Soliton amplification in gain medium governed by Ginzburg–Landau equation

Abstract

With the modified Hirota method, analytic soliton solutions for the generalized cubic complex Ginzburg–Landau equation with variable coefficients are derived for the first time. Based on the analytic solutions, soliton amplification is realized by choosing corresponding parameters properly. Besides, physical effects affecting the soliton amplification are discussed. Furthermore, stability analysis is presented. Results in this paper may be of value in further understanding the soliton amplification in fiber laser, and helpful for the generation of supercontinuum.

1 Introduction

Solitons are regarded as valid tools in optical communications due to their properties in the stable propagation during the long-distance transmission [1]. Because of the actual transmission losses, the distortion of solitons consequently occurs with energy attenuated [2–6]. To solve that problem, research interests on optical communications in gain medium have been stimulated by the introduction of erbium-doped fiber amplifiers [7–11]. Since then, the soliton amplification has been hot research topic investigated on both theoretically and experimentally in the past two decades [12–29].

Some investigations on soliton amplification have been applying different methods. In gain medium, the effects of two-photon absorption (TPA) and gain dispersion on the soliton propagation are investigated by adopting Rayleigh’s dissipation function in the framework of variational approach [1]. In Ref. [30], soliton amplification has been studied with the nonlinear optical amplifier. The property of amplification has been researched by introduction of two-stage erbium-doped fiber [31]. An analytic study on soliton amplification in inhomogeneous optical fibers as well as in inhomogeneous optical waveguides has been presented [17–19]. Different physical effects affecting soliton amplification have been discussed [20]. Dispersion management has been applied successfully both in the oscillator and amplifier, allowing dissipative soliton generation and amplification [32]. The standard Ginzburg–Landau (GL) equation containing both gain dispersion and gain saturation term has been used to describe the amplification process of solitons [1]. To date, some researches on the cubic complex Ginzburg–Landau equation (CGLE) have been done. In the last century, Ref. [33] has summarized and extended the works on coherent structures in the one-dimensional CGLE and its generalizations, with the existence and competition of fronts, pulses, sources and sinks being completely studied. In Ref. [34], a comprehensive description of various aspects of the CGLE chaotic dynamics has been provided by studying the relationship between modulated amplitude waves and large-scale chaos. As one of the studied nonlinear equations in the physics community, an overview of some phenomena described by the CGLE in one to three dimensions has been given in order to study the relevant solutions and gain insight into nonequilibrium phenomena in spatially extended systems [35]. In the recent work, two categories (pulses and snakes) of dissipative solitons have been found. Furthermore, the dependence of both their shape and stability on the physical parameters of the cubic–quintic CGLE has been analyzed [36]. The normalized form of the governing equation of fundamental soliton propagation in gain medium is as follows [37].

$$\begin{aligned}&i\frac{\partial u}{\partial x}+\frac{1}{2}(1-id)\frac{\partial ^{2}u}{\partial \tau ^{2}}+\left| u \right| ^{2}u\nonumber \\&\quad +\,iK\left| u \right| ^{2}u-\frac{i}{2}\mu u=0 \end{aligned}$$

(1)

where $u(x,\tau ),\mu ,d$ and $K$ represent the optical field amplitude, gain coefficient, gain dispersion and normalized TPA coefficient, respectively.

However, the analytic soliton solutions of variable-coefficient CGLE via the modified Hirota method have not been reported before. To be more generalized, we use the variable-coefficient CGLE as the master equation describing the soliton propagation in gain medium [38]:

$$\begin{aligned}&i\frac{\partial u}{\partial x}-\left[ \frac{1}{2}d(x)+i\xi (x)\right] \frac{\partial ^{2}u}{\partial \tau ^{2}}\nonumber \\&\quad +\,[\gamma (x)-i\chi (x)]\left| u \right| ^{2}u-ih(x)u=0 \end{aligned}$$

(2)

here, $u(x,\tau )$ is the optical field amplitude, $x$ is the normalized propagation distance and $\tau$ is the retarded time. The distributed parameters $d(x)$, $\xi (x)$, $\gamma (x)$, $\chi (x)$, $h(x)$, which are functions of the propagation distance $x$, are related to the group-velocity dispersion (GVD), gain dispersion, self-phase modulation (SPM), TPA and linear gain (loss).

In this paper, via the modified Hirota method, Eq. (2) will be studied analytically for the first time. Analytic soliton solutions will be derived. According to the solutions obtained, corresponding parameters will be chosen to realize soliton amplification with the physical effects such as the gain coefficient and gain dispersion being discussed.

The paper is arranged as follows. In Sect. 2, the analytic soliton solution for Eq. (2) will be derived with the modified Hirota method [39]. In Sect. 3, the amplified solitons will be shown, with the influence of gain coefficient and gain dispersion being discussed. Stability analysis will be made in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Analytic soliton solutions for Eq. (2)

Transformations facilitating the application of the modified Hirota method are [39–42]

$$\begin{aligned} u(x,\tau )=\frac{g(x,\tau )}{f(x,\tau )^{1+i\alpha }} \end{aligned}$$

(3)

where $g(x,\tau )$ is a complex differentiable function, and $\alpha ,f(x,\tau )$ are assumed to be real.

By virtue of symbolic computation, bilinear forms for Eq. (2) can be derived as

$$\begin{aligned}&iD_{x,\alpha } g\cdot f-\left[ \frac{1}{2}d(x)+i\xi (x)\right] D_{\tau ,\alpha }^2 g\cdot f\nonumber \\&\quad -\,ih(x)g\cdot f=0\end{aligned}$$

(4)

$$\begin{aligned}&\left[ \frac{1}{2}d(x)+i\xi (x)\right] (1+i\alpha )(2+i\alpha )D_{\tau ,\alpha }^2 f\cdot f \nonumber \\&\quad +\,2[\gamma (x)-i\chi (x)]g\cdot g^{*}=0 \end{aligned}$$

(5)

$D_{x,\alpha }$ and $D_{\tau ,\alpha }^2$ are the Hirota’s bilinear operators, which can be defined by [39, 40].

$$\begin{aligned}&(D_x^m D_\tau ^n )_\alpha (g\cdot f) \nonumber \\&\quad =\left[ \frac{\partial }{\partial x}-(1+i\alpha )\frac{\partial }{\partial {x}'}\right] ^{m}\left[ \frac{\partial }{\partial \tau }-(1+i\alpha )\frac{\partial }{\partial {\tau }'}\right] ^{n}\nonumber \\&\qquad \times g(x,\tau )f({x}',{\tau }')|_{{x}'=x,{\tau }'=\tau } \end{aligned}$$

(6)

Bilinear forms (4), (5) can be solved by the following power series expansions for $g(x,\tau )$ and $f(x,\tau )$

$$\begin{aligned} g(x,\tau )= & {} \varepsilon g_1 (x,\tau )+\varepsilon ^{2}g_2 (x,\tau )+\varepsilon ^{3}g_3 (x,\tau )\\&+\,\varepsilon ^{4}g_4 (x,\tau )+\varepsilon ^{5}g_5 (x,\tau )+\cdots \\ f(x,\tau )= & {} 1+\varepsilon f_1 (x,\tau )+\varepsilon ^{2}f_2 (x,\tau )+\varepsilon ^{3}f_3 (x,\tau )\\&+\,\varepsilon ^{4}f_4 (x,\tau )+\varepsilon ^{5}f_5 (x,\tau )+\cdots \\ \end{aligned}$$

However, we find that the even powers of $\varepsilon$ in $g(x,\tau )$ and odd powers of $\varepsilon$ in $f(x,\tau )$ equaling to zero can meet the recursion relations in the process of calculation. For the sake of simplicity, we directly set $g(x,\tau )$ and $f(x,\tau )$ in the following form:

$$\begin{aligned} g(x,\tau )= & {} \varepsilon g_1 (x,\tau )+\varepsilon ^{3}g_3 (x,\tau )\nonumber \\&+\varepsilon ^{5}g_5 (x,\tau )+\cdots \end{aligned}$$

(7)

$$\begin{aligned} f(x,\tau )= & {} 1+\varepsilon ^{2}f_2 (x,\tau )+\varepsilon ^{4}f_4 (x,\tau )\nonumber \\&+\,\varepsilon ^{6}f_6 (x,\tau )+\cdots \end{aligned}$$

(8)

where $\varepsilon$ is a formal expansion parameter. Substituting expressions (7), (8) into bilinear forms (4), (5) and equating coefficients of the same powers of $\varepsilon$ to zero yield the recursion relations for $g_n (x,\tau )^{,}s$ and $f_n (x,\tau )^{,}s$. Then, analytic solution for Eq. (2) can be obtained.

For the analytic soliton solution of Eq. (2), $g_1(x,\tau )$ are assumed to be in the following form [43–46]:

$$\begin{aligned} g_1 (x,\tau )= & {} \exp (\theta )\end{aligned}$$

(9)

$$\begin{aligned} \theta= & {} (a_1 +ia_2 )\tau +[b_1 (x)+ib_2 (x)]x\nonumber \\&+\,(k_1 +ik_2 ) \end{aligned}$$

(10)

with $a_j,k_j,(j=1,2)$ are real constants, and $b_j (x),(j=1,2)$ are differentiable functions to be determined. Substituting $g_1(x,\tau )$ into the resulting set of linear partial differential equations which refer to the above recursion relations yielded by equating coefficients of the same powers of $\varepsilon$ to zero, given in recursion relations of ‘Appendix’, and after some calculations, we can get the constraints on the parameters:

$$\begin{aligned} b_1 (x)= & {} \frac{\int {\left[ a_1 a_2 d(x)\!+\!h(x)\!+\!a_1^2 \xi (x)\!-\!a_2^2 \xi (x)\right] dx} }{x} \nonumber \\ b_2 (x)= & {} \frac{\int {\left[ a_2^2 d(x)-a_1^2 d(x)+4a_1 a_2 \xi (x)\right] dx} }{2x} \nonumber \\ f_2 (x,\tau )= & {} \sigma (x)\exp (\theta +\theta ^{*}) \end{aligned}$$

(11)

where $\theta ^{*}$ is the conjugate of $\theta$,

$$\begin{aligned}&\gamma (x)=2a_1^2 \left[ (\alpha ^{2}-2)d(x)+6\alpha \xi (x)\right] \sigma (x)\\&\chi (x)=2a_1^2 \left[ 3\alpha d(x)-2(\alpha ^{2}-2)\xi (x)\right] \sigma (x)\\&\sigma (x)\!=\!\eta \exp \left\{ {\int {\left[ \!-\!2a_1^2 \alpha d(x)\!-\!2h(x)\!+\!\frac{2\left( \!-a_1^2 \alpha \!+\!a_1^2 \alpha ^{3}\right) \xi (x)}{\alpha }\right] } dx} \right\} \\&a_2 =\alpha a_1,\\&g_n (x,\tau )=0\qquad (n=3,5,7,\ldots ),\\&f_n (x,\tau )=0\qquad (n=4,6,8,\ldots ), \end{aligned}$$

Without loss of generality, we set $\varepsilon =1$, and the analytic soliton solution can be expressed as:

$$\begin{aligned}&u(x,\tau )=\frac{g(x,\tau )}{f(x,\tau )^{1+i\alpha }}=\frac{g_1 (x,\tau )}{[1+f_2 (x,\tau )]^{1+i\alpha }}\nonumber \\&=\frac{\exp \left\{ {k_1 \!+\! ik_2 +a_1 \tau \!+\! ia_1 \tau \alpha \!+\!\frac{1}{2}ia_1^2 \int {[(\alpha ^{2}-1)d(x)\!+\! 4\alpha \xi (x)]dx\!+\!\int {[a_1^2 \alpha d(x)\!+\!h(x)-a_1^2 (\alpha ^{2}-1)\xi (x)]dx} } } \right\} }{[1+\eta e^{2(k_1 +a_1 \tau )}]^{1+i\alpha }}\nonumber \\ \end{aligned}$$

(12)

3 Results and discussions

With appropriate parameters in solution (12), soliton solutions and the amplification of solitons can be obtained in gain medium. First, we choose all the parameters as constants. And then, we change them to variable coefficients to find more fascinating properties. We choose the combination of sine and cosine functions as the variable coefficients, leading to the periodical amplification of solitons.

3.1 Soliton solution

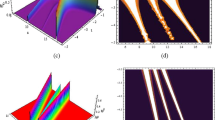
As is shown in Fig. 1a, we set $\alpha =0.13,a_1=0.114,d(x)=0.46,h(x)=0.12$,

$$\begin{aligned} \xi (x)=-9.45,k_1 =0.92,k_2 =-0.92,\eta =1.1 \end{aligned}$$

The amplitude of pulse keeps stable along the line of propagation. Soliton solution has been obtained under this condition. Besides, the amplitude of solitons remains unchanged during the propagation. On one hand, the nonlinear effect (SPM) can counterbalance the effect of GVD; on the other hand, the gain dispersion, along with TPA, restricts the amplification of the pulse due to its dissipative nature, reaching the equilibrium with gain effects to a certain extent.

Fig. 1

a Evolution of solitons derived from solution (12). Parameters are $\alpha =0.13,a_1 =0.114,d(x)=0.46,h(x)=0.12, \quad \xi (x)=-9.45,k_1 =0.92,k_2 =-0.92,\eta =1.1$ b Soliton amplification in gain medium. Parameters are the same with (a) except $h(x)=0.13$

3.2 Soliton amplification affected by the gain coefficient

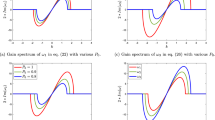
We just change the value of gain coefficient such as $h(x)=1.3$ (or $h(x)=1.4$), keeping other parameters unchanged as shown in Figs. 1b and 2a. From Figs. 1b and 2a, we can obviously see that the soliton is amplified during the propagation by changing the value of $h(x)$. Intuitively, the parameter plays an important role in determining the properties of solitons. One reasonable interpretation is that with GVD and SPM achieving a balance, the effect of gain coefficient is greater than the effect of gain dispersion. As a result, the amplification of solitons is realized.

Fig. 2

a Amplification of solitons derived from solution (12) with the same parameters as those given in Fig. 1(b), but with $h(x)=0.14$; b Comparison of soliton profiles $(\xi (x)=-9.45,h(x)=0.14)$ at $\hbox {z}=0$ (black solid line) and $\hbox {z}=40$ (red dash-dotted line)

Furthermore, the degree of soliton amplification can be controlled by different values of gain coefficient in the gain medium in the case of other coefficients unchanged. Because the greater the value of gain coefficient is, the more remarkable the energy compensation is due to the gain effect. At $\hbox {z}=0$, the amplitude of soliton in Fig. 1b is about 0.2, which is the same with that in Fig. 2a. However, at $\hbox {z}=40$, the value of the latter (increased to about 1.2) is much larger than that of the former (increased to about 0.5). A higher value of gain efficient indicates a higher amplification of solitons along the fibers of propagation. Thereby, we can adjust the parameter of gain coefficient to achieve soliton amplification.

Next, variable coefficients will be chosen as the parameters as shown in Fig. 4. Similar to that shown in Figs. 4b and 2a, the gain coefficient plays the same role in soliton amplification as is shown in Fig. 4. The choice of the periodic function [$d(x)$ and $\xi (x)$] leads to the periodic amplification. The gain coefficient is also powerful enough to be the dominant factor to control the soliton amplification (the same with the case of constant coefficient discussed above).

3.3 Soliton amplification affected by the gain dispersion

When the absolute value of gain dispersion $\xi (x)$ changes, if we keep the gain coefficient unchanged, the amplification can also be influenced as shown in Figs. 2 and 3. At $\hbox {z}=40$, when $\xi (x)=-9.8$, the amplitude of solitons is lower than that when $\xi (x)=-9.45$. It suggests that the gain dispersion coefficient can weaken the amplification of solitons. Physically, this behavior can be understood by noting that the gain dispersion can restrict the soliton amplification due to its dissipative nature. The existence of gain dispersion $\xi (x)$ can make the equivalent loss coefficient become larger in the gain medium. As a result, the amplitude of solitons is attenuated during the propagation if we do not consider the gain effect in the gain medium.

Fig. 3

a Amplification of solitons derived from solution (12) with the same parameters as those given in Fig. 2 (a), but with $\xi (x)=-9.8$; b Comparison of soliton profiles ($\xi (x)=-9.8,h(x)=0.14$,) at $\hbox {z}=0$ (blue solid line) and $\hbox {z}=40$ (green dash-dotted line)

Fig. 4

a Amplification of solitons derived from solution (12) in the gain medium. Parameters are $a_1=0.11,d(x)=-0.46cos(0.30x),h(x)=0.01,\xi (x)=10.45cos(0.30x),k_1 =0.92,k_2 =-10.92,\eta =1.02$ and $\alpha =0.10$; b Amplification of solitons derived from solution (10) in the gain medium with the same parameters as those given in (a), but with $h(x)=0.015$

4 Stability analysis

4.1 Regions where the growth/decay exists based on the parameters $\xi (x)$

Soliton solution has been obtained under appropriate parameters (Fig. 1a). Our research shows that if we keep other parameters unchanged, and just change the value of $\xi (x)$, the growth/decay can be obtained. When we set $\xi (x)>-9.45$, the growth (amplification) is realized. And when we set $\xi (x)<-9.45$, the decay exists.(see Fig. 5)

Fig. 5

a Growth (amplification) of solitons with the same parameters as those given in Fig. 1 (a), but with $\xi (x)>-9.45$ (e.g., $\xi (x)=-9$); b Decay of solitons with the same parameters as those given in Fig. 1 (a), but with $\xi (x)<-9.45$ (e.g., $\xi (x)=-10$)

Different from the so-called “exploding solitons,” found in numerical simulations [47, 48] and experimentally confirmed in a passively mode-locked solid laser [49], our research indicates that the soliton amplification is continuous with the increase of z. The exploding solitons explode at a certain point, break down into multiple pieces, and subsequently recover their original shape [50]. However, in this paper, the soliton can be amplified continuously and stably, which can be confirmed by expanding the range of z (from 0 to 400, see Fig. 6a). It is notable that no matter how large the range of z is, we can choose the value of $\xi (x)$ to make the soliton amplification finite at the end.

Fig. 6

a Amplification of solitons without the Gaussian white noise from solution (12); b Amplification of solitons with the Gaussian white noise from solution (12). Parameters are the same with Fig. 1 (a), except $\xi (x)$=$-$9.4

4.2 Stability analysis with white noise

The stability analysis is one of the significant issues in the nonlinear wave physics. And it is involved in plasma physics [51], hydrodynamics [52] as well as nonlinear optics [53]. In this part, we will study the stability of soliton amplification by embedding white noise, which is subject to Gaussian distribution [54]. We set the amplitude of embedded white noise to be 0.01(Fig. 6b). By comparison between Fig. 6a, b, Gaussian white noise has very little impact on the shape and amplitude of the soliton. And the soliton amplification is still continuous, just with slight perturbation. Undoubtedly, the stability is useful to the soliton amplification during the soliton propagation.

5 Conclusions

The generalized cubic complex Ginzburg–Landau equation with variable coefficient[see Eq. (2)], which can be used to describe the amplification of solitons in gain medium, has been investigated analytically. A simple and straightforward method of modified Hirota method has been proposed, with which the bilinear forms (4)–(5) for Eq. (2) have been derived, and the analytic soliton solution (12) has been obtained after some symbolic computation. Amplification of solitons in gain medium has been studied (see Figs. 1, 2, 3, 4). According to the solution, with appropriate parameters, the stable soliton has been obtained. By changing the arbitrary parameters, we achieve the amplification of solitons. At last, we have discussed as well as analyzed the influences of gain dispersion coefficient $\xi (x)$ and gain coefficient $h(x)$ on soliton amplification. Through the comparison between the amplitudes of soliton at $x=0$ and at $x=40$, we find that the gain effect can stimulate the soliton amplification while the gain dispersion restricts the soliton amplification. This is the result of their opposite effects. We hope the results are helpful for the experimental research on fiber lasers and supercontinuum generation.

Appendix

1.1 Generalized Hirota method

It is very difficult to find exact solutions of nonlinear differential equations, since the superposition principle does not hold in them. One way to solve a nonlinear differential equation is to find a transformation to a linear equation. The Hirota method is to translate nonlinear differential equations into linear differential equations by means of a dependent variable transformation to a rational function g/ f [55]. With the help of $D$-operator, which is defined by

$$\begin{aligned} D_x^m D_\tau ^n (g\cdot f)= & {} \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial {x}'}\right) ^{m}\left( \frac{\partial }{\partial \tau }-\frac{\partial }{\partial {\tau }'}\right) ^{n}\\&\times g(x,\tau )f({x}',{\tau }')|_{{x}'=x,{\tau }'=\tau } \end{aligned}$$

we can get

$$\begin{aligned} \frac{\partial }{\partial x}\frac{g}{f}= & {} \frac{D_x g\cdot f}{f^{2}}; \nonumber \\ \frac{\partial ^{2}}{\partial x^{2}}\frac{g}{f}= & {} \frac{D_x^2 g\cdot f}{f^{2}}-\frac{g}{f}\frac{D_x^2 f\cdot f}{f^{2}}; \nonumber \\ \frac{\partial ^{3}}{\partial x^{3}}\frac{g}{f}= & {} \frac{D_x^3 g\cdot f}{f^{2}}-3\frac{D_x g\cdot f}{f^{2}}\frac{D_x^2 f\cdot f}{f^{2}} \end{aligned}$$

(13)

Take the KdV equation for example

$$\begin{aligned} \frac{\partial u}{\partial t}+6u\frac{\partial u}{\partial x}+\frac{\partial ^{3}u}{\partial x^{3}}=0 \end{aligned}$$

By putting $u=\hbox {g}/\hbox {f}$ and making use of (13), the KdV equation may be rewritten as

$$\begin{aligned}&\frac{D_t g \cdot f}{f^{2}}+6\frac{g}{f}\frac{D_x g\cdot f}{f^{2}}+\frac{D_x^3 g\cdot f}{f^{2}}\\&\quad -3\frac{D_x g\cdot f}{f^{2}}\frac{D_x^2 f\cdot f}{f^{2}}=0 \end{aligned}$$

The above equation can be reorganized as

$$\begin{aligned} \frac{D_t g\cdot f+D_x^3 g\cdot f}{f^{2}}+\frac{3D_x g\cdot f(2gf-D_x^2 f\cdot f)}{f^{4}}=0 \end{aligned}$$

According to the form of denominator $f^{2}$ and $f^{4}$, it can be decoupled into the bilinear form:

$$\begin{aligned} (D_t +D_x^3 )g\cdot f= & {} 0 \\ D_x^2 f\cdot f-2g\cdot f= & {} 0 \end{aligned}$$

Another typical example is the nonlinear Schrödinger equation:

$$\begin{aligned} i\frac{\partial u}{\partial x}=\frac{1}{2}\frac{\partial ^{2}u}{\partial t^{2}}-N^{2}\left| u \right| ^{2}u \end{aligned}$$

Through the same process with KdV equation, the nonlinear Schrödinger equation may be rewritten as

$$\begin{aligned}&\frac{2iD_x g\cdot f-D_t^2 g\cdot f}{f^{2}}\\&\quad +\frac{g\cdot f(D_t^2 f\cdot f+2N^{2}\left| g \right| ^{2})}{f^{4}}=0 \end{aligned}$$

According to the form of denominator$f^{2}$ and $f^{4}$, it can be decoupled into the bilinear form:

$$\begin{aligned} (2iD_x -D_t^2 )g\cdot f= & {} 0 \\ D_t^2 f\cdot f+2N^{2}\left| g \right| ^{2}= & {} 0 \end{aligned}$$

In the next work, we can solve the bilinear form by the power series expansions for $g(x,\tau )$ and $f(x,\tau )$. As a result, the soliton solution of KdV equation/ nonlinear Schrödinger equation can be relatively easy to solve.

1.2 Recursion relations

$$\begin{aligned}&\varepsilon :h(x)g_1 -g_{1x} -\frac{1}{2}id(x)g_{1tt} +\xi (x)g_{1tt} =0.\\&\varepsilon ^{2}:(2\gamma (x)-2\hbox {i}\chi (x))\left| {g_1 } \right| ^{2} \\&\quad -(\alpha ^{2}-3\hbox {i}\alpha -2)(d(x)+2\hbox {i}\xi (x))f_{2tt} =0 \\&\varepsilon ^{3}:-2\hbox {i}h(x)f_2 g_1 +2(1+\hbox {i}\alpha )(d(x)+2\hbox {i}\xi (x))f_{2t} g_{1t}\\&\quad +(-\hbox {i}+\alpha )g_1 (2f_{2x} +(\alpha -\hbox {i})(d(x)+2\hbox {i}\xi (x))f_{2tt}) \\&\quad +f_2 (2\hbox {i}g_{1x} -(d(x)+2\hbox {i}\xi (x))g_{1tt} =0 \\&\varepsilon ^{4}:f_{2t} ^{2}-f_2 f_{2tt} =0 \end{aligned}$$