Stabilization of fractional-order coupled systems with time delay on networks

Abstract

Stabilization problem for a class of fractional-order nonlinear coupled systems on networks is addressed in the paper. By using Kirchhoff’s matrix tree theory and comparison principle, a state feedback control law is presented to stabilize such systems. The controller design approach could be adapted to many classes of fractional-order delayed coupled systems in ecology, biology and engineering. An example is presented to illustrate the effectiveness of our proposed method.

1 Introduction

A wide variety of physical, biological and artificial complex dynamical systems can be characterized by coupled systems of nonlinear differential equations about networks, such as neural networks on artificial intelligence, complex ecosystems, the spread of infectious diseases, nonlinear oscillators on lattices and so on. The networks can be viewed as directed graphs from the viewpoint of mathematics, which are composed of vertices and directed arcs connecting them. Now, coupled systems on networks(CSNs) have attracted considerable attention from both mathematicians and engineers. Some fundamental and interesting problems on CSNs have been considered, for instance, stability [1], control [2], synchronization [3], consensus [4], clustering [5], phase transitions and bifurcations [6].

In practice, information interaction between individuals within a complex network is in general not instantaneous, the finite speed of signal transmission over a distance gives rise to a finite time delay. Therefore, time delays are considered as ubiquitous in networks. Time delays may decrease the quality of the system and even lead to oscillation, divergence, and instability. The dynamics of complex networks with delays have become a topic of both theoretical and practical importance and have been extensively studied in recent years. See Refs. [7,8,9,10,11,12,13].

Note that above results mainly focus on integer-order CSNs models, in which dynamical behavior of the vertex system is described by integer-order differential equations. With the rapid development of fractional calculus and its applications, fractional-order derivatives have been proven to provide an excellent instrument to characterize memory and hereditary properties of system variables, such as anomalous diffusion, time-dependent materials and processes with long-range dependence, allometric scaling laws, as well as power law in complex systems. This is because it not only takes into account the history of the process involved but also carries its impact to present and future development of the process. Some scholars have employed fractional-order derivative operators into the classical CSNs model to form fractional-order CSNs one and believed that it is an important improvement in accuracy, for instances, fractional-order neural networks [14, 15], fractional-order epidemic systems [16, 17], fractional-order ecosystem [18, 19], fractional-order synchronous motors [20] and fractional-order complex networks [21, 22]. In recent years, more and more researchers are being devoted into investigating stability and control of these systems. From another point of view, these existing results about stability and control of integer-order CSNs with time delay have been developed with the help of constructing traditional Lyapunov–Krasovskii functional and linear matrix inequality (LMI) approach. However, the method and these results could not be extended easily and applied to fractional-order cases, since similar method has not been well developed for fractional-order CSNs. To analyze stability of delayed fractional-order CSNs is still a formidable problem. As we all know, there are few results on stabilization of fractional-order CSNs with delay in the existing literatures.

Motivated by the above discussions, in the paper, by using results from graph theory and the comparison theorem for fractional-order linear delayed system, a linear feedback controller design scheme for stabilizing a class of fractional-order CSNs with time delay is presented. The main contributions of this paper lie in three aspects. First, stabilization of fractional-order nonlinear delayed system on networks is considered; Second, Kirchhoff’s matrix tree theory in graph theory and the comparison theorem for fractional-order linear delayed systems are adopted to obtain the control scheme; Third, the obtained result is associated with the topological property of network and has more value in the design and applications of fractional-order delayed CSNs.

The rest of the paper is organized as follows. The network model is introduced, and some necessary definitions, lemmas and hypotheses are given in Sect. 2. Stabilization criteria for fractional-order coupled systems with delay on networks are presented in Sect. 3. An example and its simulations are obtained in Sect. 4. Finally, the paper is concluded in Sect. 5.

2 Preliminaries and model description

In the section, some notations, definition, lemma and necessary basic concepts and theorems on graph theory are presented.

The fractional-order integro-differential operator is the generalized concept of integer-order integro-differential operator. As we all know, the initial conditions for fractional differential equations with Caputo derivatives take on the same forms as those for integer-order differential equations, which have well-understood physical meanings. Another aspect is that Caputo derivative of a constant is equal to zero, that is not the case for the Riemann–Liouville derivative. Therefore, in this paper, Caputo fractional derivative operator is adopted [23], which is described as follows

$$\begin{aligned} D^\alpha x(t)=\frac{1}{\varGamma (n-\alpha )}\int _a^t(t-\tau )^{n-\alpha -1}x^{(n)}(\tau )d\tau , \end{aligned}$$

where $n-1<\alpha <n$, n is an integer, $D^\alpha$ denotes Caputo derivative operator, $\varGamma (\cdot )$ is the Gamma function.

Since the coupled system considered in this paper is built on a directed graph, some basic concepts and notations on graph theory are necessary to be introduced, which can be found in [1] and [24].

A directed graph $G=(V, E)$ contains a set $V=\{1, 2,\ldots , n\}$ of vertices and a set E of arcs (i, j) leading from initial vertex i to terminal vertex j. A subgraph H of G is said to be spanning if H and G have the same vertex set. A digraph G is weighted if each arc (j, i) is assigned a positive weight $a_{ij}$. Here $a_{ij}>0$ if and only if there exists an arc from vertex j to vertex i in G. The weight W(H) of a subgraph H is the product of the weights on all its arcs. A directed path P in G is a subgraph with distinct vertices $\{i_1, i_2,\ldots , i_m\}$ such that its set of arcs is $\{(i_k, i_{k+1}) : k=1, 2, \ldots , m-1\}$. If $i_m=i_1$, we call P a directed cycle. A digraph G is strongly connected if, for any pair of distinct vertices, there exists a directed path from one to the other. Given a weighted digraph G with n vertices, define the weight matrix $A =(a_{ij})_{n\times n}$ whose entry $a_{ij}$ equals the weight of arc (j, i) if it exists, and 0 otherwise. Denote the directed graph with weight matrix A as (G, A). The Laplacian matrix of (G, A) is defined as $L=(l_{ij})_{n\times n}$, where $l_{ij}=-a_{ij}$ for $i\ne j$ and $p_{ij}=\sum _{k\ne j}a_{ik}$ for $i=j$. Let $c_i$ denote the cofactor of the $i-$th diagonal element of L. The following result is standard in graph theory, which is called Kirchhoff’s tree theorem [1].

Lemma 1

[1] Assume $n\ge 2$. Then the following identity holds:

$$\begin{aligned}&\sum _{i,j=1}^nc_ia_{ij}F_{ij}(x_i,x_j)\\&\quad =\sum _{Q\in \mathbb {Q}}W(Q)\sum _{(s,r)\in E(C_Q)}F_{rs}(x_r,x_s), \end{aligned}$$

here $F_{ij}(x_i,x_j), i\le i,j \le n$, are arbitrary functions, $\mathbb {Q}$ is the set of all spanning unicyclic graphs of (G, A), W(Q) is the weight of Q, and $C_Q$ denotes the directed cycle of Q.

Moreover, a weighed digraph (G, A) is said to be balanced if $W(C)=W(-C)$ for all directed cycle C. Here, $-C$ denotes the reverse of C and is constructed by reversing the direction of all arcs in C. For a unicyclic graph Q with cycle $C_Q$, let $\tilde{Q}$ be the unicyclic graph obtained by replacing $C_Q$ with $-C_Q$. Suppose that (G, A) is balanced, then $W(Q)=W(\tilde{Q})$. In this case, Lemma 1 can be rewritten as the following lemma.

Lemma 2

[1]

$$\begin{aligned}&\sum _{i,j=1}^nc_ia_{ij}F_{ij}(x_i,x_j)=\frac{1}{2}\sum _{Q\in \mathbb {Q}}W(Q)\\&\quad \sum _{(s,r)\in E(C_Q)}\left[ F_{rs}(x_r,x_s)+F_{sr(u_s,u_r)}\right] . \end{aligned}$$

Given a network represented by digraph G with n vertices, $n\ge 2$, each vertex has its own internal dynamics and these vertex dynamics are coupled based on directed arcs in G. In this paper, each vertex dynamics is described by the following fractional-order nonlinear delayed systems:

$$\begin{aligned} D^\alpha x_i(t)= & {} f_i(x_i(t),x_i(t-\tau ))\nonumber \\&+\sum _{j=1}^na_{ij}(x_j(t)-x_i(t)),\quad i=1,2,\ldots ,n,\nonumber \\ \end{aligned}$$

(1)

where $0<\alpha \le 1$, $x_i(t)\in R^{m}$ is the state variable of ith dynamical node at time t. $a_{ij}$ represents the influence of node j on node i, $a_{ij}=0$ if there exists no arc from node j to node i in G. $f_i(\cdot )\in R^{m\times m}\rightarrow R ^{m}$ is a continuous function. Function $f_i$ is Lipschitz-continuous with Lipschitz constant $l_i>0$, i.e., $\Vert f_i(x,y)-f_i(\bar{x},\bar{y})\Vert \le l_i(\Vert x-\bar{x}\Vert +\Vert y-\bar{y}\Vert )$ for all $x, y,\bar{x},\bar{y}\in R^m$. $\tau$ is the system delay at each node. It is assumed that the initial conditions of network (1) are given by $x_i(t)=\phi _i(t)$, $-\tau \le t\le 0$.

Assume that system (1) admits an equilibrium point $x^*=(x^*_1,x^*_2,\ldots ,x^*_n)^T$, where $x^*_i=(x^*_{i1},x^*_{i2},\ldots , x^*_{im})\in R^{m}(i=1,2,\ldots ,n)$, which satisfies the following equation,

$$\begin{aligned} D^\alpha x^*_i=f_i(x^*_i,x^*_i). \end{aligned}$$

(2)

In order to force all states of the complex dynamical network to the objective equilibrium point $x^*$, controllers $u_i(t)$ are added to the node i. Denote $y_i(t)=x_i(t)-x^*_i$ and design $u_i(t)=-K_iy_i(t)$, where $K_i=diag(k_{i1},k_{i2},\ldots ,k_{im})$ are feedback gain matrices to be determined later, then we can obtain the controlled dynamical network as follows:

$$\begin{aligned} D^\alpha y_i(t)= & {} f_i(y_i(t)+x^*_i,y_i(t-\tau )+x^*_i)-f_i(x^*_i,x^*_i)\nonumber \\&+\sum _{j=1}^na_{ij}(y_j(t)+x^*_j-(y_i(t)+x^*_i))\nonumber \\&-\sum _{j=1}^na_{ij}(x^*_j-x^*_i)-K_iy_i(t). \end{aligned}$$

(3)

Obviously, to illustrate that all states of the complex dynamical network can be stabilized to the objective equilibrium point $x^*$, it is sufficient to prove stability of the origin of system (3). To this end, the following lemmas are presented firstly.

Lemma 3

[25] Let $x(t)\in R^n$ be a continuous and differentiable function. Then, for any time instant $t\ge t_0$

$$\begin{aligned} D^\alpha \big (x^T(t)x(t)\big )\le 2x^T(t)D^\alpha x(t), \ \ \ \ \ \forall \alpha \in (0,1). \end{aligned}$$

Lemma 4

[26] Consider the following fractional-order differential inequality with time delay

$$\begin{aligned} \left\{ \begin{aligned}&D^\alpha V(t)\le -aV(t)+bV(t-\tau ), \ \ t>0,\\&V(t)=\varphi (t), t\in [-\tau ,0], \end{aligned} \right. \end{aligned}$$

and the linear fractional-order differential systems with time delay

$$\begin{aligned} \left\{ \begin{aligned}&D^\alpha W(t)=-aW(t)+bW(t-\tau ), \ \ t>0,\\&W(t)=\varphi (t), t\in [-\tau ,0], \end{aligned} \right. \end{aligned}$$

(4)

where $W(t)\in R$ and $V(t)\in R$ are continuous and nonnegative in $[0,+\infty )$, and $\varphi (t)\ge 0, t\in [-\tau , 0]$. If $a>0$ and $b>0$, then

$$\begin{aligned} V(t)\le W(t), t\in [0,+\infty ). \end{aligned}$$

Lemma 5

[27] For fractional-order linear delayed systems (4), if $a>b$, the zero solution of system (4) is Lyapunov globally asymptotically stable.

3 Main results

In this section, a sufficient criterion is presented to stabilizing the fractional-order coupled system on networks based on state feedback controller.

Theorem 1

Assume that (G, A) in (1) is strongly connected. If feedback gain matrices $K_i=diag(k_{i1},k_{i2},\ldots ,k_{im})$ satisfy

$$\begin{aligned} \min _{1\le i\le n}\left\{ 2k_i-3l_i\right\} >\max _{1\le i\le n}\{l_i\}, \end{aligned}$$

(5)

where $k_i=\min _{1\le j\le m}\{k_{ij}\}$, then system (1) will approach and stabilize to equilibrium point $x^*$ asymptotically.

Proof

Constructing an auxiliary function $V(t)=\sum _{i=1}^nc_iy_i^T(t)y_i(t)$, where $c_i$ denotes the cofactor of the i-th diagonal element of L. If (G, A) is strongly connected, then $c_i>0$ for any $1\le i\le n$[1]. It follows from Lemma 3 that

$$\begin{aligned}&D^{\alpha }V(t)=D^{\alpha }\left( \sum _{i=1}^nc_iy_i^T(t)y_i(t)\right) \nonumber \\&\quad \le \sum _{i=1}^n2 c_iy^T_i(t)\big [(f_i(y_i(t)+x^*_i,y_i(t-\tau )+x^*_i)\nonumber \\&\qquad -f_i(x^*_i(t),x^*_i))+\sum _{j=1}^na_{ij}(y_j(t)+x^*_j-(y_i(t)+x^*_i))\nonumber \\&\qquad -\sum _{j=1}^na_{ij}(x^*_j-x^*_i)-K_iy_i(t)\big ]\nonumber \\&\quad \le \sum _{i=1}^nc_i\big [2\Vert y_i(t)\Vert \times \Vert (f_i(x_i(t),x_i(t-\tau ))-f_i(x^*_i,x^*_i))\Vert \nonumber \\&\qquad +\,2\sum _{j=1}^na_{ij}y^T_i(t)(y_j(t)-y_i(t))-2y^T_i(t)K_iy_i(t)\big ]\nonumber \\&\quad \le \sum _{i=1}^nc_i\big [2\Vert y_i(t)\Vert \times (l_i\Vert y_i(t)\Vert +l_i\Vert y_i(t-\tau )\Vert )\nonumber \\&\qquad +\,2\sum _{j=1}^na_{ij}y^T_i(t)(y_j(t)-y_i(t))-2y^T_i(t)K_iy_i(t)\big ]\nonumber \\&\quad \le \sum _{i=1}^nc_i\big [3l_iy_i^T(t)y_i(t)+l_iy_i^T(t-\tau )y_i(t-\tau )\nonumber \\&\qquad +\sum _{j=1}^na_{ij}\big (-(y_i(t)-y_j(t))^T(y_i(t)-y_j(t))\nonumber \\&\qquad +\,y_j^T(t)y_j(t)-y_i^T(t)y_i(t)\big )-2k_iy^T_i(t)y_i(t)\big ]\nonumber \\&\quad \le \sum _{i=1}^nc_i\big [3l_iy_i^T(t)y_i(t)-2k_iy_i^T(t)y_i(t)\nonumber \\&\qquad +\,l_iy_i^T(t-\tau )y_i(t-\tau )\nonumber \\&\qquad +\sum _{j=1}^na_{ij}\big (y_j^T(t)y_j(t)-y_i^T(t)y_i(t)\big )\big ]\nonumber \\&\quad \le -\min _{1\le i\le n}\left\{ 2k_i-3l_i\right\} \sum _{i=1}^nc_iy_i^T(t)y_i(t)\nonumber \\&\qquad +\max _{1\le i\le n}\{l_i\}\sum _{i=1}^nc_iy_i^T(t-\tau )y_i(t-\tau )\nonumber \\&\qquad +\sum _{i,j=1}^nc_ia_{ij}(y_j^T(t)y_j(t)-y_i^T(t)y_i(t))\nonumber \\&\quad =-aV(x(t))+bV(x(t-\tau ))\nonumber \\&\qquad +\,\sum _{i,j=1}^nc_ia_{ij}F_{ij}(y_i,y_j), \end{aligned}$$

(6)

where $a=\min _{1\le i\le n}\{2k_i-3l_i\}$, $b=\max _{1\le i\le n}\{l_i\}$ and $F_{ij}(y_i,y_j)=y_j^T(t)y_j(t)-y_i^T(t)y_i(t)$.

Along every directed cycle C of the weight digraph (G, A), one has

$$\begin{aligned}&\sum _{(s,r)\in E(C_Q)}F_{rs}(y_r,y_s)\nonumber \\&\quad =\sum _{(s,r)\in E(C_Q)}(y_s^T(t)y_s(t)-y_r^T(t)y_r(t))=0. \end{aligned}$$

(7)

It follows from Lemma 1, (6) and (7) that

$$\begin{aligned}&D^{\alpha }V(t) \le -aV(x(t))+bV(x(t-\tau ))\nonumber \\&\quad \quad +\sum _{i,j=1}^nc_ia_{ij}F_{ij}(y_i,y_j){=}-aV(x(t)){+}bV(x(t{-}\tau ))\nonumber \\&\quad \quad +\sum _{Q\in \mathbb {Q}}W(Q)\sum _{(s,r)\in E(C_Q)}F_{rs}(y_r,y_s)\nonumber \\&\quad =-aV(x(t))+bV(x(t-\tau ))\nonumber \\&\quad \quad +\sum _{Q\in \mathbb {Q}}W(Q)\sum _{(s,r)\in E(C_Q)}(y_s^T(t)y_s(t)-y_r^T(t)y_r(t))\nonumber \\&\quad =-aV(x(t))+bV(x(t-\tau )). \end{aligned}$$

(8)

Now, in view of system (4), Lemma 5 and condition (5), if $a>b$, W(t) is Lyapunov globally asymptotically stable. It follows from Lemma 4 that $V(t)\le W(t)$, which means that $V(t)=\sum _{i=1}^nc_iy_i^T(t)y_i(t)\rightarrow 0(t\rightarrow \infty )$. That is, the equilibrium point $x^*$ is asymptotically stable. $\square$

Remark 1

In Theorem 1, the condition that weight digraph (G, A) is strongly connected is indispensable, which indicates the obtained result is associated with the topological property of network. In fact, if the weighted digraph (G, A) is not strongly connected, only parts of vertices system can be stabilized, which implies that the whole controlled network may not be stable. An example is given to illustrate the case.

Consider a weighted digraph (G, A) with 3 vertices which is not strongly connected, where $A=(a_{ij})_{3\times 3}=\left( \begin{array}{ccc} 0 &{} 2 &{} 1 \\ 1 &{} 0 &{} 2 \\ 0 &{} 0 &{} 0 \end{array} \right)$, it is easy to obtain the Laplacian matrix of (G, A), $L=(l_{ij})_{3\times 3}=\left( \begin{array}{ccc} 3 &{} -2 &{} -1 \\ -1 &{} 3 &{} -2 \\ 0 &{} 0 &{} 0 \end{array} \right)$. By simple computation, one has $c_1=c_2=0,c_3=7$. Obviously, from the proof process of Theorem 1 and constructed auxiliary function V(t), the stability of the third controlled vertex can be obtained, but the stability of the whole controlled networks cannot be guaranteed. So from the complex networks point of view, the condition on strong connectedness of the networks is necessary and important.

Remark 2

Suppose that weight digraph (G, A) is balanced, It follows from Lemma 2 and proof of Theorem 1 that Theorem 1 holds if digraph (G, A) is strongly connected and balanced.

Remark 3

[28,29,30,31,32] discussed synchronization of fractional-order complex networks, but without considering the time delays in the dynamical nodes.

Remark 4

As we know, in many real-world complex networks, there often exist the unknown system parameters and topological structure. Therefore, it is very necessary to develop an effective method to identify the network topological structure and system parameters. Some effective approaches for parameter identification proposed in [33,34,35,36,37,38] may be used. Here, the controlled fractional-order dynamical networks with known system parameters and fixed topological structure are only considered.

Fig. 1

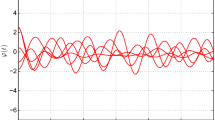
Chaotic behaviors of fractional-order system (9) with order $\alpha =0.98$

4 Numerical example

In this section, to verify and demonstrate the effectiveness of the proposed methods, a simple numerical example is presented.

Fig. 2

Time response curves of state $x_1(t)$ in the controlled system (10) with $\alpha =0.98$

Fig. 3

Time response curves of state $x_2(t)$ in the controlled system (10) with $\alpha =0.98$

Fig. 4

Time response curves of state $x_3(t)$ in the controlled system (10) with $\alpha =0.98$

Fig. 5

Time response curves of state $x_4(t)$ in the controlled system (10) with $\alpha =0.98$

Fig. 6

Time response curves of state $x_5(t)$ in the controlled system (10) with $\alpha =0.98$

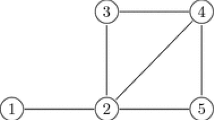
Consider a simple network with 5 nodes, the fractional-order dynamical equation of each node is described by the following fractional-order Chua oscillators [39]

$$\begin{aligned} D^\alpha x(t)= & {} f(x(t),x(t-\tau ))\nonumber \\= & {} Ax(t)+g_1(x(t))+g_2(x(t-\tau )), \end{aligned}$$

(9)

where $\alpha =0.98$, $x(t)=(x_1(t), x_2(t), x_3(t))^T\in R^3$, $g_1(x(t))=(-\frac{1}{2}a(m_1-m_2)|x_1(t)+1|-|x_1(t)-1|, 0, 0)^T\in R^3.$ $g_2(x(t-\tau ))=(0, 0, -bc\sin (vx_1(t-\tau )))^T\in R^3$, $A=\left( \begin{array}{ccc} -a(1+m_2) &{} a &{} 0\\ 1 &{} -1 &{} 1\\ 0 &{} -b &{} -\omega \\ \end{array} \right)$, $a=10$, $b=19.53$, $\omega =0.1636$, $m_1=-1.4325$, $m_2=-0.7831$, $v=0.5$, $c=0.2$, $\tau =0.2$. System (9) displays a chaotic attractor in Fig. 1. It is easy to verify that $l_i=21.9888$ (i $=$ 1, 2, 3, 4, 5).

The controlled networks consists of 5 nodes fractional-order delayed Chua system can be rewritten as follow

$$\begin{aligned} D^\alpha x_i(t)= & {} f(x_i(t),x_i(t-\tau ))\nonumber \\&+\,\sum _{j=1}^5g_{ij}(x_j-x_i)+u_i, \end{aligned}$$

(10)

where $g_{13}=g_{14}=g_{21}=g_{24}=g_{25}=g_{51}=g_{52}=1$, $g_{31} = g_{32}= g_{35}=g_{53}=g_{54}=2$, $g_{12}=g_{15}= g_{23}= g_{34}=g_{42}=g_{45}=0$, $g_{41}=g_{43}=3$. Thus, we can obtain the Laplace matrix $L=\left( \begin{array}{ccccc} 2 &{} 0 &{} -1 &{} -1 &{} 0\\ -1 &{} 3 &{} 0 &{} -1 &{} -1 \\ -2 &{} -2 &{} 6 &{} 0 &{} -2 \\ -3 &{} 0 &{} -3 &{} 6 &{} 0\\ -1 &{} -1 &{} -2 &{} -2 &{} 6 \end{array} \right)$, it is easy to obtain that $c_1=426,c_2=126,c_3=153,c_4=116,c_5=72$. When $u_i(t)=0$, system admits an equilibrium point $x^*=0$. According to Theorem 1, let $K_i=diag(45,45,45)$, which satisfies $\min _{1\le i\le n}\{2k_i-3l_i\}=24.0336>21.9888=\max _{1\le i\le n}\{L_i\}$. In the simulation, the initial conditions are $x_i(0)=(i+1, i+2, i+3)^T(1\le i \le 5)$. Figs. 2, 3, 4, 5 and 6 show the state response of each node of the controlled dynamical network, respectively, from which it can be seen that all the states can be stabilized to equilibrium point $x^*=0$.

5 Conclusions

This paper is focused on the stabilization of fractional-order dynamical coupled systems with time delay on network. A sufficient condition for stabilizing such systems by using linear feedback and graph theory has been presented. Future work is to give controller design method for fractional-order delayed systems with delay coupling on network via linear delayed feedback control.