Hollow ring-like soliton and dipole soliton in ($\varvec{2+1}$)-dimensional $\varvec{\mathcal {PT}}$-symmetric nonlinear couplers with gain and loss

Abstract

By means of the Hirota bilinear method, we obtain the hollow ring-like soliton and dipole soliton solutions of the coupled nonlinear Schrödinger equation in the ($2+1$)-dimensional inhomogeneous ${\mathcal {PT}}$-symmetric nonlinear couplers. Based on these analytical solutions, we investigate the compression behaviors of hollow ring-like soliton and dipole soliton in a diffraction decreasing system with exponential profile.

1 Introduction

Solitons were intensively studied in various fields including nonlinear optics, plasma physics, condensed matter physics and quantum physics as the self-localized robust and long-lived nonlinear solitary wave objects [1–6]. Recently, many works have focused on more complex localized structures [7–9]. One of them is the dipole soliton (DS) with two symmetrical humps. The theoretical prediction of DSs was firstly made in Ref. [10], and it was soon observed experimentally in Ref. [11].

In 1998, Bender et al. [12] introduced the ${\mathcal {PT}}$ symmetry, which requires that the potential satisfies $V(x) =V^*(-x)$ with $*$ denoting the complex conjugation. Since Christodoulides and co-workers [13] did the pioneering theoretical research about the ${\mathcal {PT}}$ symmetry in optics, soliton dynamics in ${\mathcal {PT}}$-symmetric potentials were intensively studied [7, 8, 14–16]. Moreover, dynamical properties of solitons in ${\mathcal {PT}}$-symmetric nonlinear couplers were also extensively discussed [17–19]. However, the completely localized structures in x and y directions were hardly reported in ($2+1$)-dimensional ${\mathcal {PT}}$-symmetric coupled systems.

In this paper, we study the coupled nonlinear Schrödinger equation (CNLSE) in the ($2+1$)-dimensional inhomogeneous ${\mathcal {PT}}$-symmetric nonlinear couplers and obtain the hollow ring-like soliton and DS solutions by means of the Hirota bilinear method. Based on these analytical solutions, we analyze the dynamical behaviors of hollow ring-like soliton and DS in a diffraction decreasing system (DDS) with exponential profile.

2 Model and soliton solution

In order to improve the conventional twin core coupler [20], the nonlinear coupler with gain and loss was presented and realized in experiment [21, 22]. In this structure, two optical waveguides are close proximity each other. One guide has a certain amount of gain, and the other one has an equal amount of loss. In a real waveguide, the inhomogeneous core medium exists [23], and thus the propagation of soliton in this inhomogeneous ${\mathcal {PT}}$-symmetric coupled systems can be governed by the following variable-coefficient CNLSE [24]

$$\begin{aligned}&\mathrm{i}u_z+\frac{1}{2}\beta (z) \nabla ^2_\bot u+\left[ \chi _1(z)|u|^{2}+\chi (z)|v|^2\right] u \nonumber \\&\quad =\lambda (z)(-v+\mathrm{i}\gamma u),\nonumber \\&\mathrm{i}v_z+\frac{1}{2}\beta (z) \nabla ^2_\bot v+\left[ \chi (z)|u|^{2}+\chi _1(z)|v|^2\right] v \nonumber \\&\quad =\lambda (z)(-u-\mathrm{i}\gamma v), \end{aligned}$$

(1)

where u(z, x, y) and v(z, x, y) denote two normalized complex mode fields in two parallel planar waveguides, z and x, y represent dimensionless propagation and transverse coordinates, the transverse Laplacian operator $\nabla ^2_\bot =\frac{\partial ^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial ^2}{\partial \phi ^2}$ with the radius $r=\sqrt{x^2+y^2}$ and the azimuthal angle $\phi =\arctan (y/x)$. In Eq. (1), from the left to right, these terms account for diffraction, nonlinearly coupled terms of the self-phase-modulation (SPM) and cross-phase-modulation (XPM) and the coupling between the modes propagating in the two waveguides. The opposite signs of the $\gamma$ term in the second term of right side describe the ${\mathcal {PT}}$-balanced gain in the first equation of Eq. (1) and loss in the second equation of Eq. (1). If the gain/loss term is small enough, e.g. $\gamma \le 1$, the energy through linear coupling is transferred from the core with gain to the lossy one, and modes can be excited in the system by input beams but do not arise spontaneously. Here we discuss this case.

We search for the ${\mathcal {PT}}$-symmetric ($+$) and ${\mathcal {PT}}$-antisymmetric (−) axisymmetric cylindrical-beam solutions of Eq. (1) in the form

$$\begin{aligned} u(z,r,\phi )= & {} U(z,r)\Phi (\phi )\exp \left[ \mathrm{i}\sqrt{1-\gamma ^2} \int _0^z\lambda (s)\hbox {d}s\right] \nonumber \\ v(z,r,\phi )= & {} \pm u(z,r,\phi )\exp {[\pm \mathrm{i}\arcsin (\gamma )]}. \end{aligned}$$

(2)

Inserting Eq. (2) into Eq. (1), the separation of variables leads to the following two equations:

$$\begin{aligned}&-\frac{1}{\Phi }\frac{\mathrm{d}^2\Phi }{\mathrm{d}\phi ^2}=m^2, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{2r^2}{\beta U}\left[ \mathrm{i}\frac{\partial U}{\partial z}+\frac{1}{2}\beta \left( \frac{\partial ^2U}{\partial r^2}+\frac{1}{r}\frac{\partial U}{\partial r}\right) \right. \nonumber \\&\quad \left. +\,(\chi +\chi _1) |\Phi |^2|U|^2U\right] =m^2. \end{aligned}$$

(4)

Obviously, solution to Eq. (3) can be expressed as

$$\begin{aligned} \Phi =\cos (m\phi )+\mathrm{i}q\sin (m\phi ), \end{aligned}$$

(5)

where parameter $q\in [0 ,1]$ determines the modulation depth of the beam, and the topological charge $m\ge 0$ is an integer [25]. Note that solution (5) is an approximate solution of Eq. (3), and it is valid for weak nonlinearities or for large values of q ($\sim$1) because the last term in the left of Eq. (4) is $\phi$-dependence and spoils the assumed separation of variables.

Therefore, integrating over $\phi$ from 0 to $2\pi$ and considering m being an integer, Eq. (4) changes into an averaged equation

$$\begin{aligned}&\frac{2r^2}{\beta U}\left[ \mathrm{i}\frac{\partial U}{\partial z}+\frac{1}{2}\beta \left( \frac{\partial ^2U}{\partial r^2}+\frac{1}{r}\frac{\partial U}{\partial r}\right) \right. \nonumber \\&\quad \left. +(\chi +\chi _1) (1+q^2)|U|^2U\right] =m^2. \end{aligned}$$

(6)

According to the Hirota bilinear method [25], inserting $U=r\frac{g(r,z)}{f(r,z)}$ with the complex and real functions g(r, z) and f(r, z) into Eq. (6), we have

$$\begin{aligned}&\left( \mathrm{i}rD_z+\frac{1}{2}\beta rD_r^2+\frac{3}{2}\beta D_r\right) (g\cdot f)=0, \end{aligned}$$

(7)

$$\begin{aligned}&D_r^2(f\cdot f)=(1+q^2)\frac{\chi +\chi _1}{\beta }r^2gg^*, \end{aligned}$$

(8)

with $m=1$ and the Hirota’s bilinear derivative operator $D_r^n(g\cdot f)=(\frac{\partial }{\partial r}-\frac{\partial }{\partial r'})^ng(z,r)f(z',r')|_{z'=z,r'=r}.$

In order to obtain fundamental soliton solutions, we expand functions g(r, z) and f(r, z) as power series of a formal expansion parameter $\epsilon$, and truncate g(r, z) as $g(r,z)=\epsilon g_1(r,z)$ and f(r, z) as $f(r,z)=1+\epsilon ^2 f_2(r,z)$ [25]. Inserting these expressions into Eqs. (7) and (8), we obtain

$$\begin{aligned}&\epsilon :\ \left( \mathrm{i}rD_z+\frac{1}{2}\beta rD_r^2+\frac{3}{2}\beta D_r\right) (g_1\cdot 1)=0,\nonumber \\&\epsilon ^2:\ D_r^2(1\cdot f_2)=\left( 1+q^2\right) \frac{\chi +\chi _1}{\beta }r^2g_1g_1^*,\nonumber \\&\epsilon ^3:\ \left( \mathrm{i}rD_z+\frac{1}{2}\beta rD_r^2+\frac{3}{2}\beta D_r\right) (g_1\cdot f_2)=0,\nonumber \\&\epsilon ^4:\ D_r^2(f_2\cdot f_2)=0. \end{aligned}$$

(9)

Solving Eq. (9) yields

$$\begin{aligned} g_1= & {} g_{10}\alpha ^2(z)\exp \left[ \alpha (z)r^2+M_0\right] ,\nonumber \\ f_2= & {} (1+q^2)\frac{\chi (z) +\chi _1(z)}{\beta (z)}H(z)\nonumber \\&\times \left[ \frac{e^{M(z)r^2}}{2M^2(z)} +\frac{\mathrm{i}\sqrt{\pi }r \mathrm{erf}\left[ \mathrm{i}r\sqrt{H(z)}\right] }{4H^{3/2}(z)}\right] \end{aligned}$$

(10)

where $M(z)=g_{10}^2\exp (2M_0)/[c^2+4D^2(z)],H(z) =2c/[c^2+4D^2(z)],\alpha (z)=1/[c-2\mathrm{i}D(z)],D(z)=\int _0^z\beta (s)\hbox {d}s$ with the error function $\hbox {erf}(x)$, and three constants $c,M_0,g_{10}$.

From results (2), (5) and (10), ${\mathcal {PT}}$-symmetric (+) and ${\mathcal {PT}}$-antisymmetric (−) axisymmetric cylindrical-beam solutions of equations (1) can be expressed as

(11)

When we solve Eqs. (7) and (8), g(r, z) and f(r, z) are truncated to $g_1 (r,z)$ and $f_2 (r,z)$ respectively, and this truncation cannot be exact. Moreover, solution $\Phi$ expressed as (5) is also not be exact. Therefore, solution (11) is an analytical but approximate solution.

3 Dynamical behaviors of hollow ring-like soliton and dipole soliton

In the following, we discuss the dynamical behaviors of hollow ring-like soliton and dipole soliton in a DDS with exponential profile [26]

$$\begin{aligned} \beta (z)= & {} \beta _{0}\exp (-\sigma z),\chi (z)=\chi _{0}\exp (-\delta z),\chi _1(z)\nonumber \\= & {} \chi _{10}\exp (-\delta z), \end{aligned}$$

(12)

where $\beta _{0}$ and $\chi _{0},\chi _{10}$ are three positive parameters related to diffraction and nonlinearity, respectively, $\sigma >0$ corresponds to DDS and $\delta$ is exponential parameter of nonlinearity.

We fix constants c and $M_0$ as $c=1.5$ and $M_0=3$. For $q = 1$ in solution (11), we obtain a hollow ring-like soliton. One example of this typical structure is shown in Fig. 1, where the axisymmetric radial intensity ($I=|u|^2$) is zero at the center, and the distributions of the optical field are independent of the azimuthal angle. From Fig 1a, b, in the course of evolution in the DDS, this nonstationary ring is compressed in a self-similar manner, the amplitude adds and the width attenuates in the radial direction. ${\mathcal {PT}}$-antisymmetric structure corresponding to Fig. 1b is shown in Fig. 1c.

Fig. 1

(Color online) The compression of hollow ring-like soliton at a $z=0$ and b $z=20$, c ${\mathcal {PT}}$-antisymmetric structure corresponding to (b) when $y=0$. Parameters are chosen as $q=1,g_{10}=1,c=1.5,M_0=3,\beta _0=0.5,\chi _0=0.3, \chi _{10}=0.2,\sigma =0.2,\delta =0.25$

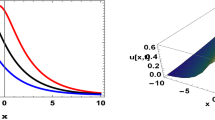
If we set q as other values, different localized structures can be constructed. For example, when $q=0$, the DS with two symmetrical humps also appears zero domain at the center. In Fig. 2a, b, with the evolution in the DDS, the structure shrinks in the radial direction and its peak gradually strengthens. When $q=0.75$, we can obtain another structure, that is, the ring soliton with two lobes. From Fig. 2c, d, with the evolution in the DDS, the smaller the radius of the stripes, the stronger the optical intensity of the ring soliton with two lobes.

Fig. 2

(Color online) The compression of dipole soliton at a, c $z=0$ and b, d $z=20$. Parameters are chosen as a, b $q=0$ and c, d $q=0.75$. Other parameters are chosen as the same as those in Fig. 1

4 Conclusions

In conclusion, by means of the Hirota bilinear method, we derive the hollow ring-like soliton and DS solutions of the CNLSE in the ($2+1$)-dimensional inhomogeneous ${\mathcal {PT}}$-symmetric nonlinear couplers. Based on these analytical solutions, we also study the compression behaviors of hollow ring-like soliton and DS in a DDS with exponential profile. Our analysis and results may have potential values for certain applications of synthetic ${\mathcal {PT}}$-symmetric systems in condensed matter physics and nonlinear optics.