Non-lane-discipline-based car-following model considering the effects of two-sided lateral gaps

Abstract

This study proposes a new car-following model that considers the effects of two-sided lateral gaps on a road without lane discipline. In particular, a car-following model is proposed to capture the impacts from the lateral gaps of the leading vehicles on both sides of the following vehicle. Linear stability analysis of the proposed model is performed using the perturbation method to obtain the stability condition. Nonlinear analysis is performed using the reductive perturbation method to derive the modified Korteweg de Vries equation to describe the density wave propagation. Results from numerical experiments illustrate that the proposed car-following model has larger stable region compared to a car-following model that considers the effect of lateral gap on only one side. Also, it is able to more rapidly dissipate the effect of a perturbation such as a sudden stimulus from a leading vehicle. In addition, the findings of this study provide insights in analyzing system performance of a non-lane-discipline road system in the future.

1 Introduction

Traffic flow modeling based on the fluid-dynamic approach can date back to 1950s, which aims to model the flow and interactions in the traffic stream considering the similar characteristics between traffic flow and the fluid dynamics [1–3]. In the literature, various microscopic and macroscopic traffic flow models have been proposed. At the microscopic level, each individual vehicle is represented as a particle and the vehicular traffic is treated as a system of interacting particles. The car-following theory is used to describe the interactions between each pair of leading and following vehicles [4–8].

In the car-following theory, the relationship between the leading vehicle and the following vehicle is based on the following vehicle decelerating or accelerating in response to a stimulus from the leading vehicle [8]. Bando et al. [9] propose a car-following model in which the concept of optimal velocity (OV) is introduced based on the assumption that the desired velocity of the following vehicle is determined by its space headway with the leading vehicle. Helbing and Tilch [10] calibrate the OV model using the empirical follow-the-leader data and develop a generalized force (GF) model by considering the impact of lower leading vehicle velocity on the behavior of the following vehicle. However, neither the OV model nor the GF model can explain the following traffic phenomena described by Treiber et al. [11]: In reality, when the leading vehicle is much faster than the following vehicle, the following vehicle will not decelerate even when its headway is lower than the safe space headway. Consequently, Jiang et al. [12, 13] argue that the impact of relative speed between the leading and the following vehicles on the behavior of following vehicle should be considered explicitly. They propose a full velocity difference (FVD) model by considering both positive and negative velocity differences. However, the FVD model does not study the effects of the lateral gaps on vehicular traffic flow. By considering multiple attributes of leading vehicles, other car-following models have since been developed, such as the FVAD model [14], MVD model [15], MHVD model [16], MHVAD model [17] and so on (see [8] for a review). Other car-following models [18–23] have also been proposed in the literature.

A key assumption in car-following theory is that vehicles follow the lane discipline and move in the middle of the lane. However, this assumption may not be valid in many developing countries where lanes may not be clearly demarcated on a road though multiple vehicles can travel in parallel. That is, the notion of a lane does not exist, and consequently, the middle of a lane is not meaningful either. Therefore, the aforementioned car-following models cannot be readily applied [24]. A common situation in such non-lane-based traffic environment is that vehicles are positioned off the center-line of the road. The off-center effect will cause lateral gaps between vehicles, and the lateral gap may increase with the road width. Hence, there is the need to study the impact of lateral gaps on the behavior of the following vehicles [25, 26]. Jin et al. [25] propose a non-lane-based full velocity difference car-following (NLBCF) model to analyze the impact of the lateral gap on one side on the car-following behavior. They illustrate that considering the one-sided lateral gap can improve the stability of the traffic flow. However, the NLBCF model cannot distinguish the right-side and the left-side lateral gaps. In addition, the main properties of the NLBCF model are derived based on linear perturbation analysis only, without conducting a nonlinear analysis. The nonlinear analysis is an important aspect in the study of car-following models [27–36]. The linear stability analysis can provide the conditions under which a small perturbation of a stationary state can dissipate over time. However, as the traffic system is a nonlinear strongly coupled complex system, conducting nonlinear analysis can characterize density wave profiles under larger perturbations [27]. In particular, the Korteweg de Vries (KdV) equation can be used to find exact solutions such as solitons by applying the inverse scatting transform [27]. Kurtz et al. [28] derive the KdV equation from the hydrodynamic model and show that the traffic soliton appears near the neutral stability line. Komatsu et al. [29] deduce the modified KdV (mKdV) equation from the OV model. Nagatani [30] and Li et al. [31] also investigate a car-following model with next-nearest-neighbor interaction through nonlinear analysis and derive the mKdV equation. Ge et al. [32] perform nonlinear analysis to a car-following model. Lei et al. [33] and Yu et al. [34] also perform nonlinear analysis to obtain kink–antikink density waves of an OV-based traffic flow model. Kurtze et al. [35] and Lv et al. [36] analyze the solitons and kinks for a general car-following model.

The literature review heretofore illustrates the importance of incorporating lateral gaps for modeling non-lane-discipline traffic flow as well as improving the stability of car-following models. However, considering the lateral gap on only one side is restrictive because in many non-lane-discipline road systems, more than two vehicles travel on the road in parallel as shown in Fig. 1. Hence, there is the need to analyze the behavior of the following vehicle by considering the lateral gaps on both sides to address the more general scenario in non-lane-discipline roads. The focus of this study is on the effects of two-sided lateral gaps on the vehicular traffic flow. The FVD model does not consider the effects of lateral gap. The NLBCF model considers the effects of a one-sided lateral gap, but cannot be used under the scenarios with two-sided lateral gaps. Additionally, no nonlinear analysis has been conducted for the NLBCF model.

Fig. 1

Car-following with two-sided lateral gaps

Motivated by the scenarios with two-sided lateral gaps, we propose a generalized model considering the effects of two-sided lateral gaps of the following vehicle in a road system without lane discipline. Theoretical analyses show that the FVD and NLBCF models are special cases of the proposed model. The linear stability of the proposed model is analyzed using the perturbation method to obtain the stability condition. Theoretical and simulation analyses verify that the stability region of the proposed model is improved compared to those of the OV, FVD and NLBCF models under the same condition. The nonlinear analysis of the proposed model is performed using the reductive perturbation method to obtain the corresponding mKdV equation, which can describe the density wave propagation such that the traffic congestion pattern and its evolution can be better understood. Finally, the numerical experiments conducted in this study verify that the capability of perturbation rejection of the proposed model is improved compared to that of the NLBCF model under the same condition.

The rest of this paper is organized as follows: Sect. 2 proposes a new car-following model considering the effects of two-sided lateral gaps. Section 3 performs the linear stability analysis of proposed model using the perturbation method. Section 4 conducts the nonlinear analysis using the reductive perturbation method. Section 5 presents the numerical experiments and comparisons. The final section concludes this study.

2 Dynamic model

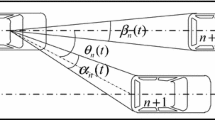
In this study, it is assumed that all vehicles travel on a road without lane discipline as shown in Fig. 1. Hence, vehicle may not travel in the middle of the road or follow any lane discipline. The dashed lines in the figure indicate the center lines associated with the various vehicles and are used in the modeling process.

The leading vehicle (i.e., vehicle $n+3$ in Fig. 1) is traveling in front of the following vehicle (i.e., vehicle $n$ in Fig. 1). The vehicle traveling on the right side of the road (i.e., vehicle $n+1$ in Fig. 1) and the vehicle traveling on the left side of the road (i.e., vehicle $n+2$ in Fig. 1) constitute two lateral gaps with respect to the following vehicle $n$. Denote $\hbox {Lg}_{n,n+1}$ as the lateral gap between the following vehicle $n$ and the vehicle traveling on the right side $n+1$ and $\hbox {Lg}_{\max }$ as the lateral gap between the vehicles traveling on the right side and on the left side of the following vehicle $n$. Then, the ratio $p_n =\hbox {Lg}_{n,n+1} /\hbox {Lg}_{\max } \in [0,1]$ indicates the relative location of the following vehicle $n$ with respect to the two extreme lateral locations of vehicles $n+1$ and $n+2$. Note that, as the following vehicle $n$ and the leading vehicle $n+3$ may not align with each other, there may be another lateral gap constituted by these two vehicles. However, this study does not focus on the effects from this lateral gap on the following vehicle.

A new car-following model considering the effects of two-sided lateral gaps can be developed based on the FVD model as follows

$$\begin{aligned} a_n (t)&= \alpha \left\{ U\left[ \Delta x_{n,n+1} (t),\Delta x_{n,n+2} (t),\Delta x_{n,n+3} (t)\right] \right. \nonumber \\&\left. -\,\,v_n (t)\right\} +\kappa G\left[ \Delta v_{n,n+1} (t),\Delta v_{n,n+2} (t),\right. \nonumber \\&\left. \Delta v_{n,n+3} (t)\right] \end{aligned}$$

(1)

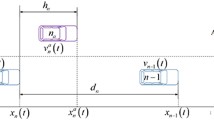
where $x_n (t)>0,v_n (t)>0$ and $a_n (t)$ represent the position $(\hbox {m})$, velocity $\hbox {(m/s)}$ and acceleration $(\hbox {m/s}^{2})$ of the vehicle $n$, respectively. $t\in {\mathbb {{R}}}$ represents the time $\hbox {(s)}$. $\alpha \in {\mathbb {{R}}}$ ($\alpha =1/\tau >0)$ is the sensitivity coefficient of a driver to the difference between the optimal and the current velocities. $\kappa \in {\mathbb {{R}}} (\kappa =\lambda /\tau \ge 0)$ represents the sensitivity coefficient of response to the stimulus $G(\cdot ,\cdot ,\cdot )$. $\Delta x_{n,n+1} (t)\equiv x_{n+1} (t)-x_n (t)$ and $\Delta v_{n,n+1} (t)\equiv v_{n+1} (t)-v_n (t)$ are the longitudinal space headway and the velocity difference between the leading vehicle $n+1$ and the following vehicle $n$ at time $t$ , respectively. $\Delta x_{n,n+2} (t)\equiv x_{n+2} (t)-x_n (t)$ and $\Delta v_{n,n+2} (t)\equiv v_{n+2} (t)-v_n (t)$ are the longitudinal space headway and the velocity difference between the leading vehicle $n+2$ and the following vehicle $n$ at time $t$ , respectively. $\Delta x_{n,n+3} (t)\equiv x_{n+3} (t)-x_n (t)$ and $\Delta v_{n,n+3} (t)\equiv v_{n+3} (t)-v_n (t)$ are the longitudinal space headway and the velocity difference between the leading vehicle $n+3$ and the following vehicle $n$ at time $t$ , respectively.

Considering the two-sided lateral gaps from center-line of the following vehicle, the function $U(\cdot ,\cdot ,\cdot )$ and $G(\cdot ,\cdot ,\cdot )$ can be represented as

$$\begin{aligned}&U\left[ \Delta x_{n,n+1} (t),\Delta x_{n,n+2} (t),\Delta x_{n,n+3} (t)\right] \nonumber \\&\quad =\left\{ {\begin{array}{l} V\left[ (1-2p_n )\Delta x_{n,n+1} (t)+2p_n \Delta x_{n,n+3} (t)\right] \;\;\; \\ \quad \hbox {Lg}_{n,n+1} \in \left[ 0,0.5\hbox {Lg}_{\max } \right] \\ V\!\left[ (2p_n \!-\!1)\Delta x_{n,n+2} (t)+2(1\!-\!p_n )\Delta x_{n,n\!+\!3} (t)\right] \\ \quad \hbox {Lg}_{n,n+1} \in \left[ 0.5\hbox {Lg}_{\max } ,\hbox {Lg}_{\max } \right] \\ \end{array}} \right. \nonumber \\\end{aligned}$$

(2)

$$\begin{aligned}&G\left[ \Delta v_{n,n+1} (t),\Delta v_{n,n+2} (t),\Delta v_{n,n+3} (t)\right] \nonumber \\&\quad =\left\{ {\begin{array}{l} (1-2p_n )\Delta v_{n,n+1} (t)+2p_n \Delta v_{n,n+3} (t)\\ \quad \hbox {Lg}_{n,n+1} \in \left[ 0,0.5\hbox {Lg}_{\max } \right] \\ (2p_n -1)\Delta v_{n,n+2} (t)+2(1-p_n )\Delta v_{n,n+3} (t)\;\;\;\\ \quad \hbox {Lg}_{n,n+1} \in \left[ 0.5\hbox {Lg}_{\max } ,\hbox {Lg}_{\max } \right] \\ \end{array}} \right. \nonumber \\\end{aligned}$$

(3)

$$\begin{aligned}&V(\Delta x)=0.5v_{\max } \left[ \tanh (\Delta x-h_c )+\tanh (h_c )\right] \end{aligned}$$

(4)

$$\begin{aligned}&p_n =\frac{\hbox {Lg}_{n,n+1} }{\hbox {Lg}_{\max } } \end{aligned}$$

(5)

where $V(\cdot )$ is the optimal velocity function, $v_{\max }$ is the maximal speed of the vehicle, $h_c$ is the safe longitudinal space headway, and $\tanh (\cdot )$ is the hyperbolic tangent function [9]. $p_n$ is the parameter representing the effect of lateral gap. The value of $\hbox {Lg}_{\max }$ can be chosen as 3.6 m to be consistent with the typical road width [25].

Based on Eqs. (2)–(5), Eq. (1) can be reformulated as:

Case 1 $\hbox {Lg}_{n,n+1} \in [0,0.5\hbox {Lg}_{\max } ]$

$$\begin{aligned} a_n (t)&= \alpha \left\{ V\left[ (1-2p_n )\Delta x_{n,n+1} (t)+2p_n \Delta x_{n,n+3} (t)\right] \right. \nonumber \\&\left. -\,\,v_n (t)\right\} +\kappa \left[ (1-2p_n )\Delta v_{n,n+1} (t)\right. \nonumber \\&\left. +\,\,2p_n \Delta v_{n,n+3} (t)\right] ; \end{aligned}$$

(6)

Case 2 $\hbox {Lg}_{n,n+1} \in [0.5\hbox {Lg}_{\max } ,\hbox {Lg}_{\max } ]$

$$\begin{aligned} a_n (t)&= \alpha \left\{ V\left[ (2p_n -1)\Delta x_{n,n+2} (t)\right. \right. \nonumber \\&\left. \left. \!+\,2(1-p_n )\Delta x_{n,n+3} (t)\right] \;-v_n (t)\right\} \nonumber \\&+\,\kappa \left[ (2p_n -1)\Delta v_{n,n+2}(t)\right. \nonumber \\&\left. \!+\,2(1-p_n )\Delta v_{n,n+3} (t)\right] . \end{aligned}$$

(7)

Based on Eqs. (6) and (7), three specific conditions can be analyzed:

• (i) If $\hbox {Lg}_{n,n+1} =0$ , then $p_n =0$ , which represents the vehicle $n$ will follow vehicle $n+1$ , then the model becomes

  $$\begin{aligned} a_n (t)=\alpha V[\Delta x_{n,n\!+\!1} (t)\!-\!v_n (t)\}\!+\!\kappa \Delta v_{n,n+1} (t);\nonumber \\ \end{aligned}$$

  (8)

• (ii) If $\hbox {Lg}_{n,n+1} =0.5\hbox {Lg}_{\max }$, then $p_n =0.5$, which represents the vehicle $n$ follow vehicle $n+3$, then the model becomes

  $$\begin{aligned} a_n (t)\!=\!\alpha V[\Delta x_{n,n\!+\!3} (t)\!-\!v_n (t)\}+\kappa \Delta v_{n,n+3} (t);\nonumber \\ \end{aligned}$$

  (9)

• (iii) If $\hbox {Lg}_{n,n+1} =\hbox {Lg}_{\max },$ then $p_n =1,$ which represents the vehicle $n$ follow vehicle $n+2$, then the model becomes

  $$\begin{aligned} a_n (t)\!=\!\alpha V[\Delta x_{n,n+2} (t)\!-\!v_n (t)\}+\kappa \Delta v_{n,n+2} (t).\nonumber \\ \end{aligned}$$

  (10)

Remark 1

Eqs. (6) and (7) indicate that if the impact of lateral gaps on only one-sided is considered, the model is similar to the NLBCF model in [25]; and if $\hbox {Lg}_{n,n+1} =0$, $\hbox {Lg}_{n,n+1} =0.5\hbox {Lg}_{\max }$, or $\hbox {Lg}_{n,n+1} =\hbox {Lg}_{\max }$, the model is deduced to FVD model in [12]. Therefore, the FVD model and the NLBCF model are some special cases of the proposed model.

In addition, Eqs. (6) and (7) can be rewritten using the asymmetric forward difference [18, 25] to facilitate stability analyses of the proposed model as:

Case 1 $\hbox {Lg}_{n,n+1} \in \left[ 0,0.5\hbox {Lg}_{\max } \right]$

$$\begin{aligned} x_n (t+2\tau )&= x_n (t+\tau )+\tau V\left[ (1-2p_n )\Delta x_{n,n+1} (t)\right. \nonumber \\&\left. +\,\,2p_n \Delta x_{n,n+3} (t)\right] +\tau \lambda \left\{ (1-2p_n )\right. \nonumber \\&\times \,\,\left[ \Delta x_{n,n+1} (t+\tau )-\Delta x_{n,n+1} (t)\right] \nonumber \\&\left. +\,\,2p_n \left[ \Delta x_{n,n+3} (t+\tau )\!-\!\Delta x_{n,n\!+\!3} (t\right] \right\} ;\nonumber \\ \end{aligned}$$

(11)

Case 2 $\hbox {Lg}_{n,n+1} \in [0.5\hbox {Lg}_{\max } ,\hbox {Lg}_{\max } ]$

$$\begin{aligned}&x_n (t+2\tau )=x_n (t+\tau )+\tau \left\{ V\left[ (2p_n -1)\right. \right. \nonumber \\&\quad \left. \times \,\, \Delta x_{n,n+2} (t)+2(1-p_n )\Delta x_{n,n+3} (t)\right] \nonumber \\&\quad +\,\,\tau \lambda \left\{ (2p_n -1)\left[ \Delta x_{n,n+2} (t+\tau )-\Delta x_{n,n+2} (t)\right] \right. \nonumber \\&\quad \left. +\,\,2(1-p_n )\left[ \Delta x_{n,n+3} (t+\tau )-\Delta x_{n,n+3} (t)\right] \right\} .\nonumber \\ \end{aligned}$$

(12)

3 Linear stability analysis

The stability of the proposed model is analyzed under the following assumption.

Assumption 1

The initial state of the traffic flow is steady, and all vehicles in the traffic move with the identical space headway and the optimal velocity.

Based on this assumption, the stability analysis is conducted in two cases:

Case 1 $\hbox {Lg}_{n,n+1} \in \left[ 0,0.5\hbox {Lg}_{\max } \right]$

Following Assumption 1, the position solution to the steady flow is:

$$\begin{aligned} x_n^0 (t)=hn+V(h,3h)t \end{aligned}$$

(13)

where $V(h,3h)=V[(1-2p_n )\cdot h+2p_n \cdot 3h]$ is the optimal velocity in uniform traffic flow and $h$ is the steady headway, $x_n^0 (t)$ is the position of the $n$th vehicle in steady state.

Adding a small disturbance $y_n (t)$ to the steady-state solution $x_n^0 (t)$ , i.e.,

$$\begin{aligned} y_n (t)=x_n (t)-x_n^0 (t). \end{aligned}$$

(14)

Substituting Eq. (14) into Eq. (11) and linearizing the resulting equation using the Taylor expansion, it deduces:

$$\begin{aligned}&y_n (t+2\tau )=y_n (t+\tau )+\tau V^{\prime }(h,3h)\left[ (1-2p_n )\right. \nonumber \\&\quad \left. \times \, \Delta y_{n,n+1} (t)+2p_n \Delta y_{n,n+3} (t)\right] \nonumber \\&\quad +\,\,\tau \lambda \left\{ (1-2p_n )\left[ \Delta y_{n,n+1} (t+\tau )-\Delta y_{n,n+1} (t)\right] \right. \nonumber \\&\left. \quad +\,\,2p_n \left[ \Delta y_{n,n+3} (t+\tau )-\Delta y_{n,n+3} (t\right] \right\} . \end{aligned}$$

(15)

Set $y_n (t)$ be in the Fourier models, i.e.,$\, y_n (t)=A\exp (\hbox {ik}n+zt)$, substituting it in Eq. (15) and we have

$$\begin{aligned} e^{2\tau z}&= e^{\tau z}+\tau V^{\prime }(h,3h)\left[ (1-2p_n )(e^{{\mathrm{i}}k}-1)\right. \nonumber \\&\left. +\,\,2p_n (e^{{\mathrm{3i}}k}-1)\right] +\tau \lambda \left[ (1-2p_n )(e^{\tau z}-1)\right. \nonumber \\&\left. \,\,\times \,(e^{{\mathrm{i}}k}-1)+2p_n (e^{\tau z}-1)(e^{{\mathrm{3i}}k}-1)\right. ]. \end{aligned}$$

(16)

Let $z=z_1 (\hbox {i}k)+z_2 (\hbox {i}k)^{2}+\cdots$ and expand it to the second term of $(\hbox {i}k)$, we obtain

$$\begin{aligned}&1+2\tau z_1 (ik)+\left( 2\tau z_2 +2\tau ^{2}z_1^2 \right) (ik)^{2}=1+\tau z_1 (ik)\nonumber \\&\quad +\left( \tau z_2 +\frac{1}{2}\tau ^{2}z_1^2\right) (ik)^{2}\;+\tau V^{\prime }(h,3h)(1-2p_n )\nonumber \\&\quad \times \left( ik\!+\!\frac{1}{2}(ik)^{2}\right) +2\tau V^{\prime }(h,3h)p_n \left( 3ik+\frac{9}{2}(ik)^{2}\right) \nonumber \\&\quad +\,\tau ^{2}\lambda (1-2p_n )z_1 (ik)^{2}\;\hbox {+\,6}\tau ^{2}\lambda p_n z_1 (ik)^{2}. \end{aligned}$$

(17)

Therefore,

$$\begin{aligned} \left\{ {\begin{array}{l} \tau z_1 = \tau V^{\prime }(h,3h)(1-2p_n ) + 6\tau V^{\prime }(h,3h)p_n \\ 2\tau z_2 +2\tau ^{2}z_1^2 = \tau z_2 +\frac{1}{2}\tau ^{2}z_1^2 + \frac{1}{2}\tau V^{\prime }(h,3h)\\ (1-2p_n ) + 9\tau V^{\prime }(h,3h)p_n + \tau ^{2}\lambda \\ (1-2p_n )z_1 \hbox {+6}\tau ^{2}\lambda p_n z_1 . \\ \end{array}} \right. \end{aligned}$$

(18)

Consequently

$$\begin{aligned} \left\{ {\begin{array}{l} z_1 = V^{\prime }(h,3h)(1 + 4p_n ) \\ z_2 = \frac{1 + 16p_n }{2}V^{\prime }(h,3h) + \tau V^{\prime }(h,3h)(1 + 4p_n )^{2}\\ (\lambda -\frac{3}{2}V^{\prime }(h,3h)). \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(19)

Thus, the neutral stability condition is given by

$$\begin{aligned} \tau = \frac{1 + 16p_n }{\left[ 3V^{\prime }(h,3h)-2\lambda \right] (1 + 4p_n )^{2}}. \end{aligned}$$

(20)

For small disturbance with long wavelengths, the uniform traffic flow is unstable in the condition that

$$\begin{aligned} \tau >\frac{1 + 16p_n }{\left[ 3V^{\prime }(h,3h)-2\lambda \right] (1 + 4p_n )^{2}}. \end{aligned}$$

(21)

Case 2 $\hbox {Lg}_{n,n+1} \in [0.5\hbox {Lg}_{\max } ,\hbox {Lg}_{\max } ]$

Using the similar method in Case 1, the position solution to the stability flow is:

$$\begin{aligned} x_n^0 (t)=hn+V(2h,3h)t \end{aligned}$$

(22)

where $V(2h,3h)=V[(2p_n -1) \cdot 2h+2(1-p_n ) \cdot 3h]$ is the optimal velocity in uniform traffic flow. The neutral stability condition is obtained as

$$\begin{aligned} \tau = \frac{(7-5p_n )}{2\left[ 3V^{\prime }(2h,3h)-2\lambda \right] (2-p_n )^{2}}. \end{aligned}$$

(23)

And the uniform traffic flow in this case is unstable when

$$\begin{aligned} \tau > \frac{(7-5p_n )}{2\left[ 3V^{\prime }(2h,3h)-2\lambda \right] (2-p_n )^{2}}. \end{aligned}$$

(24)

Based on Eqs. (20) and (23), we obtain

• (i) If $\hbox {Lg}_{n,n+1} =0$, then $p_n =0$, thus the neutral stability condition is

  $$\begin{aligned} \tau = \frac{1}{3V^{\prime }(h)-2\lambda }; \end{aligned}$$

  (25)

• (ii) If $\hbox {Lg}_{n,n+1} =0.5\hbox {Lg}_{\max },$ then $p_n =0.5$, thus the neutral stability condition is

  $$\begin{aligned} \tau = \frac{1}{3V^{\prime }(3h)-2\lambda }; \end{aligned}$$

  (26)

• (iii) If $\hbox {Lg}_{n,n+1} =\hbox {Lg}_{\max },$ then $p_n =1$, thus the neutral stability condition is

  $$\begin{aligned} \tau = \frac{1}{3V^{\prime }(2h)-2\lambda }. \end{aligned}$$

  (27)

Remark 2

According to Eqs. (20), (23), (25)-(27), we can verify the effectiveness of the proposed model and the correctness of the stability analysis. Moreover, Eq. (25) is the neutral stability condition of the FVD model in [12], and Eq. (27) is the neutral stability condition of the NLBCF model in [25] with $p_n =1$.

Fig. 2

Neutral stability lines in the space headway-sensitivity coefficient diagram with different $(\lambda ,p_n )$

Figure 2 is the critical curves between sensitivity coefficient $\alpha$ and the space headway with respect to different values of ($\lambda ,p_n )$. In Fig. 2, the space formed by the sensitivity coefficient and the space headway is divided into two regions (stable region and unstable region) by the critical curve. Specifically, the region over each critical curve is the stable region in which the traffic flow is stable; the remainder is the unstable region in which density waves emerge. In addition, if $\lambda =0,p_n =0$ , the proposed model is reduced to the OV model in [9] and if $\lambda \ne 0,p_n =0$ , the proposed model is reduced to the FVD model in [12] while if $\lambda \ne 0,p_n \in [0,0.5]$ or $\lambda \ne 0,p_n \in [0.5,1]$ , the proposed model is reduced to the NLBCF model in [25]. Moreover, Fig. 3 shows the sensitivity of critical points for the neutral stability lines as a function of $\lambda$ and $p_n$. Figure 3 also shows that the sensitivity coefficient obtains the maximum values under the condition of $\lambda =0$ , which can also be verified by Fig. 2.

To conclude, we can find that (i) the stability region of the uniform traffic flow will been enlarged with the increase of parameter $\lambda$ in the case of the same value of parameter $p_n$; (ii) the critical curve will be shifted left from the initial state (i.e., $\lambda =0,p_n =0)$ with the increase of parameter $p_n$; and (iii) the steady dynamics of the uniform traffic flow will be improved by considering the two-sided lateral gaps compared with OV model, FVD model and NLBCF model under the same condition.

Fig. 3

Critical points for the neutral stability lines

4 Nonlinear analysis

To verify the nonlinear characteristics of the proposed model, the weakly nonlinear wave equation of the jam formation is derived using the reductive perturbation method [27–36]. Starting from the definition, the small scaling parameters $\varepsilon (0<\varepsilon \ll 1)$ and new quantities have to be defined, i.e., the slow space, time variables $X$ and $T$ and perturbation $R$. To investigate the slowly varying behavior of slow scales near the critical point $\alpha =\alpha _c$, $h=h_c$ in the unstable region, the scaling between variables $X$, $T$ and $R$ are chosen such that [27–36]:

$$\begin{aligned} \left\{ {\begin{array}{l} X=\varepsilon (n+bt) \\ T=\varepsilon ^{3}t \\ \Delta x_n (t)=h_c +\varepsilon R(X,T) \\ \end{array}} \right. \end{aligned}$$

(28)

where $b$ is an arbitrary constant that will be specified later and $\Delta x_n (t)\equiv \Delta x_{n,n+1} (t)=\Delta x_{n+1} (t)-\Delta x_n (t)$.

Case 1 $\hbox {Lg}_{n,n+1} \in \left[ 0,0.5\hbox {Lg}_{\max } \right]$

Let us start by Eqs. (6) and rewrite it with the reductive perturbation method as follows

$$\begin{aligned}&\Delta x(t+2\tau )=\Delta x(t+\tau )+\tau \left\{ V\left[ (1-2p_{n+1} )\Delta x_{n+1,n+2} (t)\right. \right. \nonumber \\&\quad \left. +\,\,2p_{n+1} \Delta x_{n+1,n+4} (t)\right] -V[(1-2p_n )\Delta x_{n,n+1} (t)\nonumber \\&\quad \left. +\,\, 2p_n \Delta x_{n,n+3} (t)]\right\} +\lambda \tau \left\{ \left[ (1-2p_{n+1} )\left( \Delta x_{n+1,n+2} (t+\tau )\right. \right. \right. \nonumber \\&\quad \left. -\,\,\Delta x_{n+1,n+2} (t)\right) +2p_{n+1} \left( \Delta x_{n+1,n+4} (t+\tau )\right. \nonumber \\&\quad \left. \left. -\,\, \Delta x_{n+1,n+4} (t)\right) \right] -\left[ (1-2p_n )\left( \Delta x_{n,n+1} (t+\tau )\right. \right. \nonumber \\&\quad \left. \left. \left. -\,\,\Delta x_{n,n+1} (t)\right) +2p_n (\Delta x_{n,n+3} (t+\tau )-\Delta x_{n,n+3} (t))\right] \right\} .\nonumber \\ \end{aligned}$$

(29)

Substituting Eq. (28) into Eq. (29) and making the Taylor expansions to the fifth order of $\varepsilon$, we have

$$\begin{aligned}&\varepsilon ^{2}\beta _1 \partial _X R+\varepsilon ^{3}\beta _2 \partial _X^2 R+\varepsilon ^{4}\left( \beta _3 \partial _T R+\beta _4 \partial _X^3 R\right. \nonumber \\&\quad \left. +\,\beta _5 \partial _X R^{3}\right) \!+\!\varepsilon ^{5}\left( \beta _6 \partial _X \partial _T R\!+\!\beta _7 \partial _X^4 R\!+\!\beta _8 \partial _X^2 R^{3}\right) \!=\!0.\nonumber \\ \end{aligned}$$

(30)

The coefficients $\beta _i (i=1,2, \ldots ,8)$ are given in the Table 1,

Table 1 The coefficients $\beta _i$ of the proposed model

where $\partial _X =\frac{\partial }{\partial _X },\partial _T =\frac{\partial }{\partial _T },\partial _X \partial _T =\frac{\partial ^{2}}{\partial _X \partial _T },V^{\prime }=\frac{\hbox {d}V(\Delta x)}{\hbox {d}\Delta x}|_{\Delta x=h_c }$ and $V^{\prime \prime \prime }=\frac{\hbox {d}^{\hbox {3}}V(\Delta x)}{\hbox {d}\Delta x^{3}}|_{\Delta x=h_c }$.

By taking $b=V^{\prime }(1+4p_n )$ , the second-order term of $\varepsilon$ is eliminated from Eq. (30) and near the critical point $(\alpha _c ,h_c )$, the neighborhood of the critical point $\tau _c$ is considered as follows [27–36]

$$\begin{aligned} \frac{\tau }{\tau _c }=1+\varepsilon ^{2} \end{aligned}$$

(31)

where $\tau _c =\frac{1 + 16p_n }{(3V^{\prime }-2\lambda )(1 + 4p_n )^{2}}$. And let

$$\begin{aligned} \partial _X \partial _T R&= \frac{1+52p_n +\lambda (3+48p_n )(1+4p_n )}{6}V^{\prime }\partial _X^4 R\nonumber \\&+\,\,\frac{1}{6}V^{\prime \prime \prime }\left[ \left( 1+16p_n^3 \right) \partial _X^2 R^{3}+O(\varepsilon )\right. \!. \end{aligned}$$

(32)

Then Eq. (30) becomes

$$\begin{aligned} \partial _T R&- \frac{1+52p_n +\lambda (3+48p_n )(1+4p_n )}{6}V^{\prime }\partial _X^3 R\nonumber \\&-\,\,\frac{1}{6}V^{\prime \prime \prime }\left[ \left( 1+16p_n^3 \right) \partial _X R^{3}+O(\varepsilon )=0.\right. \nonumber \\ \end{aligned}$$

(33)

In order to get the standard mKdV equation, the following transformations are introduced [27–36]:

$$\begin{aligned} T^{\prime }=g_1 T,\;\;\;R=\sqrt{g_1 /g_2 }R^{\prime } \end{aligned}$$

(34)

where

$$\begin{aligned} g_1&= \frac{1+52p_n +\lambda (3+48p_n )(1+4p_n )}{6}V^{\prime },\\ g_2&= -\frac{1}{6}V^{\prime \prime \prime }\left[ \left( 1+16p_n^3 \right) \right. \end{aligned}$$

with $1+52p_n +\lambda (3++48p_n )(1+4p_n )\ge 0,(0\le \lambda \le 1)$. Substituting (35) into (34), the regularized equation is referred

$$\begin{aligned} \partial _{T^{\prime }} R^{\prime }-\partial _X^3 R^{\prime }+\partial _X R^{\prime 3}+O(\varepsilon )=0. \end{aligned}$$

(35)

If $O(\varepsilon )$ is ignored, Eq. (35) is just the mKdV equation and the kink–antikink solution according to the general solution is derived:

$$\begin{aligned} R^{\prime }_0 (X,T^{\prime })=\sqrt{c}\tanh \sqrt{\frac{c}{2}}\left( X-cT^{\prime }\right. ). \end{aligned}$$

(36)

Suppose $R^{\prime }(X,T^{\prime })=R^{\prime }_0 (X,T^{\prime })+R^{\prime }_1 (X,T^{\prime })$ with the consideration of $O(\varepsilon )$ , the existence condition of $R^{\prime }_0 (X,T^{\prime })$ is presented to obtain the propagation speed $c$ in Eq. (37) as [29]

$$\begin{aligned} (R^{\prime }_0 ,M[R^{\prime }_0 ])&= \int _{-\infty }^{+\infty } \hbox {d}XR^{\prime }_0 (X,T^{\prime })\nonumber \\&\times \, M\left[ R^{\prime }_0 (X,T^{\prime })\right] =0 \end{aligned}$$

(37)

where $M[R^{\prime }_0 ]=c_1 \partial _X^2 R^{\prime }+\frac{c_2 }{2}\partial _X^4 R^{\prime }-\frac{c_3 }{2}\partial _X^2 R^{\prime 3}$ and

$$\begin{aligned} c_1&= \frac{\lambda }{1+52p_n +\lambda (3+48p_n )(1+4p_n )},\nonumber \\ c_2&= \frac{1}{1+52p_n +\lambda (3+48p_n )(1+4p_n )},\;c_3 =1. \end{aligned}$$

Using the integral method, we can obtain the propagation speed $c=\frac{2c_1 }{2c_2 +3c_3 }$ , and the amplitude $A$ of the kink–antikink solution is

$$\begin{aligned} A&= \left[ \frac{1+52p_n +\lambda (3+48p_n )(1+4p_n )}{3}\right. \nonumber \\&\left. \times \left( \frac{\alpha _c }{\alpha }-1\right) c \right] ^{1/2} \end{aligned}$$

(38)

where $\alpha _c =\frac{1}{\tau _c }=\frac{(3V^{\prime }-2\lambda )(1 + 4p_n )^{2}}{1+16p_n }$. Thus, the following kink–antikink soliton solution of the mKdV equation is obtained by

$$\begin{aligned}&R(X,T)=\left[ {-\frac{2\left[ 1+52p_n +\lambda (3+48p_n )(1+4p_n )\right] }{3\left( 1+16p_n^3 \right) V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\quad \times \;\tanh \sqrt{\frac{c}{2}}\left( X-\frac{1+52p_n +\lambda (3+48p_n )(1+4p_n )}{6}V^{\prime }cT\right) .\nonumber \\ \end{aligned}$$

(39)

Therefore, the kink–antikink soliton solution to the space headway is

$$\begin{aligned}&\Delta x_n =h_c +\left[ {-\frac{2\left[ 1+52p_n +\lambda (3+48p_n )(1+4p_n )\right] }{3\left( 1+16p_n^3 \right) V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\quad \times \tanh \sqrt{\frac{c}{2}}\left( X-\frac{1+52p_n +\lambda (3+48p_n )(1+4p_n )}{6}V^{\prime }cT\right) .\nonumber \\ \end{aligned}$$

(40)

If $p_n =0$, we have

$$\begin{aligned} \Delta x_n&= h_c +\left[ {-\frac{2(1+3\lambda )}{3V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\times \tanh \sqrt{\frac{c}{2}}\left( X-\frac{1+3\lambda }{6}V^{\prime }cT\right) . \end{aligned}$$

(41)

If $p_n =0.5$, we have

$$\begin{aligned} \Delta x_n&= h_c +\left[ {-\frac{6(1+3\lambda )}{V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\times \tanh \sqrt{\frac{c}{2}}\left[ {X-\frac{9(1+3\lambda )}{2}V^{\prime }cT} \right] . \end{aligned}$$

(42)

Case 2 $\hbox {Lg}_{n,n+1} \in \left[ 0.5\hbox {Lg}_{\max } ,\hbox {Lg}_{\max } \right]$

Similarly, Eq. (7) can be rewritten as follows

$$\begin{aligned}&\Delta x(t+2\tau )=\Delta x(t+\tau )+\tau \left\{ V\left[ (2p_{n+1} -1)\right. \right. \nonumber \\&\quad \left. \times \Delta x_{n+1,n+3} (t)+2(1-p_{n+1} )\Delta x_{n+1,n+4} (t)\right] \nonumber \\&\quad \left. -\,V\left[ (2p_n {-}1)\Delta x_{n,n\!+\!2} (t)+2(1{-}p_n )\Delta x_{n,n+3} (t)\right] \right\} \nonumber \\&\quad +\,\,\lambda \tau \left\{ \left[ (2p_{n+1} -1)\left[ \Delta x_{n+1,n+3} (t+\tau )\right. \right. \right. \nonumber \\&\quad \left. -\,\Delta x_{n+1,n+3} (t)\right] +2(1{-}p_{n+1} )\left[ \Delta x_{n+1,n+4} (t+\tau )\right. \nonumber \\&\quad \left. \left. -\,\Delta x_{n+1,n+4} (t)\right] \right] {-}[(2p_n {-}1)[\Delta x_{n,n+2} (t+\tau )\nonumber \\&\quad \left. -\,\Delta x_{n,n+2} (t)\right] +2(1{-}p_n )\left[ \Delta x_{n,n+3} (t+\tau )\right. \nonumber \\&\quad \left. \left. \left. -\,\,\Delta x_{n,n+3} (t)\right] \right] \right\} . \end{aligned}$$

(43)

Substituting Eq. (28) into Eq. (43) and applying the Taylor expansions to the fifth order of $\varepsilon$, we have

$$\begin{aligned}&\varepsilon ^{2}\gamma _1 \partial _X R+\varepsilon ^{3}\gamma _2 \partial _X^2 R+\varepsilon ^{4}\left( \gamma _3 \partial _T R+\gamma _4 \partial _X^3 R\right. \nonumber \\&\left. +\,\gamma _5 \partial _X R^{3}\right) \!+\!\varepsilon ^{5}\left( \gamma _6 \partial _X \partial _T R\!+\!\gamma _7 \partial _X^4 R\!+\!\gamma _8 \partial _X^2 R^{3}\right) =0\nonumber \\ \end{aligned}$$

(44)

The coefficients $\gamma _i (i=1,2,\ldots ,8)$ are given in the Table 2.

Table 2 The coefficients $\gamma _i$ of the proposed model

By taking $b=V^{\prime }(4-2p_n )$ , the second-order term of $\varepsilon$ is eliminated from Eq. (44) and near the critical point $(\alpha _c ,h_c )$. The neighborhood of the critical point $\tau _c$ is considered as follows [27–36]

$$\begin{aligned} \frac{\tau }{\tau _c }=1+\varepsilon ^{2} \end{aligned}$$

(45)

where $\tau _c =\frac{7-5p_n }{2(3V^{\prime }-2\lambda )(2-p_n )^{2}}$. And let

$$\begin{aligned}&\partial _X \partial _T R=\frac{23-19p_n +\lambda (42-30p_n )(2-p_n )}{3}\nonumber \\&\quad \times V^{\prime }\partial _X^4 R\!+\!\frac{1}{3}V^{\prime \prime \prime }\left[ \left( 1\!+\!4(1-p_n )^{3}\right) \partial _X^2 R^{3}\!+\!O(\varepsilon ).\right. \nonumber \\ \end{aligned}$$

(46)

Then Eq. (44) becomes

$$\begin{aligned}&\partial _T R-\frac{23-19p_n +\lambda (42-30p_n )(2-p_n )}{3}\nonumber \\&V^{\prime }\partial _X^3 R\!-\!\frac{1}{3}V^{\prime \prime \prime }\left[ \left( 1\!+4(1-p_n )^{3}\right) \partial _X R^{3}\!+\!O(\varepsilon )\!=\!0\right. .\nonumber \\ \end{aligned}$$

(47)

In order to get the standard mKdV equation, the following transformations are introduced [27–36]:

$$\begin{aligned} T^{\prime }=\psi _1 T,\;\;\;R=\sqrt{\psi _1 /\psi _2 }R^{\prime } \end{aligned}$$

(48)

where

$$\begin{aligned} \psi _1&= \frac{23-19p_n +\lambda (42-30p_n )(2-p_n )}{3}V^{\prime },\\ \psi _2&= -\frac{1}{3}V^{\prime \prime \prime }\left[ 1+4(1-p_n )^{3}\right] \end{aligned}$$

with $23-19p_n +\lambda (42-30p_n )(2-p_n )\ge 0,(0\le \lambda \le 1)$. Substituting (47) into (46), the regularized equation is referred

$$\begin{aligned} \partial _{T^{\prime }} R^{\prime }-\partial _X^3 R^{\prime } +\partial _X R^{\prime 3}+O(\varepsilon )=0 \end{aligned}$$

(49)

If $O(\varepsilon )$ is ignored, Eq. (48) is just the mKdV equation and the kink–antikink solution according to the general solution is derived:

$$\begin{aligned} R^{\prime }_0 (X,T^{\prime })=\sqrt{c}\tanh \sqrt{\frac{c}{2}}(X-cT^{\prime }) \end{aligned}$$

(50)

Suppose $R^{\prime }(X,T^{\prime })=R^{\prime }_0 (X,T^{\prime })+R^{\prime }_1 (X,T^{\prime })$ with the consideration of $O(\varepsilon )$ , the existence condition of $R^{\prime }_0 (X,T^{\prime })$is presented to obtain the propagation speed $c$ in Eq. (50) as [29]

$$\begin{aligned} (R^{\prime }_0 ,M[R^{\prime }_0 ])&= \int _{-\infty }^{+\infty } {\hbox {d}XR^{\prime }_0 (X,T^{\prime })M[R^{\prime }_0 (X,T^{\prime })]}\nonumber \\&= 0 \end{aligned}$$

(51)

where $M[R^{\prime }_0 ]=c_1 \partial _X^2 R^{\prime }+\frac{c_2 }{2}\partial _X^4 R^{\prime }-\frac{c_3 }{2}\partial _X^2 R^{\prime 3}$ and

$$\begin{aligned} c_1&= \frac{\lambda }{23-19p_n +\lambda (42-30p_n )(2-p_n )},\\ c_2&= \frac{1}{23-19p_n +\lambda (42-30p_n )(2-p_n )},\\ c_3&= 1. \end{aligned}$$

Using the integral method, we can obtain the propagation speed $c=\frac{2c_1 }{2c_2 +3c_3 }$ , and the amplitude $A$ of the kink–antikink solution is

$$\begin{aligned} A&= \left[ \frac{23-19p_n +\lambda (42-30p_n )(2-p_n )}{3}\right. \nonumber \\&\left. \times \left( \frac{\alpha _c }{\alpha }-1\right) c \right] ^{1/2} \end{aligned}$$

(52)

where $\alpha _c =\frac{1}{\tau _c }=\frac{2(3V^{\prime }-2\lambda )(2-p_n )^{2}}{7-5p_n }$. Thus, the following kink–antikink soliton solution of the mKdV equation is obtained by

$$\begin{aligned}&R(X,T)\nonumber \\&\quad =\left[ {-\frac{2[23-19p_n +\lambda (42-30p_n )(2-p_n )]}{3(1+4(1-p_n )^{3})V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\quad \quad \times \tanh \sqrt{\frac{c}{2}}\left( X\right. \\&\quad \quad \left. -\frac{23-19p_n +\lambda (42-30p_n )(2-p_n )}{3}V^{\prime }cT\right) .\nonumber \end{aligned}$$

(53)

Therefore, the kink–antikink soliton solution to the space headway is

$$\begin{aligned}&\Delta x_n =h_c\nonumber \\&\quad +\,\left[ {\!-\!\frac{46-38p_n \!+\!2\lambda (42-30p_n )(2-p_n )]}{3[1\!+\!4(1\!-\!p_n )^{3}]V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\quad \times \,\tanh \sqrt{\frac{c}{2}}\left( X\right. \\&\quad \left. -\,\frac{23-19p_n +\lambda (42-30p_n )(2-p_n )}{3}V^{\prime }cT\right) .\nonumber \end{aligned}$$

(54)

If $p_n =0.5$ , we have

$$\begin{aligned} \Delta x_n&= h_c +\left[ {-\frac{6(1+3\lambda )}{V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\times \tanh \sqrt{\frac{c}{2}}\left( X-\frac{9(1+3\lambda )}{2}V^{\prime }cT\right) . \end{aligned}$$

(55)

If $p_n =1$ , we have

$$\begin{aligned} \Delta x_n&= h_c +\left[ {-\frac{8(1+3\lambda )}{3V^{\prime \prime \prime }}V^{\prime }c} \right] ^{1/2}\nonumber \\&\times \tanh \sqrt{\frac{c}{2}}\left( X-\frac{2(1+3\lambda )}{3}V^{\prime }cT\right) . \end{aligned}$$

(56)

Remark 3

Through the nonlinear analysis, the mKdV equation of the proposed model is derived, which represents the kink wave under the unstable condition. And the kink solution represents the coexisting phase which includes both freely moving phase and jamming phase, and the headways of the two phases are given by $\Delta x_n =h_c -A$ and $\Delta x_n =h_c +A$, respectively.

5 Numerical experiments

Based on the foregoing theoretical analyses, numerical experiments are carried out to verify the proposed model described by Eqs. (6) and (7) and demonstrate the dynamic performance. Suppose that there are $N$ vehicles distributed homogeneously on a road under a periodic boundary condition and the lateral gap is a constant for all vehicles. The initial conditions are set as follows [18, 25]:

$$\begin{aligned}&\Delta x_{n,n+1} (t)\left| {_{t=0} } \right. =\Delta x_{n,n+1} (t)\left| {_{t=1}} \right. \nonumber \\&\qquad \quad =4.0 \hbox { for } n\ne 0.5N \hbox { and } n\ne 0.5N+1 \nonumber \\&\Delta x_{n,n+1} (t)\left| {_{t=0} } \right. =\Delta x_{n,n+1} (t)\left| {_{t=1}} \right. \nonumber \\&\qquad \quad =4.0-0.5 \hbox { for } n=0.5N \nonumber \\&\Delta x_{n,n+1} (t)\left| {_{t=0} } \right. =\Delta x_{n,n+1} (t)\left| {_{t=1}} \right. \nonumber \\&\qquad \quad =4.0+0.5 \hbox { for } n=0.5N+1 \end{aligned}$$

(57)

And to calculate the initial values of $\Delta x_{n,n+2} (t)$ and $\Delta x_{n,n+3} (t)$ , we define that

$$\begin{aligned} \Delta x_{n,n+2} (t)&\equiv \Delta x_{n,n+1} (t)+\Delta x_{n+1,n+2} (t),\Delta x_{n,n+3} (t)\\&\equiv \Delta x_{n,n+1} (t)+\Delta x_{n+1,n+2} (t)\\&+\Delta x_{n+2,n+3} (t) \end{aligned}$$

Moreover, the total number of vehicles $N=100$ and the related parameters are chosen as $v_{\max } =2\hbox {m/s,}\;h_c =4m$ and $\alpha =1/\tau =2\hbox {s}^{-1}$ [18, 25].

Figure 4 shows the space headway evolution after $10^{4}$ time steps and the corresponding profile at the time step $t=10^{4}$ with parameter $\lambda =0.02$. The curves in Fig. 4 are the profiles of corresponding three-dimensional diagrams at the time step $t=10^{4}$.

Fig. 4

Space headway evolution after $10^{4 }$ time steps and the profile at $t=10^{4}$ with $\lambda =0.02$ , where a, c, e, g, i are the outputs from the one-sided lateral gap condition while b, d, f, h, j are the outputs from the two-sided lateral gaps condition with $p_n =0,0.02,0.1,0.2,1.0$ , respectively

In Fig. 4, the parameter $p_n$ is set as 0, 0.02, 0.1, 0.2 and 1.0. The subfigures on the left-hand side of Fig. 4, i.e.: Fig. 4a, c, e, g, i, are the simulation results based on the NLBCF model in [25]. The subfigures on the right-hand side of Fig. 4, i.e.: Fig. 4b, d, f, h, j, are the simulation results based on the proposed model considering two-sided lateral gaps. The comparisons are mainly to demonstrate the capability of perturbation rejection in the vehicular traffic flow. By comparing the results under one-sided lateral gap and two-sided lateral gaps conditions, the main findings are summarized as follows:

• (i) Under the one-sided lateral gap condition, as shown in Fig. 4a, c, e, the stop-and-go traffic appears with parameter $p_n =0,0.02,0.1$, while the stop-and-go traffic disappears with parameter $p_n =0.1$ under the two-sided lateral gaps condition as shown in Fig. 4b, d, f. This accounts for the condition that when small perturbations (57) are put into the uniform flow, they will be amplified with time and the uniform flow will eventually evolve toward a heterogeneous flow. The jams in Fig. 4a, b are the most serious in NLBCF model [25] and the proposed model, where there are no effects of lateral gaps. And when the effects of lateral gaps are considered, the stability of traffic flow can be improved. As shown in Fig. 4c, e, d, f, the amplitudes of perturbations decrease with the increase of $p_n$ , and the traffic flow can evolve toward a homogeneous flow in NLBCF model with $p_n =0.2$[25] and in the proposed model with $p_n =0.1$ under the condition of $\lambda =0.02$.

• (ii) Figure 4f–j indicate that the effects of two-sided lateral gaps can improve the stability of traffic flow. The introduction of effects of the two-sided lateral gaps is necessary traffic flow.

• (iii) According to Fig. 4e, f, the dynamic performance of the proposed model is better than that of NLBCF model [25]. That is to say traffic flow described by the proposed model can overcome the effects of small perturbations such as the sudden acceleration or deceleration with smaller value of parameter $p_n$ than that of NLBCF model. This is because the NLBCF model only considers the effect of one-sided lateral gap while the proposed model considers the effect of two-sided lateral gaps, which implies that the rich information of leading and lateral vehicles can enhance the performance of car-following model.

• (iv) The density waves in Fig. 4a–j always propagate backwards. This has been observed in reality and reported in relevant studies [9–26].

6 Conclusions

Considering the effects of two-sided lateral gaps of the following vehicle in a road without lane discipline, a new car-following model is proposed. Theoretical analysis proves that the FVD model and the one-sided lateral gap non-lane-based NLBCF model are special cases of the proposed model. Compared with NLBCF model, the stability region is enlarged through the linear stability analysis using the perturbation method and the corresponding mKdV equation of the proposed model is derived through nonlinear analysis using the reductive perturbation method to describe the density wave propagation. Additionally, results from simulation-based numerical experiments show that the proposed mode is able to more rapidly dissipate the effect of a perturbation such as a sudden acceleration or deceleration of a leading vehicle.

Note that the proposed model does not consider the scenario that the leading vehicle in the middle of a road has lateral gap with respect to the following vehicle. For some specifically cases, this gap may impact the following vehicle behavior. This leads to one of the future research directions. In addition, the results of this study illustrate the effects of lateral gaps on the stability of traffic flow. These findings motivate us to study the impacts of lateral gaps on the energy consumption of vehicular flow in non-lane-discipline road system in the future.