1 Introduction

Potential applications of robotic systems have motivated the researchers to design new models and develop robust controllers in order to improve their reliabilities. Among the robotic systems, unmanned aerial vehicles (UAV) have received great attention in the last decade and many applications are reported, including traffic monitoring, search and rescue, fire monitoring [16, 38]. The researches generally involve designing reliable controllers, developing efficient actuators and using the precise sensors. The sensory system for these vehicles generally includes the global positioning systems (GPSs) and the inertial measurement units (IMUs). This sensory unit provides attitude and angular velocity information, reliable for a control process. However, it is difficult to estimate an accurate linear velocity information [22]. In addition, the GPSs provide only a course position information and are not useful in indoor environments.

Many researches have been conducted recently to provide locomotion and environmental information for autonomous UAVs, especially in GPS-denied workspaces. In this regard, simultaneous localization and mapping (SLAM) techniques are developed to build a map of the environment [26], and different sensory systems are utilized. In the recent years, vision sensor is considered as a reliable, lightweight and low-cost system, which in combination with an IMU system can provide useful translational velocity information and also can be effectively used in localization of a vehicle with respect to its environment. Many applications have been reported in using the vision system for UAVs including obstacle avoidance [34], pose estimation [25], SLAM [7], line tracking [23] and positioning [28].

Controlling the UAVs using visual data started from the late 1990s. Direct implementation of visual information in the feedback control is called visual servoing which is mainly classified into two approaches including position-based visual servoing (PBVS) and image-based visual servoing (IBVS). In the first method, 3D pose information of the target is reconstructed from visual data using estimation algorithms. Generally these algorithms require a priori information from the geometric model of the observed target. The application of this method on the aerial robots has been reported in several works including [4, 5, 11]. In the second approach, the controller is designed based on the dynamics of image features in the image plane. This approach is more attractive since it is robust against camera calibration errors and does not require 3D information of the image, and hence, it is computationally simple with respect to PBVS. However, this approach still requires the depth information of the image and needs more challenge in designing the controller.

Unlike the implementation of visual servo approaches on traditional manipulators, it is recommended to consider the dynamics of the whole system in designing an IBVS approach for UAVs [8]. This is a challenging problem since these vehicles are generally underactuated. In most of the available works, passivity properties of spherical image moments are exploited to design a dynamic IBVS controller for UAVs [6, 12, 14, 15]. However, spherical image features do not generally provide satisfactory behavior for the robot motion in vertical axis [27]. To overcome this conditioning problem, the authors have proposed a method in [18], which utilizes perspective image moments, and the controller is designed for their dynamics in a suitably oriented image plane. This approach is also followed and experimentally validated by the researchers in [9, 10, 36].

The other difficulty in designing an IBVS controller for the aerial vehicles is the lack of precise information of the linear velocity, which is an input for the image dynamics. Considering the unreliable linear velocity information obtained from an IMU system, optic flow of image features is used in [22] as a cue of the translational velocity and the dynamics of the system are expressed based on the dynamics of spherical optic flow. However, the approach does not consider the error in estimation of the optic flow from low-quality image information and it has the conditioning problem mentioned above. An observer-based method has been presented in [21], where the method considers a partial dynamics of the system and provides only a basin of attraction for it. A method using a nonlinear observer is also presented in [24], which assumes that the image depth is known. The full dynamic IBVS approach, presented in [1], assumes that a geometric model of the object is known in prior, from which the image depth information is not required. All of the mentioned controllers require the yaw angle of the UAV where the estimated value is generally unreliable.

In this paper, an IBVS approach is designed to control the translational motion of the quadrotor UAV, considering the full dynamics of the system. Image features are selected from appropriate combination of perspective image moments and reprojected on a suitably defined virtual image plane. These features provide efficient trajectories in both image and Cartesian space and also do not require a geometric model of the target. The proposed scheme utilizes a nonlinear observer to estimate the flow of image features as the linear velocity cue and only assumes the orientation and angular velocity available for feedback. The controller is robust with respect to parametric uncertainty of the translational dynamics associated with depth information of the image. Furthermore, using the robust integral of the sign of the error (RISE) method [35], the controller compensates for unmodeled dynamics and disturbances in the rotational dynamics. The approach exploits passivity properties of the image dynamics in the virtual image plane to avoid the use of the yaw information of the quadrotor. The designed force input for the translational dynamics is bounded which helps to keep the target points in the field of view of the camera. Some auxiliary variables are exploited to simplify the design procedure and the Lyapunov-based stability analysis guarantees the convergence of system errors to zero. Simulation results are provided to illustrate the effectiveness of the proposed approach. This work is an extension to the authors’ previous works on observer-based IBVS control of the quadrotor [17, 20] in which only the translation dynamics of the vehicle are considered.

The rest of the paper is organized as follows. Section 2 presents the kinematic and dynamic models of the quadrotor helicopter. In Sect. 3, the image features are introduced and their dynamics in the new image plane are presented. The proposed robust IBVS controller is given in Sect. 4. Simulation results are presented in Sect. 5. Finally, conclusions are given in Sect. 6.

2 Kinematics and dynamics of the robot

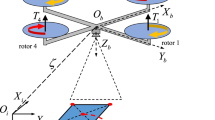
This section describes the kinematics and dynamics of the quadrotor helicopter. For this purpose, two coordinate frames are considered (Fig. 1). Inertial frame \({\mathcal {I}}=\left\{ O_i,X_i,Y_i,Z_i\right\} \) and body-fixed frame \({\mathcal {B}}=\left\{ O_b,X_b,Y_b,Z_b\right\} \) which is attached to the center of mass of the robot.

Fig. 1
figure 1

A quadrotor helicopter and coordinate frames

Full size image

Center of the frame \({\mathcal {B}}\) is located in position \(\varvec{\zeta }=\left[ x\;y\;z\right] ^{\top }\) with respect to the inertial frame and its attitude is given by the rotation matrix \({\mathbf {R}}:{\mathcal {B}}\rightarrow {\mathcal {I}}\). The rotation matrix depends on the three Euler angles \(\phi \), \(\theta \) and \(\psi \) denoting, respectively, the roll, pitch and yaw. The following property is satisfied for the rotation matrix:

Property 1

For any vector \({\mathbf {u}}\in \mathfrak {R}^3\) and the rotation matrix \({\mathbf {R}}\) one has

$$\begin{aligned} {\mathbf {R}}\mathbf{sk }\left( {\mathbf {u}}\right) {\mathbf {R}}^{\top }=\mathbf{sk }\left( {\mathbf {Ru}}\right) . \end{aligned}$$

The notation \(\mathbf{sk }\left( \cdot \right) \) is the skew-symmetric matrix such that for any vectors \({\mathbf {u}}_1, {\mathbf {u}}_2\in \mathfrak {R}^3\), \(\mathbf{sk }\left( {\mathbf {u}}_1\right) {\mathbf {u}}_2={\mathbf {u}}_1\times {\mathbf {u}}_2\), where \(\times \) denotes the vector cross-product. A skew-symmetric matrix has the following property:

Property 2

For a given skew-symmetric matrix \(\varvec{\varLambda }_{n\times n}\) and a vector \({\mathbf {u}}\in \mathfrak {R}^n\), the relation \({\mathbf {u}}^{\top }\varvec{\varLambda }{\mathbf {u}}=0\) is satisfied.

The kinematics of the quadrotor can be expressed by [33]

$$\begin{aligned} \dot{\varvec{\zeta }}= & {} {\mathbf {RV}}\nonumber \\ \dot{{\mathbf {R}}}= & {} {\mathbf {R}}\mathbf{sk } \left( \varvec{\Omega }\right) . \end{aligned}$$
(1)

where \({\mathbf {V}}\in \mathfrak {R}^3\) and \(\varvec{\Omega }=\left[ \varOmega _1\; \varOmega _2\; \varOmega _3\right] ^{\top }\in \mathfrak {R}^3\) are, respectively, the linear and angular velocities of the quadrotor in the body-fixed frame. Also, the time derivatives of the Euler angles are given by

$$\begin{aligned} \left[ \begin{array}{lll} \dot{\phi }\\ \dot{\theta }\\ \dot{\psi } \end{array}\right] =\left[ \begin{array}{lll} 1 &{} s_\phi t_\theta &{} c_\phi t_\theta \\ 0 &{} c_\phi &{} -s_\phi \\ 0 &{} \frac{s_\phi }{c_\theta } &{} \frac{c_\phi }{c_\theta } \end{array}\right] \left[ \begin{array}{lll} \varOmega _1\\ \varOmega _2\\ \varOmega _3 \end{array}\right] \end{aligned}$$
(2)

where \(s_{\phi }\equiv \sin \left( \phi \right) \), \(c_a\equiv \cos \left( a\right) \) and \(t_\theta \equiv \tan \left( \theta \right) \).

On the other hand, the dynamics of a general 6DOF rigid body, with the mass of m and the constant symmetric inertia matrix \({\mathbf {J}}\in \mathfrak {R}^{3\times 3}\) around the center of mass, with respect to the frame \({\mathcal {B}}\), can be written as follows [14, 37]:

$$\begin{aligned}&\dot{{\mathbf {V}}}=-\varvec{\Omega } \times {\mathbf {V}}+{\mathbf {F}} \end{aligned}$$
(3)
$$\begin{aligned}&{\mathbf {J}}\dot{\varvec{\Omega }}=-\varvec{\Omega } \times {\mathbf {J}}\varvec{\Omega }+\varvec{{\varDelta }}+\varvec{\tau } \end{aligned}$$
(4)

where \({\mathbf {F}}\in \mathfrak {R}^3\) and \(\varvec{\tau }\in \mathfrak {R}^3\) are, respectively, the force and torque vectors in the frame \({\mathcal {B}}\), and \(\varvec{{\varDelta }}\) is the unmodeled dynamics and/or external disturbances. The inertia matrix is diagonal, i.e., \({\mathbf {J}}={\text {diag}}\left( J_{xx},J_{yy},J_{zz}\right) \), when \(O_b\) coincides with the body’s principal axis of inertia. The following assumption is considered for \(\varvec{{\varDelta }}\):

Assumption 1

The unknown time varying disturbance \(\varvec{{\varDelta }}\left( t\right) \) and its first two time derivatives are bounded, i.e., \(\varvec{{\varDelta }}\left( t\right) \), \(\dot{\varvec{{\varDelta }}}\left( t\right) \), \(\ddot{\varvec{{\varDelta }}}\left( t\right) \in \mathcal {L}_{\infty }\).

The quadrotor actuators generate a single actuation of trust force \(U_1\), and full actuation of the torque \(\varvec{\tau }=\left[ U_2\;U_3\;U_4\right] ^{\top }\), which demonstrates underactuated dynamic of the system. The force input \({\mathbf {F}}\) in (3) is as follows:

$$\begin{aligned} {\mathbf {F}}=-\frac{1}{m}U_1{\mathbf {E}}_3+g {\mathbf {R}}^{\top }{\mathbf {e}}_3 \end{aligned}$$
(5)

where \({\mathbf {E}}_3={\mathbf {e}}_3=\left[ 0\; 0\; 1\right] ^{\top }\) are the unit vectors in the body-fixed frame and the inertial frame, respectively. The input \({\mathbf {F}}\) is an intermediary input for the translational dynamics (Eq. 3), and to control these dynamics it is also necessary to control the tilting of the robot through the rotational dynamics (Eq. 4). However, it is clear from (5) that the translational dynamics do not depend on the yaw angle. Therefore, the yaw dynamic can be controlled independently.

3 Image features and their dynamics

Spherical and perspective projections are usually used for vision-based control of aerial vehicles. Based on experimental results reported in [6], image features obtained from perspective image moments provide better results comparing to spherical image moments, but stability problem is not solved for the case of perspective image moments. To guarantee the stability of the system, the authors have proposed a method in [18] in which, using only the roll and pitch angles of the robot (through the rotation matrix \({\mathbf {R}}_{\phi \theta }\) which specifies a rotation, respectively, about \(X_i\) and \(Y_i\) axes and depends on \(\phi \) and \(\theta \) angles), perspective image points are suitably reprojected on an image plane parallel to the target, called virtual plane. Based on the selected image features in the new image plane, it is possible to design a stable full dynamic image-based controller for the underactuated UAVs while preserving a good behavior of the robot in Cartesian space. This paper uses the same imaging method and exploits the image features presented in [19], which are obtained from a planar object as follows:

$$\begin{aligned} q_x=q_{z}\frac{^{\mathcal {V}}u_g}{\lambda },\quad q_y=q_z\frac{^{\mathcal {V}}n_g}{\lambda },\quad q_z=\sqrt{\frac{a^*}{a}} \end{aligned}$$
(6)

where \(^{\mathcal {V}}u_g\) and \(^{\mathcal {V}}n_g\) are the coordinates of the center of gravity of the target in the oriented image plane, \(\lambda \) is the focal length of the camera, a is defined as \(a={}^{\mathcal {V}}\mu _{20}+{}^{\mathcal {V}}\mu _{02}\), where \({}^{\mathcal {V}}\mu _{ij}\) is the centered moment of the target in the virtual image plane, and \(a^*\) is the value of a in the desired position. Knowing that \(z\sqrt{a}=\frac{1}{\rho }\sqrt{a^{*}}\), where \(\rho \) is the inverse of the normal distance of the camera from the target in the desired position [32], the dynamics of the features in the virtual image plane can be written as follows [19]:

$$\begin{aligned} \dot{{\mathbf {q}}}=-\mathbf{sk } \left( \dot{\bar{\varvec{\psi }}}\right) {\mathbf {q}}-\rho {\mathbf {v}} \end{aligned}$$
(7)

where \({\mathbf {q}}=\left[ q_x\;q_y\;q_z\right] ^{\top }\) is the vector of image features defined in (6), \(\dot{\bar{\varvec{\psi }}}=\left[ 0\;0\;\dot{\psi }\right] ^{\top }\) and \({\mathbf {v}}={\mathbf {R}}_{\phi \theta }{\mathbf {V}}\) is the linear velocity of the camera (or of the robot if their frames are coincident) in the virtual frame (a frame attached to \(\mathcal {B}\) and rotated by \({\mathbf {R}}_{\phi \theta }\)). In some works (e.g., [27] and [1]), the value of \(\rho \) is assumed to be available. However, to know this parameter, a measurement of the area of the object or depth of the image in the desired position is required which are not available in most applications. An adaptive scheme is presented in this paper in order to compensate for the unknown value of this parameter. In addition, the dynamics (7) possess the passivity properties mentioned in [14]. These properties will be exploited in the next section to design an IBVS controller without using the yaw information of the UAV.

4 Image-based visual servo controller

In this section, a robust IBVS controller is presented for the translational motion of the quadrotor. The controller is robust with respect to unknown depth of the image and external disturbances. Furthermore, the proposed approach requires neither the yaw angle of the robot nor the linear velocity measurements. The control objective is to design the thrust \(U_1\) and the torque \(\varvec{\tau }\) inputs in order to move the camera, attached to the quadrotor, to match the observed image features with those obtained from a stationary object in a desired position. In order to stabilize the yaw dynamic of the quadrotor, the controller tracks a desired angular velocity around the vertical axis of the vehicle \(Z_b\).

In the design procedure, it is assumed that the camera frame (attached to its center of projection) is coincident with the quadrotor body-fixed frame, \({\mathcal {B}}\). This assumption can be easily released by using the transformation between the frames. In order to preserve the passivity properties of the image dynamics, the desired image features are considered as follows:

$$\begin{aligned} {\mathbf {q}}_d= \left[ q_{dx}\;q_{dy}\;q_{dz} \right] ^{\top }=\left[ 0\;0\;q_{dz} \right] ^{\top }. \end{aligned}$$

Selecting these desired features is equivalent to have the barycenter of the target at the center of image which is common in vision-based control of UAVs. [1, 6, 14]. Now, the image error for the translational motion control of the robot is defined as follows:

$$\begin{aligned} \varvec{\delta }={\mathbf {q}}-{\mathbf {q}}_d . \end{aligned}$$

Using (7), the dynamics of the image error vector will be

$$\begin{aligned} \dot{\varvec{\delta }}=-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\delta }-\rho {\mathbf {v}}. \end{aligned}$$
(8)

Now, let define the scaled linear velocity as follows:

$$\begin{aligned} \varvec{\nu }=\rho {\mathbf {v}}. \end{aligned}$$
(9)

which is the translational optic flow in the virtual image plane and can be computed through (8) by measuring optic flow of image features \(\dot{\varvec{\delta }}\) and compensating the rotational term \(\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \). Several methods of optic flow computation is well investigated in the literature [31, 41]. However, the aim of this paper is to estimate it through a nonlinear observer and consider the error of the estimation in the stability analysis.

Considering the definition in (9) and using the translational dynamics of the robot (3), expressed in the virtual frame, equation (8) and the dynamics of \(\varvec{\nu }\) can be written as [20]

$$\begin{aligned} \dot{\varvec{\delta }}= & {} -\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\delta }-\varvec{\nu } \end{aligned}$$
(10)
$$\begin{aligned} \dot{\varvec{\nu }}= & {} -\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\nu }-\rho {\mathbf {f}}+\rho g{\mathbf {e}}_3 \end{aligned}$$
(11)

where \({\mathbf {f}}\) is the input for these dynamics (the translational dynamics of \(\varvec{\delta }\)), which is defined as

$$\begin{aligned} {\mathbf {f}}=\frac{1}{m}{\mathbf {R}}_{\phi \theta }U_1{\mathbf {E}}_3. \end{aligned}$$
(12)

Now, inspired from the method in [2, 3], the new variables are defined as follows:

$$\begin{aligned} \varvec{\xi }= & {} \hat{\varvec{\delta }}-\varvec{\delta }-\varvec{\varsigma }_1 \end{aligned}$$
(13)
$$\begin{aligned} {\mathbf {r}}= & {} \varvec{\nu }-\hat{\varvec{\nu }}-\varvec{\varsigma }_2 \end{aligned}$$
(14)

where \(\hat{\varvec{\delta }}\) and \(\hat{\varvec{\nu }}\) are, respectively, the estimates of \(\varvec{\delta }\) and \(\varvec{\nu }\) which, together with the auxiliary variables \(\varvec{\varsigma }_1\) and \(\varvec{\varsigma }_2\), are defined as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\hat{\varvec{\delta }}}=-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \hat{\varvec{\delta }}-\hat{\varvec{\nu }}\\ \dot{\hat{\varvec{\nu }}}=-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \hat{\varvec{\nu }}+\hat{\rho }k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) -\hat{\rho }k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) \\ \quad +\,l_1\varvec{\varsigma }_1+l_2\varvec{\varsigma }_2\\ \dot{\varvec{\varsigma }}_1=-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\varsigma }_1+\varvec{\varsigma }_2\\ \dot{\varvec{\varsigma }}_2=-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\varsigma }_2-l_1\varvec{\varsigma }_1-l_2\varvec{\varsigma }_2\\ \quad +\,2k_1\varvec{\xi }+k_2\varvec{\vartheta }-\varvec{\chi }\\ \dot{\hat{\rho }}={\text {Proj}}\left( \mu \right) \end{array} \right. \end{aligned}$$
(15)

in which \(k_p\), \(k_d\), \(k_1\), \(k_2\), \(l_1\) and \(l_2\) are positive constants, \(\hat{\rho }\) is the estimate of \(\rho \), the variable \(\varvec{\chi }\) is an additional input vector to be defined later, and the operator \({\text {Proj}}\left( \cdot \right) \) is a continuous projection operator, similar to what is defined in [19], which is used to ensure \(\hat{\rho }\) to be strictly positive. Also, in (15)

$$\begin{aligned} \mu&= \gamma \left( {\mathbf {r}} -\varvec{\vartheta }\right) ^{\top }\left( k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) -k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) \right. \nonumber \\&\left. \quad -\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3\right) , \end{aligned}$$
(16)

and

$$\begin{aligned} {\mathbf {h}}\left( {\mathbf {u}}\right) =\frac{{\mathbf {u}}}{\sqrt{1+{\mathbf {u}}^{\top }{\mathbf {u}}}}. \end{aligned}$$
(17)

Furthermore, the auxiliary variable \(\varvec{\vartheta }\) is given by

$$\begin{aligned} \dot{\varvec{\vartheta }}=-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\vartheta }-k_1\varvec{\xi }-k_2\varvec{\vartheta }. \end{aligned}$$
(18)

Now, using (10), (11) and (15), the dynamics of \(\varvec{\xi }\) and \({\mathbf {r}}\) can be written as

$$\begin{aligned} \dot{\varvec{\xi }}= & {} -\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) \varvec{\xi }+{\mathbf {r}} \end{aligned}$$
(19)
$$\begin{aligned} \dot{{\mathbf {r}}}= & {} -\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) {\mathbf {r}}-\rho {\mathbf {f}}+\rho g{\mathbf {e}}_3-\hat{\rho }k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) +\hat{\rho }k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) \nonumber \\&-2k_1\varvec{\xi }-k_2\varvec{\vartheta }+\varvec{\chi }. \end{aligned}$$
(20)

Since the dynamics of the quadrotor UAV is underactuated, the input \({\mathbf {f}}\) cannot provide full actuation for the translational dynamics of the system. In fact, this is an intermediary input for the translational dynamics, and hence, it is also necessary to consider the rotational dynamics in order to control the translational degrees of freedom. Therefore, in the sequel, first a desired input \({\mathbf {f}}\) will be designed for the translational dynamics and then a controller for the rotational dynamics will be introduced to track the desired \({\mathbf {f}}\).

The desired value of \({\mathbf {f}}\) is proposed as follows:

$$\begin{aligned} {\mathbf {f}}_d=g{\mathbf {e}}_3-k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) +k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) . \end{aligned}$$
(21)

Now, using (12) and knowing the fact that for the Euclidean norm \(\left\| \cdot \right\| \), the relation \(\left\| {\mathbf {R}}_{\phi \theta }{\mathbf {E}}_3\right\| = 1\) is satisfied, the trust input \(U_1\) can be extracted as follows:

$$\begin{aligned} U_1=m\left\| {\mathbf {f}}_d\right\| . \end{aligned}$$
(22)

Therefore, from (12), one has

$$\begin{aligned} {\mathbf {f}}_d=\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }\right) _d{\mathbf {E}}_3 \end{aligned}$$
(23)

in which \(\left( {\mathbf {R}}_{\phi \theta }\right) _d\) is the desired orientation and should be tracked to reach the desired position. Using (23), the desired roll and pitch angles of the robot can be computed for a given \({\mathbf {f}}_d=\left[ f_{xd}\;f_{yd}\;f_{zd}\right] ^{\top }\) as follows:

$$\begin{aligned} \phi _d=\tan ^{-1}\left( \frac{-f_{yd}}{\sqrt{f_{xd}^2+f_{zd}^2}}\right) , \qquad \theta _d=\tan ^{-1}\left( \frac{f_{xd}}{f_{zd}}\right) \end{aligned}$$
(24)

provided that \(U_1\ne 0\). If \(f_{zd}\) satisfies

$$\begin{aligned} f_{zd}> 0 \end{aligned}$$
(25)

then, according to (22) and (24), \(U_1\) is always positive and the desired angles \(\phi _d\) and \(\theta _d\) are inside the open interval \(\left( -\frac{\pi }{2},\frac{\pi }{2}\right) \). It can be discovered from (21) that the condition (25) is satisfied if

$$\begin{aligned} \left( k_p+k_d\right) <g. \end{aligned}$$
(26)

Remark 1

It is clear that the bounded nature of (21), as the primary role, guarantees the extraction of \(\phi _d\) and \(\theta _d\). It is also worth noting that the bounded input for the translational dynamics limits the tilting of the aircraft which helps to keep the object in the field of view of the camera [13].

The error between \({\mathbf {f}}\) and \({\mathbf {f}}_d\) can be considered as

$$\begin{aligned} {\mathbf {f}}-{\mathbf {f}}_d=\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3. \end{aligned}$$
(27)

At this point, the auxiliary variable \(\varvec{\chi }\) is defined as

$$\begin{aligned} \varvec{\chi }=\hat{\rho }\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3, \end{aligned}$$

and (20) and (21) are used to rewrite the dynamics of \({\mathbf {r}}\) as follows:

$$\begin{aligned} \dot{{\mathbf {r}}}=&-\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}}\right) {\mathbf {r}}-2k_1\varvec{\xi }-k_2\varvec{\vartheta } +\tilde{\rho }\left[ k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) -k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) \right. \nonumber \\&\left. -\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3\right] \end{aligned}$$
(28)

with \(\tilde{\rho }=\rho -\hat{\rho }\).

The right-hand side of (27) can be written as

$$\begin{aligned} \frac{U_1}{m}\left( \tilde{{\mathbf {R}}}_{\phi \theta }-{\mathbf {I}}\right) \left( {\mathbf {R}}_{\phi \theta }\right) _d{\mathbf {E}}_3 \end{aligned}$$

in which \(\tilde{{\mathbf {R}}}_{\phi \theta }={\mathbf {R}}_{\phi \theta }\left( {\mathbf {R}}_{\phi \theta }\right) ^{\top }_d\) and \({\mathbf {I}}\) is a \(3\times 3\) indentity matrix. In fact, \({\left( \tilde{{\mathbf {R}}}_{\phi \theta }-{\mathbf {I}}\right) }\) reflects the attitude error which has to be minimized through the rotational dynamics controller, in order to reach the desired position. To compensate for this error, the unit-quaternion representation of attitude is used in this paper.

The unit-quaternion \({\mathbf {Q}}_0=\left[ \eta _0\;\varvec{\eta }^{\top }\right] ^{\top }\) is a four-element vector, composed of a scalar \(\eta _0\in \mathfrak {R}\) and a vector \(\varvec{\eta }\in \mathfrak {R}^3\), satisfying the unity constraint: \(\eta _0^2+\varvec{\eta }^{\top }\varvec{\eta }=1\) [29]. In this view, the rotation matrix \({\mathbf {R}}\) defines a rotation \(\alpha \) around the unit vector \({{\mathbf {u}}}\in \mathfrak {R}^3\) which can be described by a unit-quaternion \(\bar{{\mathbf {Q}}}=\left[ \bar{\eta }_0\;\bar{\varvec{\eta }}^{\top }\right] ^{\top }\) such that \(\bar{\eta }_0=\cos \left( \alpha /2\right) \), and \(\bar{\varvec{\eta }}={{\mathbf {u}}}\sin \left( \alpha /2\right) \). The relation can be obtained as: \({\mathbf {R}}=\left( \bar{\eta }_0^2-\bar{\varvec{\eta }}^{\top }\bar{\varvec{\eta }}\right) {\mathbf {I}}+2\bar{\varvec{\eta }}\bar{\varvec{\eta }}^{\top }+2\bar{\eta }_0 \mathbf{sk }\left( \bar{\varvec{\eta }}\right) \). Multiplication between two unit-quaternions, \({\mathbf {Q}}_1=\left[ \eta _{0_1}\;\varvec{\eta }_1^{\top }\right] ^{\top }\) and \({\mathbf {Q}}_2=\left[ \eta _{0_2}\;\varvec{\eta }_2^{\top }\right] ^{\top }\) is defined as:

$$\begin{aligned} {\mathbf {Q}}_1\otimes {\mathbf {Q}}_2=&\left[ \left( \eta _{0_1}\eta _{0_2}-\varvec{\eta }_1^{\top }\varvec{\eta }_2\right) ,\;\right. \\&\left. \quad \left( \eta _{0_1}\varvec{\eta }_2+\eta _{0_2}\varvec{\eta }_1+\mathbf{sk }\left( \varvec{\eta }_1\right) \varvec{\eta }_2\right) ^{\top }\right] ^{\top }. \end{aligned}$$

Also, the inverse of a unit-quaternion is defined by \({\mathbf {Q}}_0^{-1}=\left[ \eta _0\;-\varvec{\eta }^{\top }\right] ^{\top }\).

With the above definition, \(\tilde{{\mathbf {R}}}_{\phi \theta }\) can be described by a unit-quaternion, \(\tilde{{\mathbf {Q}}}=\left[ \tilde{\eta }_0\;\tilde{\varvec{\eta }}^{\top }\right] ^{\top }\), defined by \({\mathbf {Q}}\otimes {\mathbf {Q}}_d^{-1}\) which are, respectively, related to \({\mathbf {R}}_{\phi \theta }\) and \(\left( {\mathbf {R}}_{\phi \theta }\right) _d\). These quaternions can be obtained through the equivalent Euler angles, where for \({\mathbf {Q}}_d\) the relation is as follows:

$$\begin{aligned} {\mathbf {Q}}_d=\left( \begin{array}{c} \cos \left( \phi _d/2\right) \cos \left( \theta _d/2\right) \\ \sin \left( \phi _d/2\right) \cos \left( \theta _d/2\right) \\ \cos \left( \phi _d/2\right) \sin \left( \theta _d/2\right) \\ -\sin \left( \phi _d/2\right) \sin \left( \theta _d/2\right) \\ \end{array} \right) . \end{aligned}$$

Based on the above development, the attitude control objective is achieved when \(\tilde{\varvec{\eta }}\) converges to zero, which is identical to coincidence of \({\mathbf {Q}}\) with \({\mathbf {Q}}_d\). One can easily conclude that when \(\tilde{\varvec{\eta }}\) is zero, \(\tilde{\eta }_0\) will be \(\pm 1\) where both of these values represent the same physical orientation. Therefore, to design the controller, the kinematics of \(\tilde{{\mathbf {Q}}}\) will be required which can be written as [40]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\tilde{\varvec{\eta }}}=\frac{1}{2}\left( \tilde{\eta }_0{\mathbf {I}}+\mathbf{sk }\left( \tilde{\varvec{\eta }}\right) \right) \tilde{\varvec{\varOmega }}\\ \dot{\tilde{\eta }}_0=-\frac{1}{2}\tilde{\varvec{\eta }}^{\top }\tilde{\varvec{\varOmega }} \end{array} \right. \end{aligned}$$
(29)

where \(\tilde{\varvec{\varOmega }}\) is the angular velocity error which is defined as follows:

$$\begin{aligned} \tilde{\varvec{\varOmega }}=\left( {\mathbf {R}}_{\phi \theta }\right) _d\left( \varvec{\varOmega }_{\phi \theta }-\left( \varvec{\varOmega }_{\phi \theta }\right) _d\right) \end{aligned}$$
(30)

in which \(\varvec{\varOmega }_{\phi \theta }\) and \(\left( \varvec{\varOmega }_{\phi \theta }\right) _d\) are, respectively, the angular velocity and the desired angular velocity corresponding to the rotation matrices \({\mathbf {R}}_{\phi \theta }\) and \(\left( {\mathbf {R}}_{\phi \theta }\right) _d\). The velocity \(\varvec{\varOmega }_{\phi \theta }\) can be computed from the angular velocity of the quadrotor (available from gyroscopes), through the following relation:

$$\begin{aligned} \varvec{\varOmega }_{\phi \theta }=\varvec{\varOmega }-{\mathbf {R}}^{\top }_{\phi \theta }\dot{\bar{\varvec{\psi }}}. \end{aligned}$$
(31)

The desired angular velocity for the first two elements of \(\left( \varvec{\varOmega }_{\phi \theta }\right) _d=\left[ \left( \varOmega _{\phi \theta }\right) _{d1}\;\left( \varOmega _{\phi \theta }\right) _{d2}\;\left( \varOmega _{\phi \theta }\right) _{d3}\right] ^{\top }\) can be obtained by computing the time derivative of \({\mathbf {f}}_d\). To obtain a full desired angular velocity information, it is assumed that a bounded value of \(\left( \varOmega _{\phi \theta }\right) _{d3}\) is already defined. Furthermore, the following assumption is considered:

Assumption 2

Following the assumption considered in [39], it is assumed that the first three time derivatives of \(\left( \varOmega _{\phi \theta }\right) _{di}\), for \(i=1,2,3\), are bounded.

Now, using (1), (4) and Property 1, the time derivative of \(\tilde{\varvec{\varOmega }}\) can be written as

$$\begin{aligned} \dot{\tilde{\varvec{\varOmega }}}={\mathbf {N}}+{\mathbf {B}}\varvec{\tau }+\left( {\mathbf {R}}_{\phi \theta }\right) _d{\mathbf {J}}^{-1}\varvec{{\varDelta }}-\left( {\mathbf {R}}_{\phi \theta }\right) _d\left( \dot{\varvec{\varOmega }}_{\phi \theta }\right) _d \end{aligned}$$
(32)

where the vector function \({\mathbf {N}}\) and the matrix \({\mathbf {B}}\) are given by

$$\begin{aligned}&{\mathbf {N}}=\mathbf{sk }\left( \left( {\mathbf {R}}_{\phi \theta }\right) _d\left( \varvec{\varOmega }_{\phi \theta }\right) _d\right) \tilde{\varvec{\varOmega }}\\&\qquad +\left( {\mathbf {R}}_{\phi \theta }\right) _d\left( -{\mathbf {J}}^{-1}\varvec{\varOmega \times {\mathbf {J}}\varvec{\varOmega }}-\dot{{\mathbf {R}}}_{\phi \theta }^{\top }\dot{\bar{\varvec{\psi }}}-{\mathbf {R}}_{\phi \theta }^{\top }\varvec{\varGamma }_1\right) \\&{\mathbf {B}}=\left( {\mathbf {R}}_{\phi \theta }\right) _d\left( {\mathbf {J}}^{-1}-{\mathbf {R}}_{\phi \theta }^{\top }\varvec{\varGamma }_2\right) \end{aligned}$$

with \(\varvec{\varGamma }_1\) and \(\varvec{\varGamma }_2\) are defined in the “Appendix 1.” It should be mentioned that, the vector \({\mathbf {N}}\) depends on available signals, and the matrix \({\mathbf {B}}\) is invertible. It is also worth mentioning that, for \({\mathbf {T}}\triangleq \frac{1}{2}\left( \tilde{\eta }_0{\mathbf {I}}+\mathbf{sk }\left( \tilde{\varvec{\eta }}\right) \right) \), \(\left\| {\mathbf {T}}{\mathbf {x}}\right\| =\left\| {\mathbf {x}}\right\| ,\;\forall {\mathbf {x}}\in \mathfrak {R}^3\), which, according to (29), means that the convergence of \(\tilde{\varvec{\varOmega }}\) to zero is equivalent to the convergence of \(\dot{\tilde{\varvec{\eta }}}\).

Now, to design the attitude tracking controller, the following auxiliary variables are introduced:

$$\begin{aligned} \varvec{\sigma }_1= & {} \tilde{\varvec{\varOmega }}+\alpha _1\tilde{\varvec{\eta }} \end{aligned}$$
(33)
$$\begin{aligned} \varvec{\sigma }_2= & {} \dot{\varvec{\sigma }}_1+\alpha _2\varvec{\sigma }_1 \end{aligned}$$
(34)

where \(\alpha _1\) and \(\alpha _2\) are positive constants. It should be noted that, the filtered error \(\varvec{\sigma }_2\) is not measurable, since it depends on \(\ddot{\tilde{\varvec{\eta }}}\). Using (29) and (32), the open-loop tracking error system can be obtained as follows:

$$\begin{aligned} \varvec{\sigma }_2=&{\mathbf {N}}+{\mathbf {B}}\varvec{\tau }+\left( {\mathbf {R}}_{\phi \theta }\right) _d{\mathbf {J}}^{-1}\varvec{{\varDelta }}-\left( {\mathbf {R}}_{\phi \theta }\right) _d\left( \dot{\varvec{\varOmega }}_{\phi \theta }\right) _d\nonumber \\&+\alpha _1{\mathbf {T}}\tilde{\varvec{\varOmega }}+\alpha _2\varvec{\sigma }_1 \end{aligned}$$
(35)

For the open-loop dynamics (35), the following controller is proposed:

$$\begin{aligned} \varvec{\tau }=&-{\mathbf {B}}^{-1}\left[ {\mathbf {N}}+\alpha _1{\mathbf {T}}\tilde{\varvec{\varOmega }}+\left( \alpha _2+k_s\right) \varvec{\sigma }_1\right. \nonumber \\&\left. \quad \qquad +\int \limits _{0}^{t}\left[ k_s\alpha _2\varvec{\sigma }_1\left( \bar{t}\right) +\varrho {\text {sgn}}\left( \varvec{\sigma }_1\left( \bar{t}\right) \right) \right] {\text {d}}\bar{t}\right] \end{aligned}$$
(36)

where \(k_s\) and \(\varrho \) are positive constants. Now, substituting (36) in (35) and using (34), the time derivative of (35) can be computed as

$$\begin{aligned} \dot{\varvec{\sigma }}_2=-k_s\varvec{\sigma }_2-\varrho {\text {sgn}}\left( \varvec{\sigma }_1\right) +{\mathbf {N}}_d \end{aligned}$$
(37)

where \({\mathbf {N}}_d\in \mathfrak {R}^3\) is defined as

$$\begin{aligned} {\mathbf {N}}_d=&\left( \dot{{\mathbf {R}}}_{\phi \theta }\right) _d{\mathbf {J}}^{-1}\varvec{{\varDelta }}+\left( {\mathbf {R}}_{\phi \theta }\right) _d{\mathbf {J}}^{-1}\dot{\varvec{{\varDelta }}}\\&-\left( \dot{{\mathbf {R}}}_{\phi \theta }\right) _d\left( \dot{\varvec{\varOmega }}_{\phi \theta }\right) _d-\left( {\mathbf {R}}_{\phi \theta }\right) _d\left( \ddot{\varvec{\varOmega }}_{\phi \theta }\right) _d. \end{aligned}$$

Note that, according to Assumptions 1 and 2, the following inequalities can be considered:

$$\begin{aligned} \left\| {\mathbf {N}}_d\right\| \le \zeta _1,\qquad \left\| \dot{{\mathbf {N}}}_d\right\| \le \zeta _2 \end{aligned}$$

where \(\zeta _1\) and \(\zeta _2\) are positive constants.

Before presenting the main result of this paper, the following lemmas are presented:

Lemma 1

Let the auxiliary function \(\mathcal {L}\left( t\right) \in \mathfrak {R}\) be defined as follows:

$$\begin{aligned} \mathcal {L}\triangleq \varvec{\sigma }_2^{\top }\left( {\mathbf {N}}_d-\varrho {\text {sgn}}\left( \varvec{\sigma }_1\right) \right) . \end{aligned}$$

If the control gain \(\varrho \) is selected to satisfy the following sufficient condition:

$$\begin{aligned} \varrho >\zeta _1+\frac{1}{\alpha _2}\zeta _2, \end{aligned}$$
(38)

then

$$\begin{aligned} \int _{0}^{t}\mathcal {L}\left( \bar{t}\right) {\text {d}}\bar{t} \le \varrho \left| \varvec{\sigma }_{1i}\left( 0\right) \right| -\varvec{\sigma }_1\left( 0\right) ^{\top }{\mathbf {N}}_d\left( 0\right) \end{aligned}$$

where the subscript \(i=1,2,3\) denotes the ith element of the vector.

Proof

The proof is given in [35]. \(\square \)

Lemma 2

The extended Barbalat lemma [30]. Suppose that \(x\left( t\right) \) to be a solution for the differential equation \(\dot{x}=a\left( t\right) +b\left( t\right) \) where \(a\left( t\right) \) is a uniformly continuous function. If \(x\left( t\right) \) when \(t\rightarrow \infty \) has a bounded constant value and \(\lim \limits _{t\rightarrow \infty }b\left( t\right) =0\), then one will have: \(\lim \limits _{t\rightarrow \infty }\dot{x}\left( t\right) =0\) and \(\lim \limits _{t\rightarrow \infty }a\left( t\right) =0\).

Lemma 3

Consider a nonlinear system defined by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{\mathbf {x}}}_1=k_1\mathbf{sk }\left( {\mathbf {u}}_1\right) {\mathbf {x}}_1-{\mathbf {x}}_2\\ \dot{{\mathbf {x}}}_2=k_2\mathbf{sk }\left( {\mathbf {u}}_2\right) {\mathbf {x}}_2+l_1b\left( t\right) {\mathbf {h}}\left( {\mathbf {x}}_1\right) \\ \quad -\,l_2b\left( t\right) {\mathbf {h}}\left( {\mathbf {x}}_2\right) +\varvec{\epsilon } \end{array} \right. \end{aligned}$$
(39)

where \({\mathbf {h}}\left( \cdot \right) \) is defined as in (17), \({\mathbf {u}}_1,{\mathbf {u}}_2\in \mathfrak {R}^3\) are bounded signals, \({\mathbf {x}}_1,{\mathbf {x}}_2\in \mathfrak {R}^3\) and \(k_1\) and \(k_2\) are constant values. Let the continuous scalar function \(b\left( t\right) \) to be bounded and positive for all \(t>0\), i.e., \(b_m< b\left( t\right) < b_M\) with constants \(b_M>b_m>0\) such that \(\frac{1}{b_m}<<\infty \). In addition, \(\dot{b}\left( t\right) \) is bounded and \(\dot{b}\left( t\right) \rightarrow 0\). Also, consider \(l_1\) and \(l_2\) to be positive constants and let \(\varvec{\epsilon }\) to be bounded for all \(t>0\) and converges to zeros as \(t\rightarrow \infty \). Then \({\mathbf {x}}_1\) and \({\mathbf {x}}_2\) are bounded and converge to zero as time goes to infinity.

Proof

The proof is given in the “Appendices 2.” \(\square \)

Now, the following theorem for IBVS control of the quadrotor is stated:

Theorem 1

Consider the image and the quadrotor dynamics defined by (4), (10) and (11) with their inputs as \(U_1\) and \(\varvec{\tau }\). Let the inputs to be defined through (22) and (36) with \(k_p\) and \(k_d\) satisfying (26). Then starting from the initial conditions, all states of the system are bounded and the error signals converge to zero as time goes to infinity provided that

$$\begin{aligned} \alpha _1>\frac{1}{2},\quad \alpha _2>1,\quad k_s>\frac{1}{2}. \end{aligned}$$
(40)

Proof

Let the auxiliary function \(P\left( \varvec{\sigma }_1,t\right) \in \mathfrak {R}\) be defined as follows:

$$\begin{aligned}&P\triangleq \varrho \sum \limits _{i=1}^{3}\left| \varvec{\sigma }_{1i}\left( 0\right) \right| -\varvec{\sigma }_1\left( 0\right) ^{\top }{\mathbf {N}}_d\left( 0\right) -\int _{0}^{t}\mathcal {L}\left( \bar{t}\right) {\text {d}}\bar{t} \end{aligned}$$
(41)

where \(\mathcal {L}\) is defined in Lemma 1. It can be easily verified from Lemma 1 that if the condition for \(\varrho \) in (38) is satisfied, \(P\left( t\right) \ge 0\).

Now, the following Lyapunov function is considered to proof the theorem:

$$\begin{aligned} L&= \frac{1}{2}k_1\varvec{\xi }^{\top }\varvec{\xi }+\frac{1}{2}\varvec{\vartheta }^{\top }\varvec{\vartheta }+\frac{1}{2}\left( {\mathbf {r}}-\varvec{\vartheta }\right) ^{\top }\left( {\mathbf {r}}-\varvec{\vartheta }\right) \nonumber \\&\quad +2\left( 1-\tilde{\eta }_0\right) +\frac{1}{2}\varvec{\sigma }_1^{\top }\varvec{\sigma }_1+\frac{1}{2}\varvec{\sigma }_2^{\top }\varvec{\sigma }_2+P+\frac{1}{2\gamma }\tilde{\rho }^2.\nonumber \\ \end{aligned}$$
(42)

Then, using (18), (19), (28), (29), (34), (37) and (41) the time derivative of (42) can be written as

$$\begin{aligned} \dot{L}=&-k_2\varvec{\vartheta }^{\top }\varvec{\vartheta }-\alpha _1\tilde{\varvec{\eta }}^{\top }\tilde{\varvec{\eta }}-\alpha _2\varvec{\sigma }_1^{\top }\varvec{\sigma }_1-k_s\varvec{\sigma }_2^{\top }\varvec{\sigma }_2\nonumber \\&+\tilde{\varvec{\eta }}^{\top }\varvec{\sigma }_1+\varvec{\sigma }_1^{\top }\varvec{\sigma }_2+\tilde{\rho }\left[ \left( {\mathbf {r}}-\varvec{\vartheta }\right) ^{\top }\left( k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) \right. \right. \nonumber \\&\left. \left. -\,k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) -\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3\right) -\frac{\dot{\hat{\rho }}}{\gamma }\right] . \end{aligned}$$
(43)

Substituting the adaptive law (16) in (43), and using the fact that,

$$\begin{aligned} {\mathbf {x}}_1^{\top }{\mathbf {x}}_2\le \frac{1}{2}\left\| {\mathbf {x}}_1\right\| ^2+\frac{1}{2}\left\| {\mathbf {x}}_2\right\| ^2, \quad \forall {\mathbf {x}}_1,{\mathbf {x}}_2\in \mathfrak {R}^n, \end{aligned}$$

an upper bound can be obtained for \(\dot{L}\) as

$$\begin{aligned} \dot{L}\le&-k_2\left\| \varvec{\vartheta }\right\| ^2-\left( \alpha _1-\frac{1}{2}\right) \left\| \tilde{\varvec{\eta }}\right\| ^2-\left( \alpha _2-1\right) \left\| \varvec{\sigma }_1\right\| ^2\nonumber \\&-\left( k_s-\frac{1}{2}\right) \left\| \varvec{\sigma }_2\right\| ^2. \end{aligned}$$
(44)

At this step, it is shown that \(\tilde{\varvec{\eta }}\), \(\varvec{\sigma }_1\) and \(\varvec{\sigma }_2\) converge to zero and \(\dot{\bar{\varvec{\psi }}}\) is bounded. Provided that (40) is satisfied, (44) can be written as

$$\begin{aligned} \dot{L}\le -\beta _1\left\| {\mathbf {x}}_3\right\| ^2\le 0 \end{aligned}$$
(45)

where \({\mathbf {x}}_3\triangleq \left[ \tilde{\varvec{\eta }}^{\top }\; \varvec{\sigma }_1^{\top }\;\varvec{\sigma }_2^{\top }\right] ^{\top }\) and

$$\begin{aligned} \beta _1=\min \left\{ \alpha _1-\frac{1}{2},\alpha _2-1,k_s-\frac{1}{2}\right\} . \end{aligned}$$

Equation (45) indicates that \(\varvec{\xi }\), \(\varvec{\vartheta }\), \({\mathbf {r}}\), \(\tilde{\varvec{\eta }}\), \(\varvec{\sigma }_1\), \(\varvec{\sigma }_2\) and \(\tilde{\rho }\) are bounded and then one has

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\beta _1\int ^{t}_{t_0}{\mathbf {x}}_3^{\top }{\mathbf {x}}_3{\text {d}}\bar{t}\le L\left( t_0\right) -L\left( \infty \right) <\infty . \end{aligned}$$

In addition, it can be verified from (33) that \(\tilde{\varvec{\varOmega }}\) is bounded, then \(\dot{\tilde{\varvec{\eta }}}\) is bounded from (29). Also, it can be seen from (34) and (37) that \(\dot{\varvec{\sigma }}_1\) and \(\dot{\varvec{\sigma }}_2\) are bounded. Therefore, \({\mathbf {x}}_3\) is uniformly continuous, and applying Barbalat lemma indicates that \(\tilde{\varvec{\eta }}\), \(\varvec{\sigma }_1\) and \(\varvec{\sigma }_2\) converge to zero asymptotically. Hence, it can be concluded that \(\tilde{{\mathbf {R}}}_{\phi \theta }\rightarrow {\mathbf {I}}\) and \(\tilde{\eta }_0\rightarrow \pm 1\). On the other hand, since \(\tilde{\varvec{\varOmega }}\) and \(\left( \varOmega _{\phi \theta }\right) _{d3}\) are bounded, it can be verified from (30) that the third element of the vector \(\varvec{\varOmega }_{\phi \theta }\) is also bounded. Therefore, from (31), \(\left( \varOmega _3-\cos \phi \cos \theta \dot{\psi }\right) \) is bounded. By exploiting (2), it can be verified that \(\dot{\psi }\) and hence \(\dot{\bar{\varvec{\psi }}}\) are bounded.

Now, again, (44) can be written as

$$\begin{aligned} \dot{L}\le -k_2\left\| \varvec{\vartheta }\right\| ^2\le 0. \end{aligned}$$

From (18), it can be seen that \(\dot{\varvec{\vartheta }}\) is bounded. Hence, \(\varvec{\vartheta }\) is uniformly continuous, and by applying Barbalat lemma it can be concluded that \(\varvec{\vartheta }\rightarrow {\mathbf {0}}\) and \(\dot{\varvec{\vartheta }}\rightarrow {\mathbf {0}}\) from (18). From (19), \(\dot{\varvec{\xi }}\) is bounded, and hence \(\varvec{\xi }\) is continuous. Therefore, applying Lemma 2 to (18) indicates that \(\varvec{\xi }\) converges to zero.

To simplify the demonstration of the convergence of \(\varvec{\varsigma }_1\) and \(\varvec{\varsigma }_2\) to zero, consider the change of variables \(\bar{\varvec{\varsigma }}_1={\mathbf {R}}_\psi \varvec{\varsigma }_1\) and \(\bar{\varvec{\varsigma }}_2={\mathbf {R}}_\psi \varvec{\varsigma }_2\), where \({\mathbf {R}}_\psi \) specifies a rotation about \(Z_i\) axis, and hence depends on \(\psi \). Considering this change of variables and also the above development, from (15) one has \(\dot{\bar{\varvec{\varsigma }}}_1=\bar{\varvec{\varsigma }}_2\) and

$$\begin{aligned} \ddot{\bar{\varvec{\varsigma }}}_1=-l_1\bar{\varvec{\varsigma }}_1-l_2\dot{\bar{\varvec{\varsigma }}}_1+\varvec{\varepsilon } \end{aligned}$$

which is a linear system with an asymptotically vanishing perturbation \(\varvec{\varepsilon }\). Therefore, it can be easily verified that \(\bar{\varvec{\varsigma }}_1\) and \(\bar{\varvec{\varsigma }}_2\), and hence \(\varvec{\varsigma }_1\) and \(\varvec{\varsigma }_2\), are bounded and converge to zero. Based on the above results, one can write the dynamics of \(\hat{\varvec{\delta }}\) and \(\hat{\varvec{\nu }}\) as in (39). Thus, from the result of Lemma 3 one can conclude that \(\hat{\varvec{\delta }}\) and \(\hat{\varvec{\nu }}\) are bounded and \(\hat{\varvec{\delta }}\rightarrow {\mathbf {0}}\) and \(\hat{\varvec{\nu }}\rightarrow {\mathbf {0}}\). It can also be concluded from (15) that \(\dot{\hat{\varvec{\delta }}}\) and \(\dot{\hat{\varvec{\nu }}}\) converge to zero. Equation (28) implies that \(\dot{{\mathbf {r}}}\) is bounded and then \({\mathbf {r}}\) is continuous. Therefore, applying Lemma 2 to (19) indicates that \(\dot{\varvec{\xi }}\rightarrow {\mathbf {0}}\) and \({\mathbf {r}}\rightarrow {\mathbf {0}}\). Convergence of \(\varvec{\delta }\) and \(\varvec{\nu }\) to zero can be, respectively, concluded from (13) and (14). Therefore, (10) and (11) imply that \(\dot{\varvec{\delta }}\rightarrow {\mathbf {0}}\) and \(\dot{\varvec{\nu }}\rightarrow {\mathbf {0}}\). Also, from (16) \(\dot{\hat{\rho }}\) converges to zero. From the above results, it can be easily verified that the torque input (36) is also bounded and this ends the proof. \(\square \)

Remark 2

The adaptation law (16) contains \({\mathbf {r}}\) which is unavailable. Integrating (16), the projection of the following equivalent version of it can be obtained in which all signals are measurable:

$$\begin{aligned} \hat{\rho } =&\hat{\rho }\left( 0\right) +\gamma \int ^{t}_{0}\left( {\mathbf {r}}-\varvec{\vartheta }\right) ^{\top }\left( k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) -k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) \right. \\&\left. \quad -\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3\right) {\text {d}}\bar{t}\\ =&\hat{\rho }\left( 0\right) +\gamma \int ^{\varvec{\delta }\left( t\right) }_{\varvec{\delta }\left( 0\right) }\left( k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) -k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) \right. \\&\left. \quad -\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3\right) ^{\top }{\text {d}}\bar{\varvec{\delta }}\\&\quad +\gamma \int ^{t}_{0}\left( -\mathbf{sk }\left( \dot{\bar{\varvec{\psi }}} \right) \varvec{\delta }-\hat{\varvec{\nu }}- \varvec{\varsigma }_2-\varvec{\vartheta }\right) ^{\top }\left( k_p{\mathbf {h}}\left( \hat{\varvec{\delta }}\right) \right. \\&\quad \left. -\,k_d{\mathbf {h}}\left( \hat{\varvec{\nu }}\right) -\frac{U_1}{m}\left( {\mathbf {R}}_{\phi \theta }-\left( {\mathbf {R}}_{\phi \theta }\right) _d\right) {\mathbf {E}}_3\right) {\text {d}}\bar{t}. \end{aligned}$$

5 Simulation results

In this section, simulations are presented to demonstrate the effectiveness of the proposed robust visual servo controller. Simulations are done in MATLAB and SIMULINK environment. Parameters of the dynamic model of the quadrotor, Eqs. (3) and (4), are considered as \(m=2~\hbox {kg}\), \(g=9.81~{\hbox {m}/\hbox {s}^{2}}\) and \({\mathbf {J}}={\text {diag}}\left( 0.0081,0.0081,0.0142\right) ~{\hbox {kgm}^{2}/\hbox {rad}^{2}}\). Visual information includes four points related to the four vertexes of a rectangle, which are used to calculate the image features defined in (6). The vertexes of the rectangle are located at \(\left( 0.25,0.2,0\right) ~\hbox {m}\), \(\left( 0.25,-0.2,0\right) ~\hbox {m}\), \(\left( -0.25,0.2,0\right) ~\hbox {m}\) and \((-0.25,-0.2,0) \hbox {m}\) with respect to the inertial frame. These points are projected with perspective projection on a digital image plane with focal length divided by pixel size (identical in both horizontal and vertical axes of the image plane) equal to 213 and the principal point located at (80,60).

The sampling rate for the visual information is considered to be 50 Hz, while this rate for the rest of the system is 100 Hz. The uncertainty \(\varvec{{\varDelta }}\left( t\right) \) in (4) is modeled by a sinusoidal signal with different phases for each channel and amplitude equal to 0.1. The aircraft is assumed to start in a hover position with the object in the field of view of the camera. The initial position of the quadrotor is considered to be at \(\left( -1.5,0.7,-7\right) ~\hbox {m}\) with respect to the inertial frame, and the desired image features are obtained at \(\left( 0,0,-5\right) ~\hbox {m}\). The simulation parameters for the controller and observers are given in Table 1.

Table 1 Simulation parameters
Full size table
Fig. 2
figure 2

Simulation 1: Object point trajectories in the image plane. u and n represent the horizontal and vertical axes of the image plane

Full size image

In the first simulation, the visual and inertial measurements are assumed to be ideal. The results of this simulation are presented in Figs. 2, 3, 4, 5, 6 and 7.

Fig. 3
figure 3

Simulation 1: Time evolution \(\varvec{\delta }\) and its estimate

Full size image
Fig. 4
figure 4

Simulation 1: Time evolution of \(\varvec{\nu }\) and its estimate

Full size image
Fig. 5
figure 5

Simulation 1: Time evolution of the auxiliary variables

Full size image
Fig. 6
figure 6

Simulation 1: Time evolution of the orientation and angular velocity errors

Full size image
Fig. 7
figure 7

Simulation 1: Time evolution of the quadrotor Cartesian coordinates

Full size image

In order to evaluate the performance of the proposed controller in a more realistic condition, in the second simulation, the visual and angular velocity information are augmented with noise. The covariance of noise is \(2\times 10^{-4}\) and 2 for the angular velocity and visual information, respectively. Results are presented in Figs. 8 and 9. The results demonstrate that the presented approach performs well in spite of considerable amount of measurement noise in the system.

Fig. 8
figure 8

Simulation 2: Object point trajectories in the image plane

Full size image
Fig. 9
figure 9

Simulation 2: Time evolution of \(\varvec{\delta }=\left[ \delta _1\;\delta _2\;\delta _3\right] ^{\top }\)

Full size image

6 Conclusion

In this paper, an IBVS controller has been developed for translational motion control of the quadrotor helicopter. This paper aims to design a bounded-input output feedback controller for the translational dynamics of the quadrotor and a robust controller for the rotational dynamics. The visual features are defined using perspective image moments, which are projected on a suitably oriented image plane, in order to have decoupled kinematics for the translational motion. The features can be obtained from a limited number of visual landmarks, and hence, the proposed approach has its interest when a few information is available from the environment, while a SLAM technique can introduce an alternative simple controller with rich information from the workspace. Translational optic flow of the image features is considered as the linear velocity cue and estimated through a nonlinear observer. The controller uses an adaptive scheme in order to compensate for the unknown depth information of the image and utilizes the RISE method to alleviate the effect of disturbances. Furthermore, the controller exploits the passivity properties of the dynamics of the translational optic flow, in order to not to use the yaw information of the quadrotor. Lyapunov-based stability analysis is presented to guarantee that the error signals converge to zero in the presence of disturbances. Simulation examples illustrate the effectiveness of the proposed IBVS approach even in the presence of noise corrupting the inertial and image data.