1 Introduction

Quadrotor UAV (QUAV) has been widely used in autonomous detection [1, 2], payload transportation [3], target tracking [4], and other missions because of its vertical takeoff and landing characteristics. In these missions, the QUAV needs to have the ability of autonomous flight, and the primary task to achieve the autonomous flight of the QUAV is to obtain their spatial position information. The traditional QUAV combines low-cost GPS (Global Positioning System) and low-cost IMU (inertial measurement unit) to obtain its position information. However, this positioning method will not provide reliable position feedback when the QUAV is in an indoor, low latitude, and complex urban environment [5]. The most common way to solve this problem is to combine it with visual technology. Under this scheme, QUAV usually carries a low-cost monocular camera. The rich visual information provided by the camera can help us achieve QUAV target tracking [6, 7].

Using images to obtain the position and attitude information of the robot is called visual servoing [8]. Visual servoing technology has two branches: position-based visual servoing (PBVS) and image-based visual servoing (IBVS). PBVS requires complete spatial data for 3D reconstruction, which requires high computational power and is unsuitable for small QUAV. IBVS calculates the position and attitude information according to the selected image features. IBVS does not require the accuracy of the camera and has better robustness to calibration error and image noise [9], so it is suitable for small QUAV. It should be pointed out that due to the underactuated characteristics of QUAV, the dynamics and image of QUAV are coupled, so the IBVS of QUAV is more challenging than the full actuated system [10].

The earliest IBVS of QUAV was started by Nicolas [9], who realized image-based visual servoing of static targets using the optical flow feature. Due to optical flow features, the coupling degree of the QUAV visual servoing will be improved [11]. Researchers begin to try to use invariant features, such as image moments [12, 13]. Image moments contain many features, such as point features and line features. In addition, image moments are scale invariant. Taking advantage of this feature and introducing the concept of a virtual camera plane, Hamed and Giuseppe [14] eliminate the coupling of pitch angle and roll angle, reducing the complexity of controller design and designing an adaptive controller. Subsequently, image moment features in the virtual camera plane are widely used [15,16,17].

Because most QUAVs use low-cost monocular cameras for image-based visual servo, it will lead to the inability to obtain image depth information accurately. To solve this problem, Hamed Jabbari and Jungwon estimated the linear velocity of QUAV in the virtual camera plane [16]. This method uses an observer to compensate for the depth information of the image. After that, Zheng and Wang discussed the IBVS of QUAV under slope conditions [17]. They designed a nonlinear velocity observer to estimate the linear velocity information of QUAV. The linear velocity observer derived from the virtual plane can avoid acquiring depth information. Then they use the backstepping method to design the controller and prove the global asymptotic stability for the first time.

The above methods are designed for static targets. However, QUAV has an urgent need for tracking moving targets. Due to the lack of accurate prior parameters of moving targets, it is more challenging to track unpredictable targets. S. Masoud and A.Abdollah designed an indirect adaptive neural controller for QUAV using a radial basis function (RBF) neural network to enable QUAV to track moving targets [18]. After that, Masoud and Hamed Jabbari [19] used an artificial neural network to process the speed of moving targets and considered the influence of external interference. Ning [20] uses error symbol compensated robust integral (DCRISE) feedback control to design a visual servoing controller for moving targets, which improves the system’s robustness. Zhiqiang and Xuchao [21] use a higher-order differentiator to estimate the motion parameters of the moving target and transfer the parameters as feedforward to the design stage of the controller. This method eliminates the coupling of the controller to the motion parameters. Moreover, it should be noted that the QUAV often needs better system response capability when facing autonomous flight missions [22].

In the current research, the discussion on the convergence of the system controller is mainly asymptotic convergence. As time tends to infinity, the system state reaches the equilibrium point. Alexis [23] proposed a finite-time controller for position control, which realized the hover control of QUAV in a finite time . Tian et al. [24] applied a multivariable hyper twist algorithm to realize the attitude control of QUAV and proved the stability through theory and experiments. Harshavarthini [25] uses Lyapunov–Krasovskii functional to design a finite-time fault-tolerant controller for the attitude of the QUAV. Gajbhiye [26] considered the finite-time control of the slung payload transportation of QUAV and proposed a geometric finite-time inner–outer loop control strategy. Wenwu [27] uses the homogeneous theory to design the finite-time position controller and the finite-time attitude controller of QUAV so that QUAV can realize hovering control in a finite time. Guanglei and Guangbo [28] designed a finite-time controller using the nonsingular terminal sliding mode to realize the finite-time control of QUAV image-based visual servoing. We use a table to summarize the above research work, as shown in Table 1. We consider these methods through three dimensions: the convergence rate of the controller, whether to consider the depth information of targets, and whether to discuss external disturbances.

Table 1 Comparison of control methods
Full size table

We can see that no control scheme can simultaneously satisfy the requirements of tracking a moving target, finite-time convergence, considering the target’s depth information, and verifying the disturbance. We propose a control scheme based on global finite-time stability to solve this problem. First, we use a nonlinear high-order tracking differentiator to estimate the parameters of moving objects. Using the backstepping method, we design a novel nonlinear global finite-time linear velocity observer for image depth information acquisition. Finally, we use the backstepping method to design the global finite-time controller of the system.

The main contributions of this paper are as follows:

  1. (1)

    We propose the global finite-time control scheme used for the image-based visual servoing of a moving target for the first time. In this scheme, we use a nonlinear tracking differentiator to estimate the parameters of the moving target. Then a global finite-time nonlinear linear velocity observer is designed using the backstepping method. Finally, we use the backstepping method to design the global finite-time controller of the QUAV.

  2. (2)

    To solve the problem of acquiring the image depth information of a monocular camera in the image-based visual servoing of a moving target, we propose a global finite-time nonlinear linear velocity observer. The depth information of the QUAV relative to the target is estimated by estimating the linear velocity of the altitude axis in the virtual camera plane.

  3. (3)

    The numerical simulation and ROS gazebo simulation results show high error convergence performance and better tracking control performance.

The rest of this paper is organized as follows. In Sect. 2, we introduce the QUAV and the image moment dynamics. In Sect. 3, we introduce the design of the controller. In Sect. 4, the simulation experiment of the proposed control scheme is carried out. Finally, our conclusions are given in Sect. 5.

2 Modeling of QUAV and image moment

In this section, we will introduce the dynamic modeling of QUAV and image moment feature dynamics.

2.1 Quadrotor model

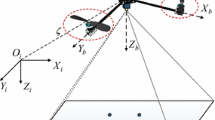
This section considers using two frames to describe the translation and rotation motion of the QUAV (see Fig. 1). The inertial frame \({I} = \left\{ {{O_i},{X_i},{Y_i},{Z_i}} \right\} \) is assumed to be fixed at a point on the earth. We assume that the mass center of the quadrotor UAV is the origin of the body-fixed frame \({B} = \left\{ {{O_b},{X_b},{Y_b},{Z_b}} \right\} \). Moreover, we assume that the quadrotor UAV is always a rigid body. The position of the origin of the body frame B in the inertial frame is expressed as \({\zeta } = {\left( {x,y,z} \right) ^T}\). We use three Euler angles \(\phi \), \(\theta \), and \(\psi \) to represent the rotation between two frames. \({\textbf{R}}:{B} \rightarrow {I}\) is the rotation matrix between two frames.

Fig. 1
figure 1

Inertial frame I and body frame B

Full size image

Assumption 1

The roll and pitch angles belong to \(\left( -\frac{\pi }{2},\frac{\pi }{2} \right) \), and the yaw angle belongs to \(\left( -\pi ,\pi \right) \).

The mass of the QUAV is m and the inertia is \(\textbf{J} = diag\{[J_{xx}, J_{yy}, J_{zz}]\}\). The linear velocity and angular velocity in the body-fixed frame of the QUAV are expressed as \(\textbf{V} \in {{{\mathbb {R}}}^{3}}\) and \({\omega } = {\left( {{\omega _1},{\omega _2},{\omega _3}} \right) ^T} \in {{{\mathbb {R}}}^{3}}\). According to [29,30,31], the kinematics and dynamics equations used to describe QUAV with disturbance are expressed as follows:

$$\begin{aligned} {\dot{\zeta }}&={\textbf{RV}} \end{aligned}$$
(1)
$$\begin{aligned} {\dot{\textbf{R}}}&={\textbf{Rsk}}\left( {\omega } \right) \end{aligned}$$
(2)
$$\begin{aligned} m\dot{\textbf{V}}&=-m{\omega }\times \textbf{V}+\textbf{F} \end{aligned}$$
(3)
$$\begin{aligned} {\textbf{J}}\dot{\omega }&=-{\omega }\times {\textbf{J}}\omega +{\tau } \end{aligned}$$
(4)
$$\begin{aligned} \textbf{F}&=-{{U}_{1}}{{\textbf{E}}_{3}}+mg{{{\textbf{R}}}^{T}}{{\textbf{e}}_{3}} \end{aligned}$$
(5)

where \(\textbf{sk}\left( {\omega } \right) \) is skew symmetric matrix, which means that \(\textbf{sk}\left( \textbf{a}\right) \textbf{b}=\textbf{a}\times \textbf{b}\), \(\textbf{a} \in {{{\mathbb {R}}}^{3}}\) and \(\textbf{b}\in {{{\mathbb {R}}}^{3}}\) are arbitrary vectors, and \(\times \) denotes the vector cross product. g is the gravity acceleration. \(\textbf{F} \in {{{\mathbb {R}}}^{3}}\) is the force. \({\tau } \in {{{\mathbb {R}}}^{3}}\) is the torque. \(U_1\) is the total thrust.

2.2 Image dynamics

This section also uses the image moment feature based on a virtual camera. First, we assume a camera frame \(C = \left\{ {{O_C},{X_C},{Y_C},{Z_C}} \right\} \), which coincides with the body-fixed frame of the QUAV. We assume that the camera is fixed at the mass center of the quadrotor and has a downward FOV. The virtual camera frame \(\nu \) is the same as the actual camera frame. However, the roll angle and pitch angle of the virtual camera frame are always zero, and the yaw angle is consistent with the actual orientation of the quadrotor (see Fig. 2).

Fig. 2
figure 2

Camera frame C and the virtual camera frame \(\nu \)

Full size image

We assume that there is a fixed point \({}^I\textbf{P} = {\left[ {{}^Ix,{}^Iy,{}^Iz} \right] ^T}\) in the inertia frame, and it is represented as \({}^C\textbf{P} = {\left[ {{}^Cx,{}^Cy,{}^Cz} \right] ^T}\) in the camera frame and as \({}^\nu \textbf{P} = {\left[ {{}^\nu x,{}^\nu y,{}^\nu z} \right] ^T}\) in the virtual camera frame. Therefore, we get

$$\begin{aligned} {}^\nu \textbf{P}\left( t \right) = {\textbf{R}}_\psi ^T\left( t \right) \left( {{}^I\textbf{P}- {O_\nu }\left( t \right) } \right) \end{aligned}$$
(6)

where \({\textbf{R}}_\psi ^T\) is a rotation matrix used to describe rotation around the \(Z-\)axis, \(\psi \) denotes yaw angle. Then, we get

$$\begin{aligned} \begin{aligned} {}^{\nu }\dot{\textbf{P}}&=\frac{{\textrm{d}}{\textbf{R}}_{\psi }^{T}}{{\textrm{d}}t}\left( {}^{I}\textbf{P}-{{O}_{\nu }} \right) -{\textbf{R}}_{\psi }^{T}\frac{{\textrm{d}}{{O}_{\nu }}}{{\textrm{d}}t}+{\textbf{R}}_{\psi }^{T}\frac{{\textrm{d}}}{{\textrm{d}}t}{}^{I}\textbf{P} \\&=-sk\left( \dot{\psi }{{e}_{3}} \right) {\textbf{R}}_{\psi }^{T}\left( {}^{I}\textbf{P}-{{O}_{\nu }} \right) -{\textbf{R}}_{\psi }^{T}{{{\dot{O}}}_{\nu }}+{\textbf{R}}_{\psi }^{T}{}^{I}{\dot{\textbf{P}}} \\&=-sk\left( \dot{\psi }{{e}_{3}} \right) {\textbf{R}}_{\psi }^{T}\left( {}^{I}\textbf{P}-{{O}_{\nu }} \right) -\textbf{v}+\textbf{d} \end{aligned} \end{aligned}$$
(7)

where \({\dot{O}_\nu }\) denotes the linear velocities of camera and virtual frameworks in the inertia frame. \(\textbf{v} = {\left[ {{}^{\nu }{v_x},{}^{\nu }{v_y},{}^{\nu }{v_z}} \right] ^T}\) is the linear velocity of camera framework in the virtual frame, and \(\textbf{d}\left( t \right) ={{\left[ v_{x}^{d},v_{y}^{d},v_{z}^{d} \right] }^{T}}\) is the velocity vector of a moving point in the virtual frame.

According to the perspective projection model, the projection of point \(\textbf{P}\) onto the virtual camera plane can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {}^{\nu }u = \lambda \frac{{{}^{\nu }x}}{{{}^{\nu }z}} \\ \\ {}^{\nu }n = \lambda \frac{{{}^{\nu }y}}{{{}^{\nu }z}} \end{array} \right. \end{aligned}$$
(8)

where \(\lambda \) is focal length and \(\left( {{}^{\nu }u,{}^{\nu }n} \right) \) are the point coordinates in the virtual camera frame. From (7) and (8), one obtains

$$\begin{aligned} \begin{bmatrix} {}^{\nu }\dot{u} \\ {}^{\nu }\dot{n} \end{bmatrix} = \begin{bmatrix} { - \frac{\lambda }{{{}^{\nu }z}}} &{} 0 &{} {\frac{{{}^{\nu }u}}{{{}^{\nu }z}}} \\ 0 &{} { - \frac{\lambda }{{{}^{\nu }z}}} &{} {\frac{{{}^{\nu }n}}{{{}^{\nu }z}}} \end{bmatrix} \begin{bmatrix} {}^{\nu }{v_x} -v_{x}^{d} \\ {}^{\nu }{v_y} -v_{y}^{d} \\ {}^{\nu }{v_z} -v_{z}^{d} \end{bmatrix} + \begin{bmatrix} {}^{\nu }n \\ - {}^{\nu }u \end{bmatrix} {{\dot{\psi }}}. \end{aligned}$$
(9)

Suppose that there are N stationary points in a level plane in the inertial frame, which are subject to the following assumptions.

Assumption 2

The observed target is a planar object that locates at a level plane of inertial frame and its binary image is obtained by segmentation algorithm.

Assumption 3

Image points are always in the field of view(FOV) of the camera.

Assumption 4

The sensor can get an accurate measurement value in the controller design stage.

Remark 1

Assumptions 3 and 4 are difficult to guarantee in the natural environment. These two assumptions are added here only to ensure that in the simulation experiment, the image features will always remain in the camera FOV, and each sensor can also accurately give feedback.

Then according to [13], we can get that the image moment features are as follows:

$$\begin{aligned} {q_x} = {q_z}\frac{{{}^{\nu }{u_g}}}{\lambda },{q_y} = {q_z}\frac{{{}^{\nu }{n_g}}}{\lambda },{q_z} = \sqrt{\frac{{{a^*}}}{a}} \end{aligned}$$
(10)

where \({}^{\nu }{u_g} = \frac{1}{N}\sum \nolimits _{k = 1}^N {{}^{\nu }{u_k}} \) and \({}^{\nu }{n_g} = \frac{1}{N}\sum \nolimits _{k = 1}^N {{}^{\nu }{n_k}} \). \({}^{\nu }{u_k}\) and \({}^{\nu }{n_k}\) are the two components of the kth point. \(a = {}^{\nu }{\mu _{02}} + {}^{\nu }{\mu _{20}}\) and \({}^{\nu }{\mu _{ij}} = \sum \nolimits _{k = 1}^N {{\left( {{}^{\nu }{u_k} - {}^{\nu }{u_g}} \right) }^i}\left( {{}^{\nu }{n_k} - {}^{\nu }{n_g}} \right) ^j\). The desired value of a is \(a^*\).

Based on (9) and (10), the dynamics of the image features are defined as follows [14]:

$$\begin{aligned} \dot{\textbf{q}} = - \textbf{sk}\left( {{\dot{\psi }} \mathbf {e_3}} \right) \textbf{q} - \frac{1}{{{z^*}}}\textbf{v} + \frac{1}{{{z^*}}}\textbf{d} \end{aligned}$$
(11)

where \(\textbf{q} = {\left[ {{q_x},{q_y},{q_z}} \right] ^T}\). \(z^*\) is the desired altitude.

In order to control the yaw motion of quadrotor UAV, we select the image feature \(q_\psi \) to describe the corresponding motion according to [12], which is defined as follows:

$$\begin{aligned} {q_\psi } = \frac{1}{2}\arctan \left( {\frac{{2{}^{\nu }{\mu _{11}}}}{{{}^{\nu }{\mu _{20}} - {}^{\nu }{\mu _{02}}}}} \right) \end{aligned}$$
(12)

where the time derivative of \(q_\psi \) is \({\dot{q}_\psi } = - {\dot{\psi }} + \Delta _{\psi }\), and \(\Delta _{\psi }\) is the equivalent of an undefined term that indicates the velocity of the target in the yaw direction.

3 Controller design

This section first gives the closed-loop error equation of the system and then gives the design of the target trajectory observer and the design of the linear velocity finite-time observer in the plane of the virtual camera. Finally, we give the design process of the global finite-time controller. Figure 3 shows the block diagram of the whole system.

The following lemmas are useful to derive our main results.

Lemma 1

[32] Consider the nonlinear system \(\dot{x} = f\left( x\right) , f(0) = 0, x \in {{{\mathbb {R}}}^{n}}\), where \(f(\cdot ):{{{\mathbb {R}}}^{n}} \rightarrow {{{\mathbb {R}}}^{n}}\) is continuous function. Suppose that there exists a positive definite continuous function V(x) such that

$$\begin{aligned} \dot{V}(x) + c V^{\alpha }(x) \le 0, \end{aligned}$$

where \(c > 0\) and \(\alpha \in (0,1)\). Then, the system is finite-time stable. In addition, the finite convergence time T(x) satisfies that

$$\begin{aligned} T(x) \le \frac{V^{1-\alpha }(x(0))}{c(1-\alpha )}. \end{aligned}$$

Lemma 2

[33] For any real numbers \(x_i,i=1,\ldots ,n\) and \(b \in \left( 0,1 \right] \) the following inequality holds:

$$\begin{aligned} {{\left( |{{x}_{1}} |+\cdots +|{{x}_{n}} |\right) }^{b}}\le {{|{{x}_{1}} |}^{b}}+\cdots +{{|{{x}_{n}} |}^{b}}. \end{aligned}$$

When \(b = p/q \le 1\), where \(p>0,q>0\) are odd integers,

$$\begin{aligned} |{{x}^{b}}-{{y}^{b}} |\le {{2}^{1-b}}{{|x-y |}^{b}}. \end{aligned}$$

Lemma 3

[34] For real variables x, y, and any positive constants a, b, c, the following inequality is true.

$$\begin{aligned} {{|x |}^{a}}{{|y |}^{b}}\le \frac{a}{a+b}c{{|x |}^{a+b}}+\frac{b}{a+b}{{c}^{-\frac{a}{b}}}{{|y |}^{a+b}}. \end{aligned}$$
Fig. 3
figure 3

Structure diagram of the system

Full size image

3.1 Image feature error dynamics

We define the desired image features as follows:

$$\begin{aligned} {\textbf{q}_d} = {\left( {q_x^d,q_y^d,q_z^d} \right) ^T} = {\left( {0,0,1} \right) ^T},q_\psi ^d = 0 . \end{aligned}$$

Therefore, the image moment feature errors of translational motion are as follows:

$$\begin{aligned} {\textbf{q}_1} = \textbf{q} - {\left( {0,0,1} \right) ^T}. \end{aligned}$$

Taking the derivative of the above formula and using (11), we can obtain the following dynamics

$$\begin{aligned} {{{\dot{\textbf{q}}}}_{1}}&=-\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}}-\frac{1}{{{z}^{*}}}\textbf{v} + \frac{1}{{{z^*}}}\textbf{d} \end{aligned}$$
(13)
$$\begin{aligned} {\dot{\textbf{v}}}&=-\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) \textbf{v}+\textbf{f} \end{aligned}$$
(14)
$$\begin{aligned} {{{{\dot{\textbf{R}}}}}_{\phi \theta }}&={{{\textbf{R}}}_{\phi \theta }}\textbf{sk}\left( {\omega } \right) -\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{{\textbf{R}}}_{\phi \theta }} \end{aligned}$$
(15)
$$\begin{aligned} {\textbf{J}}\dot{\omega }&=-{\omega }\times {\textbf{J}}\omega +{\tau } \end{aligned}$$
(16)

where \(\textbf{f}=-{{{\textbf{R}}}_{\phi \theta }}{{U}_{1}}{{\textbf{E}}_{3}}/m+g{{\textbf{e}}_{3}} = \left[ f_x,f_y,f_z \right] ^T,{{\textbf{R}}}_{\phi \theta } = {\textbf{R}}_{\theta } {\textbf{R}}_{\phi }\).

3.2 Trajectory observer

Before designing the controller, we need to estimate the trajectory parameters. The standard method uses a high-order differentiator, but the high-order differentiator is sensitive to noise. Therefore, we use the nonlinear tracking differentiator proposed by Han and Wang, proving its stability. The general form of the nonlinear tracking differentiator with the input v(t) is as follows [35]:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{{\dot{x}}}_{1}}={{x}_{2}} &{} \\ \cdots &{} \\ {{{\dot{x}}}_{n-1}}={{x}_{n}} &{} \\ {{{\dot{x}}}_{n}}={{R}^{n}}f\left( {{x}_{1}}-v\left( t \right) ,\frac{{{x}_{2}}}{R},\cdots ,\frac{{{x}_{n}}}{{{R}^{n-1}}} \right) &{} \end{array}\right. } \end{aligned}$$
(17)

where \(x_1\) tracks the origin signal v(t) and \(x_{i+1} (i>0)\) is the estimation of ith-order derivative. R is a coefficient to determine the rate of convergence for (17). The function \(f\left( \cdot \right) \) is suggested by Han and Wang as follows [35]:

$$\begin{aligned} \begin{aligned} f\left( \cdot \right) =&\text {fal}\left( {{x}_{1}},{{\alpha }_{1}},\Delta \right) +\text {fal}\left( {{x}_{2}},{{\alpha }_{2}},\Delta \right) \\&+\cdots +\text {fal}\left( {{x}_{n}},{{\alpha }_{n}},\Delta \right) \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} \text {fal}\left( {{x}_{i}},{{\alpha }_{i}},\Delta \right) \,= \,{\left\{ \begin{array}{ll} {{|{{x}_{i}} |}^{{{\alpha }_{i}}}}\text {sign}\left( {{x}_{i}} \right) , &{} |{{x}_{i}} |>\Delta \\ z/{{\Delta }^{1-{{\alpha }_{i}}}}, &{} |{{x}_{i}} |<\Delta ,\Delta >0 \end{array}\right. } \end{aligned}$$
(19)

\(\alpha _i\) is a coefficient to reflect the degree of the nonlinearity, and \(\alpha _i = 1\) is corresponding to the linear case. \(\Delta \) is used to determine the linear interval, which can prevent vibration when the system is in the neighborhood of origin point.

For our system, the velocity of the target object is \(\textbf{d}\), its estimated value is \(\hat{\textbf{d}}\), and the estimation error is \(\tilde{\textbf{d}}\). Therefore, the following observer is designed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{{\dot{x}}}_{1}}={{x}_{2}} &{} \\ {{{\dot{x}}}_{2}}={{x}_{3}} &{} \\ {{{\dot{x}}}_{3}}={{x}_{4}} &{} \\ {{{\dot{x}}}_{4}}={{R}^{4}}f\left( {{x}_{1}}-{\tilde{d}},\frac{{{x}_{2}}}{R},\frac{{{x}_{3}}}{{{R}^{2}}},\frac{{{x}_{4}}}{{{R}^{3}}} \right) &{} \\ \end{array}\right. } \end{aligned}$$
(20)

where \({{x}_{1}}=\hat{\textbf{d}},{{x}_{2}}=\dot{\hat{\textbf{d}}},{{x}_{3}}=\ddot{\hat{\textbf{d}}},{{x}_{4}}=\dddot{\hat{\textbf{d}}}\).

3.3 Finite-time velocity observer

In order to compensate for the depth information of the monocular camera, estimate the linear velocity in the virtual plane, and ensure the convergence performance of the observer, we design a finite-time linear velocity observer (FTO).

Theorem 1

The velocity observer and the corresponding update law are defined as follows:

$$\begin{aligned} {{\dot{\hat{\textbf{q}}}}_{1}}&=-\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}}-\frac{1}{{{z}^{*}}}{\hat{\textbf{v}}}+\frac{1}{{{z}^{*}}}\textbf{d}+{{k}_{1}}{{{\tilde{\textbf{q}}}}_{1}^{\frac{5}{7}}} \end{aligned}$$
(21)
$$\begin{aligned} {\dot{\hat{\textbf{v}}}}&=-\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {\hat{\textbf{v}}}+\textbf{f}-\frac{1}{{{z}^{*}}}{{{\tilde{\textbf{q}}}}_{1}}+\frac{{{k}_{2}}}{{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}} \end{aligned}$$
(22)

where \({{{\dot{\hat{\textbf{q}}}}}_{1}}\) and \({\dot{\hat{\textbf{v}}}}\) are the estimated values of \(\textbf{q}_1\) and \(\textbf{v}\), respectively. \(k_1\) and \(k_2\) are positive constant. \(\tilde{\textbf{q}}_{1}^{\frac{5}{7}}={{\left[ \tilde{q}_{11}^{\frac{5}{7}},\tilde{q}_{12}^{\frac{5}{7}},\tilde{q}_{13}^{\frac{5}{7}} \right] }^{T}}\) and \({{{\tilde{\textbf{v}}}}^{\frac{5}{7}}}={{\left[ \tilde{v}_{1}^{\frac{5}{7}},\tilde{v}_{2}^{\frac{5}{7}},\tilde{v}_{3}^{\frac{5}{7}} \right] }^{T}}\). \({{{\tilde{\textbf{q}}}}_{1}}\) and \({{{{\tilde{\textbf{v}}}}}}\) are the corresponding estimation errors, which define as follows:

$$\begin{aligned} {{{\tilde{\textbf{q}}}}_{1}}&= \mathbf {{q}_1} - \hat{\textbf{q}}_{\textbf{1}} \end{aligned}$$
(23)
$$\begin{aligned} {{{{\tilde{\textbf{v}}}}}}&= \mathbf {{v}} - {\hat{\textbf{v}}}. \end{aligned}$$
(24)

This linear velocity observer is globally finite-time stable.

Proof

We first take the time derivatives of (23) and (24) then substitute (13) and (14), respectively. We can get the following expression:

$$\begin{aligned} {{\dot{\tilde{\textbf{q}}}}_{1}}&={{\dot{\textbf{q}}}_{1}}-{{\dot{\hat{\textbf{q}}}}_{1}}=-\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-{{k}_{1}}\tilde{\textbf{q}}_{1}^{\frac{5}{7}} \end{aligned}$$
(25)
$$\begin{aligned} \dot{\tilde{\textbf{v}}}&=\dot{\textbf{v}}-{\dot{\hat{\textbf{v}}}}=-\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {\tilde{\textbf{v}}}+\frac{1}{{{z}^{*}}}{{\tilde{\textbf{q}}}_{1}}-\frac{{{k}_{2}}}{{{z}^{*}}}{{{\tilde{\textbf{v}}}}^{\frac{5}{7}}}. \end{aligned}$$
(26)

Now we choose a Lyapunov candidate function

$$\begin{aligned} L=\frac{1}{2}\tilde{\textbf{q}}_{1}^{T}{{\tilde{\textbf{q}}}_{1}}+\frac{1}{2}{{{\tilde{\textbf{v}}}}^{T}}{\tilde{\textbf{v}}} = \frac{1}{2}\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) . \end{aligned}$$
(27)

Taking the derivative of time for (27). Then substitute (21) and (22) into to (27), we can get the following:

$$\begin{aligned} \begin{aligned} \dot{L}&=-\tilde{\textbf{q}}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+{{{{\tilde{\textbf{v}}}}}^{T}}\frac{1}{{{z}^{*}}}{{{\tilde{\textbf{q}}}}_{1}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \\&=-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \end{aligned} \end{aligned}$$
(28)

where r is a design parameter.  (28) is definite negative. Inspired by [17] and [33], we can select a set of design parameters as follows:

$$\begin{aligned} {{\beta }_{1}}&=2\min \left\{ {{k}_{1}},\frac{{{k}_{2}}}{{{z}^{*}}} \right\} \end{aligned}$$
(29)
$$\begin{aligned} n&=3 \end{aligned}$$
(30)
$$\begin{aligned} r&=\frac{4n}{2n+1}=\frac{12}{7} \end{aligned}$$
(31)
$$\begin{aligned} \alpha&=\frac{2n}{2n+1}=\frac{6}{7} \end{aligned}$$
(32)

where \(n=3\) represents the order of the system. Then, we use the parameter (29) in (28), and we can get

$$\begin{aligned} \dot{L}&=-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \nonumber \\&\le -{{\beta }_{1}}\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \le 0 \end{aligned}$$
(33)

So far, we have been able to prove that the observer can be globally asymptotically stable (GAS). We continue to prove that it can be globally finite-time stable (GFTS). Scaling the (27), we can get

$$\begin{aligned} \begin{aligned} L&=\frac{1}{2}\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) \\&\le 2\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) . \end{aligned} \end{aligned}$$
(34)

Combining (33) and (34) , and using Lemma 2, we can get

$$\begin{aligned} \begin{aligned} {{L}^{\alpha }}&\le {{2}^{\alpha }}{{\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }} \\&\le 2{{\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }}\le 2\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \end{aligned} \end{aligned}$$
(35)

where \(r = 2\alpha \). And then, we select a function as follows:

$$\begin{aligned} \begin{aligned} \dot{L}+\frac{{{\beta }_{1}}}{4}{{L}^{\alpha }}\le&-{{\beta }_{1}}\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \\&+\frac{{{\beta }_{1}}}{2}\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \\ \le&-\frac{{{\beta }_{1}}}{2}\left( \sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \le 0 . \end{aligned} \end{aligned}$$
(36)

The result means that \(\dot{L}\le -\frac{{{\beta }_{1}}}{4}{{L}^{\alpha }}\) holds. That is, we can find a Lyapunov function satisfying Lemma 1. So far, the proposed velocity observer is globally finite-time stable (GFTS). \(\square \)

3.4 Finite-time controller

We mainly use the backstepping scheme to design the IBVS controller of QUAV, and we need to use the proposed velocity observer.

We define the first Lyapunov function:

$$\begin{aligned} V_1 = \frac{1}{2} \textbf{q}^{T}_{1}\textbf{q}_1. \end{aligned}$$

By substituting (13), we can get the time derivative of the Lyapunov function

$$\begin{aligned} \begin{aligned} \dot{V}_1&= \textbf{q}^{T}_{1}\left( -\textbf{sk}\left( \dot{\psi } \textbf{e}_3 \right) \textbf{q}_1 - \frac{1}{z^*} \textbf{v} + \frac{1}{{{z}^{*}}}\textbf{d} \right) \\&= -\textbf{q}^{T}_{1}\frac{1}{z^*}\left( {\tilde{\textbf{v}}} + {\hat{\textbf{v}}} + \textbf{d} \right) . \end{aligned} \end{aligned}$$
(37)

We treat \({\hat{\textbf{v}}}\) as a virtual control input, and choose \({{{\hat{\textbf{v}}}}^{d}}={{c}_{1}}\textbf{q}_{1}^{\frac{5}{7}} + \textbf{d} , c_1>0, \textbf{q}_{1}^{\frac{5}{7}}={{\left[ q_{11}^{\frac{5}{7}},q_{12}^{\frac{5}{7}},q_{13}^{\frac{5}{7}} \right] }^{T}}\). According to the standard backstepping scheme, it is necessary to continue to define new error terms \(\textbf{q}_2\)

$$\begin{aligned} {{\textbf{q}}_{2}}=\textbf{q}_{1}^{\frac{5}{7}}-\frac{1}{{{c}_{1}}}{\hat{\textbf{v}}} + \frac{1}{{{c}_{1}}}\textbf{d}. \end{aligned}$$
(38)

Update \(\dot{V}_1\) in (37) using (38)

$$\begin{aligned} {{\dot{V}}_{1}}=-\textbf{q}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}+\textbf{q}_{1}^{T}\frac{{{c}_{1}}}{{{z}^{*}}}{{\textbf{q}}_{2}}. \end{aligned}$$
(39)

Then we define the second Lyapunov function

$$\begin{aligned} {{V}_{2}}={{V}_{1}}+\frac{1}{2}\textbf{q}_{2}^{T}{{\textbf{q}}_{2}}+L. \end{aligned}$$
(40)

Since we need to get the time derivative of (40), we need to get the time derivative of \(\textbf{q}_2\) first. Taking the time derivative of (38), then substituting (13) and (22) into it, we can get

$$\begin{aligned} \begin{aligned} {{{\dot{\textbf{q}}}}_{2}}=&-\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}}+\frac{1}{{{c}_{1}}}\dot{\textbf{d}} \\&-\frac{5}{7{{z}^{*}}}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{v}-\frac{{{k}_{2}}}{{{c}_{1}}{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}}+\frac{1}{{{c}_{1}}{{z}^{*}}}{{{\tilde{\textbf{q}}}}_{1}} \\&+\frac{5}{7{{z}^{*}}}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{d}-\frac{1}{{{c}_{1}}}\textbf{f}+\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) \frac{1}{{{c}_{1}}}{\hat{\textbf{v}}} \end{aligned} \end{aligned}$$
(41)

where \(\textbf{q}_{1}^{-\frac{2}{7}}\text {=}{{\left[ q_{11}^{-\frac{2}{7}},q_{12}^{-\frac{2}{7}},q_{13}^{-\frac{2}{7}} \right] }^{T}}\). Now we can get the time derivative of the second Lyapunov function. Taking the time derivative of (40), then substituting (39), (41) and (33) into it, we can get

$$\begin{aligned} {{{\dot{V}}}_{2}}=&{{{\dot{V}}}_{1}}+\textbf{q}_{2}^{T}{{{\dot{\textbf{q}}}}_{2}}+\dot{L}\nonumber \\ =&-\textbf{q}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-\textbf{q}_{2}^{T}\frac{{{k}_{2}}}{{{c}_{1}}{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}} \nonumber \\&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \nonumber \\&+\textbf{q}_{2}^{T}\left( -\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}} \right. \nonumber \\&-\frac{5}{7{{z}^{*}}}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{v}+\frac{5}{7{{z}^{*}}}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{d} \nonumber \\&+\frac{{{c}_{1}}}{{{z}^{*}}}{{\textbf{q}}_{1}}+\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) \frac{1}{{{c}_{1}}}{\hat{\textbf{v}}}-\frac{1}{{{c}_{1}}}\textbf{f} \nonumber \\&\left. +\frac{1}{{{c}_{1}}{{z}^{*}}}{{{\tilde{\textbf{q}}}}_{1}}+\frac{1}{{{c}_{1}}}\dot{\textbf{d}} \right) \end{aligned}$$
(42)

We can also prove that (42) is also GFTS.

Theorem 2

Considering \(\textbf{f}\) as a virtual control input and design \(\textbf{f}\) as follows:

$$\begin{aligned} \begin{aligned} \frac{1}{{{c}_{1}}}{{\textbf{f}}_{d}}=&\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \left( -\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}}-\frac{1}{{{z}^{*}}}\textbf{v} + \frac{1}{{{z}^{*}}}\textbf{d} \right) \\&+{{k}_{3}}\textbf{q}_{2}^{\frac{5}{7}}+\frac{{{c}_{1}}}{{{z}^{*}}}{{\textbf{q}}_{1}}+\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) \frac{1}{{{c}_{1}}}{\hat{\textbf{v}}} \\&+\frac{1}{{{c}_{1}}}\dot{\textbf{d}}+\frac{1}{{{c}_{1}}{{z}^{*}}}{{{\tilde{\textbf{q}}}}_{1}} \end{aligned} \end{aligned}$$
(43)

\(\dot{V}_2\) is definite negative, and the system is GFTS.

Proof

Substituting (43) into (42), we can obtain

$$\begin{aligned} \begin{aligned} {{{\dot{V}}}_{2}}=&-\textbf{q}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-\textbf{q}_{2}^{T}\frac{{{k}_{2}}}{{{c}_{1}}{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}}-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}} \\&-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}. \end{aligned} \end{aligned}$$
(44)

Using Lemma 3 to scale (44). The parameters are \(a=b=c=1\), then we can get

$$\begin{aligned} \begin{aligned} {{{\dot{V}}}_{2}}\le&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \\&-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}} -\frac{1}{2{{z}^{*}}}\left( \textbf{q}_{1}^{T}{{\textbf{q}}_{1}}+{{{{\tilde{\textbf{v}}}}}^{T}}{\tilde{\textbf{v}}} \right) \\&-\frac{{{k}_{2}}}{2{{c}_{1}}{{z}^{*}}}\left( \textbf{q}_{2}^{T}{{\textbf{q}}_{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{\frac{10}{7}}} \right) \\ \le&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}. \end{aligned} \end{aligned}$$
(45)

where \(-\textbf{q}_{\textbf{1}}^{\textbf{T}}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}\le -\frac{1}{2{{z}^{*}}}\left( \textbf{q}_{\textbf{1}}^{\textbf{T}}{{\textbf{q}}_{1}}+{{{{\tilde{\textbf{v}}}}}^{T}}{\tilde{\textbf{v}}} \right) ,{{z}^{*}}<0\).

Now use Lemma 2 for (45) and scale (40) simultaneously, then combine the results of the two equations, and we can get

$$\begin{aligned} {{{\dot{V}}}_{2}}\le&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}\nonumber \\&-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}\nonumber \\ \le&-{{\beta }_{2}}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}+\sum \limits _{i=1}^{3}{q_{2i}^{r}} \right) \end{aligned}$$
(46)
$$\begin{aligned} V_{2}^{\alpha }=&\left( \frac{1}{2}\sum \limits _{i=1}^{3}{q_{1i}^{2}}+\frac{1}{2}\sum \limits _{i=1}^{3}{q_{2i}^{2}} \right. \nonumber \\&{{\left. +\frac{1}{2}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\frac{1}{2}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }}\nonumber \\ \le&{{2}^{\alpha }}{{\left( \sum \limits _{i=1}^{3}{q_{1i}^{2}}+\sum \limits _{i=1}^{3}{q_{2i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }} \nonumber \\ \le&2{{\left( \sum \limits _{i=1}^{3}{q_{1i}^{2}}+\sum \limits _{i=1}^{3}{q_{2i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }} \nonumber \\ \le&2\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{q_{2i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \end{aligned}$$
(47)
$$\begin{aligned} {{{\dot{V}}}_{2}}&+\frac{{{\beta }_{2}}}{4}V_{2}^{\alpha } \nonumber \\ \le&-{{\beta }_{2}}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}+\sum \limits _{i=1}^{3}{q_{2i}^{r}} \right) \nonumber \\&+\frac{{{\beta }_{2}}}{2}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{q_{2i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \nonumber \\ =&-\frac{{{\beta }_{2}}}{2}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{q_{2i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right) \nonumber \\ \le&0. \end{aligned}$$
(48)

The result means that \(\dot{V}_2 \le -\frac{\beta _2}{4}V^{\alpha }_{2}\) holds, where \({{\beta }_{2}}=2\min \left\{ \frac{{{c}_{1}}}{{{z}^{*}}},{{k}_{1}},\frac{{{k}_{2}}}{{{z}^{*}}},{{k}_{3}} \right\} \). So far, we have proved that \(V_2\) is GFTS. \(\square \)

Remark 2

If we use the small angle assumption, we can get the desired attitude of the QUAV through the following equation

$$\begin{aligned} {{\theta }_{d}}&=\arctan \left( \frac{{{f}^d_{x}}}{{{f}^d_{z}}-g} \right) , \\ {{\phi }_{d}}&=\arctan \left( -\frac{\cos {{\theta }_{d}}{{f}^d_{y}}}{{{f}^d_{z}}-g} \right) . \end{aligned}$$

However, this paper does not adopt this assumption, so it is necessary to continue the backstepping design to obtain the desired angular velocity.

Continue to define the third error term

$$\begin{aligned} {{\textbf{q}}_{3}}=\frac{1}{{{k}_{3}}{{c}_{1}}}\textbf{f}-\frac{1}{{{k}_{3}}{{c}_{1}}}{{\textbf{f}}_{d}}. \end{aligned}$$
(49)

Update \(\dot{V}_2\) in (42) using (43)

$$\begin{aligned} \begin{aligned} {{{\dot{V}}}_{2}}=&-\textbf{q}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-\textbf{q}_{2}^{T}\frac{{{k}_{2}}}{{{c}_{1}}{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}}-{{k}_{3}}\textbf{q}_{3}^{T}{{\textbf{q}}_{2}} \\&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}} \\&-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}. \end{aligned} \end{aligned}$$
(50)

Then we define the third Lyapunov function

$$\begin{aligned} {{V}_{3}}={{V}_{2}}+\frac{1}{2}\textbf{q}_{3}^{T}{{\textbf{q}}_{3}}. \end{aligned}$$
(51)

Using (50) and (49), we can get the time derivative of \(V_3\)

$$\begin{aligned} \begin{aligned} {{{\dot{V}}}_{3}}=&{{{\dot{V}}}_{2}}+\textbf{q}_{3}^{T}{{{\dot{\textbf{q}}}}_{3}} \\ =&-\textbf{q}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-\textbf{q}_{2}^{T}\frac{{{k}_{2}}}{{{c}_{1}}{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}}-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}} \\&-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \\&+\textbf{q}_{3}^{T}\left( \frac{1}{{{k}_{3}}{{c}_{1}}}{\dot{\textbf{f}}}-\frac{1}{{{k}_{3}}{{c}_{1}}}{{{{\dot{\textbf{f}}}}}_{d}}-{{k}_{3}}{{\textbf{q}}_{2}} \right) \end{aligned} \end{aligned}$$
(52)

where \(\frac{1}{{{c}_{1}}}{{{\dot{\textbf{f}}}}_{d}}\) is expressed as follows:

$$\begin{aligned} \frac{1}{{{c}_{1}}}{{{{\dot{\textbf{f}}}}}_{d}}=&\frac{10}{49}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{9}{7}} \right) \textbf{diag}\left( {{{\dot{\textbf{q}}}}_{1}} \right) \textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}}\nonumber \\&+\frac{10}{49}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{9}{7}} \right) \textbf{diag}\left( {{{\dot{\textbf{q}}}}_{1}} \right) \frac{1}{{{z}^{*}}}\textbf{v} \nonumber \\&+\frac{10}{49}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{9}{7}} \right) \textbf{diag}\left( {{{\dot{\textbf{q}}}}_{1}} \right) \frac{1}{{{z}^{*}}}\textbf{d}\nonumber \\&-\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \frac{1}{{{z}^{*}}}\dot{\textbf{v}} +\frac{1}{{{c}_{1}}{{z}^{*}}}{{{\dot{\tilde{\textbf{q}}}}}_{1}}\nonumber \\&+\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \frac{1}{{{z}^{*}}}\dot{\textbf{d}} +\frac{1}{{{c}_{1}}}\ddot{{\textbf{d}}}\nonumber \\&-\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{sk}\left( \ddot{\psi }{{\textbf{e}}_{3}} \right) {{\textbf{q}}_{1}} \nonumber \\&-\frac{5}{7}\textbf{diag}\left( \textbf{q}_{1}^{-\frac{2}{7}} \right) \textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) {{{\dot{\textbf{q}}}}_{1}}\nonumber \\&+\frac{5}{7}{{k}_{3}}\textbf{q}_{2}^{-\frac{2}{7}}{{{\dot{\textbf{q}}}}_{2}}+\textbf{sk}\left( \ddot{\psi }{{\textbf{e}}_{3}} \right) \frac{1}{{{c}_{1}}}{\hat{\textbf{v}}} \nonumber \\&+\frac{{{c}_{1}}}{{{z}^{*}}}{{{\dot{\textbf{q}}}}_{1}}+\textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) \frac{1}{{{c}_{1}}}{\dot{\hat{\textbf{v}}}} . \end{aligned}$$
(53)

Theorem 3

Considering \(\dot{\textbf{f}}\) as the control input and design \(\dot{\textbf{f}}\) as follows:

$$\begin{aligned} {\dot{\textbf{f}}}=-{{c}_{1}}{{k}_{3}}{{k}_{4}}\textbf{q}_{3}^{\frac{5}{7}}+{{c}_{1}}k_{3}^{2}{{\textbf{q}}_{2}}+{{{\dot{\textbf{f}}}}_{d}} \end{aligned}$$
(54)

\(\dot{V}_3\) is definite negative, the system is GFTS.

Proof

Substituting (54) into (52), we can get

$$\begin{aligned} \begin{aligned} {{{\dot{V}}}_{3}}=&{{{\dot{V}}}_{2}}+\textbf{q}_{3}^{T}{{{\dot{\textbf{q}}}}_{3}} \\ =&-\textbf{q}_{1}^{T}\frac{1}{{{z}^{*}}}{\tilde{\textbf{v}}}-\textbf{q}_{2}^{T}\frac{{{k}_{2}}}{{{c}_{1}}{{z}^{*}}}{{{{\tilde{\textbf{v}}}}}^{\frac{5}{7}}}-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}} \\&-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}} \\&-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{4}}\sum \limits _{i=1}^{3}{q_{3i}^{r}} . \end{aligned} \end{aligned}$$
(55)

Using Lemma 3 to scale (55), we can get

$$\begin{aligned} {{{\dot{V}}}_{3}}\le&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}} \nonumber \\&-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}-{{k}_{4}}\sum \limits _{i=1}^{3}{q_{3i}^{r}}\nonumber \\&-\frac{1}{2{{z}^{*}}}\left( \textbf{q}_{1}^{T}{{\textbf{q}}_{1}}+{{{{\tilde{\textbf{v}}}}}^{T}}{\tilde{\textbf{v}}} \right) \nonumber \\&-\frac{{{k}_{2}}}{2{{c}_{1}}{{z}^{*}}}\left( \textbf{q}_{2}^{T}{{\textbf{q}}_{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{\frac{10}{7}}} \right) \nonumber \\ \le&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}} \nonumber \\&-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}-{{k}_{4}}\sum \limits _{i=1}^{3}{q_{3i}^{r}}. \end{aligned}$$
(56)

Using Lemma 2 for (56) and scaling (51), we can obtain

$$\begin{aligned} {{{\dot{V}}}_{3}}\le&-\frac{{{c}_{1}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{q_{1i}^{r}}-{{k}_{1}}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}\nonumber \\&-\frac{{{k}_{2}}}{{{z}^{*}}}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-{{k}_{3}}\sum \limits _{i=1}^{3}{q_{2i}^{r}}-{{k}_{4}}\sum \limits _{i=1}^{3}{q_{3i}^{r}} \nonumber \\ \le&{{\beta }_{3}}\left( -\sum \limits _{i=1}^{3}{q_{1i}^{r}}-\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}} \right. \nonumber \\&\left. -\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}}-\sum \limits _{i=1}^{3}{q_{2i}^{r}}-\sum \limits _{i=1}^{3}{q_{3i}^{r}} \right) \end{aligned}$$
(57)
$$\begin{aligned} V_{3}^{\alpha }=&\left( \frac{1}{2}\sum \limits _{i=1}^{3}{q_{1i}^{2}}+\frac{1}{2}\sum \limits _{i=1}^{3}{q_{2i}^{2}} \right. +\frac{1}{2}\sum \limits _{i=1}^{3}{q_{3i}^{2}}\nonumber \\&{{\left. +\frac{1}{2}\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\frac{1}{2}\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }}\nonumber \\ \le&2\left( \sum \limits _{i=1}^{3}{q_{1i}^{2}}+\sum \limits _{i=1}^{3}{q_{2i}^{2}} \right. +\sum \limits _{i=1}^{3}{q_{3i}^{2}}\nonumber \\&{{\left. +\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{2}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{2}} \right) }^{\alpha }} \end{aligned}$$
(58)
$$\begin{aligned} {{{\dot{V}}}_{3}}+\frac{{{\beta }_{3}}}{4}V_{3}^{\alpha }\le&-{{\beta }_{3}}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right. \nonumber \\&\left. +\sum \limits _{i=1}^{3}{q_{2i}^{r}}+\sum \limits _{i=1}^{3}{q_{3i}^{r}} \right) \nonumber \\&+\frac{{{\beta }_{3}}}{2}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right. \nonumber \\&\left. +\sum \limits _{i=1}^{3}{q_{2i}^{r}}+\sum \limits _{i=1}^{3}{q_{3i}^{r}} \right) \nonumber \\ =&-\frac{{{\beta }_{3}}}{2}\left( \sum \limits _{i=1}^{3}{q_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{q}_{1i}^{r}}+\sum \limits _{i=1}^{3}{\tilde{v}_{i}^{r}} \right. \nonumber \\&\left. +\sum \limits _{i=1}^{3}{q_{2i}^{r}}+\sum \limits _{i=1}^{3}{q_{3i}^{r}} \right) \le 0 . \end{aligned}$$
(59)

The result means that \({{\dot{V}}_{3}}\le -\frac{{{\beta }_{3}}}{4}V_{3}^{\alpha }\) holds, where \({{\beta }_{3}}=2\min \left\{ \frac{{{c}_{1}}}{{{z}^{*}}},{{k}_{1}},\frac{{{k}_{2}}}{{{z}^{*}}},{{k}_{3}},{{k}_{4}} \right\} \). The \(V_3\) is GFTS. \(\square \)

So far, we have obtained the controller, but we also need to obtain the angular velocity and thrust that can be directly used to control the QUAV. Since in the virtual camera frame, the force \(\textbf{f}\) of the QUAV is expressed as

$$\begin{aligned} \textbf{f}=\frac{-{{{\textbf{R}}}_{\phi \theta }}{{U}_{1}}{{\textbf{E}}_{3}}}{m}+g{{\textbf{e}}_{3}}. \end{aligned}$$
(60)

By taking the time derivative of (60) and substituting (15), we can get

$$\begin{aligned} \textbf{sk}\left( \dot{\psi }{{\textbf{e}}_{3}} \right) \left( mg{{\textbf{e}}_{3}}-m\textbf{f} \right) -m{\dot{\textbf{f}}}={{{\textbf{R}}}_{\phi \theta }}\left[ \begin{matrix} {{\omega }_{2}}{{U}_{1}} \\ -{{\omega }_{1}}{{U}_{1}} \\ {{{\dot{U}}}_{1}} \\ \end{matrix} \right] . \end{aligned}$$
(61)

Finally, we only need to combine (61) and (54) to obtain the desired thrust \(U_1\) and desired angular velocity \(\omega _1, \omega _2\) respectively.

Remark 3

This paper only studies the controller of translational motion obtained from the image moment features in the virtual camera plane. When we get the desired angular velocity, we can use a PD or PID controller to realize the translation control of the QUAV in the horizontal and altitude directions.

After the above process, we get the controller to control the translational motion, and we also need to get the controller to control the yaw motion. The image feature error is defined as

$$\begin{aligned} q_4 = q_{\psi } -q^d_{\psi } \end{aligned}$$

where \(q^d_{\psi }\) is the desired value. According to (12), we can get

$$\begin{aligned} \dot{q}_4 = -{\dot{\psi }} + \Delta _{\psi }. \end{aligned}$$
(62)

Theorem 4

Design the control input as

$$\begin{aligned} {{\omega }_{3}}=\left( {{k}_{5}}q_{4}^{\frac{1}{3}} + \Delta _{\psi } -\frac{\sin \phi }{\cos \theta }{{\omega }_{2}} \right) \frac{\cos \theta }{\cos \phi } \end{aligned}$$
(63)

with \(k_5 > 0\), the image feature error \(q_4\) while converge to zero in a finite-time.

Proof

The relationship between the time derivative of Euler angles and angular velocity is as follows:

$$\begin{aligned} \begin{bmatrix} {\dot{\phi }} \\ {\dot{\theta }} \\ {\dot{\psi }} \\ \end{bmatrix} =\left[ \begin{matrix} 1 &{} \sin \phi \tan \theta &{} \cos \phi \tan \theta \\ 0 &{} \cos \phi &{} \sin \phi \\ 0 &{} \sin \phi /\cos \theta &{} \cos \phi /\cos \theta \\ \end{matrix} \right] \begin{bmatrix} {{\omega }_{1}} \\ {{\omega }_{2}} \\ {{\omega }_{3}} \\ \end{bmatrix}. \end{aligned}$$
(64)

From (64), we have

$$\begin{aligned} \dot{\psi }=\frac{\sin \phi }{\cos \theta }{{\omega }_{2}}+\frac{\cos \phi }{\cos \theta }{{\omega }_{3}}. \end{aligned}$$
(65)

Now we choose a Lyapunov function

$$\begin{aligned} V_{\psi } = \frac{1}{2} q^2_4. \end{aligned}$$
(66)

Then we take the time derivative of (66) and substitute (63) (65) into it, we get

$$\begin{aligned} {{{\dot{V}}}_{\psi }}={{q}_{4}}\left( -\dot{\psi } + \Delta _{\psi } \right) =-{{k}_{5}}q_{4}^{r}. \end{aligned}$$
(67)

By scaling (66) and combining the results with (67), we can get

$$\begin{aligned}&V_{\psi }^{\alpha }={{\left( \frac{1}{2}q_{4}^{2} \right) }^{\alpha }}\le {{\left( 2q_{4}^{2} \right) }^{\alpha }}\le 2q_{4}^{r} , \end{aligned}$$
(68)
$$\begin{aligned}&{{{\dot{V}}}_{\psi }}+\frac{{{k}_{5}}}{4}V_{\psi }^{\alpha }=-{{k}_{5}}q_{4}^{r}+\frac{{{k}_{5}}}{2}q_{4}^{r}=-\frac{{{k}_{5}}}{2}q_{4}^{r}\le 0. \end{aligned}$$
(69)

The result means that \({{\dot{V}}_{\psi }}\le -\frac{{{k}_{5}}}{4}V_{\psi }^{\alpha }\) holds, and the \(V_{\psi }\) is GFTS. Finally, we can get that \(q_4\) will converge to zero in a finite time. \(\square \)

Remark 4

In the actual QUAV system, yaw motion control is usually regarded as an independent channel. Therefore, according to the characteristics of its dynamic model and image moment error model, the design parameters of the yaw motion controller are selected as follows:

$$\begin{aligned} n=1 , r=\frac{4n}{2n+1}=\frac{4}{3}, \alpha =\frac{2n}{2n+1}=\frac{2}{3}. \end{aligned}$$

Remark 5

After the above controller design process, we can use Lemma 1 to describe the convergence time of the system quantitatively. Recall that convergence time T(x) as follows:

$$\begin{aligned} T(x) \le \frac{V^{1-\alpha }(x(0))}{c(1-\alpha )}. \end{aligned}$$
(70)

Then the convergence time of the translation motion and the yaw motion can be expressed as follows:

$$\begin{aligned} {{T}_{1}}\left( x \right) \le \frac{V_{3}^{\frac{1}{7}}\left( \textbf{q}_1\left( 0 \right) \right) }{{{\beta }_{3}}/28} \end{aligned}$$
(71)
$$\begin{aligned} {{T}_{2}}\left( x \right) \le \frac{V_{\psi }^{\frac{1}{3}}\left( {{q}_{4}}\left( 0 \right) \right) }{{{k}_{5}}/12} \end{aligned}$$
(72)

where \(\textbf{q}_1\left( 0 \right) \) and \({{q}_{4}}\left( 0 \right) \) represent the corresponding initial state of the system, respectively.

Remark 6

In the controller design stage, the rotor of QUAV is assumed to be ideal. For the control allocation of the actuator, since the four rotors can produce a single thrust \(U_1\) and a full torque vector \({\tau }={{\left( {{\tau }_{1}},{{\tau }_{2}},{{\tau }_{3}} \right) }^{T}}\) for rotation, we can use the following equation to obtain the desired angular velocity of the four rotors.

$$\begin{aligned} \begin{aligned} F&=-{{U}_{1}}{{E}_{3}}+mg{{R}^{T}}{{e}_{3}} \\&=\left[ \begin{matrix} 0 \\ 0 \\ b\left( n_{1}^{2}+n_{2}^{2}+n_{3}^{2}+n_{4}^{2} \right) \\ \end{matrix} \right] +mg{{R}^{T}}{{e}_{3}} \\ \end{aligned} \end{aligned}$$
(73)
$$\begin{aligned} \begin{aligned} {\tau }&=\left[ \begin{matrix} {{\tau }_{1}} \\ {{\tau }_{2}} \\ {{\tau }_{3}} \\ \end{matrix} \right] =\left[ \begin{matrix} bl\left( n_{4}^{2}-n_{2}^{2} \right) \\ bl\left( n_{3}^{2}-n_{1}^{2} \right) \\ dl\left( n_{2}^{2}+n_{4}^{2}-n_{1}^{2}-n_{3}^{2} \right) \\ \end{matrix} \right] \\ \end{aligned} \end{aligned}$$
(74)

where \(n_1, n_2,n_3\), and \(n_4\) denote the angular velocity of the front, right, rear, and left rotor, respectively. b and d are the thrust and drag factors. l is the distance between each rotor center and the center of mass of the QUAV.

4 Simulation

In order to verify the effectiveness of the proposed controller, we set up four groups of simulations. In the first group, we apply the proposed method to static targets to ensure that our method can be applied in static scenarios. We apply the proposed method to a moving target in the second group. We compare the proposed method with the previous methods in the third group. In the fourth group, we conduct a simulation comparison in Robot Operating System (ROS) gazebo environment. The model parameters of the QUAV and the camera are shown in Table 2.

Table 2 Simulation parameters
Full size table

The first three groups of simulation are numerical simulations conducted in MATLAB R2019b of Windows \(10\times 64\). The fourth group of ROS Gazebo moving target simulation was conducted under Ubuntu 18.04 amd64. The simulation calculation platform parameter is Intel i7-8700k with 64GB RAM.

4.1 Numerical simulation of the stationary target

The selection of control parameters of the controller is shown in Table 3. It should be noted that the current desired image moment can be obtained when the QUAV is at position \((0,0,-4)\text {m}\) in the inertial frame I with attitude \((0,0,0) \text {rad}\). Therefore, the desired height is \(z^* = -4 \text {m}\). The numerical simulation is divided into two groups: one without external disturbance and the other with external disturbance \(\textbf{dt}={{\left[ 0.2\sin \left( t \right) ,0.2\sin \left( t \right) ,0.2\sin \left( t \right) \right] }^{T}}\text {m}\cdot {{\text {s}}^{\text {-2}}}\).

Table 3 Control parameters
Full size table
Fig. 4
figure 4

Numerical simulation of the stationary target without external disturbance

Full size image
Fig. 5
figure 5

Numerical simulation of the stationary target with external disturbance

Full size image

Figure 4 shows the performance of the proposed control method on static targets without external disturbance. Figure 4a shows that QUAV finally hovers at the position of \((0,0,-4)\text {m}\), and Fig. 4b shows that the attitude of QUAV is \((0,0,0) \text {rad}\). Figure 4c shows the convergence of the image moment characteristic error in the plane of the virtual camera. It can be seen that the proposed control method can make the system reach the desired state, and it can be seen from the yaw feature that the system is stable in a finite time. Figure 4d shows the linear velocity in the virtual plane. We can see that the designed linear observer can accurately estimate the actual linear velocities of QUAV. Figure 4e, f shows the trajectories of feature points in the virtual camera plane and the actual camera plane, respectively. Through the axis of the trajectories, we can find that theoretically, using a low-cost 1080p resolution camera in practice is enough to deal with the current visual servoing task. Figure 4g, h shows the thrust input and torque input of the system, respectively. Figure 4i, j, k shows the observation state of the target motion observer in three axes, respectively. Figure 4l shows the space trajectory of the QUAV. We can see that the target observer can accurately estimate the motion state of the target.

Figure 5 shows the performance of the proposed control method on static targets with external disturbance. We can see that although we impose external disturbances on the system, the system is robust to external disturbances.

4.2 Numerical simulation of the moving target

Firstly, we give the motion constraint equation of the target, and its trajectory in space is a square in the xOy plane. The simulation results are shown in Fig. 6.

The motion constraint equation as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{v}_{x}}=0.2\,\text {m/s},{{v}_{y}}=0\,\text {m/s}, &{} t\in \left( 0,10 \right] \,\text {s} \\ {{v}_{x}}=0\,\text {m/s},{{v}_{y}}=0.2\,\text {m/s}, &{} t\in \left( 10,20 \right] \,\text {s} \\ {{v}_{x}}=-0.2\,\text {m/s},{{v}_{y}}=0\,\text {m/s}, &{} t\in \left( 20,30 \right] \,\text {s} \\ {{v}_{x}}=0\,\text {m/s},{{v}_{y}}=-0.2\,\text {m/s}, &{} t\in \left( 30,40 \right] \,\text {s} \end{array}\right. }. \end{aligned}$$
(75)

The target is always kept in the xOy plane during movement, i.e., \(v_z = 0\,\text {m/s}\). At the same time, the target does not spin at any angle, that is, \(\omega _z = 0\,\text {rad/s}\). The numerical simulation is divided into two groups, one without external disturbance and the other with external disturbance \(\textbf{dt}={{\left[ 0.2\sin \left( t \right) ,0.2\sin \left( t \right) ,0.2\sin \left( t \right) \right] }^{T}}\text {m}\cdot {{\text {s}}^{\text {-2}}}\).

Fig. 6
figure 6

Numerical simulation of the moving target without external disturbance

Full size image
Fig. 7
figure 7

Numerical simulation of the moving target with external disturbance

Full size image

We focus on the following aspects for this simulation:

  1. (1)

    Image moment feature error.

  2. (2)

    Linear velocity observer.

  3. (3)

    Target trajectory observer.

Figure 6c shows the convergence of image moment characteristic error. We can see some weak fluctuations in the figure due to the QUAV tracking the target to the inflection point, but they can quickly converge to the desired value. Figure 6d shows the linear velocity in the plane of the virtual camera. We can see that the proposed finite-time linear velocity observer can also accurately estimate the linear velocity of QUAV in the scene of target motion. Figure 6i, j, k shows the situation of the target trajectory observer. We can see that in the scene of target motion, the target trajectory observer can also accurately estimate the motion parameters of the target. Figure 7 shows the performance of the proposed control method on moving targets with external disturbance. We can also see that the system is robust to external disturbances. Finally, Fig. 7l shows the spatial trajectory of QUAV. We can find that there is no time delay in the proposed control method for tracking the moving target.

To further illustrate the effectiveness of our proposed method, we also carried out a group of nonlinear target tracking simulations. The target trajectory parameters are as follows:

$$\begin{aligned} {{v}_{x}}\left( t \right) =-\sin \left( t \right) \,\text {m}/\text {s},{{v}_{y}}\left( t \right) =\cos \left( t \right) \,\text {m}/\text {s}\text {.} \end{aligned}$$
(76)
Fig. 8
figure 8

Numerical simulation of the nonlinear moving target

Full size image

Figure 8 shows the numerical simulation results for nonlinear moving targets. Because we use a nonlinear tracking differentiator, we can get the motion trajectory estimation parameters of the target, so the system shows adaptability to nonlinear moving targets. Therefore, we can verify the effectiveness of the proposed control method for tracking nonlinear moving targets.

Fig. 9
figure 9

Image moment feature errors under three control methods. “VO” means “VE-backstepping” method

Full size image
Fig. 10
figure 10

Control inputs under three control methods

Full size image
Table 4 IAE and ISDE of numerical simulation
Full size table
Table 5 IAU and ISDU of numerical simulation
Full size table

4.3 Comparative simulation of moving targets

In order to better illustrate the performance of the proposed method, we conducted a set of comparative experiments. The methods involved in the comparison include the artificial neural network method proposed by Masoud [19], which is noted as RBFNN. The other method uses the target observer proposed by Zhiqiang [21], which is noted as VE-backstepping. The methods selected here all use the same dynamic model and image moment features in the virtual camera plane. At the same time, to quantitatively illustrate the performance of the proposed method, we use the four indicators proposed by Jing and Qiang [36, 37] to analyze the control method. Our method is noted as VE-FTO-FTC.

The four indices are as follows:

  1. (1)

    Integrated Absolute Error (IAE). It is used to measure the tracking performance of the control method.

    $$\begin{aligned} {\textrm{IAE}}=\int {|e\left( t \right) |}{\textrm{d}}t. \end{aligned}$$
  2. (2)

    Integrated Square Error (ISDE). It shows the fluctuation degree of tracking error.

    $$\begin{aligned} {\textrm{ISDE}}=\int {{{\left( e\left( t \right) -{\bar{e}}\left( t \right) \right) }^{2}}{\textrm{d}}t} \end{aligned}$$

    where \({\bar{e}}\) is the mean of the error.

  3. (3)

    Integrated Absolute Control (IAU). It shows the intervention of the controller.

    $$\begin{aligned} {\textrm{IAU}}=\int {|u\left( t \right) |}{\textrm{d}}t. \end{aligned}$$
  4. (4)

    Integrated Square Control (ISDU). It is used to measure the fluctuation degree of control signal.

    $$\begin{aligned} {\textrm{ISDU}}=\int {{{\left( u\left( t \right) -{\bar{u}}\left( t \right) \right) }^{2}}{\textrm{d}}t} \end{aligned}$$

    where \({\bar{u}}\) is the mean of the control input.

Remark 7

IAE represents the accumulation of absolute error, and the smaller this indicator is, the stronger the control effect is. ISDE represents the variance of error, which describes the fluctuation of error. When the control effect of the controller is more robust, the value is smaller. Similarly, IAU describes the accumulation of controllers. The higher the value, the stronger the control effect. ISDU is the variance of the controller. The more significant the value, the better the control intervention effect.

Figures 9 and 10 show the image moment feature errors and control inputs under three control methods, respectively. Figure 10 shows the control effect of our proposed method. However, the superiority of our proposed control method cannot be better demonstrated only by the data plots. Therefore, we use the above four indicators and obtain Tables 4 and 5.

As shown in Table 4, our control method has smaller IAE and ISDE, which means that our method can make the system reach the desired value as soon as possible. In addition, Table 5 shows that our proposed control method has large IAU and ISDE, which means that our method has a better control effect.

4.4 Simulation experiment in ROS gazebo

Fig. 11
figure 11

ROS gazebo simulation environment

Full size image
Table 6 ROS gazebo simulation parameters
Full size table
Table 7 Control parameters in ROS gazebo
Full size table
Table 8 IMU parameters in ROS gazebo
Full size table

The simulation parameters in ROS gazebo are shown in Table 6. And Table 7 shows the control parameters in ROS gazebo. Since the environment of the ROS gazebo is close to the actual environment, we suggest selecting relatively small control parameters. The simulation environment we use is Prometheus framework [38], which is developed based on MAVROS. We need to build our scenario to use this environment, as shown in Fig. 9a. For the requirements of the visual servoing task, we design the ground markers as shown in Fig. 9b.

In the ROS gazebo, the sensor parameters of QUAV are provided by the IMU module of the gazebo. It should be noted that the module can add Gaussian white noise to simulate the measurement noise. These parameters are ROS default, and we have not modified these parameters. Table 8 shows the parameters of the sensors.

Fig. 12
figure 12

Simulation in ROS gazebo

Full size image
Fig. 13
figure 13

Time charts of image moment feature error under three control schemes

Full size image

In the simulation process, we first make QUAV fly to the initial position and maintain the initial attitude. After that, the QUAV will hover in this position and wait for the command of the visual servoing. After receiving the start command, the QUAV starts to enter the IBVS task independently. At the same time, the system will record the current data of the QUAV for subsequent analysis. The motion constraint equation as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{v}_{x}}=0.5\,\text {m/s},{{v}_{y}}=0\,\text {m/s}, &{} t\in \left( 0,17\right] \,\text {s} \\ {{v}_{x}}=0\,\text {m/s},{{v}_{y}}=0.5\,\text {m/s}, &{} t\in \left( 17,34\right] \,\text {s} \\ {{v}_{x}}=-0.5\,\text {m/s},{{v}_{y}}=0\,\text {m/s}, &{} t\in \left( 34,51\right] \,\text {s} \\ {{v}_{x}}=0\,\text {m/s},{{v}_{y}}=-0.5\,\text {m/s}, &{} t\in \left( 51,68\right] \,\text {s} \end{array}\right. }. \end{aligned}$$

The target is always kept in the xOy plane during movement, i.e., \(v_z = 0\,\text {m/s}\). At the same time, the target does not spin at any angle, that is, \(\omega _z = 0\,\text {rad/s}\).

As shown in Fig. 12c, the proposed control method can also converge the image feature error to the expected value in the ROS gazebo. Figure 12d shows that the designed finite-time observer can estimate the linear velocity of QUAV more accurately. Figure 12g shows the spatial trajectory of QUAV. It can be seen that the control effect is ideal. It should be noted that in Fig. 12b, the attitude angle in the figure has oscillated, but its range is within 2 degrees. Therefore, we think the QUAV can be in hovering mode.

We also conducted comparative experiments in ROS gazebo, and the comparative methods are still RBFNN and VE-backstepping. Figure 13 shows the variation of image moment feature error with time under three control schemes. We also use IAE and ISDE to analyze the performance of the controller. Table 9 shows the result.

Table 9 IAE and ISDE of ROS gazebo simulation
Full size table

The above simulation experiments show that the proposed control method has better control convergence, and the designed finite-time observer can also accurately estimate the linear velocity in the virtual image plane of the QUAV. However, parameters such as system quality, inertia, and camera focal length are not easy to obtain in practice. Therefore, we need to further discuss these problems in the future.

5 Conclusion

In this paper, we propose a novel image-based visual servoing control scheme combining target motion differentiator, finite-time observer, and finite-time controller, and we apply the scheme to the research of moving target tracking of QUAV. We use the differentiator to estimate the target motion parameters and transfer the parameters to the controller to ensure that the system can track the target in real time. Aiming to acquire camera depth information and the linear velocity of QUAV, we design a finite-time observer to compensate for this information. Finally, we design the global finite-time controller of the system using the simplified backstepping method. We have made assumptions about the visibility of the target, but in practice, the target is likely to be out of the field of view of the camera. At the same time, we do not conduct real machine experiments. Therefore, we plan to consider the target visibility constraint in future research and real machine verification.