Localization of a Drone for Landing Using Image-Based Visual Servoing with Image Moments

Abstract

The automated operation of Unmanned Aerial Vehicles (UAVs) has become increasingly important, and one key step in the procedure is the accurate landing of such vehicles. A major problem is that when trying to design a control algorithm for the landing procedure, it is difficult to accurately measure the 3D pose of the vehicle with respect to the local environment. Three dimensional pose estimation and subsequent corrections in velocity to design the control system was omitted by using an image-based visual servoing controller. Another important development is choosing the appropriate visual features which ensures convergence to desired position. The proposed controller with image moments as features was able to converge and land the vehicle accurately using only the image moments as the visual features from two fiducial markers without any local position or global position information. The proposed method has been verified using simulations considering an existing model of UAV.

Riby Abraham Boby and Alexandr Klimchik were supported by RSF research grant No. 22-41-02006.

1 Introduction

Unmanned aerial vehicles (UAVs) have many useful applications ranging from surveillance [1], search [2], agriculture [3] to border patrol [4], and mapping [5]. In these applications, fully autonomous UAVs play an important and key role, because they perform tasks without the guidance of humans. The majority of drones come with a variety of sensors, including Inertial Measurement Units (IMUs), GPS, compasses, barometers, monocular, stereo cameras, and LIDAR sensors, among others. These sensors are used to localize the drone and to gather information about the surroundings in order to map or avoid the various obstacles around the drone. The key point is to ensure that the drone has a high autonomy level with the use of robust and reliable navigation systems [6] and accurate localization. An important requirement to achieving this level of autonomy is to guarantee the takeoff as well as the landing phases to be totally autonomous. More importantly during the landing phase, the vehicle has to land safely on the landing platform [7]. There are two kinds of landing sites, the first one is that which is known to the vehicle before hand and the vehicle should reach it with the local positioning information [8]. The second kind is that where the vehicle has to land in unseen or unknown environments [9]. In the first kind, the landing site is made from easily recognizable marker or markers so that it can be easily detected when the vehicle has reached the boundary of the landing site. The landing phase then is activated when the camera detects the special characteristics of the marker. In the second kind, the criteria of flatness, spaciousness, and surface robustness are used to determine the best landing places. Landing platforms are used for the first case where we know before hand the special characteristics of the platform and use it to perform the landing strategy. One of the most promising methods for extending the operational range of UAVs with the least amount of vehicle modification is to use landing platforms. Additionally, automatic landing platforms could carry out tasks like picking up or loading goods, data exchange and processing, etc., in addition to the battery charge or replacement function [10]. There are two types of landing platforms which are the stationary type and the moving type. This work will focus on the first kind of landing site, which will be a set of markers known beforehand, and the platform will be stationary.

There are solutions in the literature based on motion capture systems [11] or other sensors [12]. Additionally, several articles on moving targets focused on how a flying aircraft and a ground vehicle worked together to plan the landing maneuver [14, 15]. In this work however, it is assumed that the vehicle has no communication with the platform. Another article [16] demonstrates an onboard computer vision system for estimating a UAV’s pose in relation to a landing target based on a coarse-to-fine approach using a monocular camera. Different methods can be thought of to land the drone after detecting the marker of the landing platform such as image-based visual servoing [17, 18] which involves the use of computer vision data to regulate a robot’s movements. Though popularly used methods rely on calculating the pose of the drone after detecting the landmark and then transforming the pose from 3D camera coordinates into 3D world coordinates, it might lead to unnecessary errors if the camera is not calibrated properly. Some of these steps can be skipped with the help of visual servoing. The control needs to be modified to get the 2D image coordinates as input; this will make the process more robust to tiny calibration errors, which will be significant while transforming into world coordinates.

2 Methodology

In Image Based Visual Servoing (IBVS) [17, 18], the time variation $\boldsymbol{\dot{s}}$ of the visual features $\textbf{s}$ can be linearly expressed with respect to the relative velocity of the camera $\mathbf {v_c}$. The control is created to ensure that the visual features decouple exponentially to reach the required value $\mathbf {s^*}$, where $\mathbf {L_s}$ is the interaction matrix associated with $\textbf{s}$, and considering an eye-in-hand system observing a static object, then

$$\begin{aligned} \mathbf {v_c} = - \lambda {\mathbf {\widehat{L}_s}^\dagger } \,(\textbf{s} -\mathbf {s^*}),~\boldsymbol{\dot{s}} = \mathbf {L_s} \mathbf {v_c}, \end{aligned}$$

(1)

where ${\mathbf {\widehat{L}_s}^\dagger }$ is an approximation of $\mathbf {L_s}$ and its pseudo-inverse, $\lambda$ is a positive gain responsible for the time to convergence. Given the mounting details and the UAV’s center of mass, this velocity twist vector needs to be rotated and translated.

The key here is the selection of the visual features to ensure the convergence of the controller to the desired position, one might select the individual corner points of an aruco markers as visual features, but the image moments of that marker were chosen instead. The reason is that image moments provide general representation of any object that can be segmented in an image. They are also more intuitive and meaningful than just the corners of an object [19, 20]. For a discrete set of n image points, the moments $m_{ij}$ and and the centered moments $\mu _{ij}$ are defined by [21]:

$$\begin{aligned} m_{ij} = \sum ^n_{k=1} x^i_k y^j_k,~\mu _{ij} = \sum ^n_{k=1} (x_k - x_g)^i (y_k - y_g)^j, \end{aligned}$$

(2)

where n is the number of image points, $x_g = \frac{m_{10}}{n}$, $y_g = \frac{m_{01}}{n}$ and $m_{00} = n$. It is known that these centered moments are invariant to 2D translational motion.

Next, interaction matrix may be defined. If planar objects are taken into account and for each object point, the degenerate case when the camera optical center is on the plane is excluded $1/Z = A x + B y + C$. For any point in the image, the velocity $\boldsymbol{x_k}$ is given from [17]. Using 1 to set $s = \boldsymbol{x_k}$ we obtain:

$$\begin{aligned} \dot{x_k} & = - (A x_k + B y_k + C) v_x + x_k (A x_k + B y_k + C) v_z + x_k y_k \omega _x \nonumber \\ {} & \quad - (1 +x_k^2) \omega _y + y_k \omega _z \end{aligned}$$

(3)

$$\begin{aligned} \dot{y_k} & = - (A x_k + B y_k + C) v_y + y_k (A x_k + B y_k + C) v_z -x_k y_k \omega _y \nonumber \\ {} & \quad + (1 +y_k^2) \omega _x + x_k \omega _z. \end{aligned}$$

(4)

The first two components of the interaction matrix that relate $x_g$ and $y_g$:

$$\begin{aligned} L_{x_g} &= \begin{bmatrix} - \frac{1}{Z_g} & 0 & x_{g_{vz}} & x_{g_{\omega x}} & x_{g_{\omega y}} & y_{g} \end{bmatrix},~ L_{y_g} &= \begin{bmatrix} 0 & - \frac{1}{Z_g} & y_{g_{vz}} & y_{g_{\omega x}} & y_{g_{\omega x}} & -x_{g}. \end{bmatrix} \end{aligned}$$

(5)

From the observations taken from [21], the centered moments will be invariant to tranlsational motions if $A = B = 0$ that happens when the object and the image plane are parallel to each other.

In [19, 22], to control the three translational motions these visual features have been selected: $x_g$, $y_g$ the center of gravity and the area of the object in the image a. Based on [21] the interaction matrix can be expressed as

$$\begin{aligned} L_{x_g} &= \begin{bmatrix} - C & 0 & C x_g & \epsilon _1 & -(1+\epsilon _2) & y_{g} \end{bmatrix},~ L_{y_g} &= \begin{bmatrix} 0 & - C & C y_g & 1+\epsilon _3 & - \epsilon _1 & -x_{g} \end{bmatrix},~\nonumber \\ L_{a} &= \begin{bmatrix} 0 & 0 & 2 a \delta C & 3 a \delta y_g & -3 a \delta x_g & 0. \end{bmatrix} \end{aligned}$$

(6)

A modification to this interaction matrix will be made by adding normalization in the form $a_n = z^* \sqrt{\frac{a^*}{a}}, \, \,x_n = a_n x_g , \, \, \text {and} y_n = a_n y_g$, where $a^*$ is the desired area of the object in the desired image, and $z^*$ is the desired depth between the camera and the object in the image. The resulting interaction matrix elements after the modification will be

$$\begin{aligned} \begin{bmatrix} L_{x_n} \\ L_{y_n} \\ L_{a_n} \end{bmatrix} = \begin{bmatrix} - 1 &{} 0 &{} 0 &{} a_n \epsilon _{11} &{} -a_n(1+\epsilon _{12}) &{} y_n \\ 0 &{} - 1 &{} 0 &{} a_n(1+\epsilon _{21}) &{} - a_n\epsilon _{22} &{} -x_n\\ 0 &{} 0 &{} -1 &{} -a_n \epsilon _{31} &{} a_n \epsilon _{32} &{} 0. \end{bmatrix} \end{aligned}$$

(7)

This new interaction matrix has a decoupling property to control the three translational velocities, and the three features have the same dynamics. For discrete objects, since $\mu _{20} + \mu _{02}$ is invariant to 2D rotation and translation [21] $a = \mu _{20} + \mu _{02}, \, \, a^* = \mu _{20}^* + \mu _{02}^*$. Since the high-level control of the drone can only control 4 dofs, $v_x$, $v_y$, $v_z$ and yaw rate, so we will keep only those columns from the full interaction matrix resulting in

$$\begin{aligned} \begin{bmatrix} L_{x_n} \\ L_{y_n} \\ L_{a_n} \end{bmatrix} = \begin{bmatrix} - 1 &{} 0 &{} 0 &{} y_n \\ 0 &{} - 1 &{} 0 &{} -x_n\\ 0 &{} 0 &{} -1 &{} 0. \end{bmatrix} \end{aligned}$$

(8)

In [19, 22], to control the three rotational motions, these visual features have been selected: the orientation of the object in the image $\alpha = \frac{1}{2} \arctan 2({{2\mu _{11}},({\mu _{20}-\mu _{02}}}))$ and two moment invariants $c_i$, $c_j$ chosen from combination of image momments that are invariant to 2D translation, rotation, and scale. A modification to the general form of the orientation of the object has been made to be specific to the orientation of the fiducial marker. The algorithm detects the four corners with a fixed order, the new angle will be the angle between the first corner, and the third corner of the detected marker: $\alpha = \arctan 2(({y_2 - y_1}),({x_2 - x_1}))$. The interaction matrix has the following form:

$$\begin{aligned} \begin{bmatrix} L_{c_i} \\ L_{c_k} \\ L_{\alpha } \end{bmatrix} = \begin{bmatrix} 0 &{} 0 &{} 0 &{} c_{i_{\omega x}} &{} c_{i_{\omega y}} &{} 0 \\ 0 &{} 0 &{} 0 &{} c_{j_{\omega x}} &{} c_{j_{\omega y}} &{} 0 \\ 0 &{} 0 &{} 0 &{} \alpha _{\omega x} &{} \alpha _{\omega _y} &{} -1 \end{bmatrix} \end{aligned}$$

(9)

Since we only need to control the yaw rate, only the last row with the 4th and 5th columns removed will be used i.e., $L_{\alpha } = \begin{bmatrix} 0 & 0 & 0 & -1 \end{bmatrix}$. Finally, the following interaction matrix will be used in the IBVS approach based on our 4 DOFs high-level control:

$$\begin{aligned} \begin{bmatrix} L_{x_n} \\ L_{y_n} \\ L_{a_n} \\ L_\alpha \end{bmatrix} = \begin{bmatrix} - 1 &{} 0 &{} 0 &{} y_n \\ 0 &{} - 1 &{} 0 &{} -x_n\\ 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1. \end{bmatrix} \end{aligned}$$

(10)

The full set of new visual features $s = [x_n,\, y_n,\, a_n,\, \alpha ]$ and the corresponding error vector $e = \begin{bmatrix} x_n - z^*x_g^* & y_n - z^*y_g^* & a_n - z^* & \alpha - \alpha ^*. \end{bmatrix}^T$

The following approximation to the interaction matrix has proven to have a good performance in practice [18, 23] ${\mathbf {\widehat{L}_s}^\dagger } = \frac{1}{2} ( L_{s(s)}^\dagger + L_{s(s^*)}^\dagger )$, where $L_{s(s)}^\dagger$ is the interaction matrix computed from the measured features, while $L_{s(s*)}^\dagger$ is computed from the desired features.

According to the findings of [26], the velocity components created by the controller employing this interaction matrix do not have significant oscillations and give a smooth trajectory in the image and in three dimensions. The gain $\lambda$ in the proposed controller is adaptive, which means the error value controls the magnitude of the gain $\lambda = (\lambda _{\max } - \lambda _{\min })(\frac{||{e}||}{||{e_{\max }}||}) + \lambda _{\min }$, where $\lambda _{\max }$, $\lambda _{\min }$ are the maximum and minimum values of the gain respectively. At time t, $||{e}||$ is the norm of the error vector and at the start of the program, $||{e_{\max }}||$ is defined as the max. error in the control loop according to [25], where the authors show the effect and smoothness of adaptive gains in different visual servoing scenarios. This was adopted in this work.

Fig. 1

Iris drone and fiducial markers

3 Evaluation and Discussion

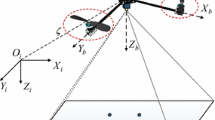
The current environment contains an Iris drone [27] inside a Gazebo world, equipped with a down-facing camera and two ArUcO markers with sizes 0.176 and 0.05 m, respectively, the code was written as a ROS package [24]. The environment is depicted in Fig. 1. The first marker will localize the drone at a $h= 0.6$ m and centered with respect to the marker, and the second marker will localize it with $h=0.25$ m and centered. The threshold of the norm of error was empirically chosen as 0.1 m and 0.015 m.

The algorithm will do the following: Firstly, detect the larger ArUcO marker in order to localize the drone at the desired $h=0.6$ m. Once detected, the IBVS module will initialize and recursively guide the drone to the desired location until the error threshold is reached. Second, once the first error threshold is reached and the second marker is detected, the IBVS module will initialize again with the new parameters to recursively guide the drone to the next desired location at $h=0.25$ m. Later, once the second error threshold is reached, the motors are turned off for landing.

Algorithm 1

Landing algorithm with IBVS

In the main experiment, the value of the parameters: $\lambda _{\max } = 1.0$ and $\lambda _{\min } = 0.5$. The drone starts at the world position $x = \begin{bmatrix} 0.2 & 0.2 & 2 \end{bmatrix}$, with the positions measured in meters. The desired height for the first marker is $h=0.6$ m and the final position of the drone is $x = \begin{bmatrix} 0.205 & 0.203 & 0 \end{bmatrix}$. The results of the IBVS algorithm for each marker in the experiment are shown in Fig. 2a–c for marker 1 and Fig. 2d–f for marker 2.

Fig. 2

Simulation results

In case of rough localization, we can see that the controller converges with decoupled error and reaches the error threshold in about 8 s with the low maximum gain, the trajectories are also smooth and there are no irregularities in the control signal. While using second marker in the stage of fine localization, from the data in the graphs we can notice the noisy nature of the drone and the problem becomes much harder for the controller due to the low error signal and the fine-positioning required to land. The system is converged in about 6 s.

4 Conclusion

This article proposed an image-based visual servoing controller for UAV that was able to converge and land the vehicle accurately using only the image moments as the visual features from two fiducial markers. This could be done without any local position or global position information helping the controller. The only step needed before the deployment of the controller is the learning step of the desired height and image moments that will be used as a reference for the controller. Once the desired image moments and height are known, the controller will stabilize and guide the drone to land on the predefined set of markers. The convergence of the UAV to the desired position has been verified through simulations. In the future, the methodology may be extended to handle a moving platform and land on it.