Keywords

1 Introduction

Rotary cranes are widely used to transfer heavy and large cargoes in construction sites and factories docks. Rotary cranes are typical nonlinear underactuated electromechanical systems [1, 2]. Especially, the luffing motion of the boom could cause swing oscillations during the transportation process. The swing oscillations may reduce work efficiency and cause accidents. It is crucial to design an efficient control method that can eliminate the payload swing oscillations while fast and accurate positioning.

Due to complex centrifugal force and friction generated by the luffing motion of the boom, it is difficult to control rotary cranes systems. Besides the high coupling between the luffing motion of the boom and swing of payload, the nonlinear dynamics of rotary cranes become more complicated with double-pendulum effects which exist in the case that the payload is suspended with the hook by rigging cable or the mass of the hook is similar to the mass of payload [3, 4]. The anti-swing while positioning control of the rotary crane system is a challenge problem.

The existing control approaches have made some progress in the control of the rotary crane system. Some open-loop control methods, including input shaping methods [5, 6] and trajectory planning control method [7,8,9], are used to suppress the payload oscillations for rotary crane systems. However, open-loop control methods lack of status feedback signals, thus making them less robust of external disturbance. Compared with the open-loop control methods, closed-loop control method improves robustness to disturbances and system parametric uncertainties by using feedback signals. Therefore, many researchers are devoted to closed-loop control in recent years, such as sliding mode control method [10,11,12], intelligent control methods [13, 14] and stabilization/regulation control methods [15, 16].

The aforementioned research work based on single-pendulum model failed to work for the double-pendulum rotary crane system, which couples boom luffing motion, hook swing and payload swing. Several control methods are devoted to solve the anti-swing and positioning control problems for double-pendulum rotary crane system. An input-shaping controller is designed for human-operated double-pendulum rotary crane [17]. However, input-shaping control method is open-loop control method, which is sensitive to the system parametric uncertainties. In order to solve the problems of robustness for crane system, a simple robust control method is obtained to against different cable lengths [18]. An adaptive nonlinear tracking control method is presented for double-pendulum rotary crane, even in the case of uncertain payload masses, cable lengths and external disturbances [19].

Although existing control approaches have made some progresses, few of them can completely guarantee the state constraints problems. In the practical rotary crane system, the angular acceleration and the angular velocity for boom are restricted within reasonable ranges to ensure that control inputs are constrained within the hardware limits. Many approaches considering state constraints are presented for the other cranes [20,21,22], which cannot be directly applied to control a double-pendulum rotary crane. The control problems of considering state constraints for double-pendulum rotary crane is still at an early stage. To the best of our knowledge, only an energy-shaped based (ESB) nonlinear control method is obtained considering control torque constraints for double-pendulum rotary crane systems [23]. An arctangent function is added to nonlinear controller to make the control torque in the bounded coordination. However, the actual rotary crane is different from the rotary crane in the laboratory, which uses torque signals to control the system [24]. The actual rotary crane uses variable-frequency control signals to drive motor with suitable angular acceleration/velocity in the boom luffing motion process. The angular acceleration/velocity of the driving motor should be constrained in the corresponding ranges to satisfy the state constraints and safety requirement.

Aiming at anti-swing and positioning control problem for the double-pendulum rotary crane system subject to state constraints, a nonlinear coupling-based motion trajectory planning control method is proposed in this paper. Inspired by trajectory planning control method for overhead cranes [25], the proposed boom luffing angular acceleration trajectory can be divided two parts: positioning angular acceleration trajectory and swing-eliminating angular acceleration trajectory. The positioning angular acceleration trajectory development considers the state constraints, such as maximum angular acceleration/velocity of the boom luffing motion. The swing-eliminating angular acceleration trajectory has no influence on the positioning performance of boom luffing motion. Lyapunov techniques and LaSalle’s invariance are used to proof the control system stability. Some simulation results are given to show the effectiveness and robustness of the proposed nonlinear coupling-based motion trajectory planning control method.

The main contributions of this paper are presented as follows:

  1. 1)

    To the best of our knowledge, the proposed method is the first nonlinear coupling-based motion trajectory planning method for rotary crane with double-pendulum effect.

  2. 2)

    By using the proposed method, the state variable (angular acceleration/velocity of the boom luffing motion) can be limited within a preset reasonable range during the whole operation process. It is very simple and effective to the actual rotary crane in practice.

The rest of this paper is organized as follows. Section 2 provides dynamic model and analysis of rotary crane with double-pendulum effect. Then, Sect. 3 discusses the development of nonlinear coupling-based motion trajectory planning control method. After that, several groups of simulations are presented to verify the performance of proposed control method in Sect. 4. Finally, Sect. 5 gives some conclusions for the whole paper.

2 Modeling and Dynamics of Double-Pendulum Rotary Crane

2.1 Model of a Double-Pendulum Rotary Cranes

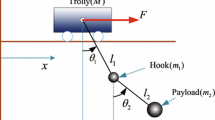
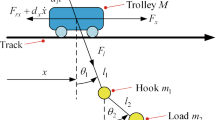
Figure 1 gives the underactuated dynamic model of the double pendulum-rotary crane system, whose dynamical equations are presented as follows:

$$ \begin{gathered} \left( {\frac{1}{3}m_{b} + m_{h} + m_{p} } \right)l_{b}^{2} \ddot{\phi } + (m_{h} + m_{p} )l_{b} l_{s} \ddot{\alpha }\sin (\alpha - \phi ) + (m_{h} + m_{p} )l_{b} l_{s} \dot{\alpha }^{2} \cos (\alpha - \phi ) \hfill \\ + \;m_{p} l_{r} l_{b} \ddot{\beta }\sin (\beta - \phi ) + m_{p} l_{r} l_{b} \dot{\beta }^{2} \cos (\beta - \phi ) + (\frac{1}{2}m_{b} + m_{h} + m_{p} )gl_{b} \cos \phi = u, \hfill \\ \end{gathered} $$
(1)
$$ \begin{gathered} (m_{h} + m_{p} )l_{s}^{2} \ddot{\alpha } + (m_{h} + m_{p} )l_{b} l_{s} \ddot{\phi }\sin (\alpha - \phi ) - (m_{h} + m_{p} )l_{b} l_{s} \dot{\phi }^{2} \cos (\alpha - \phi ) \hfill \\ + \;m_{p} l_{r} l_{s} \ddot{\beta }\cos (\alpha - \beta ) + m_{p} l_{r} l_{s} \dot{\beta }^{2} \sin (\alpha - \beta ) + (m_{h} + m_{p} )gl_{s} \sin \alpha = 0, \hfill \\ \end{gathered} $$
(2)
$$ \begin{gathered} m_{p} l_{b} l_{r} \ddot{\phi }\sin (\beta - \phi ) - m_{p} l_{b} l_{r} \dot{\phi }^{2} \cos (\beta - \phi ) + m_{p} gl_{r} \sin \beta \hfill \\ + \;m_{p} l_{r}^{2} \ddot{\beta } + m_{p} l_{b} l_{r} \ddot{\alpha }\cos (\alpha - \beta ) - m_{p} l_{r} l_{s} \dot{\alpha }^{2} \sin (\alpha - \beta ) = 0, \hfill \\ \end{gathered} $$
(3)

where \(\phi\) donates the boom luffing motion angles. \(\alpha\) and \(\beta\) represent the swing angles of hook and payload, respectively. \(m_{h}\) and \(m_{p}\) donate the mass of hook and payload, respectively. The length and the mass of the boom are denoted by \(l_{b}\) and \(m_{b}\). \(l_{s}\) is the suspension cable length. \(l_{r}\) is the rigging cable length. \(u\) is the actuating torque controlling boom luffing motion.

Fig. 1.
figure 1

Dynamics model of double-pendulum rotary crane

Full size image

We make the following reasonable assumptions based on the actual application of the rotary crane [18, 19, 23,24,25].

Assumption 1:

The hook and payload swing angles satisfy following conditions during the boom operation process:

$$ {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha ,\beta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}. $$
(4)

Assumption 2:

The suspension cable and the rigging cable are rigid bodies. Their mass is ignored.

Considering the state constraints, the boom luffing motion angular acceleration/velocity are bounded in the sense that:

$$ \ddot{\phi }_{\min } \le \ddot{\phi } \le \ddot{\phi }_{\max } ,\dot{\phi }_{\min } \le \dot{\phi } \le \dot{\phi }_{\max } , $$
(5)

where \(\ddot{\phi }_{\max } (\ddot{\phi }_{\min } )\) donates the maximum (minimum) angular acceleration and \(\dot{\phi }_{\max } (\dot{\phi }_{\min } )\) donates the maximum (minimum) angular velocity.

2.2 Dynamic Analysis

The swing angles of hook and payload are usually kept as small values in practice. Therefore, the approximate linearization of the double-pendulum rotary crane dynamics is reasonable [26]. The nature frequencies of the payload swing motion can be obtained by the linearized dynamics model [17]:

$$ w_{1,2} = \sqrt {\frac{g}{2}(1 + R)\frac{{l_{r} + l_{s} }}{{l_{r} l_{s} }} \mp \gamma } , $$
(6)

where \(\gamma = \sqrt {\left( {1 + R} \right)^{2} \left( {\frac{{l_{r} + l_{s} }}{{l_{r} l_{s} }}} \right)^{2} - 4\left( {\frac{1 + R}{{l_{r} l_{s} }}} \right)}\), \(R = \frac{{m_{p} }}{{m_{h} }}\).

The natural frequencies not only depend on the lengths of suspension cable and rigging cable but also depend on the masses of hook and payload. The rotary cranes transfer the different kinds of payloads in practice. The payload mass \(m_{p}\) and suspension cable length \(l_{s}\) are usually changed for different work task. The rigging cable length \(l_{r}\) and hook mass \(m_{h}\) are kept the same values. To simplify this problem, R is defined as the ratio of payload mass \(m_{p}\) to hook mass \(m_{h}\). Figure 2 shows the two nature frequencies as a function of the suspension cable length \(l_{s}\) and mass ratio R.

Fig. 2.
figure 2

Variation of the payload swing frequencies

Full size image

In Fig. 2, on the one hand, the nature frequency w1 changes very little for different mass ratio R and suspension cable length \(l_{s}\). The nature frequency w2 has a strong dependence on mass ratio R and suspension cable length \(l_{s}\). The nature frequency w2 changes greatly because the mass ratio changes slightly. On the other hand, the nature frequency w2 is bigger than the nature frequency w1. Thus, the nature frequency w2 has a big influence on double-pendulum rotary crane control system. In brief, we should pay more attention to provide robustness to changes in the nature frequency w2.

3 Trajectory Planning

The rotary crane system transfers the payload from the starting position to the target position. The boom moves to the desired angle accurately. Moreover, the payload and hook should suppress the swing oscillations during the whole operation. Therefore, we need to design a motion trajectory including positioning component and swing-eliminating component:

$$ \ddot{\phi }_{f} = \ddot{\phi }_{p} + \ddot{\phi }_{s} , $$
(7)

where \(\ddot{\phi }_{f}\) donates the boom final angular acceleration trajectory, \(\ddot{\phi }_{p}\) is the boom positioning angular acceleration trajectory, \(\ddot{\phi }_{s}\) represents the swing-eliminating angular acceleration trajectory.

Fig. 3.
figure 3

An overall flow diagram of the proposed method

Full size image

An overall flow diagram of the proposed nonlinear coupling-based motion trajectory planning method for the double-pendulum rotary crane with state constraints is shown in Fig. 3.

3.1 Positioning Trajectory Planning

In order to keep the soft start and smooth operation of the boom, a S-shape smooth luffing motion positioning trajectory are usually chosen for the rotary crane system. We design a trapezoid-like angular acceleration positioning trajectory:

$$ \ddot{\phi }_{p} = \left\{ {\begin{array}{*{20}c} {\frac{{\ddot{\phi }_{\max } }}{{t_{j} }}t} & {0 \le t \le t_{j} ,} \\ {\ddot{\phi }_{\max } } & {t_{j} < t \le t_{j} + t_{a} ,} \\ { - \frac{{\ddot{\phi }_{\max } }}{{t_{j} }}\left( {t - 2t_{j} - t_{a} } \right)} & {t_{j} + t_{a} < t \le 2t_{j} + t_{a} ,} \\ { - \frac{{\ddot{\phi }_{\max } }}{{t_{j} }}\left( {t - 2t_{j} - t_{a} - t_{c} } \right)} & {2t_{j} + t_{a} + t_{c} < t \le 3t_{j} + t_{a} + t_{c} ,} \\ { - \ddot{\phi }_{\max } } & {3t_{j} + t_{a} + t_{c} < t \le 3t_{j} + 2t_{a} + t_{c} ,} \\ {\frac{{\ddot{\phi }_{\max } }}{{t_{j} }}\left( {t - 4t_{j} - 2t_{a} - t_{c} } \right)} & {3t_{j} + 2t_{a} + t_{c} < t \le 4t_{j} + 2t_{a} + t_{c} ,} \\ 0 & {t \in other.} \\ \end{array} } \right. $$
(8)

where \(t_{j}\) is acceleration (deceleration) change duration, \(t_{a}\) donates acceleration (deceleration) hold duration, \(t_{c}\) is the constant velocity duration, \(\ddot{\phi }_{\max }\) is the maximum angular acceleration under the boom luffing motion state constraints. The profile of the trapezoid-like angular acceleration positioning trajectory is given in Fig. 4. \(\ddot{\phi }_{\max }\) is a state constraint variable, which is related to the physical parameters of the system. The main problem to be solved below is how to determine the values of tj, ta and tc given in Fig. 4.

Fig. 4.
figure 4

Schematic profile for the boom positioning angular acceleration trajectory

Full size image

By some integration operation, the boom luffing motion positioning maximum angular velocity \(\dot{\phi }_{p\max }\) and final angle \(\phi_{p}\) are calculated as:

$$ \dot{\phi }_{{{\text{p}} \max }} = \int_{0}^{{T_{1} }} {\ddot{\phi }_{p} } {\text{d}} t = \ddot{\phi }_{\max } \left( {t_{j} + t_{a} } \right), $$
(9)
$$ \phi_{p} = \int_{0}^{{T_{2} }} {\int_{0}^{{T_{2} }} {\ddot{\phi }_{p} } } {\text{d}} t{\text{d}} t = \ddot{\phi }_{\max } \left( {t_{j} + t_{a} } \right)\left( {2t_{j} + t_{a} + t_{c} } \right), $$
(10)

where \(T_{1} = 2t_{j} + t_{a} ,T_{2} = 4t_{j} + 2t_{a} + t_{c} .\)

We need to further determine the values of acceleration (deceleration) change duration \(t_{j}\), acceleration (deceleration) hold duration ta and constant velocity duration \(t_{c}\). In order to increase the robustness to the double-pendulum rotary crane system nature frequency \(w_{1,2}\), the acceleration (deceleration) change duration \(t_{j}\) is obtained as:

$$ t_{j} = \frac{2\pi }{{\max \left( {w_{1,2} } \right)}}. $$
(11)

The boom luffing motion angular velocity is limited in practice because of the physical constraints. Therefore, the positioning trajectory planning should pay more attention to the rotary crane system state constraints. \(\dot{\phi }_{\max }\) is the maximum angular velocity under the boom luffing motion state constraints. \(\phi_{d}\) is the boom luffing motion final target angle. The acceleration (deceleration) hold duration \(t_{a}\) and the constant velocity duration \(t_{c}\) are obtained from (9) and (10) as:

$$ t_{a} = \frac{{\dot{\phi }_{\max } }}{{\ddot{\phi }_{\max } }} - t_{j} , $$
(12)
$$ t_{c} = \frac{{\phi_{d} }}{{\ddot{\phi }_{\max } \left( {t_{j} + t_{a} } \right)}} - \left( {2t_{j} + t_{a} } \right). $$
(13)

Remark 1:

The acceleration (deceleration) change duration \(t_{j}\) is calculated by the system nature frequency \(w_{1,2}\). The acceleration (deceleration) hold duration \(t_{a}\) and constant velocity duration \(t_{c}\) are calculated by final target angle \(\phi_{d}\), maximum angular velocity \(\dot{\phi }_{\max }\) and maximum angular acceleration \(\ddot{\phi }_{\max }\). Therefore, we can adjust \(t_{j}\), \(t_{a}\) and \(t_{c}\) to ensure the constrains on the boom luffing motion positioning angular acceleration \(\ddot{\phi }_{p}\) and velocity \(\dot{\phi }_{p}\).

3.2 Swing-Eliminating Trajectory Planning

The double-pendulum rotary crane dynamic equation indicates the kinematic coupling relationship among boom luffing, hook swing and payload swing. This kinematic coupling relationship is the basis of the proposed swing-eliminating trajectory planning method in this paper. When the boom luffing angle moves to target position \(\phi_{d}\), the following clear kinematic coupling relationship can be obtained by calculating the Eq. (2) and (3):

$$ \begin{gathered} \left[ {l_{s}^{2} \dot{\alpha } + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r} l_{s} \dot{\beta }} \right]\ddot{\alpha } + \left[ {\frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r} l_{s} \dot{\alpha } + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r}^{2} \dot{\beta }} \right]\ddot{\beta } + gl_{s} \dot{\alpha }\sin \alpha \hfill \\ + \;\frac{{m_{p} }}{{m_{h} + m_{p} }}gl_{r} \dot{\beta }\sin \beta = - l_{b} l_{s} \left[ {\frac{{m_{p} }}{{m_{h} + m_{p} }}\dot{\beta }\sin \left( {\beta - \phi_{d} } \right) + \dot{\alpha }\sin \left( {\alpha - \phi_{d} } \right)} \right]\ddot{\phi }. \hfill \\ \end{gathered} $$
(14)

In order to suppress the hook and payload swing when the boom moves, the swing-eliminating angular acceleration trajectory is designed based on the kinematic coupling relationship (14):

$$ \ddot{\phi }_{s} = k\left[ {\frac{{m_{p} }}{{m_{h} + m_{p} }}\dot{\beta }\sin \left( {\beta - \phi_{d} } \right) + \dot{\alpha }\sin \left( {\alpha - \phi_{d} } \right)} \right], $$
(15)

where \(k \in \Re^{ + }\) is a positive control gain. The proposed swing-eliminating angular acceleration trajectory \(\ddot{\phi }_{s}\) has the following properties:

Theorem 1:

The proposed swing-eliminating angular acceleration trajectory \(\ddot{\phi }_{s}\) not only has no influence on the positioning of the boom, but also suppresses the swing of the hook and the payload.

$$ \mathop {\lim }\limits_{t \to \infty } \left[ {\begin{array}{*{20}c} {\phi_{s} } & \alpha & \beta & {\dot{\phi }_{s} } & {\dot{\alpha }} & {\dot{\beta }} & {\ddot{\phi }_{s} } & {\ddot{\alpha }} & {\ddot{\beta }} \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{T} . $$
(16)

Proof:

Firstly, a function \(V(t)\) is chosen as the Lyapunov function candidate.

$$ V(t) = \frac{1}{2}l_{s}^{2} \dot{\alpha }^{2} + \frac{1}{2}\frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r}^{2} \dot{\beta }^{2} + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{s} l_{r} \dot{\alpha }\dot{\beta } + l_{s} g\left( {1 - \cos \alpha } \right) + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r} g\left( {1 - \cos \beta } \right). $$
(17)

Using arithmetic and geometric mean inequality, (17) is calculated as:

$$ V(t) \ge \sqrt {\frac{{m_{p} }}{{m_{h} + m_{p} }}} l_{s} l_{r} \left| {\dot{\alpha }\dot{\beta }} \right| + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{s} l_{r} \dot{\alpha }\dot{\beta } + l_{s} g\left( {1 - \cos \alpha } \right) + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r} g\left( {1 - \cos \beta } \right). $$
(18)

In order to analysis the positive definiteness of the \(V(t)\), we need to discuss the following two case by the values of \(\dot{\alpha }\dot{\beta }\):

Case 1: \(\dot{\alpha }\dot{\beta } \ge 0\). It is easy to obtained:

$$ \begin{gathered} \sqrt {\frac{{m_{p} }}{{m_{h} + m_{p} }}} l_{s} l_{r} \left| {\dot{\alpha }\dot{\beta }} \right| + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{s} l_{r} \dot{\alpha }\dot{\beta } + l_{s} g\left( {1 - \cos \alpha } \right) \hfill \\ + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r} g\left( {1 - \cos \beta } \right) \ge 0. \hfill \\ \end{gathered} $$
(19)

Case 2: \(\dot{\alpha }\dot{\beta } < 0\). The right half of formula (18) can be rewritten as:

$$ \begin{gathered} \left( {\sqrt {\frac{{m_{p} }}{{m_{h} + m_{p} }}} - 1} \right)\sqrt {\frac{{m_{p} }}{{m_{h} + m_{p} }}} l_{s} l_{r} \dot{\alpha }\dot{\beta } + l_{s} g\left( {1 - \cos \alpha } \right) \hfill \\ + \frac{{m_{p} }}{{m_{h} + m_{p} }}l_{r} g\left( {1 - \cos \beta } \right) \ge 0. \hfill \\ \end{gathered} $$
(20)

According to formula (18), we can get:

$$ V(t) \ge 0. $$
(21)

Therefore, the Lyapunov function candidate \(V(t)\) is positive definite function.

By taking the time derivative of (17) and using (14), we get the following results:

$$ \dot{V}(t) = - l_{b} l_{s} \left[ {\frac{{m_{p} }}{{m_{h} + m_{p} }}\dot{\beta }\sin \left( {\beta - \phi_{d} } \right) + \dot{\alpha }\sin \left( {\alpha - \phi_{d} } \right)} \right]\ddot{\phi }_{s} . $$
(22)

Hence, by inserting (14) into (22), it can be obtained that

$$ \dot{V}(t) = - l_{b} l_{s} k\left[ {\frac{{m_{p} }}{{m_{h} + m_{p} }}\dot{\beta }\sin \left( {\beta - \phi_{d} } \right) + \dot{\alpha }\sin \left( {\alpha - \phi_{d} } \right)} \right]^{2} \le 0, $$
(23)

which implies that:

$$ V(t) \le V(0) < < + \infty . $$
(24)

It is obvious that V(t) is always nonnegative. Additionally, noticing that V(0) is bounded, it is easy to infer that:

$$ V(t) \in L_{\infty } . $$
(25)

The initial conditions are chosen as:

$$ \phi_{s} (0) = 0,\alpha (0) = 0,\beta (0) = 0,\dot{\phi }_{s} (0) = 0,\dot{\alpha }(0) = 0,\dot{\beta }(0) = 0. $$
(26)

In order to accomplish the Theorem 1 proof, we define the \(\Omega\) as the set where \(\dot{V}(t) = 0\).

$$ \Omega = \left\{ {(\phi_{s} ,\alpha ,\beta ,\dot{\phi }_{s} ,\dot{\alpha },\dot{\beta },\ddot{\phi }_{s} ,\ddot{\alpha },\ddot{\beta })\left| {\dot{V}(t) = 0} \right.} \right\}. $$
(27)

Further, let \(\psi\) as the largest invariant set in \(\Omega\). In the largest invariant set \(\psi\), we can obtain from (23) obviously:

$$ \frac{{m_{p} }}{{m_{h} + m_{p} }}\dot{\beta }\sin \left( {\beta - \phi_{d} } \right) + \dot{\alpha }\sin \left( {\alpha - \phi_{d} } \right) = 0. $$
(28)

By inserting (28) into (15), it can be obtained that:

$$ \ddot{\phi }_{s} = 0. $$
(29)

By some integration operation and using (29), we can get the following results:

$$ \dot{\phi }_{s} = \int_{0}^{t} {\ddot{\phi }_{s} } {\text{d}} t + \dot{\phi }_{s} (0) = 0, $$
(30)
$$ \phi_{s} = \int_{0}^{t} {\dot{\phi }_{s} } {\text{d}} t + \phi_{s} (0) = 0. $$
(31)

The integral of (28) in time can be calculated as:

$$ \begin{gathered} \int_{0}^{t} {\frac{{m_{p} }}{{m_{h} + m_{p} }}\dot{\beta }\sin \left( {\beta - \phi_{d} } \right) + \dot{\alpha }\sin \left( {\alpha - \phi_{d} } \right)} \hfill \\ = \frac{{m_{p} }}{{m_{h} + m_{p} }}\cos \left[ {\beta (0) - \phi_{d} } \right] + \cos \left[ {\alpha (0) - \phi_{d} } \right] \hfill \\ - \frac{{m_{p} }}{{m_{h} + m_{p} }}\cos \left[ {\beta (t) - \phi_{d} } \right] - \cos \left[ {\alpha (t) - \phi_{d} } \right] = 0. \hfill \\ \end{gathered} $$
(32)

By inserting (26) into (32), it can be obtained that:

$$ \begin{gathered} \cos \phi_{d} \left\{ {\frac{{m_{p} }}{{m_{h} + m_{p} }}\left[ {1 - \cos \beta (t)} \right] + \left[ {1 - \cos \alpha (t)} \right]} \right\} \hfill \\ - sin\phi_{d} \left[ {\frac{{m_{p} }}{{m_{h} + m_{p} }}\sin \beta (t) + \sin \alpha (t)} \right] = 0. \hfill \\ \end{gathered} $$
(33)

Solving the above trigonometric function equation, the following results can be obtained:

$$ \alpha = 2n\pi ,\beta = 2n\pi , $$
(34)

where n is an integer to be determined. Considering the limiting condition \({{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha ,\beta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\) in the Eq. (4), we can get n = 0. Thus, it is clear that:

$$ \alpha = 0,\beta = 0. $$
(35)

By taking the time derivative of (35), it can be obtained that:

$$ \dot{\alpha } = 0,\dot{\beta } = 0 \Rightarrow \ddot{\alpha } = 0,\ddot{\beta } = 0. $$
(36)

By summarizing the above equations in (29), (30), (31), (35) and (36), the following results can be obtained in the maximum invariant \(\psi\): \(\phi_{s} = 0,\alpha = 0,\beta = 0,\dot{\phi }_{s} = 0,\dot{\alpha } = 0,\dot{\beta } = 0,\ddot{\phi }_{s} = ,\ddot{\alpha } = 0,\ddot{\beta } = 0\). The maximum invariant set \(\psi\) only contains closed-loop equilibrium points. Therefore, the LaSalle’s invariance theorem can be directly proved the control objectives in the Theorem 1 [27]. □

Remark 2:

The positioning angular acceleration \(\ddot{\phi }_{p}\) and velocity \(\dot{\phi }_{p}\) are limited within a certain range by the adjustment time \(t_{j}\), \(t_{a}\) and \(t_{c}\). From Eq. (16), it can be seen that the swing-eliminating angular acceleration \(\ddot{\phi }_{s}\) and velocity \(\dot{\phi }_{s}\) has no influence on the positioning of the boom. The final motion trajectory consists of positioning component and swing-eliminating component. Therefore, the final angular acceleration \(\ddot{\phi }_{f}\) and velocity \(\dot{\phi }_{f}\) of the boom are limited by the state constraints.

4 Simulation Results and Analysis

This section provides the test in the simulation software Matlab/Simulink and Webots, which is closer to the actual situation of the rotary crane system. The simulation in Matlab/Simulink is easily for testing the feasibility and accuracy of the proposed motion trajectory control strategy. And the simulation in Webots is convenient for monitoring the boom position and hook/payload swing angles. The simulation environment is shown in the Fig. 5.

The double pendulum rotary crane physical parameters are: mb = 1 kg, mh = 0.2 kg, mp = 0.3 kg, lb = 1.5m, ls = 0.4 m, lr = 0.24 m, g = 9.8 m/s2.

Fig. 5.
figure 5

Simulation environment with Matlab/Simulink and Webots

Full size image

4.1 Comparative Simulation

Two cases of numerical simulations are carried out to verify the effectiveness of the proposed nonlinear coupling-based motion trajectory planning method.

Case 1:

Swing-eliminating effectiveness. We compare the proposed motion trajectory \(\phi_{f}\) with positioning trajectory \(\phi_{p}\) to verify the swing-eliminating effectiveness. For the proposed motion trajectory, the positive control gain is obtained as \(k = 1.2\) by trial and error to get best control performance.

Figure 6 shows the simulation results for swing-eliminating effectiveness of the proposed motion trajectory. It is clear from Fig. 5 that the payload and hook swing oscillations when the boom reaches the target position using the positioning trajectory \(\phi_{p}\) without any swing-eliminating. In contrast, the proposed motion trajectory \(\phi_{f}\) not only accurately achieves the positioning performance of the boom luffing motion, but also effectively suppresses the swing of the hook and payload.

Fig. 6.
figure 6

Simulation environment with Matlab/Simulink and Webots

Full size image

Case 2:

Different control methods. We compare the proposed motion trajectory planning method with a traditional PD control method and an ESB control method.

The traditional PD control method is designed:

$$ u = (\frac{1}{2}m_{b} + m_{h} + m_{p} )gl_{b} \cos \phi - k_{p1} e - k_{d1} \dot{e}, $$
(37)

where kp1, kd1 are control gains. e is defined as the boom luffing motion error signal, and \(e = \phi - \phi_{d} ,\dot{e} = \dot{\phi }\).

For the literature completeness, the expression of ESB control method in [24] is given:

$$ u = (\frac{1}{2}m_{b} + m_{h} + m_{p} )gl_{b} \cos \phi - k_{p2} \arctan \left( \xi \right) - k_{d2} \arctan \left( {\dot{\xi }} \right) $$
(38)

where kp2, kd2 are control gains, and \(\xi = e + \frac{{m_{p} l_{r} }}{{\left( {m_{h} + m_{p} } \right)l_{b} }}\cos \phi_{d} \left[ {\frac{{\left( {m_{h} + m_{p} } \right)l_{s} }}{{m_{p} l_{r} }}\alpha + \beta } \right],\;\dot{\xi } = \dot{e} + \frac{{m_{p} l_{r} }}{{\left( {m_{h} + m_{p} } \right)l_{b} }}\cos \phi_{d} \left[ {\frac{{\left( {m_{h} + m_{p} } \right)l_{s} }}{{m_{p} l_{r} }}\dot{\alpha } + \dot{\beta }} \right].\)

In order to get the suitable control performance for the double-pendulum rotary crane, the control gains in the comparative control methods are obtained by trial and error without too much difficulty. The control gains are obtained as \(k_{p1} = 2,k_{d1} = 5,k_{p2} = 2,k_{d2} = 4.2\). The double pendulum rotary crane system state constraints are: \(\ddot{\phi }_{\max } = 8\deg /s^{2} ,\,\,\ddot{\phi }_{\min } = - 8\deg /s^{2} ,\,\,\dot{\phi }_{\max } = 16\deg /s,\,\,\dot{\phi }_{\min } = 0\deg /s,\,\,\phi_{d} = 60\deg\).

The comparative simulation results of different control methods are presented in Fig. 7. There are five indicates to show the control performance in Table 1. It can be seen from comparative simulation results, by applying the proposed method, the boom luffing motion angle reaches the target position rapidly and accurately with suitable states. The maximum angular acceleration \(\ddot{\phi }_{\max }\) and the maximum angular velocity \(\dot{\phi }_{\max }\) are in the limit range of the sate constraints. However, the maximum angular acceleration/ velocity of PD and ESB control method are much bigger than the state constraints conditions. Compared with the traditional PD control method, the proposed method reduces the swing amplitude of the hook by 38.76%, the swing amplitude of the payload by 42.78%, and the adjustment time by 3.63 s. Compared with the ESB control method, the proposed nonlinear coupling-based motion trajectory planning method reduces the swing amplitude of the hook by 26.35%, the swing amplitude of the payload by 30.63%, and the adjustment time by 2.18 s. Therefore, the proposed nonlinear coupling-based motion trajectory planning control method has the better control performance than the comparative control methods.

Table 1. Performance indicates for comparative simulation: case 2-different control methods.
Full size table
Fig. 7.
figure 7

Results of comparative simulation: case 2-different control methods

Full size image

4.2 Robustness Verification

In order to testify the robustness of the proposed method, two cases of simulations are implemented by parameters uncertainties and external disturbance.

Case 1: Changing the system parameters. Payload mass and suspension cable length are changed: mp = 0.6 kg, ls = 0.1 m.

Fig. 8.
figure 8

Results of robustness verification: case 1-changing system parameters

Full size image

As shown in Fig. 8, the proposed method can effectively transfer payload with different masses and different suspension cable lengths. The simulation results are similar with Fig. 7, which proves that the control performance of the proposed strategy is not influenced by the payload mass changes basically. Meanwhile, the proposed method has better anti-swing control performance than comparative control methods.

Case 2: Adding external disturbance. A maximum amplitude of 5 deg sinusoid disturbance is added to the double pendulum system from 10 s to 10.5 s. A maximum amplitude of 5° random disturbance is added to the double pendulum system from 16 s to 16.5 s.

Fig. 9.
figure 9

Results of robustness verification: case 2-adding external disturbances

Full size image

As Fig. 9 shows, although all control methods can eliminate external disturbances within 2 s, only proposed strategy still realizes accurate positioning and effective anti-swing without state constraints. The compared controllers are still worse, and even the boom luffing motion angular acceleration/velocity exceeds state constraints.

5 Conclusions

In order to solve the problem of the positioning and anti-swing for double-pendulum rotary crane under state constraints effects, this paper proposes a nonlinear coupling-based motion trajectory planning control method. First, the Lagrange’s method is used to establish the dynamic model of the underactuated double-pendulum rotary crane. Then, we design the angular acceleration positioning trajectory of the boom luffing motion that satisfies the state constraints. The swing-eliminating angular acceleration trajectory is presented based on the kinematic coupling relationship among the boom luffing motion angels, hook swing angles and payload swing angles. The proposed motion trajectory is obtained by combining with the positioning trajectory and the swing-eliminating trajectory. The Lyapunov techniques and LaSalle’s invariance are supported to proof the control system stability. At last, several groups of numerical simulations verify the effectiveness and robustness of the proposed nonlinear coupling-based motion trajectory planning control method. In the future research, we will pay attention to the control problems of rotary crane system under time/energy constraints conditions.