Introduction

Underactuated mechanical systems, which have fewer actuators than degrees of freedom, are extensively applied in various industrial fields in recent years [1,2,3,4,5,6,7,8,9,10,11]. The overhead crane system, as a typical mechanical underactuated system, has been widely used in railway transportation, iron and steel chemical industry, port and other places, the main work of which is driving the payload smoothly and safely to its destination. Similar to other underactuated mechanical systems, the fact that the payload can be only indirectly controlled by the motion of the trolley brings a great challenge for the control of the overhead crane system.

Recently, a lot of control strategies have been presented for overhead crane systems. Specially, to suppress the swing of the payload, some energy-based approaches are developed for overhead crane systems [12,13,14]. In fact, the parameters of mechanical systems cannot be accurately known and the mechanical systems usually suffer from external disturbances. For the purpose of addressing the above mentioned issues, the adaptive control technology [15,16,17] and the sliding mode control technology [18, 19] are applied to the control of overhead crane systems. Moreover, some open-loop control strategies, including input shaping methods [20,21,22] and some methods based on trajectory planning [23, 24], are also developed to realize the control objectives for overhead cranes. Besides the traditional nonlinear approaches, some intelligent control algorithms are also presented to address the control problems of overhead crane systems in recent years [25,26,27,28].

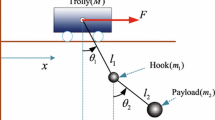
It is worthwhile to point out that above-mentioned approaches model the overhead crane system as the single-pendulum model with the assumption that the payload and the hook are regarded as one mass point. For this assumption, the hook mass and the distance between the payload and hook are ignored. However, in practical overhead crane systems, the payload is usually connected to a hook through the steel cable, which means that there is a certain distance between the hook and the payload. In addition, the hook mass connected to the trolley is usually large, which cannot be neglected. Therefore, the hook and the payload will exhibit different swings and the single-pendulum assumption does not hold when the mass of the hook is too large and the distance between the payload and hook is not negligible. Therefore, the overhead crane systems behave double-pendulum dynamics (as shown in Fig. 1), which greatly increases the complexity of the dynamic model for the overhead crane system and even makes the methods presented for single-pendulum cranes invalid. To this end, some results have been reported in [29,30,31,32,33] to address the control issue of double-pendulum overhead crane systems. Especially, for the double-pendulum overhead cranes, Ref. [31] propose a new quasi-proportional integral derivative control method. For the purpose of improving the performance index, some optimal control approaches are also applied to double-pendulum cranes in [34,35,36].

For double-pendulum overhead cranes, the fact that three degrees of freedom need to be controlled by one control input makes the control problem for the overhead crane systems extremely challenging. Although some excellent and constructive works have been reported in the literature, some issues need to be solved. In particular, the interconnection and damping assignment passivity-based control (IDA-PBC) technique is used to the control of underactuated systems, where control methods are designed by solving a series of partial differential equations [14]. The passivity-based control is usually used to construct a suitable Lyapunov function for the double-pendulum overhead cranes, however, the energy damping rate only depends on the trolley [37]. To enhance the coupling behavior among the trolley movement, the hook swing, and the payload swing, a novel energy-coupling-based control method is introduced in [38], where the system dynamic model of the overhead crane needs to be linearized when making control design and stability analysis. With the motivation to address these problems, a new enhanced anti-swing control law is developed with the consideration of double-pendulum dynamics. More precisely, firstly, we implement some basic transformations on the system dynamics and the acceleration variable is regarded as the auxiliary control input to be designed. Next, both an elaborate Lyapunov function and a corresponding auxiliary control input are introduced. Subsequently, the final control strategy is developed for the double-pendulum overhead crane system. After that, the stability of the closed-loop system and the convergence of the system states are strictly analyzed using Lyapunov theory and LaSalle’s invariance theorem. At last, the developed method is tested in Matlab/Simulink to demonstrate its effectiveness and robustness.

The rest sections of this paper are outlined as follows. In Sect. 2, the dynamic model of the overhead crane system is provided. In Sect. 3, controller design and corresponding stability analysis are given. Simulation tests are included in Sect. 4. Finally, some conclusions are made in Sect. 5.

Dynamic Model of the Overhead Crane System

Fig. 1
figure 1

Structure of the double-pendulum overhead crane system

Full size image

In this paper, we consider the double-pendulum overhead crane system as shown in Fig. 1. By employing the Euler–Lagrange approach, the double-pendulum overhead crane system can be described with the following dynamics [31]

$$\begin{aligned}&m_1\ddot{x} +m_2{\ddot{\theta }}_1\cos \theta _1 - m_2{\dot{\theta }_1^2}\sin \theta _1\nonumber \\&\qquad +m_3{\ddot{\theta }}_2 \cos \theta _2 - m_3 {{\dot{\theta }}_2^2}\sin \theta _2 =F \end{aligned}$$
(1)
$$\begin{aligned}&m_2{\ddot{x}}\cos \theta _1 +m_2l_1{\ddot{\theta }}_1+m_4{\ddot{\theta }}_2\cos (\theta _1-\theta _2)\nonumber \\&\qquad + m_4{{\dot{\theta }}_2^2}\sin (\theta _1-\theta _2)+m_2g\sin \theta _1 =0 \end{aligned}$$
(2)
$$\begin{aligned}&m_3{\ddot{x}}\cos \theta _2 +m_4{\ddot{\theta }_1}\cos (\theta _1-\theta _2)+m_3{l_2}{\ddot{\theta }_2} \nonumber \\&\qquad - m_4{\dot{\theta }_1^2}\sin (\theta _1-\theta _2)+m_3g\sin \theta _2 =0 \end{aligned}$$
(3)

where x(t), \(\theta _1(t)\), \(\theta _2(t)\) represent the trolley displacement, hook swing angle and payload swing angle, respectively; the acceleration constant of the gravity is expressed by g; the driving force is represented by F(t); \(m_1, m_2, m_3, m_4\) are system parameters, the explicit expressions of which are described as follows

$$\begin{aligned}&m_1=(m_c+m_h+m_p), m_2=(m_h+m_p)l_1 \\&m_3=m_p l_2, m_4=m_pl_1l_2 \end{aligned}$$

where \(m_c\), \(m_h\), \(m_p\) represent the mass of the trolley, hook and payload, respectively; \(l_1\) is the length of the rope; \(l_2\) denotes the distance between the hook center and the payload center.

In this paper, the following auxiliary variables are introduced for the simplicity of the subsequent analysis process

$$\begin{aligned} \begin{array}{lll} S_1=\sin \theta _1, &{} S_2=\sin \theta _2 , &{} S_{12}=\sin (\theta _1- \theta _2) \\ C_1=\cos \theta _1, &{} C_2=\cos \theta _2, &{} C_{12}=\cos (\theta _1 -\theta _2) \end{array} \end{aligned}$$

Then, the equations of the dynamic (1)-(3) can be rewritten into a compact form as follows

$$\begin{aligned} M_{11} {\ddot{x}} + M_{12} {\ddot{\varvec{}\theta }}+ V_1&= F \end{aligned}$$
(4)
$$\begin{aligned} M_{21} {\ddot{x}}+ M_{22} {\ddot{\varvec{}\theta }} + V_2&={0} \end{aligned}$$
(5)

where

$$\begin{aligned}&{\varvec{}\theta } =[\theta _1 ~~ \theta _2]^{\mathrm T}, ~M_{11}= m_1 \\&M_{12}=M_{21}^{\mathrm T}= [m_2 C_1 ~~ m_3 C_2 ],~V_1=- m_2{\dot{\theta }_1^2}S_1-m_3 {{\dot{\theta }}_2^2}S_2 \\&M_{22}=\left[ \begin{array}{cc} m_2 l_1 &{} m_4 C_{12} \\ m_4 C_{12} &{} m_2 l_2 \end{array} \right] ,~ V_{2}=\left[ \begin{array}{c} m_2gS_1 +m_4{{\dot{\theta }}_2^2}S_{12} \\ m_3gS_2-m_4{{\dot{\theta }}_1^2}S_{12} \end{array} \right] \end{aligned}$$

The main objectives of the double-pendulum overhead crane are driving the payload smoothly and safely to its destination and ensuring no residual swing of the payload and hook. To realize the objectives of the system, we will design a nonlinear control strategy to position the trolley to the specified location and suppress the swing of the hook and payload, which means

$$\begin{aligned} \lim _{t \rightarrow \infty } \left[ x ~~ \theta _1 ~~ \theta _2 ~~ \dot{x} ~~ {\dot{\theta }}_1 ~~ {\dot{\theta }}_2 \right] ^{\mathrm T} = \left[ x_d ~~ 0 ~~ 0 ~~ 0 ~~ 0 ~~ 0 \right] ^{\mathrm T} \end{aligned}$$
(6)

where \(x_d \in {{\mathbb {R}}}\) is the specified location of the trolley.

For practical cranes, the following assumption is reasonably made [29, 31].

Assumption 1

The swing of the hook and payload is within \(- \frac{\pi }{2} \le \theta _1,\theta _2 \le \frac{\pi }{2}\).

Main Results

In this section, a nonlinear control strategy will be developed to realize the control objectives of the double-pendulum overhead crane system. Moreover, rigorous stability analysis of the closed-loop system will be given to demonstrate the feasibility of the presented control method.

Controller Design

First, a partial feedback linearizing control law is derived as follows based on (4) and (5)

$$\begin{aligned} F=(M_{11}-M_{12}M_{22}^{-1}M_{21})\upsilon + V_1 - M_{12}M_{22}^{-1}V_2 \end{aligned}$$
(7)

where \(v(t)=\ddot{x}(t)\) is an auxiliary signal which should be designed. Thus, we could design a suitable acceleration signal \(\ddot{x}(t)\) to obtain the desired controller.

For the double-pendulum overhead crane system, the total mechanical energy of which is

$$E_{\textrm{hp}}=~\frac{1}{2}m_2{l_1}{\dot{\theta }_1^2}+\frac{1}{2}m_3{l_2}{{\dot{\theta }}_2^2} +{m_4}{\dot{\theta }_1}{{\dot{\theta }}_2}C_{12} +m_2g(1-C_1)+m_3g(1-C_2)$$
(8)

Then, the derivative of \(E_{hp}(t)\) can be obtained as follows

$$\begin{aligned} {\dot{E}}_{\textrm{hp}}=&~m_2 l_1 {{\dot{\theta }}_1} {\ddot{\theta }_1} + m_3 l_2 {{\dot{\theta }}_2}{\ddot{\theta }_2} + m_4 {\ddot{\theta }_1} {{\dot{\theta }}_2}{C_{12}} \nonumber \\&+ m_4 {{\dot{\theta }}_1} {\ddot{\theta }_2}{C_{12}} -m_4 {{\dot{\theta }}_1^2}{{\dot{\theta }}_2}{S_{12}}+ m_4 {{\dot{\theta }}_1}{{\dot{\theta }}_2^2}{S_{12}}\nonumber \\&+m_2 g {\dot{\theta }_1} S_1 +m_3 g {{\dot{\theta }}_2} S_2 \end{aligned}$$
(9)

Meanwhile, inserting (2) and (3) into \(\dot{E}_{hp}(t)\) leads to

$$\begin{aligned} {\dot{E}}_{\textrm{hp}}= - (m_2{{\dot{\theta }}_1}C_1 + m_3{\dot{\theta }_2}C_2) \cdot \upsilon \end{aligned}$$
(10)

Based on v(t) and \(\dot{E}_{hp}(t)\), the following Lyapunov function candidate is introduced

$$\begin{aligned} V(t)= \frac{1}{2}k_p (e_x - k_v m_2 S_1 -k_v m_3 S_2)^2 + \frac{1}{2}{\dot{x}}^2 + k_vE_{\textrm{hp}} \end{aligned}$$
(11)

where \(k_p, k_v \in {{\mathbb {R}}}^+\) are constants and \(e_x(t)\) is the positioning error, that is

$$\begin{aligned} e_x=x-x_d \end{aligned}$$
(12)

Next, taking the derivative of V(t) along the closed-loop system (1)-(3) and making some algebraic manipulations yields

$$\begin{aligned}&{\dot{V} }(t)= ({\dot{x}} - k_v m_2 {{\dot{\theta }}_1}C_1 -k_v m_3 {\dot{\theta }_2}C_2) \left( \upsilon \nonumber \right. \\&\qquad \left. + k_p (e_x - k_v m_2 S_1 -k_v m_3 S_2) \right) \end{aligned}$$
(13)

wherein the conclusion of (10) is used.

Based on (13), the following auxiliary input signal is designed

$$\begin{aligned} \upsilon =&- k_p (e_x - k_v m_2 S_1 -k_v m_3 S_2) -k_d ({\dot{x}} \nonumber \\&\qquad - k_v m_2 {{\dot{\theta }}_1}C_1 -k_v m_3 {{\dot{\theta }}_2}C_2) \end{aligned}$$
(14)

where \(k_d\in {{\mathbb {R}}}^+\) is a constant. By inserting the above control scheme (14) into (7), one can get the controller as follows

$$\begin{aligned} F=&~(M_{11}-M_{12}M_{22}^{-1}M_{21}) (- k_p (e_x - k_v m_2 S_1 -k_v m_3 S_2) \nonumber \\&-k_d ({\dot{x}} - k_v m_2 {{\dot{\theta }}_1}C_1 -k_v m_3 {\dot{\theta }_2}C_2)) + V_1 - M_{12}M_{22}^{-1}V_2 \end{aligned}$$
(15)

Stability Analysis

In this section, to prove the stability of the closed-loop system and the convergence of the states, the following theorem is introduced.

Theorem 1

The developed nonlinear control method ensures the control objectives of the double-pendulum overhead crane system are achieved, that is

$$\begin{aligned} \lim _{t \rightarrow \infty } \left[ e_x ~~ \theta _1 ~~ \theta _2 ~~ \dot{x} ~~ {\dot{\theta }}_1 ~~ {\dot{\theta }}_2 \right] ^{\mathrm T} = \left[ 0 ~~ 0 ~~ 0 ~~ 0 ~~ 0 ~~ 0 \right] ^{\mathrm T} \end{aligned}$$
(16)

Proof

First, the following Lyapunov function candidate given in (11) is introduced

$$\begin{aligned} V(t)= \frac{1}{2}k_p \left( e_x - k_v m_2 S_1 -k_v m_3 S_2 \right) ^2 + \frac{1}{2}{\dot{x}}^2 + k_vE_{\textrm{hp}} \end{aligned}$$

Taking the time derivative of V(t), applying the conclusion of (10), and substituting the devised control law (15) into the resulting equation lead to

$$\begin{aligned} {\dot{V}}(t) = -k_d\left( {\dot{x}} - k_v m_2 {{\dot{\theta }}_1}C_1 -k_v m_3 {{\dot{\theta }}_2}C_2 \right) ^2\le 0 \end{aligned}$$
(17)

which means that \(V(t) \in {{\mathcal {L}}}_\infty\) and the closed-loop system is stable in the Lyapunov sense. Furthermore, the following conclusion can be derived

$$\begin{aligned} x, \dot{x}, \theta _1, {\dot{\theta }}_1, \theta _2 , {\dot{\theta }}_2\in {{\mathcal {L}}}_\infty \end{aligned}$$
(18)

To demonstrate that the origin is the only equilibrium point, the following invariant set is introduced based on LaSalle’s invariance principle

$$\begin{aligned} {{\mathcal {S}}} =\left\{ (x, \dot{x}, \theta _1, {\dot{\theta }}_1, \theta _2 , {\dot{\theta }}_2) \mid \dot{V}(t)=0 \right\} \end{aligned}$$
(19)

According to (19), one can obtain the following conclusion

$$\begin{aligned} {\dot{x}} - k_v m_2 {{\dot{\theta }}_1}C_1 -k_v m_3 {{\dot{\theta }}_2}C_2= 0 \end{aligned}$$
(20)

it is clear from (20) that

$$\begin{aligned} e_x - k_v m_2 S_1 -k_v m_3 S_2 = \alpha _1 \end{aligned}$$
(21)

where \(\alpha _1 \in {{\mathbb {R}}}\) is a constant. Thus, one can derive from (14), (20) and (21) that

$$\begin{aligned} \ddot{x} =\upsilon&= - k_p (e_x - k_v m_2 S_1 -k_v m_3 S_2) = -k_p \alpha _1 \end{aligned}$$
(22)

Then, we assume that \(\upsilon (t)\ne 0\) and it can be concluded that

$$\begin{aligned} \dot{x}(t) \rightarrow \left\{ \begin{array}{ll} -\infty &{} \upsilon (t)<0,\\ +\infty &{} \upsilon (t)>0, \end{array}\right. \quad {\textrm{as}} \quad t \rightarrow \infty \end{aligned}$$
(23)

The conclusion of (23) means that x(t) will go infinity when t goes infinity, which contradicts the result of (18). Therefore, the supposition of \(\upsilon (t)\ne 0\) is invalid, which further makes the following equality hold

$$\begin{aligned} \ddot{x}=\upsilon =- k_p (e_x - k_v m_2 S_1 -k_v m_3 S_2) =0 \end{aligned}$$
(24)

Analogously, one can get the following conclusion from (24)

$$\begin{aligned} \left. \begin{array}{l} \dot{x} =\alpha _2 \\ e_x=k_v m_2 S_1 +k_v m_3 S_2 \end{array} \right\} \Longrightarrow \dot{x}=0 \end{aligned}$$
(25)

where \(\alpha _2 \in {{\mathbb {R}}}\) is a constant. It is derived from (25) that

$$\begin{aligned} m_2 S_1 +m_3 S_2 = \alpha _3 \Longrightarrow m_2 {{\dot{\theta }}_1}C_1 + m_3 {{\dot{\theta }}_2}C_2 =0 \end{aligned}$$
(26)

where \(\alpha _3 \in {{\mathbb {R}}}\) is a constant. To guarantee \(\alpha _3 =0\), the sum of (2) and (3) is written as

$$\begin{aligned}&\frac{\mathrm d}{{\mathrm d}t}\left[ m_2 l_1{{\dot{\theta }}_1} +m_3{l_2}{{\dot{\theta }}_2} +m_4({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}\right] =-m_2 g S_1 - m_3 g S_2 \end{aligned}$$
(27)

Integrating both sides of (27) yields

$$\begin{aligned} m_2 l_1{{\dot{\theta }}_1} +m_3{l_2}{{\dot{\theta }}_2} +m_4({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}= - \alpha _3 g t + \alpha _4 \end{aligned}$$
(28)

where \(\alpha _4\in {{\mathbb {R}}}\) is a constant. It can be derived that \(\alpha _3=0\) from the conclusion of (18). Therefore, the following equalities hold

$$\begin{aligned}&m_2 S_1 +m_3 S_2 = 0 \end{aligned}$$
(29)
$$\begin{aligned}&m_2 l_1{{\dot{\theta }}_1} +m_3{l_2}{{\dot{\theta }}_2} +m_4({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}= \alpha _4 \end{aligned}$$
(30)

According to the triangular transformation formula, one can rewrite the item \(({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}\) of (30) as follows

$$\begin{aligned} ({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}&= ({{\dot{\theta }}_1}+{{\dot{\theta }}_2})(C_1C_2 +S_1 S_2) \nonumber \\&= ({{\dot{\theta }}_1} C_1 C_2 + {{\dot{\theta }}_2}S_1 S_2) + ({{\dot{\theta }}_1} S_1 S_2 + {{\dot{\theta }}_2}C_1 C_2) \end{aligned}$$
(31)

which further implies from (26) and (30) that

$$\begin{aligned} ({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}&= -\frac{m_3}{m_2}({\dot{\theta }_2} {C_2^2} + {{\dot{\theta }}_2}{S_2^2}) -\frac{m_2}{m_3}({{\dot{\theta }}_1} {S_1^2} + {{\dot{\theta }}_1}{C_1^2}) \nonumber \\&= -\frac{m_3}{m_2}{{\dot{\theta }}_2}-\frac{m_2}{m_3}{{\dot{\theta }}_1} \end{aligned}$$
(32)

Substituting the resulting expression of (32) into (30) for \(({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}\) and utilizing the expressions of \(m_2, m_3, m_4\) lead to

$$\begin{aligned}&m_2 l_1{{\dot{\theta }}_1} +m_3{l_2}{{\dot{\theta }}_2} +m_4({{\dot{\theta }}_1}+{{\dot{\theta }}_2})C_{12}\nonumber \\&\quad = m_2 l_1{{\dot{\theta }}_1} +m_3{l_2}{{\dot{\theta }}_2} -m_4\left( \frac{m_3}{m_2}{\dot{\theta }_2}+\frac{m_2}{m_3}{{\dot{\theta }}_1} \right) \nonumber \\&\quad = \left( m_3 l_2 - \frac{m_4 m_3}{m_2}\right) {{\dot{\theta }}_2} =\alpha _4 \end{aligned}$$
(33)

Analogously, it is clear that

$$\begin{aligned} \alpha _4 =0 ,~{\dot{\theta }}_2= 0 \end{aligned}$$
(34)

which, along with (29) and (30), further indicates that

$$\begin{aligned} {\dot{\theta }}_1 =0 \end{aligned}$$
(35)

Based on (2), (3) and the conclusions that

$$\begin{aligned} \ddot{x} =0,~{\dot{\theta }}_1 =0 ,~{\dot{\theta }}_2 =0,~\ddot{\theta }_1 =0 ,~\ddot{\theta }_2 =0 \end{aligned}$$
(36)

Then, based on Assumption 1, one can obtain that

$$\begin{aligned} S_1 =0, ~ S_2=0 \Longrightarrow \theta _1=0 ,~\theta _2=0 \end{aligned}$$
(37)

By summarizing the results in (37), (21), (22) and (24), we can draw the conclusion that

$$\begin{aligned} e_x=0 \Longrightarrow x=x_d \end{aligned}$$
(38)

Hence, the conclusion of the theorem is proven.

Simulation Results

In this section, a series of digital simulation tests are included using Matlab/Simulink to demonstrate the control performance of the developed control law. Specially, three groups of simulation tests will be carried out. For the first group, the LQR method and an existing nonlinear control method designed in [31] are selected for a comparison study. For the second group, the control performance of the proposed method with different system parameters and desired positions will be examined. For the third group, the robustness of the proposed method with respect to different external disturbances will be examined.

Fig. 2
figure 2

Simulation results for the LQR method, the existing nonlinear method, and the presented approach

Full size image
Fig. 3
figure 3

Simulation results for the presented approach (15) with respect to Case 1

Full size image
Fig. 4
figure 4

Simulation results for the presented approach (15) with respect to Case 2

Full size image
Fig. 5
figure 5

Simulation results for the presented approach (15) with respect to different disturbances

Full size image

Comparative Simulation

First, we set the initial condition as \([x(0)~ \theta _1(0)~ \theta _2(0)]^{\mathrm T}=[0~0~0]^{\mathrm T}\). The parameters of the system are adopted as

$$\begin{aligned} l_1=0.8\,\textrm{m}, l_2=0.2\,\textrm{m},~m_c=10\,\textrm{kg},~ m_h=0.2\,\textrm{kg}, m_p=3\,\textrm{kg}, g=9.8\,\mathrm{kg/ s^2 } \end{aligned}$$

and the desired position is set as \(x_d=2.4\,\textrm{m}\). The control gains of the presented approach are adopted as

$$\begin{aligned} k_p=1,~k_d=2,~k_v=0.6 \end{aligned}$$

For simplicity, the expressions of the LQR method and the existing nonlinear control method are not given here. The simulation results of the three methods are displayed in Fig. 2.

It can be observed from Fig. 2 that the LQR method, the existing nonlinear control method and the developed method can make the trolley reach the specified position rapidly. However, we can also observe the fact that both the LQR method and the existing nonlinear control method need more time to eliminate the hook swing and even can not eliminate the payload swing, which affects work efficiency and sometimes causes payload damages in some cases. The comparative simulation results of this group show that the proposed control method possesses superior control performance.

Stabilization of Different Conditions

For the second simulation test, we will evaluate the control performance of the developed control law with different conditions. Specially, we will examine the performance of the devised control law with the following cases.

Case 1

The desired position is changed from \({x_d=2.4\,\textrm{m}}\) to \({x_d=1.8\,\textrm{m}}\). The initial condition is zero. The system parameters and control gains are selected as the same as those in the comparative simulation part.

Case 2

The system parameters are changed to \(m_c=7\,\textrm{kg}\), \(m_h=0.1\,\textrm{kg}\), \(m_p=1\,\textrm{kg}\), \(l_1=0.4\,\textrm{m}\), \(l_2=0.1\,\textrm{m}\), \(g=9.8\,\mathrm{kg/s^2}\). The initial condition is zero. The desired position and control gains are chosen as the same as those in the comparative simulation part.

The simulation results of this group are displayed in Figs. 3 and 4, respectively. We can observe from Figs. 3 and 4 that the swing of the hook and payload is successfully suppressed and eliminated with different conditions. The simulation results show that the proposed method has good performance regardless of whether the desired position or system parameters are changed.

Robustness Examination

To examine the robustness of the proposed control method with respect to different external disturbances, we add three kinds of disturbances to the payload. Specifically, random disturbances are imposed on the payload between 10 and \(15\,\textrm{s}\), sinusoid disturbances are imposed on the payload between 22 and \(24\,\textrm{s}\), and impulsive disturbances are imposed on the payload between 30 and \(30.1\,\textrm{s}\), all with the amplitude of \(2^\circ\). All of other conditions are chosen as the same as those in the comparative simulation part.

The simulation results of this group are shown in Fig. 5. From the obtained simulation results, one can find that three types of external disturbances are all eliminated by the proposed control method, which indicates satisfactory robustness with respect to uncertain disturbances.

Conclusions

In this study, a new enhanced anti-swing control strategy is developed for overhead crane systems with double-pendulum dynamics. The presented control algorithm has both the theoretical and practical significance. On the one hand, the double pendulum-dynamics of the overhead crane system is taken into consideration to improve the applicability in practical engineering. On the other hand, a novel control strategy is presented to suppress the payload swing and hook swing. Compared with existing approaches for the double-pendulum overhead crane control, digital simulation results have shown that the presented approach has excellent performance.