Keywords

1 Introduction

Chaotic systems are defined as nonlinear dynamical systems which are sensitive to initial conditions, topologically mixing and with dense periodic orbits. Sensitivity to initial conditions of chaotic systems is popularly known as the butterfly effect. Small changes in an initial state will make a very large difference in the behavior of the system at future states.

The Lyapunov exponent is a measure of the divergence of phase points that are initially very close and can be used to quantify chaotic systems. It is common to refer to the largest Lyapunov exponent as the Maximal Lyapunov Exponent (MLE). A positive maximal Lyapunov exponent and phase space compactness are usually taken as defining conditions for a chaotic system.

Some classical paradigms of 3-D chaotic systems in chaos literature are Lorenz system [1], Rössler system [2], ACT system [3], Sprott systems [4], Chen system [5], Lü system [6], Liu system [7], Cai system [8], Chen-Lee system [9], Tigan system [10], etc.

Many new chaotic systems have been discovered in the recent years such as Zhou system [11], Zhu system [12], Li system [13], Wei-Yang system [14], Sundarapandian systems [15, 16], Vaidyanathan systems [17–32], Pehlivan system [33], Sampath system [34], Pham system [35], etc.

Chaos theory and control systems have many important applications in science and engineering [36–41]. Some commonly known applications are oscillators [42, 43], lasers [44, 45], chemical reactions [46–48, 48–50], biology [51–58], ecology [59, 60], encryption [61, 62], cryptosystems [63, 64], mechanical systems [65–69], secure communications [70–72], robotics [73–75], cardiology [76, 77], intelligent control [78, 79], neural networks [80–82], finance [83, 84], memristors [85, 86], etc.

Synchronization of chaotic systems is a phenomenon that occurs when two or more chaotic systems are coupled or when a chaotic system drives another chaotic system. Because of the butterfly effect which causes exponential divergence of the trajectories of two identical chaotic systems started with nearly the same initial conditions, the synchronization of chaotic systems is a challenging research problem in the chaos literature.

Major works on synchronization of chaotic systems deal with the complete synchronization of a pair of chaotic systems called the master and slave systems. The design goal of the complete synchronization is to apply the output of the master system to control the slave system so that the output of the slave system tracks the output of the master system asymptotically with time.

Pecora and Carroll pioneered the research on synchronization of chaotic systems with their seminal papers [87, 88]. The active control method [89–99] is typically used when the system parameters are available for measurement.

Adaptive control method [100–115] is typically used when some or all the system parameters are not available for measurement and estimates for the uncertain parameters of the systems.

Sampled-data feedback control method [116–119] and time-delay feedback control method [120–122] are also used for synchronization of chaotic systems. Backstepping control method [123–130] is also used for the synchronization of chaotic systems, which is a recursive method for stabilizing the origin of a control system in strict-feedback form.

Another popular method for the synchronization of chaotic systems is the sliding mode control method [131–140], which is a nonlinear control method that alters the dynamics of a nonlinear system by application of a discontinuous control signal that forces the system to “slide” along a cross-section of the system’s normal behavior.

In this research work, we describe a ten-term novel 4-D four-wing chaotic system with four quadratic nonlinearities. Section 2 describes the 4-D dynamical model and phase portraits of the novel four-wing chaotic system. Section 3 describes the dynamic analysis of the novel four-wing chaotic system. We shall show that the novel four-wing chaotic system has a unique equilibrium at the origin, which is a saddle-point. Thus, the origin is an unstable equilibrium of the novel four-wing chaotic system.

The Lyapunov exponents of the novel 4-D four-wing chaotic system are obtained as \(L_1 = 5.6253\), \(L_2 = 0\), \(L_3 = -5.4212\) and \(L_4 = -53.0373\). Thus, the maximal Lyapunov exponent of the novel four-wing chaotic system is obtained as \(L_1 = 5.6253\). The large value of \(L_1\) indicates that the novel four-wing system is highly chaotic. Since the sum of the Lyapunov exponents of the novel chaotic system is negative, it follows that the novel chaotic system is dissipative. Also, the Kaplan-Yorke dimension of the novel four-wing chaotic system is obtained as \(D_{KY} = 3.0038\).

Section 4 describes the adaptive synchronization of the identical novel chaotic systems with unknown parameters. The adaptive feedback control and synchronization results are proved using Lyapunov stability theory [141]. MATLAB simulations are depicted to illustrate all the main results for the 4-D novel four-wing chaotic system. Finally, Sect. 5 gives a summary of the main results derived in this work.

2 A Novel 4-D Four-Wing Chaotic System

In this work, we announce a novel 4-D four-wing chaotic system described by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} - a x_1 + x_2 x_3 + p x_4 \\ \dot{x}_2 &{} = &{} a x_2 - x_1 x_3 - p x_4 \\ \dot{x}_3 &{} = &{} - b x_3 + x_1 x_2 \\ \dot{x}_4 &{} = &{} - c x_4 + x_1 x_3 \\ \end{array} \right. \end{aligned}$$
(1)

In (1), \(x_1, x_2, x_3, x_4\) are the states and a, b, c, p are constant, positive parameters.

The 4-D system (1) is chaotic when the parameter values are taken as

$$\begin{aligned} a = 17, \ \ b = 50, \ \ c = 5, \ \ p = 2 \end{aligned}$$
(2)

For numerical simulations, we take the initial state of the chaotic system (1) as

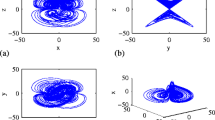
$$\begin{aligned} x_1(0) = 1.5, \ \ \ x_2(0) = 1.8, \ \ \ x_3(0) = 1.2, \ \ x_4(0) = 1.4 \end{aligned}$$
(3)

The novel 4-D chaotic system (1) exhibits a strange, four-wing chaotic attractor. Figure 1 describes the 3-D projection of the four-wing chaotic attractor of the novel 4-D chaotic system (1) on \((x_1, x_2, x_3)\) space. Figure 2 describes the 3-D projection of the four-wing chaotic attractor of the novel 4-D chaotic system (1) on \((x_1, x_2, x_4)\) space.

Figure 3 describes the 3-D projection of the four-wing chaotic attractor of the novel 4-D chaotic system (1) on \((x_1, x_3, x_4)\) space. Figure 2 describes the 3-D projection of the four-wing chaotic attractor of the novel 4-D chaotic system (1) on \((x_2, x_3, x_4)\) space.

Fig. 1
figure 1

3-D projection of the novel four-wing chaotic system on \((x_1, x_2, x_3)\) space

Full size image
Fig. 2
figure 2

3-D projection of the novel four-wing chaotic system on \((x_1, x_2, x_4)\) space

Full size image
Fig. 3
figure 3

3-D projection of the novel four-wing chaotic system on \((x_1, x_3, x_4)\) space

Full size image

3 Analysis of the Novel 4-D Four-Wing Chaotic System

This section gives the qualitative properties of the novel 4-D four-wing chaotic system (1) proposed in this research work.

3.1 Dissipativity

We write the system (1) in vector notation as

$$\begin{aligned} \dot{x} = f(x) = \left[ \begin{array}{c} f_1(x) \\ f_2(x) \\ f_3(x) \\ f_4(x) \\ \end{array} \right] , \end{aligned}$$
(4)

where

$$\begin{aligned} \left. \begin{array}{ccl} f_1(x) &{} = &{} - a x_1 + x_2 x_3 + p x_4 \\ f_2(x) &{} = &{} a x_2 - x_1 x_3 - p x_4 \\ f_3(x) &{} = &{} - b x_3 + x_1 x_2 \\ f_4(x) &{} = &{} - c x_4 + x_1 x_3 \\ \end{array} \right. \end{aligned}$$
(5)

We take the parameter values as in the chaotic case, viz.

$$\begin{aligned} a = 17, \ \ b = 50, \ \ c = 5, \ \ p = 2 \end{aligned}$$
(6)

The divergence of the vector field f on \(\mathrm{I\!R}^4\) is obtained as

$$\begin{aligned} \text {div} \ f = {\partial f_1(x) \over \partial x_1} + {\partial f_2(x) \over \partial x_2} + {\partial f_3(x) \over \partial x_3} + {\partial f_4(x) \over \partial x_4} = - (b + c) = -\mu \end{aligned}$$
(7)

where

$$\begin{aligned} \mu = b + c = 55 > 0 \end{aligned}$$
(8)

Let \(\varOmega \) be any region in \(\mathrm{I\!R}^4\) with a smooth boundary. Let \(\varOmega (t) = \varPhi _t(\varOmega )\), where \(\varPhi _t\) is the flow of the vector field f.

Let V(t) denote the hypervolume of \(\varOmega (t)\).

By Liouville’s theorem, it follows that

$$\begin{aligned} {dV(t) \over dt} = \int \limits _{\varOmega (t)} \ (\text {div} f) dx_1 \, dx_2 \, dx_3 \, dx_4 \end{aligned}$$
(9)

Substituting the value of \(\text {div} f\) in (9) leads to

$$\begin{aligned} {dV(t) \over dt} = - \mu \int \limits _{\varOmega (t)} \ dx_1 \, dx_2 \, dx_3 \, dx_4 = - \mu V(t) \end{aligned}$$
(10)

Integrating the linear differential equation (10), V(t) is obtained as

$$\begin{aligned} V(t) = V(0) \exp (-\mu t), \ \ \text {where} \ \ \mu = 55 > 0. \end{aligned}$$
(11)

From Eq. (11), it follows that the hypervolume V(t) shrinks to zero exponentially as \(t \rightarrow \infty \).

Thus, the novel chaotic system (1) is dissipative. Hence, any asymptotic motion of the system (1) settles onto a set of measure zero, i.e. a strange attractor.

3.2 Rotation Symmetry

It is easy to see that the novel 4-D chaotic system (1) is invariant under the change of coordinates

$$\begin{aligned} (x_1, x_2, x_3, x_4) \mapsto (- x_1, - x_2, x_3, - x_4) \end{aligned}$$
(12)

Since the transformation (12) persists for all values of the system parameters, it follows that the novel 4-D chaotic system (1) has rotation symmetry about the \(x_3\)-axis and that any non-trivial trajectory must have a twin trajectory.

3.3 Equilibria

The equilibrium points of the novel chaotic system (1) are obtained by solving the nonlinear equations

$$\begin{aligned} \left. \begin{array}{cclcl} f_1(x) &{} = &{} - a x_1 + x_2 x_3 + p x_4 &{} = &{} 0 \\ f_2(x) &{} = &{} a x_2 - x_1 x_3 - p x_4 &{} = &{} 0 \\ f_3(x) &{} = &{} - b x_3 + x_1 x_2 &{} = &{} 0 \\ f_4(x) &{} = &{} - c x_4 + x_1 x_3 &{} = &{} 0 \\ \end{array} \right. \end{aligned}$$
(13)

We take the parameter values as in the chaotic case, viz.

$$\begin{aligned} a = 17, \ \ b = 50, \ \ c = 5, \ \ p = 2 \end{aligned}$$
(14)

Solving the nonlinear system of Eq. (13) with the parameter values (14), we obtain a unique equilibrium point at the origin, i.e.

$$\begin{aligned} E_0 = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] \end{aligned}$$
(15)

The Jacobian matrix of the novel chaotic system (1) at \(E_0\) is obtained as

$$\begin{aligned} J_0 = J(E_0) = \left[ \begin{array}{rrrr} -17 &{} 0 &{} 0 &{} 2 \\ 0 &{} 17 &{} 0 &{} -2 \\ 0 &{} 0 &{} -50 &{} 0 \\ 0 &{} 0 &{} 0 &{} -5 \\ \end{array} \right] \end{aligned}$$
(16)

The matrix \(J_0\) has the eigenvalues

$$\begin{aligned} \lambda _1 = - 50, \ \ \lambda _2 = -17, \ \ \lambda _3 = -5, \ \ \lambda _4 = 17 \end{aligned}$$
(17)

This shows that the equilibrium point \(E_0\) is a saddle-point, which is unstable (Fig. 4).

Fig. 4
figure 4

3-D projection of the novel four-wing chaotic system on \((x_2, x_3, x_4)\) space

Full size image

3.4 Lyapunov Exponents and Kaplan-Yorke Dimension

We take the initial values of the novel four-wing system (1) as in (3), viz.

$$\begin{aligned} x_1(0) = 1.5, \ \ x_2(0) = 1.8, \ \ x_3(0) = 1.2, \ \ x_4(0) = 1.4 \end{aligned}$$
(18)

We also take the parameter values of the novel four-wing system (1) as in the chaotic case (2), viz.

$$\begin{aligned} a = 17, \ \ b = 50, \ \ c = 5, \ \ p = 2 \end{aligned}$$
(19)

Then the Lyapunov exponents of the novel four-wing system (1) are numerically obtained as

$$\begin{aligned} L_1 = 5.6253, \ \ L_2 = 0, \ \ L_3 = -5.4212, \ \ L_4 = -53.0373 \end{aligned}$$
(20)

Since \(L_1 + L_2 + L_3 + L_4 = - 52.8332 < 0\), the system (1) is dissipative.

Also, the Kaplan-Yorke dimension of the system (1) is obtained as

$$\begin{aligned} D_{KY} = 3 + {L_1 + L_2 + L_3 \over | L_4 |} = 3.0038 \end{aligned}$$
(21)

Figure 5 depicts the dynamics of the Lyapunov exponents of the novel 4-D four-wing chaotic system (1).

From Fig. 5, it is seen that the Maximal Lyapunov Exponent (MLE) of the novel 4-D four-wing chaotic system (1) is \(L_1 = 5.5623\), which is a large value. Thus, the novel 4-D four-wing chaotic system (1) exhibits strong chaotic properties.

Fig. 5
figure 5

Dynamics of the Lyapunov exponents of the novel four-wing chaotic system

Full size image

4 Adaptive Synchronization of the Identical Novel Four-Wing Chaotic Systems

This section derives new results for the adaptive synchronization of the identical novel four-wing chaotic systems with unknown parameters.

The master system is given by the novel four-wing chaotic system

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} - a x_1 + x_2 x_3 + p x_4 \\ \dot{x}_2 &{} = &{} a x_2 - x_1 x_3 - p x_4 \\ \dot{x}_3 &{} = &{} - b x_3 + x_1 x_2 \\ \dot{x}_4 &{} = &{} - c x_4 + x_1 x_3 \\ \end{array} \right. \end{aligned}$$
(22)

where \(x_1, x_2, x_3, x_4\) are state variables and a, b, c, p are constant, unknown, parameters of the system.

The slave system is given by the controlled novel chaotic system

$$\begin{aligned} \left. \begin{array}{ccl} \dot{y}_1 &{} = &{} - a y_1 + y_2 y_3 + p y_4 + u_1 \\ \dot{y}_2 &{} = &{} a y_2 - y_1 y_3 - p y_4 + u_2 \\ \dot{y}_3 &{} = &{} - b y_3 + y_1 y_2 + u_3 \\ \dot{y}_4 &{} = &{} - c y_4 + y_1 y_3 + u_4 \\ \end{array} \right. \end{aligned}$$
(23)

where \(y_1, y_2, y_3, y_4\) are state variables and \(u_1, u_2, u_3, u_4\) are adaptive controls to be designed.

The synchronization error is defined as

$$\begin{aligned} \left. \begin{array}{ccl} e_1 &{} = &{} y_1 - x_1 \\ e_2 &{}= &{} y_2 - x_2 \\ e_3 &{} = &{} y_3 - x_3 \\ e_4 &{} = &{} y_4 - x_4 \\ \end{array} \right. \end{aligned}$$
(24)

A simple calculation yields the error dynamics

$$\begin{aligned} \left. \begin{array}{ccl} \dot{e}_1 &{}= &{} - a e_1 + p e_4 + y_2 y_3 - x_2 x_3 + u_1 \\ \dot{e}_2 &{}= &{} a e_2 - p e_4 - y_1 y_3 + x_1 x_3 + u_2 \\ \dot{e}_3 &{}= &{} - b e_3 + y_1 y_2 - x_1 x_2 + u_3 \\ \dot{e}_4 &{}= &{} - c e_4 + y_1 y_3 - x_1 x_3 + u_4 \\ \end{array} \right. \end{aligned}$$
(25)

We consider the adaptive control law given by

$$\begin{aligned} \left. \begin{array}{ccl} u_1 &{}= &{} \hat{a}(t) e_1 - \hat{p}(t) e_4 - y_2 y_3 + x_2 x_3 - k_1 e_1 \\ u_2 &{}= &{} - \hat{a}(t) e_2 + \hat{p}(t) e_4 + y_1 y_3 - x_1 x_3 - k_2 e_2 \\ u_3 &{}= &{} \hat{b}(t) e_3 - y_1 y_2 + x_1 x_2 - k_3 e_3 \\ u_4 &{}= &{} \hat{c}(t) e_4 - y_1 y_3 + x_1 x_3 - k_4 e_4 \\ \end{array} \right. \end{aligned}$$
(26)

where \(\hat{a}(t), \hat{b}(t), \hat{c}(t), \hat{p}(t)\) are estimates for the unknown parameters a, b, c, p, respectively, and \(k_1, k_2, k_3, k_4\) are positive gain constants.

The closed-loop control system is obtained by substituting (26) into (25) as

$$\begin{aligned} \left. \begin{array}{ccl} \dot{e}_1 &{} = &{} - [ a - \hat{a}(t) ] e_1 + [ p - \hat{p}(t) ] e_4 - k_1 e_1 \\ \dot{e}_2 &{} = &{} [ a - \hat{a}(t) ] e_2 - [ p - \hat{p}(t) ] e_4 - k_2 e_2 \\ \dot{e}_3 &{} = &{} - [ b - \hat{b}(t) ] e_3 - k_3 e_3\\ \dot{e}_4 &{} = &{} - [ c - \hat{c}(t) ] e_4 - k_4 e_4\\ \end{array} \right. \end{aligned}$$
(27)

To simplify (27), we define the parameter estimation error as

$$\begin{aligned} \left. \begin{array}{ccl} e_a(t) &{} = &{} a - \hat{a}(t) \\ e_b(t) &{} = &{} b - \hat{b}(t) \\ e_c(t) &{} = &{} c - \hat{c}(t) \\ e_p(t) &{} = &{} p - \hat{p}(t) \\ \end{array} \right. \end{aligned}$$
(28)

Using (28), the closed-loop system (27) can be simplified as

$$\begin{aligned} \left. \begin{array}{ccl} \dot{e}_1 &{} = &{} - e_a e_1 + e_p e_4 - k_1 e_1 \\ \dot{e}_2 &{} = &{} e_a e_2 - e_p e_4 - k_2 e_2 \\ \dot{e}_3 &{} = &{} - e_b e_3 - k_3 e_3\\ \dot{e}_4 &{} = &{} - e_c e_4 - k_4 e_4\\ \end{array} \right. \end{aligned}$$
(29)

Differentiating the parameter estimation error (28) with respect to t, we get

$$\begin{aligned} \left. \begin{array}{ccl} \dot{e}_a &{} = &{} - \dot{\hat{a}} \\ \dot{e}_b &{} = &{} - \dot{\hat{b}} \\ \dot{e}_c &{} = &{} - \dot{\hat{c}} \\ \dot{e}_p &{} = &{} - \dot{\hat{p}} \\ \end{array} \right. \end{aligned}$$
(30)

Next, we find an update law for parameter estimates using Lyapunov stability theory.

Consider the quadratic Lyapunov function defined by

$$\begin{aligned} V(e_1, e_2, e_3, e_4, e_a, e_b, e_c, e_p) = {1 \over 2} \, \sum \limits _{i = 1}^4 e_i^2 + {1 \over 2} \, \left( e_a^2 + e_b^2 + e_c^2 + e_p^2 \right) \end{aligned}$$
(31)

Differentiating V along the trajectories of (29) and (30), we get

$$\begin{aligned} \left. \begin{array}{ccl} \dot{V} &{} = &{} - k_1 e_1^2 - k_2 e_2^2 - k_3 e_3^2 - k_4 e_4^2 + e_a \left[ e_2^2 - e_1^2 - \dot{\hat{a}} \right] \\ &{} &{} +\,e_b \left[ - e_3^2 - \dot{\hat{b}} \right] + e_c \left[ - e_4^2 - \dot{\hat{c}} \right] + e_p \left[ (e_1 - e_2) e_4 - \dot{\hat{p}} \right] \end{array} \right. \end{aligned}$$
(32)

In view of Eq. (32), an update law for the parameter estimates is taken as

$$\begin{aligned} \left. \begin{array}{ccl} \dot{\hat{a}} &{} = &{} e_2^2 - e_1^2 \\ \dot{\hat{b}} &{} = &{} - e_3^2 \\ \dot{\hat{c}} &{} = &{} - e_4^2 \\ \dot{\hat{p}} &{} = &{} (e_1 - e_2) e_4 \\ \end{array} \right. \end{aligned}$$
(33)

Theorem 1

The identical novel 4-D four-wing chaotic systems (22) and (23) with unknown system parameters are globally and exponentially synchronized for all initial conditions \(x(0), y(0) \in \mathrm{I\!R}^4\) by the adaptive control law (26) and the parameter update law (33), where \(k_i, (i = 1, 2, 3, 4)\) are positive constants.

Proof

The result is proved using Lyapunov stability theory [141].

We consider the quadratic Lyapunov function V defined by (31), which is positive definite on \(\mathrm{I\!R}^8\).

Substitution of the parameter update law (33) into (32) yields

$$\begin{aligned} \dot{V} = - k_1 e_1^2 - k_2 e_2^2 - k_3 e_3^2 - k_4 e_4^2, \end{aligned}$$
(34)

which is a negative semi-definite function on \(\mathrm{I\!R}^8\).

Therefore, it can be concluded that the synchronization error vector e(t) and the parameter estimation error are globally bounded, i.e.

$$\begin{aligned} \left[ \begin{array}{cccccccc} e_1(t)&e_2(t)&e_3(t)&e_4(t)&e_a(t)&e_b(t)&e_c(t)&e_p(t) \end{array} \right] ^T \in \mathbf {L}_\infty . \end{aligned}$$
(35)

Define

$$\begin{aligned} k = \min \left\{ k_1, k_2, k_3, k_4 \right\} \end{aligned}$$
(36)

Then it follows from (34) that

$$\begin{aligned} \dot{V} \le - k \Vert e \Vert ^{2} \ \ \text {or} \ \ k ||\mathbf {e} ||^2 \le - \dot{V} \end{aligned}$$
(37)

Integrating the inequality (37) from 0 to t, we get

$$\begin{aligned} k \int \limits _0^t \ ||\mathbf {e}(\tau ) ||^2 \, d\tau \, \le \, - \int \limits _0^t \ \dot{V}(\tau ) \, d\tau = V(0) - V(t) \end{aligned}$$
(38)

From (38), it follows that \(\mathbf {e}(t) \in \mathbf {L}_2\).

Using (29), it can be deduced that \(\dot{\mathbf {e}}(t) \in \mathbf {L}_\infty \).

Thus, using Barbalat’s lemma [141], we can conclude that \(\mathbf {e}(t) \rightarrow 0\) exponentially as \(t \rightarrow \infty \) for all initial conditions \(\mathbf {e}(0) \in \mathrm{I\!R}^4\).

Hence, we have proved that the identical novel 4-D four-wing chaotic systems (22) and (23) with unknown system parameters are globally and exponentially synchronized for all initial conditions \(x(0), y(0) \in \mathrm{I\!R}^4\) by the adaptive control law (26) and the parameter update law (33).

This completes the proof. \(\square \)

For numerical simulations, the parameter values of the novel systems (22) and (23) are taken as in the chaotic case, viz.

$$\begin{aligned} a = 17, \ \ b = 50, \ \ c = 5, \ \ p = 2 \end{aligned}$$
(39)

The gain constants are taken as

$$\begin{aligned} k_1 = 5, \ \ k_2 = 5, \ \ k_3 = 5, \ \ k_4 = 5 \end{aligned}$$
(40)

The initial values of the parameter estimates are taken as

$$\begin{aligned} \hat{a}(0) = 5.3, \ \ \hat{b}(0) = 14.9, \ \ \hat{c}(0) = 20.1, \ \ \hat{p}(0) = 17.8 \end{aligned}$$
(41)

The initial values of the master system (22) are taken as

$$\begin{aligned} x_1(0) = 12.4, \ \ x_2(0) = -21.3, \ \ x_3(0) = 6.1, \ \ x_4(0) = -7.3 \end{aligned}$$
(42)

The initial values of the slave system (23) are taken as

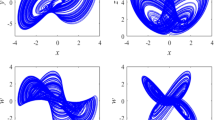
$$\begin{aligned} y_1(0) = 1.5, \ \ y_2(0) = 12.8, \ \ y_3(0) = 23.9, \ \ y_4(0) = -18.5 \end{aligned}$$
(43)

Figures 6, 7, 8 and 9 show the complete synchronization of the identical chaotic systems (22) and (23).

Figure 6 shows that the states \(x_1(t)\) and \(y_1(t)\) are synchronized in two seconds (MATLAB).

Figure 7 shows that the states \(x_2(t)\) and \(y_2(t)\) are synchronized in two seconds (MATLAB).

Figure 8 shows that the states \(x_3(t)\) and \(y_3(t)\) are synchronized in two seconds (MATLAB).

Figure 9 shows that the states \(x_4(t)\) and \(y_4(t)\) are synchronized in two seconds (MATLAB).

Figure 10 shows the time-history of the synchronization errors \(e_1(t)\), \(e_2(t\)), \(e_3(t)\), \(e_4(t)\). From Fig. 10, it is seen that the errors \(e_1(t)\), \(e_2(t)\), \(e_3(t)\) and \(e_4(t)\) are stabilized in two seconds (MATLAB).

Fig. 6
figure 6

Synchronization of the states \(x_1\) and \(y_1\)

Full size image
Fig. 7
figure 7

Synchronization of the states \(x_2\) and \(y_2\)

Full size image
Fig. 8
figure 8

Synchronization of the states \(x_3\) and \(y_3\)

Full size image
Fig. 9
figure 9

Synchronization of the states \(x_4\) and \(y_4\)

Full size image
Fig. 10
figure 10

Time-history of the synchronization errors \(e_1, e_2, e_3, e_4\)

Full size image

5 Conclusions

In this research work, we announced a ten-term novel 4-D four-wing chaotic system with four quadratic nonlinearities. We described the qualitative analysis of the novel 4-D four-wing chaotic system. We showed that the novel four-wing chaotic system has a unique equilibrium point at the origin, which is a saddle-point. Thus, origin is an unstable equilibrium of the novel chaotic system. We also showed that the novel four-wing chaotic system has a rotation symmetry about the \(x_3\) axis. Thus, it follows that every non-trivial trajectory of the novel four-wing chaotic system must have a twin trajectory. The Lyapunov exponents of the novel 4-D four-wing system were obtained as \(L_1 = 5.6253\), \(L_2 = 0\), \(L_3 = -5.4212\) and \(L_4 = -53.0373\). Thus, the maximal Lyapunov exponent of the novel four-wing chaotic system is seen as \(L_1 = 5.6253\). The large value of \(L_1\) indicates that the novel four-wing system is highly chaotic. Since the sum of the Lyapunov exponents of the novel chaotic system is negative, the novel chaotic system is dissipative. Also, the Kaplan-Yorke dimension of the novel four-wing chaotic system was obtained as \(D_{KY} = 3.0038\). Finally, we derived new results for the adaptive synchronization of the identical novel 4-D four-wing chaotic systems with unknown parameters. The adaptive synchronization result was proved using Lyapunov stability theory. MATLAB simulations were shown to illustrate all the main results for the novel 4-D four-wing chaotic system.