1 Introduction

The first chaotic attractor in a 3D autonomous system was discovered in 1963 and was called the Lorenz chaotic system [1]. The Rössler chaotic system [2] and the Rössler hyperchaotic system [3] were reported in 1976 and 1979, respectively. In 1999, Chen and Ueta [4] reported a 3D chaotic system that was not topologically equivalent to the Lorenz chaotic system and was called the Chen chaotic system. Lü and Chen constructed a 3D chaotic system in 2002 that was not equivalent to the Lorenz and Chen chaotic systems and was called the Lü chaotic system [5]. Up to now, many chaotic and hyperchaotic systems have been proposed in the past decades [6–18].

In chaos theory, the equilibria of an autonomous dynamical system are significant for understanding its nonlinear dynamics, especially for the Šil’nikov type of chaos [19]. Most known chaotic and hyperchaotic systems have one to three equilibrium points, such as the systems mentioned above. Some chaotic and hyperchaotic systems have more than three equilibria [7, 8]. Some chaotic and hyperchaotic systems have no equilibrium points [10, 11]. Up to now, most chaotic and hyperchaotic systems reported previously have just a limited number or a countable number of isolated equilibria. Thus, a natural and interesting question is: does a chaotic or hyperchaotic system possess an infinite uncountable number of equilibria? Clearly, the answer to this question is of both academic significance and practical importance. A positive answer to this question is given in this paper. A thorough study of such kind of chaotic systems may be helpful to understand the complicated mechanisms of chaos and hyperchaos. For chaotic systems with infinitely many equilibria, there seems to be no study on chaotic encryption or decryption, so it may be more security.

Motivated by the above discussions, we report a 4D chaotic system with infinitely many equilibrium points based on the 3D Lü chaotic system in this paper. The dynamical behavior of this chaotic system is obtained. The periodic orbit, chaotic, and hyperchaotic attractors are emerged in this 4D chaotic system. Moreover, horseshoe and entropy in this 4D chaotic system are also discussed by means of topological horseshoe theory and numerical computation.

The organization of this paper is as follows. In Sect. 2, a 4D chaotic system with infinitely many equilibria is introduced, and the dynamical behavior of this chaotic system is discussed. The horseshoe and entropy for the 4D chaotic system are investigated in Sect. 3. The conclusion is given in Sect. 4.

2 A 4D chaotic system with infinitely many equilibria

Lü and Chen reported a 3D chaotic system in 2002, which is not diffeomorphic to the Lorenz and Chen chaotic systems and is defined as

$$ \begin{cases} \dot{x}_{1} = a(x_{2} - x_{1}),\\ \dot{x}_{2} = cx_{2} - x_{1}x_{3},\\ \dot{x}_{3} = - bx_{3} + x_{1}x_{2}. \end{cases} $$
(1)

When the parameters a=36, b=3, and c=20, the chaotic attractor of system (1) is shown in Fig. 1.

Fig. 1
figure 1

The chaotic attractor of system (1) for a=36, b=3, and c=20

Full size image

Based on the Lü chaotic system (1), we construct a 4D nonlinear system, which is described as follows:

$$ \begin{cases} \dot{x}_{1} = 36(x_{2} - x_{1}) + x_{4},\\ \dot{x}_{2} = cx_{2} - x_{1}x_{3},\\ \dot{x}_{3} = - 3x_{3} + x_{1}x_{2},\\ \dot{x}_{4} = 18x_{1} - 0.5x_{4}, \end{cases} $$
(2)

where 4≤c≤33.

In the Lü system (1), c is a typical parameter, which has been studied extensively in many papers and is most familiar to the readers. So, in our system (2), we choose this parameter in our discussion so that the readers could compare our results with the classical Lü system.

Obviously, system (2) is invariant under the transformation

$$(x_{1},x_2,x_3,x_4) \leftrightarrow (-x_{1},-x_2,x_3,-x_4). $$

In the following, we will show that system (2) is dissipative and there exists an attractor in system (2).

Calculating the variation of the small element volume V(t) in the state space, we have

$$\nabla V(t) = \sum_{i = 1}^{4} \frac{\partial\dot{x}_{i}}{\partial x_{i}} = - 39.5 + c < 0. $$

So, system (2) is dissipative, and there exists an attractor in system (2).

Solving the following algebraic equations, we can obtain the real equilibria of system (2):

$$\begin{cases} 36(x_{2} - x_{1}) + x_{4} = 0,\\ cx_{2} - x_{1}x_{3} = 0,\\ - 3x_{3} + x_{1}x_{2} = 0,\\ 18x_{1} - 0.5x_{4} = 0. \end{cases} $$

Obviously, the real equilibria of system (2) are (x 1,x 2,x 3,x 4)=(x 1,0,0,36x 1), where x 1 is a real number. So, system (2) has an infinite number of real equilibria. Moreover, the real equilibria are the coordinate axis x 1 of the subspace (x 1,x 2,x 3), the coordinate axis x 4 of the subspace (x 2,x 3,x 4), and the straight line (x 4=36x 1) in the subspace (x 1,x 2,x 4) or subspace (x 1,x 3,x 4). So, system (2) is different from all the previous chaotic and hyperchaotic systems, which implies that a new 4D system with infinitely many equilibria has been obtained.

The Jacobian J at all equilibrium points is

$$J = \left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} - 36 & 36 & 0 & 1\\ 0 & c & - x_{1} & 0\\ 0 & x_{1} & - 3 & 0\\ 18 & 0 & 0 & - 0.5 \end{array} \right ), $$

and its eigenvalues are λ 1=0, λ 2=−36.5, and \(\lambda_{ \pm} = 0.5(c - 3) \pm0.5\sqrt{(c - 3)^{2} - 4(x_{1}^{2} - 3c)}\), respectively.

Since c−3>0, we can derive the following conclusions:

  1. (1)

    if \((c - 3)^{2} - 4 (x_{1}^{2} - 3c ) \le0\), then \(\operatorname{Re} (\lambda_{ \pm} ) > 0\).

  2. (2)

    if \(0 < (c - 3)^{2} - 4 (x_{1}^{2} - 3c ) \le(c - 3)^{2}\), then \(\operatorname{Re} ( \lambda_{ \pm} ) > 0\).

  3. (3)

    if \((c - 3)^{2} - 4 (x_{1}^{2} - 3c ) > (c - 3)^{2}\), then \(\operatorname{Re} ( \lambda_{ +} ) > 0\).

Therefore, all equilibrium points in system (2) are unstable.

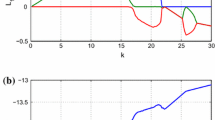
The dynamical behavior of system (2) can be characterized by its Lyapunov-exponent spectrum. The Lyapunov-exponent spectrum of system (2) is increasing with respect to parameter c, which is shown in Fig. 2. According to Fig. 2, we can yield:

  1. (1)

    The hyperchaotic attractor is emerged in system (2) for 13<c≤16.75, where λ 1>λ 2>0, λ 3=0, λ 4<0, and λ 1+λ 2+λ 4<0. Setting the parameter c=14, the Lyapunov exponents of system (2) are λ 1=0.24014, λ 2=0.08613, λ 3=0, and λ 4=−25.826, respectively. The Lyapunov dimension of system (2) is D L =3+(λ 1+λ 2)/|λ 4|=3.0126, so system (2) is fractal. The hyperchaotic attractor for the parameter c=14 is shown in Fig. 3.

  2. (2)

    The chaotic attractor is emerged in system (2) for 16.75<c≤21.2 and 21.5<c≤27.5, where λ 1>0, λ 2=0, λ 3<0, λ 4<0, and λ 1+λ 3+λ 4<0. Setting the parameter c=25, the Lyapunov exponents of system (2) are λ 1=1.5919, λ 2=0, λ 3=−0.34582, and λ 4=−15.747, respectively. The Lyapunov dimension of system (2) is D L =3+λ 1/|λ 3+λ 4|=3.0989, so system (2) is fractal. The chaotic attractor for parameter c=25 is shown in Fig. 4.

  3. (3)

    The periodic orbit is emerged in system (2) for 4≤c≤13, 21.2<c≤21.5, and 27.52<c≤33, where λ 1=0, λ 2<0, λ 3<0, and λ 4<0. Setting the parameter c=5, the Lyapunov exponents of system (2) are λ 1=0, λ 2=−0.47057, λ 3=−0.47057, and λ 4=−33.556, respectively. The periodic orbit for the parameter c=5 is shown in Fig. 5.

Fig. 2
figure 2

Diagram of the Lyapunov exponent spectrum as parameter c varies

Full size image
Fig. 3
figure 3

The hyperchaotic attractor of system (2) with system parameter c=14

Full size image
Fig. 4
figure 4

The chaotic attractor of system (2) with system parameter c=25

Full size image
Fig. 5
figure 5

The periodic orbit of system (2) with system parameter c=5

Full size image

According to the above mentioned, we obtained a 4D nonlinear system with infinitely many equilibria. The hyperchaos and chaotic are emerged in this 4D nonlinear system. We obtained the exact range of the parameter c, which guarantees the existence of hyperchaos, so that the reader may change this parameter to control the hyperchaos.

3 Computer-assisted verification of hyperchaos

From the analysis in Sect. 2 we found out that system (2) is hyperchaotic for the parameter c=14, and two positive Lyapunov exponents are λ 1=0.24014 and λ 2=0.08613, respectively. However, the numerical errors during the computation are unavoidable, and the second Lyapunov exponent is not large enough to tolerate such errors. So, the readers may ask whether it is indeed positive or not.

Generally, the existence of chaos and hyperchaos can be studied by Shil’nikov’s theorems, which guarantee the existence of infinitely many Smale horseshoes. This method has been applied to a multitude of 4D dynamical systems, such as real quadratic dynamics in the context of competitive modes [20], the Shil’nikov chaos in the 4D Lorenz–Stenflo system [21], and so on. In our case, we will propose a rigorous proof of the existence of hyperchaos in system (2) by directly finding topological horseshoes with two-directional expansion in the phase space of its corresponding Poincaré map.

First, we review some theoretical criteria of topological horseshoes and then present our main result.

Let X be a metric space, B a compact subset of X, and let there exist m mutually disjoint compact subsets B 1,B 2,…,B m of B. For each B i , let \(B_{i}^{1}\) and \(B_{i}^{2}\) be its two fixed disjointed connected nonempty compact subsets contained in the boundary ∂B i , and let the map f be continuous on each B i .

Definition 1

[22] A connected subset Γ of B i is said to be a separation of \(B_{i}^{1}\) and \(B_{i}^{2}\), denoted by \(\varGamma\updownarrow (B_{i}^{1}, B_{i}^{2})\), if for any connected subset L∈B i with \(L \cap B_{i}^{1} \ne\varPhi\) and \(L \cap B_{i}^{2} \ne\varPhi\), we have L∩Γ≠Φ.

Definition 2

[22] We say that f(Γ) separates B i , denoted by f(Γ)↦B j , if there exists a compact subset Γ′ of Γ such that \(f(\varGamma') \updownarrow(B_{j}^{1},B_{j}^{2})\).

Definition 3

[23] We say that f:B i ↦B j is a codimension-one crossing with respect to two pairs (\(B_{i}^{1},B_{i}^{2}\)) and (\(B_{j}^{1},B_{j}^{2}\)) if for each compact subset Γ⊂B i that satisfies \(\varGamma\updownarrow (B_{i}^{1}, B_{i}^{2})\), we have f(Γ)↦B j .

Theorem 1

[23] If the codimension-one crossing relation f:B i ↦B j , holds for 1≤i,j≤m, then there exists a compact invariant set K⊂B such that f|K is semi-conjugate to the m-shift mapping. Then the entropy of f satisfies \(\operatorname{ent}(f) \ge\log m\).

Since the condition of this theorem is too conservative, it is hard to find a horseshoe of this kind in practical systems. So we use the following practical corollary, which has been successfully applied in a number of chaotic and hyperchaotic systems [8, 24, 25].

Corollary 1

[22] Suppose that the map f:B→X satisfies the following assumptions:

  1. (1)

    There exist two mutually disjoint compact subsets B 1 and B 2 of B, and f m|B 1 and f n|B 2 are differential homeomorphisms, where m,n∈Z +.

  2. (2)

    f m(B 1) ↦ B 1, f m(B 1) ↦ B 2, and f n(B 2) ↦ B 1.

Then there exists a compact invariant set K⊂B such that f 2m+n|K is semi-conjugate to 2-shift dynamics and the topological entropy of f satisfies \(\operatorname{ent}(f) \ge\frac{1}{2m + n}\log2\).

Since f in the above horseshoe corollary is a homeomorphism, we are going to study a Poincaré map of system (2). By taking the hyperplane

$$\varPi= \bigl\{ x = (x_{1},x_{2},x_{3},x_{4}) \vert x_{4} = 0,\dot{x}_{4} < 0 \bigr\} $$

as a Poincaré cross-section, the corresponding Poincaré map P:Π→Π can be defined as follows: for each x∈Π, P(x) is taken to be the first return point in P under the flow of the dynamical system with the initial condition x.

Unlike many other studies on topological horseshoes for two-dimensional chaotic maps [6, 26–28], generally, due to the high dimensionality, it is very difficult to find a topological horseshoe directly. Fortunately, Li and Tang [29] proposed a remarkable method to detect a horseshoe with two-directional expansions effectively by deducting the dimension along the direction of contraction.

According to the algorithm, we find a horseshoe by three steps.

  1. (1)

    Since the attractor of the Poincaré map is very close to a curved surface whose equation x 1=s(x 2,x 3) can be easily fitted in MATLAB, we obtain the following two-dimensional projective system:

    $$\begin{aligned} \left ( \begin{array}{c} x_{2}\\ x_{3} \end{array} \right )_{n + 1} =& \varphi \left ( \left ( \begin{array}{c} x_{2}\\ x_{3} \end{array} \right )_{n} \right ) \\ =& \left ( \begin{array}{c@{\quad }c@{\quad }c} 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right )P\left ( \left ( \begin{array}{c} s(x_{2},x_{3})\\ x_{2}\\ x_{3} \end{array} \right )_{n} \right ). \end{aligned}$$
    (3)
  2. (2)

    By several attempts we find a horseshoe with two directional expansions of the above projective system by choosing two quadrilaterals in the x 2 ox 3 plane. The four vertices of the first quadrilateral in terms of (x 2,x 3) are as follows:

    $$\begin{aligned} &{[ - 6.211927593,19.187952363]^{T},} \\ &{[ - 6.194265221,18.681381786]^{T},} \\ &{[ - 4.436859217,19.070264249]^{T},} \\ &{[ - 4.763613097,19.459146712]^{T}.} \end{aligned}$$

    The four vertices of the second one are as follows:

    $$\begin{aligned} &{[ - 4.163092452,19.187952363]^{T},} \\ &{[ - 4.516339890,18.875823108]^{T},} \\ &{[ - 3.854000944,18.696732410]^{T},} \\ &{[ - 3.562571807,18.906524265]^{T}.} \end{aligned}$$
  3. (3)

    We construct the three-dimensional horseshoe of the map P utilizing the projective horseshoe by projecting the planar horseshoe back to the three-dimensional space.

For clarity, we rotate the coordinates via the following Householder transform:

$$\mathbf{y} = [y_{1},y_{2},y_{3}]^{T} = \mathbf{H}[x_{1},x_{2},x_{3}]^{T}, $$

where

$$\mathbf{H} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.598888177 & 0.365362777 & - 0.712631034\\ 0.365362777 & 0.667200138 & 0.649117875\\ - 0.712631034 & 0.649117875 & - 0.266088315 \end{array} \right ], $$

so that the direction of contraction is parallel to the y 3-axis. Finally, we have two blocks B 1 and B 2 in the phase space of the Poincaré map P, as shown in Figs. 6(a) and 7(a). It is not hard to get the following theorem.

Fig. 6
figure 6

P 2(B 1) separates B 1 and B 2 under system (2) at c=14

Full size image
Fig. 7
figure 7

P 3(B 2) separates B 1 under system (2) at c=14

Full size image

Theorem 2

For the Poincaré map P:Π→Π, there exists a closed invariant set Λ⊂B 1∪B 2 on which P 6|Λ is semiconjugate to the 2-shift, and \(\operatorname{ent}(P) \ge \frac{1}{6}\log2\).

Proof

According to Corollary 1, we only need to show that B 1, B 2 and their images under P 2 and P 3, respectively, satisfy the following relationships about the codimension-one crossing:

$$\begin{aligned} &{P^2(B_{1}) \mapsto B_{2},\qquad P^2(B_{1}) \mapsto B_{2}, \quad \mbox{and} } \\ &{P^{3}(B_{2}) \mapsto B_{1}.} \end{aligned}$$

The geometrical relations of B 1, B 2, and P 2(B 1) is shown in Fig. 6. Figure 6(a) is a 3D view, which suggests that P 2(B 1) expands in two directions and transversely intersects both blocks B 1 and B 2. Figure 6(b) is a side view, which shows that the intersection happens between their top and bottom surfaces, i.e., (\(B_{1}^{t},B_{1}^{b}\)) and (\(B_{2}^{t},B_{2}^{b}\)). Figure 6(c) is a top view, which shows that the side surfaces of B 1 are mapped outside B 1 and B 2. In this way, for each separation S of (\(B_{1}^{t},B_{1}^{b}\)), f(S)∩B 1 must be a separation of (\(B_{1}^{t},B_{1}^{b}\)), and f(S)∩B 2 must be a separation of (\(B_{2}^{t},B_{2}^{b}\)). Then we have

$$P^{2}(B_{1}) \mapsto B_{1},\qquad P^{2}(B_{1}) \mapsto B_{2}, $$

according to Definitions 2 and 3. Similarly, we can have the codimension-one crossing about P 3(B 2)↦B 1 from Fig. 7.

Since system (2) is smooth, i.e., the system has a unique solution from each initial condition, Figs. 6 and 7 also show that P 2|B 1 and P 3|B 2 are both continuous, so they must be homeomorphisms. Then, it follows from the corollary that there exists a compact invariant set Λ⊂B 1∪B 2 such that P 6|Λ is semiconjugate to the 2-shift, and the topological entropy of P is not less than \(\operatorname{ent}(P) \ge\frac{1}{6}\log2\).

Since P 2|B 1 and P 3|B 2 both expands in two directions, the expansions along each trajectory in Λ are also in two directions, so there must exist two positive Lyapunov exponents. Therefore, the system is hyperchaotic. □

4 Conclusion

A 4D chaotic system with infinitely many equilibria is reported in this paper. The Lyapunov-exponent spectrum is yielded. The periodic orbit, chaotic, and hyperchaotic attractor can been found in this nonlinear system. By means of topological horseshoe theory and numerical computation, a topological horseshoe with two-directional expansions is also obtained, which ensures that system (2) is a hyperchaos system for a suitable system parameter c.

Although chaos and hyperchaos have been found in many 4D systems with limit number of isolated equilibria, our chaotic system has infinitely many nonisolated equilibria, which is a significant difference. So our work may be useful for better understanding of the chaotic mechanism. On the other hand, our system can generate hyperchaos, which may be also useful in chaos engineering, e.g., in chaos encryption, chaos communications, etc. Synchronization of a chaotic system with infinitely many equilibria is also an interesting topic.