Abstract
This chapter deals with the stabilization of a nominal and uncertain time-delay systems using state feedback control law.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
This chapter deals with the stabilization of a nominal and uncertain time-delay systems using state feedback control law. Next, Load-Frequency Control (LFC) of an interconnected power systems with communication delay based on two different control configurations (i) pure state feedback (one-term control) and (ii) pure state feedback as well as delayed state feedback (two-term control) is considered by exploring the \(H_{\infty }\) performance criterion in the design procedure.
Note that, the stabilization condition for time-delay systems is obtained by directly extending the results of delay-dependent stability (or robust stability) conditions of TDS. The results of new stabilization conditions are validated by considering the numerical examples and compared with existing methods.
3.1 Introduction
As discussed in Chap. 2, the stability analysis of time-delay systems has been proposed for developing delay-dependent results in LMI framework based on LK functional approach with a tighter bounding technique. A significant research attention has been devoted to the delay-dependent studies owing to the fact that, in the delay-independent stability notion there is no upper limit to the time-delay, so often results are regarded as conservative. In true sense an unbounded time-delay is not so realistic to physical or engineering systems. In sequel, the stabilization (or robust stabilization) conditions are derived in a delay-dependent framework.
The earlier results on robust stabilization (and/or stabilization) based on delay-independent as well as on Ricatti equation approach are recalled [1,2,3,4] and [5]. Some of the results on delay-dependent robust stabilization (and/or stabilization) in an LMI framework can be found in [6,7,8,9,10,11,12], and [13], note that the condition derived in [6] is based on Lyapunov-Razumikhin approach. In [7, 8] and [13], stabilizing conditions were derived using LK functional approach adopting first model transformation and they are expected to give conservative result with or without uncertainties as model transformation introduces additional dynamics [14] and [15]. The stabilizing conditions obtained in [9, 11, 12] and [10] are all NLMI. In [12], and [9] the non-linear matrix (NLMI) conditions were solved using cone complementarity linearization algorithm [16], which is an iterative algorithm, while in [11] and [10] a fixed relaxation matrix is introduced to transform NLMI condition to LMI condition. Possibly it is one of the probable reason for conservativeness in the stabilizing results. The robust stabilizing (and/or stabilizing) conditions in [14] and [10] have been obtained for polytopic uncertain systems based on descriptor method.
In this chapter, an improved few significant delay-dependent robust stabilization (and/or stabilization) conditions for the system (3.1) (and/or (3.6)) in an LMI framework are presented in the form of theorems. The robust stabilization condition of an uncertain time-delay system (3.1) can be obtained from robust stability conditions by substituting \(A=A+BK\), or one can obtain the robust stabilization condition from the derived stabilization condition depending upon the type of bounding inequalities to eliminate the uncertain time-varying matrices.
3.2 Problem Statement
Consider an uncertain linear time-delay systems described by the following state equations
where, \(x(t)~\in ~\mathcal {R}^{n}\) is the state vector, \(u(t)~\in ~\mathcal {R}^{m}\) is the control input, and \(\phi (t)\) is the initial condition. The matrices \(A,~A_{d},~B,~C\) and D are known real constant matrices of appropriate dimensions which describe the nominal system of (3.1), and \(\Delta A(t),~\Delta A_{d}(t)\) and \(\Delta B(t)\) are real matrix function representing time-varying parameter uncertainties. The delay d(t) is time-varying and satisfies following conditions.
The parametric uncertainties are assumed to be norm bounded type of the form:
where, \(F_{a}(t)~\in ~\mathcal {R}^{m_{a}\times p_{a}}, F_{b}(t)~\in ~\mathcal {R}^{m_{b}\times p_{b}}\) and \(F_{d}(t)~\in ~\mathcal {R}^{m_{d}\times p_{d}}\) are unknown real time-varying matrices with Lebesgue measurable elements satisfying the conditions:
and, \(D_{a}, D_{d}, E_{a}, E_{b}\) and \(E_{d}\) are known real constant matrices that characterize how the uncertain parameters in \(F_{a}(t), F_{b}(t)\) and \(F_{d}(t)\) enter the nominal system and input matrices.
If the uncertainties \(\Delta A(t)~= 0, \Delta A_{d}(t)~= 0\) and \(\Delta B(t)~= 0\), then the uncertain system (3.1) reduces to nominal time-delay system described as,
Stabilization
Given a scalar \(d_{u}~>~0\), find a control law \(u(t)=Kx(t)\) for the system (3.6) such that the closed loop system is asymptotically stable for any time-delay d(t) satisfying \(0~\le ~d(t)~\le ~d_{u}\). This problem is known in the literature as stabilization problem.
Robust Stabilization
[21] Given a scalar \(d_{u}~>~0\), find a control law \(u(t)=Kx(t)\) for the system (3.1), such that the closed loop system is asymptotically stable for any time-delay d(t) satisfying \(0~\le ~d(t)~\le ~d_{u}\). This problem is known in the literature as robust stabilization problem.
3.3 Delay-Dependent Stabilization of Nominal TDS
In this section, some existing state feedback stabilization sufficient conditions for system (3.6) using LK approach are presented in the form of theorems.
Assumption 3.1
The necessary condition for delay-dependent stabilization is that, \((A+A_{d},~B)\) is stabilizable.
Theorem 3.1
(Corollary 3.2 [7]) Consider the system (3.6) with a constant delay \(d(t)\equiv d\), satisfying the condition \(0\le d(t) \le d_{u}\), the system is stabilizable with the control law \(u(t)=YX^{-1}x(t)\), if there exist matrices \(X=X^{T}>0, Y\) and a scalar \(\beta ~>~0\) such that the following LMI holds:
where, \(Q_{c}=X(A+A_{d})^{T}+(A+A_{d})X+BY+Y^{T}B^{T}\).
Remark 3.1
The condition has been derived using first model transformation, hence the transformed system becomes,
where, \(\zeta (t)\) is the new state variable of the transformed system. Any solution of the system (3.6) with \(d(t)=d\) and \(u(t)=0\) is also the solution of the above equation [7]. Thus, the LK function is chosen in accordance with the transformed system which is of the form,
where, \(W(\zeta ,~t)=\int _{-d}^{0}\{(1+\alpha ^{-1})\int _{t+\theta }^{t}\parallel A\zeta (s)\parallel ^{2}ds+\int _{t+\theta -d}^{t}\parallel A_{d}\zeta (s)\parallel ^{2}ds\}d\theta \)
Finding the time-derivative of \(V(\zeta ,~t)\), using bounding lemma (Lemma 2.1) for the cross terms and Schwartz inequality for quadratic integral terms, and finally using the change of variables (\(X=P^{-1}~and~\beta =\frac{1}{1+\alpha ^{-1}}\)) in \(\dot{V}(\zeta ,~t)\) one can obtain the stabilization condition in (3.7) with the use of Schur-complement.
The stability conditions (2.52) and (2.53) discussed in Theorem 2.5 is extended to obtain the stabilization condition which is presented below in the form of theorem.
Theorem 3.2
([9]) If there exist \(L=L^{T}~>~0, M, N, R, V\) and \(W=W^{T}~>~0\) such that following LMI holds:
Then the system (3.6) with the control law \(u(t)=VL^{-1}x(t)\) is asymptotically stable for any constant time-delay \(0\le d(t)\le d_{u}\).
Proof
Substituting \(u(t)=Kx(t)\) in (3.6) gives closed-loop system,
where, \(A_{c}=A+BK\). One can now replace A in (2.52)Footnote 1(corresponding stability condition) with \(A+BK\), then pre- and post-multiplying (2.52) and (2.53) by \(diag\{P^{-1},~P^{-1},~Z^{-1}\}\) and \(diag\{P^{-1},~P^{-1}\}\) respectively and finally applying adopting following change of variables as indicated below,
one can obtain the stabilization condition in (3.8) and (3.9) with standard algebraic manipulations.
Remark 3.2
It can be observed that the resulting condition is not an LMI due to the presence of the term \(LR^{-1}L\) in (3.9), hence it is not possible to solve this condition using any standard solver of LMI toolbox of MATLAB for obtaining delay bound \(d_{u}\). However, this difficulty can be overcome by substituting \(R=L\) in (3.8) and (3.9) which transforms it to LMI condition, but the estimate of delay bound will be conservative in this case. To obtain better delay bound estimate cone complementarity algorithm was introduced in [16] and it is adopted in [9] and [12]. The detailed discussion on iterative non-linear minimization problem can be found in [9]. In this theorem the time-delay is assumed to be constant (i.e, \(d(t)=d\) in (3.6) which makes \(\dot{d}(t)~=\mu ~=0\)).
Theorem 3.3
([10]) The state feedback control law \(u(t)=Kx(t)\) asymptotically stabilizes the system (3.6) for all the delays satisfying the condition (3.3), if there exist a diagonal matrix \(\epsilon _{1}I \in \mathcal {R}^{n\times n}\), such that the following LMIs hold: \(Q_{1}~=Q^{T}>~0, Q_{2},~Q_{3}, \bar{S}=\bar{S}^{T},~\bar{R}=\bar{R}^{T}~>~0, \bar{Z}=\left[ \begin{array}{cc} \bar{Z_{11}} &{} \bar{Z_{12}} \\ \bar{Z_{12}^{T}} &{} \bar{Z_{13}} \\ \end{array} \right] \) and \(\bar{Y}\) matrices with appropriate dimensions, that satisfy the following LMIs,
where, \((1,1)=Q_{2}+Q_{2}^{T}+d_{u}Z_{11}\),
\((1,2)=Q_{3}-Q_{2}^{T}+Q_{1}A^{T}+\epsilon _{1}A_{d}^{T}+d_{u}Z_{12}+\bar{Y^{T}}B^{T}\),
\((2,2)=-Q_{3}-Q_{3}^{T}+d_{u}Z_{13}\).
Proof
The condition stated above is obtained by extending the stability theorem in [10], here a brief sketch of the formulation is presented as a part proof, the details can be found in [10].
Consider the system (3.6) with \(u(t)=0\) satisfying the condition (3.3). The system in descriptor form by substituting \(x(t-d(t))=x(t)-\int _{t-d(t)}^{t}\dot{x}(s)ds\) can be written as,
this can also be expressed as
where, \(\bar{x}(t)=\left[ \begin{array}{cc} x^{T}(t) &{} y^{T}(t) \\ \end{array} \right] ^{T}\), \(E=diag \{I,~~0\}\).
Following LK functional is selected for the descriptor system in (3.13),
where, \(P=\left[ \begin{array}{cc} P_{1} &{} 0 \\ P_{2} &{} P_{3} \\ \end{array} \right] , P_{1}>0,~EP=P^{T}E~\ge ~0\)
Finding the time-derivative of (3.14), one can obtain the following
Using bounding Lemma 2.3 (Moon’s Bounding Lemma) for the cross term in (3.15), one can rewrite (3.15) as
To treat the last term of (3.16), substitute \(\int _{t-d(t)}^{t}\dot{x}(s)^{T}ds=\{x^{T}(t)-x^{T}(t-d(t))\}\), applying the bounding Lemma 2.1 and with little algebraic manipulations one can obtain
where, \(\Upsilon =\left[ \begin{array}{c} Y \\ 0 \\ \end{array} \right] +\left[ \begin{array}{c} Y \\ 0 \\ \end{array} \right] ^{T}+\left[ \begin{array}{cc} -A_{d}^{T}P_{2}+P_{2}^{T}A_{d} &{} -A_{d}^{T}P_{3}\\ \star &{} 0 \\ \end{array} \right] \).
Substituting the RHS of the above inequality in the last term of (3.16) one can obtain the following:
where, \(\Psi =P^{T}\left[ \begin{array}{cc} 0 &{} I \\ A &{} -I \\ \end{array} \right] +\left[ \begin{array}{cc} 0 &{} A^{T} \\ I &{} -I \\ \end{array} \right] P+d_{u}Z+\left[ \begin{array}{cc} S &{} 0 \\ 0 &{} d_{u}R \\ \end{array} \right] +\left[ \begin{array}{c} Y \\ 0 \\ \end{array} \right] +\left[ \begin{array}{c} Y \\ 0 \\ \end{array} \right] ^{T}\),
\(Z=\left[ \begin{array}{cc} Z_{11} &{} Z_{12} \\ \star &{} Z_{13} \\ \end{array} \right] \), and \(Y=\left[ \begin{array}{cc} Y_{11} &{} Y_{12} \\ \end{array} \right] \).
If the LMIs,
then the system (3.6) with \(u(t)=0\) is asymptotically stable. The LMI (3.18) is due to the use of Moons bounding inequality lemma 2.3 for replacing the quadratic integral term that arises out of derivative of LK functional. Now, replacing the matrix A by \(A+BK\) in the LMI (3.18).
Defining \(P^{-1}=Q=\left[ \begin{array}{cc} Q_{1} &{} 0 \\ Q_{2} &{} Q_{3} \\ \end{array} \right] \) and pre- and post multiply (3.18) by \(\Delta =diag\{Q,~~I\}\) and \(\Delta ^{T}\) respectively, pre- and post multiply (3.19) by \(diag\{R^{-1},~Q^{T}\}\) and \(diag\{R^{-1},~Q\}\) respectively. Choosing following linear changes in variables \(Q^{T}ZQ=\bar{Z}, S^{-1}=\bar{S}, R^{-1}=\bar{R}\) and \(\bar{Y}=\epsilon _{1}A_{d}^{T}[\bar{P}_{2},~~\bar{P}_{3}]\) with \(\epsilon _{1}~I\) a block diagonal matrix. Now, it is now straight forward to obtain the LMI condition in (3.10) and (3.11), which are the required stabilizing condition for the time-delay systems (3.6). The state feedback gain is computed by the relation \(K=\bar{Y}Q_{1}^{-1}\).
Remark 3.3
The selection of \(\bar{Y}\) matrix in the stabilization formulation helps to avoid the NLMI stabilization condition. The stabilization results presented in [12] reveal the fact that, descriptor system formulation of the problem in this case helped to obtain better results than that of [9].
The stability condition (2.94)–(2.95) discussed in Theorem 2.12 (for system \(\sigma _{2}\)) is extended to obtain the stabilization condition which is presented in the form of theorem below.
Theorem 3.4
(Theorem 2, [12]) Given the scalars \(d_{u}~>~0, \mu ~>~0\), the system (3.6) is asymptotically stabilizable with the state-feedback controller, \(u(t)=YX^{-1}x(t)\) for any time-delay satisfying the condition (3.3) if there exist symmetric positive matrices \(\bar{P},~\bar{Q},~\bar{R},~\bar{T},~\bar{Z}\) and matrices \(S_{i},~(i=1,...,4),~Y\) with appropriate dimensions satisfying the following, LMI conditions:
and,
where, \(\bar{\Omega }_{11}=XA^{T}+AX+Y^{T}B^{T}+BY+\bar{R}+\bar{S}_{1}^{T}+\bar{S}_{1}\), \(\bar{\Omega }_{12}=A_{d}X-\bar{S}_{1}^{T}+\bar{S}_{2}\)
\(\bar{\Omega }_{14}=\bar{P}_{12}-\bar{S}_{1}^{T}+\bar{S}_{4}\), \(\bar{\Omega }_{17}=XA^{T}+Y^{T}B^{T}\), \(\bar{\Omega }_{22}=-(1-\mu )\bar{R}+\mu \bar{T}-\bar{S}_{2}-\bar{S}_{2}\)
\(\bar{\Omega }_{24}=-\bar{S}_{2}^{T}-\bar{S}_{4}\), \(\bar{\Omega }_{34}=\bar{P}_{22}-\bar{Q}_{12}-\bar{S}_{3}^{T}\) \(\bar{\Omega }_{44}=-\bar{Q}_{22}-\bar{S}_{4}^{T}-\bar{S}_{4}\)
Proof
The stabilization condition (3.21) has been obtained by extending the stability condition (2.95) stated in Theorem 2.12 of Chap. 2. A brief illustration is given as a part of proof for this theorem. Starting with the stability condition (2.95) one can first apply Schur-complement to obtain

Now, Pre- and post-multiplying (3.22) with \(diag\{X,~X,~X,~X,~X,~X,~X\}\), where \(X=P_{11}^{-1}\) and denoting \(X(.)X=\bar{(.)}\), (where (.) indicates any matrix variable) one can get,
Using Lemma 2.1 for any positive definite matrix Z, the last two terms of (3.23) can be bounded with inequality constraints as
where, \(\Pi _{1}=[AX,~A_{d}X,~0,~0,~0,~0,~0]\), \(\Pi _{2}=[0,~0,~\bar{P}_{12},~0,~d_{u}\bar{Q}_{12}^{T},~d_{u}\bar{Q}_{22},~0]\), and
The block matrices in \(\bar{\Lambda }_{0}\) are expressed as

Substituting (3.24) into (3.23) and replacing A with \((A+BK)\) and then applying Schur-complement one can easily obtain the stabilizing condition (3.21).
Remark 3.4
One can observe in the condition (3.21) that, the (8, 8) block (\(XZ^{-1}X\)) is nonlinear, so standard LMI tools cannot be used to solve this matrix inequalities. Thus cone complementarity algorithm proposed in [16] is used to find the feasible solution of this problem. This linearization iterative algorithm gives suboptimal value of the delay upper bound estimate.
The stability conditions (for system \(\sigma _{2}\) with the condition (2.7)) obtained in (2.85) discussed in Theorem 2.11 is extended to obtain the stabilization condition that is presented below in the form of theorem. This stabilization theorem is formulated by the present author in NLMI framework for the purpose of investigating the effect of more free weighting matrices on the convergence of cone-complementarity problem with the use of same number of bounding inequalities.
Theorem 3.5
Given the scalars \(d_{u}~>~0, \mu ~>~0\), the system (3.6) is asymptotically stabilizable with the state-feedback controller, \(u(t)=SY^{-1}x(t)\) for any time-delay satisfying the condition (3.3), if there exist symmetric positive definite matrices \(Y,~X,~Q_{R}\), any free matrices \(T_{R},~T_{S}\) and S with appropriate dimensions satisfying the following, LMI conditions:
where, \(\Theta _{11}=YA^{T}+AY+BS+S^{T}B^{T}+T_{R}+T_{R}^{T}+Q_{R}\), \(\Theta _{12}=A_{d}Y-T_{R}+T_{S}^{T}\),
\(\Theta _{13}=d_{u}(YA^{T}+S^{T}B^{T})\), \(\Theta _{22}=-T_{S}-T_{S}^{T}-(1-\mu )Q_{R}\).
Proof
Considering the stability condition (2.85) of Theorem 2.11, using Schur-complement on it one can write the condition as
where, \(\Omega _{11}=A^{T}P+PA+T_{1}+T_{1}^{T}+Q_{1}\), \(\Omega _{12}=PA_{d}-T_{1}+T_{2}^{T}\),
\(\Omega _{13}=d_{u}A^{T}Q_{2}\), \(\Omega _{22}=-T_{2}-T_{2}^{T}-(1-\mu )Q_{1}\).
Using state-feedback control law \(u(t)=Kx(t)\) to the system (3.6) and replace A matrix by \((A+BK)\) matrix in (3.26), yields the condition
where, \(\Xi _{11}=A^{T}P+PA+T_{1}+T_{1}^{T}+Q_{1}+PBK+K^{T}B^{T}P\), \(\Omega _{12}=PA_{d}-T_{1}+T_{2}^{T}\),
\(\Xi _{13}=d_{u}A^{T}Q_{2}+d_{u}K^{T}B^{T}Q_{2}\), \(\Omega _{22}=-T_{2}-T_{2}^{T}-(1-\mu )Q_{1}\).
Pre- and post-multiplying (3.27) by \(diag\{P^{-1},~P^{-1},~Q_{2}^{-1},~P^{-1}\}\), and adopting following changes in variables,
\(P^{-1}=Y,~~Q_{2}^{-1}=X,~~KP^{-1}=KY=S,~~P^{-1}T_{1}P^{-1}=T_{R},~~P^{-1}T_{2}P^{-1}=T_{S},\) and \(~~P^{-1}Q_{1}P^{-1}=Q_{R}\), where \(Y=Y^{T}~>~0\) and \(X=X^{T}~>~0\), and substituting this change of variables in (3.27) one obtains the LMI condition in (3.25).
Remark 3.5
One can observe in the condition (3.25) that the (4,4) block is not linear in matrix variable, rather it is a nonlinear, hence the obtained condition is not an LMI and the standard routine of LMI Toolbox of \(MATLAB^{\circledR }\) [17] cannot be used to obtain the feasible solution set.
For obtaining feasible solution, one can easily transform this NLMI condition into an LMI by assuming \(X=Y\), but the stabilizing results will tend to be conservative [9]. An iterative cone-complementarity algorithm in [16] has been used to solve this NLMI problem which can yield less conservative stabilizing results compared to that of the former assumption (\(X=Y\)), but the estimate of delay upper bound and the state feedback gains obtained are suboptimal.
The iterative cone-complementarity for solving the NLMI condition (3.25) is illustrated in brief below:
Let us fix,
Substituting (3.28) in (3.25), one can write
Using Schur-complement to (3.28), one can rewrite
Now defining, \(D=L^{-1},~J=Y^{-1},~N=X^{-1}\), one can rewrite (3.30) as
Again, one can have the following valid identities valid, \(DL=I,~JY=I,~~NX=I\). Thus, in view of the identities defined, one can write it in the form of matrix inequalities as,
Now, one can solve (3.25) as a linear minimization problem as:
\(\qquad \qquad \qquad \qquad \) \(Minimize~~Trace~~(LD+YJ+XN)\)
\(\qquad \qquad \qquad \qquad \;\)subject to. (3.29), (3.31), and (3.32)
This routine is iteratively implemented by incrementing the value of the delay bound \(d_{u}\) in small steps and checking the feasible solution of (3.28) at each step, the algorithm stops at a value of \(d_{u}\) where the condition (3.28) is not satisfied.
For convenience of the discussion of the main results of this chapter, some preliminaries including few definitions, basic theorems on stabilization of time-delay systems which are related to the main results are presented in previous sections.
3.4 Main Results on Delay-Dependent Stabilization of Nominal TDS
The stabilization condition is obtained by directly extending the stability condition (2.130)–(2.134) discussed in Theorem 2.18.
Theorem 3.6
Given a scalar \(0\le d(t)\le d_{u}\) (where \(d_{u}>0\)), the system (3.6) for \(0<\mu <1\) is asymptotically stabilizable with the state-feedback controller, \(u(t)=Kx(t)~(K=YZ^{-1})\) for any time-delay satisfying the condition (3.3), if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R},\bar{T}\), and any free matrices \(\bar{M}_{i},~\bar{L}_{i}~(i=1,2,3)\) and Z with appropriate dimensions such that the following LMIs hold:
and,
where,

Proof
This is an extension of the stability conditions derived in Theorem 2.18. Replacing matrix A by \(A_{c}=A+BK\) in the matrix \(\Omega \) (see (2.134)) and set the free variables \(G_{1}=G\) and \(G_{2}=\alpha G\). In 2.157 the (6,6) block contains \(-G_{2}-G_{2}^{T}\) which indicates that for negativity of that block the matrix \(G_{2}\) must be positive definite, thus in this view for guaranteing the negativity of the LMI here, matrix \(G_{2}=\alpha G\) must also be positive definite which in turns will guarantee the term \(-\alpha (G+G^{T})\) as negative definite.
Now pre-multiply the matrix \(\Omega \) in (2.134) by \(diag[G^{-T},~G^{-T},~G^{-T},~G^{-T},~G^{-T},~G^{-T}]\) and post-multiply by \(diag[G^{-1},~G^{-1},~G^{-1},~G^{-1},~G^{-1},~G^{-1}]\) and subsequently pre-multiply \(\left[ \begin{array}{cc} P_{11} &{} P_{12} \\ \star &{} P_{22} \\ \end{array} \right] \) and \(\left[ \begin{array}{cc} Q_{11} &{} 0\\ 0 &{} Q_{22} \\ \end{array} \right] \) by \(diag[G^{-T},~G^{-T}]\) and post-multiply the same matrices by \(diag[G^{-1},~G^{-1}]\) one can obtain the LMIs in (3.33)–(3.35) with the following changes in variables \(G^{-1}=Z, G^{-1}(.)G^{-1}=\bar{(.)}\) and \(KZ=Y\).
Note that, the stabilizing conditions obtained here are convex combination of LMI conditions.
To obtain a realizable solution of gain matrix K for a particular delay bound, one needs to impose constraint on Y and Z matrices that limit the size of the gain matrix K, and it is expressed as
Imposing constraint on matrix Y in the following form
or,
Similarly imposing constraint on matrix \(Z^{-1}\) in the following form
or,
To find the optimal value of the gain K for a particular delay upper bound \(d_{u}\) and \(\alpha \), following minimization problem is considered,
Minimize \(\delta +\beta \)
subject to (3.33)–(3.35), (3.38), (3.40), \(P_{11}=P_{11}>0, R_{i}>0, T>0\).
Next the stabilization condition for \(\mu =0\) is obtained from the conditions (3.33)–(3.35) by substituting \(\mu =0\). The stabilization condition is presented below in the form of corollary.
Numerical Implementation of the Algorithm: The above minimization algorithm is solved using the ‘mincx’ solver of the LMI toolbox of \(MATLAB^{\circledR }\) along with ‘fminsearch’ routine to tune the value of parameter \(\alpha \) for a particular delay value. The numerical implementation of the algorithm is presented in the form of flow chart as shown in Fig. 3.1.
Corollary 3.1
Given \(d_{u}~>~0\), the system (3.6) for \(\mu =0\) is asymptotically stabilizable with the state-feedback controller, \(u(t)=Kx(t)~(K=YZ^{-1})\) for any time-delay satisfying the condition (3.3), if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R}\), and any free matrices \(\bar{M}_{i},~\bar{L}_{i}~(i=1,2,3)\) and Z with appropriate dimensions satisfying the following LMI constraints:
and,
where, the elements of \(\bar{\Omega }\) matrix is same as defined in the Theorem 3.6.
The proof of this corollary is straight forward and can be obtained from Theorem 3.6 by substituting \(\mu =0\). The solution of the state feedback gain matrix is obtained in a similar manner using optimization algorithm presented in Theorem 3.6 subject to the constraints (3.41)–(3.43).
Numerical Example 3.1
([12]) Consider the system (3.6) with the following constant matrices
The eigenvalues of the matrix \([A+A_{d}]\) is not Hurwitz and hence the open-loop system is unstable. The proposed stabilization result is compared with the existing LMI based methods and presented in Table 3.1.
Remark 3.6
As pointed out above that the open-loop system considered in Numerical Example 3.1 is unstable, but the eigenvalues of closed-loop system (\(A+BK\) matrix) is found to be stable, on the other hand the eigenvalues of (\(A+BK-A_{d}\)) is not Hurwitz thus indicating that the closed-loop system is not delay-independently stable [12].
Remark 3.7
For a particular delay value \(d_{u}= 7 secs\) the parameter \(\alpha \) is tuned using ‘fminsearch’ to find the optimal value of the gain K as presented in the flowchart (Fig. 3.1). The variation of parameter \(\alpha \) with respect to the control energy (represented as \(\parallel K \parallel _{2}\)) is shown in the Fig. 3.2.
Remark 3.8
The controller gain K and the delay upper bound \(d_{u}\) for the system described in Example 3.1 using the proposed Corollary 3.1 are presented in Table 3.1. The effectiveness of the designed state feedback controller is obvious from the values of \(d_{u}\) and K compared to the existing methods.
Remark 3.9
Comparison of stabilizing results (\(d_{u}~and~K\)) for Example 3.1 is presented in Table 3.2. One can observe that the number of decision variables used in [12] is more than that of Theorem 3.5, more decision variables indicates use of more free matrices in establishing the stability condition. But, both the methods uses same number of bounding inequalities for obtaining the LMI condition. In view of the above reasons, probably the stabilizing condition in [12] acquired enhanced delay upper bound with sizeable iterations compared to Theorem 3.5. It must be noted here that, the scope of improvement of Theorem 3.5 is still open in terms of enhancing the delay bound by introducing more free matrices and its associated state vectors.
Another significant reason for better stabilizing result for \(\mu =0\) in [12] is due to the use of a matrix variable \(Q_{12}\) (expressing relationship between the state vectors x(s) and \(\dot{x}(s)\)). This parameter is not used in our stability formulation. The reason for not using this variable is that it can enhance the result of delay bound only for the case \(\mu =0\) but for other \(\mu \) values it fails to improve the results and subsequently incorporates more number of decision variables in the formulation.
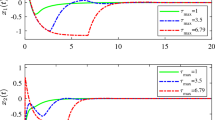
Open-loop simulation of system in Example 3.1
Closed-loop simulation of system in Example 3.1
The simulation results of the system in Numerical Example 3.1 for constant delay (i.e, \(\mu =0\)), considering \(d_{u}=8.0~secs.\) with and without controller are presented in Fig. 3.3 and Fig. 3.4 respectively. It may be observed that the open-loop time-delay system response is unstable whereas the closed-loop system response with the state feedback gain \(K=[-75.3591,~-83.9332]\) and \(d_{u}=8 secs\) stabilizes the unstable system.
3.5 Delay-Dependent Robust Stabilization of an Uncertain TDS
In this section, the robust stabilization problem for uncertain time-delay system described in (3.1)–(3.2) is considered using state feedback control law (i.e, \(u(t)=Kx(t)\)). The structure of the uncertainty is described in (3.4)–(3.5) and satisfying the delay and its derivative conditions are mentioned in (3.3). The robust stabilization conditions for the systems in (3.1)–(3.2) with norm bounded uncertainties can be found in the literatures [6,7,8,9,10, 12, 21] and [19], whereas the conditions derived for polytopic uncertainties can be found in [11, 14, 18, 22].
Next, two existing robust stabilization algorithms for an uncertain system in (3.1) are presented in the form of the theorem, which are significant for developing an improved stabilization conditions.
The delay-dependent robust stabilization theorem presented below is obtained from the robust stability conditions (2.211)–(2.212) discussed in Theorem 2.21 under state feedback control law.
Theorem 3.7
([9]) If there exist matrices \(L~>~0,~M,~N,~R,~V,~W~>~0\) and positive scalars \(\epsilon _{1},~\epsilon _{2},....,\epsilon _{6}\) such that,

then the system in (3.1)–(3.2) with the control law \(u(t)=VL^{-1}x(t)\) is asymptotically stable for any constant time-delay d satisfying the condition \(0\le d\le d_{u}\) and all admissible uncertainties defined in (3.4)–(3.5).
Remark 3.10
The proof of this theorem is straightforward as it is an extension of the robust stability condition stated in Theorem 2.21 and hence omitted. The derived condition is a NLMI, it is solved using iterative cone-complementarity algorithm as discussed in [9]. The nature of time-delay is assumed to be constant.
The delay-dependent robust stability condition (2.219)–(2.221) discussed in Theorem 2.23 has been extended for solution of robust stabilization problem using state feedback control law and is presented below in the form of theorem.
Theorem 3.8
([12]) Given the scalars \(d_{u}~>~0,~\mu ~>~0~\), system (3.1)–(3.2) is robustly asymptotically stabilizable with the memoryless state-feedback controller, \(u(t)=YX^{-1}x(t)\) for any time-delay satisfying (3.3) and for the admissible uncertainties (3.4) satisfying (3.5) if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R},~\bar{T},~\bar{Z}\) matrices \(\bar{S}_{i}, (i=1,2,...,4),~Y\) and scalars \(\epsilon _{i}^{'}s (i=1,..,4)\) satisfying the following LMIs:
where, \(\bar{\Sigma }_{11}=XA^{T}+AX+Y^{T}B^{T}+BY+\bar{R}+\bar{S}_{1}^{T}+\bar{S}_{1}+\Delta \)
\(~~~~~\bar{\Sigma }_{12}=A_{d}X-S_{1}^{T}+\bar{S}_{2}^{T}\); \(\bar{\Sigma }_{14}=\bar{P}_{12}-\bar{S}_{1}^{T}+\bar{S}_{4}\); \(\bar{\Sigma }_{17}=XA^{T}+Y^{T}B^{T}+\Delta \)
\(~~~~~\bar{\Sigma }_{22}=-(1-\mu )\bar{R}+\mu \bar{T}-S_{2}^{T}-\bar{S}_{2}\); \(\bar{\Sigma }_{24}=-\bar{S}_{2}^{T}-\bar{S}_{4}\); \(\bar{\Sigma }_{34}=\bar{P}_{22}-\bar{Q}_{12}-S_{3}^{T}\)
\(~~~~~\bar{\Sigma }_{44}=-\bar{Q}_{22}-S_{4}^{T}-\bar{S}_{4}\); \(\bar{\Sigma }_{77}=-\bar{Z}+\Delta \); \(\Delta =\epsilon _{1}D_{a}D_{a}^{T}+\epsilon _{2}D_{d}D_{d}^{T}+\epsilon _{3}D_{b}D_{b}^{T}\)
Proof
Replacing \(A,~A_{d}\) and B with \(A(t),~A_{d}(t)\) and B(t) as defined in (3.4) respectively in the stabilization condition (3.21) of (Theorem 3.4) and then decomposing the resulting matrix inequality into nominal and uncertain parts which will take the form:
where, \(\bar{\Sigma }_{unc}=D_{3}F_{a}(t)E_{3}+D_{4}F_{d}(t)E_{4}+D_{5}F_{b}(t)E_{5}\)
\(D_{3}=[D_{a}^{T}~0~0~0~0~0~D_{a}^{T}~0~0]^{T}, D_{4}=[D_{d}^{T}~0~0~0~0~0~D_{d}^{T}~0~0]^{T}\),
\(D_{5}=[D_{b}^{T}~0~0~0~0~0~D_{b}^{T}~0~0]^{T}, E_{3}=[E_{a}X~0~0~0~0~0~D_{a}^{T}~0~0]\),
\(E_{4}=[0~E_{d}X~0~0~0~0~D_{a}^{T}~0~0], E_{5}=[E_{b}Y~0~0~0~0~0~D_{a}^{T}~0~0]\).
Using Lemma 2.6 on the last two terms of (3.48) and then using Schur-complement one can get (3.47).
Remark 3.11
If uncertainties are described as \(D_{a}=D_{d}=D\) and \(F_{a}(t)=F_{d}(t)=F(t)\) and \(\Delta B(t)=0\), then the robust stabilizability condition is reduced to following corollary.
Corollary 3.2
Given the scalars \(d_{u}~>~0,~\mu ~>~0~\epsilon >0\), system (3.1)–(3.2) is robustly asymptotically stabilizable with the memoryless state-feedback controller, \(u(t)=YX^{-1}x(t)\) for any time-delay satisfying (3.3) and for the admissible uncertainties defined above (in Remark 3.11) if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R},~\bar{T},~\bar{Z}\) and any matrices \(\bar{S}_{i}, (i=1,2,...,4),~Y\) such that the condition (3.46) as well as the LMI holds:
where, \((1,1)=\bar{\Sigma }_{11}|_{\Delta =0}+\epsilon DD^{T}, (1,7)=\bar{\Sigma }_{17}|_{\Delta =0}+\epsilon DD^{T}\), \((7,7)=-Z+\epsilon DD^{T}\).
Note: Delay-dependent robust stabilization condition for \(\mu =0\) can be obtained from corollary 3.2 by substituting the value of \(\mu =0\) and \(T=0\) in (3.49).
For better understanding of the main results of this chapter, some basic theorems on robust stabilization of time-delay systems relevant to the main results are presented in preceding section.
3.6 Main Results on Delay-dependent Robust Stabilization of an Uncertain TDS
In this section, two different robust stabilization conditions for an uncertain TDS (3.1)are derived (i) in a nonlinear matrix inequality (NLMI) framework and (ii) in a linear matrix inequality (LMI) framework, which are presented in the form of theorems below. The effectiveness of the proposed stabilization criteria is validated by comparing the results with existing methods.
Theorem 3.9
([23]) System (3.1) with the state feedback control law \(u(t)=Kx(t)\) is stabilizable if there exist symmetric positive-definite matrices \(Y,~X,~Q_{r}\) and any free matrices \(T_{r},~T_{s}\) and S, positive scalars \(\epsilon _{1},~\epsilon _{2},~\epsilon _{3}\) and \(d_{u}\), such that the following LMI conditions holds:

Proof
Consider an uncertain time-delay system (3.1) satisfying the delay and its derivative conditions (3.3), to prove the above robust stabilizability condition we consider following LK functional candidate is considered.
Finding the time-derivative of (3.53) and substituting the value of \(\dot{x}(t)\) from (3.1) with \(u(t)=Kx(t)\), one can get

The time-derivative of (3.54) and (3.54) are
and,
The last integral term of (3.57) is approximated as
Using Lemma 2 of [24], (3.58) may be written as
Substituting the value of \(\dot{x}(t)\) from (3.1) and applying state feedback control law (i.e. \(u(t)=Kx(t)\)) in the first term of (3.57) and subsequently approximating the integral term by (3.59), one can obtain after simple algebraic manipulations the following expression for \(\dot{V}_{3}(t)\) as
where, \(\Upsilon _{11}=d_{u}(A(t)+B(t)K)^{T}Q_{2}(A(t)+B(t)K)+T_{1}+T_{1}^{T}\);
\(~~~~~~~~~~~~\Upsilon _{22}=d_{u}A_{d}(t)^{T}Q_{2}A_{d}(t)-T_{2}-T_{2}^{T}\);
\(~~~~~~~~~~~~\Upsilon _{12}=d_{u}(A(t)+B(t)K)^{T}Q_{2}A_{d}(t)-T_{1}+T_{2}^{T}\).
Now, in view of (3.57) and invoking (3.55), (3.56) and (3.60) one obtains
where, \(\Lambda _{11}=(A(t)+B(t)K)^{T}P+P(A(t)+B(t)K)+d_{u}(A(t)+B(t)K)^{T}Q_{2}(A(t)+B(t)K)\)
\(~~~~~~~~~~~~~~~~~~~~+T_{1}+T_{1}^{T}+Q_{1}\);
\(~~~~~~~~~~~~\Lambda _{22}=d_{u}A_{d}(t)^{T}Q_{2}A_{d}(t)-T_{2}-T_{2}^{T}-(1-\mu )Q_{1}\);
\(~~~~~~~~~~~~\Lambda _{12}=PA_{d}(t)+d_{u}(A(t)+B(t)K)^{T}Q_{2}A_{d}(t)-T_{1}+T_{2}^{T}\).
Now, for stability \(\dot{V}(t)\) must be less than zero, i.e, the following conditions must be satisfied
Using Schur-complement equation (3.62) can be rewritten as
where, \(\Pi _{11}=(A(t)+B(t)K)^{T}P+P(A(t)+B(t)K)+T_{1}+T_{1}^{T}+Q_{1}\); \(\Pi _{12}=PA_{d}(t)-T_{1}+T_{2}^{T}\);
\(~~~~~~~~~~~\Pi _{13}=d_{u}(A(t)+B(t)K)^{T}Q_{2}\); \(\Pi _{22}=-T_{2}-T_{2}^{T}-(1-\mu )Q_{1}\); \(\Pi _{23}=d_{u}A_{d}^{T}Q_{2}\).
Pre- and post-multiplying (3.63) by \(diag\{P^{-1},~P^{-1},~Q_{2}^{-1},~P^{-1}\}\) and defining the linear changes in variables as \(Y=P^{-1},~X=Q_{2}^{-1},~KY=S,~YT_{1}Y=T_{r},~YT_{2}Y=T_{s}\) and \(YQ_{1}Y=Q_{r}\), one obtain,
where, \(W_{11}=YA^{T}(t)+A(t)Y+B(t)S+S^{T}B^{T}(t)+T_{r}+T_{r}^{T}+Q_{r}\); \(W_{12}=A_{d}(t)Y-T_{r}+T_{s}^{T}\); \(W_{13}=d_{u}YA^{T}(t)+d_{u}S^{T}B^{T}(t)\); \(W_{22}=-T_{s}-T_{s}^{T}-(1-\mu )Q_{r}\).
The matrices A(t) and \(A_{d}(t)\) in (3.64) are replaced by \((A+\Delta A(t)\) and \((A_{d}+\Delta A_{d}(t)\) with (3.4) and then decomposing the (3.64) as nominal and uncertain parts as
where,

Rearranging (3.65) one may write
where,
Applying Lemma 2.6 thrice on (\(J_{u}+J_{u}^{T}\)) term of (3.66), eliminates the uncertain matrices \(F_{a}(t),~F_{b}(t)\) and \(F_{d}(t)\), and one obtains the LMI condition (3.50).
Remark 3.12
If uncertainties are described as \(D_{a}=D_{d}=D\) and \(F_{a}(t)=F_{d}(t)=F(t)\) and \(\Delta B(t)=0\), then the robust stabilizability condition is reduced to following corollary.
Corollary 3.3
System (3.1) with state feedback control law \(u(t)=Kx(t)\) is stabilizable if there exist (a) symmetric positive-definite matrices \(Y,~X,~Q_{r}\) and (b) any free matrices \(T_{r},~T_{s}\) and S, positive scalars \(\epsilon \) and \(d_{u}\), such that the following LMI conditions holds:

Remark 3.13
The Stabilizability conditions in (3.50) and (3.67) are NLMIs due to the presence of nonlinear term \(YX^{-1}Y\). In order to solve numerical such NLMIs cone-complementarity algorithm [16] has been used here.
Next, the step-by-step numerical implementation of cone complementarity algorithm is used to solve this NLMI problem.
Algorithmic Computation:
Let us fix
substituting (3.68) in (3.67), one can rewrite
using Schur-complement to (3.68), one can write
Now defining, \(D=L^{-1},~J=Y^{-1},~N=X^{-1}\), one can rewrite (3.70) as
Again, one can have the following valid identities, \(DL=I,~JY=I,~~NX=I\). Thus, in view of the identities defined, one can write it in the form of matrix inequalities as
As the nonlinear LMI condition in 3.67 cannot be solved as a feasibility problem by standard routine of LMI toolbox of MATLAB, so the NLMI in (3.67) can be solved as a cone complementarity problem suggested in [16] which is recast as
Minimize Trace(\(LD+YJ+XN\))
subject to (3.67), (3.71) and (3.71)
Such problems are solved by considering the linear approximation of (\(Trace~LD+YJ+XN\)) in the form \(Trace~(D_{0}L+L_{0}D+J_{0}Y+Y_{0}J+N_{0}X+X_{0}N\)) at a given point (\(D_{0}, L_{0}, J_{0}, Y_{0}, N_{0}, X_{0}\)) [16]. Note that, (3.72) confronts the exact solution when these are at the boundary, i.e., the inequalities are rank-deficient. Now we are ready to present algorithmic steps of the linearization algorithm.
Algorithmic Steps
Step 1: Select initially a small value of delay bound \(d_{u}\) and set \(j=0\).
Step 2: Find a feasible set of \((D_{0},~J_{0},~L_{0},~Y_{0},~N_{0},~S_{0},~T_{r0},~T_{s0},~X_{0},~ Q_{r0},~\epsilon _{0})\) satisfying (3.68), (3.71) and (3.72) with \(Y>0\) and \(X>0\).
Step 3: Solve the following LMI optimization problem for the variables \((D,~J,~L,~Y,~N, ~S,~T,~T,~X,~Q,\epsilon )\)
Minimize Trace (\(LD_{j}+DL_{j}+YJ_{j}+JY_{j}+XN_{j}+NX_{j}\)) subject to (3.68), (3.71) and (3.72) with \(Y>0\) and \(X>0\). The LMIs are solved using the standard routines available with LMI toolbox of MATLAB [6].
Set (\(D_{j+1}=D,~L_{j+1}=L,~J_{j+1}=J,~Y_{j+1}=Y,~N_{j+1}=N,~X_{j+1}=X\)).
Step 4: If \(L_{j-1} \le Y_{j}X_{j}^{-1}Y_{j}\) is satisfied then increase \(d_{u}\) by small value and go to Step 2. If this is condition is not satisfied within a prespecified number of iterations then stop. Otherwise set j=j+1 and go to step 3.
The above algorithmic steps are presented in the form of flow-chart in Fig. 3.5 for better understanding of the numerical implementation of the algorithm for stabilization problem of time-delay system.
An LMI based robust stabilizing conditions are derived next by extending the stabilizing conditions obtained in Theorem 3.6 and its associated corollaries.
Theorem 3.10
Given the scalar \(d_{u}~>~0\), the system (3.1) for \(0<\mu <1\) is asymptotically robustly stabilizable with the state-feedback controller, \(u(t)=YZ^{-1}x(t)\) for any time-delay satisfying the condition (3.3) with admissible uncertainties, if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R},\bar{T}\), and any free matrices \(\bar{M}_{i},~\bar{L}_{i}~(i=1,2,3), Z\) and the scalars \(\epsilon _{i}>0, (i=1,2)\) with appropriate dimensions satisfying the following LMI constraints:
and,
where,

Proof
Replace A and \(A_{d}\) matrices in the \(\bar{\Omega }\) block matrix of the stabilizing condition (3.34)–(3.35) by \(A+D_{a}F_{a}E_{a}\) and \(A_{d}+D_{d}F_{d}E_{d}\) respectively, this replacement will give rise to a new matrix of the form,
where, \(\bar{\Omega }_{nom}=\bar{\Omega }\) and the \(\bar{\Omega }_{unc}\) is defined below,

Further one can rewrite (3.77) in the form,
where,
and
Now using Lemma 3.2 one can write (3.78) as,
Substituting (3.79) in (3.76) one can get following block matrices,
now using Schur-complement twice on the block matrices in (3.80) provides the robust-stabilizing condition (3.74)–(3.75), rest of the LMIs are same as in stabilization theorem as they do not contain any system matrices in it.
To obtain a realizable solution of gain matrix \(K=YZ^{-1}\) for a particular delay bound, one can impose constraint on the size of matrix K elements as,
with
and
the above two constraints (3.83) and (3.84) further can be rewritten as
and
To find the value of the gain K for a particular delay upper bound \(d_{u}\) and \(\alpha \) following minimization problem is proposed:
Minimize \(\delta +\beta \)
s.t. (3.73)–(3.75), \(P_{11}=P_{11}>0, R_{i}>0, T>0\) and \(\epsilon _{i}>0,~i=1,2\)
If \(D_{a}=D_{d}=D\) and \(F_{a}(t)=F_{d}(t)=F(t)\) then the resulting norm bounded uncertainties will take the form \(\Delta A = DFE_{a}\) and \(\Delta A_{d} = DFE_{d}\), the robust stabilizing condition with norm bounded uncertainties for \(0<\mu <1\) can be stated in the form of corollary presented below:
Corollary 3.4
Given the scalars \(d_{u}~>~0\), the system (3.1) with \(\Delta B=0\) for \(0<\mu <1\) is asymptotically robustly stabilizable with the state-feedback controller \(u(t)=YZ^{-1}x(t)\) for any time-delay satisfying the condition (3.3) with admissible uncertainties, if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R},\bar{T}\), and any free matrices \(\bar{M}_{i},~\bar{L}_{i}~(i=1,2,3)\),Z and a scalar \(\epsilon >0\) with appropriate dimensions satisfying the following LMI constraints:
and,
where, the elements of \(\bar{\Omega }_{per}\) are all same as defined in Theorem 3.10 except the terms,

The proof this corollary is straightforward and can be obtained in a similar manner as in Theorem 3.10, by replacing A and \(A_{d}\) matrices with \(A+DFE_{a}\) and \(A_{d}+DFE_{d}\) respectively and along with the choices of the matrix E defined above and the matrix D as
If \(\mu =0\) (delay-derivative) and the uncertainties are as defined in the Corollary 3.4 then one can get robust stabilizing condition directly from Corollary 3.4 by substituting \(\mu =0\).
Corollary 3.5
Given the scalars \(d_{u}~>~0\), the system (3.1) with \(\Delta B=0\) for \(0<\mu <1\) is asymptotically robustly stabilizable with the state-feedback controller, \(u(t)=YZ^{-1}x(t)\) for any time-delay satisfying the condition (3.3) with admissible uncertainties, if there exist symmetric positive definite matrices \(\bar{P},~\bar{Q},~\bar{R},\bar{T}\), and any free matrices \(\bar{M}_{i},~\bar{L}_{i}~(i=1,2,3)\),Z and a positive scalar \(\epsilon \) with appropriate dimensions satisfying the following LMI constraints,
and,
where, the elements of \(\bar{\Omega }_{per}\) are all same as defined in Theorem 3.10, whereas following term gets modified in view of the structure of uncertainty assumed for obtaining this corollary

Remark 3.14
It may be noted that both the corollaries 3.4 and 3.5 are equivalently same and can be applied for robust stabilization of time-delay systems with admissible uncertainties (with \(\Delta B=0\)) for \(0\le \mu \le 1\). The LMIs (3.88) and (3.89) involved in corollary 3.4 are replaced by the lower dimensional LMIs (3.91) and (3.92). While a sequence Schur-complement is employed on them, this indeed requires less number of LMI variables and in turn improves the upper bound estimate.
Numerical Example 3.2
[6, 12] Consider an uncertain time-delay system,
Note: Minimization algorithm as discussed in Theorem 3.10 is considered along with the delay-dependent robust stabilization conditions obtained in Corollary 3.4 and 3.5 for computing the delay bound \(d_{u}\) and the stabilizing gain matrix K.
(n= Order of the system and m= number of inputs).
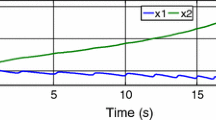
Closed-loop simulation of system in Example 3.2
Control input of system in Example 3.2
The simulation results of the system considered in Example 3.2 (for a constant delay, i.e, \(\mu =0\)) are obtained by considering the uncertainty matrix as in [12],
The considered uncertain TDS is found to be unstable under open-loop with time-delay set to \(d_{u}=1.3~seconds\). Now applying the stabilizing control law with state feedback gain \(K=~[-1.1923,~-4.1754]\) and the corresponding \(d_{u}=1.3\) seconds (see Table 3.4), the system responses are shown in the Fig. 3.6 and its corresponding control input plot is shown in Fig. 3.7. It may be mentioned that, proposed corollary 3.3 provides less control effort as well as less number of iterations are required compared to existing method [12] for the same value of delay upper bound \(d_{u}=1.3 ~secs\).
Numerical Example 3.3
Consider an uncertain time-delay system, [6, 12]
Responses of an uncertain TDS described in Numerical Example 3.3 are obtained with the following data; \(F_{a}(t)=F_{d}(t)=F(t)=I\) (as \(\parallel F(t)\parallel \le 1\)) and the time-varying delay of value \(d(t)=0.2+0.5 sin(t)\) (Fig. 3.8). Under open-loop the system response is found to be unstable as shown in the Fig. 3.9, it is stabilized using \(K=[-105.4272,~-69.6643]\) for the delay \(d_{u}=0.7 sec, \mu =0s.5\) (see Table 3.5). The closed-loop system response is shown in Fig. 3.10.
Time-varying delay considered for Example 3.3
Open-loop simulation of system in Example 3.3
Closed-loop simulation of system in Example 3.3
Remark 3.15
The robust stabilization results obtained using Corollary 3.3 (in a NLMI framework) for the systems described in Examples 3.2 and 3.3 are presented in Tables 3.4 and 3.6 respectively. One can observe from Table 3.5 that proposed stabilizing controllers provide less conservative delay bound \(d_{u}\) and less control effort \(\parallel K \parallel _{\infty }\) than those obtained using delay-dependent stabilization criteria with or without system uncertainties. Furthermore, it can be noted from Table 3.6 that the proposed stabilizing controller while solved via NLMI framework provides significant reduction in number of iterations to achieve the same delay bound estimate and thus it is computationally more attractive than the existing methods due to the number of decision variables involved in the derivation is less.
Remark 3.16
One can observe in Table 3.4 and 3.6 that, robust stabilizing condition in [12] could not achieve better delay bound and realizable gain K compared to proposed method due to the fact that, (i) the robust controller synthesis in [12] is carried out using three different bounding inequalities in order to obtain the LMI condition and (ii) use of more number of decision variables. Thus use of more number of bounding inequalities as well as decision variables results into conservative estimate of the delay bound for an uncertain system.
We would also like to mention here that, in [12] on account of the use of \(Q_{12}\) term in the LK function for deriving the stability criterion leads to complicated robust stabilization condition requiring more bounding inequalities to be used. It is needless to mention that a better stability analysis may not prove beneficial to obtain better stabilizing results due to its computational limitations.
Remark 3.17
The robust stabilization results obtained using Corollarys 3.4 and 3.5 (LMI based stabilization conditions) for the systems described in Examples 3.2 and 3.3 are presented in Tables 3.3 and 3.5 respectively. One can observe that the proposed LMI based controller could compute realizable state feedback gain with an enhanced delay upper bound compared to the existing results which are mainly due to (i) solving the proposed LMI conditions along with gain minimization routine [27], and (ii) use of more free matrices to express the relationship between various state vectors.
3.7 State Feedback \(H_{\infty }\) Control of TDS
While designing controller, the primary objective is to construct systems with guaranteed cost performance measure. A popular performance measure of a stable linear time-invariant system is the \(H_{\infty }\) norm of its transfer function. Reliable control problems for time-delay systems using LMI technique. The \(H_{\infty }\) control theory has gained significant advances over past few decades [28, 29] and references cited therein.
The problem of \(H_{\infty }\) control of linear delay system with delayed state feedback has become the focus of research just over a decade and has been investigated in delay-independent framework [30,31,32] and [33].
Some of the delay-dependent \(H_{\infty }\) control of time-delay system with or without parametric uncertainties can be found in [14, 18, 21, 34,35,36], and [22]. The work in [14, 18, 36], and [22] and references cited therein are all based on descriptor method, while the methods in [21, 34], and [35] are all based on first model transformation and expected to give conservative results due to the presence of additional dynamics in the model transformation discussed earlier in Chap. 2.
In this chapter, a state feedback \(H_{\infty }\) control of a nominal time-delay system is dealt in presence of disturbance input.
3.7.1 Problem Statement
Consider a general class of linear time-delay systems described by the following state equations
where, \(x(t)~\in ~\mathcal {R}^{n}\) is the state vector, \(u(t)~\in ~\mathcal {R}^{m}\) is the control input, \(w(t)~\in ~\mathcal {R}^{p}\) is the exogenous disturbance which belongs to \(\mathcal {L}_{2}~[0,\infty ], z(t)~\in ~\mathcal {R}^{q}\) is the regulated output, and \(\phi (.)\) is the initial condition. The matrices \(A,~A_{d},~B,~D,~C\) and F are known real constant matrices of appropriate dimensions. The delay d(t) is time-varying and satisfies the condition (3.3).
The state feedback \(H_{\infty }\) control problem consists of two parts, (i) firstly, one develops the condition of \(H_{\infty }\) performance analysis for an unforced system (3.93) with \(u(t)=0\), such that the said system is stable with disturbance attenuation \(\gamma \) (where \(\gamma ~>~0\) is a scalar) subject to zero initial condition and \(\parallel z \parallel _{2}~<~\gamma \parallel w \parallel _{2}\) for any non zero exogenous input w(t), and (ii) secondly, the obtained condition in (i) is further extended to design of a \(H_{\infty }\) state feedback control law \(u(t)=Kx(t)\) such that the resultant close-loop system is asymptotically stable and transfer function from w to z satisfy \(\parallel T_{wz} \parallel _{\infty }~<~\gamma \). Specifically, the problem of \(H_{\infty }\) control can be defined as given below.
State Feedback H-Infinity Control
[21] For given scalars \(d_{u}~>~0\) and \(\gamma ~>~0\), find a state feedback control law \(u(t)=Kx(t)\) for the system (3.93)–(3.94) such that the resulting closed loop system is asymptotically stable and satisfying the disturbance attenuation \(\gamma \) for any time-delay d(t) with \(0~\le ~d(t)~\le ~d_{u}\). In this case the system (3.93)–(3.94) is said to be stabilizable with the disturbance attenuation \(\gamma \).
In [18] and [14] it has been demonstrated that the choice of appropriate LK functional and selection of suitable bounding technique for approximating the cross terms arising out of the LK functional derivatives are the two important factors for deriving less conservative delay bound as well as for achieving the \(H_{\infty }\) performance conditions.
3.8 Stabilization of LFC Problem for Time-Delay Power System Based on \(H_{\infty }\) Approach
Load frequency control (LFC) is of importance in electric power system operation to damp frequency and voltage oscillations originated from load variations of real and reactive powers. Many control strategies, e.g., Proportional-Integral (PI) control [37,38,39], control using state feedback [33, 40,41,42,43], variable structure control [44], adaptive control [45], have been investigated to obtain a suitable LFC strategy. In view of the structure of existing power system model used for LFC [33, 38, 40,41,42, 44, 45] and [43], the area control error (ACE) is used as a control input to suppress the frequency deviation automatically. In general, the ACE signals are sought through high speed communication channel and may involve negligible communication delay. In [38, 42, 46,47,48], the need for open communication network has been highlighted that may cause a significant amount of communication delay present in the ACE signal. However, to the best of our knowledge, there are only few literature which investigate the LFC design problem considering communication delay in the ACE signal since such a design has only been considered in [48]. In this section, the design of LFC problem based on \(H_{\infty }\) controller with communication delays in the ACEs is considered.
The control structures suggested for stability analysis of interconnected power system are, (i) Decentralized control (ii) Quasi-Decentralized control (iii) Centralized Control and (iv) Hierarchial or Multilevel control [41]. Literature reveals that, the load-frequency control (LFC) of an inter-connected power system with or without time-delays are based on decentralized control structures [38, 40, 43, 48,49,50] and references cited therein, which is a network of local controller receiving local signals at each sub-system and sends control signals to the same subsystem, whereas a centralized control consists of one controller that uses all systems outputs to generate each system input, example of one such control structure in power system is wide-area-measurement-system (WAMS) centralized control [41] and references cited therein. So, far no works have been reported on application of delay-dependent \(H_{\infty }\) state feedback control using centralized LFC control structure for an interconnected time-delay power system in an LMI frame work, but the delay-independent \(H_{\infty }\) state feedback control formulation for a linear interconnected time-delay power system can be found in [48] for LFC problem and in [42] for power system stabilizer (PSS) control problem. In this thesis an attempt has been made to design a delay-dependent \(H_{\infty }\) state feedback controller using centralized LFC control structure such that the interconnected power system asymptotically stable and satisfying norm from exogenous input w(t) to regulated output z(t).
The state-feedback controllers used for LFC may be classified, on the basis of whether delayed state (in addition to the present state) information have been used or not in implementing two types of controllers—(a) one-term controller (no delayed state) and (b) two-term controller (with delayed state) [33, 42, 48]. Note that, the latter one may yields better performance due to the use of past state information. However, existing designs of such two-term controllers [33, 42, 48] consider only delay-independent design technique. Such designs consider the delay at infinity as a special case of it and yields conservative results. Clearly, the controller performance may be improved if one considers these delayed states belong to only the recent past times. This can be reflected in the design if the delay is considered to be limited and correspondingly delay-dependent design approach is made. Design of a two-term state feedback LFC for an interconnected power system having two areas is considered in this thesis. The system model under consideration takes care of the time-delays in the ACE signals as state delays. With the proper selection of Lyapunov-Krasovskii functional and use of tighter bounding inequality constraints, the system under consideration is asymptotically stable while two-term controller is designed with and without delayed state information via LMI framework with a view to achieve closed-loop system performance requirements \(\gamma \).
Let \(\gamma ~>~0\) be a given constant, then the system (3.1)–(3.2) is said to be with \(H_{\infty }\) performance index no larger than \(\gamma \) if, the system (3.1) is asymptotically stable subject to \(x(0)=0\), then the transfer function matrix satisfies,
Equation (3.96) is equivalent to \(\int _{0}^{\infty }z^{T}(t)z(t)dt~\le ~\gamma ^{2}~\int _{0}^{\infty }w^{T}(t)w(t)dt,~~\forall \omega \).
Remark 3.18
Note that, \(\gamma \) is a load disturbance rejection measure of the controller. Clearly, the system performance is better as \(\gamma \) is smaller and this indicates better the disturbance rejection. Therefore, for obtaining an optimal \(H_{\infty }\) controller one attempts to minimize the \(\gamma \) in order to have minimal effect of the load variation in the system performance.
In next following two sections, mathematical model of an interconnected time delayed LFC system is considered. Next, a two-term controller design criterion is proposed for the solution of LFC problem with the inequality 3.95 describes restraint disturbance ability.
3.8.1 Load-Frequency Control (LFC) of Power Systems with Communication Delay
A two-area interconnected power system model with communication delays is shown in Fig. 3.11, both the areas are identical in structure but having different generation capacities. The notations used for the ith area, \((i=1,2)\), are given in the following.
Further, \(d_{i}\) represents communication delays present in the ith-area that arises in the ACEs due to the time taken in measuring frequency and tie line power flow from remote terminal units (RTUs) to local control center. Note that, the local controller is a PI controller that is embedded in the system as an integral part of the model.
The dynamics of the two-area interconnected LFC model with communication delay is shown in Fig. 3.11 and it may be described in state space form (for \(i,~j=1,2\) and \(i\ne j\))
where, \(\Delta P_{ij}=-\Delta P{ji}\). Now, defining a state vector as,
The above equations (3.97)–(3.101) may be represented in a compact form as:
where, \(d_{i}(t)\) is a time-varying delay in the model, but in the LFC model it is assumed to be of constant nature and \(w(t) = \Delta P_{d}(t) = [\Delta P_{d1},~\Delta P_{d2}]^{T}\) is a load disturbance vector and the constant matrices associated with the (3.102) and (3.103) are given below:
The objective of the control problem for system (3.102) and (3.103) is to design a suitable control law u(t) such that, the closed-loop system exhibits good load-disturbance rejection property in the sense that it attains certain \(H_{\infty }\) performance, which will be discussed in succeeding sections on load-frequency controller synthesis.
The detailed discussion on need for evolution of LFC model under dergulated power market scenario for interconnected power system involving communication delay can be found in [51].
3.8.2 Existing \(H_{\infty }\) Control Design For LFC Model
In this section, the \(H_{\infty }\) control design technique (one-term and two-term controller) of [33] for the solution of LFC problem (subsection (3.8.1)) is presented briefly. It must be mentioned here that, the \(H_{\infty }\) control strategy of [33] has been applied in [48] and [42] that are designed based on delay-independent stability analysis approach. The system model in [33] as well as in [42] and [48] considers a single state time-delay, and it is presented as:
Two types of control strategies are discussed in [42] for the solutions of PSS and LFC problems. The structure of both one-term and two-term controllers are described as One-term:
Two-term:
for the solution of \(H_{\infty }\) LFC problem satisfying the \(H_{\infty }\) performance index no larger than ‘\(\gamma \)’.
3.8.2.1 One-Term \(H_{\infty }\) Control
Theorem 3.11
[33, 42] and [48] The system described in (3.104) with the control law (3.106) is asymptotically stable and \(\parallel T_{wy}\parallel \le \gamma , \gamma >0\) for any time-delay d, if there exist matrices, \(Y=Y^{T}>0,~\bar{Q}_{1}=\bar{Q}_{1}^{T}>0\), such that the following LMI is satisfied provided (A, B) is stabilizable,
where, \(W_{11}=AY+Y^{T}A^{T}+BS+S^{T}B^{T}+\bar{Q}_{1}\). The state feedback controller law is given by \(u(t)=Kx(t)\) with \(K=SY^{-1}\).
3.8.2.2 Two-Term \(H_{\infty }\) Control
Theorem 3.12
[33, 42] and [48] The system described in (3.104) with the control law (3.107) is asymptotically stable and \(\parallel T_{wy}\parallel \le \gamma , \gamma >0\) for any time-delay d, if there exist matrices, \(Y=Y^{T}>0,~\bar{Q}_{1}=\bar{Q}_{1}^{T}>0\), positive scalars \(\sigma \) and \(\kappa \), such that the following LMI is satisfied provided (A, B) is stabilizable,
where, \(W_{11}=AY+Y^{T}A^{T}+BS+S^{T}B^{T}+\bar{Q}_{1}\). The state feedback control law is given by \(u(t)=Kx(t)+K_{d}x(t-d)\) with \(K=SY^{-1}\), and \(K_{d}=VY^{-1}\).
3.9 Main Results on \(H_{\infty }\) Based LFC of an Interconnected Time-Delay Power System
In this section, the existing delay-independent one-term as well as two-term control design techniques discussed above are extended for an interconnected power system LFC problem having multiple delays (see equations (3.102)–(3.103)). An improved feedback delay-dependent \(H_{\infty }\) two-term controller is proposed for LFC of an interconnected power systems with the constraint on \(H_{\infty }\) performance index ‘\(\gamma \)’.
3.9.1 One-Term \(H_{\infty }\) Control
As pointed out earlier that, the design of one-term controller in [33, 42] and [48] can be applied to a single time-delay systems (or equivalently to one-area LFC model). An extension of the result of [42] to LFC problem of an interconnected two-area power system model (3.102)–(3.103) is presented in the form of following lemma.
Lemma 3.1
The system described in (3.102)–(3.103) with the control law (3.106) is asymptotically stable and \(\parallel T_{wy}\parallel \le \gamma , \gamma >0\) for any time-delay d, if there exist matrices, \(Y=Y^{T}>0,~\bar{Q}_{i}=\bar{Q}_{i}^{T}>0, (i=1,2)\), such that the following LMI is satisfied provided (A, B) is stabilizable
where, \(W_{11}=AY+Y^{T}A^{T}+BS+S^{T}B^{T}+\sum _{i=1}^{2}\bar{Q}_{i}\).
The state feedback control law is given by \(u(t)=Kx(t)\) with \(K=SY^{-1}\).
Proof
The proof of Lemma 3.1 is straightforward following [42] and hence omitted.
The result of LMI condition for one-term control in (3.110) can be further extended for an n-interconnected power systems as,
where, \(M_{11}=AY+Y^{T}A^{T}+BS+S^{T}B^{T}+\sum _{i=1}^{n}\bar{Q}_{i}\)
3.9.2 Two-Term \({H}_{\infty }\) Control
A two-term \(H_{\infty }\) controller design using delay-independent analysis for power system stabilizer (P.S.S) model has been considered in [42]. In this section, the result of [42] is adopted for solution of time-delay LFC control problem (3.102) and its delay-independent stabilization is presented below in the form of lemma. However in the design stage, similar to [42] one can consider the d in (3.107) as \(d \in max[d_{1},~d_{2}]\). In the present synthesis, assume \(d=d_{2}\) so the closed loop system (3.102) with the control law (3.107) becomes
where, \(A_{c}=A+BK\) and \(A_{d2c}=A_{d2}+BK_{d}\).
Lemma 3.2
System (3.112) with the controller (3.107) and assumption \(d=d_{2}\) satisfies the \(H_{\infty }\) performance defined in (3.95), if there exist positive definite symmetric matrices \(Y,~\bar{Q}_{1}, \bar{Q}_{2}\) and any matrices S, V, positive scalars \(\sigma \) and \(\kappa \), such that the following LMI holds:
where, \(\Theta _{11}=AY+Y^{T}A^{T}+BS+S^{T}B^{T}+\bar{Q}_{1}+\bar{Q}_{2}\). The corresponding \(H_{\infty }\) two-term controller gains may then be obtained as \(K=SY^{-1}\) and \(K_{d}=VY^{-1}\).
Remark 3.19
Note that, if \(d_{2}\rightarrow \infty \) then feedback delay ‘d’ also tends to infinity and this situation is equivalent to delay-independent one-term controller design. Hence, at this limiting situation the use of delayed states in feedback term is insignificant. This fact has been observed by solving two-area LFC problem using LMI (3.114).
The proposed feedback delay-dependent \(H_{\infty }\) two-term control strategy in the form of following theorem is presented, where the two-term control law (3.107) in the present situation is modified to
where, \(\tau \) is the delay in feedback signal and its upper bound is unknown.
Remark 3.20
Here, \(\tau \) is a feedback delay involved in the control law, which is not equal to that of the state delay \(d_{i}~(i=1,2)\) available in the system model. In all the existing \(H_{\infty }\) control formulations irrespective of delay-independent analysis [33, 42, 48] or delay-dependent [14, 18, 22] and [21], the delay information used in the LK functional is the state delay of the system model, whereas in the present synthesis, the designed controller uses a delayed state information ‘\(\tau \)’ in the LK functional corresponding to the delay-dependent term. The modification of the control law (3.115) leads to the choice of a new delay-dependent LK functional that avoids the demerit of the limiting situation (as mentioned in Remark (3.19), thus in practice, it is suitable for the solution of LFC problem. To the best of the present author knowledge, the stabilization of two-area LFC problem satisfying \(H-{\infty }\) performance bound based on proposed delay-dependent control strategy in LMI framework has not been reported so far in literature.
Theorem 3.13
The system (3.102)–(3.103) with the controller (3.115) is asymptotically stable and satisfies the \(H_{\infty }\) performance (3.95), if there exist positive definite matrices \(X,~\bar{Q}_{i}~(i=1,2..4)\) and matrices \(S,~Y,~\bar{T}_{i} (i=1,2), V\) and positive scalars \(\gamma , \tau \) such that the following LMI holds:
where, \(\Lambda _{11}=YA^{T}+AY+BS+S^{T}B^{T}+\bar{Q}_{1}+\bar{Q}_{2}+\bar{Q}_{3}+\bar{T}_{1}+\bar{T}_{1}^{T}\),
\(~~~~~~\Lambda _{14}=BV+YA^{T}+BS+S^{T}B^{T}-\bar{T}_{1}+\bar{T}_{2}^{T}\), \(\Lambda _{15}=-Y^{T}+X+YA^{T}+S^{T}B^{T}\), and
\(~~~~~~\Lambda _{44}=BV+V^{T}B^{T}-\bar{T}_{2}-\bar{T}_{2}^{T}-\bar{Q}_{3}\).
Proof
The closed-loop system with the implementable control law (3.115) is expressed as:
where, \(A_{c}=A+BK\) and \(B_{\tau }=BK_{\tau }\).
It is assumed that the pair (A, B) is stabilizable. As the design of \(H_{\infty }\) controller is delay-dependent with respect to feedback delay ‘\(\tau \)’ one needs to choose appropriately LK functional of the form:
Finding the time-derivative of (3.118) one can get,
Now, to approximate the quadratic integral term \(-\int _{t-\tau }^{t}\dot{x}^{T}(s)Q_{4}\dot{x}(s)ds\) in (3.119) one can use Lemma 2 of [23] which yields
Now, for a free matrix G of appropriate dimension following equality is valid,
On expansion of (3.121), one can get
where, \(\xi (t)=[x^{T}(t),~x^{T}(t-d_{1}),~x^{T}(t-d_{2}),~x^{T}(t-\tau ),~\dot{x}^{T}(t)]^{T}\) and

Using the bounding Lemma 2.1, one can treat the cross term \(2\xi ^{T}(t)\left[ \begin{array}{ccccc} G^{T} &{} 0 &{} 0 &{} G^{T} &{} G^{T} \\ \end{array} \right] ^{T}Dw(t)\) in (3.122) and rewrite it as
where, \(\gamma \) is any positive scalar quantity. Invoking (3.120) and (3.123) in (3.119), one can obtain

Using Schur-complement one can easily rewrite (3.124) as,
where, \(\Psi =\left[ \begin{array}{ccccccc} \psi _{11} &{} GA_{d1} &{} GA_{d2} &{} \psi _{14} &{} \psi _{15} &{} T_{1} &{} GD \\ \star &{} 0 &{} 0 &{} \psi _{24} &{} \psi _{24} &{} 0 &{} 0\\ \star &{} 0 &{} 0 &{} \psi _{34} &{} \psi _{35} &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \psi _{44} &{} \psi _{45} &{} T_{2} &{} GD \\ \star &{} \star &{} \star &{} \star &{} \psi _{55} &{} 0 &{} GD\\ \star &{} \star &{} \star &{} \star &{} \star &{} -\tau ^{-1}Q_{4} &{} 0\\ \star &{} \star &{} \star &{} \star &{} \star &{} 0 &{} -\gamma ^{2}I\\ \end{array} \right] \)
In (3.125), if \(\dot{V}(t)\) is negative definite then it is guaranteed that the system considered in (3.102) is stabilizable with the control law (3.115). In case of \(H_{\infty }\) state feedback control with \(x(0)=0\), and additional constraint \(\parallel z(t)\parallel _{2}~\le \gamma \parallel w(t)\parallel _{2,} \gamma ~>~0\) that describes the restraint disturbance ability must be included in the delay-dependent stability condition (3.125). One can rewrite (3.125) as,
Integrate (3.126) from \(0~to~\infty \) on both the sides, it follows then
Substituting \(z(t)=C~x(t)\) in (3.127), one can rewrite
After simple algebraic manipulation of (3.128) one can rewrite it as
If we define the \(H_{\infty }\) performance index as
thus in view of (3.130) one can write
Now, in view of (3.131) and (3.129) it is obvious that following is true,
Using Schur-complement one can rewrite (3.133) equivalently as,
If \(\Omega ~<~0\) in (3.134), then it guarantees both \(\dot{V}(t)<0\) as well as \(J_{wz}<0\) thus satisfying the condition of (3.96). Now, substitute \(A_{c}=A+BK\) and \(B_{\tau }=BK_{\tau }\) in (3.133) first, then pre- and post-multiplying (3.133) by \(\{G^{-1}, G^{-1}, G^{-1}, G^{-1}, G^{-1}, G^{-1}, I, I\}\) and its transpose respectively and adopting following linear changes of variables,

After carrying out above linear changes of matrix variables in \(\Omega \) matrix, one can obtain \(\Lambda ~<~0\) in (3.116) which is the required stabilizing condition for the LFC system. This completes the proof. \(\blacksquare \)
Remark 3.21
Note that, one may obtain controller gains using \(K=SY^{-1}\) and \(K_{\tau }=VY^{-1}\) from feasible solution of (3.116) for a specified \(\gamma \). However, by defining \(\bar{\gamma }=\gamma ^{2}\) and then obtaining a solution of (3.116) by minimizing \(\bar{\gamma }\) yields an optimal controller in the sense that \(\gamma \) gets optimized. But such optimal controllers generally have high gains and significantly amplify noises causing performance degradation. However, these high control gains may be reduced if one attempts to obtain a suboptimal controller by exploiting the trade-off between the control gains and the \(H_{\infty }\) performance index \(\gamma \). An attempt is made to design such suboptimal controllers by minimizing the \(\gamma \) as well as restricting the size of the control gains K and \(K_{\tau }\) simultaneously. Such an attempt is not new in literature, for example see [27], where suboptimal controllers have been obtained to avoid the problem that arises due to high control gains. For this purpose, note that, computing the control gains K and \(K_{\tau }\) involves the LMI variables S, V and Y . In view of this, one can define the following multi-objective optimization algorithm for computing the controller gains and simultaneously the \(H_{\infty }\) performance index \(\gamma \).
Multi-objective Optimization Algorithm:
Minimize \(\bar{\gamma }+p+s+v\)
\(~subject~to~~(3.117),~\left[ \begin{array}{cc} sI &{} S \\ \star &{} I \\ \end{array} \right] ,~\left[ \begin{array}{cc} vI &{} V \\ \star &{} I \\ \end{array} \right] ,~\left[ \begin{array}{cc} Y &{} I \\ \star &{} pI \\ \end{array} \right] \ge 0\),
\(~~~~~~~~~~~~~~~~~~~\bar{\gamma }>0,~p>0,~s>0,~and~v>0\)
3.9.3 Simulation Results
To illustrate the effectiveness of the proposed LFC \(H_{\infty }\) control problem satisfying performance index ‘\(\gamma \)’, the following two-area power system model has been considered. The area-1 is equivalent to a single generator and area-2 is equivalent to 4-interconnected generator units as in ([48]). The plant parameters are given as follows,
Area -1 (Parameters are in p.u):
\(T_{ch1}=0.3~sec,~T_{g1}=0.1~sec,~R_{1}=0.05,~D_{1}=1,~M_{1}=10,~k_{1}=0.5\), and
\(\frac{1}{T_{p1}}=\frac{D_{1}}{M_{1}},~T_{p1}=\frac{M_{1}}{D_{1}},~\frac{k_{p1}}{T_{p1}}=\frac{1}{M_{1}},~ k_{p1}=\frac{1}{D_{1}},~B_{1}=\frac{1}{R_{1}}+D_{1}\)
Area -2 (Parameters are in p.u):
\(T_{ch2}=0.17~sec,~T_{g2}=0.4~sec,~R_{2}=0.05,~D_{2}=1.5,~M_{2}=12,~k_{2}=0.5\), and
\(T_{p2}=\frac{M_{2}}{D_{2}},~ \frac{k_{p2}}{T_{p2}}=\frac{1}{M_{2}},~k_{p2}=\frac{1}{D_{2}},~B_{2}=\frac{4}{R_{2}}+D_{2}\)
Open-loop simulation: Without control input (i.e, \(u(t)=0\)) the system in (3.102) with \(d_{1}=0.1~sec\) and \(d_{2}=0.6~sec\) is simulated with constant load disturbances of 1 p.u in both the areas. It can be observed that the frequency deviations \(\Delta f_{1}(t)\) and \(\Delta f_{2}(t)\) of the system are unstable as shown in the Fig. (3.12). It must be mentioned here that the PI controllers are inherently involved in the respective areas of the system model (3.102), (see Fig. 3.11).
Closed-loop simulation: The designed \(H_{\infty }\) controller gains for the LFC problem are computed by solving the LMI conditions using ‘mincx’ optimization solver of LMI control toolbox ([17]).
One-term control: Solving the LMI in (3.110), one obtains the \(\gamma \) as 0.4493 and the corresponding gain matrix K as:
Delay-independent two-term control [33, 42]: Solving the LMI in (3.114) with the choice \(\sigma =1\) and \(\kappa =1\), the control gains are obtained as:
Remark 3.22
It is mentioned in the Remark 4.4 of [33] that, the direct implementation of the LMI (59) of Theorem 4.2 for the system considered in (50a) will yield smisleading result for computing the controller gain associated with the delayed term due to the fact that (1,1) entry of the LMI (59) does not contain a symmetric term associated with the variable V which in turn yields \(V=[0]\) and consequently \(K_{d}=VY^{-1}=[0]\), this fact can be observed in the result presented above for delay-independent two-term control.
To overcome this difficulty an iterative optimization procedure has been suggested in [33] by introducing some additional terms in the (1,1) entry of the LMI condition (3.114) to minimize the \(\gamma \). The drawbacks of this iterative algorithm are:
-
(i)
selecting the initial conditions for several scalar tuning parameters involved in the LMI (like \(\kappa \) and \(\sigma \))
-
(ii)
selecting the arbitrary initial Y matrix
-
(ii)
selecting predetermined tolerance for \(\parallel Y^{*}-Y^{j}\parallel < \delta \).
As these selections are arbitrary and has no specific guidelines, so one can conclude that the accuracy of the solution is not guaranteed immediately from the solution of this algorithm.
Also the result presented for PSS problem in [42] returned a \(K_{d}\) matrix whose elements are very small whereas the elements of the K matrix are relatively very large (of the order of \(10^{5}\)), the same trend of the gain matrices are observed in the results presented above (delay-independent two-term controller) for the LFC problem.
The above drawbacks of the delay-independent two-term controller design have been eliminated in the proposed delay-dependent two-term control algorithm (i) introducing an arbitrary finite delay ‘\(\tau \)’ in the feedback-loop that consequently avoids the limiting situation of delay-independent design (i.e, when state delay tends to infinity the feedback loop is still closed as ‘\(\tau \)’ is finite) and (ii) use of modified LMI conditions are established along with the solution of multi-objective optimization algorithm.
Proposed delay-dependent two-term control: Delay-dependent two-term \(H_{\infty }\) controller gains are obtained by solving the multi-objective optimization algorithm presented in Theorem 3.13. This yields controller gains as,
The corresponding \(\gamma \) is 4.0124.
Now, simulation results for one-term and delay-dependent two-term controllers with different load disturbances are compared in terms of performances. First, considering the unit-step load disturbance, the variations in frequency deviations in both the areas are shown in Fig. 3.13 whereas the control inputs are presented in Fig. 3.14. Next, the simulation results of the closed-loop system for time-varying disturbance are presented in Figs. 3.15 and 3.16. From these results, it is clear that the transient response of the proposed delay-dependent two-term controller is superior than the one-term controller and in both the cases the disturbance rejection capability appears to be nearly same at the steady-state condition.
Remark 3.23
A linear model of LFC problem for an interconnected power system with communication delay is considered with zero initial condition for the stabilization and disturbance rejection problem. A closed loop simulation study of proposed two-term controller for the same system under non-zero initial conditions is carried out, the result reveals that there is a tendency for the system to deteriorate the transient response little bit, but the disturbance rejection capability will not be lost i.e, the steady state response is similar to that under zero initial condition.
3.10 Conclusions
The first part of this chapter discusses stabilization and robust stabilization of a linear time-varying delay system with state delay in the feedback control law. Improved delay-dependent stabilization as well as robust stabilization conditions in an LMI and NLMI frameworks have been derived for the linear time-delay system. The proposed delay-dependent LMI based stabilization as well as robust stabilization conditions are formulated using both convex combination of LMIs and improved bounding technique along with the multi-objective optimization algorithm to compute the controller gains for a given delay upper bound. On the other hand, the NLMI based proposed delay-dependent stabilization condition (Theorem 3.5) is formulated with much lesser decision variables and could not yield delay upper bound estimate comparable to that of [12] while solving through cone-complementarity algorithm. It may be emphasized here that the extension of the NLMI stabilization condition (Theorem 3.5) for an uncertain TDS requires lesser bounding inequalities thus yielding improved robust stabilization results than that of [12]. Several numerical examples are considered to illustrate the effectiveness of the proposed delay-dependent stabilizing conditions to achieve improved delay upper bound and lesser control effort.
The last part of this chapter dealt with \(H_{\infty }\) state feedback controller for the solution of LFC problem of an interconnected power system with communication delays in an LMI framework. It must be mentioned at this stage that, the existing results of \(H_{\infty }\) state feedback controller design are all based on delay-dependent formulation with delayed states in feedback signals and however, these results have not been utilized to solve LFC problem yet. The \(H_{\infty }\) controller that has been applied so far for an LFC problem of a multi-area inter-connected power system is delay-independent one with decentralized control structures having (i) one-term control and (ii) two-term control. The proposed two-term \(H_{\infty }\) controller based on performance index ‘\(\gamma \)’ is delay-dependent formulation with respect to the feedback delays and not the state delays as opposed to other existing delay-dependent \(H_{\infty }\) controller designs. Simulation results of an LFC of a two-area inter-connected power system are presented to show the effectiveness of (i) the proposed two-term delay-dependent controller over delay-independent one in terms of the control effort, (ii) implementation of LMI conditions are less complex computationally compared to the results presented in [33, 42] and [48] and (iii) the superiority of the proposed two-term controller over one-term controller under different types of load-disturbances.
References
J.C. Shen, B.S. Chen, F.C. Kung, Memoryless stabilization of uncertain dynamic delay system: Ricatti equation approach. IEEE Trans. Autom. Control 36, 638–640 (1991)
S. Phoojaruenchanachai, K. Furuta, Memoryless stabilization of uncertain linear system including time-varying sate delay. IEEE Trans. Autom. Control 37, 1022–1026 (1992)
M.S. Mahmoud, N.F. Al-muthairi, Quadratic stabilization of continuous time system with the state delay and norm bounded uncertainties. IEEE Trans. Autom. Control 39, 2135–2139 (1994)
A. Trinh, M. Aldeen, Stabilization of uncertain dynamic delay system by memoryless state feedback controllers. Int. J. Control 56, 1525–1542 (1994)
A. Trinh, M. Aldeen, “Robust stabilization and disturbance attenuation for uncertain time-delay systems,” in European Control conference, 1993, pp. 0 – 0
X. Li, C.E. de Souza, Criteria for robust stability and stabilization of uncertain linear systems with state delays. Automatica 33, 1657–1662 (1997)
X. Li, C.E. de Souza, Delay-dependent robust stability and stabilization of uncertain linear delay system:a linear matrix inequality approach. IEEE Trans. Autom. Control 42, 1144–1148 (1997)
Y.Y. Cao, Y.X. Sun, C. Cheng, Delay-dependent robust stabilizion of uncertain systems with multiple state delays. IEEE Trans. Autom. Control 43, 1608–1612 (1998)
Y.S. Moon, P. Park, W.H. Kwon, Y.S. Lee, Delay-dependent robust stabilization of uncertain state delayed system. Int. J. control 74, 1447–1455 (2001)
E. Fridman, U. Shaked, An improved stabilization method for linear time-delay system. IEEE Trans. Autom. Control 47, 1931–1937 (2002)
E. Fridman, U. Shaked, Parameter dependent stability and stabilization of uncertain time-delay systems. IEEE Trans. Autom. Control 48, 861–866 (2003)
M.N.A. Parlakci, Improved robust stability criteria and design of robust stabilizing controller for uncertain linear time-delay system. Int. J. Robust Nonlinear Control 16, 599–636 (2006)
M.N.A. Parlakci, Delay-dependent stability and state feedback stabilization criterion for linear time delay system, in International Conference on Modeling and Simulation, Coimbator-Vol.2, 2007, pp. 963 – 968
M.N.A. Parlakci, Delay-dependent stability and \(H_{\infty }\) control: Constant and time-varying delays. Int. J. Control 76, 48–60 (2003)
K. Gu, S.I. Niculescu, Additional dynamics in transformed time-dealy systems. IEEE Trans. Autom. Control 45, 00–00 (2000)
E. Ghaoui, F. Oustry, M.A. Rami, A cone-complementary linearization algorithm for static output feedback and related problems. IEEE Trans. Autom. Control 42, 1171–1176 (1997)
P. Gahinet, A. Nemirovski, A.J. Laub, M. Chilali, LMI control toolbox users guide (Mathworks, Cambridge, 1995)
E. Fridamn, U. Shaked, A descriptor system approach to \(H_{\infty }\) control of linear time-delay systems. IEEE Trans. Autom. Control 47, 253–270 (2002)
S. Xu, J. Lam, Y. Zou, Delay-dependent guaranteed cost control for uncertain system with state and input delays. IEE Proc. Control Theory Appl. 153, 307–313 (2006)
T. Li, L. Guo, Y. Zhang, Delay-range-dependent robust stability and stabilization for uncertain systems with time-varying delay. Int. J. Robust Nonlinear Control 18, 1372–1387 (2008)
C.E. de Souza, X. Li, Delay-dependent robust \(H_{\infty }\) control of uncertain linear state-delayed systems. Automatica 35, 1313–1321 (1999)
V. Suplin, E. Fridman, U. Shaked, \(H_{\infty }\) control of linear uncertain time-delay systems-a projection approach. IEEE Trans. Autom. Control 31, 680–685 (2006)
R. Dey, S. Ghosh, G. Ray, A. Rakshit, State feedback stabilization of uncertain linear time-delay systems: A nonlinear matrix inequality appraoch. Numer. Linear Algebra with Appl. 18(3), 351–361 (2011)
R. Dey, G. Ray, S. Ghosh, A. Rakshit, Stability analysis for contious system with additive time-varying delays: A less conservative result. Appl. Mathematics Comput. 215, 3740–3745 (2010)
S. Niculescu, A.T. Neto, J.M. Dion, L. Dugard, Roust stability and stabilization of uncertain linear systems with state delay: Multiple delay case \({(I)}\), in IFAC symposium on Robust control Design, 1994
J.W. Ko, P.G. Park, Delay-dependent robust stabilization for systems with time-varying delays. Int. J. Control Autom. Sys. 7, 711–722 (2009)
D.D. Siljak, D.M. Stipanovic, A.I. Zecevic, Robust decentralized turbine/governor control using linear matrix inequalities. IEEE Trans. Power Sys. 17, 715–722 (2002)
P.P.K.J.C. Doyle, K. Glover, B.A. Francis, State-space solutions to the standard \(H_{2}\) and \(H_{\infty }\) control problems. IEEE Trans. Autom. Control 34, 831–927 (1989)
B.A. Francis, A course in \(H_{\infty }\) Control Theory (Springer Verlag, New York, 1987)
H.H. Choi, M.J. Chung, Observer-based \(H_{\infty }\) controller design for state delayed linear system. Automatica 32, 1073–1075 (1996)
S.W.K.J.H. Lee, W.H. Kwon, Memoryless \(H_{\infty }\) controller for state delayed systems. IEEE Trans. Autom. Control 39, 159–162 (1994)
S. Niclescu, C. E. D. Souza, J. M. Dion, L. Dugard, Robust \(H_{\infty }\) memoryless control of uncertain linera systems with time-varying delay, in Proceedings of 1995 Euoropean Control Conference, Rome, 1995, pp. 1814 – 1819
M.S. Mahmoud, M. Zribi, \(H_{\infty }\) controllers for linearized time-delay systems using LMI. J. Optim. Theory and Appl. 100, 89–112 (1999)
M.S. Mahmoud, M. Zribi, “Robust stabilization and \({H}_{\infty }\) controlfor uncertain linear time-delay system: An \(\text{LMI}\) approach,” in \(13^{th}\) IFAC World Congress, San Francisco, 1996, pp. 113 – 118
Y.Y. Cao, Y.X. Sun, J. Lam, Delay-dependent robust \({H}_{\infty }\) control for uncertain system with time-varying delays. IEE Proc. of CTA 145, 338–344 (1998)
X. Li, E. Fridman, U. Shaked, Robust \(H_{\infty }\) control of distributed delay systems with application to combustion control. IEEE Trans. Autom. control 46, 1930–1933 (2001)
G. Ray, A.N. Prasad, G.D. Prasad, Design of robust lfc for interconnected power system based on singular value decomposition method. Electric Power Syst. Res. 37, 209–219 (1996)
H. Bevrani, T. Hiyama, Robust decentralized \(\text{ PI }\) based \(\text{ LFC }\) design for time-delay system. Energy Conversion Manage. 49, 193–204 (2008)
T.C. Yang, H. Cimen, Q.M. Zhu, Decentralized \(\text{ LFC }\) design based on structured singular value. IEE Proc. Generation, Transm. Distribution 145, 7–14 (1998)
D. Rerkpreedapong, A. Feliachi, “Decentralized \(H_{\infty }\) load frequency control using lmi control toolbox,” in IEEE proceedings of the circuit and systems (ISCAS’03), 2003, pp. 411 – 414
D. Dotta, A.S. Silva, I.C. Decker, Wide-area measurements-based two-level control design considering signal transmission delay. IEEE Trans. Power Sys. 24, 208–216 (2009)
M. Zribi, M.S. Mahmoud, M. Karkoub, T.T. Lie, \(H_{\infty }\) controller for linearized time-delay power system. IEE proc. Generation Transm. Distribution 147, 401–403 (2000)
T. Ishii, G. Shirai, G. Fujita, Decentralized load frequency based on \(H_{\infty }\) control. Electr. Eng. Japan 136, 28–38 (2001)
A.Y. Sivaramakrishnan, M.V. Hariharan, M.C. Srisailam, Design of variable structure load frequency controller using pole placement technique. IEEE Trans. Autom. Control 14, 487–498 (1984)
C.T. Pan, C.M. Liaw, An adaptive controller for power system \(\text{ LFC }\). IEEE Trans. Power Sys. 14, 122–128 (1989)
E.A.A. Nedzad, N ERC compliant decentralized \(\text{ LFC }\) design using \(\text{ MPC }\). IEEE Power Eng. Soc. Gen. Meeting 2, 13–17 (2003)
S. Bhowmick, K. Tomsovic, A. Bose, Communication models for third party \(\text{ LFC }\). IEEE Trans. Power Sys. 19, 543–548 (2004)
X. Yu, K. Tomsovic, Application of linear matrix inequalities for load frequency control with communication delay. IEEE Trans. Power Sys. 19, 1508–1515 (2004)
H. Jiang, H. Cai, J.F. Dorsey, Z. Qu, Towards a globally robust decentralized control for large-scale power systems. IEEE Trans. Control Sys. Technol. 5, 309–319 (1997)
G.J. Li, T.T. Lie, C.B. Soh, G.H. Yang, Decentralized \(H_{\infty }\) control for power system stability enhancement. Electr. Power and Energy Sys. 20, 453–464 (1998)
R. Dey, S. Ghosh, G. Ray, A. Rakshit, \(h_\infty \) load frequency control of interconnected power system with communication delays. Electr. Power Energy Sys. 42, 672–684 (2012)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this chapter
Cite this chapter
Dey, R., Ray, G., Balas, V.E. (2018). Stabilization of Time-Delay Systems. In: Stability and Stabilization of Linear and Fuzzy Time-Delay Systems. Intelligent Systems Reference Library, vol 141. Springer, Cham. https://doi.org/10.1007/978-3-319-70149-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-70149-3_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70147-9
Online ISBN: 978-3-319-70149-3
eBook Packages: EngineeringEngineering (R0)