1 Introduction

Over the past years, chaos systems have been widely studied in various fields. In engineering applications, chaotic behavior is undesirable [1, 2] and should be regulated or suppressed to improve control performance. Chaos systems are often used as keys for secure communications or information processing because, although a chaos system is deterministic, its long-term behavior is impossible to predict [3]. Controlling the chaos systems is a real challenge because they are sensitive to initial conditions, highly nonlinear, irregular, and complex [4].

Recently, several types of controllers for the control and synchronization of chaos systems have been proposed: fuzzy sliding mode control [5–7], linear matrix inequality (LMI) based stabilization [8, 9], fuzzy disturbance observer [10], particle swarm optimization (PSO) based fractional fuzzy control [11], radial-neural-network-based control [12], finite time control using fractional calculus [13–19], and linear coupling and pragmatical adaptive tracking [20]. However, these approaches tend to require either a high level of mathematical background or heavy computing power, restricting their practical applications despite their high performance. Sometimes, field engineers find the complexity of the algorithm hard to handle or encounter tuning difficulties.

It is worth noting that time-delay control (TDC) is simpler in form and easier to implement for controlling and synchronizing chaos systems than the above-mentioned techniques. TDC was first introduced to control robot manipulators [21, 22]. TDC eliminates unknown dynamics and disturbance using time-delay estimation (TDE), which employs one-step delayed state variables and control input, and then applies the desired error dynamics [21–25]. With TDE, the control structure and the effect of tuning parameters are transparent to designers. TDC has been proved to be numerically efficient, practically effective in controlling and synchronizing chaos systems, and robust against parametric perturbation [26].

To further improve control and synchronization performance using TDE, we must first consider the characteristics of chaotic systems. Chaos systems are highly nonlinear and irregular; the state variables of chaos systems vary slowly for some time, but, sometimes, they change abruptly. The flow of unified chaos systems [27] is described as multiple orbits circulating around the stationary points [28]. The instance the center and size of the orbits are changed, the system dynamics tends to rapidly change. Hence, the approximation capability of TDE instantaneously weakens, degrading the control accuracy of TDC.

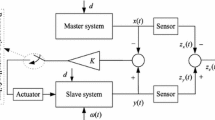
In this paper, we propose a supervising switching controller (SSC) for TDC to enhance the control and synchronization accuracy of chaos systems. SSC is designed to adjust the switching gain in proportion to TDE errors in order to counteract them. When the dynamics of a chaos system is rapidly changing, the supervising controller increases the switching gain. If the state variables move slowly, SSC decreases the switching gain towards zero. In our proposed technique, a saturation function is used instead of the signum function to avoid chattering the control input. We prove stability using the Lyapunov analysis method. Further, the results of a simulation showed that TDE-SSC is indeed effective and feasible. Thus, our proposed technique is a simple, numerically efficient, robust, and highly accurate solution for controlling and synchronizing chaos systems. The proposed technique is successfully implemented for stabilization of three-dimensional chaotic Arneodo systems [19, 29] via a single variable control input. Simulation results show the effectiveness and applicability of the proposed control technique.

To demonstrate the practicality of our proposed technique, we simulate a chaotic masking technique for secure communications [30]. A secret information signal is masked by a chaos system at the transmitter side, and then it is sent to a public communication channel. To recover the original information, the chaos system at the receiver side must be synchronized with the chaos system at the transmitter side. We show that the reconstruction accuracy depends significantly on the synchronization accuracy, and the proposed TDE-SSC indeed reduces loss of the original information compared with the TDC.

The remainder of this paper is organized as follows. In Sect. 2, we propose TDE-SSC for the control and synchronization of chaos systems, and prove that the closed-loop system is stable with the proposed TDE-SSC. Section 3 presents a simulation for the control of a Lorenz system [31]. Stabilization of three-dimensional chaotic Arneodo systems with a single variable control input is given in Sect. 4. In Sect. 5, the Lorenz system is synchronized with Lü’s system [32]. In Sect. 6, we present an example of chaotic masking used for secure communication. Finally, in Sect. 7 we conclude this paper.

2 Design of controllers for chaos systems

2.1 Time-delay control

Consider a class of nonlinear systems:

$$ \dot{\bf x}_{t}={\bf f}_{t}+{\bf u}_{t}, $$
(1)

where \({\bf x}_{t}=[x_{1,t},x_{2,t},\ldots ,x_{n,t}]^{T}=[x(t),x^{(1)}(t),\ldots, x^{(n-1)}(t)]^{T}\), \({\bf f}_{t}={\bf f}({\bf x}_{t})=[f_{1}({\bf x}_{t}),f_{2}({\bf x}_{t}),\ldots,f_{n}({\bf x}_{t})]^{T}\), and \({\bf u}_{t}={\bf u}({\bf x}_{t})=[u_{1}({\bf x}_{t}),u_{2}({\bf x}_{t}),\ldots,u_{n}({\bf x}_{t})]^{T}\). Suppose that \({\bf x}_{t}\in[t_{0},t_{f})\times D\subset R^{n}\) and \({\bf f}\) is a Lipschitz function on D. That is, there exist \({\boldsymbol{\delta}}^{*}=[\delta _{1}^{*},\delta_{2}^{*},\ldots, \delta_{n}^{*}]^{T}\) and \(0<\delta_{i}^{*}\) such that

$$\begin{aligned} &\sup_{{\bf x},{\bf y}\in D}\bigl \Vert f_i({\bf x})-f_i({\bf y})\bigr \Vert \leq \delta_{i}^*\cdot\|{\bf x}-{\bf y}\|. \end{aligned}$$
(2)

In order to design a controller for the system tracking a desired trajectory \({\bf x}_{m,t}\), we first estimate \({\bf f}_{t}\) from TDE as

$$ {\bf f}_t\approx{\bf f}_{t-L}=\dot{\bf x}_{t-L}-{ \bf u}_{t-L}, $$
(3)

where L is a small time delay, which is given as the sampling time of a control microprocessor. Using TDE, a TDC controller is designed as

$$ {\bf u}_t=\underbrace{-\dot{\bf x}_{t-L}+{\bf u}_{t-L} }_{\text{TDE of }-{\bf f}_t} +\underbrace{ \dot{\bf x}_{m,t}+{\bf K} {\bf e}_{t} }_{\substack{\text {Pole placement}\\\text{control}}}, $$
(4)

where \({\bf e}_{t}={\bf x}_{t}-{\bf x}_{m,t}\) and \({\bf K}\) is a matrix used to assign stable closed-loop poles. By substituting \({\bf u}_{t}\) in (1), the closed-loop system becomes

$$ \dot{\bf e}_{t}={\bf K} {\bf e}_{t}+{\bf f}_t-{\bf f}_{t-L}. $$
(5)

Hence, if the TDE error \(\|{\bf f}_{t}-{\bf f}_{t-L}\|\) is sufficiently small, then the closed-loop system follows the desired error dynamics characterized by the pole placement gain \({\bf K}\).

2.2 Design of TDE-SSC

In order to enhance the accuracy of TDC, we propose the following TDE-SSC:

$$ \begin{aligned} {\bf u}_t&=\underbrace{-\dot{\bf x}_{t-L}+{\bf u}_{t-L} }_{\text{TDE}} +\underbrace{ \dot{\bf x}_{m,t}+{\bf K} {\bf e}_{t} }_{\substack{\text {Pole placement}\\\text{control}}} +\underbrace{ { \bf r}_t }_{\text{SSC}}, \end{aligned} $$
(6)

where \({\bf r}_{t}=[r_{1,t},r_{2,t},\ldots,r_{n,t}]^{T}\) is the vector signal of SSC that compensates for the TDE error and is expressed as

$$\begin{aligned} r_{i,t}&=-\hat{\delta}_{i,t}\cdot\|{\bf x}_{t}-{\bf x}_{t-L}\|\cdot\text {sgn}\bigl({\bf e}^T_{t}{\bf Pb}_i\bigr), \end{aligned}$$
(7a)
$$\begin{aligned} \dot{\hat{\delta}}_{i,t}&=\gamma_i\cdot\|{\bf x}_{t}-{\bf x}_{t-L}\| \cdot\bigl|{\bf e}^T_{t}{ \bf Pb}_i\bigr|, \end{aligned}$$
(7b)

where \(0\leq\hat{\delta}_{i,t}\leq\hat{\delta}_{i}^{\max}\) is used to estimate the maximum gain, γ i >0 is an adaptation gain, \({\bf P}={\bf P}^{T}>0\) is the solution of the algebraic Riccati equation of \({\bf K}^{T}{\bf P}+{\bf P}{\bf K}+q\cdot{\bf I}=0\) for a given q>0 and an identity matrix \({\bf I}\), and

$$ {\bf I}= \left [ \begin{array}{cccc} {\bf b}_1;&{\bf b}_2;&\ldots&;{\bf b}_n \end{array} \right ]. $$
(8)

In (6), the high order term \(\dot{\bf x}_{t-L}\) can be calculated by numerical differentiation, as \(\dot{\bf x}_{t-L}\approx {({\bf x}_{t}-{\bf x}_{t-L})}/{L}\).

The switching gain in (7a) can be approximated as

$$ \|{\bf x}_t-{\bf x}_{t-L}\|\approx L\cdot\|\dot{\bf x}_{t}\|, $$
(9)

by using the finite divided difference method as given in [33]. If the system dynamics is rapidly changing, then the switching amplitude increases but if the state variables converge to the steady state, then the switching amplitude decreases to zero. Using this property of the proposed switching gain, we can suppress the chattering. A large γ i updates \(\hat{\delta}_{i,t}\) quickly but it tends to overestimate \(\delta^{*}_{i}\). On the other hand, a small γ i can avoid the overestimation but \(\hat{\delta}_{i,t}\) will only be slowly updated.

The following theorem shows that the tracking error of the closed-loop system converges to zero.

Theorem 1

The closed-loop control system (1)–(6), and (7a), (7b) converges in the sense that

$$\lim_{t\rightarrow\infty}\|{\bf e}_{t}\|=0. $$

Proof

Let us consider the following Lyapunov function V t :

$$ V_t=\frac{1}{2}{\bf e}^T_{t}{\bf Pe}_{t}+\frac{1}{2}\cdot\tilde{\boldsymbol{\delta}}_t^T{ \bf\varGamma}\tilde{\boldsymbol{\delta}}_t, $$
(10)

where \(\tilde{\boldsymbol{\delta}}_{t}=\hat{\boldsymbol{\delta}}_{t}-{\boldsymbol{\delta}}^{*}=[\tilde{\delta}_{1,t},\tilde{\delta }_{2,t},\ldots,\tilde{\delta}_{n,t}]^{T}\), \(\hat{\boldsymbol{\delta}}_{t}=[\hat{\delta}_{1,t},\hat{\delta}_{2,t},\ldots,\hat{\delta}_{n,t}]\), and \({\bf\varGamma}=\text{diag}(\gamma_{1}^{-1},\gamma_{2}^{-1},\ldots,\gamma _{n}^{-1})\) is a diagonal matrix. Then we have

$$\begin{aligned} \dot{V}_t\leq&-q\cdot\|{\bf e}_{t}\|^2+{\bf e}^T_{t}{\bf P}\cdot ({\bf f}_{t}-{\bf f}_{t-L}+{\bf r}_t ) +\tilde{\boldsymbol{\delta}}_t^T{\bf\varGamma}\dot{\hat{\boldsymbol{\delta}}}_t. \end{aligned}$$
(11)

By using (2), we obtain

$$\begin{aligned} \|f_{i,t}-f_{i,t-L}\|&\leq \delta_i^*\cdot\|{\bf x}_t-{\bf x}_{t-L}\| \\ &= (\hat{\delta}_{i,t}-\tilde{\delta}_{i,t} )\cdot\|{\bf x}_t-{\bf x}_{t-L}\|. \end{aligned}$$
(12)

Hence, it follows from (11) that

$$\begin{aligned} \dot{V}_t& \leq-q\cdot\|{\bf e}_{t}\|^2 \\ &\quad {}+\sum_{i=1}^n \bigl\{ \hat{ \delta}_{i,t}\cdot\|{\bf x}_t-{\bf x}_{t-L}\|\cdot|{ \bf e}^T_{t}{\bf Pb}_i|+{\bf e}^T_t{\bf Pb}_i\cdot r_{i,t} \bigr \} \\ &\quad {}+\sum_{i=1}^n \biggl[\frac{1}{ \gamma_i}\tilde{\delta}_{i,t} \\ &\quad {}\times \bigl\{\dot {\hat{ \delta}}_{i,t}-\gamma_i\cdot\|{\bf x}_t-{\bf x}_{t-L}\|\cdot\bigl|{\bf e}^T_{t}{\bf Pb}_i\bigr| \bigr\} \biggr]. \end{aligned}$$
(13)

Substituting (7a) and (7b) in the above equation yields

$$\begin{aligned} \dot{V}_t&\leq -q\cdot\|{\bf e}_{t}\|^2. \end{aligned}$$
(14)

Hence, there exists a positive constant c such that

$$ \int_{0}^t\|{\bf e}_\tau \|^2\,d\tau\leq c\cdot\bigl\{|V_0|-|V_t|\bigr\}\leq c \cdot |V_0|<\infty, $$
(15)

from which it follows that \(\lim_{t\rightarrow\infty}\int_{0}^{t}\|{\bf e}_{\tau}\|\,d\tau\) exists and is finite. By using Barbalat’s lemma [34], we can then show that \(\| {\bf e}_{t}\|\rightarrow0\) as t→∞. □

Remark 1

The boundary layer approach helps to reduce the high-frequency action in the proposed controller. That is, the switching boundary is smoothed out by replacing the signum function with a saturation function [35]:

$$ \text{sat} \biggl(\frac{x}{\epsilon} \biggr)= \begin{cases} x&\text{if}~|x|\leq\epsilon,\\ \text{sign}(x)&\text{if}~\epsilon<|x|, \end{cases} $$
(16)

where ϵ>0. Because ϵ is proportional to the upper bound of the synchronization error, it should be carefully selected.

3 Control of the Lorenz system

The Lorenz system to be controlled [26, 36–38] (Fig. 1) is expressed as follows:

$$ \begin{aligned} \dot{x}_{1,t}&=\sigma\cdot(x_{2,t}-x_{1,t})+d_{1,t}, \\ \dot{x}_{2,t}&=r\cdot x_{1,t}-x_{2,t}-x_{1,t} \cdot x_{3,t}+d_{2,t}+u_{2,t}, \\ \dot{x}_{3,t}&=x_{1,t}\cdot x_{2,t}-b\cdot x_{3,t}, \end{aligned} $$
(17)

where σ=10, b=8/3, and r=28. According to [28], the Lorenz system has a bounded, zero volume, and a globally attracting set. Hence, \(\|{\bf f}_{t}\|\) is bounded for all 0≤t. Let d 1,t =d 2,t =0.5⋅cos(5πt) be disturbances [37] and \({\bf x}_{0}=[10,10,10]^{T}\). The desired position trajectory is given as

$$ {\bf x}_{m,t}= \begin{cases} [8.50,8.50,27.09]^T,&5\leq t<10,\\ [12,12,54]^T,&10\leq t\leq20. \end{cases} $$
(18)

The control input u 2,t is designed as

$$\begin{aligned} u_{2,t}=-\dot{x}_{2,t-L}+u_{t-L}+k_1\cdot e_{1,t}+k_2\cdot e_{2,t}+r_{2,t}, \end{aligned}$$
(19)

where k 1=−10, k 2=−50, L=1 ms, γ=100, \({\bf P}=[2.61~0.05;~0.05~0.01]\), and q=1. The control input is applied to the system after 5≤t.

Fig. 1
figure 1

Phase portrait of the uncontrolled Lorenz system

Full size image

Figure 2 shows the state variables and the phase portrait of the controlled Lorenz system. It can be seen that the proposed controller drives the state variables of the Lorenz system to the desired position. The supervising controller reduces the switching gain to zero as x 1,t and x 2,t converge to the desired position x m,1=x m,2=8.50 (Fig. 3). It increases the switching gain again when the desired position is changed to x m,1=x m,2=12 after 10≤t s.

Fig. 2
figure 2

The controlled Lorenz system. The state variables converge to the desired position trajectory \({\bf x}_{m,1}^{T}=[8.5,8.5,27.09]\) for 5≤t≤10, and \({\bf x}_{m,2}^{T}=[12,12,54]\) for 10≤t≤20; a is the initial position; the controller activated at t=5 drives the state variables from b to c located at \({\bf x}_{m,1}\) and then to d located at \({\bf x}_{m,2}\)

Full size image
Fig. 3
figure 3

The control input u 2,t and the switching amplitude of SSC r 2,t ; the u 2,t is activated after 5≤t; and r 2,t impulsively increases when the desired position is changed

Full size image

4 Control of the Arneodo system

The Arneodo chaos system to be controlled [19, 29] is expressed as follows:

$$ \begin{aligned} \dot{x}_{1,t}&=x_{2,t}+\delta f_t+u_t, \\ \dot{x}_{2,t}&=x_{3,t}, \\ \dot{x}_{3,t}&=5.5x_{1,t}-3.5x_{2,t}-x_{3,t}-x_{1,t}^3, \end{aligned} $$
(20)

where δf t is a disturbance given as

$$\begin{aligned} \delta f_t&=0.12\sin(4t)x_{2,t}+0.18\cos(3t)x_{1,t} \\ &\quad {}+0.15 \cos(5t). \end{aligned}$$
(21)

In [19], it was shown that if x 1,t =0, then we have

$$ \begin{aligned} \dot{x}_{2,t}&=x_{3,t}, \\ \dot{x}_{3,t}&=-3.5x_{2,t}-x_{3,t}, \end{aligned} $$
(22)

which is asymptotically stable. The control input u t is designed as

$$ u_{t}=-\dot{x}_{1,t-L}+u_{t-L}+k\cdot x_{1,t}+r_t, $$
(23)

where \(-\dot{x}_{1,t-L}+u_{t-L}\) is to estimate and eliminate the disturbance δf t , and the desired dynamics k⋅x 1,t is applied to the system; the switching input r t , (7a), (7b), is designed to compensate the TDE error. The initial value of the system are given as x 1,0=0.15, x 1,0=−0.10, and x 3,0=0.20. The sampling time and gains are selected as L=1 ms, k=−0.01, γ=100, \({\bf P}=50\), and q=1. As a result, x 1,t converges to zero, and the closed-loop system is asymptotically stable.

Figure 4 shows that the state variables of the Arneodo system with TDE-SSC is asymptotically stable. The control input converges to zero as state variable reduces to zero (Fig. 5).

Fig. 4
figure 4

State variables of the Arneodo system: the TDE-SSC stabilizes the state variables to zero

Full size image
Fig. 5
figure 5

The control input of TDE-SSC

Full size image

5 Chaos synchronization between Lorenz and Lü systems

The Lorenz system to be synchronized with the Lü systems is given as

$$ \begin{aligned} \dot{x}_{1,t}&=(\sigma+\delta\sigma)\cdot (x_{2,t}-x_{1,t})+d_{1,t}+u_{1,t}, \\ \dot{x}_{2,t}&=(r+\delta r)\cdot x_{1,t}-x_{2,t}-x_{1,t} \cdot x_{3,t}+d_{2,t}+u_{2,t}, \\ \dot{x}_{3,t}&=x_{1,t}\cdot x_{2,t}-(b+\delta b)\cdot x_{3,t}+d_{3,t}+u_{3,t}, \end{aligned} $$
(24)

where δσ=0.1, δr=0.1, and δb=0.2 denote the corresponding perturbation of the parameters σ=10, r=28, and b=8/3, respectively; d 1=0.3⋅sin(x 2,t ), d 2=0.1⋅cos(x 1,t ), and d 3=0.2⋅sin(3⋅x 2,t ) are disturbances; and \({\bf x}_{0}=[0.2,0.6,1]^{T}\). The desired Lü system [32] is given as

$$ \begin{aligned} \dot{x}_{m,1,t}&=a\cdot(x_{m,2,t}-x_{m,1,t}), \\ \dot{x}_{m,2,t}&=-x_{m,1,t}\cdot x_{m,3,t}+c\cdot x_{m,2,t}, \\ \dot{x}_{m,3,t}&=x_{m,1,t}\cdot x_{m,2,t}-b\cdot x_{m,3,t}, \end{aligned} $$
(25)

where a=35, b=3, c=20, and \({\bf x}_{m,0}=[-10, -5,5]^{T}\). The control input \({\bf u}_{t}\) is designed as follows:

$$ {\bf u}_{t}=-\dot{\bf x}_{t-L}+{\bf u}_{t-L}+\dot{ \bf x}_{m,t}+{\bf K}\cdot{\bf e}_{t}+{\bf r}_{t}, $$
(26)

where \({\bf K}=\text{diag}(-50,-50,-50)\), L=1 ms, γ=25000, \({\bf P}=\text{diag}(0.01,0.01,0.01)\), and q=1. \(\dot{\bf x}_{t-L}\) is calculated by \(\dot{\bf x}_{t-L}\approx{({\bf x}_{t}-{\bf x}_{t-L})}/{L}\).

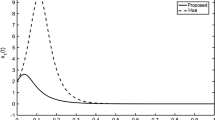
Figure 6 depicts the simulation results, which show that the Lorenz system is synchronized with the Lü system using TDE-SSC. From Fig. 7 it is clear that TDE-SSC improves the synchronization error \(\|{\bf e}_{t}\|_{2}\), where ∥⋅∥2 is a conventional 2-norm, compared with TDC [26]. Figure 8 shows that the supervising control adjusts the switching gain of r i,t roughly in proportion to the TDE error |f i,t −f i,t−L |.

Fig. 6
figure 6

The Lorenz system synchronized with the Lü system

Full size image
Fig. 7
figure 7

Synchronization errors \(\|{\bf e}_{t}\|_{2}\). The error of TDE-SSC is smaller than that of TDC

Full size image
Fig. 8
figure 8

Relationship between the TDE error and the switching gain. The switching gain is adjusted roughly in proportion to the TDE error for 9≤t≤11

Full size image

In order to reduce the chattering problem, the signum function is replaced with a saturation function, where ϵ=10−4. Figures 9 and 10 show that the chattering effect is substantially attenuated but Fig. 11 shows that the synchronization error is sufficiently small even though the signum function is replaced with the saturation function. Comparison of the root-mean-square (RMS) error of the TDE-SSC and TDC indicates that the TDE-SSC shows a better synchronization performance compared with TDC, as shown in Table 1.

Fig. 9
figure 9

Comparison of the control input of TDE-SSC with signum function and with saturation function. The control input chattering is reduced in u 3,t by using the saturation function

Full size image
Fig. 10
figure 10

The TDE error and SSC input r t . The amplitude of SSC with the saturation function is roughly proportional to the TDE error

Full size image
Fig. 11
figure 11

The synchronization errors corresponding to TDC, TDE-SSC with signum function, and TDE-SSC with saturation function

Full size image
Table 1 RMS synchronization errors for 1≤t≤20
Full size table

To show the relationship between the synchronization accuracy of the TDE-SSC and the time delay L, we repeat the above simulation with L=1, 10, 100, and 1000 ms. The synchronization error for 9≤t≤11 is plotted in Fig. 12 and its RMS error is given in Table 2, where we can see that the synchronization error was roughly proportional to the length of the time delay. In fact, as the length of the time delay increases, the TDE error f t −f t−L increases (Fig. 13). Then the increased TDE error disturbs the desired error dynamics more as shown in (5), resulting poor synchronization accuracy. It is obvious that TDE-SSC with shorter time delay guarantees higher accuracy but L cannot be infinitesimal due to CPU power limitation of the microprocessor or computer. In general, the sampling time of 1 ms is acceptable for various chaos applications.

Fig. 12
figure 12

Synchronization errors \(\|{\bf e}_{t}\|\) with L=1, 10, 100, and 1000 ms

Full size image
Fig. 13
figure 13

The TDE errors f i,t −f i,t−L with L=1, 10, and 100 ms for 9≤t≤11 (s)

Full size image
Table 2 RMS synchronization errors with L=1, 10, 100, and 1000 ms for 1≤t≤20
Full size table

6 Chaos synchronization for secure communications

In this section, we present a simulation example of a chaotic masking process as given in Fig. 14 [30]. For communication security, an information signal \({\bf m}_{t}\) is masked by adding a chaos signal \({\bf x}_{m,t}\) with a particular initial condition \({\bf x}_{m,0}\) at the transmitter side as

$$ {\bf v}_t={\bf m}_t+{\bf x}_{m,t}, $$
(27)

where \({\bf v}_{t}\) is the masked information signal. Figure 15 shows that the information signal m t =0.3sin(πt/2) is masked by adding the Lü chaos signal x m,2,t with \({\bf x}_{m,0}^{T}=[-10,-5,5]\). Then the masked information signal \({\bf v}_{t}\) is sent to a public communication channel. Any receivers in this public channel can access the masked information signal but the recovery of the original information \({\bf m}_{t}\) is only possible when the masking chaos signal \({\bf x}_{m,t}\) is known. If \({\bf x}_{m,t}\) information is available, then \({\bf m}_{t}\) can be recovered as

$$ {\bf m}_t={\bf v}_t-{\bf x}_{m,t}. $$
(28)

Since the chaos systems are unpredictable, it is impossible to estimate the parameters of the chaos system from the masked signal. An attempt to recover the original information with an arbitrarily selected parameters will fail because the chaotic signal is very sensitive to the initial condition and system parameters. Even if the initial value of the unmasking signal is slightly different from that of the original masking signal, the unmasked information is completely distorted: Fig. 16 shows the unmasked information \({\bf m}_{t}\) by subtracting the masking chaos signal with the original initial value and with a small perturbed initial value. Due to this property, the chaos system is known to be suitable for secure communication.

Fig. 14
figure 14

Structure of the chaos masking scheme

Full size image
Fig. 15
figure 15

The original signal and the corresponding masked signals masked by the Lü chaos system with \({\bf x}_{m,0}^{T}=[-10~-5~5]\)

Full size image
Fig. 16
figure 16

Unmasked information signals when there is no initial error and there is a small initial error

Full size image

For wireless communication environment, the masking signal \({\bf x}_{m,t}\) generated at the transmitter side is not directly available at the receiver side. Instead, the receiver generates the unmasking chaos signal \({\bf x}_{u,t}\) and synchronizes it with the masking signal \({\bf x}_{m,t}\) generated at the designated transmitter side. Then the original information is recovered by using the synchronized \({\bf x}_{u,t}\) as

$$\begin{aligned} \hat{\bf m}_t={\bf v}_t-{\bf x}_{u,t}, \end{aligned}$$
(29)

where \(\hat{\bf m}_{t}\) is the unmasked information signal using \({\bf x}_{u,t}\). Here, the synchronization accuracy is important to reduce the loss of the original information because \(\|{\bf m}_{t}-\hat{\bf m}_{t}\|=\|{\bf x}_{u,t}-{\bf x}_{m,t}\|\). Figure 17 presents the unmasked information signals, where \({\bf x}_{u,t}\) at the receiver side is the Lorenz system with \({\bf x}_{u,0}^{T}=[0.2,0.6,1]\) as given in the last section; \({\bf x}_{m,t}\) at the transmitter side is the Lü system with \({\bf x}_{m,0}^{T}=[-10,-5,5]\); and the TDC and the TDE-SSC with L=1, 10, and 100 ms are used for synchronization. As the length of the time delay L decreases, the loss of the original information also decreases because the controllers with a shorter time delay can provide better synchronization accuracy. Note that the results of the control system obtained by using the TDE-SSC are more robust and accurate than those of the system obtained by using the TDC.

Fig. 17
figure 17

The original information \(\hat{\bf m}_{t}\) unmasked by the synchronized Lorenz system. Compared with TDC, TDE-SSC improves the quality of the recovered signal even with a longer time delay

Full size image

7 Conclusion

In this paper, we showed that synergistic effects are achieved by combining TDE and SSC for control and synchronization of chaos systems. TDE is used to estimate nonlinearities in chaotic systems; however, relatively large TDE errors occur when the dynamics of chaos systems are rapidly changing. SSC is designed to adjust the switching gain in proportion to TDE errors in order to counteract the TDE errors. However, the use of the signum function in SSC introduces chattering in the control input. A saturation function can be used instead of the signum function in our proposed control technique. Simulation results show that the synchronization error of our proposed technique is smaller than that of TDC, and the chattering effect of our proposed control input can be substantially attenuated without severely deteriorating the synchronization performance of the signum function by using a saturation function. Our proposed technique is an easily understood, numerically efficient, robust, and accurate solution for the control and synchronization of chaos systems.