1 Introduction

To meet the demand of future space missions, the high-precision and high-stability attitude control of flexible spacecrafts has become a difficult and important problem [1]. However, unknown external and internal disturbances widely act on spacecrafts, and the inertia parameter is uncertain. Moreover, the structural vibrations of flexible appendages usually occur in rotational maneuvers [2], which seriously affect attitude control performance. These problems pose a huge challenge for attitude control system designers, and thus good control schemes are required to improve robust performance and control accuracy to solve these problems.

Over the last decades, many researchers have conducted extensive studies on the spacecraft attitude control system. Early in the 1980s, Breakwell [3] and Ben-Asher et al. [4] discussed the optimal control scheme of flexible spacecrafts for vibration suppression problems. Afterward, to improve robust performance in the presence of the unmodelled dynamics, disturbances, model uncertainty, and structural vibrations of flexible appendages, many control methods with robustness have been studied for the spacecraft attitude control system. The sliding mode control (SMC) was proposed to effectively design the attitude control system in [5–7]. However, the phenomenon of chattering caused by SMC has limited its practical applications [1]. Luo et al. [8] and Hu et al. [9] studied the \({H}_\infty \) control scheme systematically for the attitude control system to solve disturbance and vibration problems. In [10–12], a series of adaptive attitude controllers was also applied to address the tracking problem of spacecrafts in the presence of unknown control input saturation and external disturbances. Ali et al. [13] designed a nonlinear backstepping attitude controller using an inverse tangent-based tracking function for the attitude maneuver problem of spacecrafts. The feedback linearization (FBL) control approach, with its advantages of efficiency and simplicity in the nonlinearity system, was also used to improve attitude control performance in [14–16]. Moreover, a hybrid control scheme with the classic FBL and \(\mu \)-synthesis control method was designed for the control of flexible space structures that consider uncertainties and environmental disturbances [17].

As an effective disturbance attenuation control strategy, the nonlinear disturbance observer (NDO), which can estimate unknown disturbances and effectively compensate for them through feedforward, has attracted the attention of many researchers [18–22]. A composite controller with hierarchical architecture attained by combining the NDO and the SMC was studied in [19, 20], and stability of the closed-loop system was also established. Qian et al. [21] designed a flight control system for a hypersonic gliding vehicle with the help of the NDO. An NDO approach was developed in combination with the nonlinear dynamic inverse control law for a missile autopilot system [22]. The NDO can implement disturbance attenuation and is easy to combine with other traditional feedback control methods, such as the FBL, \(H_\infty \) , variable structure controller, and SMC.

In this paper, the NDO combined with the FBL approach is proposed to enhance the disturbance attenuation ability and robust performance of a flexible spacecraft attitude control. The NDO, which can estimate various unknown disturbances, is designed for feedforward compensation. Then, a FBL approach is adopted for the flexible spacecraft attitude control. Stability of the closed-loop system is analyzed using the Lyapunov method. The composite attitude control scheme improves the accommodation of uncertainties and unknown disturbances to give the spacecraft attitude control system high precision and high stability.

2 Problem formulation

To simplify the control problem, three-axis rotation is considered, and the spacecraft includes one rigid body and \(n\) flexible appendages. The rotational dynamics of the spacecraft with flexible appendages is described as follows [23]:

(1)
(2)

where \(\varvec{\omega } \) is the attitude angle velocity of the spacecraft body frame with respect to the inertia frame expressed in the body frame, \(\varvec{J}\) is the exact inertia moment of the spacecraft, \(\Delta \varvec{J}\) is the uncertainties of the inertia moment, \({\mathbf {F}}_\mathrm{sai}\) is the coupling matrix, \(\varvec{\eta } _i\) is the modal coordinate of the \(i\mathrm{th}\) flexible appendage \((i=1,2,{\ldots },n)\), \({\mathbf {u}}\) is the control torque, \({\mathbf {d}}_{0}\) is the disturbance torque produced by the space environment and unmodelled dynamics, \(\varvec{\xi } _i \) is the damping ratio of the \(i\mathrm{th}\) flexible appendage, and \(\varvec{\varOmega } _\mathrm{ai} \) is the modal frequency of the \(i\mathrm{th}\) flexible appendage; the symbol \({\mathbf {x}}^{\times }\) is a skew symmetric matrix acting on the vector \( {\mathbf {x}}= [x_{1}\; x_{2}\;x_{3}]^\mathrm{T}\) and

$$\begin{aligned} {\mathbf {x}}^{\times }=\left[ {{\begin{array}{ccc} 0&{} {-x_3 }&{} {x_2 } \\ {x_3 }&{} 0&{} {-x_1 } \\ {-x_2 }&{} {x_1 }&{} 0 \\ \end{array} }} \right] \end{aligned}$$
(3)

Combining (1) with (2), we obtain

$$\begin{aligned} {\mathbf {J}}\dot{\varvec{\omega } }&= -\varvec{\omega } ^{\times }\left( \varvec{J\omega } \right) +{\mathbf {u}}+{\mathbf {d}}_0 -\varvec{\omega } ^{\times }\left( {\sum _{i=1}^{n} {\mathbf {F}}_\mathrm{sai} \dot{\varvec{\eta } }_i } \right) \nonumber \\&\quad +\,{\mathbf {F}}_\mathrm{sai} \left( {2\varvec{\xi } _{i} \varvec{\varOmega } _\mathrm{ai} \dot{\varvec{\eta } }_i +\varvec{\varOmega } _\mathrm{ai}^2 \varvec{\eta } _i +{\mathbf {F}}_\mathrm{sai}^T \dot{\varvec{\omega } }} \right) \nonumber \\&\quad -\,\Delta {\mathbf {J}}\dot{\varvec{\omega } }-\varvec{\omega } ^{\times }\left( {\Delta \varvec{J\omega } } \right) \end{aligned}$$
(4)

From (4), we can consider

$$\begin{aligned} {\mathbf {d}}_1&= -\Delta {\mathbf {J}}\dot{\varvec{\omega } }+{\mathbf {F}}_\mathrm{sai} \left( {2\varvec{\xi } _i \varvec{\varOmega } _\mathrm{ai} \dot{\varvec{\eta } }_i +\varvec{\varOmega } _\mathrm{ai}^2 \varvec{\eta } _i +{\mathbf {F}}_\mathrm{sai}^T \dot{\varvec{\omega } }} \right) \nonumber \\&\quad -\varvec{\omega } ^{\times }\left( {\Delta \varvec{J\omega } } \right) -\varvec{\omega } ^{\times }\left( {\sum _{i=1}^{n} {\mathbf {F}}_\mathrm{sai} \dot{\varvec{\eta } }_i } \right) \end{aligned}$$
(5)

as the disturbance produced by the elastic vibration of the flexible appendages and model uncertainties, and \(\varvec{\omega }^{\times }({\mathbf {J}}\varvec{\omega } )\) as the nonlinear function.

We denote \({\mathbf {d}}={\mathbf {d}}_{0}+{\mathbf {d}}_{1}\) as the ‘equivalent’ disturbance, including external and internal disturbances, model uncertainties, and unmodelled dynamics. The rotational dynamics of the spacecraft can be rearranged in the following form:

$$\begin{aligned} {\mathbf {J}}\dot{\varvec{\omega } }=-\varvec{\omega } ^{\times }\left( \varvec{J\omega } \right) +{\mathbf {u}}+{\mathbf {d}} \end{aligned}$$
(6)

In this paper, the quaternion is used to express the attitude of the spacecraft, which is free of singularity and simpler to calculate due to the inexistence of transcendental functions [24]. The quaternion is defined by \({\mathbf {q}}=[q_{0} \; q_{1}\; q_{2}\; q_{3}]^\mathrm{T}=[q_{0}\;\hat{{\mathbf {q}}}^{T}]^\mathrm{T}\) satisfying \(\hat{{\mathbf {q}}}^{T}\hat{{\mathbf {q}}}+q_0^2 =1\), where \(q_{0}\) is the scalar component and \(\hat{{\mathbf {q}}}\in {\mathbf {R}}^{3\times 1}\) is the vector part. The attitude kinematics is given by [9]

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{q}_0 =-\frac{1}{2}\hat{{\mathbf {q}}}^{{\mathbf {T}}}\varvec{\omega }} \\ {\dot{\hat{{\mathbf {q}}}}=\frac{1}{2}\left( {\hat{{\mathbf {q}}}^{\times } \varvec{\omega } +q_{0} \varvec{\omega }} \right) } \\ \end{array} }} \right. \end{aligned}$$
(7)

3 Composite control system design

3.1 Nonlinear disturbance observer design

To design the NDO and the composite controller, the following assumptions are needed in this paper.

Assumption 1

In the spacecraft dynamics (6) and (7), all state variables can be measured, which implies that the attitude angle velocity \(\varvec{\omega } \) and the quaternion q are available for the NDO and composite controller design [8, 25].

Assumption 2

The elastic vibration and its velocity of flexible appendages are assumed to be bounded during the whole attitude control process [9]. Thus, \(\left\| {\dot{\varvec{\eta } }_i} \right\| \) and \(\left\| \varvec{\eta } _{i} \right\| \) are bounded.

Assumption 3

The ‘equivalent’ disturbance d is slow varying and bounded. Therefore, \(\dot{{\mathbf {d}}}\approx 0\) is reasonable.

To estimate the disturbance of system (6), we construct the disturbance observer as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\hat{{\mathbf {d}}}={\mathbf {z}}+{\mathbf {p}}(\varvec{\omega } )} \\ \dot{{\mathbf {z}}}=-{\mathbf {L}}(\varvec{\omega } )\left\{ {-{\mathbf {J}}^{-1}\left[ {\varvec{\omega } ^{\times }\left( {{\mathbf {J}}\varvec{\omega } } \right) } \right] +{\mathbf {J}}^{-1}{\mathbf {u}}} \right\} \\ \qquad -{\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}\left[ {{\mathbf {z}}+{\mathbf {p}}(\varvec{\omega } )} \right] \\ \end{array} }} \right. \end{aligned}$$
(8)

where \(\hat{{\mathbf {d}}}\) is the estimation of the merged disturbance \({\mathbf {d,\;p}}(\varvec{\omega } )\) is the nonlinear function, and \({\mathbf {L}}(\varvec{\omega })\) is the nonlinear observer gain function defined by

$$\begin{aligned} {\mathbf {L}}(\varvec{\omega } )=\frac{\partial {\mathbf {p}}(\varvec{\omega } )}{\partial \varvec{\omega } } \end{aligned}$$
(9)

Denoting \({\mathbf {d}}_\mathrm{e}\) as the disturbance observer error, we have

$$\begin{aligned} \dot{{\mathbf {d}}}_\mathrm{e} =\dot{{\mathbf {d}}}-\dot{\hat{{\mathbf {d}}}}\approx -\dot{\hat{{\mathbf {d}}}}=-\dot{{\mathbf {z}}}-\frac{\partial {\mathbf {p}}(\varvec{\omega } )}{\partial \varvec{\omega } }\dot{\varvec{\omega } }=-\dot{{\mathbf {z}}}-{\mathbf {L}}(\varvec{\omega } )\dot{\varvec{\omega } }\nonumber \\ \end{aligned}$$
(10)

Theorem 1

Considering the system (6) and the NDO system (8), when the nonlinear function \({\mathbf {p}}(\varvec{\omega } )\) satisfies

$$\begin{aligned} {\mathbf {p}}(\varvec{\omega } )=\left[ {{\begin{array}{l} {\lambda _{1} \left( {\omega _{1} +{\omega _{1}^{s_1 } }/{s_{1} }} \right) } \\ {\lambda _{2} \left( {\omega _{2} +{\omega _{2}^{s_2 } }/{s_{2} }} \right) } \\ {\lambda _{3} \left( {\omega _{3} +{\omega _{3}^{s_3 } }/{s_{3} }} \right) } \\ \end{array} }} \right] \end{aligned}$$
(11)

the NDO system (8) can track the disturbance d, and the estimation error \({\mathbf {d}}_\mathrm{e}\) can converge to the origin, where \(\lambda _i >0\) and \(s_{i}\) is the positive odd integer \((i=1, 2,3)\).

Proof

Select a candidate Lyapunov function (CLF) \(V_{1}\) as:

$$\begin{aligned} {\mathbf {V}}_1 =\frac{1}{2}{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {d}}_\mathrm{e} >0 \end{aligned}$$
(12)

Computing the derivative of \(V_{1}\), we have

$$\begin{aligned} \dot{{\mathbf {V}}}_1 ={\mathbf {d}}_\mathrm{e}^{T} \dot{{\mathbf {d}}}_\mathrm{e} ={\mathbf {d}}_\mathrm{e}^T \left( {-\dot{{\mathbf {z}}}-{\mathbf {L}}(\varvec{\omega } )\dot{\varvec{\omega } }} \right) \end{aligned}$$
(13)

Putting (8) into (13), we have

$$\begin{aligned} \dot{{\mathbf {V}}}_1&= {\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } )\left\{ {-{\mathbf {J}}^{-1}\left[ {\varvec{\omega } \times \left( \varvec{J\omega } \right) } \right] +{\mathbf {J}}^{-1}{\mathbf {u}}-\dot{\varvec{\omega } }} \right\} \nonumber \\&\quad +\,\,{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}\hat{{\mathbf {d}}} \end{aligned}$$
(14)

By substituting (6) into (14), (14) can be rewritten as

$$\begin{aligned} \dot{{\mathbf {V}}}_1&= -\,{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega }) {\mathbf {J}}^{-1}{\mathbf {d}}+{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}\hat{{\mathbf {d}}} \nonumber \\&= -\,{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega }){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \end{aligned}$$
(15)

From (9) and (11), we can obtain

$$\begin{aligned}&{\mathbf {L}}(\varvec{\omega } )=\nonumber \\&\left[ {{\begin{array}{ccc} {\lambda _1 \left( {1+\omega _1^{s_1 -1} } \right) }&{} 0&{} 0 \\ 0&{} {\lambda _2 \left( {1+\omega _2^{s_2 -1} } \right) }&{} 0 \\ 0&{} 0&{} {\lambda _3 \left( {1+\omega _3^{s_3 -1} } \right) } \\ \end{array} }} \right] \end{aligned}$$
(16)

Clearly, \({\mathbf {L}}(\varvec{\omega })\) is a positive definite matrix. As \({\mathbf {J}}^{-1}\) is also a positive definite matrix, when \({\mathbf {d}}_\mathrm{e}\ne \mathbf{0}\),

$$\begin{aligned} \dot{{\mathbf {V}}}_1 <0. \end{aligned}$$
(17)

The NDO system (8) can track the disturbance d, and the estimation error \({\mathbf {d}}_\mathrm{e}\) converges to the origin. The conclusion can then be obtained.

Further, from (13)–(15), we can obtain

$$\begin{aligned} \dot{{\mathbf {d}}}_\mathrm{e}=-{\mathbf {L}}(\varvec{\omega }){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \end{aligned}$$
(18)

Hence, it is easy to get the solution

$$\begin{aligned} {\mathbf {d}}_\mathrm{e}(t)={e}^{-{\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}(t-t_0 )}{\mathbf {d}}_\mathrm{e} (0) \end{aligned}$$
(19)

where \({\mathbf {d}}_\mathrm{e}(0)\) is the initial value of \({\mathbf {d}}_\mathrm{e}\). \(\square \)

Remark 1

It is obvious that the convergence rate and observation error accuracy of NDO depend on the parameters \(\lambda _{i} \) and \(s_{i}\). The larger the parameters \(\lambda _i\) and \(s_{i}\) are, the faster the convergence rate and the higher the observation error accuracy will be. However, too large parameters will lead to undesirable substantial chattering. Therefore, the parameters \(\lambda _{i}\) and \(s_{i}\) cannot be selected too large.

3.2 Composite controller design

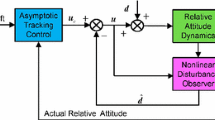
The composite controller scheme mainly consists of two parts as shown in Fig. 1: The inner loop is the merged disturbance estimation and feedforward compensation, and the outside loop is the FBL attitude controller.

Fig. 1
figure 1

Schematic of the composite attitude control system

Full size image

We denote \(\varvec{\omega }_\mathrm{e}\) as the error of the current attitude angle velocity with respect to the desired attitude angle velocity. Therefore,

$$\begin{aligned} \varvec{\omega } _\mathrm{e} =\varvec{\omega } -\varvec{\omega } _\mathrm{d} \end{aligned}$$
(20)

where \(\varvec{\omega }_\mathrm{d}\) is the desired attitude angle velocity expressed in the body frame.

The expression \(q_\mathrm{e} =[q_\mathrm{e0}\;\hat{{\mathbf {q}}}_\mathrm{e}^\mathrm{T}]^{T}\) is defined as the error quaternion of the current attitude with respect to the desired attitude. The attitude kinematics error can be written as [24]

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{q}_\mathrm{e0} =-\frac{1}{2}\hat{{\mathbf {q}}}_\mathrm{e} ^{{\mathbf {T}}}\varvec{\omega }_\mathrm{e}} \\ {\dot{\hat{{\mathbf {q}}}}_\mathrm{e} =\frac{1}{2}\left( {\hat{{\mathbf {q}}}_\mathrm{e} ^{\times }\varvec{\omega }_\mathrm{e} +q_\mathrm{e0} \varvec{\omega } _\mathrm{e} } \right) } \\ \end{array} }} \right. \end{aligned}$$
(21)

Generally, the classical FBL controller for system (6) and the attitude kinematic error system (21) without disturbances can be expressed as [15]

$$\begin{aligned} {\mathbf {u}}_\mathrm{c} =-k_1 \hat{{\mathbf {q}}}_\mathrm{e} -{\mathbf {K}}_2 \varvec{\omega } _\mathrm{e} +{\mathbf {J}}\dot{\varvec{\omega } }_\mathrm{d}+\varvec{\omega } ^{\times }\left( {\mathbf {J}}\varvec{\omega } \right) \end{aligned}$$
(22)

Therefore, the composite controller based on the FBL and NDO can be designed as

$$\begin{aligned} {\mathbf {u}}={\mathbf {u}}_\mathrm{c} -\hat{{\mathbf {d}}} \end{aligned}$$
(23)

Theorem 2

Considering the rotational dynamic system (6) and the attitude kinematic error system (21), choose the control law u as

$$\begin{aligned} {\mathbf {u}}=-k_1 \hat{{\mathbf {q}}}_\mathrm{e} -{\mathbf {K}}_2 \varvec{\omega } _\mathrm{e} +{\mathbf {J}}\dot{\varvec{\omega } }_\mathrm{d} +\varvec{\omega }^{\times }\left( {\mathbf {J}}\varvec{\omega } \right) -\hat{{\mathbf {d}}} \end{aligned}$$
(24)

and the NDO in the form of (8); then, the system (21) is in global asymptotic stability, where \(k_{1}>0\) and \({\mathbf {K}}_{2}>0\) are controller gains, \(\eta _{2}>1 /(4\eta _{1}),\eta _{1}\) is the minimum eigenvalue of \({\mathbf {L}}(\varvec{\omega }){\mathbf {J}}^{-1}\) in (15), and \(\eta _{2} \) is the minimum eigenvalue of \({\mathbf {K}}_{2}\) in (24).

Proof

Consider a candidate Lyapunov function (CLF) \(V\) as:

$$\begin{aligned} {\mathbf {V}}=k_{1} \left[ {\hat{{\mathbf {q}}}_\mathrm{e}^{T} \hat{{\mathbf {q}}}_\mathrm{e} +\left( {q_\mathrm{e0} -1} \right) ^{2}} \right] +\frac{1}{2}\varvec{\omega } _\mathrm{e}^{T} \varvec{J\omega }_\mathrm{e} +V_1 \end{aligned}$$
(25)

Similarly, by computing the derivative of \(V\) along the trajectories of (21), we can obtain

$$\begin{aligned} \dot{V}&= 2k_1 \left[ {\hat{{\mathbf {q}}}_\mathrm{e}^T \dot{\hat{{\mathbf {q}}}}_\mathrm{e} +\left( {q_\mathrm{e0} -1} \right) \dot{q}_\mathrm{e0} } \right] +\varvec{\omega } _\mathrm{e}^{T} {\mathbf {J}}\dot{\varvec{\omega } }_\mathrm{e} +{\mathbf {d}}_\mathrm{e}^{T} \dot{{\mathbf {d}}}_\mathrm{e} \nonumber \\&= k_1 \left[ {\hat{{\mathbf {q}}}_\mathrm{e}^{T} \left( {\hat{{\mathbf {q}}}_\mathrm{e} ^{\times }\varvec{\omega } _\mathrm{e} +q_\mathrm{e0} \varvec{\omega } _\mathrm{e} } \right) -\left( {q_\mathrm{e0} -1} \right) \hat{{\mathbf {q}}}_\mathrm{e} ^{\mathbf {T}}\varvec{\omega } _\mathrm{e} } \right] \nonumber \\&\quad +\,\varvec{\omega } _\mathrm{e}^{T} {\mathbf {J}}\dot{\varvec{\omega } }_\mathrm{e} +{\mathbf {d}}_\mathrm{e}^{T} \dot{{\mathbf {d}}}_\mathrm{e} \nonumber \\&= k_1 \hat{{\mathbf {q}}}_\mathrm{e} ^{T}\varvec{\omega } _\mathrm{e} +\varvec{\omega } _\mathrm{e}^{T} {\mathbf {J}}\dot{\varvec{\omega } }_\mathrm{e} +{\mathbf {d}}_\mathrm{e}^T \dot{{\mathbf {d}}}_\mathrm{e} \end{aligned}$$
(26)

In view of (13), (14), and (15), it shows that

$$\begin{aligned} \dot{V}=k_1 \hat{{\mathbf {q}}}_\mathrm{e}^{\mathbf {T}}\varvec{\omega } _\mathrm{e} +\varvec{\omega } _\mathrm{e}^{T} {\mathbf {J}}\dot{\varvec{\omega } }_\mathrm{e} -{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \end{aligned}$$
(27)

Substituting (20) into (27) gives

$$\begin{aligned} \dot{V}=k_1 \hat{{\mathbf {q}}}_\mathrm{e}^{T}\varvec{\omega } _\mathrm{e} +\varvec{\omega } _\mathrm{e}^T \left( {{\mathbf {J}}\dot{\varvec{\omega } }-{\mathbf {J}}\dot{\varvec{\omega } }_d } \right) -{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \end{aligned}$$
(28)

It is readily obtained from (6) that

$$\begin{aligned} \dot{V}&= k_1 \hat{{\mathbf {q}}}_\mathrm{e} ^{T}\varvec{\omega } _\mathrm{e} +\varvec{\omega } _\mathrm{e}^T \left( {{\mathbf {u}}+{\mathbf {d}}-\varvec{\omega } ^{\times }\left( \varvec{J\omega } \right) -{\mathbf {J}}\dot{\varvec{\omega } }_d } \right) \nonumber \\&-\,{\mathbf {d}}_\mathrm{e}^T {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \end{aligned}$$
(29)

By combining the control law (24) with (29), we have

$$\begin{aligned} \dot{V}&= k_1 \hat{{\mathbf {q}}}_\mathrm{e} ^{T}\varvec{\omega } _\mathrm{e} +\varvec{\omega } _\mathrm{e}^T ( {-k_1 \hat{{\mathbf {q}}}_\mathrm{e} -{\mathbf {K}}_{2} \varvec{\omega } _\mathrm{e} -\hat{{\mathbf {d}}}+{\mathbf {d}}} ) \nonumber \\&-\,{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \nonumber \\&= -\, \varvec{\omega } _\mathrm{e}^{T} {\mathbf {K}}_{2} \varvec{\omega } _\mathrm{e} +\varvec{\omega } _\mathrm{e}^{T} {\mathbf {d}}_\mathrm{e} -{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}{\mathbf {d}}_\mathrm{e} \end{aligned}$$
(30)

Further, the (30) can be transformed as

$$\begin{aligned} \dot{V}&\le -\eta _2 \left\| \varvec{\omega } _\mathrm{e} \right\| ^{2}+\left\| {\varvec{\omega } _\mathrm{e} } \right\| \left\| {\mathbf {d}}_\mathrm{e} \right\| -\eta _1 \left\| {\mathbf {d}}_\mathrm{e} \right\| ^{2} \nonumber \\&= -\left( {\eta _2 -\frac{1}{4\eta _1 }} \right) \left\| \varvec{\omega } _\mathrm{e} \right\| ^{2}-\left( {\frac{\left\| \varvec{\omega } _\mathrm{e} \right\| }{2\sqrt{\eta _1 }}-\sqrt{\eta _1 }\left\| {\mathbf {d}}_\mathrm{e} \right\| } \right) ^{2}\nonumber \\ \end{aligned}$$
(31)

When the following condition

$$\begin{aligned} \eta _2 -\frac{1}{4\eta _1 }>0 \end{aligned}$$
(32)

is satisfied,

$$\begin{aligned} \dot{V}\le 0 \end{aligned}$$
(33)

According to (33), it is obvious that \(V(t)\le V(0)\) and \(V\) is bounded. Then, we easily find \(\hat{{\mathbf {q}}}_\mathrm{e} ,q_\mathrm{e0},\varvec{\omega }_\mathrm{e},{\mathbf {d}}_\mathrm{e}\) are bounded form (25), that is, \(\hat{{\mathbf {q}}}_\mathrm{e}\in L_\infty ,\varvec{\omega } _\mathrm{e} \in L_\infty ,{\mathbf {d}}_\mathrm{e} \in L_\infty \). In view of (13)–(15), it is clear \(\dot{{\mathbf {d}}}_\mathrm{e}\in L_\infty \) . According to (21), it is obvious \(\hat{{\mathbf {q}}}_\mathrm{e}\in L_\infty \) and \(q_\mathrm{e0}\in L_\infty \). Therefore, \({\mathbf {u}}\in L_\infty \) is clear from (24). Further, it is reasonable \(\dot{\varvec{\omega } }\in L_\infty \) from (6), so \(\dot{\varvec{\omega } }_\mathrm{e}\in L_\infty \).

The time derivative of (30) is given by

$$\begin{aligned} \ddot{V}&= -\,2\varvec{\omega } _\mathrm{e}^{T}{\mathbf {K}}_2 \dot{\varvec{\omega } }_\mathrm{e} +\dot{\varvec{\omega } }_\mathrm{e}^{T} {\mathbf {d}}_\mathrm{e} +\varvec{\omega } _\mathrm{e}^{T} \dot{{\mathbf {d}}}_\mathrm{e} -2{\mathbf {d}}_\mathrm{e}^{T} {\mathbf {L}}(\varvec{\omega } ){\mathbf {J}}^{-1}\dot{{\mathbf {d}}}_\mathrm{e} \nonumber \\&\quad -\,{\mathbf {d}}_\mathrm{e}^{T} \dot{{\mathbf {L}}}(\varvec{\omega } ){\mathbf {J}}^{-1}{d}_\mathrm{e} \end{aligned}$$
(34)

It is clear that \(\ddot{V}\) is bounded. According to the Barbalat’s Lemma [26], \(\dot{V}\) can converge to zero as \(\hbox {t}\rightarrow \infty \). Then, the observer error \({\mathbf {d}}_\mathrm{e}\), the attitude angle velocity error \(\varvec{\omega }_\mathrm{e}\), and the attitude error \(\hat{{\mathbf {q}}}_\mathrm{e} \) can converge to origin as \(\hbox {t}\rightarrow \infty \). The composite controller can effectively track the desired attitude in the presence of various disturbances, model uncertainties, and unmodelled dynamics. The conclusion can then be obtained. \(\square \)

Remark 2

As can be seen from (19) and (31), the system convergence rate depends on \(\eta _{2} -1/(4\eta _{1} ),\lambda _i\), and \(s_{i}\). To keep the stability of the system, the parameter \(\eta _{2}>1/(4\eta _{1})\) should be satisfied first. It is obvious that the larger the parameters \(\eta _{2} ,\lambda _{i} \), and \(s_{i}\) are, the faster the system states can converge to the origin. However, too large \(\eta _{2} ,\lambda _{i}\), and \(s_{i}\) will lead to undesirable substantial chattering and require a high control input torque u, which is bounded in practice. Thus, the parameters \(\eta _{2} ,\lambda _{i} \), and \(s_{i}\) cannot be chosen too large.

4 Simulation results and discussion

In this section, the disturbance attenuation ability and robust performance of the proposed composite control algorithm for flexible spacecrafts, which combines the NDO and FBL, are discussed and demonstrated by numerical simulations. We give the instruction attitude angle and use the FBL approach, adaptive control approach, and FBL + NDO approach to compare the tracking performance of the control system.

In the simulation, the moment of inertia of the spacecraft is

$$\begin{aligned} {\mathbf {J}}=\left[ {{\begin{array}{lll} {420.8}&{} 0&{} 0 \\ 0&{} {410.6}&{} 0 \\ 0&{} 0&{} {690.7} \\ \end{array} }} \right] \hbox {kg}\cdot \hbox {m}^{2} \end{aligned}$$
(35)

Four bending modes are considered for the flexible appendages with \(\omega _{1}=0.05\,\hbox {Hz}, \omega _{2}=0.5\,\hbox { Hz}\), \(\omega _{3} =1.0\,\hbox {Hz}\), and \(\omega _{4} =2.0\,\hbox { Hz}\); damping ratio of \(\xi _{1} =0.05,\xi _{2} =0.05,\xi _{3} =0.05\), and \(\xi _{4}=0.05\); and the coupling coefficients of the four bending modes are \({\mathbf {F}}_\mathrm{sai}=[{\mathbf {F}}_\mathrm{sa1}\; {\mathbf {F}}_\mathrm{sa2}\;{\mathbf {F}}_\mathrm{sa3}\; {\mathbf {F}}_\mathrm{sa4}]\), where \({\mathbf {F}}_\mathrm{sa1}=[-0.28895\hbox {e}2 -0.39046\hbox {e}1 0.3986\hbox {e}-8]^{T}\), \({\mathbf {F}}_\mathrm{sa2}=[0.49894\hbox {e}-7 0.052219 -0.30009\hbox {e}2]^{T}\), \({\mathbf {F}}_\mathrm{sa3}=[0.16520 -4.3318 -0.87999\hbox {e}-7]^{T}\), and \({\mathbf {F}}_\mathrm{sa4}=[6.7877 0.22092\hbox {e}1 0.98309\hbox {e}-9]^{T}\). Suppose \(n_{0}\) is the orbit rate, then the space environmental disturbance torques acting on the spacecraft are supposed as follows [1]:

$$\begin{aligned} \left\{ {{\begin{array}{l} {d_{0x} =4.5\times 10^{-3}(3\cos n_0 t+1)} \\ {d_{0y} =4.5\times 10^{-3}(3\cos n_0 t+1.5\sin n_0 t)} \\ {d_{0z} =4.5\times 10^{-3}(3\sin n_0 t+1)} \\ \end{array} }} \right. \end{aligned}$$
(36)

Aside from the external merged disturbances, the disturbance form d can also represent the system uncertainties and unmodelled dynamics of a flexible spacecraft. That is, system uncertainties and unmodelled dynamics can be considered part of the disturbances, and the NDO approach can also estimate and compensate for them through feedforward. In the simulation, \(\pm 20\,\%\) perturbation of the nominal moment of inertial is considered [1]. The initial attitudes of the spacecraft are \([\varphi \; \theta \; \psi ] = [5^{\circ }\;5^{\circ }\;-5^{\circ }]\). The desired attitudes of the spacecraft are given by [11]

$$\begin{aligned} \left[ {{\begin{array}{l} {\varphi _d } \\ {\theta _d } \\ {\psi _d } \\ \end{array} }} \right] =\frac{\pi }{36}\sin \left( {\frac{\pi }{15}t} \right) \left[ {{\begin{array}{l} 0 \\ 1 \\ 0 \\ \end{array} }} \right] \end{aligned}$$
(37)

The composite control approach in Eq. (24), adaptive control approach in Ref. [25], and the pure FBL approach in Eq. (22) will control the flexible spacecraft attitude. We choose the same attitude controller parameters: \(k_{1}=27.3\) and \({\mathbf {K}}_{2}=\hbox {diag} (16.1, 28.5, 23.2)\). Meanwhile, the NDO parameters are chosen as: \(\lambda _{1} =2210,\lambda _{2} =2853,\lambda _{3} =2210\), \(s_{1}=s_{2}=s_{3}=3\); then the nonlinear function is \({\mathbf {p}}(\varvec{\omega })=[2210(\omega _{1}+{\omega _1^3 }/3)\; 2853(\omega _{2}+\omega _{2}^{3}/3)\) \(2210(\omega _{3}+{\omega _{3}^{3} }/3)]^{T}\). Suppose the maximum control torque for each axis generated by the actuators is \(u_\mathrm{max} <100(\hbox {N}\cdot \hbox {m})^{[\hbox {5}]}\). On the basis of the preceding formulation of our model, we can obtain the simulation results, respectively, as shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, and 10.

Fig. 2
figure 2

Time responses of disturbance \(d_\mathrm{x}\) and estimation

Full size image
Fig. 3
figure 3

Time responses of disturbance \(d_\mathrm{y}\) and estimation

Full size image
Fig. 4
figure 4

Time responses of disturbance \(d_\mathrm{z}\) and estimation

Full size image
Fig. 5
figure 5

Time responses of roll angle

Full size image
Fig. 6
figure 6

Time responses of pitch angle

Full size image
Fig. 7
figure 7

Time responses of yaw angle

Full size image
Fig. 8
figure 8

Time responses of FBL control torque

Full size image
Fig. 9
figure 9

Time responses of adaptive control torque

Full size image
Fig. 10
figure 10

Time responses of composite control torque

Full size image

Figures. 2, 3, and 4 indicate the time responses of the three-axis disturbances, disturbance estimations, and estimation errors. Based on the simulation results in Figs. 2, 3, and 4, all disturbances from the flexible appendages, space environment, and unmodelled dynamics can be effectively estimated by the NDO, where the estimation error is \(<\)3.2 % of the practical disturbance for the roll axis, that for the pitch axis is \(<\)2.8 %, and that for the yaw axis is \(<\)2.1 %. The effects of the disturbances on the flexible spacecraft are reduced to the lowest by the NDO through feedforward compensation.

Under the same simulation conditions, Figs. 5, 6, and 7 show that all spacecraft attitude angles have better dynamic response performance controlled by the FBL + NDO composite controller. Moreover, the attitude tracking accuracy and attitude stabilization are improved compared with those generated by the pure FBL approach and the adaptive approach in the presence of various disturbances. The roll angle tracking error is \(<8\,\times \,10^-5^{\circ }\), the pitch angle tracking error is \(<1.5\,\times \, 10^{-3^{\circ }}\), and the yaw angle tracking error is \(<3\,\times \,10^{-6^{\circ }}\).

As demonstrated in Figs. 8, 9, and 10, the composite control torque is larger at the beginning of the simulations than the FBL control torque and the adaptive control torque. The reason is that the composite controller can estimate and compensate for the disturbances. This reason also explains how the FBL + NDO approach has better dynamic response performance than the FBL approach and adaptive approach.

5 Conclusions

A composite control approach combining the NDO with the FBL is proposed for the attitude control system of flexible spacecrafts to enhance disturbance attenuation ability and robust performance. The NDO is used to estimate various unknown disturbances and compensate for them through feedforward. The FBL controller can effectively accomplish attitude control in the presence of various disturbances. Simulation results demonstrate that the NDO can estimate the disturbance and reduce the effect of the disturbances on flexible spacecrafts through feedforward compensation. The composite controller can improve robust dynamic performance and attitude control accuracy.