1 Introduction

Use of high-power-density permanent magnet synchronous motors (PMSM) in hybrid electric vehicle (HEV) presents a promising potential. This is due to attractive features such as high torque density, high efficiency, small size, fast response and reliable operation of these motors [1, 2]. In general, PMSM used for HEV are typical electromechanical coupling systems. Operation quality has a direct impact on performance and stability of driveline systems.

Installation deviation, mass eccentricity and bearing faults inevitably lead to rotor eccentricity. This is due to the mechanical connection between the rotor and gear mechanism. An asymmetric air gap results in non-uniform magnetic fields, where a transversal excitation referred to as unbalanced magnetic pull (UMP) is generated [3–5]. Unbalanced electromagnetic forces increase as eccentricity of the rotor increases, which in turn further increases the eccentricity. This leads to an unstable mechanical and magnetic coupling and is the cause for vibrations [6]. Changing magnitude of the supply current and frequency can be used to vary the coupling. When the magnitude of the current increases at higher supply frequencies, electromagnetic fields transfer energy into the mechanical system, which may lead to self-excited vibrations and rotor dynamic instability [7]. Typically, PMSM for HEV are operated over a wide range of speeds, using inverters to vary line frequency. Effects due to mechanical and magnetic coupling are significant in motors operating close to the first flexural critical speed. Due to this fact, it is important to take into account instability regions while designing the rotor, to avoid these instability regions, which lie within the range of operation speeds. In addition, with increase in operating power of the PMSM used in HEV, the problem arising due to nonlinear vibrations induced by the magnetic field becomes more serious [1]. Consequently, it is essential to analyze the nonlinear vibrations and instability taking into consideration the mechanical and magnetic coupling effects, which are of theoretical significance in the mechanical design of PMSM for HEV and fault diagnosis.

Determination of precise UMP has been a topic of an intensive research and has been reported extensively in the literature over the last several decades. UMP can be computed precisely using finite element analysis [1, 8, 9]. However, this approach is computationally expensive and is unable to provide an insight into the origin of UMP along with the key factors that influence it. Various research groups have focused on theoretical formulation of UMP and its effects on rotors in electric machines. Smith and Dorrell [10] put forward a model for assessing UMP due to rotor eccentricity for cage induction motors that take into account axial variation in the eccentricity. Guo et al. [11] analytically expressed nonlinear UMP using a range of pole pairs under no-load conditions to characterize vibration in a hydro-generator rotor. They further characterized the influences of the UMP and eccentric forces on Jeffcott rotor dynamics. Gustavsson et al. [12, 13] and Yang et al. [14] calculated UMP by considering eccentricity and axis change in a hydro-generator rotor and analyzed rotor stability and imbalance response. Huang et al. [15] investigated periodic motion, quasi-periodic motion and chaotic motion of a generator for different rotor eccentricities.

The research mentioned above focused on large-scale hydro-generators. For a permanent magnet machine, even without excitation, UMP exists due to the magnets; essentially, in this machine, UMP will increase with load and result in additional vibrations. Meanwhile, in a PMSM for HEV, there is an internal combustion engine in close proximity, operating together in a complementary manner. This gives rise to a multitude of operational and vibration frequencies that are picked up by the internal combustion engine. In addition, surface conditions of the roads act as an excitation source, which varies with the velocity of the HEV. The rotor may pick up these vibrations when the vehicle is in motion. The external disturbances act as a force at variable frequencies that can act on the rotor. Although several groups [4, 16–18] have reported on UMP from the electrical perspective, very few groups [19–21] have presented a UMP model from a mechanical and dynamics perspective. Kim et al. [19] analyzed the vibration of a PMSM rotor by considering mechanical-magnetic coupling and the influence of magnetic coupling on rotor trajectory using the finite element transfer matrix method. Ede et al. [20] calculated and measured natural frequency of high-speed brushless PMSM rotor. Ha et al. [21] studied the influence of UMP on rotor vibration for switch reluctance motors and calculated the dynamic response of the motor rotor using step-by-step integration.

As pointed out in by Jiang et al. [22], mathematical stability analysis has limitations, but offers the best chance for understanding nonlinear phenomena to allow intelligent design modifications. Stability analysis is an important topic in qualitative theory of nonlinear differential equations. Various stability types, methods and conditions are motivated by standard approaches based on the classical Floquet theory and Routh–Hurwitz criteria [23–26].

The main objective of this paper is identification and characterization of nonlinear dynamics of the UMP constituents on the radial displacement of the rotor center inside the stator bore. Characteristics of the non-sinusoidal distribution of the PMSM air gap magnetic field are analyzed. Based on these characteristics, magnetic motive force (MMF) of the air-gap magnetic field was determined based on existing theories for armature winding and permanent magnets. The air-gap permeance of the eccentricity rotor is calculated with the Fourier series expansion method. Then, taking armature reaction into consideration, UMP of PMSM was calculated and validated using FEM. The simplest mechanical model in a rotating environment, which is the Jeffcott rotor, is used here to study the dynamic response of the UMP. Furthermore, this paper explores stability issues related to PMSM for HEV. The analysis approximates the nonlinear system from our model with an appropriate linear system. An eigenvalue-based stability analysis is used which offers insights into system design parameters. The change in the electromagnetic system is expressed by electromagnetic stiffness coefficient. Analytical and numerical methods were used to study dynamic response of the Jeffcott rotor under UMP and eccentric forces. In addition, vibration characteristic of the system response are studied using amplitude–frequency curves. The trajectory of the rotor center, vibrating characteristics and dynamic response caused by UMP are summarized.

2 Unbalanced magnetic pull

Electromagnetic vibration in an eccentric rotor is induced by radial electromagnetic force, which is an UMP [27]. The air-gap magnetic field is influenced by MMF and air-gap permeance. Therefore, it is essential to analyze MMFs and permeance.

For analysis of electromagnetic forces acting on the PMSM rotor, following assumptions were made: (a) In order to consider only vibration of the rotor, the stator is assumed to be the rigid body in comparison with the rotor. (b) Permeability of the rotor iron and the stator is infinite. (c) Surface of the rotor and stator are smooth in the axial direction. (d) Air-gap magnetic field distribution is sinusoidal.

2.1 Magnetic motive force of stator and rotor

Figure 1 represents the relative position between permanent magnets and the stator armature. Where, \(\alpha \) is the angle between the centerline of a predetermined stator tooth and a centerline of a permanent magnetic pole, i.e., the relative position between the stator and rotor.

Fig. 1
figure 1

Relative position between permanent magnets and stator armature

Full size image

According to magnetic circuit principle for permanent magnet motors [28], the permanent magnet can be regarded as a constant source of MMF. The fundamental MMF of surface permanent magnet motors can be expressed as:

$$\begin{aligned} F_\mathrm{r} \left( {t,\alpha } \right)&= F_\mathrm{rm} \cos \left( {\omega t-p\alpha } \right) \nonumber \\&= \frac{4}{\pi }\frac{B_\mathrm{r} h_\mathrm{m} }{\mu _0 }\sin \left( {\frac{\alpha _p \pi }{2}} \right) \cos \left( {\omega t-p\alpha } \right) \end{aligned}$$
(1)

where, \(F_\mathrm{rm}\) is the amplitude of the fundamental MMF for the permanent magnet rotor, \(p\) is the number of pole pairs, \(B_\mathrm{r}\) is the magnetic remanence for the permanent magnet material, \(\alpha _\mathrm{p}\) is the magnetic pitch/pole ratio, \(\mu _{0}\) is the air permeability, \(h_\mathrm{m}\) is the thickness of permanent magnet magnetization direction, and \(\omega \) is the electric angular frequency.

The stator winding MMF analysis for a permanent magnet motor is similar to that of induction motors. The PMSM for the HEV is supplied using a PWM voltage source; however, the armature current is an approximate three-phase symmetrical sinusoid waveform.

According to winding theory for electric machines, the fundamental MMF of A-phase winding can be expressed as [9, 28]:

$$\begin{aligned} f_{\phi 1} \left( {\alpha ,t} \right) =\frac{4}{\pi }\frac{\sqrt{2}NK_\mathrm{w1} }{2p}I_\mathrm{m} \cos \left( {p\alpha } \right) \cos \left( {\omega t} \right) \end{aligned}$$
(2)

where \(\alpha =0\) refers to the axis of the phase winding, \(N\) is the number of series turns per phase, and \(K_\mathrm{w1}= K_\mathrm{d1}K_\mathrm{p1}\), where, \(k_\mathrm{w1}\) is the fundamental winding distribution factor. For example, when the number of slots per phase is an integer, \(K_\mathrm{d1}\) and \(K_\mathrm{p1}\) are given by:

$$\begin{aligned} k_\mathrm{p1} =\sin \frac{y_1 }{\tau }\frac{\pi }{2}\quad \hbox { and }\quad k_\mathrm{d1} =\frac{\sin q\frac{\pi }{Q_\mathrm{s} }}{q\sin \frac{\pi }{Q_\mathrm{s} }} \end{aligned}$$
(3)

where, \(y_{1}\) is the pitch of a coil, \(\tau \) is the pole pitch, \(q=Q_\mathrm{s}/2pm\) is the number of stator slots per pole per phase, \(Q_\mathrm{s}\) is the total number of slots, and \(m\) is the number of phases.

Hence, MMF of a three-phase stator winding is obtained from Eqs. (2) and (3):

$$\begin{aligned} F_\mathrm{s} \left( {\alpha ,t} \right)&= F_\mathrm{sm} \cos \left( {\omega t-p\alpha -{\varphi } _0 } \right) \nonumber \\&= 1.35\frac{Nk_w }{2p}I_\mathrm{m} \cos \left( {\omega t-p\alpha -{\varphi } } \right) \end{aligned}$$
(4)

where, \(F_\mathrm{sm}\) is the amplitude of the fundamental MMF for the excitation current of the armature reaction current of the stator, respectively, and \({\varphi }\) is the inner power factor angle.

For the case of a PMSM under symmetrical load, resultant fundamental MMF of the air gap can be expressed as:

$$\begin{aligned} F_j \left( {\alpha ,t} \right)&= F_\mathrm{r} \left( {t,\alpha } \right) +F_\mathrm{s} \left( {t,\alpha } \right) \nonumber \\&= F_\mathrm{m} \cos \left( {\omega t-p\alpha -\beta } \right) \end{aligned}$$
(5)

where,

$$\begin{aligned}&F_j =\sqrt{F_\mathrm{sm} ^{2}+F_\mathrm{rm} ^{2}-2F_\mathrm{sm} F_\mathrm{rm} \sin {\varphi } }, \\&\cos \beta ={\left( {F_\mathrm{rm} -F_\mathrm{sm} \sin {\varphi } } \right) }/{F_\mathrm{rm}} \end{aligned}$$

2.2 Air-gap permeance

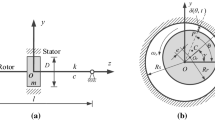
Figure 2 shows the cross section of a rotor rotating at a constant angular speed \(\varOmega \). The shadow area depicts the stator. Points \(O_\mathrm{r}\) and \(O\) refer to the geometrical centers of the rotor and stator, respectively. Figure 3 plots the Cartesian coordinate system xyz created using center \(O\) as the origin, where \(z\)-axis denotes the longitudinal coordinate of the rotor shaft, \(x\) and \(y\) represents the lateral coordinates of the rotor center. In this case, \(l\) is the length of the rotor shaft and \(R_\mathrm{r}\) is the outer radius of the rotor. The eccentricity is \(e\), and eccentricity can be static, dynamic or both.

Fig. 2
figure 2

Cross section of eccentric rotor

Full size image

Eccentricity is assumed to be identical along the longitudinal direction of the eccentric rotor. The air-gap length can be approximately expressed as

$$\begin{aligned} \delta \left( {\alpha ,t} \right) \approx \delta _0 -e\cos \left( {\theta -\theta _\mathrm{r} } \right) \end{aligned}$$
(6)

where \(\delta _{0}\) is the mean air-gap length of the machine.

The air-gap permeance can be expressed as a Fourier series [11]:

$$\begin{aligned} \varLambda \left( {\alpha ,t} \right)&= \frac{\mu _0 }{\delta \left( {\alpha ,t} \right) }=\frac{\mu _0 }{\delta _0 \left[ {1-\varepsilon \cos \left( {\alpha -\theta _\mathrm{r} } \right) } \right] } \nonumber \\&= \sum _{n=0}^\infty {\varLambda _n } \cos \left[ {n\left( {\alpha -\theta _\mathrm{r} } \right) } \right] \end{aligned}$$
(7)

where \(\varepsilon =e/\delta _{0}\) is the relative eccentricity and \(\mu _{0}\) is the air permeance.

Fig. 3
figure 3

Simply supported Jeffcott rotor system

Full size image

Fourier coefficients \(\varLambda _\mathrm{n}\) are given as

$$\begin{aligned} \varLambda _n =\left\{ \begin{array}{ll} \frac{\mu _0 }{\delta _0 \sqrt{1-\varepsilon ^{2}}} &{}\quad \left( {n=0} \right) \\ \frac{2\mu _0 }{\delta _0 \sqrt{1-\varepsilon ^{2}}}\left[ {\frac{1-\sqrt{1-\varepsilon ^{2}}}{\varepsilon }} \right] ^{n} &{}\quad \left( {n>0} \right) \\ \end{array} \right. \end{aligned}$$
(8)

Normalized magnitude of permeance can be represented by \(\bar{{\varLambda }}_n ={\varLambda _n \delta _0 }/{\mu _0 }\), and relationship between \(\bar{{\varLambda }}_n\) and relative eccentricity \(\varepsilon \) is shown in Fig. 3.

From Fig. 4, it can be seen that as the order \(n\) increases, amplitude of Fourier series decreases rapidly, and the DC component and the first-harmonic component are dominant. Simultaneously, amplitude of each Fourier series increases in relative eccentricity. When \(n>2\), magnitude of which is approximately equal to zero. Hence, if the eccentricity is assumed to be small, only the DC component, first-order and second-order components need to be taken into account.

Fig. 4
figure 4

Normalized air-gap permeance coefficient against eccentricity

Full size image

2.3 Model of unbalanced magnetic pull

After analyzing MMF and air-gap permeance, air-gap density distribution is given by [28]:

$$\begin{aligned} B_\mathrm{r} \left( {\alpha ,t} \right) =\mu _0 \frac{F}{\delta }=F_j \left( {\alpha ,t} \right) \varLambda \left( {\alpha ,t} \right) \end{aligned}$$
(9)

Substituting Eqs. (5) and (8) into Eq. (9), we can obtain Eq. (10) by keeping the first three terms of the infinite series. From Eq. (10), it can be seen that modulation of the harmonic MMF waves by air-gap permeance produces air-gap harmonic fields with different pole-pair numbers, and pole-pair number of PMSM for HEV is usually larger than 2.

$$\begin{aligned} B_\mathrm{r}&= \frac{1}{2}F_\mathrm{m} \left\{ 2\varLambda _0 \cos \left( {\omega t-p\alpha } \right) +\varLambda _1 \left[ \cos \left( \left( {p-1} \right) \alpha \right. \right. \right. \nonumber \\&\left. -\,\left( {\omega t-\theta _\mathrm{r} } \right) \right) +\cos \left( \left( {p+1} \right) \alpha -\left( {\omega t+\theta _\mathrm{r} } \right) \right) \nonumber \\&+\,\varLambda _2 \left[ \cos \left( {\left( {p-2} \right) \alpha -\left( {\omega t-2\theta _\mathrm{r} } \right) } \right) \right. \nonumber \\&\left. \left. +\,\cos \left( {\left( {p+2} \right) \alpha -\left( {\omega t+2\theta _\mathrm{r} } \right) } \right) \right] \right\} \end{aligned}$$
(10)

According to Maxwell stress tensor method, density of radial electromagnetic force acting on the rotor can be expressed as:

$$\begin{aligned} \sigma _\mathrm{r} =\frac{1}{2\mu _0 }\left( {B_\mathrm{r} ^{2}-B_t ^{2}} \right) \approx \frac{1}{2\mu _0 }B_\mathrm{r} ^{2} \end{aligned}$$
(11)

where \(B_\mathrm{r}\) is the radial component of air-gap flux density and \(B_{t}\) is the tangential component. Studies have shown that \(B_{t}\) is much smaller than \(B_\mathrm{r}\) [8]; consequently, the radial force density is determined mainly by radial flux density.

Analytical expression of radial electromagnetic force is obtained by the Maxwell stress tensor method [6, 11]

$$\begin{aligned} \left\{ {\begin{array}{l} F_{x} =\frac{R_\mathrm{r} l\pi F_\mathrm{m} ^{2}}{2\delta _0 }\frac{1}{1-\varepsilon ^{2}}\left( {\frac{1-\sqrt{1-\varepsilon ^{2}}}{\varepsilon }} \right) ^{3}\cos \theta _\mathrm{r} \\ F_{y} =\frac{R_\mathrm{r} l\pi F_\mathrm{m} ^{2}}{2\delta _0 }\frac{1}{1-\varepsilon ^{2}}\left( {\frac{1-\sqrt{1-\varepsilon ^{2}}}{\varepsilon }} \right) ^{3}\sin \theta _\mathrm{r} \\ \end{array}} \right. \end{aligned}$$
(12)

Since \([\varepsilon ^{2}]<1\), we can obtain the following expression of the power series by keeping the first two terms:

$$\begin{aligned} \frac{1}{1-\varepsilon ^{2}}\approx 1+\varepsilon ^{2} , \quad \sqrt{1-\varepsilon ^{2}}\approx 1-\frac{1}{2}\varepsilon ^{2} \end{aligned}$$
(13)

Substituting Eq. (13) into (12) and neglecting higher-order terms for order greater than three,

$$\begin{aligned} \left\{ {\begin{array}{l} F_{x} =k_\mathrm{en} \delta _0 \left( {\varepsilon +\frac{5}{4}\varepsilon ^{3}} \right) \cos \theta _\mathrm{r} \\ F_{y} =k_\mathrm{en} \delta _0 \left( {\varepsilon +\frac{5}{4}\varepsilon ^{3}} \right) \sin \theta _\mathrm{r} \\ \end{array}} \right. \end{aligned}$$
(14)

where \(k_\mathrm{en}\) is called electromagnetic stiffness coefficient and \(k_\mathrm{en} =\frac{R_\mathrm{r} l\pi \mu _0 F_\mathrm{m} ^{2}}{2\delta _0 ^{3}}\).

As seen from Eq. (14), orientation of the radial electromagnetic force points to the narrow air gap.

2.4 Comparison with finite element results

In order to validate this model, radial electromagnetic forces of PMSM for HEV due to static and dynamic eccentricity are analyzed using 2D FEA. A comparison between FEM and analytical results is presented in the following sections.

The main characteristic values used in this study are listed in Table 1. An application of this machine is the HEV drive system.

Table 1 Main parameters of PMSM
Full size table

Usually, two types of rotor eccentricities are considered: static and dynamic. Static eccentricity occurs when the rotor is not centered on the stator bore axis due to a misaligned bearing, wear or manufacturing tolerances, and it rotates on its own axis. Dynamic eccentricity is when the rotor is not centered in the stator bore, but rotates about the center of the stator bore. A dynamic eccentricity rotates at the same speed as the rotor. This could be caused by a bent shaft or manufacturing tolerances. Modeling methods of static and dynamic eccentricity are presented in [29]. The center of the stator core is shifted on the \(x\)-axis to simulate static eccentricity. When the rotor rotates, position of the narrow air gap is same. Center of rotor is moved to consider dynamic eccentricity. Since the rotating center is fixed, position of the narrow gap is rotating the rotor movement. Radial magnetic force on the air-gap contour is calculated by 2D FEA and analytical expression shown in Eq. (14).

Table 2 shows a comparison of unbalanced magnetic force obtained using FEA and the analytical model at rated load with static eccentricity. Maximum error between the FEM and analytical results is about 5 %. The results obtained by the two methods are in good agreement.

Table 2 Comparison of UMP at rated load with static eccentricity
Full size table

Direction of the unbalanced magnetic force needs to be determined. Figures 5 and 6 show the comparison of unbalanced magnetic force under 30 % eccentricity with static and dynamic eccentricity. Mechanical angle refers to the rotor rotation angle, \(F_{x}\) is the \(x\)-axis component of unbalanced magnetic force, and \(F_{y}\) is the \(y\)-axis component of unbalanced magnetic force. Figure 5 shows the unbalanced magnetic force characteristics with static eccentricity. Since the narrow air gap is located along \(x\)-axis component, i.e., \(\theta _\mathrm{r}=0\), consequently, \(F_{x}\) level is relatively high at static eccentricity, and \(F_{y}\) is approximately zero. Unbalanced magnetic force with dynamic eccentricity is shown in Fig. 6. Due to the position of the narrow air gap rotating with rotor movement, i.e., \(\theta _\mathrm{r}=\omega _\mathrm{r}t+\theta _{0}\) (\(\theta _{0}\) is the initial position angle. In this case, \(\theta _{0}=5^{{\circ }}\)), the direction of force rotates according to rotor position. Amplitude of unbalanced magnetic force is almost the same as static eccentricity due to similar eccentricity levels.

Fig. 5
figure 5

Unbalanced magnetic force with static eccentricity

Full size image
Fig. 6
figure 6

Unbalanced magnetic force with dynamic eccentricity

Full size image

3 Nonlinear dynamic model of rotor

In this section, nonlinear vibration of the rotor induced by UMP and residual mass unbalanced force are considered. The rotor of the PMSM for HEV is modeled as an ideal, simply supported Jeffcott rotor, as shown in Fig. 2. Further assumptions are made that the rotor is much shorter than the shaft and that the magnetic field in the air gap is uniformly distributed along the longitudinal direction \(Z\). Point G represents the gravity center of the rotor. Also, \(k\) and \(c\) are the rotor mechanical stiffness and mechanical damping contributed by the shaft to the rotor. The mass eccentric distance of the disk is \(a\). Differential equations for the radial vibration of the rotor can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} {m\ddot{x}+c}\dot{x}+kx=ma\varOmega ^{2}\cos \varOmega t+F_x \\ {m\ddot{y}+c}\dot{y}+ky=ma\varOmega ^{2}\sin \varOmega t+F_y \\ \end{array}} \right. \end{aligned}$$
(15)

where \(\varOmega \) is the rotating angular velocity of the rotor. For the PMSM, relationship between the rotating angular velocity \(\varOmega \), pole-pair number \(p\) and electrical frequency \(\omega \) is given by \(\varOmega = \omega /p\).

Substituting Eq. (14) into Eq. (15) leads to Eq. (16).

$$\begin{aligned} \left\{ {\begin{array}{l} {\ddot{x}+}2\xi \omega _n \dot{x}+\omega _n ^{2}\left[ {1-k_\mathrm{en} \left( {1{+}\frac{5}{4}\varepsilon ^{2}} \right) } \right] x =e\varOmega ^{2}\cos \varOmega t \\ {\ddot{y}+}2\xi \omega _n \dot{y}+\omega _n ^{2}\left[ {1-k_\mathrm{en} \left( {1{+}\frac{5}{4}\varepsilon ^{2}} \right) } \right] y = e\varOmega ^{2}\sin \varOmega t \\ \end{array}} \right. \end{aligned}$$
(16)

From Fig. 2, relationship between displacement of vibration and eccentricity is:

$$\begin{aligned} \left\{ {\begin{array}{l} x=e\cos \theta _\mathrm{r} =\delta _0 \varepsilon \cos \theta _\mathrm{r} \\ y=e\sin \theta _\mathrm{r} =\delta _0 \varepsilon \sin \theta _\mathrm{r} \\ \end{array}} \right. \end{aligned}$$
(17)

Equation (17) is put into a non-dimensional form by choosing

$$\begin{aligned}&\tau =\omega _n t, \quad \nu =\varOmega /{\omega _n }, \quad \alpha =a/{\delta _0 }, \nonumber \\&\omega _n ^{2}=k/m, \quad \xi =c/{\left( {2m\omega _n } \right) } \nonumber \\&K_n ={k_\mathrm{en} }/k, \quad X=x/{\delta _0 },\hbox { and } Y=y/{\delta _0 } \end{aligned}$$
(18)
$$\begin{aligned}&\!\!\!\! \left\{ {\begin{array}{l} {\ddot{X}+}2\xi \dot{X}+X-K_n \left( {X+\frac{5}{4}X^{3}+\frac{5}{4}XY{ }^2} \right) \\ \qquad =\alpha \nu ^{2}\cos \nu \tau \\ {\ddot{Y}+}2\xi \dot{Y}+Y-K_n \left( {Y+\frac{5}{4}Y^{3}+\frac{5}{4}X{ }^2Y} \right) \\ \qquad =\alpha \nu ^{2}\sin \nu \tau \\ \end{array}} \right. \end{aligned}$$
(19)

Equation (19) is the non-dimensional form of the equations of motion. From Eqs. (15) and (16), it can be seen that the external frequency, \(\varOmega \), is scaled by the natural frequency, \(\omega _\mathrm{n}\), of the system under consideration. This natural frequency, \(\omega _\mathrm{n}\), will vary with the stiffness of the system. From Eq. (19), it can be seen that the equation of vibration is nonlinear with mechanical and magnetic coupling terms.

4 Vibration response and stability analysis

4.1 Vibration response

Equation (19) is symmetrical; consequently, motion in the xy-plane can be investigated in complex coordinates defined by \(Z=X+iY\). Equation (19) can be rewritten in the complex form and is shown in Eq. (20)

$$\begin{aligned} \ddot{Z}+2\xi \dot{Z}+Z-K_n \left( {Z+\frac{5}{4}\bar{{Z}}Z^{2}} \right) =\alpha \nu ^{2}e^{i\nu \tau } \end{aligned}$$
(20)

In this paper, an averaging method is used to solve the periodic response [30]. Assuming the solution as \(\hbox {Z}= Be^{i(\nu \tau +{\varphi } )}\) and substituting it into Eq. (20), then the primary resonance solution is obtained.

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{B}=-\frac{K_n }{2\nu }\left( {\xi B\nu +\alpha \nu ^{2}\sin {\varphi } } \right) \\ \dot{{\varphi } }=\frac{K_n }{2\nu B}\left[ {\left( {K_n -\nu ^{2}} \right) B-\frac{5}{4}K_n B^{3}-\alpha \nu ^{2}\cos {\varphi } } \right] \\ \end{array}} \right. \end{aligned}$$
(21)

When the motor is operating in a steady state, \(\dot{B}=\dot{{\varphi } }=0\); consequently, the amplitude–frequency equation of nonlinear dynamic can be obtained:

$$\begin{aligned}&\frac{25}{16}K_n ^{2}\left( {B^{2}} \right) ^{3}+\frac{5}{2}K_n \left( {K_n -1+\nu ^{2}} \right) \left( {B^{2}} \right) ^{2} \nonumber \\&\quad +\left[ {4\xi ^{2}\nu ^{2}+} \right. \left. {\left( {1-\nu ^{2}} \right) ^{2}+K_n ^{2}-2K_n \left( {1-\nu ^{2}} \right) } \right] \nonumber \\&\quad B^{2}=\alpha ^{2}\nu ^{4} \end{aligned}$$
(22)

Meanwhile, phase frequency equation of synchronized motion is also obtained and is given as:

$$\begin{aligned} \tan {\varphi } =\frac{2\xi \nu }{\nu ^{2}-1+K_n \left( {1+\frac{5}{4}B^{2}} \right) } \end{aligned}$$
(23)

4.2 Stability condition for synchronous motion

The synchronous motion of rotor is governed by Eq. (21), and the steady-state solution is determined by amplitude \(B\) and phase \({\varphi }\). To investigate stability of the synchronous periodic motion, disturbed quantities are denoted as:

$$\begin{aligned} \tilde{B}=B-B_\mathrm{s}\quad \hbox { and }\quad \tilde{{\varphi } }={\varphi } -{\varphi } _\mathrm{s} \end{aligned}$$
(24)

Linearization of Eq. (21) at \(B=B_\mathrm{s}\) and \({\varphi }_\mathrm{s}\) yields

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\tilde{B}} \\ \dot{\tilde{{\varphi } }} \\ \end{array} \right\}&= \left[ {{\begin{array}{cc} {-\frac{K_\mathrm{n} }{2\nu }\left( {\frac{\partial F_1 }{\partial B}} \right) _\mathrm{s} }&{} {-\frac{K_\mathrm{n} }{2\nu }\left( {F_2 } \right) _\mathrm{s} } \\ {-\frac{K_\mathrm{n} }{2\nu B_\mathrm{s} }\left( {\frac{\partial F_2 }{\partial B}} \right) _\mathrm{s} }&{} {-\frac{K_\mathrm{n} }{2\nu B_\mathrm{s} }\left( {F_1 } \right) _\mathrm{s} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \tilde{B} \\ \tilde{{\varphi } } \\ \end{array}} \right\} \nonumber \\&= \mathbf{J}\left\{ {\begin{array}{l} \tilde{B} \\ \tilde{{\varphi } } \\ \end{array}} \right\} \end{aligned}$$
(25)

where

$$\begin{aligned} F_1 =8\xi \alpha \varpi , F_2 =4\left( {\frac{K_\mathrm{n} }{2}-1+\nu ^{2}} \right) B+\frac{5}{2}K_\mathrm{n} B^{3}, \end{aligned}$$

and \(()_\mathrm{s}\) stands for a quantity evaluated at the steady-state solution. \(\mathbf{J}\) is called Jacobian matrix. Eigenvalues of the Jacobian matrix are solved using the characteristic equation:

$$\begin{aligned} \lambda ^{2}+p\lambda +q=0 \end{aligned}$$
(26)

where

$$\begin{aligned} \left\{ {\begin{array}{l} p=K_\mathrm{n} \xi \\ q=\xi ^{2}\nu ^{2}+\frac{25}{16}\omega _\mathrm{n} ^{2}B_\mathrm{s} ^{4}-\frac{5\left( {1-\nu ^{2}} \right) }{K_\mathrm{n} }+\frac{\left( {1-\nu ^{2}} \right) ^{2}}{K_\mathrm{n} } \\ \end{array}} \right. \end{aligned}$$

Stability of the approximate solutions depends on the eigenvalues of the Jacobian matrix J according to the Routh–Hurwitz criterion [31]. Solutions are unstable if the real part of the eigenvalues are positive, i.e., \(p>0, q>0\).

5 Results and discussion

Some basic parameters for the system were selected as \(m=26.7\,\hbox {kg}, k=1.75\times 10^{6}\,\hbox {N/m}\). Other parameters are listed in Table 1 and calculated from the equations above.

5.1 Natural frequency of free vibration

Based on vibration theory, if nonlinear UMP is taken into account, natural frequency of the rotor system is expressed by Eq. (27). Natural frequency was found to be related to the electromagnetic stiffness coefficient and relative eccentricity.

$$\begin{aligned} f_\mathrm{n} =\frac{\omega _\mathrm{n} }{2\pi }=\frac{1}{2\pi }\sqrt{\frac{k-k_\mathrm{en} \left( {1+\frac{5}{4}\varepsilon ^{2}} \right) }{m}} \end{aligned}$$
(27)

Figure 7a shows the variation of natural frequency \(\omega _\mathrm{n}\) with relative eccentricity. A significant drop in the magnitude of \(\omega _\mathrm{n}\) was observed with increase in relative eccentricity. This indicates that UMP reduces flexural rigidity of the shaft–rotor system. Figure 7b illustrates the variation in natural frequency of rotor with respect to flux density \(B\).

Relative eccentricities are chosen as \(\varepsilon =0.25, \varepsilon =0.5\) and \(\varepsilon =0.75\). Monotonic reduction of \(\omega _\mathrm{n}\) was observed with increase in flux density. For \(\varepsilon =0.75\), decrease in natural frequency is faster than in the other two cases. It can be concluded that UMP acting on the rotor takes on a negative stiffness effect, which can be seen from Eq. (27). Consequently, drop in natural frequency beyond a certain threshold value would lead to resonance and unstable motion.

Fig. 7
figure 7

Variation of natural frequency

Full size image

5.2 Forced vibration response

In a vibrating state, amplitude of vibration is always equal to a nonzero solution. Both stable and unstable non-trivial solutions were observed. Stability of those solutions was analyzed to avoid sudden change in behavior as the parameter crosses a critical value called the bifurcation point. Sudden change in amplitude leads to catastrophic failure of the whole system. Graphical representation of the vibration amplitude for varying system control parameters was constructed.

Figure 8 illustrates a representative frequency response or a typical solution for various values of non-dimensional electromagnetic stiffness coefficient \(K_\mathrm{n}\), while keeping \(\alpha \) and \(\xi \) constant equal to 0.02 and 0.01, respectively. The value for \(K_\mathrm{n}=0\) corresponds to a linear forced vibration response. Meanwhile, \(K_\mathrm{n}>0\) correspond to a nonlinear forced vibration response. It can be seen that the effective nonlinearities of the system are of soft type. For a specific value of \(v\), the system has three solutions. Two of these solutions are stable and one is unstable. Therefore, both jumping phenomena and bifurcation occur in the system. For \(K_\mathrm{n}=0.75\) in Fig. 8, solid lines correspond to stable solutions, whereas the dotted lines correspond to unstable solutions. In the figure, arrows indicate the jumping phenomenon associated with each mode. It is worthy to note that amplitude of vibratory motion of the rotor increased with in frequency (upward sweep), and it finally reached a critical point D, which is called as saddle-node fixed bifurcation point. Any further increase in frequency beyond this point leads to a spontaneous amplitude increase to a point E, i.e., a sudden upward jump in the amplitude from lower to higher amplitude. Further increase in frequency, results in an amplitude change of the vibratory motion and it varies along the path EF. For downward sweep of the frequency, when the frequency of applied current is decreased from point F, amplitude response increases and finally reaches point C. A slight decrease in frequency at this critical point leads to a similar sudden upward jump as seen in the case of the upward sweep. Further decrease in frequency decreases the amplitude to a lower value, and a sudden downward jump is observed at point C. For specific parameters, stability analysis shows that motions on curves AB, BD and CED are stable and those on curve CD are unstable. Meanwhile, it is worthy to note that the resonance area augments and moves to the left as non-dimensional electromagnetic stiffness coefficient \(K_\mathrm{n}\) increases. It can be seen that by increasing \(K_\mathrm{n}\), amplitude decreases. Also, increasing \(K_\mathrm{n}\) results in bifurcation at a lower rotational speed.

Fig. 8
figure 8

Frequency response for different values of \(K_\mathrm{n}\) for constant values of \(\alpha \) and \(\upzeta \) constant, equal to 0.02 and 0.01, respectively

Full size image

Figure 9 demonstrates effect of damping on rotor dynamic behavior for three different values of viscous damping coefficient \(\zeta \). Increase in \(\xi \) resulted in a decrease in the amplitude response. For instance, a sharp decrease in the amplitude response from \(1.14 \delta _{0}\) to \(0.75 \delta _{0}\) was seen as \(\xi \) was increased from 0.005 to 0.01. With increase in viscous damping, amplitude response decreased due dominant terms containing the coefficients \(\alpha , k\) over the term function of \(\xi \). Meanwhile, the unstable zone reduced with increase in damping. Forward saddle-node bifurcation point and backward saddle-node bifurcation point disappear from the response curve for higher values of \(\xi \), and the system dynamics become stable.

Fig. 9
figure 9

Frequency response for different values of \(\xi \) for constant values of \(K_\mathrm{n}\) and \(\alpha \), equal to 0.25 and 0.02, respectively

Full size image

Figure 10 describes the behavior of the system with changing mass imbalance parameter \(\alpha \) changing from 0.01 to 0.05. It is worthy to note here that the pattern of response curve remains the same, but there is an increase in the amplitude response and the resonance area augments with increase in the magnitude of \(\alpha \) for the system. The backward bifurcation point starts at a lower frequency and the jump length increases with increase in the mass imbalance parameter \(\alpha \). The starting amplitude of the rotor reduces with decrease in \(\alpha \). The jumping phenomenon disappears altogether from the response curve for lower values of mass imbalance parameter \(\alpha \), and the system dynamics become stable.

Fig. 10
figure 10

Frequency response for different values of \(\alpha \) for constant values of \(K_\mathrm{n}\) and \(\xi \), equal to 0.25 and 0.01, respectively

Full size image

5.3 Numerical solutions

Response obtained using the average method is compared to results obtained by numerically solving the temporal Eq. (19). Runge–Kutta method was used in the present study. Standard fast Fourier transform (FFT) was adopted to analyze frequency composition of displacement responses to allow frequency component identification in the harmonic terms.

When the relative eccentricity is small, center of the rotor can be considered the same as the center of the stator at the initial state. A non-homogenous air gap will result when the rotor is rotating due to the mass eccentricity. Figure 11 shows the steady-state response with and without the UMP being considered for \(\varOmega =0.5 \omega _\mathrm{n}\), and conditions are similar to that shown in Fig. 8. The non-dimensional electromagnetic stiffness coefficient \(K_\mathrm{n}=0.25\). It can be seen that the vibration magnitude with UMP considered is 0.021 and is close to the analytical solution, 0.0205, obtained from Eq. (24). This indicates that the analytic solution is in good agreement with the numerical solution. Also, the vibration magnitude with UMP considered is larger in magnitude in comparison with the case when UMP was not considered. As mentioned above, the direction of UMP acting on the rotor of PMSM always points to the smallest air gap, making average trajectory size of the rotor larger. The displacement only contains a component of rotating frequency \(0.5 \omega _\mathrm{n}\).

Fig. 11
figure 11

Steady-state response for \(K_\mathrm{n}=0.25\). a Trajectory of the rotor center; b FFT for displacement

Full size image

In this case, due to the mass eccentricity, mixed eccentricity can occur. Figure 12 shows the steady-state response with UMP when \(\varOmega =0.5 \omega _\mathrm{n}\) and \(K_\mathrm{n}=0.75\). It can be seen that the shape of trajectory of the rotor center is not cyclical but similar to a heart-shaped curve. FFT shows that the dynamic response contains both the component of the rotating speed \(\varOmega \), along with the double-power frequency \(2\varOmega \). The amplitude of rotating speed \(\varOmega \) is 0.171 similar to the analytical solution of 0.175. However, the amplitude of the trajectory of the rotor center is approximately 0.23. Using a higher-order method can substantially reduce error in amplitude.

Fig. 12
figure 12

Steady-state response for \(K_\mathrm{n}=0.75\). a Trajectory of the rotor center; b FFT for displacement

Full size image

Therefore, it can be concluded that an averaging method aimed at primary resonance for weak nonlinear problems is accurate for use in the current study. Consequently, there is considerable reduction in efforts, since higher-order terms can be neglected without serious loss in the accuracy of the solution for the entire range of rotation speeds.

6 Conclusions

Based on the idea of modulating the fundamental MMF wave by air-gap permeance and Maxwell tensor method, an analytical expression of the UMP of PMSM for HEV was derived here. This was validated using FEM analysis. Predicted values for both two methods were in good agreement, and 2-D FE analysis results validated the analytical expression of the UMP.

UMP excitation was introduced into the equations of motion. Results show that the natural frequency reduced with increase in the flux density and relative eccentricity because of the negative stiffness effects caused by UMP.

An averaging method is adopted to determine the steady-state motion of the Jeffcott rotor under the influence of UMP. Stability analysis was based on the Routh–Hurwitz criterion and a numerical scheme using Runge–Kutta method. Effect of various design parameters on the mechanical behavior of the system was characterized. Numerical computations were used to validate analytic results. Following important results were achieved from this study:

  • Effective nonlinearity is of soft type for prime resonance under UMP excitation. Increasing \(K_\mathrm{n}\), i.e., UMP excitation, effect of nonlinearity on the frequency response curves was found to be dominant. The resonance area widens and moves toward the left. Working area of a PMSM used for HEV could easily move into the resonance area.

  • Saddle-node bifurcations point unstable zone were found. It is at these points that catastrophic failure of the system occurs.

  • For simple resonance condition, it was observed that increase in mass imbalance result in a increase in the amplitude response and a jump phenomenon occurs at lower frequency.

  • It was observed that the unstable zone reduced with increase in damping, and the amplitude response decreased. Saddle-node bifurcation points disappear from the response curve for a higher value of \(\xi \), and the system dynamics become stable.

  • An average method aimed at the primary resonance for weak nonlinear problems was accurate enough for the current study. Nonlinear vibration of rotor system of PMSM with double times of the rotating frequency could be excited using higher UMP excitation. Consequently, there is considerable reduction in efforts, since higher-order terms can be neglected without serious loss in accuracy of the solution for strong nonlinear problems.