1 Introduction

The design and development of electrostatically actuated microbeams/plates has been extensively studied by MEMS community to miniaturize, reduced cost, high durability and further improve the performance of transducer and actuators. The microresonator has been widely used over the years as a key component of pressure sensors, gyroscopes and RF system. At present, cantilever-based microresonators have been used as one of the most useful MEMS resonators in various applications of micro and nanotechnologies such as microswitches, sensors, microvalves and microgrippers.

In general, most of the MEMS devices are made up with either a thin beam or thin plate having cross section in the order of microns and length in the order of hundreds of microns. The air-gap between microbeam and stationary electrode is usually maintained at the range from \(10^{-3}\) to \(10^{-2}\) in order to establish an efficient electrostatic actuation. Within this range, most simple parallel capacitor formula is justified for calculating the distributed electrostatic force acting on microelement under the assumption that the surfaces of both deformable beam and electrode are locally parallel to each other. The integration of this assumption is appropriate in some way when the electrostatic actuated devices are modelled either as lumped spring–mass or as continuous microbeams model with small deflection. But, when this range is not necessarily small, typically of the order of \(10^{-2}\)–\(10^{-1}\) or even higher for designing small-size of electrically actuated devices, parallel capacitor formula becomes inappropriate and insufficient. In some applications, it is recommended to maintain a high gap-length ratio when a large deflection of the beam is anticipated that may lead a nonlinear electrostatic interaction between deformable beam and stationary electrode. In this circumstance, the employ of linear formulation is not appropriate for accurately simulating the dynamic performance as it does not consider the mid-plane stretching effect which exhibits a nonlinear electrostatic pressure distribution. A higher order approximation of electrostatic pressure is highly anticipated to build an accurate and realistic distribution of the electrostatic pressure acting on the microbeam. Several investigators have been attempting in a long period of time to improve the design characteristics by subsequent development of MEMS model and studying the associated dynamics. In the following subsection, a brief literature on the current research of modelling and dynamics of MEMS structures has been cited.

Luo and Wang [1] investigated analytically and numerically the chaotic motion in the certain frequency band of a MEMS with capacitor nonlinearity. Pamidighantam et al. [2] derived a closed-form expression for the pull-in voltage of fixed–fixed microbeams and fixed-free microbeams by considering axial stress, nonlinear stiffening, charge re-distribution and fringing fields. They carried out an extensive analysis of the nonlinearities in a micromechanical clamped–lamped beam resonator. Abdel-Rahman et al. [3] presented a nonlinear model of electrically actuated microbeams with consideration of electrostatic forcing of the air- gap capacitor, restoring force of the microbeam and axial load applied to the microbeam. The response of a resonant microbeam subjected to an electrical actuation has been investigated by Younis and Nayfeh [4]. Xie et al. [5] performed the dynamic analysis of a microswitch using invariant manifold method. They considered microswitch as a clamped–clamped microbeam subjected to a transverse electrostatic force. An analytical approach and resultant reduced-order model to investigate the dynamic behaviour of electrically actuated microbeam-based MEMS devices have been demonstrated by Younis et al. [6]. The natural frequency and responses of electrostatically actuated MEMS with time varying capacitors have been investigated by Luo and Wang [7]. Authors have demonstrated that the numerically and analytically obtained predictions were in good agreement with the findings obtained experimentally. A simplified discrete spring–mass mechanical model has been considered for the dynamic analysis of MEMS device. In Teva et al. [8], a mathematical model for an electrically excited electromechanical system based on lateral resonating cantilever has been developed. The authors obtained static deflection and the frequency response of the oscillation amplitude for different voltage polarization conditions. Kuang and Chen [9] and Najar et al. [10] studied the dynamic characteristics of nonlinear electrostatic pull-in behaviour for shaped actuators in micro-electro-mechanical systems (MEMS) using the differential quadrature method (DQM). Zhang and Meng [11] analysed the resonant responses and nonlinear dynamics of idealized electrostatically actuated microcantilever-based devices in micro-electro-mechanical systems (MEMS) by using the harmonic balance (HB) method. Rhoads et al. [12] proposed a microbeam device which couples the inherent benefits of a resonator with purely parametric excitation with the simple geometry of a microbeam. Krylov and Seretensky [13] developed higher order correction to the parallel capacitor approximation of the electrostatic pressure acting on microstructures taking into account the influence of the curvature and slope of the beam on the electrostatic pressure. The higher order approximation has validated through a comparison with analytical solutions for simple geometries as well as numerical results. Decuzzi et al. [14] investigated the dynamic response of a microcantilever beam used as a transducer in a biomechanical sensor. Here, Euler-Bernoulli beam theory was introduced to model the cantilever motion of the transducer. They also considered Reynolds equation of lubrication for the analysis of hydrodynamic interactions. A number of review papers [15–18] provided an overview of the fundamental research on modelling and dynamics of electrostatically actuated MEMS devices under working different conditions. Nayfeh et al. [19] studied that the characteristics of the pull-in phenomenon in the presence of AC loads differ from those under purely DC loads. Zhang et al. [20] furnished a survey and analysis of the electrostatic force of importance in MEMS, its physical model, scaling effect, stability, nonlinearity and reliability in details. Chao et al. [21] predicted the DC dynamics pull-in voltages of a clamped–clamped microbeam based on a continuous model. They derived the equation of motion of the dynamics model by considering beam flexibility, inertia, residual stress, squeeze film, distributed electrostatic forces and its electrical field fringing effects. Shao et al. [22] demonstrated the nonlinear vibration behaviour of a micromechanical clamped–lamped beam resonator under different driving conditions. They developed a nonlinear model for the resonator by considering both mechanical and electrostatic nonlinear effects, and the numerical simulation was verified by experimental findings. Moghimi et al. [23] investigated the nonlinear oscillations of microbeams actuated by suddenly applied electrostatic force including the effects of electrostatic actuation, residual stress, mid-plane stretching and fringing fields in modelling. Chatterjee and Pohit [24] introduced a nonlinear model of an electrostatically actuated microcantilever beam considering the nonlinearities of the system arising out of electric forces, geometry of the deflected beam and the inertial terms. Furthermore, one may use the review articles [15–18] as a source of information to the overall images about the electromechanical model of MEMS devices actuated by electrostatically and related dynamics. A detailed of perturbation techniques widely used to obtain the nonlinear solution of such kind of structures can be found in [25–27].

Nonetheless, after an extensive literature review, it has been realized that most of the previously carried out researches were dealing with eigenvalue problems exhibiting the vibrations around the deflection position of the microbeam and obtaining the natural frequencies and mode shapes by numerically solving the eigenvalue problem for various system parameters. It has been also observed that several researchers have investigated the nonlinear behaviour of micromechanical system with different boundary conditions under various driving conditions about its static beam positions [28–33]. A large number of researchers have used finite element method (FEM) simulations, analytical beam models, or lumped element models to analyse the resonating various microstructures. In addition, it has been noticed that many researchers are still considering either simply lumped spring–mass model or Euler–Bernoulli beam theory with small deflection assumption to carry out the theoretical and experimental investigation of dynamic performance of MEMS devices [34–36]. Therefore, so far enough investigation on the stability and bifurcation analysis of electrostatically driven cantilever-based MEMS device accounting the effect of mid-plane stretching and nonlinearly distributed electrostatic force between deformable microbeam and electrode under periodically applied AC potential difference has been lacking in the existing available works. Moreover, in order to enable a proper understanding, a better insight into the MEMS devices and an accurate simulation of mechanical behaviours, it is fairly important to consider a more realistic shape of the bending deflection of the microbeam and the development of resulting electrostatic pressure distribution.

Keeping these points in the mind and to the best of the author’s current knowledge, an attempt has been made to investigate the dynamic stability and bifurcation analysis of electrostatically actuated MEMS cantilever taking into account the effect of mid-plane stretching and nonlinear distribution of electrostatic pressure acting on the beam. Here primary aimed at author is to investigate the qualitative assessment of the bifurcations which usually demonstrate the locus of instability that expresses the boundary of the stable and unstable motions of the system. Even though the introduced equation of motion is similar to that of considered by Pohit and Chatterjee [24], the results obtained in the present work are completely different with the outcomes observed in the work [24] where only static and dynamic behaviour of the tip deflection of the microbeam for a wide range of applied DC voltage has been investigated. In the present work, pull-in results and its response on higher order correction of electrostatic force of the proposed model have been accomplished and compared with previously obtained finding. Furthermore, effect of the higher order correction of electrostatic pressure in the pull-in stability has also been investigated. In contrast to the work [24], spatio-temporal mathematical model of electrically excited cantilever-based MEMS resonator cantilever has been developed and further discretized into temporal equation of motion. The method of multiple scales has been used to analyse the stability and bifurcation of the steady-state responses. The effect of variation of air-gap, electrostatic forcing, and damping on the dynamic behaviour of the resonator has been investigated. The basin of attraction has been illustrated for predicting the specific steady state solution under certain initial condition in the region having multiple solutions. The solution demonstrated in this present work enables the designer to investigate the loss of stability in dynamical performance of the resonator or similar structures with respect to the electrostatic forcing.

Fig. 1
figure 1

a A pictorial diagram of microcantilever beam separated from a stationery electrode at a distance of \(d\), b a schematic diagram of a deflected resonator considering large displacements as the mid-plane stretching effect

Full size image

2 Problem formulation

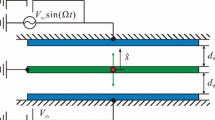
Figure 1 illustrates the pictorial diagram of a continuous microcantilever beam subjected to AC potential difference by stationery electrode. The microresonantor is modelled as a microcantilever beam in the present study as shown in Fig. 1. One end of the cantilever beam is clamped at a dielectric support and for sake of simplicity; it has assumed that the microcantilever beam has electrostatically actuated by a simple square root voltage signal \(V=\left[ {V_0 \cos \left( {\varOmega t} \right) } \right] ^{\frac{1}{2}}\) [11, 28, 29] with the objective of keeping apart the parametric effects from harmonic effects where \(V_0, \; \varOmega \) are the amplitude and frequency of AC polarization voltage, respectively. The equation of motion has been derived using Euler–Bernoulli beam neglecting the effect of variation of shear stresses across a section and rotary inertia of the beam. Under the potential difference, a transverse deflection \(v(x,t)\) and axial displacement component \(u(x,t)\) take place along the inertial direction \((x, y)\) of the displacement of the beam centroid axis. When subjected to potential difference, microbeam undergoes a large deformation and develops nonlinear deflection-dependent electrostatic pressure acting on the microcantilever beam. The variables \(v(x,t)\) and \(u(x,t)\) are pertained through a constraint equation originating from inextensibility condition \(( {1+\frac{\partial u}{\partial x}} )^{2}+( {\frac{\partial v}{\partial x}})^{2}=1\) of the beam. For large oscillation model, axial displacements \(u(x,t)\) can be explicitly written as \(u\left( {x,t} \right) =\int _0^\xi {\sqrt{1-{v}'^{2}}} \mathrm{d}x-\xi \) in term of transverse deflection \(v(x,t)\). Considering a small element at a distance\( x\) from fixed end (Fig. 1) along elastic line of the beam, bending moment \(M(s)\) can be expressed according to Euler–Bernoulli beam theory as

$$\begin{aligned} M\left( x \right) \approx E I\kappa (x). \end{aligned}$$
(1)

Here, \(E\) is elastic modulus, and \(I\) is cross-sectional moment of inertia, and nonlinear curvature \(\kappa (s)\) at any section is expressed as follows in terms of transverse deflection.

$$\begin{aligned} \kappa (x)&= \frac{\partial \phi }{\partial x} =\phi ^{/} = \left\{ {1-\left( {\frac{\partial v}{\partial x}} \right) ^{2}} \right\} \frac{\partial ^{2}v}{\partial x^{2}}\nonumber \\&\quad +\left( {\frac{\partial v}{\partial x}\frac{\partial ^{2}v}{\partial x^{2}}} \right) \frac{\partial v}{\partial x},\hbox { and }\sin (\phi )=\frac{\partial v}{\partial x}={v}^{\prime }.\nonumber \\ \end{aligned}$$
(2)

Here, \(\tan (\phi )\) is slope of the rotation \(\phi \). Taking time derivative of \(u\left( {x,t} \right) \), and \(\sin (\phi )\), expanding by using binomial expansion and eliminating terms of order higher than three one may yield the following expressions.

$$\begin{aligned} \ddot{u}\left( {x,t} \right) =\int \limits _0^\xi {\left\{ {\left( {{\dot{v}}^{\prime }} \right) ^{2}+{v}^{\prime }{\ddot{v}}^{\prime }} \right\} \mathrm{d}x}, \hbox { and } \dot{\phi }={\dot{v}}^{\prime }+\frac{1}{2}{v}^{\prime }{\dot{v}}^{\prime }. \end{aligned}$$
(3)

Hence, the potential energy due to elastic bending and kinetic energy, respectively, is expressed as

$$\begin{aligned} U_b&= \frac{1}{2}\int \limits _0^L {EI\left( {\frac{\partial \phi \left( {x,t} \right) }{\partial x}} \right) }^{2}\mathrm{d}x, \hbox { and } T\nonumber \\&= \frac{1}{2}\int \limits _0^L {\rho A\left\{ {\left( {\frac{\partial v\left( {x,t} \right) }{\partial t}} \right) ^{2}+\left( {\frac{\partial u\left( {x,t} \right) }{\partial t}} \right) ^{2}} \right\} } \mathrm{d}x.\nonumber \\ \end{aligned}$$
(4)

The potential energy stored in the beam owing to the development of higher order electrostatic pressure induced between microbeam and fixed electrode maintained at relatively large gap is expressed [12, 23, 24] as

$$\begin{aligned} U_\mathrm{e}&= -\frac{\varepsilon _0 wV^{2}}{2}\int \limits _0^L {\frac{\mathrm{d}x}{\left( {d_0 -v} \right) }}\nonumber \\&\quad -\frac{\varepsilon _0 wV^{2}}{2}\int \limits _0^L {\frac{1}{3\left( {d_0 -v} \right) }} \left\{ {\frac{\partial }{\partial x}\left( {\frac{d_0 -v}{L}} \right) } \right\} ^{2}\mathrm{d}x.\nonumber \\ \end{aligned}$$
(5)

Using the extended Hamilton’s Principle with considering Eqs. 1–5 and Taylor’s expansion, finally the beam governing equation is obtained as terms of order higher than three are eliminated in term of transverse deflection \(v\) [24].

$$\begin{aligned}&\!\!\!\rho A\ddot{v}+c\dot{v}\nonumber \\&+EI{{v}^{\prime \prime \,\prime \prime }}+EI\left[ {\left( {{v}^{\prime \prime }} \right) ^{3}+4{v}^{\prime }{v}^{\prime \prime }{v}^{\prime \prime \prime }+\left( {{v}^{\prime }} \right) ^{2}{{v}^{\prime \prime \,\prime \prime }}} \right] \nonumber \\&\quad +\rho A\left[ {{v}^{\prime }\int \limits _0^\xi {\left\{ {{\ddot{v}}^{\prime }{v}^{\prime }+\left( {{\dot{v}}^{\prime }} \right) ^{2}} \right\} \mathrm{d}\xi } } \right] \nonumber \\&\quad -\rho A\left[ {{v}^{\prime \prime }\int \limits _\xi ^L {\int \limits _0^\eta {\left\{ {{\ddot{v}}^{\prime }{v}^{\prime }+\left( {{\dot{v}}^{\prime }} \right) ^{2}} \right\} \mathrm{d}\xi } \mathrm{d}\eta } } \right] \nonumber \\&=\frac{1}{2}\frac{\varepsilon _0 bV^{2}}{\left( {d_0 -v} \right) ^{2}}+\frac{1}{2}\frac{\varepsilon _0 bV^{2}}{\left( {d_0 -v} \right) ^{2}}\nonumber \\&\quad \times \left[ {\frac{\left\{ {\left( {{v}^{\prime }} \right) ^{2}+2\left( {d_0 -v} \right) {v}^{\prime \prime }} \right\} }{3L^{2}}} \right] , \end{aligned}$$
(6)

with the boundary conditions i.e. essential or imposed and natural or dynamic boundary condition neglecting the higher order terms as

$$\begin{aligned} \begin{array}{ll} v\left( {x,t} \right) {=}\frac{\partial }{\partial x}v\left( {x,t} \right) \!=\!0&{} \hbox { at }x=0,L \\ EI\frac{\partial ^{2}}{\partial x^{2}}v\left( {x,t} \right) {=}\frac{\partial }{\partial x}\left( {EI\frac{\partial ^{2}}{\partial x^{2}}v\left( {x,t} \right) } \right) \!=\!0 &{}\hbox { at }x=0,L. \end{array} \end{aligned}$$
(7)

Here, \(v\) is transverse displacement of the beam. \(()^{\prime }\) and \(\mathop {(\,)}\limits ^{\cdot }\) stand for first derivative with respect to \(s\) and time, respectively. Here, \(EI, \rho , A, L, b\) and \(h\) are flexural rigidity, mass density, cross-sectional area, length, width and height of the beam, respectively. While \(\varepsilon _0\) is permittivity constant for free space, \(d_0\) is initial gap between microbeam and stationery electrode and \(c\) is effective viscous damping constant for this model. It may also be noted that \(\xi , \,\eta \) are the integration variables. Using nondimensional parameters \(w=( {v/{d_0 }}), s=( {x/l} ), \quad \tau =( {t/{l^{2}}})\sqrt{{EI}/{\rho A}},\, {\bar{\eta }}=( {\eta /l})\,\hbox { and} {\bar{\xi }}=( {\xi /l})\), the above Eq. (7) can be rewritten as

$$\begin{aligned}&\ddot{w}+\left( {c/\rho A} \right) \dot{w}+{{w}^{\prime \prime \, \prime \prime }}+\left( \delta \right) ^{2}\left[ \left( {{w}^{\prime \prime }} \right) ^{3}+4{w}^{\prime }{w}^{\prime \prime }{w}^{\prime \prime \prime }\right. \nonumber \\&\left. \quad +\left( {{w}^{\prime }} \right) ^{2}{{w}^{\prime \prime }}^{\prime \prime } \right] +\left( \delta \right) ^{2}\left[ {{w}^{\prime }\int \limits _0^{{\bar{\xi }}} {\left\{ {{\ddot{w}}^{\prime }{w}^{\prime }+\left( {\dot{{w}^{\prime }}} \right) ^{2}} \right\} \mathrm{d}{\bar{\xi }}} } \right] \nonumber \\&\quad -\left( \delta \right) ^{2}\left[ {{w}^{\prime \prime }\int \limits _{{\bar{\xi }}}^1 {\int \limits _0^{{\bar{\eta }}} {\left\{ {{\ddot{w}}^{\prime }{w}^{\prime }+\left( {\dot{{w}^{\prime }}} \right) ^{2}} \right\} \mathrm{d}{\bar{\xi }} } \mathrm{d}{\bar{\eta }}} } \right] \nonumber \\&\quad =\alpha \left( {1+2w+3w^{2}+\cdots } \right) \nonumber \\&\qquad -\frac{\alpha \delta }{3}\left( {2{w}^{\prime \prime }+2w{w}^{\prime \prime }+{w}^{\prime 2}+\cdots } \right) , \end{aligned}$$
(8)

with boundary conditions as

$$\begin{aligned} \begin{array}{ll} w=\frac{\partial }{\partial s}w=0&{}\hbox { at }s=0,1 \\ EI\frac{\partial ^{2}w}{\partial s^{2}}=\frac{\partial }{\partial s}\left( {EI\frac{\partial ^{2}w}{\partial s^{2}}} \right) =0&{} \hbox { at }s=0,1. \end{array} \end{aligned}$$
(9)

Here, \(\delta ={d_0 }/l,\hbox { and }\alpha =\frac{6\varepsilon _0 l^{4}V_0^2 }{Eh^{3}d_0^3 }\). The deflection of the microbeam undergoing an electrostatically actuation can be written as

$$\begin{aligned}&w\left( {s,\tau } \right) =\sum _{i=1}^n {\gamma _n \left( s \right) \varphi _n \left( \tau \right) },\,\nonumber \\&\quad n=1,2,3,\ldots ,\quad 0\le s\le 1. \end{aligned}$$
(10)

Here, \(\varphi _n \left( \tau \right) \) is the time modulation, and \(\gamma _n (s)\) is a companion function that satisfies the boundary conditions, both geometric and natural, and not necessarily the equation of motion. Here, companion function is assumed to be an eigenfunction \(\gamma _n (s)\) of the cantilever beam expressed as

$$\begin{aligned} \gamma _n \left( s \right)&\!=\!&\frac{\sin \left( {\beta _n } \right) \!+\!\sinh \left( {\beta _n } \right) }{\cos \left( {\beta _n } \right) \!+\!\cosh \left( {\beta _n } \right) }\left\{ {\cosh \left( {\beta _n s} \right) \!-\!\cos \left( {\beta _n s} \right) } \right\} \nonumber \\&\quad +\left( {\sinh \left( {\beta _n s} \right) -\sin \left( {\beta _n s} \right) } \right) . \end{aligned}$$
(11)

One may find \(\beta _n\) from the following characteristic equation.

$$\begin{aligned} 1+\cos {\beta _n} \cosh {\beta _n} =0. \end{aligned}$$
(12)

By adopting the Galerkin’s techniques, the weighting function is chosen to be the same as that of admissible function. Here author has used a single admissible trial function for solving the problem as first mode is considered to be dominant mode of the system. The partial governing equation is then discretized with single mode assumption, and it has expressed as

$$\begin{aligned} \int \limits _0^1 {R\left( {s,\tau } \right) \gamma \left( {s,\tau } \right) } =0. \end{aligned}$$
(13)

Here, \(R({s,t})\) is a nonlinear residual operator of the governing equation that can be obtained by substituting Eq. (10) into Eq. (8). For further analysis, one may obtain the following nondimensional time-dependent equation of motion neglecting higher order terms and considering viscous damping effect.

$$\begin{aligned}&\ddot{\varphi }+\varphi +\varepsilon \left( {2\zeta \dot{\varphi }+\alpha \varphi ^{3}+\beta \ddot{\varphi }\varphi ^{2}+\varGamma \dot{\varphi }^{2}\varphi } \right) \nonumber \\&=\varepsilon \left( {f\cos \varTheta \tau +h \varphi \cos \varTheta \tau +k\varphi ^{2}\cos \varTheta \tau } \right) . \end{aligned}$$
(14)

Here, \(\varTheta =\left( {\varOmega /\omega _e } \right) \). The expression for the symbolic nondimensional parameters (i.e. \(\omega _e, \zeta , \alpha , \;\beta , \;\varGamma ,\) \( f,\;h,\;k)\) in Eq. (14) is manifested below.

$$\begin{aligned} \omega _\mathrm{e}^2&= \frac{EI}{\rho Al^{4}}\left( {\frac{\int _0^1 {\gamma \left( s \right) \gamma ^{iv}\left( s \right) \mathrm{d}s} }{\int _0^1 {\gamma ^{2}( s )\mathrm{d}s} }} \right) =\frac{EI}{\rho Al^{4}}\left( {\frac{h_1 }{h_2 }} \right) , \zeta =\frac{c}{2 \varepsilon \rho A \omega _\mathrm{e} },\nonumber \\ \varepsilon \alpha&= \left( {\frac{d_0 }{l}} \right) ^{2}\left( {\frac{h_1 }{h_2 }} \right) \left( {\frac{\int _0^1 {\gamma ( s )\left( {{\gamma }^{\prime \prime }( s)} \right) ^{3}\mathrm{d}s+} 4\int _0^1 {\gamma s )\left( {{\gamma }^{\prime \prime }( s )} \right) ^{3}\mathrm{d}s} }{\int _0^1 {\gamma ^{2}( s )\mathrm{d}s} }} \right) ,\nonumber \\ \varepsilon \beta&= \left( {\frac{d_0 }{l}} \right) ^{2}\left( {\frac{\int _0^1 {{\gamma }^{\prime }( s )\gamma ( s )\left[ {\int _0^{{\bar{\xi }}} {\left\{ {{\gamma }^{\prime }\left( {{\bar{\xi }}} \right) } \right\} ^{2}\mathrm{d}{\bar{\xi }}} } \right] \mathrm{d}s-\int _0^1 {{\gamma }^{\prime \prime }( s)\gamma ( s )\left[ {\int _{{\bar{\xi }}}^1 {\int _0^{{\bar{\eta }}} {\left\{ {{\gamma }^{\prime }\left( {{\bar{\xi }}} \right) } \right\} ^{2}\mathrm{d}{\bar{\eta }}\mathrm{d}{\bar{\xi }}} } } \right] \mathrm{d}s} } }{\int _0^1 {\gamma ^{2}( s )\mathrm{d}s} }} \right) ,\nonumber \\ \varepsilon \varGamma&= \left( {\frac{d_0 }{l}} \right) ^{2}\left( {\frac{\int _0^1 {{\gamma }^{\prime }\left( s \right) \gamma ( s )\left[ {\int _0^{{\bar{\xi }}} {\left\{ {{\gamma }^{\prime }\left( {{\bar{\xi }}} \right) } \right\} ^{2}\mathrm{d}{\bar{\xi }}} } \right] \mathrm{d}s-\int _0^1 {{\gamma }^{\prime \prime }( s)\gamma ( s)\left[ {\int _{{\bar{\xi }}}^1 {\int _0^{{\bar{\eta }}} {\left\{ {{\gamma }^{\prime }\left( {{\bar{\xi }}} \right) } \right\} ^{2}\mathrm{d}{\bar{\eta }}\mathrm{d}{\bar{\xi }}} } } \right] \mathrm{d}s} } }{\int _0^1 {\gamma ^{2}( s )\mathrm{d}s} }} \right) ,\nonumber \\ \varepsilon f&= \alpha \frac{h_2 }{h_1 }\left( {\frac{\int _0^1 {\gamma ( s )\mathrm{d}s} }{\int _0^1 {\gamma ^{2}( s)\mathrm{d}s} }} \right) ,\quad \varepsilon h=\alpha \frac{h_2 }{h_1 }\left( {\frac{\int _0^1 {\gamma ^{2}( s )\mathrm{d}s-\left( {\frac{d_0 }{3l}} \right) \int _0^1 {\gamma ( s){\gamma }^{\prime \prime }( s )\mathrm{d}s} } }{\int _0^1 {\gamma ^{2}( s )\mathrm{d}s} }} \right) \nonumber \\ \varepsilon k&= \alpha \frac{h_2 }{h_1 }\left( {\frac{\int _0^1 {\gamma ^{3}\left( s \right) \mathrm{d}s-\left( {\frac{2d_0 }{3l}} \right) \int _0^1 {\left\{ {\gamma ( s)} \right\} ^{2}{\gamma }''\left( s \right) \mathrm{d}s} } }{\int _0^1 {\gamma ^{2}\left( s \right) \mathrm{d}s} }} \right) . \end{aligned}$$
(15)

The temporal equation of motion (14) comprises linear \((2 \zeta \dot{\varphi })\), cubic geometric \((\alpha q^{3})\) and inertial \((\beta q^{2 }\ddot{q}+\varGamma \dot{q}^{2} q)\) nonlinear terms, direct forced term \(f\cos \left( {\varTheta \tau } \right) \), parametric term \(h\cos \left( {\varTheta \tau } \right) \varphi \) and nonlinear parametric term \(k\cos \left( {\varTheta \tau } \right) \varphi ^{2}\). However, the temporal equation of motion (14) contains many nonlinear terms, and it is difficult to find closed-form solution. Hence, one may go for approximate solution by using the perturbation method. Here method of multiple scales is used, which has been described in the following section.

3 Perturbation technique: method of multiple scales

By using similar procedure as explained in [25–27, 31], substituting \(T_n =\varepsilon ^{n}\tau ,\, n=\hbox {0, 1, 2, 3},\ldots \) and displacement \(\varphi (\tau ;\varepsilon )=\varphi _0 \left( {T_0, T_1 } \right) +\varepsilon \varphi _1 \left( {T_0, T_1 } \right) +O\left( {\varepsilon ^{2}} \right) \) in Eq. (14) and equating the coefficients of like powers of \(\varepsilon \), one may find the following expressions:

$$\begin{aligned}&\!\!\!\!\!\hbox { Order } \varepsilon ^{0}: D_0^{2}\varphi _0 +\varphi _0 =0,\end{aligned}$$
(16)
$$\begin{aligned}&\!\!\!\hbox {Order } \varepsilon ^{1}: D_0^{2}\varphi _1 +\varphi _1 =-2 D_0 D_1 \varphi _0 -2 i\zeta \varphi _0 -\alpha \;\varphi _0^3\nonumber \\&\!\!\!\quad -\beta \left( {D_0^2 \varphi _0 } \right) \varphi _0 -\varGamma \left( {D_0 \varphi _0 } \right) ^{2}\varphi _0^2 \nonumber \\&\!\!\!\qquad +f\cos \left( {\varTheta T_0 } \right) +h\cos \left( {\varTheta T_0 } \right) \varphi _0 +k\cos \left( {\varTheta T_0 } \right) \varphi _0^2.\nonumber \\ \end{aligned}$$
(17)

General solutions of Eq. (16) can be written as

$$\begin{aligned} \varphi _0 =A(T_1 )\exp (iT_0 )+{\bar{A}}(T_1 )\exp (-iT_0 ). \end{aligned}$$
(18)

Substituting Eq. (18) into Eq. (17) leads to

$$\begin{aligned}&\!\!\!D_0^{2}\varphi _1 +\varphi _1 =-2iD_1 A\exp \left( {iT_0 } \right) -2i\zeta A\exp \left( {iT_0 } \right) \nonumber \\&\quad -3\left( {\alpha -\beta +\varGamma } \right) A^{2}{\bar{A}}\exp \left( {iT_0 } \right) \nonumber \\&\quad -\left( {\alpha -\beta -\varGamma } \right) A^{3}\exp \left( {3iT_0 } \right) +\frac{f}{2}\exp \left( {i\varTheta T_0 } \right) \nonumber \\&\quad +\frac{h}{2}A\exp i\left( {\varTheta +1} \right) T_0 +\frac{h}{2}{\bar{A}}\exp i\left( {\varTheta -1} \right) T_0 \nonumber \\&\quad +\frac{k}{2}A^{2}\exp i\left( {\varTheta +2} \right) T_0 +\frac{k}{2}A^{2}\exp i\left( {\varTheta -2} \right) T_0\nonumber \\&\quad +\frac{k}{2}A{\bar{A}}\exp \left( {i\varTheta T_0 } \right) +cc. \end{aligned}$$
(19)

Here, cc stands for the complex conjugate of preceding terms. It is clearly observed that system comprises secular terms or small divisor terms viz., terms that are directly proportional to \(\exp \left( {iT_0 } \right) \) or \(\approx \left( {i\varTheta T_0 } \right) ,\, \approx \exp i\left( {\varTheta -1} \right) T_0,\, \approx \exp i\left( {\varTheta -2} \right) T_0 \) depending on various resonance conditions. It is noteworthy that Eq. (19) will contain secular or small divisor terms when \(\varTheta \approx 1,\, \varTheta \approx 3\) or \(\varTheta \approx 2\). In the following subsections, three resonance conditions viz., primary resonance when \(\varTheta \approx 1\), principal parametric resonance condition when \(\varTheta \approx 2\), and third-order subharmonic conditions when \(\varTheta \approx 3\) have been discussed.

3.1 Primary resonance condition when \((\varTheta \approx 1)\)

Using detuning parameter \(\sigma \) to express the nearness of \(\varTheta \) to 1, one may substitute equation \(\varTheta =1+\varepsilon \sigma \), into Eq. (19) and setting \(A\) equal to \(\left( {1/2} \right) a\left( {T_1 } \right) \mathrm{e}^{i \beta (T_1 )}\) and \(\phi =\sigma T_1 -\beta \). Separating the real and imaginary terms, one may obtain a set of reduced equations as given below.

$$\begin{aligned}&{a}^{\prime }=-\zeta a+\left( {\frac{f}{2}} \right) \sin \phi +\left( {\frac{k}{8}} \right) a^{2}\sin \phi ,\end{aligned}$$
(20)
$$\begin{aligned}&a {\phi }'=a\sigma -\frac{3}{8}\left( {\alpha -\beta +\frac{\varGamma }{3}} \right) a^{3}+\left( {\frac{f}{2}} \right) \cos \phi \nonumber \\&\quad +\left( {\frac{3k}{8}} \right) a^{2}\cos \phi . \end{aligned}$$
(21)

In simple resonance condition, system has only nontrivial responses i.e. \(a\ne 0\) obtained from Eqs. (20–21). Steady-state responses have been determined by converting differential Eqs. (20–21) into set of algebraic equations by setting \({a}^{\prime }=0\), and \({\phi }^{\prime }=0\). Here, Newton’s method has used for obtaining steady-state solutions by simultaneously solving algebraic equations. Stability of the steady state responses has been analysed by investigating eigen-values of the Jacobian matrix which has been obtained by perturbing the algebraic equations with \(a=a_o +a_1 \) and \(\gamma =\gamma _0 +\gamma _1 \) where \(a_0, \gamma _0\) are singular points.

$$\begin{aligned} J=\left[ {{\begin{array}{c@{\quad }c} {-\zeta +\left( {\frac{k}{4}} \right) a_0 \sin \phi _0 }&{} {\left( {\frac{f}{2}} \right) \cos \phi _0 +\left( {\frac{k}{8}} \right) a_0^2 \cos \phi _0 } \\ {\sigma -\frac{9}{8}a_0^2 \left( {\alpha -\beta +\frac{\varGamma }{3}} \right) +\left( {\frac{9k}{8}} \right) a_0^2 \cos \phi _0 }&{} {-\left( {\frac{f}{2}} \right) \sin \phi _0 -\left( {\frac{3k}{8}} \right) a_0^2 \sin \phi _0 } \\ \end{array} }} \right] . \end{aligned}$$
(22)

System is stable if and only if all real parts of the eigen-values are negative. Now the first-order nontrivial steady-state response of the cantilever-based MEMS devices is as follows.

$$\begin{aligned} \varphi =a\cos \left( {\varTheta \tau -\phi } \right) +O\left( \varepsilon \right) +\cdots . \end{aligned}$$
(23)

3.2 Principal parametric resonance \((\varTheta \approx 2)\)

Here, one may substitute equation \(\varTheta =2+\varepsilon \sigma \), into Eq. (19) and setting \(A=\left( {1/2} \right) a\left( {T_1 } \right) e^{i \beta (T_1 )}\) and \(\phi =\sigma T_1 -\beta \). Separating the real and imaginary terms, one may obtain a set of reduced equations as given below.

$$\begin{aligned}&{a}'=-\zeta a+\left( {\frac{h}{4}} \right) a \sin \phi ,\end{aligned}$$
(24)
$$\begin{aligned}&a {\phi }'=a\sigma -\frac{3}{8}\left( {\alpha -\beta +\frac{\varGamma }{3}} \right) a^{3}+\left( {\frac{h}{2}} \right) \cos \phi . \end{aligned}$$
(25)

Here, it has been observed that system possesses both trivial and nontrivial responses determined by solving the reduced nonlinear algebraic equations at steady-state condition by using Newton’s method, simultaneously. To find the stability of the steady-state responses, one may perturb Eqs. (24–25) by substituting \(a=a_o +a_1 \) and \(\gamma =\gamma _0 +\gamma _1 \) where \(a_0, \gamma _0 \) are the equilibrium points and then investigating the eigen-values of the resulting Jacobian matrix \((J)\). The Jacobian matrix \((J)\) is given by

$$\begin{aligned} J=\left[ {{\begin{array}{cc} {-\zeta {+}\frac{h}{4}\sin \phi _0 }&{} {\frac{h}{4} a_0 \cos \phi _0 } \\ {\sigma {-}\frac{9}{8}\left( {\alpha {-}\beta +\frac{\varGamma }{3}} \right) a_0^2 {+}\frac{h}{2}\cos \phi _0 }&{} {-\frac{h}{2}a_0 \sin \phi _0 } \\ \end{array} }} \right] . \end{aligned}$$
(26)

For this case the system will be stable if and only if all the real parts of the eigen-values are negative. Now the first-order nontrivial steady-state response of the system can be given as

$$\begin{aligned} \varphi =a\cos \left( {\frac{\varTheta \tau }{2}-\phi } \right) +O\left( \varepsilon \right) +\cdots . \end{aligned}$$
(27)

3.3 Subharmonic resonance case \((\varTheta \approx 3)\)

Following similar procedure as described in Sects. 3.1 and 3.2, here one may use the detuning parameter \(\sigma \)to express the nearness of \(\varTheta \) to 3 (\(\varTheta =3+\varepsilon \sigma )\) and substituting similar A equal to \(\frac{1}{2}a\left( {T_1 } \right) e^{\left( {i \beta T_1 } \right) }\) in Eq. (19) and separating the real and imaginary parts, yields the following reduced equations.

$$\begin{aligned}&{a}^{\prime }=-\zeta a+\frac{k}{8}a^{2}\sin \phi ,\end{aligned}$$
(28)
$$\begin{aligned}&a{\phi }^{\prime }=a\sigma -\frac{3}{8}\left( {\alpha -\beta +\frac{\varGamma }{3}} \right) a^{3}+\frac{3k}{8}a^{2}\cos \phi \end{aligned}$$
(29)

Here, \(\gamma =\sigma T_1 -3\beta \). For steady-state condition, \({a}^{\prime }\) and \({\gamma }^{\prime }\) equal to zero. Similar to the primary resonance case, one may determine here the system responses numerically by solving the equations obtained after setting \({a}^{\prime }\) and \({\gamma }^{\prime }\) equal to zero using similar Newton’s method for different system parameters. It is clear that unlike primary resonance case and similar to the principle resonance conditions, here the system has both trivial and nontrivial solutions. So, stability of the steady-state response of this case can be determined by investigating the nature of the equilibrium points.

4 Numerical simulations and discussion

The nondimensional equation of motion with nondimensional design parameters of the device has been stated in Eq. (14). Therefore, this equation of motion may be used to study the dynamic behaviours for any other similar kind of electrically driven microbeam. Both static and dynamic analyses have been numerically investigated in this section. Though the static analysis has been demonstrated in order to verify the correctness of the present work obtained numerically, in dynamic analysis, the effect of air-gap length ratio \((\frac{d_0 }{l}=\delta )\), electrostatic forcing parameter \(\alpha \) which is directly proportional to the square of the amplitude of applied voltage \((V_0^2 )\) for a particular air-gap, and viscous dissipative element on the vibratory motion of the system has been examined. An effective numerical solution technique for the computation of steady-state nonlinear dynamic behaviour based on first-order method of multiple scales (MMS) has been investigated for various resonance conditions. It may be noted that in all the numerical simulations for finding the frequency response curve, the vibration amplitude \((a)\), a generalized coordinator of \(\varphi \) equal to \(v( {l,t})/\gamma ( l)\) has been considered in comparison to the beam tip deflection \(v( {l,t)})\). The simulation for finding \(a\), i.e. an amplitude for single mode discretization for different excitation frequencies, i.e. equivalently different \(\sigma \), has been reported here. Kindly note that in this present work, the values considered for the variables of forcing parameter and air-gap length are well below the value that produces the pull-in stability.

Fig. 2
figure 2

a Variations of the nondimensional tip deflection \( w|_{x=1} \) with variable \(\alpha \) for various values of \(\delta \) b effect of higher order correction of electrostatic pressure on the nondimensional tip deflection \(w|_{x=1} \) with variable \(\alpha \)

Full size image

4.1 Static analysis

In this subsection, static deflection of the tip of the microcantilever beam has been determined by directly solving the BVP by setting all time derivatives in Eq. (8) equal to zero. The two-point boundary value problem for solving the deflection of \(w\left( s \right) \) at \(s =1\) using MATLAB BVP solver (bvp4c) within relative and absolute tolerance of \(10^{-6}\). In this present work, static deflection of microcantilever beam has been only plotted in Fig. 2 that represents the stable equilibrium solutions practically achieved by the system. The stable solutions for the proposed model in pull-in results has been verified and are found to be in very good agreement with the previously obtained numerical and experimental results. The influence of nonlinear elastic deformation in the beam for investigating the static deflection of the beam under a wide range of electrostatic forces \((\alpha )\) has been illustrated. Fig. 2a exhibits a representative nondimensional deflection of the tip with voltages \((\alpha )\) for various values of \(\delta =( {{d_0 }/l})\) ranging from zero to forcing level where the pull-in stability occurs. It has been found that the estimated static pull-in voltage increases with increase in gap-length ratio \(\delta =( {{d_0 }/l})\). It is worthy to note that the pull-in results occur at lowest value of electrostatic force for the system with higher nonlinear curvature, and it has been observed that for the same parameters considered in Ref. [24], the pull-in condition starts at \(\alpha \) equal to 1.69 that represents the pull-in voltage of 66.83 compared to the pull-in voltage 66.78 obtained in Ref. [24] and 68.5 V obtained in Ref. [25], experimentally as mentioned in the work of Pohit and Chatterjee [24]. Hence, the pull-in results shown in Fig. 2 are in better agreement in comparison to the analytical results [24] and the experimental results [34]. Also the effect of higher order correction factor of electrostatic pressure shows in Fig. 2b. It has been observed that the critical point at which the structural instability (pull-in) develops is occurred at lower value of \(\alpha \) for the electrostatic pressure neglecting the effect of higher order correction. It can be observed that the nondimensional static pull-in deflection starts in the range of 0.45–0.5 as compared to value of 0.33 obtained using linear theories. Thus, the effect of nonlinear electrostatic forces with higher order correction terms operates the stability limit through the critical pull-in voltage which provides a better estimation for the design of nonpull-in devices, and the linear estimation underestimates the stability limits of the microcantilever.

4.2 Dynamic performance

4.2.1 Primary resonance condition

Here, the resonator has been excited with a frequency of the applied alternative voltage nearly equal to the fundamental frequency of the resonator. In this vibrating state, it is observed that the amplitude of vibration is always equal to a nonzero solution. Both stable and unstable nontrivial solutions are being observed. Stability of those solutions has been analysed in order to avoid the sudden change in behaviour as a parameter passes through a critical value called a bifurcation point. The sudden change in amplitude leads the catastrophic failure of the whole system. The graphical representation of vibration amplitude for varying various system control parameters has been constructed. Figure 3 illustrates a representative frequency response curves or a typical solution for various values of air-gap between resonator and stationary electrode \(( {d_0 /l})=\delta \), while the forcing parameter \(\alpha \) is keeping constant equal to 1. It is worthy to note that amplitude of vibratory motion of the resonator is increased for sweeping up the frequency, and finally it is reached to a critical point \(A\) which is called as saddle-node fixed bifurcation point. Any further increase of the frequency at this point leads a spontaneous amplitude increase to a point \(A^{/}\) i.e. a sudden upward jump in the amplitude from lower to higher amplitude. Further increase in frequency, the amplitude of vibratory motion varies along the path AB. For sweeping down condition, when the frequency of applied voltage is decreasing from point \(C\), the response amplitude goes on increasing and finally reaches a point \(D\). A slight decrease in frequency at this critical point leads a similar sudden upward jump up phenomenon. Further decrease in frequency brings down the amplitude of responses to a lower value continuously, and a sudden jump down phenomenon takes place at point \(E\). It may be observed by experimental investigation that this jump phenomenon results in developing and propagating the mechanical crack across the width of the beam, and subsequent jump up and down in response amplitude is associated with the crack growth. Simultaneously, it is observed that with increase in \(\delta \), response amplitude decreases predominantly. For instance, a sharp decrease in response amplitude from 10.59 to 0.9388 is found as \(\delta \) steps up from 0.05 to 0.3. Hence, it is noteworthy that with increase in air-gap between resonator and ground, the amplitude of responses is reduced due to the fact of dominating the terms containing the coefficients of \(f, k\) over the terms function of \(\delta \). It is observed that with increase in \(\delta \), forward saddle-node bifurcation point \(A \) and backward saddle-node bifurcation point \(E\) disappear from the response curve. Hence, sudden change in amplitude due to these critical points is reduced. The system dynamics becomes stable in forward path for higher values of \(\delta \).

Fig. 3
figure 3

Effect of varying the ratio of \(\delta \) keeping \(\alpha \) and \(\zeta \) constant equal to 1.0 and 0.1 a \(\delta =0.05\), b \(\delta =0.1\), c \(\delta =0.2\), and \(\delta =0.3\)

Full size image
Fig. 4
figure 4

Basin of attractions for a \({\bar{\omega }}=0.7\), b \({\bar{\omega }}=1.15\) as key to the Fig. 2a

Full size image

One may observe that at some frequencies in the entire frequency range from 0.5 to 1.5, theoretically more than one solution exists. For relatively small value of \(\delta \), system has two bistable regions and two single stable zones as shown in Fig. 3a, while for higher value, system has only one bi-stable region. Being existence of three solutions in Fig. 3a–d, it is desirable to check the stability of these solutions. For a specific initial condition, the behaviour of amplitude and phase has been plotted as time progresses. It has been observed from Fig. 3 that the system has two stable solutions in these regions. For specific parameters, the system possesses theoretical response as shown in Fig. 3 where the points \(P_{1},\, P_{2}\), and \(P_{3}\) are representing different amplitudes corresponding to a single frequency. It is expected that the point \(\hbox {P}_{2}\) is unstable and cannot be realised by the system physically. This observation is clearly portrayed by the representation of the basin of attractions as shown in Fig. 4 in \(a\sim \phi \) plane which is obtained by numerically solving the reduced Eqs. (20–21) for \(\varTheta \) equal to 0.7 and 1.15, respectively. Hence, inappropriate selection of initial conditions mostly leads the wrong output response. It is important for finding the appropriate condition for a specific solution that would be achieved physically by the system.

Fig. 5
figure 5

Time history for the points A, B, C and D as marked in Fig. 2b

Full size image

One may validate the results obtained by using perturbation techniques with the results obtained by numerically solving the temporal equation of motion (14). Fourth order Runge–Kutta method is used to solve the temporal equation of motion for finding the time response of the system as illustrated in Fig. 5. Four points viz., \(A,\, B,\, C\) and \(D\) identified with cross marks on the frequency response curves shown in Fig. 3b are considered for the comparison purpose. The amplitude of the periodic response obtained by numerically integrating the temporal equation is found to be 0.07517, while the amplitude obtained by using first-order method of multiple scales is observed to be 0.07164. Hence, the error in the amplitude of the response is found to be 4.92 %. Similarly, after investigation, it has been observed that the errors for other three points \(B,\, C\) and \(D\) are found to be nearly equal to 4.5 %. From the steady-state response, one may note that the result obtained by numerically solving the temporal equation of motion (14) is found to be in good agreement with that determined by using the method of multiple scales. The amount of error in amplitude can be substantially reduced by using higher order method of multiple scales. However, incorporating higher order perturbation techniques will enhance the computation process and complexity of problem. In order to avoid this complexity, first-order method of multiple scales has been employed.

Fig. 6
figure 6

Effect of varying the ratio of \(\alpha \) keeping \(\delta \) constant equal to 0.2 a \(\alpha =0.25\), b \(\alpha =0.75\), c \(\alpha =1.0\), and d \(\alpha =1.25\)

Full size image

Figure 6 describes the behaviour of the response curves with changing forcing parameter \(\alpha \) from 0.25 to 1.25. It is worthy to note that pattern of response curve remains the same, but the response amplitude is decreased as increase in forcing quantity of the system. The backward saddle-node bifurcation point starts as higher frequency and jump length increase with increase in forcing parameter \(\alpha \). The stating amplitude of the MEMS device gets higher with increase in the forcing function \(\alpha \) as shown in Fig. 6d.

Fig. 7
figure 7

Effect of varying the damping ratio \(\zeta \) keeping \(\delta \) and \(\alpha \) are constant equal to 0.2 and 0.5, respectively, a \(\zeta =0.25\), b \(\zeta =0.35\), c \(\zeta =0.365\) and d \(\zeta =0.375\)

Full size image

Figure 7 demonstrates the effect of damping on the system dynamic behaviour considering four different values of viscous damping constant \(\zeta \). With increase in damping, a slight decrease in amplitude of the response has been observed. For high value of damping, the system experiences a number of saddle-node bifurcation points because of possessing two separate response curves. Discontinuity in amplitude of the results at the critical points can be observed in the dynamic responses of the system. Furthermore, it is investigated that the upper response curve disappears for a higher value of damping, and system becomes stable.

4.2.2 Principle parametric resonance condition

In this condition, the microcantilever beam is vibrating with a frequency of the applied voltage nearly equal to the twice the fundamental frequency of the resonator. In this vibrating situation, it is observed that the amplitude of vibration may switch from zero to nonzero value and vice-versa depending upon the state of vibration being considered. Interestingly, the trivial and nontrivial solutions are found to be both stable and unstable relying on the selected value of various system control parameters and chosen frequency of the potential difference. Sudden change in amplitude has taken place because of subcritical pitchfork bifurcation point, and the discontinuity in amplitude leads the catastrophic failure of the system. The influence of forcing parameter \(\alpha \) on the dynamic behaviour of the entire system in response to the forcing frequency has been investigated in Fig. 8. With increase in forcing parameter \(\alpha \), a slight increase in response amplitude is observed. The jump length increases with increase in \(\alpha \). The pitchfork bifurcation point starts at higher frequency when the air-gap length ratio increases.

Fig. 8
figure 8

Effect of changing the value of \(\alpha \) keeping \(\delta \) and \(\zeta \)constant equal to 0.2 and 0.1, respectively, a \(\alpha =0.5\), b \(\alpha =0.75\), c \(\alpha =1.0\) and d \(\alpha =1.5\)

Full size image
Fig. 9
figure 9

Time history for the points A, B as marked in Fig. 7a

Full size image

Response obtained by using the method of multiple scales is compared with those found by numerically solving the temporal Eq. (14). Time response illustrated in Fig. 9a for point A clearly depicts that the steady-state response is stable trivial state which is same as that of observed in Fig. 8. Similarly, the amplitude of steady-state response obtained by solving the temporal Eq. (14) is same as the response shown in Fig. 9b, (point B) obtained by method of multiple scales. Time response clearly shows that the trajectory is initiated from the unstable fixed-point response and finally moves towards stable fixed-point response. Hence, these response obtained by solving the temporal equation of motion is in good agreement with those obtained by using the method of multiple scales.

Fig. 10
figure 10

Influences of changing \(( {\frac{d}{l}} )=\delta \), keeping \(\alpha \) and \(\zeta \) constant equal to 0.5 and 0.1 a \(\delta =0.2\), b \(\delta =0.3\), c \(\delta =0.4\), and \(\delta =0.5\)

Full size image

Figure 10 provides the behavioural description of response curves for four different values of \(( {d_0 /l} )=\delta \). The amplitude of response decreases with increase in air-gap \(\delta \). The unstable zone, i.e. region between supercritical and subcritical pitchfork bifurcation points, remains the same for all value of air-gaps \(\delta \), and hence, the jump up phenomenon always occurs at almost frequency.

Fig. 11
figure 11

a \(\zeta =0.2\), b \(\zeta =0.35\) while keeping \(\delta \) and \(\alpha \) are constant equal to 0.2 and 0.1, respectively

Full size image

The influences of damping on the response curves have been depicted in Fig. 11 for four different values of damping ratio \(\zeta \). A similar observation to that of explained in Fig. 9 has also been reported here. With increase in damping, the response amplitude and jump length decrease. Unlike the condition of varying air-gap, here unstable zone is reduced with increase in damping.

4.2.3 Subharmonic resonance condition

This resonance is took place when the frequency of the applied voltage is nearly equal to thrice the fundamental frequency of the resonator. It is worthy to note that the amplitude of vibration may switch from nonzero to zero value as trivial solutions are found to be stable for wide range of frequency and control parameters of the system. Similar to the primary resonance conditions, stability of the system depends on the position of critical point. Hence, the system may be brought to stable condition by simply choosing the appropriate frequency and other system parameters. Figure 12 describes the effect of changing air-gap between resonant and electrode on the frequency response curves. With increase in air-gap \(\delta \) the response amplitude is decreased, and jump down phenomenon takes place on account of saddle-node bifurcation point. The jump length is found to be decreased with increase in air-gap. Also, it has been noticed that this nonlinear phenomenon occurs at a higher value of frequency with increase in air-gap \(\delta \). From Figs. 12, 13, and 14, it may observe that with increase in forcing parameter \(\alpha \) and decrease in damping, the response amplitude is increased. Similarly, jump length will increase with increase in both forcing parameter \(\alpha \) and damping \(\zeta \).

Fig. 12
figure 12

Effect of varying the gap \(\delta \) keeping \(\alpha \) and \(\zeta \)constant equal to 1.0 and 0.1 a \(\delta =0.05\), b \(\delta =0.07\), c \(\delta =0.1\), d \(\delta =0.2\)

Full size image
Fig. 13
figure 13

Effect of changing the value of \(\alpha \) keeping \(\delta \) and \(\zeta \) constant equal to 0.2 and 0.1, respectively a \(\alpha =0.75\), b \(\alpha =1.25\)

Full size image
Fig. 14
figure 14

Frequency response curves for a \(\zeta =0.05\), b \(\zeta =0.25\) while keeping \(\delta \) and \(\alpha \) are constant equal to 0.75 and 0.75, respectively

Full size image

5 Conclusions

Unlike to the existing research, in the present work, the stability and bifurcation analysis of electrically driven microbeam has been investigated using a model accounting for mid-plane stretching and nonlinear electrostatic forcing. The present nonlinear model has strong potential to deal with the nonlinearities in the geometric of the deformable microbeam and in the electrostatic force. The pull-in results from the proposed model have been examined and are found in very good agreement with the findings previously obtained experimentally and numerically. The effect of the higher order correction of electrostatic pressure in the pull-instability has also been investigated. It has been observed that the structural instability (pull-in) occurs at a lower value of the forcing parameter when the effect of higher order correction is neglected. It may kindly note that the effect of electrostatic force with higher order correction terms operates the stability limit through the critical pull-in voltage which provides a better estimation for the design of nonpull-in devices, and the linear estimation underestimates the stability limits of the microcantilever. Effect of various design parameters on the mechanical behaviours of the system has been accomplished. Saddle-node and pitchfork bifurcations points have been found and resulting the catastrophic failure of the system. Basins of attractions are being illustrated in order to find the initial condition for a specific solution in multi-regions.

In simple resonance condition, it has been observed that with increase in air-gap distance, response amplitude goes on predominantly decreasing. The dynamic instability for sudden change in amplitude with increase in air-gap is truncated. With increase in forcing parameter and damping, the response amplitude is decreased, and a jump phenomenon occurs at higher frequency with the increase in forcing parameter.

In principle parametric resonance condition, both trivial and nontrivial solutions are found to be stable and unstable, and sudden change in amplitude takes place due to pitchfork bifurcation point. The jump length increases with increase in forcing quantity, and subcritical pitchfork point starts at higher frequency with increase in air-gap-beam length ratio. While the amplitude of response decreases with increase in air-gap, the unstable zone remains the same for all values of air-gap. But, unstable zone is reduced with increase in damping effect.

In subharmonic resonance condition, it has been found that the system may be brought to the stable condition by selecting the appropriate frequency and controlling the other design parameters. Like primary and principle parametric resonance conditions, similar investigation has been established taken into account the varying different system parameters. With increase in air-gap-length ratio, the response amplitude decreases, and jump down phenomenon has taken place due to the backward \(S\)–\(N\) bifurcation point. It may observe that with increase in electric actuation force, i.e. applying voltage for a specific value of gap length and decrease in damping, the response amplitude is increased. The obtained results can successfully be used for designing the cantilever-based electrostatically controlled microdevices in the field of MEMS application.