An investigation on lateral and torsional coupled vibrations of high power density PMSM rotor caused by electromagnetic excitation

Abstract

Electromagnetic excitation in high power density permanent magnet synchronous motors (PMSMs) due to eccentricity is a significant concern in industry; however, the treatment of lateral and torsional coupled vibrations caused by electromagnetic excitation is rarely addressed, yet it is very important for evaluating the stability of dynamic rotor vibrations. This study focuses on an analytical method for analyzing the stability of coupled lateral/torsional vibrations in rotor systems caused by electromagnetic excitation in a PMSM. An electromechanically coupled lateral/torsional dynamic model of a PMSM Jeffcott rotor is derived using a Lagrange–Maxwell approach. Equilibrium stability was analyzed using a linearized matrix of the equation describing the system. The stability criteria of coupled torsional–lateral motions are provided, and the influences of the electromagnetic and mechanical parameters on mechanical vibration stability and nonlinear behavior were investigated. These results provide better understanding of the nonlinear response of an eccentric PMSM rotor system and are beneficial for controlling and diagnosing eccentricity.

1 Introduction

The increasing popularity of permanent magnet synchronous motors (PMSMs) in machinery trains has increased interest in the electromagnetic excitation they produce as this may influence machinery vibration [1]. Motors are designed under the assumption of a uniform air gap around the rotor, but in practice, all motors operate with the rotor slightly displaced from the motor centerline, i.e., in an eccentric position. Rotor center eccentricity can generate a radially unbalanced magnetic field, while the motor operates [2]. This will result in a coupled radial and tangential excitation that pulls the motor further away from the center, inducing coupled unstable lateral and torsional vibration. In order to avoid electromechanically coupled resonance caused by variations in the electrical parameters, the existing dynamics model should be improved. This requires analyzing multiple electromechanical coupling effects determined by mechanical, electrical, and magnetic parameters. The improved model can provide theoretical guidance for structural design, optimal control over electromechanical coupling in the transmission system, and damping of active vibrations.

In the past, research on the dynamics considered a linear theory that did not account for electromechanical coupling. Some high performance PMSM-driven systems demand low vibration, low acoustic noise, and high accuracy. However, a growing number of studies show that electromagnetic coupling-induced vibration is a major concern [3, 4]. Accurate evaluation and experimental investigation of the dynamic response indicate that electromechanical coupling and nonlinear vibrations should be considered when describing vibrations in electromechanical systems [5].

Fig. 1

PMSM rotor and its coordinate system

Determining precise electromagnetic excitation is critical problem when the electromagnetic coupling dynamics is investigated. The electromagnetic excitation model was studied in the past. It is well known that electromagnetic excitation can be computed using finite element method (FEM) [6, 7]. However, FEM is time-consuming and cannot provide insight into the origin of electromagnetic excitation. Various researches have focused on theoretically describing electromagnetic excitation and its effects on rotors dynamics. Lundström [8] and Chuan [9] established an electromagnetic excitation model by considering changes in the axial eccentricity of a hydro-generator rotor, and stability of the rotor dynamics and imbalance response were analyzed. Dorrell [10] proposed a radial electrical electromagnetic excitation model that accounts for rotor eccentricity in cage induction motors. Zhang [11] theoretically investigated an electromagnetic excitation model for a motor without a load. Coupling between the dynamics and electromagnetic excitation due to dynamic and static eccentricity was analyzed.

Overall, the aforementioned research focused on large-scale electrical excitation in hydro-generators. A permanent magnet still produces radial electromagnetic excitation despite the absence of electrical excitation. The strength of electromagnetic excitation will increase with the applied load and additional vibrations. Second, an internal combustion engine operates along a PMSM with high power density in hybrid electric vehicle (HEV), which may pick up a multitude of operational and vibration frequencies from internal combustion engine. Third, pavement irregularity acts as an excitation source, which varies with the velocity of the vehicle. External disturbances apply forces to the rotor at various frequencies.

Many publications discuss radial electromagnetic excitation from an electrical perspective. Li [12] and Dorrell [13, 14] investigate the radial force density for IPM/SPM and fractional-slot brushless permanent magnet motors due to either magnetic asymmetry or static rotor eccentricity. FEM was used to account for the magnetic saturation, and the radial force density was analyzed by using Maxwell stress tensor. Others have presented a radial electrical electromagnetic excitation model from a dynamics perspective [15, 16]. Jiang et al. [15] studied rotor vibration induced by UMP for switch reluctance motors, and the dynamic response of the motor rotor was calculated by using step-by-step integration. Mao et al. [16] analyzed the influence of the rotor position error on the longitudinal vibration of the electric wheel system. FEM was also used for harmonic analysis of the stator in a low speed, direct drive PMSM in order to predict the vibration characteristics and limit vibration and noise, and unbalanced response of the rotor was analyzed [16].

Electromechanical coupling caused by electromagnetic excitation mainly primarily focuses on transverse vibration. However, coupled lateral torsional vibration arises in real rotor systems. Consequently, electromechanically coupled rotor vibration is a complicated dynamic phenomenon that can cause serious problems. Many prior studies [17,18,19,20] have addressed lateral/torsional vibration coupling theoretically, which provides an important reference for solving the lateral/torsional coupling dynamic equation and analytical method for this research work.

This study focuses on investigating nonlinear coupled lateral and torsional rotor vibrations in a high power density PMSM used for HEV caused by electromagnetic excitation. This paper is organized as follows: A nonlinear electromechanical coupling dynamic model derived from the Lagrangian–Maxwell theory is presented in Sect. 2. An autonomous nonlinear ordinary differential equation is subsequently derived by applying a symplectic transformation. The amplitude–frequency and phase–frequency characteristics of the vibration can be determined by solving multiple coupling dynamics in Sect. 3.Numerical algorithms and analytical methods for their stability analysis are introduced in Sect. 4.

2 Multiple electromechanical coupling dynamic model

2.1 Assumptions and definitions

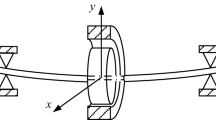
A schematic diagram of a dynamic model describing a PMSM rotor supported by rigid bearings is shown in Fig. 1. This model is based on Jeffcott’s model, which consists of a rigid disk and a massless flexible shaft. A key motivation for this simplified single-rotor model is application of PMSMs with high power density in HEV, which are slender rotating structures that are used to avoid transmission vibration. These structures are rather different from typical rotating machines because they typically experience large torsional deformation, significant imbalance, and eccentricity arising from matching with other machinery.

The equation of motion can be derived under the following assumptions: (i) Rotational motion along the x- and y-axes is neglected; (ii) the system is undamped; (iii) all elastic restoring forces are assumed to be linear; (iv) the lateral stiffness of the system $K_{xx}$ and $K_{yy}$ is assumed to be equal.

Figure 1a shows the coordinate system used in this model, where the z-axis is the longitudinal coordinate of the rotor shaft, and x and y are the lateral coordinates from the rotor axis. Figure 1b shows the cross section of a rotor rotating at a constant angular speed $\Omega$. The shadowed area depicts the stator. Points $O_{r}$ and O refer to the geometrical centers of the rotor and stator, respectively. Point Cis the center of mass of the rotor. In this case, l is the length of the rotor shaft and $R_{r}$ is the outer radius of the rotor. The eccentricity e can be static or dynamic. The mass eccentricity of the rotor is $O_{r}C=d$.

The angle between the x coordinate and vector $\overrightarrow{OO_r }$ is $\gamma$, where ${ \gamma }= \omega _{r}t + { \theta }+ { \phi }_{0}$, where $\Omega$ is the shaft rotational speed, $\theta$ is the torsional deflection angle, and ${\phi }_{0}$ is the initial deflection angle. $k_{m}=K_{xx}= K_{yy}$ is the torsional stiffness. The rotor has mass m and moment of inertia J. $\phi$$_{0}$ is assumed to be zero for simplification.

2.2 Derivation of the multiple electromechanical coupling model

The rotor rotates around $O_{r}$, while the rotor center $O_{r}$ moves with the rotor. If the position of the geometric center is (x, y), then the position of the center of mass is

$$\begin{aligned} x_m =x+d\cdot \cos \gamma , y_m =y+d\cdot \sin \gamma \end{aligned}$$

(1)

When the rotor is eccentric, cross-coupling in the coupling channel and the geometric coupling channel will cause the rotor system to vibrate. The motor is assumed to be the same as that presented in a prior study [21]. The Lagrange–Maxwell method is used to construct the Lagrangian for this system L [22]:

$$\begin{aligned} L=T-V+W_\mathrm{m} \end{aligned}$$

(2)

where T and V are the kinetic and potential energies of the system, respectively, and $W_\mathrm{m}$ is the magnetic field energy.

Total kinetic T energy is the sum of the translational kinetic energy and rotational kinetic energy:

$$\begin{aligned} T= & {} \frac{1}{2}m\left( {\dot{x}-d\dot{\phi }\sin \phi } \right) ^{2}\nonumber \\&+\frac{1}{2}m\left( {\dot{y}-d\dot{\phi }\cos \phi } \right) ^{2}+\frac{1}{2}J\dot{\phi }^{2} \end{aligned}$$

(3)

The potential Venergy of this system is:

$$\begin{aligned} V=\frac{1}{2}k_m x^{2}+\frac{1}{2}k_m y^{2} \end{aligned}$$

(4)

where $k_{m}$ is the bending stiffness coefficient, and $\phi$ is the angular displacement of the rotor.

According to the relationship between the magnetic conductance of an eccentric air gap in reference [1] and Eq. (1), the air-gap magnetic conductance is:

$$\begin{aligned} \Lambda \left( {\alpha ,t} \right)= & {} \Lambda _0 \left\{ {\left[ {1+\frac{1}{2}\left( {x^{2}+y^{2}} \right) +\frac{3}{8}\left( {x^{2}+y^{2}} \right) ^{2}} \right] } \right. \nonumber \\&+\left[ {1+\frac{3}{4}\left( {x^{2}+y^{2}} \right) } \right] \cdot \left( {x\cos \alpha +y\sin \alpha } \right) \nonumber \\&+\left[ {\frac{1}{2}\left( {x^{2}-y^{2}} \right) +\frac{1}{2}\left( {x^{4}-y^{4}} \right) } \right] \cdot \cos 2\alpha \nonumber \\&\left. {+\left[ {xy+\left( {xy^{3}-xy^{3}} \right) } \right] \cdot \sin 2\alpha } \right\} \end{aligned}$$

(5)

$\hbox {x}=\frac{e\cos \gamma }{k_\mu \cdot \delta _0 }=\frac{X}{\sigma }$ and $\hbox {y}=\frac{e\sin \gamma }{k_\mu \cdot \delta _0 }=\frac{Y}{\sigma }$ are substituted into Eq. (5), yielding the energy stored in the air gap:

(6)

The dissipative function $F_{c}$ is relatively simple and can be written as:

$$\begin{aligned} F_c =\frac{1}{2}c\left( {\dot{x}^{2}+\dot{y}^{2}} \right) \end{aligned}$$

(7)

where c is the bending damped coefficient.

X, Y, and $\phi$ are defined as generalized displacements in a fixed coordinate system. Substituting L and $F_{c}$ into the Lagrange–Maxwell equations yields:

$$\begin{aligned}&m\frac{\mathrm{d}^{2}X}{\mathrm{d}t^{2}}+c\frac{\mathrm{d}X}{\mathrm{d}t}+k_m X-\frac{f_1 }{\sigma }X-\frac{3\left( {X^{3}+XY^{2}} \right) }{2\sigma ^{3}}\nonumber \\&\quad -\,\frac{X}{2\sigma }\left( {f_2 \cos 2\omega t+f_3 \sin 2\omega t} \right) \nonumber \\&\quad -\,\frac{Y}{2\sigma }\left( {f_2 sin2\omega t-f_3 \cos 2\omega t} \right) \nonumber \\&\quad -\,\frac{X}{\sigma ^{3}}\left( {f_2 \cos 2\omega t+\lambda _3 \sin 2\omega t} \right) \nonumber \\&\quad +\,\frac{Y^{3}}{\sigma ^{3}}\left( {f_2 \sin 2\omega t-f_3 \cos 2\omega t} \right) \nonumber \\&\quad -\,\frac{3\left( {X^{2}+Y^{2}} \right) Y}{2\sigma ^{3}}\left( {f_2 \sin 2\omega t-f_3 \cos 2\omega t} \right) \nonumber \\&\quad =md\dot{\phi }^{2}\cos \phi +md\ddot{\phi }\sin \phi \nonumber \\&m\frac{\mathrm{d}^{2}Y}{\mathrm{d}t^{2}}+c\frac{\mathrm{d}Y}{\mathrm{d}t}+k_m Y-\frac{f_1 }{\sigma }Y-\frac{3\left( {X^{2}Y+Y^{3}} \right) }{2\sigma ^{3}}\nonumber \\&\quad -\,\frac{X}{2\sigma }\left( {f_2 \sin 2\omega t-\lambda _3 \cos 2\omega t} \right) \nonumber \\&\quad +\,\frac{Y}{2\sigma }\left( {f_2 \cos 2\omega t+f_3 \sin 2\omega t} \right) \nonumber \\&\quad +\,\frac{X^{3}}{\sigma ^{3}}\left( {f_2 \sin 2\omega t-f_3 \cos 2\omega t} \right) \nonumber \\&\quad +\,\frac{Y^{3}}{\sigma ^{3}}\left( {f_2 \cos 2\omega t+f_3 \sin 2\omega t} \right) \nonumber \\&\quad -\,\frac{3\left( {X^{2}+Y^{2}} \right) X}{2\sigma ^{3}}\left( {f_2 \sin 2\omega t-f_3 \cos 2\omega t} \right) \nonumber \\&\quad =md\dot{\phi }^{2}\sin \phi +md\ddot{\phi }\cos \phi \nonumber \\&J\frac{\mathrm{d}^{2}\phi }{\mathrm{d}t^{2}}-M\left( {\dot{\phi }} \right) {+}\left[ {1+\frac{X^{2}+Y^{2}}{2\sigma ^{2}}{+}\frac{3\left( {X^{2}+Y^{2}} \right) ^{2}}{8\sigma ^{4}}} \right] T_1 \nonumber \\&\quad -\,\left( {\frac{X^{2}-Y^{2}}{4\sigma ^{2}}T_2 } \right. \left. {-\frac{XY}{2\sigma ^{2}}\cdot T_3 } \right) \cdot \sin 2\omega t \nonumber \\&\quad +\,\left[ {\frac{X^{2}-Y^{2}}{4\sigma ^{2}}T_3 +\frac{XY}{2\sigma ^{2}}\cdot T_2 } \right] \cdot \cos 2\omega t \nonumber \\&\quad -\,\left( {\frac{X^{4}-Y^{4}}{4\sigma ^{2}}T_2 } \right. \left. {-\frac{X^{3}Y+XY^{3}}{2\sigma ^{4}}\cdot T_3 } \right) \cdot \sin 2\omega t \nonumber \\&\quad +\,\left[ {\frac{X^{4}-Y^{4}}{4\sigma ^{2}}T_3 +\frac{X^{3}Y+XY^{3}}{2\sigma ^{4}}\cdot T_2 } \right] \cdot \cos 2\omega t \nonumber \\&\quad =md\left( {\ddot{Y}\cos \phi -\ddot{X}\sin \phi } \right) \end{aligned}$$

(8)

Equation (8) is a nonlinear differential equation with periodic coefficients describing vibrations in the system. The coefficients $f_{1}$, $f_{2}$, $f_{3}$, $T_{1}$, $T_{2}$, and $T_{3}$ are determined from the electromagnetic parameters and the operation state of the motor, which are defined as follows:

$$\begin{aligned}&\left\{ {\begin{array}{l} f_1 =\frac{\pi \mathrm{RL}\Lambda _0 }{2\sigma }\left( {F_{sm}^2 +F_{rm}^2 -2F_{sm} F_{rm} \sin \psi } \right) \\ f_2 =\frac{\pi \mathrm{RL}\Lambda _0 }{2\sigma }\left( {F_{sm}^2 {-}F_{rm}^2 \cos 2\psi {-}2F_{sm} F_{rm} \sin \psi } \right) \\ f_3 =\frac{\pi \mathrm{RL}\Lambda _0 }{2\sigma }\left( {F_{rm}^2 \sin 2\psi -2F_{sm} F_{rm} \cos \psi } \right) \\ \end{array}} \right. \\&\left\{ {\begin{array}{l} T_1 =\pi \mathrm{RL}\Lambda _0 F_{sm} F_{rm} \cos \psi \\ T_2 =\pi \mathrm{RL}\Lambda _0 \left( {F_{rm}^2 \cos 2\psi +F_{sm} F_{rm} \sin \psi } \right) \\ T_3 =\pi \mathrm{RL}\Lambda _0 \left( {F_{sm} F_{rm} \cos \psi -F_{rm}^2 \sin 2\psi } \right) \\ \end{array}} \right. \end{aligned}$$

When a permanent magnet synchronous motor operates in the steady-state, a voltage, and power equation can be obtained from the three-phase symmetric electric vector [23], as defined in Eq. (10). These six electromagnetic coefficients describe the electromagnetic field and operating conditions of the motor and are coupled as defined in Eq. (9):

$$\begin{aligned} \left\{ {\begin{array}{l} U\sin \theta =I_q X_q +I_d R_1 \\ U\cos \theta =E_0 -I_d X_d +I_q R_1 \\ E_0 =4.44fK_{dp} N\Phi _{\delta 0} K_\Phi \\ \frac{mE_0 U}{X_d }\sin \theta +\frac{mU^{2}}{2}\left( {\frac{1}{X_q }-\frac{1}{X_d }} \right) \sin 2\theta =P_{em} \\ \end{array}} \right. \end{aligned}$$

(9)

where U is the effective voltage, $X_{d}$ and $X_{q}$ are the dq-axis synchronous reactance (a surface-type permanent magnet synchronous motor is used, thus $X_{d}=X_{q})$. $R_{1}$ is the stator winding resistance, $E_{0}$ is the fundamental back electromotive force produced by the permanent magnetic air gap, $\theta$ is the power angle, and $\psi$ is the power factor angle. $I_d =I_1 \sin \psi$, and $I_q =I_1 \cos \psi$

The lateral vibration in multiple electromechanical coupling equations is related to torsional vibration parameters, while the torsional vibration is related to transverse vibration parameters. The coefficients in the electromechanical coupling equations are determined by the structural parameters and the electromagnetic field of the PMSM. This illustrates the electromechanical coupling inherent in this dynamic model.

The angular displacement of the PMSM rotor is ${\phi }= { \omega t }+ {\theta }$. $\omega$ is the angular frequency of the armature current, and $\theta$is the relative angular displacement between the rotor pole center line and the synthetic magnetic potential. When the motor does not exhibit a synchronous oscillation, $\frac{\mathrm{d}\theta }{\mathrm{d}t}$ can be considered to change slowly, i.e., $\dot{\phi }=\left( {\omega +\dot{\theta }} \right) =\Omega$, and $\ddot{\phi }=\dot{\Omega }$

It is assumed that $Z=X+iY$, $\bar{{Z}}=X-iY$, and introducing the following parameters

$$\begin{aligned} k^{2}= & {} \frac{k_m }{m}-\frac{f_1 }{m\sigma }, \quad 2\mu =\frac{c}{m}, \quad k_1^2 =\frac{f_1 }{m}, \\ k_2^2= & {} \frac{f_2 }{m}, \quad k_3^2 =\frac{f_3 }{m} \\ N_1= & {} \frac{T_1 }{J}, \quad N_2 =\frac{T_2 }{J},\\ N_3= & {} \frac{T_3 }{J}, \quad B=\frac{M}{J}, \quad q=\frac{me}{2J} \end{aligned}$$

The second equation in Eq. (8) is multiplied by i and added to the first equation. If the damping force and electromagnetic force are small relative to the elastic force, the small terms can be moved to the right side of the equations, and a small parameter $\omega$ can be introduced into these equations. Ultimately, the coupling equations can be simplified as follows:

$$\begin{aligned}&\frac{\mathrm{d}^{2}Z}{\mathrm{d}t^{2}}+k^{2}Z\nonumber \\&\quad = \varepsilon \left[ {-2n\dot{Z}+\frac{1}{2\sigma }\left( {k_2^2 -jk_3^2 } \right) e^{i2\omega t}\cdot \bar{{Z}}} \right. \nonumber \\&\quad \quad +\,\frac{3k_1^2 }{2\sigma ^{3}}Z^{2}\bar{{Z}}+\frac{1}{4\sigma ^{3}}\left( {k_2^2 +jk_3^2 } \right) e^{-i2\omega t}\cdot Z^{3} \nonumber \\&\quad \quad +\,\frac{3}{4\sigma ^{3}}\left( {k_2^2 -jk_3^2 } \right) e^{i2\omega t}\cdot \bar{{Z}}^{2}\cdot Z\nonumber \\&\quad \quad \left. +\,r\left( {\Omega ^{2}-j\dot{\Omega }} \right) e^{i\Theta t} \right] \nonumber \\&\frac{\mathrm{d}^{2}\Omega }{\mathrm{d}t^{2}}=\varepsilon \left[ B-N_1 -\frac{N_1 }{2\sigma ^{2}}Z\bar{{Z}}-\frac{3N_1 }{8\sigma ^{4}}Z^{2}\bar{{Z}}^{2}\right. \nonumber \\&\quad \quad -\,\frac{1}{8\sigma ^{2}}\left( {N_3 -iN_2 } \right) \nonumber \\&\quad \quad \cdot \, e^{-i2\omega t}\cdot Z^{2}-\frac{1}{8\sigma ^{2}}\left( {N_2 +iN_3 } \right) e^{i2\omega t}\cdot \bar{{Z}}^{2}\nonumber \\&\quad \quad -\,\frac{1}{8\sigma ^{4}}\left( {N_3 -iN_2 } \right) \nonumber \\&\quad \quad \cdot e^{-i2\omega t}\cdot Z^{3}\bar{{Z}}-\frac{1}{8\sigma ^{4}}\left( {N_3 +iN_2 } \right) e^{i2\omega t}\cdot Z\bar{{Z}}^{3} \nonumber \\&\quad \quad \left. -iq\left( {\frac{\mathrm{d}^{2}\bar{{Z}}}{\mathrm{d}t^{2}}e^{i\Theta t}-\frac{\mathrm{d}^{2}Z}{\mathrm{d}t^{2}}e^{-i\Theta t}} \right) \right] \end{aligned}$$

(10)

These differential equations define the multiple electromechanical coupling dynamics model; they are nonlinear differential equations with periodic coefficients. The differential equations are described by parametric vibrations in nonlinear vibration theory.

Fig. 2

Critical speed as a function of $f_{1}$ for $\hbox {cos}\psi = 0.5$ and $\mu = 3.0$

Equation (8) shows that $f_{1}$ can define the unbalanced electromagnetic force in the absence of vibration. Figure 2 shows the variation in the critical speed of the motor as a function of the electromagnetic force $f_{1}$ and four different values of magnetic circuit saturation coefficients. One can see that the critical speed rapidly decreases as the unbalanced electromagnetic force $f_{1}$ increases. An unbalanced electromagnetic force causes the critical speed to vary over a larger range. The critical speed can even decrease to zero when the unbalanced electromagnetic force reaches a certain value. This is equivalent to the case where the unbalanced electromagnetic force on the rotor shaft is equal to the elastic restoring force.

3 Solving of multiple coupling dynamics

In order to focus on the electromagnetic vibration excited by the electromagnetic force, it is assumed that d= 0. It is easy to design the normal operating speed of the rotor system such that it produces resonance. The primary parametric resonance was investigated in this paper.

It is useful to express the position of the rotor in polar coordinates during analysis. In light of this, a multiple electromechanical dynamics equation can be written in polar coordinates using the transformation

$$\begin{aligned}&Z=Ae^{i\left( {\omega t+\beta } \right) } \end{aligned}$$

(11a)

$$\begin{aligned}&\dot{Z}=iA\omega e^{i\left( {\omega t+\beta } \right) } \end{aligned}$$

(11b)

$$\begin{aligned}&\frac{\mathrm{d}\phi }{\mathrm{d}t}=\Omega \end{aligned}$$

(11c)

The new variables A and $\beta$vary slowly over time. Equations (11a) and (11c) can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{Z}=\frac{\mathrm{d}A}{\mathrm{d}t}e^{i\left( {\omega t+\beta } \right) }+A\left( {i\omega +i\frac{\mathrm{d}\beta }{\mathrm{d}t}} \right) e^{i\left( {\omega t+\beta } \right) } \\ \dot{\bar{{Z}}}=\frac{\mathrm{d}A}{\mathrm{d}t}e^{-i\left( {\omega t+\beta } \right) }-A\left( {i\omega +i\frac{\mathrm{d}\beta }{\mathrm{d}t}} \right) e^{i\left( {\omega t+\beta } \right) } \\ \end{array}} \right. \end{aligned}$$

(12)

Equation (11b) can be substituted into Eq. (12), yielding the following equation:

$$\begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}t}e^{i\left( {\omega t+\beta } \right) }+iA\frac{\mathrm{d}\eta }{\mathrm{d}t}e^{i\left( {\omega t+\beta } \right) }=\varepsilon iA\left( {k-\omega } \right) e^{i\left( {\omega t+\beta } \right) } \end{aligned}$$

(13)

where $\left( {k-\omega } \right)$in Eq. (13) is known as a small parameter, and thus, a small parameter $\varepsilon$ can be added. Equation (11b) can be rewritten in the following form:

$$\begin{aligned} \ddot{Z}= & {} jk\frac{\mathrm{d}A}{\mathrm{d}t}e^{i\left( {\omega t+\beta } \right) }-Ak\omega e^{i\left( {\omega t+\beta } \right) }\nonumber \\&\quad -Ak\frac{\mathrm{d}\beta }{\mathrm{d}t}\left( {k-\omega } \right) e^{i\left( {\omega t+\beta } \right) } \end{aligned}$$

(14)

Substituting Eqs. (11) and (14) into the first equation in Eq. (10) yields

$$\begin{aligned}&jk\frac{\mathrm{d}A}{\mathrm{d}t}e^{i\left( {\omega t+\beta } \right) }-Ak\frac{\mathrm{d}\beta }{\mathrm{d}t}e^{i\left( {\omega t+\beta } \right) }\nonumber \\&\quad =\varepsilon \left[ {Ak\left( {\omega -k} \right) e^{i\left( {\omega t+\beta } \right) }} \right. -i2\mu Ake^{i\left( {\omega t+\beta } \right) } \nonumber \\&\qquad +\frac{1}{2\sigma }\left( {k_2^2 -ik_3^2 } \right) Ae^{i\left( {\omega t-\beta } \right) }+\frac{3k_1^2 }{2\sigma ^{3}}A^{3}Ae^{i\left( {\omega t+\beta } \right) } \nonumber \\&\qquad +\frac{1}{4\sigma ^{3}}\left( {k_2^2 +ik_3^2 } \right) A^{3}e^{i\left( {\omega t+3\beta } \right) }\nonumber \\&\qquad +\frac{1}{4\sigma ^{3}}\left( {k_2^2 -ik_3^2 } \right) A^{3}e^{i\left( {\omega t-\beta } \right) } \end{aligned}$$

(15)

$\frac{\mathrm{d}A}{\mathrm{d}t}$ and $\frac{\mathrm{d}\beta }{\mathrm{d}t}$can be solved by taking the real part of Eqs. (10) and (15), respectively. The standard nonlinear differential equations can be obtained by substituting Eq. (14) into the second equation in Eq. (10) as follows:

$$\begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}t}= & {} -\,\varepsilon \left[ 2\mu A\sin ^{2}\left( {\omega t+\beta } \right) +\frac{Ak_2^2 }{2\sigma k}\cos \left( {\omega t-\beta } \right) \right. \nonumber \\&\quad \cdot \sin \left( {\omega t+\beta } \right) +\frac{Ak_3^2 }{2\sigma k}\sin \left( {\omega t-\beta } \right) \nonumber \\&\quad \cdot \cos \left( {\omega t+\beta } \right) +\frac{3A^{3}k_2^2 }{4\sigma ^{3}k}\cos \left( {\omega t-\beta } \right) \nonumber \\&\quad \cdot \sin \left( {\omega t+\beta } \right) +\frac{3A^{3}k_3^2 }{4\sigma ^{3}k}\sin \left( {\omega t-\beta } \right) \nonumber \\&\quad \cdot \sin \left( {\omega t+\beta } \right) +\frac{3A^{3}k_1^2 }{2\sigma ^{3}k}\cos \left( {\omega t-\beta } \right) \nonumber \\&\quad \cdot \sin \left( {\omega t+\beta } \right) \nonumber \\ \frac{\mathrm{d}\beta }{\mathrm{d}t}= & {} -\varepsilon \left[ \left( {\omega -k} \right) +2n\sin \left( {\omega t+\beta } \right) \cdot \cos \left( {\omega t+\beta } \right) \right. \nonumber \\&+\frac{k_2^2 }{2\sigma k}\cos \left( {\omega t-\beta } \right) \cdot \cos \left( {\omega t+\beta } \right) \nonumber \\&+\frac{k_3^2 }{2\sigma k}\sin \left( {\omega t-\beta } \right) \cdot \cos \left( {\omega t+\beta } \right) \nonumber \\&+\frac{3A^{2}k_2^2 }{4\sigma ^{3}k}\cos \left( {\omega t-\beta } \right) \cdot \cos \left( {\omega t+\beta } \right) \nonumber \\&+\frac{3A^{2}k_3^2 }{4\sigma ^{3}k}\sin \left( {\omega t-\beta } \right) \cdot \cos \left( {\omega t+\beta } \right) \nonumber \\&+\frac{3A^{2}k_1^2 }{2\sigma ^{3}k}\cos ^{2}\left( {\omega t+\beta } \right) \nonumber \\ \frac{\mathrm{d}^{2}\Omega }{\mathrm{d}t^{2}}= & {} \varepsilon \left[ B-N_1 -\frac{N_1 }{2\sigma ^{2}}A^{2}-\frac{3N_1 }{8\sigma ^{4}}A^{4}\right. \nonumber \\&-\left( {\frac{A^{2}}{4\sigma ^{2}}+\frac{A^{4}}{4\sigma ^{4}}} \right) \left( {N_3 \cos 2\eta +LN_2 \sin 2\eta } \right) \nonumber \\ \end{aligned}$$

(16)

The right side of $\frac{\mathrm{d}A}{\mathrm{d}t}, \frac{\mathrm{d}\beta }{\mathrm{d}t}$, and $\frac{\mathrm{d}\Omega }{\mathrm{d}t}$ in Eq. (16) contains the small parameter, and thus, A, $\beta$, and $\Omega$ are slowly varying functions. We use the average method from nonlinear vibration theory to transform the standard nonlinear differential equations [1]. The approximate solution of Eq. (16) is

$$\begin{aligned} \left\{ {\begin{array}{l} A=a+\varepsilon F_1 \left( {t,a,\eta ,\rho } \right) \\ \beta =\eta +\varepsilon F_2 \left( {t,a,\eta ,\rho } \right) \\ \Omega =\rho +\varepsilon F_3 \left( {t,a,\eta ,\rho } \right) \\ \end{array}} \right. \end{aligned}$$

(17)

where $F_1 \left( {t,a,\eta ,\rho } \right)$, $F_2 \left( {t,a,\eta ,\rho } \right)$, and $F_3 \left( {t,a,\eta ,\rho } \right)$ are the small periodic functions. At the same time, the derivative of new variables a, $\eta$, and $\rho$ satisfies

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}a}{\mathrm{d}t}=\varepsilon Y_1 \left( {a,\eta ,\rho } \right) +\varepsilon ^{2}Y_1 ^{{*}}\left( {t,a,\eta ,\rho ,\varepsilon } \right) \\ \frac{\mathrm{d}\eta }{\mathrm{d}t}=\varepsilon Y_2 \left( {a,\eta ,\rho } \right) +\varepsilon ^{2}Y_2 ^{{*}}\left( {t,a,\eta ,\rho ,\varepsilon } \right) \\ \frac{\mathrm{d}\rho }{\mathrm{d}t}=\varepsilon Y_3 \left( {a,\eta ,\rho } \right) +\varepsilon ^{2}Y_3 ^{{*}}\left( {t,a,\eta ,\rho ,\varepsilon } \right) \\ \end{array}} \right. \end{aligned}$$

(18)

A first-order approximate solution can be obtained by substituting Eqs. (17) and (18) into (16):

$$\begin{aligned} \frac{\mathrm{d}a}{\mathrm{d}t}= & {} -\,\varepsilon \left[ \mu a+\frac{k_2^2 \left( {\sigma ^{2}+a^{2}} \right) a}{4k\sigma ^{3}}\sin 2\eta \right. \nonumber \\&\left. +\frac{k_3^2 \left( {\sigma ^{2}+a^{2}} \right) a}{4k\sigma ^{3}}\cos 2\eta \right] \nonumber \\ \frac{\mathrm{d}\eta }{\mathrm{d}t}= & {} -\,\varepsilon \left[ \left( {\omega -k} \right) +\frac{3k_1^2 a^{2}}{4k\sigma ^{3}}+\frac{k_2^2 \left( {\sigma ^{2}+2a^{2}} \right) }{4k\sigma ^{3}}\cos 2\eta \right. \nonumber \\&\left. -\frac{k_3^2 \left( {\sigma ^{2}+a^{2}} \right) a}{4k\sigma ^{3}}\sin 2\eta \right] \nonumber \\ \frac{\mathrm{d}\rho }{\mathrm{d}t}= & {} \varepsilon \left[ B-N_1 -\frac{N_1 }{2\sigma ^{2}}a^{2}-\frac{3N_1 }{8\sigma ^{4}}a^{4}\right. \nonumber \\&-\frac{N_3 }{4}\left( {\frac{a^{2}}{\sigma ^{2}}+\frac{a^{4}}{\sigma ^{4}}} \right) \cos 2\eta \nonumber \\&\left. -\frac{N_2 }{4}\left( {\frac{a^{2}}{\sigma ^{2}}+\frac{a^{4}}{\sigma ^{4}}} \right) \sin 2\eta \right] \end{aligned}$$

(19)

When the vibration is unsteady, the amplitude a, phase angle $\eta$, and angular velocity $\Omega$ change with time, and vice versa, when the vibration is steady. $\frac{\mathrm{d}a}{\mathrm{d}t}=\frac{\mathrm{d}\eta }{\mathrm{d}t}=0$ defines the condition for steady-state vibration, yielding

$$\begin{aligned}&\mu a+\frac{k_2^2 \left( {\sigma ^{2}+a^{2}} \right) a}{4k\sigma ^{3}}\sin 2\eta \nonumber \\&\quad +\frac{k_3^2 \left( {\sigma ^{2}+a^{2}} \right) a}{4k\sigma ^{3}}\cos 2\eta =0 \nonumber \\&\left( {\omega -k} \right) +\frac{3k_1^2 a^{2}}{4k\sigma ^{3}}+\frac{k_2^2 \left( {\sigma ^{2}+2a^{2}} \right) }{4k\sigma ^{3}}\cos 2\eta \nonumber \\&\quad -\frac{k_3^2 \left( {\sigma ^{2}+a^{2}} \right) a}{4k\sigma ^{3}}\sin 2\eta =0 \nonumber \\&L-N_1 -\frac{N_1 }{2\sigma ^{2}}a^{2}{-}\frac{3N_1 }{8\sigma ^{4}}a^{4}-\frac{N_3 }{4}\left( {\frac{a^{2}}{\sigma ^{2}}{+}\frac{a^{4}}{\sigma ^{4}}} \right) \cos 2\eta \nonumber \\&\quad -\frac{N_2 }{4}\left( {\frac{a^{2}}{\sigma ^{2}}+\frac{a^{4}}{\sigma ^{4}}} \right) \sin 2\eta =0 \end{aligned}$$

(20)

The amplitude–frequency and phase–frequency during steady-state vibration can be studied using Eq. (20). The transient vibration can be studied using Eq. (19). For example, the transition from resonance to transience in the resonance region can be studied. Second- and higher-order terms were neglected during the subsequent analysis. This simplifies Eq. (20) as follows:

$$\begin{aligned}&\mu a+\frac{k_2^2 a}{4k\sigma }\sin 2\eta +\frac{k_3^2 a}{4k\sigma }\cos 2\eta =0 \nonumber \\&\left( {\omega -k} \right) +\frac{3k_1^2 a^{2}}{4k\sigma ^{3}}+\frac{k_2^2 }{4k\sigma }\cos 2\eta -\frac{k_3^2 a}{4k\sigma }\sin 2\eta =0 \nonumber \\&B-N_1 -\frac{N_1 }{2\sigma ^{2}}a^{2}-\frac{N_3 a^{2}}{4\sigma ^{2}}\cos 2\eta -\frac{N_2 a^{2}}{4\sigma ^{2}}\sin 2\eta =0\nonumber \\ \end{aligned}$$

(21)

Calculation and analysis can be carried out separately in the two cases using Eqs. (20) and (21).

Table 1 Prototype parameters

4 Effects of changes in system parameters on rotor response

$\sin 2\eta$ and $\cos 2\eta _{ }$can be solved using the first and second forms of Eq. (21). The equation describing the amplitude is obtained using $\sin ^{2}2\eta +\cos ^{2}2\eta =1$:

$$\begin{aligned}&a=\sqrt{-\frac{4\sigma ^{2}}{3k_1 }\left[ {\sigma \left( {\omega -k} \right) k\pm \sqrt{\frac{k_2^2 +k_3^4 }{16}-\mu ^{2}\sigma ^{2}k^{2}}} \right] }\nonumber \\ \end{aligned}$$

(22a)

$$\begin{aligned}&\tan 2\eta =\frac{4\sigma ^{3}\mu kk_2^2 -3k_1^2 k_3^2 a^{2}-4(\omega -k)\sigma ^{3}kk_3^2 }{4\sigma ^{3}\mu kk_2^2 +3k_1^2 k_3^2 a^{2}+4(\omega -k)\sigma ^{3}kk_3^2 }\nonumber \\ \end{aligned}$$

(22b)

The boundary width of the parametric resonance region can be obtained as follows:

$$\begin{aligned}&k-\sqrt{\frac{k_2^2 +k_3^4 }{16\sigma ^{2}k^{2}}-\mu ^{2}}<\omega <k+\sqrt{\frac{k_2^2 +k_3^4 }{16\sigma ^{2}k^{2}}-\mu ^{2}}\nonumber \\ \end{aligned}$$

(23a)

$$\begin{aligned}&\Delta \omega =2\sqrt{\frac{k_2^2 +k_3^4 }{16\sigma ^{2}k^{2}}-\mu ^{2}} \end{aligned}$$

(23b)

Meanwhile, the angular velocity can be determined from the third equation in Eq. (21):

$$\begin{aligned} T=N_1 +\frac{N_1 }{2\sigma ^{2}}a^{2}+\frac{N_3 a^{2}}{4\sigma ^{2}}\cos 2\eta +\frac{N_2 a^{2}}{4\sigma ^{2}}\sin 2\eta \end{aligned}$$

(24)

Rotational equation equilibrium is defined when the following equation is satisfied:

$$\begin{aligned} B-T=0 \end{aligned}$$

(25)

In general, the mechanical parameters will not change during operation, and thus, the resonance region and amplitude shape will not change. However, the electromagnetic parameters $k_{2}$ and $k_{3}$ will vary with changes in load and other electromagnetic parameters, and thus, the region and shape of the parameter resonance determined by $k_{2}$ and $k_{3}$ will change.

A high power density PMSM and rotor were simulated with the computational parameters listed in Table 1. The characteristic curves describing amplitude–frequency [Eq. (22a)] and phase–frequency [Eq. (22a)] of multiple electromechanical coupling parameters are shown in Fig. 3. The parametric resonance amplitude curve has two branched curves AB and CD. As the excitation frequency $\omega$ increases, the amplitude curves vary along the F–D–E–B route. The amplitude jumps to point E when the excitation frequency increases to point D, indicating the parametric resonance was excited. The amplitude decreases gradually as the excitation frequency $\omega$ continues increasing along the EB branch to point B, and then, the parameter vibration disappeared completely. On the contrary, when the excitation frequency $\omega$ decreased to a small value, the amplitude curve varies along B–E–A–C–F. The parametric resonance was excited, and the amplitude increases gradually when the excitation frequency decreases to point B. The amplitude is maximized at point A and suddenly drops to point F, and resonance in the coupling parameters completely disappeared. This amplitude jump phenomenon occurs at resonance, resulting in catastrophic failure of the system.

Fig. 3

Amplitude–frequency and phase–frequency characteristic curves for various values of the periodic coefficients (cos$\psi$ = 0.5)

One can see that the phase–frequency curve is invariant outside the boundary of the parameter resonance area, and it begins to change when the excitation frequency $\omega$ varies within the resonance boundary. In particular, the phase–frequency curve exhibits jump mutation when the excitation frequency equals to resonance point. If the motor rotor operates within the parameter resonance area for a long time, fatigue damage accumulates in the rotor.

From the view of control, the PMSM can be used to regulate the stator armature current by controlling the inner power factor angle. Thus, the internal power factor angle determines different control states for the PMSM. The parametric resonance amplitude curves were compared with three different PMSM operating states, which is shown in Fig. 4. It can be seen that the amplitude and resonance region width for $\hbox {cos}{\psi }= 0.3$ is a factor 2 to 3 larger than that for $\hbox {cos}{\psi }= 0.5$ and $\hbox {cos}{\psi }= 0.6$. Consequently, the inner power factor angle plays a critical role in determining the resonance amplitude and width of the resonance region. This will stimulate resonance in the coupling parameters resonance if the internal power factor angle control is unreasonable.

Fig. 4

Comparison of the amplitude–frequency characteristics in three operating states

Fig. 5

Resonance zone boundary width $\Delta {\omega }$ in various operating states

Figure 4 shows that the internal power factor angle does not change the inclination of the resonance curve, but it has a great influence on the width of the resonance region. We then plot the resonance region boundary width $\Delta {\omega }$ in Fig. 5 while varying the inner power factor angle. $\Delta {\omega }$ has a tendency to decrease and then increase when cos$\omega$ varies from -1 to 1, and the minimum value corresponds to $\hbox {cos}{\psi }=0.6$. The minimum resonance region boundary width $\Delta \omega$ is about 10% of the maximum value. $\hbox {cos}{\psi }<0$ indicates the PMSM operates in the field enhanced area, and vice versa, when $\hbox {cos}{\psi }>0$. In order to expand the speed range, a high power density PMSM (e.g., the motor used in an electric vehicle) is usually controlled in the field weakened area. Moreover, we find that the appropriate minimum value can be found in the field weakened area. This is similar to the aforementioned resonance in the coupling parameters and is more likely to arise when the internal power factor angle control is unreasonable.

From the perspective of design, the number of turns in the coil multiplied by the current (NI, i.e., ampere-turn) is an important design parameter. Ampere-turn is the unit of magnetic potential in a magnetic circuit. According to Ampere’s law, the magnetic potential $F=\oint$Hdl reflects the ability of a current to generate a magnetic field. If compared with the power supply in a circuit, this can be understood as a “magnetic source.” The resonance region boundary width $\Delta \omega$ corresponding to variation in ampere-turn is shown in Fig. 6, which shows that $\Delta \omega$ increases first and then decreases as NI increases, and there exists a minimum value. The difference between the minimum and maximum value is nearly a factor 3. Therefore, NI has a great influence on resonance and this parameter should be considered carefully when designing a motor.

5 Stability analysis of multiple coupling dynamics

The stability of the multiple electromechanically coupled vibration system in the steady state can be analyzed by using Eqs. (19), which can be rewritten in the following form:

$$\begin{aligned} \frac{\mathrm{d}a}{\mathrm{d}t}= & {} f_1 \left( {a,\eta ,\rho } \right) \nonumber \\ \frac{\mathrm{d}\eta }{\mathrm{d}t}= & {} f_2 \left( {a,\eta ,\rho } \right) \nonumber \\ \frac{\mathrm{d}\rho }{\mathrm{d}t}= & {} f_3 \left( {a,\eta ,\rho } \right) \end{aligned}$$

(26)

In the perturbed system, $a, \eta$, and $\rho$ expressed as

$$\begin{aligned} a=a_0 +a_1 , \eta =\eta _0 +\eta _1 , \rho =\rho _0 +\rho _1 \end{aligned}$$

(27)

Fig. 6

Resonance zone boundary width $\Delta \omega$ for various values of NI

where $a_{0}$, $\eta _{0}$, and $\rho _{0}$ denote the steady-state motion of the system. These parameters are roots of the steady-state equation group as shown in Eq. (20). $a_{1}$, $\eta _{1}$, and $\rho _{1}$ denote small values relative to the motion in the steady state. According to the stability criterion of a nonlinear system [4], substituting Eqs. (27) into (26) and then expanding it to a series form yield the following variational equation:

$$\begin{aligned}&\frac{\mathrm{d}a_1 }{\mathrm{d}t}=d_{11} a_1 +d_{12} \eta _1 +d_{13} \rho _1 \nonumber \\&\frac{\mathrm{d}\eta _1 }{\mathrm{d}t}=d_{21} a_1 +d_{22} \eta _1 +d_{23} \rho _1 \nonumber \\&\frac{\mathrm{d}\rho _1 }{\mathrm{d}t}=d_{31} a_1 +d_{32} \eta _1 +d_{33} \rho _1 \end{aligned}$$

(28)

The coefficient matrix is:

$$\begin{aligned} \left| {d_{ij} } \right| =\left| {{\begin{array}{lll} {\frac{\partial f_1 ^{0}}{\partial a}}&{} {\frac{\partial f_1 ^{0}}{\partial \eta }}&{} {\frac{\partial f_1 ^{0}}{\partial \rho }} \\ {\frac{\partial f_2 ^{0}}{\partial a}}&{} {\frac{\partial f_2 ^{0}}{\partial \eta }}&{} {\frac{\partial f_2 ^{0}}{\partial \rho }} \\ {\frac{\partial f_3 ^{0}}{\partial a}}&{} {\frac{\partial f_3 ^{0}}{\partial \eta }}&{} {\frac{\partial f_3 ^{0}}{\partial \rho }} \\ \end{array} }} \right| \end{aligned}$$

(29)

where the superscript 0 indicates the value of partial derivative when $a=a_0$, $\eta =\eta _0$, and $\rho =\rho _0$.

$$\begin{aligned}&d_{11} =\left( {\frac{a}{\sigma ^{2}}+\frac{3a^{3}}{2\sigma ^{4}}} \right) N_1 -\frac{N_3 }{2}\left( {\frac{a\sigma ^{2}+2a^{2}}{\sigma ^{4}}} \right) \cdot Q_1 \\&\quad \qquad +\frac{N_2 }{2}\left( {\frac{a\sigma ^{2}+2a^{2}}{\sigma ^{4}}} \right) \cdot Q_2 \\&d_{12} =-\frac{N_3 }{2}\left( {\frac{a^{2}\sigma ^{2}+a^{4}}{\sigma ^{4}}} \right) \cdot Q_2 \\&\quad \qquad -\frac{N_2 }{2}\left( {\frac{a^{2}\sigma ^{2}+a^{4}}{\sigma ^{4}}} \right) \cdot Q_1 , d_{13} =\frac{\partial T}{\partial \Omega }, \\&Q_1 =\frac{4k\sigma ^{3}\left[ {\left( {\omega -k_a } \right) k_2^2 \left( {\sigma ^{2}+a^{2}} \right) +nk_3^2 \left( {\sigma ^{2}+2a^{2}} \right) } \right] }{\left( {\sigma ^{2}+a^{2}} \right) \left( {\sigma ^{2}+2a^{2}} \right) \left( {k_2^4 +k_3^4 } \right) }, \\&Q_2 =\frac{4k\sigma ^{3}\left[ {\left( {\omega -k_a } \right) k_3^2 \left( {\sigma ^{2}+a^{2}} \right) +nk_2^2 \left( {\sigma ^{2}+2a^{2}} \right) } \right] }{\left( {\sigma ^{2}+a^{2}} \right) \left( {\sigma ^{2}+2a^{2}} \right) \left( {k_2^4 +k_3^4 } \right) }, \\&d_{21} =\frac{2na^{2}}{\sigma ^{2}+a^{2}}, d_{22} =\frac{2a\left( {\omega -k_a } \right) \left( {\sigma ^{2}+a^{2}} \right) }{\sigma ^{2}+2a^{2}}, d_{23} =0, \\&d_{31} =\frac{\partial k_a }{\partial a}+\frac{4a\left( {\omega -k_a } \right) \left( {\sigma ^{2}+a^{2}} \right) }{\sigma ^{2}+2a^{2}}, \\&d_{32} =\frac{2n\left( {\sigma ^{2}+2a^{2}} \right) }{\sigma ^{2}+a^{2}}, d_{33} =0 \end{aligned}$$

According to the Routh–Hurwitz criterion, the sufficient and necessary condition for stability of the multiple electromechanical coupling dynamic equations is that the roots of Eq. (30) have a negative real part:

$$\begin{aligned} \lambda ^{3}+b_1 \lambda ^{2}+b_2 \lambda +b_3 =0 \end{aligned}$$

(30)

That is, $b_1 >0$, $b_3 >0$, and $b_1 b_2 -b_3 >0$, where:

$$\begin{aligned}&b_1 =-\left( {d_{11} +d_{22} +d_{33} } \right) , \\&b_2 =d_{11} d_{33} +d_{11} d_{22} +d_{22} d_{33} \\&\quad -\,d_{32} d_{23} +d_{12} d_{21} +d_{13} d_{31} \\&b_3 =d_{11} d_{23} d_{32} +d_{12} d_{21} d_{33} +d_{13} d_{22} d_{33} \\&\quad -\,d_{11} d_{22} d_{33} -d_{12} d_{23} d_{31} -d_{13} d_{21} d_{32} \end{aligned}$$

Thus, the following equations are the necessary and sufficient conditions for stability:

$$\begin{aligned} \left\{ {\begin{array}{l} \left[ {a\left( {\omega -k_a } \right) \frac{\partial k_a }{\partial a}+4\left( {\omega {-}k_a } \right) ^{2}\frac{\nu ^{2}}{\left( {1{+}2\nu ^{2}} \right) }+\frac{2n^{2}\nu ^{2}\left( {1{+}2\nu ^{2}} \right) ^{2}}{\left( {1+\nu ^{2}} \right) ^{3}}} \right] \cdot N>0 \\ 2n-N>0 \\ N^{2}-2nN-\frac{2a\left( {\omega -k_a } \right) \left( {1+\nu ^{2}} \right) }{\left( {1+2\nu ^{2}} \right) }\frac{\partial k_a }{\partial a}-\frac{8\left( {\omega -k_a } \right) ^{2}\nu ^{2}\left( {1+\nu ^{2}} \right) ^{3}}{\left( {1+\nu ^{2}} \right) ^{2}\left( {1+2\nu ^{2}} \right) ^{2}} \\ \;\;\;\;\;+\frac{2n^{2}\nu ^{2}\left( {1+2\nu ^{2}} \right) ^{3}}{\left( {1+\nu ^{2}} \right) ^{2}\left( {1+2\nu ^{2}} \right) ^{2}}>0 \\ \end{array}} \right. \end{aligned}$$

(31)

where $N=\frac{\partial T}{\partial \Omega }$, $k_a =k-\frac{3k_1 a^{2}}{4k\sigma ^{3}}$, and $\nu =\frac{a}{\sigma }$.

Fig. 7

Stability of the characteristic curve for amplitude frequency

Figure 7 shows the stability of the multiple electromechanical coupling steady-state parameters in three electromagnetic states. With regard to the right branch curve, ${\partial k_a }/{\partial a}<0$ and ${\omega }- k_{a} > 0$. If $N < 0$, Eq. (31) shows that the right branch curve is unstable for small amplitude when the amplitude exceeds a certain value. As can be seen in Fig. 7, line BC in the right branch curve is stable and large amplitude line AB and small amplitude line CD are unstable. With regard to the left branch curve, ${\partial k_a }/{\partial a}<0, {\omega }- k_{a} <0$. If $N < 0$, the first equation in Eq. (31) does not satisfy the stability condition. If $N>$ 0, the second equation in Eq. (31) does not satisfy the stability condition. Consequently, we can reach the conclusion that entire left branch of the curve is unstable. For example, points $P_{1}$ and $P_{2}$ represent two different amplitudes corresponding to a single frequency for specific parameters. It is expected that point $P_{2}$ is unstable and cannot be physically reached by the system.

Fig. 8

Time history for the points B, C, $P_{1}$, and $P_{3}$ as marked in Fig. 7b

One may validate the results obtained from the analytical method with the results obtained by numerically solving Eq. (10). The fourth-order Runge–Kutta method was used to solve Eq. (10) in order to determine the temporal response of the system, as illustrated in Fig. 7b. Four points B, C, $P_1$, and $P_3$ identified with cross-marks on the frequency response curves shown in Fig. 7b are chosen for comparison. The numerical calculation results of the four points are shown in Fig. 8. Take point B as an example, the amplitude of the periodic response obtained by numerically integrating Eq. (10) is found to be 0.7517, while the amplitude obtained by using analytical method is observed to be 0.7164 in Fig. 8a. Hence, the error in the response amplitude is found to be 4.92%. Similarly, after investigation, one finds that the errors for other three points $P_{1}$, $P_{3}$, and C are nearly 4.6%. From the steady-state response, one may note that the result obtained by numerically solving Eq. (10) is found to be consistent with that determined using the analytical method. The error in the amplitude can be substantially reduced by using the higher-order method of multiple scales and the high-order terms in Eq. (20). However, incorporating higher-order terms will increase the computational complexity of the problem. The first-order method of multiple scales and Eq. (21) were used in order to avoid this complexity.

To illustrate the effect of coupling between lateral and torsional vibration, Fig. 9 shows the amplitude–frequency characteristic curves without considering lateral/torsional coupling. By comparing Figs. 7 and 9, it can be seen that the amplitude–frequency curve is obviously different. In addition, when transverse–torsional coupling is considered, there are three instability regions, while there is only one instability region when transverse–torsional coupling is considered. Therefore, coupling between lateral and torsional vibration has a great influence on the vibration of the rotor system.

Fig. 9

Amplitude–frequency characteristic curves without considering lateral/torsional vibration coupling

Fig. 10

Rotation stability at equilibrium

Stability analysis of the rotational equilibrium is shown in Fig. 10. This figure shows that the electromagnetic torque T is a function of amplitude a, in accordance with Eq. (19). As mentioned above, there are two resonance branches (left and right), and thus, the electromagnetic torque T will also exhibit two branch curves ($T_{1}$ and $T_{2})$ in Fig. 10, respectively. Regarding the stability of the right branch line $T_{1}$, the segment CF is stable, while segment AC is unstable.

Curves $B_{1}$, $B_{2}$, and $B_{3}$ represent three kinds of load curves. The two load curves intersect the electromagnetic torque curve $T_{1}$ at a stable points D and E. The motor can run stably at a certain speed in these two situations. On the contrary, the two load curves also intersect the electromagnetic torque curve $T_{1}$ at unstable points I and J, meaning that the PMSM is not stable in these two situations. When the load curve is steeper, e.g., when the slope of the $B_{3}$ curve is larger than that of $T_{1}$, curve $B_{3}$ intersects the electromagnetic torque curves $T_{1}$ and $T_{2}$ at the unstable points, and thus, the motor is unstable in this load condition.

6 Conclusions

Nonlinear coupling between lateral and torsional vibrations in a high power density PMSM rotor caused by electromagnetic excitation was investigated in this study. A multiple electromechanical coupling dynamic model of an eccentric PMSM rotor was derived using Lagrange–Maxwell theory. An average method was used to determine steady-state motion of the rotor under the influence of electromagnetic excitation. Stability analysis was performed using the Routh–Hurwitz criterion and a numerical scheme with the Runge–Kutta method. The effect of design and control parameters on the dynamic behavior of the system was characterized. We arrive at the following important results:

• A significant reduction in the magnitude of the critical speed was observed as the unbalanced electromagnetic excitation induced by electromechanical coupling increased. One can conclude that electromagnetic excitation acting on the rotor produces negative stiffness. Consequently, the natural frequency decreased below a certain threshold, leading to resonance and unstable motion.

• The conditions for stable resonance were determined. The resonance curve for the coupling parameters contains two branch curves. The left branch is stable, while the right branch is only partially stable. Parametric resonance can be stimulated when the excitation frequency increases to a certain degree and range. In particular, an amplitude jump phenomenon arises within the resonant area. Numerical calculations were used to validate the analytic results.

• The phase–frequency curve is invariant outside the boundary of the parameter resonance area. When the excitation frequency was set equal to the resonance point, the phase–frequency curve exhibits jump mutation. If the motor rotor operates within the parameter resonance area for a long time, the rotor may experience fatigue damage.

• The control and design parameters of the motor have great influence on the resonance amplitude and width of the resonance region for the rotor system. Parametric resonance will occur, and the width of the resonance region will change if control over the internal power factor angle is unreasonable or the value of NI in the motor is inappropriate.

• The operating conditions and external load conditions on a high power density PMSM have greater influence on the stability of the multiple electromechanical coupling dynamics. The electromagnetic state of the motor and the rate of change in the external load may cause the system to enter the unstable operating area.

The results provide a theoretical basis for design and control of electromechanical systems that use PMSMs.