EM algorithm-based identification of a class of nonlinear Wiener systems with missing output data

Abstract

This paper is concerned with the problem of parameter estimation for nonlinear Wiener systems in the stochastic framework. Based on the expectation–maximization (EM) algorithm in dealing with the incomplete data, it is applied to estimate the parameters of nonlinear Wiener models considering the randomly missing outputs. By means of the EM approach, the parameters and the missing outputs can be estimated simultaneously. To obtain the noise-free output in the linear subsystem of the Wiener model, the auxiliary model identification idea is adopted here. The simulation results indicate the effectiveness of the proposed approach for identification of a class of nonlinear Wiener models.

1 Introduction

Many industrial processes have the feature of nonlinearity and dynamic nature [1, 2]. Some nonlinear systems are too complicated for researchers to study their corresponding performances. System identification is to find a system model based on measured data [3, 4] and is basis for signal processing, process monitoring and optimization [5, 6]. So-called block-oriented models, such as Wiener and Hammerstein models, can be used to approximate many nonlinear dynamic processes and have a simple structure as well [7, 8]. The Wiener model can be represented by a dynamic linear subsystem followed by a nonlinear static block. It is a reasonable model for a distillation column, a pH control process, a linear system with a nonlinear measurement device, etc. [9]. In the field of system identification, many least-squares-based identification methods and their extension versions have been developed to cope with the identification issues for Wiener systems [10–12]. Wigren [13, 14] proposed a recursive prediction error identification algorithm to identify the nonlinear Wiener model, and the convergence property of the algorithm was established. Wang et al. [15, 16] proposed auxiliary model-based and gradient-based iterative identification algorithms for Wiener or Hammerstein nonlinear systems.

Xiong et al. [17] derived an iterative numerical algorithm for modeling a class of output nonlinear Wiener systems. Westwick and Verhaegen [18] extended the multivariable output-error state space subspace model identification schemes to identify Wiener systems. Hagenblad et al. [9] proposed a maximum-likelihood method with general consistency property for identification of Wiener models. Among the literatures mentioned above, most of the contributions were derived from the same assumption that the input–output measurement data are available at every sampling instant. That is to say, the measurement data set for identification are complete.

Because of the growing scale and complexity of process industry, data missing problem is commonly encountered and should be handled carefully because of its negative effects imposed on the process identification and control [19]. There are many reasons for data missing such as a sudden mechanical fault, hardware measurement failures, data transmission malfunctions and losses in network communication [20, 21]. In such cases, the standard least-squares-based identification algorithm cannot be applied to estimate the system parameters directly. Ding et al. [22] presented an auxiliary model-based least-squares algorithm and hierarchical least-squares identification algorithm to identify the parameters of dual-rate systems, which can be seen as a special case, but may not be directly applied to identification with irregularly or randomly missing data. Then, the recursive least-squares algorithm combined with an auxiliary model was derived to cope with possibly irregularly missing outputs through output-error models and convergence properties were established simultaneously [23]. They derived the parameter estimation algorithm for systems with scarce measurements which are extension from dual-rate systems through gradient-based algorithm [24]. An output-error method is used [25] to identify systems with slowly and irregularly sampled output data. It was proven that when the system is in the model set, the consistence and minimum variance property of the output-error model can be obtained.

On the other hand, some works on irregularly or randomly missing data problems under the statistical framework have been paid great attention since 1990’s. Isaksson [26] studied parameter estimation of an ARX model when the measurement information may be incomplete by using several methods including the Kalman filtering and smoothing, maximum-likelihood estimation, and a new method so-called the expectation–maximization (EM) algorithm. A simplified iteration of data reconstruction and ARX parameter estimation were proposed in [27]. Raghavan and Gopaluni et al. [28] studied the EM-based state space model identification problems with irregular output sampling and presented some simulations, laboratory-scale and industrial case studies. Xie et al. [29] proposed a new EM algorithm-based approach to estimate an FIR model for multirate processes with random delays. Because of the feature of the statistical properties and the simplicity to realize, the EM algorithm has been used in linear parameter varying (LPV) soft sensor development and nonlinear parameter varying systems with irregularly missing output data [30–32].

The objective of this paper is to handle parameter identification and output estimation problems for nonlinear Wiener systems with randomly missing output data using the EM algorithm. The auxiliary model identification idea is utilized to estimate the noise-free output iteratively in the linear dynamic subsystem and the parameter estimation and missing output estimation are handled simultaneously in the EM algorithm.

The remainder of this paper is organized as follows. Section 2 introduces the identification model of nonlinear Wiener models and the data missing patterns. In Sect. 3, the auxiliary model identification idea is used to estimate the noise-free output of the dynamic linear subsystem in the nonlinear Wiener model. Based on this idea, the identification algorithm under the framework of the EM algorithm to deal with randomly missing output data is derived. Section 4 provides an illustrative example to show the effectiveness of the proposed algorithm. Finally, we draw some conclusions in Sect. 5.

2 Problem statement

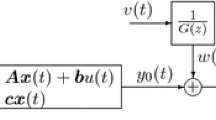
Consider the stochastic Wiener model as shown in Fig. 1 with randomly missing output data. It is composed of a linear dynamic subsystem followed by a static nonlinear block. Assume that $\{u(t),t=1,2,\ldots ,N\}$ is the input sequences of the system, $\{y(t),t=1,2,\ldots ,N\}$ is the measurable output but randomly missing with certain percentage, ${e(t)}$ is a white noise sequence with zero mean and variance $\sigma ^2$, and $A(z^{-1})$ and $B(z^{-1})$ are polynomials in the unit backward shift operator, namely $z^{-1}y(t)=y(t-1)$.

Fig. 1

The Wiener nonlinear system [23]

The linear dynamic subsystem takes the form,

$$\begin{aligned} x(t)&=\frac{B(z^{-1})}{A(z^{-1})}u(t) \nonumber \\&=-a_{1}x(t-1)+\cdots -a_{n}x(t-a_n)\nonumber \\&\quad + b_{1}u(t-1) +\cdots +b_{n}u(t-b_n) \nonumber \\&=\varphi _p^{T}(t)\vartheta _p, \end{aligned}$$

(1)

where $A(z^{-1})$ and $B(z^{-1})$ are polynomials defined as

$$\begin{aligned} A(z^{-1})&=1+a_1 z^{-1}+a_2 z^{-2}+\cdots +a_n z^{-a_n}, \nonumber \\ B(z^{-1})&=b_1 z^{-1}+b_2 z^{-2}+\cdots +b_n z^{-b_n}. \end{aligned}$$

(2)

For this class of Wiener systems, the static nonlinear block $f(\cdot )$ is generally assumed to be the sum of nonlinear basis functions based on a known basis $f = (f_1,f_2,\ldots ,f_n)$:

$$\begin{aligned} y(t)&=f(x(t))+e(t) \nonumber \\&=r_1 f_1(x(t))+r_2 f_2(x(t))\nonumber \\&\quad +\cdots +r_{n_r}f_{n_r}(x(t))+e(t) \end{aligned}$$

(3)

Here, we assume that the nonlinear function $f(\cdot )$ can be represented by the polynomial with the order $r$:

$$\begin{aligned} f(x(t))&=r_1 x(t)+r_2 x^2(t)+\cdots +r_{n_r}x^{n_r}(t) . \end{aligned}$$

(4)

As seen from Fig. 1, the linear noise-free block output $x(t)$ is the input of the nonlinear block in the nonlinear Wiener system. A direct substitution of $x(t)$ from Eqs. (1) to (4) would result in a very complex expression. Therefore, the key-term separation principle is incorporated to simplify this problem, namely the first coefficient of the nonlinear block is fixed to 1, i.e., $r_1=1$. Then, the system output $y(t)$ can be written as

$$\begin{aligned} y(t)&=x(t)+\sum _{i=2}^{n_r} r_i x^i(t)+e(t) \nonumber \\&=\varphi _p^T(t)\vartheta _p+\varphi _r^T(t)\vartheta _r+e(t) \nonumber \\&=\varphi ^T(t)\vartheta +e(t), \end{aligned}$$

(5)

where the information vector $\varphi (t)$ includes $\varphi _p(t)$ is defined as:

$$\begin{aligned} \varphi _p(t)&=\left[ -x(t-1),~ -x(t-2),\ldots , ~-x(t-n_a)\right. \nonumber \\&\quad \ \left. ~u(t-1),~ u(t-2),\ldots , ~u(t-n_b)\right] ^T \nonumber \\&\quad \ \times \in \mathbb {R}^{n_a+n_b}\nonumber \\ \vartheta _p&=\left[ a_1, ~a_2,\ldots , ~a_{n_a}~ b_1,~ b_2,\ldots ,~ b_{n_b} \right] ^T\nonumber \\&\quad \ \times \in \mathbb {R}^{n_a+n_b}\nonumber \\ \varphi _r(t)&=\left[ x^2(t),\ldots ,~ x^{n_r}(t)\right] ^T \in \mathbb {R}^{n_r-1}\nonumber \\ \vartheta _r&=\left[ r_2,\ldots ,~ r_{n_r} \right] ^T \in \mathbb {R}^{n_r-1} \nonumber \\ \varphi (t)&=\left[ \varphi _p^T(t), ~~ \varphi _r^T(t) \right] ^T \in \mathbb {R}^{n_a+n_b+n_r-1} \nonumber \\ \vartheta&=\left[ \vartheta _p, ~~\vartheta _r\right] ^T \in \mathbb {R}^{n_a+n_b+n_r-1} \end{aligned}$$

(6)

The missing data problem is very common in process industry. In this article, we assume that the causes for the missing outputs are unknown and believe that the occurrence of missing outputs does not depend on any input and output. This means part of the outputs is missing completely at random (MCAR) [20]. Thereafter, the data $Y$ are divided into two parts, the randomly missing output $Y_\mathrm{mis}=\{y_t\}_{t=m_1,\ldots ,m_{\alpha }}$ and the observed output sequence $Y_\mathrm{obs}=\{y_t\}_{t=o_1,\ldots ,o_{\beta }}$. So, the identification problem considered under the EM framework is to estimate the parameters $\vartheta =\{\vartheta _p,\vartheta _r\}$ and the noise variance $\sigma ^2$ based on the following data set:

$$\begin{aligned} C_\mathrm{obs}&= \{Y_\mathrm{obs},U \},\end{aligned}$$

(7)

$$\begin{aligned} C_\mathrm{mis}&= \{Y_\mathrm{mis}\}. \end{aligned}$$

(8)

3 The EM algorithm-based identification approach

3.1 The EM algorithm revisited

The EM algorithm is an ideal candidate for solving estimation problems for the maximum-likelihood estimate in the presence of missing data. The core idea behind the EM algorithm is to introduce hidden or missing variables to make the maximum-likelihood estimates tractable [33]. The observed data set $C_\mathrm{obs}$ with missing data set $C_\mathrm{mis}$ performs a series of iterative optimizations. The steps including E-step and M-step proceed as follows [33]:

• 1) Initialization: initialize the value of the model parameter vector $\varTheta ^{0}$.

• 2) E-step: given the parameter estimate $\varTheta ^{s}$ obtained in the previous iteration, calculate the Q-function

  $$\begin{aligned} Q(\varTheta | \varTheta ^{s})&=E_{C_\mathrm{mis}|C_\mathrm{obs},\varTheta ^{s}}\{\log p(C_\mathrm{obs},C_\mathrm{mis})|\varTheta )\}, \end{aligned}$$

• 3) M-step: calculate the new parameter estimate $\varTheta ^{s+1}$ by maximizing $Q(\varTheta | \varTheta ^{s})$ with respect to $\varTheta$. That is

  $$\begin{aligned} \varTheta ^{s+1}&= \arg \max _{\varTheta } Q(\varTheta |\varTheta ^{s}). \end{aligned}$$

The procedure including E-step and M-step is carried out iteratively until the change in parameters after each iteration is within a specified tolerance level. The value of the Q-function is ensured to be non-decreasing at each iteration. The convergence of the EM algorithm has been proved by Wu [34].

3.2 The application of auxiliary model approach

Because $x(t)$ in the information vector $\varphi _p(t)$ are unknown and are also included in $\varphi _r(t)$ and $\varphi (t)$, the calculation of E-step cannot be applied to Eq. (5) directly. The solution is to construct an auxiliary model or reference model $B_a(z^{-1})/A_a(z^{-1}))$ using the system input $u(t)$, where $B_a(z^{-1})$ and $A_a(z^{-1})$ have the same order with $B(z^{-1})$ and $A(z^{-1})$ [35]. The main idea of auxiliary model approach can be described as shown in Fig. 2.

$$\begin{aligned} x_a(t)&=\frac{B_a(z^{-1})}{A_a(z^{-1})}u(t)\nonumber \\&=-a_{1}x_a(t-1)+\cdots -a_{n}x_a(t-a_n)\nonumber \\&\quad + b_{1}u(t-1)+\cdots +b_{n}u(t-b_n) \nonumber \\&=\varphi _a^T(t)\vartheta _a, \end{aligned}$$

(9)

where $\varphi _a(t)$ and $\vartheta _a$ are the information vector and the parameter vector of the auxiliary model, respectively. If we replace these unknown $x(t)$ in the information vector $\varphi _p(t)$ with output $x_a(t)$ of the auxiliary model, then the identification problem of $\vartheta$ can be solved by using $u(t)$, $y(t)$ and $x_a(t)$. It is noticed that the output $x_a(t)$ of the auxiliary model denoted by $\hat{x}(t)$ is used here as the estimate of $x(t)$. Define

$$\begin{aligned} \hat{\varphi }_p(t)&=\left[ -\hat{x}(t-1),-\hat{x}(t-2), \ldots , -\hat{x}(t-n_a),\right. \nonumber \\&\quad \left. u(t-1), u(t-2),\ldots , u(t-n_b)\right] ^T \nonumber \\ \hat{\varphi }_r(t)&=\left[ \hat{x}^2(t),\ldots ,~ \hat{x}^{n_r}(t) \right] ^T \nonumber \\ \hat{\varphi }(t)&=\left[ \hat{\varphi }_p^T(t), ~~ \hat{\varphi }_r^T(t) \right] ^T \end{aligned}$$

(10)

In identification, we use $\hat{\varphi }(t)$ to replace $\varphi (t)$, and based on the renewed and complete the information vectors, the EM algorithm can be carried out to identify the parameters of the Wiener model.

Fig. 2

The Wiener nonlinear system with the auxiliary model [23]

3.3 The mathematical formulation of the identification problem with EM algorithm

In this section, the EM algorithm is applied to solve the identification problem. The unknown parameters are $\varTheta =\{\vartheta , \sigma ^2\}$. The complete log likelihood function can be first decomposed using the probability chain rule as follows:

$$\begin{aligned} \log p(Y,U|\varTheta )&=\log p(Y|U,\varTheta )p(U|\varTheta ) \end{aligned}$$

(11)

The first term $p(Y|U,\varTheta )$ can be decomposed into

$$\begin{aligned}&p(Y|U,\varTheta )=p(y_{1:N}|u_{1:N},\varTheta )\nonumber \\&\!\quad =p(y_N|y_{N-1:1},u_{1:N},\varTheta ) p(y_{N-1:1}|u_{1:N},\varTheta )\nonumber \\&\!\quad =p(y_N|y_{N-1:1},u_{1:N},\varTheta )p(y_{N-1}|y_{N-2:1},u_{1:N},\varTheta )\nonumber \\&\!\quad \quad \times \ldots p(y_2|y_1,u_{1:N},\varTheta ) p(y_1|u_{1:N},\varTheta )\nonumber \\&\!\quad =\prod _{t=1}^{N} p(y_t|y_{t-1:1},u_{1:N},\varTheta )\nonumber \\&\!\quad =\prod _{t=1}^{N} p(y_t|u_{t-1:1},\varTheta ). \end{aligned}$$

(12)

Here, $\prod _{t=1}^{N} p(y_t|y_{t-1:1},u_{1:N},\varTheta )$ can be simplified to $\prod _{t=1}^{N} p(y_t|u_{t-1:1},\varTheta )$ based on the fact that $y_t$ only depends on the previous input sequence, namely $u_{t-1:1}$ and the parameter $\varTheta$. Since the input $U$ of the system is the measurable data and is independent of the parameter $\varTheta$, the second term $p(U|\varTheta )$ is constant defined as $C$. Therefore, the log likelihood function can be written as

$$\begin{aligned} \log p(Y,U|\varTheta )&=\log p(Y|U,\varTheta )p(U|\varTheta ) \nonumber \\&=\sum _{t=1}^{N}\log p(y_t|u_{t-1:1},\varTheta )+\log C \nonumber \\&=\sum _{t=m_1}^{m_\alpha }\log p(y_t|u_{t-1:1},\varTheta )\nonumber \\&\quad +\sum _{t=o_1}^{o_\beta }\log p(y_t|u_{t-1:1},\varTheta )+\log C.\nonumber \\ \end{aligned}$$

(13)

The Q-function can be obtained by calculating the expectation of the complete-data log likelihood function over the missing variable $Y_\mathrm{mis}$,

$$\begin{aligned}&Q(\varTheta |\varTheta ^s)=E_{C_\mathrm{mis}|C_\mathrm{obs},\varTheta ^s}\left\{ \log p(U,Y|\varTheta )\right\} \nonumber \\&\quad =E_{Y_\mathrm{mis}|C_\mathrm{obs},\varTheta ^s}\left\{ \sum _{t=m_1}^{m_\alpha }\log p(y_t|u_{t-1:1},\varTheta )\right. \nonumber \\&\quad \quad \ \left. +\sum _{t=o_1}^{o_\beta }\log p(y_t|u_{t-1:1},\varTheta ) +\log C\right\} \nonumber \\&\quad = \sum _{t=m_1}^{m_\alpha } \int p(y_t|C_\mathrm{obs},\varTheta ^s)\log p(y_t|u_{t-1:1},\varTheta ) \mathrm{d} y_t\nonumber \\&\quad \quad \ +\sum _{t=o_1}^{o_\beta } \log p(y_t|u_{t-1:1},\varTheta ) +\log C. \end{aligned}$$

(14)

Based on Eq. (5) and the Gaussian white noise assumption, we have

$$\begin{aligned} p(y_t|u_{t-1:1},\varTheta )\!=\!\frac{1}{\sqrt{2\pi \sigma ^{2}}}\exp \left\{ \frac{-(y_{t}-\varphi ^{T}(t)\vartheta )^2}{2\sigma ^2}\right\} . \end{aligned}$$

(15)

The problem left is to calculate the integral term $\int p(y_t|C_\mathrm{obs},\varTheta ^s)\log p(y_t|u_{t-1:1},\varTheta ) \mathrm{d}y_t$ in the Q-function. Based on the definitions of the first order and second order moments, the integral term can be calculated as

$$\begin{aligned}&\int p(y_t|C_\mathrm{obs},\varTheta ^s)\log p(y_t|u_{t-1:1},\varTheta )\mathrm{d} y_t\nonumber \\&\quad =\int p(y_t|C_\mathrm{obs},\varTheta ^s)\log \frac{1}{\sqrt{2\pi \sigma ^{2}}}\nonumber \\&\qquad \times \exp \frac{-(y_{t}-\varphi ^{T}(t)\vartheta )^2}{2\sigma ^2}\mathrm{d} y_t\nonumber \\&\quad =-\frac{1}{2}\log (2\pi \sigma ^{2})-\frac{1}{2\sigma ^{2}}\int p(y_t|C_\mathrm{obs},\varTheta ^s)\nonumber \\&\qquad \times (y_{t}-\varphi ^{T}(t)\vartheta )^2 \mathrm{d}y_{t}\nonumber \\&\quad =-\frac{1}{2}\log (2\pi \sigma ^{2})-\frac{1}{2\sigma ^{2}}((\sigma ^s)^{2} +(\varphi ^{T}(t)\vartheta ^s)^{2})\nonumber \\&\qquad +\frac{1}{\sigma ^{2}}(\varphi ^{T}(t)\vartheta )(\varphi ^{T}(t)\vartheta ^s)-\frac{1}{2\sigma ^{2}}(\varphi ^{T}(t)\vartheta )^{2}\nonumber \\&\quad =-\frac{1}{2}\log (2\pi \sigma ^{2})-\frac{1}{2\sigma ^{2}}((\sigma ^s)^{2}\nonumber \\&\quad +(\varphi ^{T}(t)\vartheta -\varphi ^{T}(t)\vartheta ^s)^{2}) \end{aligned}$$

(16)

Substituting Eqs. (15) and (16) into Eq. (14), we have

$$\begin{aligned} Q(\varTheta |\varTheta ^s)&=\sum _{t=m_1}^{m_\alpha } \left\{ -\frac{1}{2}\log (2\pi \sigma ^{2}) -\frac{1}{2\sigma ^{2}}((\sigma ^s)^{2}\right. \nonumber \\&\quad \left. +(\varphi ^{T}(t)\vartheta -\varphi ^{T}(t)\vartheta ^s)^{2}\right\} \nonumber \\&\quad +\sum _{t=o_1}^{o_\beta }\left\{ -\frac{1}{2}\log (2\pi \sigma ^2)-\frac{1}{2\sigma ^2}\right. \nonumber \\&\quad \left. \times (y_t-\varphi ^{T}(t)\vartheta )^2\right\} +\log C. \end{aligned}$$

(17)

The following step is to obtain the estimates of all the unknown parameters, that is M-step. Taking the gradient of $Q(\varTheta |\varTheta ^{(s)})$ with respect to $\vartheta$ and $\sigma ^2$, respectively and setting them to zeros, the estimate of $\varTheta$ can be derived as

$$\begin{aligned} \vartheta ^{s+1}&=\frac{\sum _{t=m_1}^{m_\alpha }\varphi (t)\varphi ^{T}(t)\vartheta ^s+\sum _{t=o_1}^{o_\beta }\varphi (t)y(t)}{\sum _{t=1}^{N}\varphi (t)\varphi ^{T}(t)} \end{aligned}$$

(18)

$$\begin{aligned} (\sigma ^{2})^{s+1}=\frac{\sum _{t=m_1}^{m_\alpha } ( (\sigma ^s)^2+(\varphi ^T(t)\vartheta ^{s+1}-\varphi ^T(t)\vartheta ^s )^2 )+ \sum _{t=o_1}^{o_\beta } ( y_t-\varphi ^T(t)\vartheta ^{s+1})^2 }{N} \end{aligned}$$

(19)

The detailed derivations of Eqs. (18) and (19) are given in Appendix.

Since the $\{x(t)\}_{t=1,\ldots ,N}$ in the information vector $\varphi (t)$ are unknown, they can be estimated by using the auxiliary model identification idea. Here, the auxiliary model in Eq. (9) is constructed based on the parameter estimates obtained in previous iteration. Therefore, the estimate of the information vector $\varphi (t)$ can be constructed based on Eq. (10). The new parameter estimates can be calculated by substituting $\varphi (t)$ with $\hat{\varphi }(t)$ in Eqs. (18) and (19):

$$\begin{aligned} \vartheta ^{s+1}=\frac{\sum _{t=m_1}^{m_\alpha }\hat{\varphi }(t)\hat{\varphi }^{T}(t)\vartheta ^s+\sum _{t=o_1}^{o_\beta }\hat{\varphi }(t)y(t)}{\sum _{t=1}^{N}\hat{\varphi }(t)\hat{\varphi }^{T}(t)}, \end{aligned}$$

(20)

$$\begin{aligned} (\sigma ^{2})^{s+1}=\frac{\sum _{t=m_1}^{m_\alpha } ( (\sigma ^s)^2+(\hat{\varphi }^T(t)\vartheta ^{s+1}-\hat{\varphi }^T(t)\vartheta ^s )^2 )+ \sum _{t=o_1}^{o_\beta } ( y_t-\hat{\varphi }^T(t)\vartheta ^{s+1})^2 }{N}. \end{aligned}$$

(21)

3.4 The summary of the proposed identification algorithm

The proposed approach for nonlinear Wiener models taking the randomly missing outputs into account using the EM algorithm can be summarized as follows:

• 1) Set $s=1$ and initialize the parameter vector $\vartheta$ and the variance $\sigma ^2$.

• 2) Calculate the estimates of $\{ x(t)\}_{t=1,\ldots ,N}$ according to Eq. (9) with the parameters obtained in the previous iteration.

• 3) Update the estimates of the parameter $\vartheta ^{s+1}$ and the variance $(\sigma ^2)^{s+1}$ according to Eqs. (20) and (21), respectively.

• 4) Set $s=s+1$ and repeat step 2 to step 3 until convergence.

4 Simulation sample

Considering the following Wiener nonlinear system with the linear subsystem given as follows,

$$\begin{aligned} x(t)&=\frac{B(z^{-1})}{A(z^{-1})}u(t), \nonumber \\ A(z^{-1})&=1\!+\!a_1 z^{-1}\!+\!a_2 z^{-2}\!=\! 1\!+\!0.58z^{-1}\!+\!0.41z^{-2} \nonumber \\ B(z^{-1})&=b_1 z^{-1}+b_2 z^{-2} =-0.18z^{-1}+0.44z^{-2} \end{aligned}$$

(22)

and the nonlinearity is described by

$$\begin{aligned} f(x(t))&=r_1 x(t)+r_2 x^2(t)+\cdots +r_{n_r}x^{n_r}(t) \nonumber \\&=x(t)-0.45x^2(t)+0.25x^3(t) \end{aligned}$$

(23)

The output of the Wiener system $y(t)$ can be expressed as

$$\begin{aligned} y(t)=f(x(t))+e(t) \end{aligned}$$

(24)

For this example system, the parameter vector of the Wiener model to be identified is $\vartheta =[0.58,~0.41, -0.18,~0.44,~-0.45,~0.25]$. The input sequence $u(t)$ and output sequence $y(t)$ are generated by simulation, and $e(t)$ is a white noise process with zero mean and variance $0.001$ added to the output. The input–output data of the system are given in Fig. 3. Setting the missing rate of the output data at around 12.5 %, the proposed method is applied to identify the six parameters and noise variance simultaneously. The initial values of vector $\vartheta$ and variance $\sigma ^2$ are $[0.45,~0.5,~-0.2,~0.5,~-0.41,~0.41]$ and 0.05, respectively. The estimated parameters versus iteration are shown in Fig. 4. It can be seen that the proposed EM-based identification algorithm has good performances since the parameter estimates approach the real ones after a few iterations. The noise variance trajectory is shown in Fig. 5. It is clear that almost all the parameters are close to the real value after 10 iterations.

Fig. 3

The input and output data

Fig. 4

The EM estimates of the Wiener model parameters with output missing 15 %

Fig. 5

The EM estimate of the noise with output missing 15 %

To illustrate the effectiveness of the proposed method in dealing with the randomly data missing, the simulation is also carried out with the missing rate of the output at around 25 and 50 %, respectively. The simulation results are shown from Figs. 6, 7, 8 and  9. It is noticed that the proposed approach keeps a good identification performance when the missing data are near the half of the whole output sequence. To evaluate the performance of the proposed algorithm, the relative error (RE) of the estimated parameter criterion can be used and is defined as:

$$\begin{aligned} \mathrm{RE}= \sqrt{ \frac{\Vert \hat{\varTheta }-\varTheta \Vert }{\Vert \varTheta \Vert } } \end{aligned}$$

(25)

From Table 1, we can see that with the increase in the missing rate, the relative error becomes larger.

Fig. 6

The EM estimates of the Wiener model parameters with output missing 25 %

Fig. 7

The EM estimate of the noise with output missing 25 %

Fig. 8

The EM estimates of the Wiener model parameters with output missing 50 %

Fig. 9

The EM estimate of the noise with output missing 50 %

Table 1 Parameter estimates after 30 iterations under different missing rates

5 Conclusions

This paper considers the parameter identification for a class of nonlinear Wiener models in the stochastic framework and takes the randomly missing output problem into account. To deal with the missing outputs, the EM algorithm is employed to estimate the parameters and the noise variance simultaneously and the unknown noise-free outputs are estimated by using the auxiliary model identification idea [36, 37]. Thereafter, the identification problem is formulated under the framework of the EM algorithm. A numerical example is provided to demonstrate the effectiveness of the proposed algorithm. The proposed algorithm can be extended to study identification problem of other linear systems [38–42] and nonlinear systems [43–45].

Appendix: Detailed derivation of Eqs.(18) and (19)

The Q-function in Eq. (17) can be further written as

$$\begin{aligned}&Q(\varTheta |\varTheta ^s)=\sum _{t=m_1}^{m_\alpha }\left\{ -\frac{1}{2}\log (2\pi \sigma ^{2})-\frac{1}{2\sigma ^{2}}((\sigma ^s)^{2}\right. \nonumber \\&\quad \left. +(\varphi ^{T}(t)\vartheta -\varphi ^{T}(t)\vartheta ^s)^T(\varphi ^{T}(t)\vartheta -\varphi ^{T}(t)\vartheta ^s)\right\} \nonumber \\&\quad +\sum _{t=o_1}^{o_\beta }\left\{ -\frac{1}{2}\log (2\pi \sigma ^{2})-\frac{1}{2\sigma ^{2}}(y_t-\varphi ^T(t)\vartheta )^T\right. \nonumber \\&\quad \left. (y_t-\varphi ^T(t)\vartheta )\right\} +\log C. \end{aligned}$$

(26)

Taking the gradient of $Q(\varTheta |\varTheta ^s)$ with respect to $\vartheta$ and setting it to zero,

$$\begin{aligned} \frac{\partial Q(\varTheta |\varTheta ^s)}{\partial \vartheta }&=\sum _{t=m_1}^{m_\alpha }\left\{ -\frac{1}{2\sigma ^{2}}(2 \varphi (t)\varphi ^{T}(t)\vartheta \right. \nonumber \\&\quad \left. -2\varphi (t)\varphi ^{T}(t)\vartheta ^s)\right\} \nonumber \\&\quad +\sum _{t=o_1}^{o_\beta }\left\{ -\frac{1}{2\sigma ^{2}}(2\varphi (t)\varphi ^{T}(t)\vartheta \right. \nonumber \\&\quad \left. -2\varphi (t)y_t)\right\} \nonumber \\&=0 \end{aligned}$$

(27)

Through keeping the terms that not related with $\vartheta$ at the right side, Eq. (27) can be written as

$$\begin{aligned}&\sum _{t=m_1}^{m_\alpha } \varphi (t)\varphi ^{T}(t)\vartheta +\sum _{t=o_1}^{o_\beta } \varphi (t)\varphi ^{T}(t)\vartheta \nonumber \\&\quad = \sum _{t=m_1}^{m_\alpha } \varphi (t)\varphi ^{T}(t)\vartheta ^s+\sum _{t=o_1}^{o_\beta }\varphi _t y_t \end{aligned}$$

(28)

Then, the new estimate of parameter $\vartheta$ can be obtained as:

$$\begin{aligned} \vartheta ^{s+1}=\frac{\sum _{t=m_1}^{m_\alpha }\varphi (t)\varphi ^{T}(t)\vartheta ^s+\sum _{t=o_1}^{o_\beta }\varphi (t)y(t)}{\sum _{t=1}^{N}\varphi (t)\varphi ^{T}(t)} \end{aligned}$$

(29)

Taking the gradient of $Q(\varTheta |\varTheta ^s)$ with respect to $\sigma ^2$ and setting it to zero,

$$\begin{aligned} \frac{\partial Q(\varTheta |\varTheta ^s)}{\partial \sigma ^2}&=\sum _{t=m_1}^{m_\alpha }\left\{ -\frac{1}{2\sigma ^{2}} + \frac{1}{2\sigma ^4} \left[ (\sigma ^s)^{2}\right. \right. \nonumber \\&\quad \left. \left. +(\varphi ^{T}(t)\vartheta -\varphi ^{T}(t)\vartheta ^s)^{2}\right] \right\} \nonumber \\&\quad +\,\sum _{t=o_1}^{o_\beta } \left\{ -\frac{1}{2\sigma ^{2}} + \frac{1}{2\sigma ^4}(y_t-\varphi ^T(t)\vartheta )^2 \right\} \nonumber \\&=0. \end{aligned}$$

(30)

Through keeping the two terms including $\sigma ^2$ at the left side, the Eq. (30) can be written as:

$$\begin{aligned}&\sum _{t=m_1}^{m_\alpha } \sigma ^2 + \sum _{t=o_1}^{o_\beta } \sigma ^2=N \cdot \sigma ^2\nonumber \\&\quad =\sum _{t=m_1}^{m_\alpha } \left\{ (\sigma ^s)^{2}+(\varphi ^{T}(t)\vartheta -\varphi ^{T}(t)\vartheta ^s)^{2}\right\} \nonumber \\&\qquad +\sum _{t=o_1}^{o_\beta } (y_t-\varphi ^T(t)\vartheta )^2 \end{aligned}$$

(31)

Then, the estimation of parameter $\sigma ^2$ can be obtained as:

$$\begin{aligned} (\sigma ^{2})^{s+1}=\frac{\sum _{t=m_1}^{m_\alpha } ( (\sigma ^s)^2+(\varphi ^T(t)\vartheta ^{s+1}-\varphi ^T(t)\vartheta ^s )^2 )+ \sum _{t=o_1}^{o_\beta } ( y_t-\varphi ^T(t)\vartheta ^{s+1})^2 }{N}\end{aligned}$$

(32)