1 Introduction

For conventional discrete-time sampled-data systems, the input and output are sampled at a single rate and the sampling intervals are assumed to be equally spaced in time [1, 3–6]. In practice, different variables of a system may be sampled at different sampling rates [2, 22] and the sampling frequency may be varying, namely, non-equally spaced in time. The non-uniform sampling scheme has advantages over the uniform one, such as always preserving controllability and observability in discretization when a non-uniformly sampled system is described by a lifted state-space model [11, 17].

Literature on non-uniformly sampled multirate systems includes the generalized predictive control [26], the fault detection and isolation with non-uniformly sampled data [18, 19], the system reconstruction from non-uniformly sampled discrete-time systems [11], etc. Recently, the non-uniformly sampled multirate system identification has attracted much attention. Using lifting technique which is a standard tool of dealing with multirate systems, Ding et al. proposed a hierarchical identification method [11] for the lifted state-space model of the non-uniformly sampled systems [20].

The direct input–output representation is frequently considered when dealing with the non-uniformly sampled systems. Zhu et al. proposed the output error method for slowly and irregularly sampled system [35]. Ding et al. developed the partially coupled stochastic gradient algorithm for non-uniformly sampled-data systems [10]. Liu et al. proposed a recursive least squares algorithm for non-uniformly sampled systems with the aid of an auxiliary model [21]. See also [32–34] and the references therein.

Most of the existing systems can be modeled by state-space equations [12, 14], and the subspace identification methods are quite effective for the identification of state-space models of single-rate discrete-time linear systems [15, 16, 24, 27, 28]. This paper is concerned with the extension of the subspace identification from dual-rate sampled systems [25] to non-uniformly sampled multirate systems. The main purpose of this paper is to develop a subspace identification method that could cope with the causality constraints.

The rest of this paper is organized as follows. In Sect. 2, the lifted state-space model is derived by using the lifting technique, and the identification problem is discussed. Further, a subspace identification algorithm taking the causality constraints into consideration is presented in Sect. 3. In Sect. 4, a simulation example is illustrated for the proposed algorithm. Finally, some concluding remarks are offered in Sect. 5.

2 Problem Description

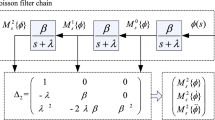
Consider a class of periodically non-uniformly sampled systems as depicted in Fig. 1 [11, 26], where S c is a continuous process,

$$ S_c:\ \begin{cases} \dot{\boldsymbol{x}}(t)=\boldsymbol {A}_c \boldsymbol{x}(t) +\boldsymbol {B}_cu(t),\\ y(t) = \boldsymbol {C}_c\boldsymbol{x}(t) +D_cu(t), \end{cases} $$
(1)

\(\boldsymbol{x}(t)\in\mathbb{R}^{n}\) is the state vector, \(u(t)\in\mathbb{R}\) is the control input, \(y(t)\in\mathbb{R}\) is the system output, A c ,B c ,C c ,D c the matrices with proper dimensions; \(\mathcal {H}_{T}\) and S T are the non-uniformly periodical zero-order holder and sampler with the frame period T, and with the updating and sampling intervals {τ 1,τ 2,…,τ p }, namely, the zero-order holder/sampler non-uniformly updates/samples at time t=kT+t i , i=1,2,…,p, k=0,1,2,… , where t i :=τ 1+τ 2+⋯+τ i (t 0=0), thus the frame period T:=τ 1+τ 2+⋯+τ p .

Fig. 1
figure 1

The periodically non-uniformly sampled systems

Full size image

In the kth period [kT,(k+1)T), the control input u(t) and output y(t) are non-uniformly updated at time t=kT+t i (i=0,1,2,…,p−1), the non-uniformly updating properties [10, 11] are

$$ u(t)= \begin{cases} u(kT), & kT\le t<kT+t_1,\\ u(kT+t_1), & kT+t_1\le t<kT+t_2,\\ \quad\vdots& \\ u(kT+t_{p-1}), & kT+t_{p-1}\le t<(k+1)T. \end{cases} $$
(2)

The system input and output are updated by {τ 1,τ 2,…,τ p } periodically, thus the discrete-time system from the input to output is a time-varying single-input single-output system. By the lifting technique, p inputs are grouped and p outputs are listed together to form \(\underline{\boldsymbol{u}}\) and \(\underline{\boldsymbol {y}}\), leading to a time-invariant multi-input multi-output system:

$$ S:\ \begin{cases} \boldsymbol{x}(kT+T)=\boldsymbol {A}\boldsymbol{x}(kT) +\boldsymbol {B}\underline{\boldsymbol{u}}(kT),\\ \underline{\boldsymbol {y}}(kT) = \boldsymbol {C}\boldsymbol{x}(kT) +\boldsymbol {D}\underline{\boldsymbol{u}}(kT), \end{cases} $$
(3)

with the available non-uniformly sampled data {u(kT+t i ),y(kT+t i ), i=0,1,2,…,p−1}.

Referring to the method in [11] and discretizing (3) yields

$$\begin{aligned} \boldsymbol{x}(kT+T) =&\mathrm {e}^{\boldsymbol {A}_cT}\boldsymbol{x}(kT)+\int^{(k+1)T}_{kT}\mathrm {e}^{\boldsymbol {A}_c((k+1)T-\tau)} \boldsymbol {B}_cu(\tau)\,\mathrm {d}\tau \end{aligned}$$
(4)
$$\begin{aligned} =:&\boldsymbol {A}\boldsymbol{x}(kT)+\sum _{i=1}^{p}\boldsymbol {B}_iu(kT+t_{i-1}), \end{aligned}$$
(5)
$$\begin{aligned} =:&\boldsymbol {A}\boldsymbol{x}(kT)+\boldsymbol {B}\underline{\boldsymbol{u}}(kT), \end{aligned}$$
(6)

where

$$\begin{aligned} \boldsymbol {A} :=&\mathrm {e}^{{\scriptsize \boldsymbol {A}}_cT}\hbox{$\in{\mathbb{R}}^{n\times n}$}, \end{aligned}$$
(7)
$$\begin{aligned} \boldsymbol {B} :=&[\boldsymbol {B}_1, \boldsymbol {B}_2, \ldots, \boldsymbol {B}_p]\in{\mathbb{R}}^{n\times p}, \end{aligned}$$
(8)
$$\begin{aligned} \boldsymbol {B}_i :=&\mathrm {e}^{{\scriptsize \boldsymbol {A}}_c(T-t_i)}\int ^{\tau_i}_0\mathrm {e}^{{\scriptsize \boldsymbol {A}}_ct}\,\mathrm {d}t \boldsymbol {B}_c, \end{aligned}$$
(9)
$$\begin{aligned} \underline{\boldsymbol{u}}(kT) :=& \bigl[u(kT),\ u(kT+t_1),\ \ldots,\ u(kT+t_{p-1}) \bigr]^{\tiny \mathrm {T}} \in{\mathbb{R}}^{p}. \end{aligned}$$
(10)

Because of the non-uniformly zero-order holder in system (1), it is easy to obtain

$$\begin{aligned} \boldsymbol{x}(kT+t_i) =&\mathrm {e}^{\boldsymbol {A}_ct_i} \boldsymbol{x}(kT)+\int^{kT+t_i}_{kT} \mathrm {e}^{\boldsymbol {A}_c(kT+t_i-\tau)}\boldsymbol {B}_cu(\tau)\,\mathrm {d}\tau \\ =&\mathrm {e}^{\boldsymbol {A}_ct_i}\boldsymbol{x}(kT) \\ &{}+[\boldsymbol {B}_1, \boldsymbol {B}_2,\ldots ,\boldsymbol {B}_i] \bigl[u(kT), u(kT+t_1), \ldots, u(kT+t_{i-1})\bigr]^{\tiny \mathrm {T}}. \end{aligned}$$
(11)

The output equation is given by

$$\begin{aligned} y(kT+t_i) =&\boldsymbol {C}_c \boldsymbol{x}(kT+t_i)+D_cu(kT+t_i) \\ =&\boldsymbol {C}_c\mathrm {e}^{\boldsymbol {A}_ct_i}\boldsymbol{x}(kT)+[ \boldsymbol {C}_c\boldsymbol {B}_1,\boldsymbol {C}_c\boldsymbol {B}_2, \ldots ,\boldsymbol {C}_c\boldsymbol {B}_i]\underline{\boldsymbol{u}}(kT) +D_cu(kT+t_i) \\ =:&\boldsymbol {C}_i\boldsymbol{x}(kT)+[D_1,D_2, \ldots,D_i, D_c] \left[ \begin{array}{c} {u(kT)}\\ {u(kT+t_1)}\\ {\vdots}\\ {u(kT+t_{i-1})}\\ {u(kT+t_i)} \end{array}\right], \end{aligned}$$
(12)

where \(\boldsymbol {C}_{i}=:\boldsymbol {C}_{c}\mathrm {e}^{\boldsymbol {A}_{c}t_{i}}\), D i =:C c B i , i=1,2,…,p−1. Thus, we obtain the lifted state-space model in (3) for the multirate system, where

$$\begin{aligned} \underline{\boldsymbol {y}}(kT) =& \bigl[y(kT),\ y(kT+t_1), \ldots, y(kT+t_{p-1}) \bigr]^{\tiny \mathrm {T}}\in{\mathbb{R}}^{p}, \end{aligned}$$
(13)
$$\begin{aligned} \boldsymbol {C} =& \left[ \begin{array}{c} {\boldsymbol {C}_c}\\ {\boldsymbol {C}_1}\\ { \boldsymbol {C}_2}\\ {\vdots}\\ {\boldsymbol {C}_{p-1}} \end{array}\right]\in {\mathbb{R}}^{p\times n} \end{aligned}$$
(14)
$$\begin{aligned} \boldsymbol {D} =& \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c}D_c & 0 & \ldots& \ldots& 0\\ D_1 & D_c & & & \vdots\\ D_1 & D_2 & \ddots& & \vdots\\ \vdots& & \ddots& D_c & 0\\ D_1 & D_2 & \ldots& D_{p-1} & D_c \end{array} \right ]\in{\mathbb{R}}^{p\times p}. \end{aligned}$$
(15)

Replacing the lifted output \(\underline{\boldsymbol {y}}(kT)\) by the lifted noise-contaminated one \(\underline{\boldsymbol{z}}(kT)\) and omitting the frame period T yields

$$ \begin{cases}\boldsymbol{x}(k+1)=\boldsymbol {A}\boldsymbol{x}(k) +\boldsymbol {B}\underline{\boldsymbol{u}}(k),\\ \underline{\boldsymbol{z}}(k) = \boldsymbol {C}\boldsymbol{x}(k) +\boldsymbol {D}\underline{\boldsymbol{u}}(k)+\underline{\boldsymbol{v}}(k), \end{cases} $$
(16)

with \(\underline{\boldsymbol{v}}(k):=[v(k), v(k+t_{1}), \ldots, v(k+t_{p-1})]^{\tiny \mathrm {T}}\in{\mathbb{R}}^{p}\) the lifted noise vector.

3 Subspace Identification Method

Given the periodically non-uniformly sampled data {u(kT+t i ),z(kT+t i ), i=0,1,2,…,p−1}, the lifted input and output data are \(\{\underline{\boldsymbol{u}}(k), \underline{\boldsymbol{z}}(k)\}\), while the input and output block Hankel matrices can be defined as

$$\begin{aligned} \boldsymbol {U}_{0|l-1} :=& \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c}\underline{\boldsymbol{u}}(0)& \underline {\boldsymbol{u}}(1) & \dots& \underline{\boldsymbol{u}}(N-1)\\ \underline{\boldsymbol{u}}(1) & \underline{\boldsymbol{u}}(2) &\dots& \underline{\boldsymbol{u} }(N)\\ \vdots& \vdots& &\vdots\\ \underline{\boldsymbol{u}}(l-1) & \underline{\boldsymbol{u}}(l) & \ldots& \underline{\boldsymbol{u}}(l+N-2) \end{array} \right ]\in{\mathbb{R}}^{lp\times N}, \end{aligned}$$
(17)
$$\begin{aligned} \boldsymbol {Z}_{0|l-1} :=& \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \underline{\boldsymbol{z}}(0)& \underline{\boldsymbol{z}}(1) & \ldots& \underline{\boldsymbol{z}}(N-1)\\ \underline{\boldsymbol{z}}(1) & \underline{\boldsymbol{z}}(2) &\ldots& \underline{\boldsymbol{z}} (N)\\ \vdots& \vdots& &\vdots\\ \underline{\boldsymbol{z}}(l-1) & \underline{\boldsymbol{z}}(l) & \ldots& \underline{\boldsymbol{z}}(l+N-2) \end{array} \right ]\in{\mathbb{R}}^{lp\times N}, \end{aligned}$$
(18)

where l is strictly greater than the dimension n of state vector, N is sufficiently large, the indices 0 and l−1 denote the arguments of the upper-left and lower-left elements, respectively.

U l|2l−1 and Z l|2l−1 can be defined in a similar way. The block Hankel matrices U 0|l−1 and Z 0|l−1 are usually called the past inputs and outputs, respectively, whereas the block Hankel matrices U l|2l−1 and Z l|2l−1 are called the future inputs and outputs, respectively. Define , the LQ decomposition of the input and output block Hankel matrices can be performed as

$$ \left[ \begin{array}{c} {\boldsymbol {U}_{l|2l-1}}\\ {\boldsymbol {W}_p}\\ { \boldsymbol {Z}_{l|2l-1}}\end{array}\right]= \left [ \begin{array}{c@{\quad }c@{\quad }c}\boldsymbol {R}_{11}& 0 & 0\\ \boldsymbol {R}_{21} & \boldsymbol {R}_{22} & 0\\ \boldsymbol {R}_{31} & \boldsymbol {R}_{32} & 0 \end{array}\right] \left[ \begin{array}{c} {\boldsymbol {Q}^{\tiny \mathrm {T}}_1}\\ { \boldsymbol {Q}^{\tiny \mathrm {T}}_2}\\ {\boldsymbol {Q}^{\tiny \mathrm {T}}_3} \end{array}\right] $$
(19)

where \(\boldsymbol {R}_{11}\in{\mathbb{R}}^{lp\times lp}\), \(\boldsymbol {R}_{22}\in {\mathbb{R}}^{2lp\times2lp}\), \(\boldsymbol {Q}_{1}, \boldsymbol {Q}_{3}\in{\mathbb{R}}^{N\times lp}\), \(\boldsymbol {Q}_{2}\in{\mathbb{R}}^{N\times2lp}\).

Defining ξ as the oblique projection of Z l|2l−1 onto W p along U l|2l−1, with the above LQ decomposition, we have

$$ \boldsymbol {\xi }=\boldsymbol {R}_{32}\boldsymbol {R}^{\dagger}_{22} \boldsymbol {W}_p, $$
(20)

† denoting the pseudo inverse. The details are referred to Theorem 6.3 in [16], and thus omitted here.

Let the SVD of ξ be

$$ \boldsymbol {\xi }=[\boldsymbol {U}_1, \boldsymbol {U}_2] \left[ \begin{array}{c@{\quad }c}{ \boldsymbol {\varSigma }_1}& {\bf0}\\ {\bf0}& {\bf0} \end{array}\right] \left[ \begin{array}{c} {\boldsymbol {V}^{\tiny \mathrm {T}}_1}\\ {\boldsymbol {V}^{\tiny \mathrm {T}}_2}\end{array}\right]= \boldsymbol {U}_1\boldsymbol {\varSigma }_1 \boldsymbol {V}^{\tiny \mathrm {T}}_1. $$
(21)

Defining the state sequence X l :=[x(l),x(l+1),…,x(l+N−1)], we have the estimated state sequence

$$ \hat{\boldsymbol {X}}:=\bigl[\hat{\boldsymbol{x}}(l), \hat{\boldsymbol{x}}(l+1), \ldots, \hat{\boldsymbol{x} }(l+N-1)\bigr]\in{\mathbb{R}}^{n\times N}. $$
(22)

By defining

$$\begin{aligned} \hat{\boldsymbol {X}}_{l+1} :=&\bigl[\hat{\boldsymbol{x}}(l+1), \hat{\boldsymbol{x}}(l+2), \ldots, \hat{\boldsymbol{x} }(l+N-1)\bigr]\in{\mathbb{R}}^{n\times(N-1)}, \end{aligned}$$
(23)
$$\begin{aligned} \hat{\boldsymbol {X}}_l :=&\bigl[\hat{\boldsymbol{x}}(l), \hat{\boldsymbol{x}}(l+1), \ldots, \hat{\boldsymbol{x} }(l+N-2)\bigr]\in{\mathbb{R}}^{n\times(N-1)}, \end{aligned}$$
(24)
$$\begin{aligned} \boldsymbol {U}_{l|l} :=&\bigl[\underline{\boldsymbol{u}}(l), \underline{\boldsymbol{u}}(l+1),\ldots, \underline{\boldsymbol{u}}(l+N-2)\bigr]\in{\mathbb{R}}^{p\times (N-1)}, \end{aligned}$$
(25)
$$\begin{aligned} \boldsymbol {Z}_{l|l} :=&\bigl[\underline{\boldsymbol{z}}(l), \underline{\boldsymbol{z}}(l+1),\ldots, \underline{\boldsymbol{z}}(l+N-2)\bigr]\in{\mathbb{R}}^{p\times(N-1)}, \end{aligned}$$
(26)

it follows that

$$ \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l+1}}\\ {\boldsymbol {Z}_{l|l}}\end{array}\right]= \left[ \begin{array}{c@{\quad }c} {\boldsymbol {A}}& {\boldsymbol {B}}\\ {\boldsymbol {C}}& {\boldsymbol {D}} \end{array}\right] \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l}}\\ { \boldsymbol {U}_{l|l}}\end{array}\right], $$
(27)

then the system matrices can be estimated by using the least-squares technique,

$$ \left[ \begin{array}{c@{\quad }c} {\hat{\boldsymbol {A}}}& {\hat{\boldsymbol {B}}}\\ {\hat{\boldsymbol {C}}}& {\hat{\boldsymbol {D}}}\end{array}\right]= \left\{ \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l+1}}\\ {\boldsymbol {Z}_{l|l}}\end{array}\right]^{\tiny \mathrm {T}} \left[ \begin{array}{c} {\hat{ \boldsymbol {X}}_{l+1}}\\ {\boldsymbol {Z}_{l|l}}\end{array}\right] \right\}^{-1} \left[ \begin{array}{c} {\hat{ \boldsymbol {X}}_{l+1}}\\ {\boldsymbol {Z}_{l|l}}\end{array}\right]^{\tiny \mathrm {T}} \left[ \begin{array}{c} {\hat{ \boldsymbol {X}}_{l}}\\ {\boldsymbol {U}_{l|l}}\end{array}\right]. $$
(28)

Note that the upper triangular blocks in D are zero, namely, the zero-entries of this upper triangular block in D do not need to be identified, but the upper triangular blocks may not equal zero in \(\hat{\boldsymbol {D}}\). In order to tackle this causality constraint for the lifted model, we propose a two-stage way to estimate the matrices (A,B,C,D).

From (27), one can get the estimates of (A,B) by solving the following least-squares form:

$$ \hat{\boldsymbol {X}}_{l+1}=[\boldsymbol {A}, \boldsymbol {B}] \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l}}\\ {\boldsymbol {U}_{l|l}}\end{array}\right]. $$
(29)

To obtain the non-zero subblock matrices in D, we decompose the matrix Z l|l in (26) and U l|l in (25) into p row vectors according to their row dimension,

$$ \boldsymbol {Z}_{l|l}:= \left[ \begin{array}{c} {\boldsymbol {Z}_1}\\ { \boldsymbol {Z}_2}\\ {\vdots}\\ {\boldsymbol {Z}_p}\end{array}\right],\qquad \boldsymbol {U}_{l|l}:= \left[ \begin{array}{c} {\boldsymbol {U}_1}\\ {\boldsymbol {U}_2}\\ {\vdots}\\ {\boldsymbol {U}_p}\end{array}\right], $$
(30)

From Equation (14) and

$$ \boldsymbol {Z}_{l|l}=[\boldsymbol {C}, \boldsymbol {D}] \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l}}\\ {\boldsymbol {U}_{l|l}}\end{array}\right], $$
(31)

we have

$$\begin{aligned} \boldsymbol {Z}_1 =&[\boldsymbol {C}_c, D_c] \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l}}\\ {\boldsymbol {U}_1}\end{array}\right], \end{aligned}$$
(32)
$$\begin{aligned} \boldsymbol {Z}_2 =&[\boldsymbol {C}_1, D_1, D_c] \left[ \begin{array}{c} {\hat{\boldsymbol {X}}_{l}}\\ {\boldsymbol {U}_1}\\ {\boldsymbol {U}_2}\end{array}\right], \end{aligned}$$
(33)
$$\begin{aligned} \vdots& \\ \boldsymbol {Z}_p =&[\boldsymbol {C}_{p-1}, D_1, D_2,\ldots, D_{p-1}, D_c] \left[ \begin{array}{c} {\hat {\boldsymbol {X}}_{l}}\\ {\boldsymbol {U}_1}\\ {\boldsymbol {U}_2}\\ {\vdots}\\ {\boldsymbol {U}_p}\end{array}\right]. \end{aligned}$$
(34)

Note that D c can be estimated by solving (32), thus it can be used to estimate D 1 in (33), and the rest unknown entries in D can be estimated in a similar way.

4 Example

Consider a continuous process model described by

$$G(s)=\frac{1}{100s^2+10s+1}, $$

its canonical state space form being

$$S_c:\ \begin{cases}\dot{\boldsymbol{x}}(t)=\left[ \begin{array}{c@{\quad }c} {-0.1}&{-0.1}\\ {1}&{0}\end{array}\right]\boldsymbol{x}(t) + \left[ \begin{array}{c} {1}\\ {0}\end{array}\right]u(t),\\ z(t) = [0,0.01]\boldsymbol{x}(t)+v(t). \end{cases} $$

Taking p=2, τ 1=0.618 s, τ 2=0.382 s, hence, t 1=τ 1=0.618 s, t 2=τ 1+τ 2=T=1 s. Then the corresponding lifted state-space model is

$$\begin{aligned} \boldsymbol{x}(kT+T) =&\boldsymbol {A}\boldsymbol{x}(kT) +\boldsymbol {B}\underline{\boldsymbol{u}}(kT) \\ =&\left[ \begin{array}{c@{\quad }c} {0.9002}& {-0.0095}\\ {0.9500}& {0.9952}\end{array}\right]\boldsymbol{x}(kT) + \left[ \begin{array}{c@{\quad }c} {0.5753} &{0.37470}\\ {0.4113}& {0.07203}\end{array}\right] \left[ \begin{array}{c} {u(kT)}\\ {u(kT+t_1)}\end{array}\right] \\ \left[ \begin{array}{c} {z(kT)}\\ {z(kT+t_1)}\end{array}\right] =& \left[ \begin{array}{c@{\quad }c} {0}& {0.01}\\ {0.005989}& {0.009981}\end{array}\right]\boldsymbol{x}(kT) \\ & +\left[ \begin{array}{c@{\quad }c} {0}& {0}\\ {0.004113}& {0}\end{array}\right] \left[ \begin{array}{c} {u(kT)}\\ {u(kT+t_1)}\end{array}\right] + \left[ \begin{array}{c} {v(kT)}\\ {v(kT+t_1)}\end{array}\right]. \end{aligned}$$

The input signals u(kT) and u(kT+t 1) are taken as two random signal sequences with zero mean and unit variances and two uncorrelated noise sequences with zero mean and variances σ 2=0.102. The noise terms are independent of the inputs.

With the non-uniformly sampled input and output data, we apply the modified subspace identification method respectively to the above lifted model and to the following single-rate model, as follows.

Taking T=1 s for a single-rate sampled system yields the discrete-time state-space model

$$ S_d:\ \begin{cases}\boldsymbol{x}(kT+T)= \left[ \begin{array}{c@{\quad }c} {0.9783}&{-0.0095}\\ {0.95}&{0.9952}\end{array}\right]\boldsymbol{x}(kT) +\left[ \begin{array}{c} {0.95}\\ {0.4833}\end{array}\right]u(kT),\\ z(kT) = [0,0.01]\boldsymbol{x}(kT)+v(kT). \end{cases} $$

The step responses of the identified lifted system and single-rate system are shown in Figs. 2–3: The lifted model can capture the actual system dynamics better than the single-rate model does. The estimated poles of the lifted model and the single-rate model are listed in Table 1: the estimated poles of the lifted model are closer to the actual system poles than that of the single-rate model.

Fig. 2
figure 2

The step responses of the actual system and the estimated model under non-uniform sampling

Full size image
Fig. 3
figure 3

The step responses of the actual system and the estimated model under single-rate sampling

Full size image
Table 1 The estimated poles of the lifted model and the single-rate model
Full size table

Furthermore, the Bode diagrams of the actual system and the estimated systems are shown in Figs. 4–5. This indicates that the estimated lifted model can achieve satisfactory results.

Fig. 4
figure 4

The Bode diagrams of the actual system and the estimated system

Full size image
Fig. 5
figure 5

The Bode diagrams of the actual system and the estimated single-rate system

Full size image

5 Conclusions

We have discussed the identification methods for periodically non-uniformly sampled system. By using the lifting technique, we propose a two-stage subspace identification method to identify the lifted state-space models, the advantages of the proposed method lie in that:

  • The lifted system can be estimated by using non-uniformly sampled data directly, thus it can achieve better performance than the single-rate one.

  • The developed algorithm can tackle the casuality constraints in the lifted state-space model.

The proposed method can be extended to other linear or nonlinear systems [7–9, 13, 23, 29–31].