1 Introduction

In many practical applications, it is important to design an effective controller for a dynamical system and at the same time consider the influence of the system constraints. Constraints are ubiquitous in realistic systems and demonstrate themselves as nonlinear saturation, physical stoppages, as well as increasing productivity demands and tighter environmental regulations, etc. Violation of the constraints during operation may result in performance degradation, hazards, or system damage. Thus, the study on constraint-handling methods in control design and analysis has attracted many researchers from various fields in science and engineering, due to theoretical challenges and importance in real-world applications.

There exist various techniques to deal with the constrained control problems for linear systems and nonlinear systems [1–7]. Most of the results in the literature are dependent on the notions of set invariance and admissible set control [8, 9], and other methods include model predictive control [10], reference governors [11]. Recently, barrier Lyapunov functions have been proposed in [12, 13] to handle the control problems with state or output constraints. [13] also proposed asymmetrical barrier Lyapunov functions to handle an asymmetric output constraint. However, a problem with the control design presented in [13] is that the asymmetric barrier Lyapunov function used in the first step of the control design procedure is of a switching type, a \(C^1\) function. Consequently, the subsequent stabilizing functions must be of a high power of the output tracking error. This is somewhat undesirable and could increase the control effort and decrease the robustness of the controlled system.

On the other hand, as a special class of hybrid systems, switched systems have attracted considerable attention during the last decade because of its importance from both theoretical and practical points of views [14–23]. Stability analysis and control synthesis are two fundamental problems in the study of switched systems for which many contributions have been proposed [24–33]. However, as a valuable problem which has great practical significance, the tracking problem of switched dynamical systems subject to output tracking error constraints has been paid little attention so far. For instance, it is necessary to ensure the noncontactness between the rotor and stator in the control of a magnetic bearing with possible switching models [34]. Another example is to guarantee no contact between the movable and fixed electrodes when controlling the electrostatic parallel plate microactuators [35]. Furthermore, the \(H_\infty \) property analysis of switched systems is an interesting issue. However, most of the results related to this problem have been focused on the linear case, and for the nonlinear case, the results depend mainly on the solution of HJI inequalities [36].

Motivated by the aforementioned observations, this article presents a controller design method to handle the output-constrained tracking control (OCTC) and state-constrained \(H_\infty \) control (SCHC) problems for nonlinear switched systems in strict feedback form. Under an appropriate condition on the output tracking error and the simultaneous domination assumption, the output tracking error is always within a pre-specified limit range. The key to the success of our control design method is the introduction of smooth and/or \(p\)-times differentiable unbounded functions that are incorporated in the output tracking error transformation. Moreover, the SCHC prolem for a class of disturbed nonlinear switched systems in strict feedback form is also considered. The contributions of this article lie in that: (i) it should be noted that the results obtained in this paper is not a simple parallel extension of [37]. Because in each step of the controller design procedure, we must choose a common virtual control law to counteract the influence of switched subsystems on the performance of closed-loop system, which is different with [37]; (ii) in comparison with the barrier Lyapunov function approach proposed in [13], no switchings are needed in our proposed controller even if the constraint is asymmetric; (iii) in the simulation, we further add a practical application to demonstrate the effectiveness of the proposed design scheme.

Notations: We use the following notations throughout this paper. \(R_ +\) denotes the set of nonnegative real numbers, \(R^n\) stands for the \(n\)-dimensional real Euclidean vector space, and \(\Vert \bullet \Vert \) represents the Euclidean vector norm. We also denote \(\bar{x}_i = \left[ {x_1 ,x_2, \ldots ,x_i } \right] ^T,\) \(\bar{z}_i = \left[ {z_1 ,z_2 , \ldots , z_i } \right] ^T\) and \(\widetilde{y} _{d_i } \!=\! \left[ y_d, {y_d^{\left( 1 \right) } ,y_d^{\left( 2 \right) } , \ldots , y_d^{\left( i \right) }} \right] ^T\), for a positive integer \(i.\)

2 System description and problem statement

In this paper, we discuss a class of nonlinear switched systems of the following form:

$$\begin{aligned} \dot{x}_i&= f_i^{\sigma ( t )} ( {\bar{x}_i } ) + x_{i + 1} , \quad i=1,2,\cdots ,n-1, \nonumber \\ \dot{x}_n&= f_n^{\sigma ( t )} ( {\bar{x}_n } ) + g^{\sigma ( t )} ( {\bar{x}_n } )u, \nonumber \\ y&= x_1 , \end{aligned}$$
(1)

where \(x_1 ,x_2 , \ldots ,x_n\) are the states, \(u = \Big [ {u_1 ,u_2, \ldots },{u_q } \Big ]^T \in R^q\) and \(y \in R\) are the input and output respectively. \(\sigma \left( t \right) :\left[ {0,\infty } \right) \rightarrow I_m = \left\{ {1, 2,\cdot \cdot \cdot ,m} \right\} \) is the switching signal. For all \(i = 1,2, \ldots ,n\) and \(k = 1,2, \ldots ,m\), the functions \(f_i^k ,g^k\) are smooth with \(g^k \left( {\bar{x}_n } \right) \ne 0,\forall \bar{x}_n \in R^n\). We assume that the state of the system (1) does not jump at the switching instants, i.e., the trajectory \(x(t)\) is everywhere continuous.

In this paper, we first deal with the following OCTC problem.

The OCTC problem: For the system (1), under arbitrary switchings, design a continuous feedback controller \(u\) that forces the output \(y\) of the system (1) to track a reference trajectory \({y_d}(t)\) such that:

  1. (1)

    Asymptotic tracking is accomplished, i.e.,

    $$\begin{aligned} {\lim _{t \rightarrow \infty }}(y(t) - {y_d}(t)) = 0. \end{aligned}$$
    (2)
  2. (2)

    The output tracking error is within a pre-specified limit range, i.e.,

    $$\begin{aligned} -\underline{L}\le y(t) - {y_d}(t) \le \bar{L} \end{aligned}$$
    (3)

    for all \(t \ge {t_0} \ge 0\), where \(\underline{L}\) and \(\bar{L}\) are strictly positive constants. If \(\underline{L}=\bar{L}\), the constraint (3) is referred to as a symmetric constraint. If \(\underline{L}\ne \bar{L}\), the constraint (3) is referred to as an asymmetric constraint.

  3. (3)

    All signals of the closed-loop system (1) are bounded.

In this paper, we adopt the following assumptions to develop the main results.

Assumption 1

The functions \(g^k \left( {\bar{x}_n } \right) \!=\! \left[ g^{k,1} \left( {\bar{x}_n } \right) ,\right. g^{k,2} \left. \left( {\bar{x}_n } \right) , \ldots , g^{k,q} \left( {\bar{x}_n } \right) \right] ,k\!\!=\!\!1,2,\ldots ,m\) are known. Further, for each \(j \in \left\{ {1, 2,\ldots , q} \right\} \), assume that \(\min _{k \in \left\{ {1, 2,\ldots , m} \right\} } g^{k,j} \left( {\bar{x}_n } \right) \ge 0, \forall \bar{x}_n \in R^n\) or \(\max _{k \in \left\{ {1, 2,\ldots , m} \right\} } g^{k,j} \left( {\bar{x}_n } \right) \le 0,\forall \bar{x}_n \in R^n\). For convenience, denote

$$\begin{aligned} M&= \left\{ {j \!\in \! \left\{ {1,2, \ldots , q} \right\} | {\hbox {min}} _{k \in \left\{ {1, 2,\ldots ,m} \right\} } g^{k,j} \left( {\bar{x}_n } \right) \!\ge \! 0} \right\} , \nonumber \\ F&= \left\{ {j \in \left\{ {1,2, \ldots ,q} \right\} |j \notin M} \right\} . \end{aligned}$$
(4)

Assumption 2

At the initial time \(t_0\), there exist strictly positive constants \(\underline{L}_1<\underline{L}\) and \({\bar{L}_1} < \bar{L}\), such that

$$\begin{aligned} - \underline{L }_1 \le y(t) - {y_d}(t) \le {\bar{L}_1}. \end{aligned}$$
(5)

Assumption 3

The reference trajectory \({y_d}(t)\) and their time derivatives \(\dot{y}_d(t),\ddot{y}_d(t),\ldots ,y_d^{(n)}(t)\) are bounded.

We review two definitions and two relevant lemmas that will be used in the sequel.

Definition 1

[37]  A scalar function \(h(x,a,b)\) is said to be a \(p\)-times differentiable step function if it enjoys the following properties:

  1. (1)

    \(h(x,a,b) = 0,\quad \forall - \infty < x \le a,\)

  2. (2)

    \(h(x,a,b) = 1,\quad \forall b \le x < + \infty ,\)

  3. (3)

    \(0 < h(x,a,b) < 1,\quad \forall x \in (a,b),\)

  4. (4)

    \(h(x,a,b)\) is \(p\) times differentiable with respect to \(x\),

  5. (5)

    \({h'}(x,a,b) > 0,\quad \forall x \in (a,b),\)

  6. (6)

    \({h'}(x,a,b) \ge {\delta _1}({\rho _1}) > 0,\forall x \in (a + {\rho _1},b - {\rho _1}),\) with \(0 < {\rho _1} < \frac{{b - a}}{2},\) where \(p\) is a positive integer, \(x \in R\) , \(a\) and \(b\) are constants such that \(a < 0 < b,{h'}(x,a,b) = \frac{{\partial {h'}(x,a,b)}}{{\partial x}}\) and \({\delta _1}({\rho _1})\) is a positive constant depending on the positive constant \({\rho _1}\). Furthermore, if the function \(h(x,a,b)\) is infinite times differentiable with respect to \(x\), then it is said to be a smooth step function.

Lemma 1

[37]  Let the scalar function \(h(x,a,b)\) be defined as

$$\begin{aligned} h(x,a,b){=}\frac{{\int _\mathrm{{a}}^x {f(\tau - a)f(b - \tau )d\tau } }}{{\int _\mathrm{{a}}^b {f(\tau - a)f(b - \tau )d\tau } }} \end{aligned}$$
(6)

with \(a\) and \(b\) being constants such that \(a < 0 < b\), and the function \(f(y)\) being defined as follows:

$$\begin{aligned} \begin{array}{rcll} f(y) &{}=&{} 0,&{}\quad { if} \,\,y\, \le \,0,\\ f(y) &{}=&{} g(y),&{}\quad { if} \,\, y\, >\, 0, \end{array} \end{aligned}$$
(7)

where \(g(y)\) is a single-valued function that enjoys the following properties:

  1. (a)

    \(g(\tau - a)f(b - \tau ) > 0,\quad \forall \tau \in (a,b),\)

  2. (b)

    \(g(\tau - a)f(b - \tau ) \ge {\delta _2}({\rho _2}) > 0,\forall \tau \in (a + {\rho _2},b - {\rho _2}),\) with \(0 < {\rho _2} < \frac{{b - a}}{2},\)

  3. (c)

    \(g(y)\) is \(p\) times differentiable with respect to \(y\), and \({\lim _{y \rightarrow {0^ + }}}\frac{{{\partial ^k}g(y)}}{{\partial {y^k}}} = 0,k = 1,2, \ldots ,p - 1,\) with \(p\) being a positive integer and \({\delta _2}({\rho _2})\) is a positive constant depending on the positive constant \({\rho _2}\). Then, the function \(h(x,a,b)\) is a p-times differentiable step function. Moreover, if \(g(y)\) in (7) is replaced by \(g(y)\mathrm{{ = }}{\mathrm{{e}}^{ - 1/y}}\) then property (4) in Definition 1 is replaced by \((4)'\), i.e., \(h(x,a,b)\) is a smooth step function.

Remark 1

It is worth pointing out that the function \(g(y)\) in (7) can be chosen as \(g(y)\mathrm{{ = }}{\mathrm{{y}}^p},\) \(g(y)\mathrm{{ = tanh(y}}{\mathrm{{)}}^p},\) \(g(y)\mathrm{{ = arctan(}}{\mathrm{{y}}^p})\), etc. It is easy to check that these functions satisfy all the properties (a)-(c) listed in Lemma 1.

Definition 2

[37]  A function \(\Psi (x,a,b)\) is said to be a \(p\)-times differentiable unbounded function if it holds the following properties:

  1. (1)

    \(\mathrm{{x}} = 0 \Leftrightarrow \Psi (x,a,b) = 0,\)

  2. (2)

    \({\lim _{x \rightarrow {a^ - }}}\Psi (x,a,b) = - \infty ,{\lim _{x \rightarrow {b^ + }}}\Psi (x,a,b) = \infty ,\)

  3. (3)

    \(\Psi (x,a,b)\) is p-times differentiable with respect to \(x\), for all \(x \in (a,b),\).

  4. (4)

    \({\Psi ^{'}}(x,a,b) > 0,\forall x \in (a,b),\)

  5. (5)

    \({\Psi ^{'}}(x,a,b) \ge {\delta _3}({\rho _3}) > 0,\forall x \in (a + {\rho _3},b - {\rho _3}),\) with \(0 < {\rho _3} < \frac{{b - a}}{2},\)

where \(p\) is a positive integer, \(a\) and \(b\) are constants such that \(a < 0 < b\), \({\Psi ^{'}}(x,a,b) = \frac{{\partial \Psi (x,a,b)}}{{\partial x}}\), and \({\delta _3}({\rho _3})\) is a positive constant depending on the positive constant \(\rho _3\). Moreover, if \( p = \infty \), then the function \(\Psi (x,a,b)\) is said to be a smooth unbounded function.

Remark 2

If \(a{= - }b\) in the function \(\Psi (x,a,b)\), then it is easy to get many \(p\)-times differentiable unbounded functions. An example is the function \(\tan ( - \frac{\pi }{{2a}}x)\). If \(a \ne \mathrm{{ - }}b\), it is more difficult to find a \(p\)-times differentiable unbounded function. However, we can construct a \(p\)-times differentiable unbounded function by using the \(p\)-times differentiable step function in Definition 1 with the following lemma.

Lemma 2

[37] Let the scalar function \(\Psi (x,a,b)\) be defined as

$$\begin{aligned} \Psi (x,a,b) = \bar{\Psi }(\varphi (x,a,b)) - \bar{\Psi }(\varphi (0,a,b)), \end{aligned}$$
(8)

where the function \(\varphi (x,a,b)\) is defined as follows:

$$\begin{aligned} \varphi (x,a,b) = \varepsilon (2h(x,a,b) - 1) \end{aligned}$$
(9)

with \( \varepsilon \) being a positive constant, \(h(x,a,b)\) being the p-times differentiable step functions in Definition 1. The function \(\bar{\Psi }(\xi )\) is such that

  1. (1)

    \(\xi = 0 \Leftrightarrow \bar{\Psi }(\xi ) = 0,\)

  2. (2)

    \({\lim _{\xi \rightarrow - {\varepsilon ^ - }}}\bar{\Psi }(\xi ) = - \infty ,{\lim _{\xi \rightarrow {\varepsilon ^ + }}}\bar{\Psi }(\xi ) = \infty ,\)

  3. (3)

    \(\bar{\Psi }(\xi )\) is p-times differentiable with respect to \(\xi \), for all \(\xi \in ( - \varepsilon ,\varepsilon ),\).

  4. (4)

    \({\bar{\Psi }^{'}}(\xi ) > 0,\forall \xi \in ( - \varepsilon ,\varepsilon ),\)

  5. (5)

    \({\bar{\Psi }^{'}}(\xi ) > {\delta _4}({\rho _4}) > 0,\forall \xi \in (a + {\rho _4},b - {\rho _4}),\) with \(0 < {\rho _4} < \frac{{b - a}}{2},\)

where \({\bar{\Psi }^{'}}(\xi ) = \frac{{\partial \bar{\Psi }(\xi )}}{{\partial \xi }} > 0,\forall \xi \in ( - \varepsilon ,\varepsilon )\), and \({\delta _4}({\rho _4})\) is a positive constant depending on the positive constant \({\rho _4}\). Then, the function \(\Psi (x,a,b)\) is a \(p\)-times differentiable unbounded function. Moreover, if \(h(x,a,b)\) is a smooth step function, then the function \(\Psi (x,a,b)\) is a smooth unbounded function.

Remark 3

As an example, we provide a \(p\)-times differentiable unbounded function \( \Psi (x,a,b)\) as \(\Psi (x,a,b)\mathrm{{ = }}\tan [\frac{\pi }{2}(2h(x,a,b) - 1)] - \tan [\frac{\pi }{2}(2h(0,a,b) - 1)].\)

Lemma 3

[38] (Barbalat’ s Lemma) Consider a differentiable function \(h(t)\). If \( \lim _{t \rightarrow \infty } h(t)\) is finite and \(\dot{h}(t)\) is uniformly continuous, then \(\lim _{t \rightarrow \infty } \dot{h}(t) = 0.\)

3 Tracking control

In this subsection, under the simultaneous domination assumption, we present a controller design approach to solve the OCTC problem of the system (1) by applying the \(p\)-times differentiable unbounded function in Definition 2 and the well-known backstepping technique.

First, we use the following change of coordinates:

$$\begin{aligned} {z_1} = \Psi ({x_{1d}},a,b), \end{aligned}$$
(10)

where \({x_{1d}} = {x_1} - {y_d} = y - {y_d}\) is the output tracking error, \(\Psi ({x_{1d}},a,b)\) is a \(p\)-times differentiable unbounded function with \(p \ge n - 1,\) and the constants \(a\) and \(b\) are chosen such that

$$\begin{aligned} -\underline{L} \le a < - \underline{L }_1 ,\overline{L}_1 < b \le \bar{L}. \end{aligned}$$
(11)

Based on the properties of \(\Psi ({x_{1d}},a,b)\) shown in Definition 2, we conclude that if we are able to design a control input \(u\) such that \({\lim _{t \rightarrow \infty }}{z_1}(t) = 0\) and keep all signals of the corresponding closed-loop system bounded for a bounded \({z_1}({t_0})\), then the output tracking control problem of the system (1) is solved. It is seen that \({z_1}({t_0})\) is bounded under the choice of the constants \(a\) and \(b\) in (11), the assumption on the initial output tracking error in (5), and the properties of the function \(\Psi ({x_{1d}},a,b)\) listed in Definition 2.

Differentiating both sides of (10) in conjunction with the system (1), we can rewrite them in the form:

$$\begin{aligned} {{{\dot{z}}}_1}&= \Psi '({x_{1d}},a,b)(f_1^{\sigma ( t )}\left( {{x_1}} \right) + {x_2} - {{\dot{y}}_d}), \nonumber \\ \dot{x}_i&= f_i^{\sigma ( t )} ( {\bar{x}_i } ) + x_{i + 1} , \quad i=2,3,\ldots ,n-1, \nonumber \\ \dot{x}_n&= f_n^{\sigma ( t )} ( {\bar{x}_n } ) + g^{\sigma ( t )} ( {\bar{x}_n } )u, \nonumber \\ y&= x_1 , \end{aligned}$$
(12)

\(Step\,1.\) We consider the following collection of auxiliary \(z_1\)- equations:

$$\begin{aligned} {\dot{z}}_1&= \Psi '({x_{1d}},a,b)(f_1^{k}\left( {{x_1}} \right) + {x_2} - {{\dot{y}}_d}),\nonumber \\&k = 1,2, \quad \ldots , m. \end{aligned}$$
(13)

Define \(V_1({z_1}) = \frac{1}{2}z_1^2\). Viewing \(x_2\) as the virtual input of the system (13), we say that these first-order subsystems are simultaneously dominatable if there exists a common smooth stabilizing function \(\phi _1 \left( { x_1,z_1 , \widetilde{y}_{d_1 } } \right) = \phi _1^* \left( { x_1,y_d } \right) + \dot{y}_d\) such that, along the solutions of the subsystems in (13),

$$\begin{aligned} \dot{V}_1\left( {z_1 } \right)&= z_1 \dot{z}_1 = z_1 \Psi '({x_{1d}},a,b)( f_1^k \left( { x_1 } \right) \nonumber \\&\quad +\,\phi _1^* \left( { x_1 ,y_d } \right) )< 0,\quad \forall {z_1} \ne 0, \nonumber \\&\quad k = 1, 2,\ldots ,m. \end{aligned}$$
(14)

Define

$$\begin{aligned} d_1^k \left( { x_1,z_1 , \widetilde{y}_{d_1 } } \right)&= z_1 \Psi '({x_{1d}},a,b)( f_1^k \left( { x_1 } \right) \nonumber \\&\quad +\,\phi _1^* \left( { x_1 ,y_d } \right) ),\nonumber \\&\quad k = 1,2, \ldots , m. \end{aligned}$$
(15)

With \(V_1 \left( {z_1 } \right) \), the control design for the first step is completed if a common smooth stabilizing function \(x_2 = \phi _1 \left( { x_1,z_1 , \widetilde{y}_{d_1 } } \right) \) is found.

\(Step\,i\) (for \(i = 2, \ldots ,n - 1\)). Define

$$\begin{aligned}&z_i = x_i - \phi _{i - 1} \left( {\bar{x}_{i - 1} ,\bar{z}_{i - 1} , \widetilde{y}_{d_{i - 1} } } \right) , \nonumber \\&V_i \left( {\bar{z}_i } \right) = V_{i - 1} \left( {\bar{z}_{i - 1} } \right) + \frac{1}{2}\left( {x_i - \phi _{i - 1} } \right) ^2 \ = \frac{1}{2}\sum \limits _{j = 1}^i {z_j^2 } .\nonumber \\ \end{aligned}$$
(16)

Then, we consider the following collection of auxiliary \(({z_1},{z_2}, \ldots ,{z_i})\)-equations:

$$\begin{aligned} {\dot{z}}_1&= \Psi {'}({x_{1d}},a,b)(f_1^{k}\left( {{x_1}} \right) + {x_2} - {{\dot{y}}_d}),\nonumber \\ \dot{z}_2&= f_2^k \left( {\bar{x}_2 } \right) + x_{3} - \frac{{\partial \phi _{ 1} }}{{\partial x_1 }}\left( f_1^k \left( { x_1 } \right) +x_{2} \right) \nonumber \\&- \sum \limits _{j = 0}^{1} {\frac{{\partial \phi _{1} }}{{\partial y_d^{(j)} }}y_d^{(j + 1)} } , \nonumber \\&\ldots \nonumber \\ \dot{z}_i&= f_i^k \left( {\bar{x}_i } \right) + x_{i + 1} - \sum \limits _{j = 1}^{i - 1} {\frac{{\partial \phi _{i - 1} }}{{\partial x_j }}\left( {x_{j + 1} + f_j^k \left( {\bar{x}_j } \right) } \right) } \nonumber \\&- \sum \limits _{j = 0}^{i - 1} {\frac{{\partial \phi _{i - 1} }}{{\partial y_d^{(j)} }}y_d^{(j + 1)} } ,\nonumber \\ k&= 1,2, \ldots , m. \end{aligned}$$
(17)

With the candidate Lyapunov function \(V_i \left( {\bar{z}_i } \right) \) and taking \(x_{i + 1}\) as the virtual input of the system (17), we say that the \(i\)th-order subsystems are simultaneously dominatable if there exists a common smooth stabilizing function \(x_{i + 1} = \phi _i \left( {\bar{x}_i ,\bar{z}_i ,\widetilde{y}_{d_i } } \right) \), such that along the solutions of the subsystems in (17),

$$\begin{aligned} \dot{V}_i \left( {\bar{z}_i } \right)&= \sum \limits _{j = 1}^i {z_j } \dot{z}_j = \sum \limits _{j = 1}^i {d_j^k } \left( {\bar{x}_i ,\bar{z}_i ,\widetilde{y}_{d_i } } \right) < 0,\nonumber \\&\quad \quad \forall \bar{z}_i \ne 0 ,k = 1,2, \ldots , m, \end{aligned}$$
(18)

where, for \(j = 2, \ldots ,i,\)

$$\begin{aligned}&d_2^k \left( {\bar{x}_2 ,\bar{z}_2 ,\widetilde{y}_{d_2 } } \right) = z_2 \left( {\Psi 'z_1+ \phi _2 + f_2^k \left( {\bar{x}_2 } \right) }\right. \nonumber \\&\quad \left. {- \frac{{\partial \phi _1 }}{{\partial x_1 }}\left( {x_2 + f_1^k \left( { x_1 } \right) } \right) - \sum \limits _{l = 0}^1 {\frac{{\partial \phi _1 }}{{\partial y_d^{(l)} }}y_d^{(l + 1)} } } \right) , \nonumber \\&d_j^k \left( {\bar{x}_j ,\bar{z}_j ,\widetilde{y}_{d_j } } \right) = z_j \left( z_{j - 1} + \phi _j + f_j^k \left( {\bar{x}_j } \right) \right. \nonumber \\&\quad \left. - \sum \limits _{l = 1}^{j - 1} {\frac{{\partial \phi _{j - 1} }}{{\partial x_l }}\left( {x_{l + 1} \!+\! f_l^k \left( {\bar{x}_l } \right) } \right) \!-\! \sum \limits _{l = 0}^{j - 1} {\frac{{\partial \phi _{j - 1} }}{{\partial y_d^{(l)} }}y_d^{(l + 1)} } } \!\right) .\nonumber \\ \end{aligned}$$
(19)

With the constructed \(V_i \left( {\bar{z}_i } \right) \), the control design for the \(i\)th step is completed if a common smooth stabilizing function \(x_{i + 1} = \phi _i \left( {\bar{x}_i ,\bar{z}_i ,\widetilde{y}_{d_i } } \right) \) is found.

By this procedure, we say that the subsystems of (12) are simultaneously dominatable if the \((n-1)\)th step is completed. In this case, we design a continuous feedback controller at the final step.

\(Step\,n\). Define

$$\begin{aligned}&\dot{z}_n = x_n - \phi _{n - 1} \left( {\bar{x}_{n-1} ,\bar{z}_{n-1},\widetilde{y}_{d_{n-1} } } \right) , \nonumber \\&V_n \left( {\bar{z}_n } \right) = V_{n - 1} \left( {\bar{z}_{n - 1} } \right) + \frac{1}{2}\left( {x_n - \phi _{n - 1} } \right) ^2 = \frac{1}{2}\sum \limits _{i = 1}^n {z_i^2 }.\nonumber \\ \end{aligned}$$
(20)

It is obvious that \(V_n \left( {\bar{z}_n } \right) \) is positive definite and radially unbounded in \({({z_1},{z_2}, \ldots ,{z_n})^T}\). Thus, along the solutions of the \(k\)th subsystem in (20), we have

$$\begin{aligned} \dot{V}_n&= \sum \limits _{i = 1}^n {z_i \dot{z}_i } =\sum \limits _{i = 1}^{n - 1} {d_i^k } \left( {\bar{x}_i ,\bar{z}_i,\widetilde{y}_{d_i } } \right) \nonumber \\&\quad + z_n \Big (z_{n - 1} + f_n^k \left( {\bar{x}_n } \right) + g^k \left( {\bar{x}_n } \right) u \nonumber \\&- \sum \limits _{j = 1}^{n - 1} {\frac{{\partial \phi _{n - 1} }}{{\partial x_j }}\left( {x_{j + 1} + f_j^k \left( {\bar{x}_j } \right) } \right) } \nonumber \\&- \sum \limits _{j = 0}^{n - 1} {\frac{{\partial \phi _{n - 1} }}{{\partial y_d^{(j)} }}y_d^{(j + 1)} } \Big ) \nonumber \\&= a_k\left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n } } \right) + b_k \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n } } \right) u , \end{aligned}$$
(21)

where

$$\begin{aligned} a_k \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n } } \right)&= \sum \limits _{i = 1}^{n - 1} {d_{i,k} } \left( {\bar{x}_i ,\bar{z}_i,\widetilde{y}_{d_i } } \right) \nonumber \\&+\, z_n (z_{n - 1} + f_n^k \left( {\bar{x}_n } \right) \nonumber \\&-\,\sum \limits _{j = 1}^{n - 1} {\frac{{\partial \phi _{n - 1} }}{{\partial x_j }}\left( {x_{j + 1} + f_j^k \left( {\bar{x}_j } \right) } \right) } \nonumber \\&-\, \sum \limits _{j = 0}^{n - 1} {\frac{{\partial \phi _{n - 1} }}{{\partial y_d^{(j)} }}y_d^{(j + 1)} } ) , \nonumber \\ b_k \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right)&= z_n g^k \left( {\bar{x}_n } \right) . \end{aligned}$$
(22)

In view of the above discussions and the simultaneous domination condition, a continuous feedback controller for system (1) can be designed in the following form:

$$\begin{aligned} u \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right)&= \left[ u_1\left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) , u_2\left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) ,\right. \nonumber \\&\quad \left. \ldots ,u_q\left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) \right] ^{T}, \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{array}{lll} u_j \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) \nonumber \\ \quad = \left\{ \begin{array}{ll} \hbox {min} _{i \in \left\{ {1,2, \ldots , m} \right\} } \left\{ {p_{i,j} \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) } \right\} ,\,&{} \quad \mathrm{if} \quad z_n > 0 \\ \hbox {max} _{i \in \left\{ {1, 2,\ldots , m} \right\} } \left\{ {p_{i,j} \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} }\right) } \right\} ,\,&{} \quad \mathrm{if}\quad z_n < 0\,\,\\ &{}\quad \mathrm{for} \,j\,\in \,M \\ 0,&{} \quad \mathrm{if} \quad z_n= 0 \\ \end{array} \right. \\ \end{array}\nonumber \\ \end{aligned}$$
(24)

and

$$\begin{aligned} \begin{array}{lll} u_j \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) \\ \quad = \left\{ \begin{array}{ll} \hbox {max}_{i \in \left\{ {1, 2,\ldots , m} \right\} } \left\{ {p_{i,j} \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} }\right) } \right\} , &{} \quad \mathrm{if}\quad z_n > 0 \\ \hbox {min}_{i \in \left\{ {1,2, \ldots ,m} \right\} } \left\{ {p_{i,j} \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) } \right\} , &{} \quad \mathrm{if}\quad z_n < 0,\\ &{}\quad \mathrm{for}\, j\, \in \, F \\ 0,&{}\quad \mathrm{if} \quad z_n = 0 \\ \end{array} \right. \\ \end{array}\quad \nonumber \\ \end{aligned}$$
(25)

with

$$\begin{aligned} p_k \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} }\right)&= \left[ p_{k,1} \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) , p_{k,2}\left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) , \right. \nonumber \\&\quad \left. \ldots , p_{k,q} \left( {\bar{x}_n ,\bar{z}_n,\widetilde{y}_{d_n} } \right) \right] ^{T} \nonumber \\&= \left\{ \begin{array}{ll} - b_k^T \frac{{\max \left\{ {a + b_k b_k^T ,0} \right\} }}{{b_k b_k^T }}, &{}\quad \mathrm{if}\quad z_n \, \ne 0 \\ 0,&{}\quad \mathrm{if}\quad z_n \, =\, 0.\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(26)

Lemma 4

Consider the system (12). Suppose that all subsystems of (12) are simultaneously dominatable. Then, a continuous feedback controller (23) can be designed such that along the solutions of all closed-loop subsystems

$$\begin{aligned} \dot{ V }_n( \bar{z}_n ) < 0,\quad \forall \bar{z}_n \ne 0 \end{aligned}$$
(27)

holds, where \( V_n( \bar{z}_n ) \) is the Lyapunov function obtained in (20). Thus, \( V_n (\bar{z}_n)\) is a common Lyapunov function (CLF) for the system (12).

Proof

The proof is similar to the proof of Lemma 3 in [29].\(\square \)

Now, we summarize the main result of this subsection in the following theorem.

Theorem 1

Suppose that Assumption 1-3 are satisfied. If the simultaneous domination assumption holds, then the OCTC problem of the system (1) is solved by the controller \(u\) designed as in (23) under arbitrary switchings. Moreover, the output tracking error \(x_{1d}(t)\) locally exponentially converges to zero.

Proof

  1. (i)

    First, we show that all \({z_i},i = 1,2, \ldots ,n\) are bounded. It follows from \(\dot{V}_n < 0\) in Lemma 4 that \(V_n \left( t \right) < V_n \left( 0 \right) , \forall t> t_0\ge 0\). This means that

    $$\begin{aligned} \frac{1}{2}\sum \limits _{j = 1}^n {z_j^2 \left( t \right) } < \frac{1}{2}\sum \limits _{j = 1}^n {z_j^2 \left( t_0 \right) } \end{aligned}$$
    (28)

    Under the initial condition specified in (3), and the choice of the constants \(a\) and \(b\) in (11), the right-hand side of (28) is bounded. This implies that the left-hand side of (28) must be bounded. It is easy to infer that the boundedness of the left-hand side of (28) implies that all \({z_i},i = 1,2, \ldots ,n\) are bounded. Then, boundedness of all \({x_i},i = 1,2, \ldots ,n\) follows from the boundedness of all \(z_i\), \(y_d^{(i)}(t)\), smooth property of all functions \(f_i^k (\overline{x}_i),g^k(\overline{x}_n),\phi _i \left( {\bar{x}_i ,\bar{z}_i ,\widetilde{y}_{d_i } } \right) \), and differentiable property of \( \Psi ({x_{1d}},a,b)\). With \(\bar{x}_n \left( t \right) ,\bar{z}_n \left( t \right) , \widetilde{y}_{d_n }\) bounded, we can infer that the continuous controller \(u\left( t \right) \) in (23) is bounded. Hence, all closed-loop signals are bounded.

  2. (ii)

    Since \(\left| {{z_1}} \right| \) is bounded for all \(t > t_0 \ge 0\), the output tracking error \({x_{1d}}(t)\) never reaches its boundary values \(a\) and \(b\), i.e., \({x_{1d}} \in (a,b)\) for all \(t > t _0 \ge 0\). This in turn implies from (11) and \(\underline{L }_1 \le \underline{L} \), \(\overline{L}_1 \le \bar{L}\) (Assumption 2) that \({x_{1d}}(t)\) is always in its constraint range, i.e., \( \underline{L }_1 \le {x_{1d}}(t) \le \overline{L}_1\) for all \(t > t_0 \ge 0\).

  3. (iii)

    From the fact that \(\bar{x}_i \left( t \right) ,\bar{z}_i \left( t \right) ,i = 1, 2,\ldots ,n\) are bounded, it can be checked from (20) that \(\ddot{V}_n\left( t \right) \) is bounded, which means that \(\dot{V}_n\left( t \right) \) is uniformly continuous. Then, applying Lemma 3, leads to \(\bar{z}_i \left( t \right) \rightarrow 0\) as \(t \rightarrow \infty \), which means \(y(t) \rightarrow y_d(t)\) as \(t \rightarrow \infty \).

  4. (iv)

    Now, by using the Taylor expansion of the function \(\Psi ({x_{1d}},a,b)\) about \({x_{1d}}(t) = 0\) with a notice of Property (5) of the function \(\Psi ({x_{1d}},a,b)\), Property (6) of the function \(h({x_{1d}},a,b)\), and the construction of the function \(\Psi ({x_{1d}},a,b)\) (see Lemma 2), it can be shown that there exists a strictly positive constant \({\delta _5}({\rho _5})\) depending on the positive constant \({\rho _5}\) with \(0 < {\rho _5} > \frac{{b - a}}{2},\) such that

    $$\begin{aligned} \quad {\delta _5}({\rho _5})\left| {{x_{1d}}(t)} \right| \le \left| {\Psi ({x_{1d}},a,b)} \right| ,\quad t > {t_1}>t_0\nonumber \\ \end{aligned}$$
    (29)

    where \(t_1\) is a fixed number. By definition \({z_1} = \Psi ({x_{1d}},a,b)\), a combination of (23) and \(z_1\rightarrow 0\) gives

    $$\begin{aligned} \quad \left| {{x_{1d}}(t)} \right| \le \frac{{\left| {\Psi ({x_{1d}}(t),a,b)} \right| }}{{{\delta _5}({\rho _5})}} = \frac{{\left| {{z_1}(t)} \right| }}{{{\delta _5}({\rho _5})}} \rightarrow 0\nonumber \\ \end{aligned}$$
    (30)

    which implies \(x_{1d}(t)\) converges to zero asymptotically.

\(\square \)

4 \(H_\infty \) control

In this subsection, the above OCTC design method is extended to the state-constrained \(H_\infty \) control (SCHC) problem of the following disturbed switched nonlinear systems:

$$\begin{aligned} {{\dot{x}}_i}&= f_i^{\sigma \left( t \right) }\left( {{{\bar{x}}_i}} \right) + {x_{i + 1}} + a_i^{\sigma \left( t \right) }\left( {{{\bar{x}}_i}} \right) \omega ,\nonumber \\&\quad i = 1,2, \ldots ,n - 1,\nonumber \\ {{\dot{x}}_n}&= f_n^{\sigma \left( t \right) }\left( {{{\bar{x}}_n}} \right) + u + a_n^{\sigma \left( t \right) }\left( {{{\bar{x}}_n}} \right) \omega ,\nonumber \\ y&= {h^{\sigma \left( t \right) }}\left( {{{\bar{x}}_n}} \right) + {d^{\sigma \left( t \right) }}\left( {{{\bar{x}}_n}} \right) \omega , \end{aligned}$$
(31)

where \(x_1 ,x_2 , \ldots ,x_n\) are the states, \(u \in R\) and \(y \in R^{n_p}\) are the input and output respectively. \(\omega \in R^{n_{\omega }}\) represents the disturbance input of function class \(\omega \in L_2[0,+\infty )\).The switching signal \(\sigma \left( t \right) \) is the same as the one for system (1). All functions are smooth functions satisfying \( f_i^k ( 0 ) = 0,\) \(a_i^k( 0 ) = 0,\) \(h^k (0) = 0,d^k (0) = 0 \) for \(\forall k \in I_m,\) \(i = 1, \ldots ,n \).

The switching signal \(\sigma \left( t \right) \) can be characterized by the switching sequence

$$\begin{aligned} \sum&= \big \{ { x_0^T ;\left( {i_0 ,t_0 } \right) ,\left( {i_1 ,t_1 } \right) , \ldots ,} \left( {i_k ,t_k } \right) ,\ldots ,\\&\quad \left. |i_k \in M, k \in I_m \right\} , \end{aligned}$$

in which \(t_0\) is the initial time, \(x_0^T \) is the initial state. When \(t \in [ {t_k ,t_{k + 1} } )\), \(\sigma \left( t \right) = i_k\), that is, the \(i_k\)th subsystem is active, and the trajectory \(x(t)\) of the switched system (1) is the trajectory of the \(i_k\)th subsystem.

Assumption 4

For \(i = 1,2, \ldots ,n,\)

$$\begin{aligned} \left| {{f_i^k}\left( {{{\bar{x}}_i}} \right) } \right| \le \left( {{{\left| {{x_1}} \right| }} + {{\left| {{x_2}} \right| }} + \ldots + {{\left| {{x_i}} \right| }}} \right) \mu _i^k\left( {{{\bar{x}}_i}} \right) , \end{aligned}$$
(32)

where \(\mu _i^k\left( {{{\bar{x}}_i}} \right) \) are a set of known nonnegative smooth functions.

Assumption 5

The controlled output \(y\) of the system (31) is of the form

$$\begin{aligned} y = h^k ( x_1 ) + d^k ( \bar{x}_n )\omega ,\quad k \in I_m, \end{aligned}$$
(33)

where \(h^k ( x_1 )\) are smooth real functions with \(h^k ( 0 ) = 0\) and \( d^k ( \bar{x}_n )\) are uniformly bounded, i.e.,

$$\begin{aligned} \Vert {d^k ( \bar{x}_n )} \Vert \le \gamma _d ,\quad \forall \bar{x}_n^T \in R^n ,k \in I_m, \end{aligned}$$
(34)

where \(\gamma _d\) is some positive constant.

Assumption 6

At the initial time \({t_0}\), there exist strictly positive constants \(\underline{L}_1<\underline{L}\) and \({ \overline{L}_1} < \overline{L}\) such that

$$\begin{aligned} -\underline{L}_1 \le {{x}_{1}}({t_0}) \le \overline{L}_1, \end{aligned}$$
(35)

where \({x_1}({t_0})\) is the initial value of the state \(x_1\).

Assumption 7

The \(p\)-times differentiable unbounded function in Definition 1 is strictly monotonic and satisfies

$$\begin{aligned} \Psi (x,a,b)=x[1 + \chi (x,a,b)], \end{aligned}$$
(36)

where \(\chi (x)\) is a nonnegative smooth function.

Lemma 5

[39]  For any positive real numbers \(c, d\) and any real-valued function \(\rho (x,y) > 0 \),

$$\begin{aligned} \left| x \right| ^a \left| y \right| ^d&\le \frac{a}{{a + d}}\rho (x,y)\left| x \right| ^{a + d} \nonumber \\&+ \frac{d}{{a + d}}\rho ^{ - a/d} (x,y)\left| y \right| ^{a + d} . \end{aligned}$$
(37)

The state-constrained \(H_\infty \) control (SCHC) problem to be addressed in this paper is stated as follows: given a constant \(\gamma \ge 0\), find, if possible, a state feedback controller \(u = u ( \bar{x}_n )\) with \(u(0)=0\) such that the resulting closed-loop system (31) with \(u ( \bar{x}_n )\) satisfies the following:

  1. (i)

    when \(w \equiv 0\), the closed-loop system (31) is asymptotically stable in a domain at the equilibrium under arbitrary switchings.

  2. (ii)

    when \(w \equiv 0\), the state \(x_1\) is within a pre-specified limit range, i.e.,

    $$\begin{aligned} -\underline{L}\le x_1 (t) \le \overline{L} \end{aligned}$$
    (38)

    for all \(t \ge {t_0} \ge 0\), where \(\underline{L}\) and \( \overline{L}\) are strictly positive constants.

  3. (iii)

    for every disturbance \(\omega \in L_2\), the response of the closed-loop system (1) starting from the initial state \(\bar{x}_n (0)\in R^n\) is such that

    $$\begin{aligned} \int _0^T {y^T (t )y(t )d} t \!\le \gamma ^2 \int _0^T {\omega ^T (t )\omega (t)d}t \!+\! V(x_0^T).\nonumber \\ \end{aligned}$$
    (39)

    where \(V: R^n \rightarrow R^+\) is a function with \(V(0) = 0\).

We are now in position to state the main result of this subsection.

Theorem 2

Consider the disturbed switched system (31) satisfying Assumptions 4-7. Then, the SCHC problem is solvable under arbitrary switchings for any scalar \(\gamma >\gamma _d\).

Proof

The main ingredients of the proof are recursive constructions of both a common Lyapunov function and a smooth-state feedback controller by backstepping.   \(\square \)

\(Step1.\) Similarly to Theorem 1, we apply a change of coordinates:

$$\begin{aligned} {z_1} = \Psi ({x_{1}},a,b), \end{aligned}$$
(40)

where \(\Psi ({x_{1}},a,b)\) is a \(p\)-times differentiable unbounded function with \(p \ge n - 1.\)

Differentiating both sides of (40) in conjunction with the system (31), one can rewrite them in the form:

$$\begin{aligned} {{{{\dot{z}}}}_1}&= \Psi '({x_{1}},a,b)(f_1^k \left( { x_1}\right) + x_{2}+a_1^k\left( {{{\bar{x}}_1}} \right) \omega ), \nonumber \\ {{\dot{x}}_i}&= f_i^k\left( {{{\bar{x}}_i}} \right) + {x_{i + 1}} + a_i^k\left( {{{\bar{x}}_i}} \right) \omega ,\quad i = 2,3, \ldots ,n,\nonumber \\ y&= {h^k}\left( {{{ x}_1}} \right) + {d^k}\left( {{{\bar{x}}_n}} \right) \omega ,\quad k\in I_m. \end{aligned}$$
(41)

Using (31), we can calculate from Assumption 5 that

$$\begin{aligned}&y^T y - \delta _1^2 \omega ^T \omega \nonumber \\&\quad \le ( {1 + \frac{{\gamma _d^2 }}{{\gamma _1^2 }}} )h_k^T \left( {x _1 } \right) h_k \left( {x _1 } \right) - \gamma _2^2 \omega ^T \omega . \end{aligned}$$
(42)

where \({\delta _1} \), \(\gamma _1\) and \(\gamma _2\) are positive constants satisfying \({\gamma _d} < {\delta _1} < \gamma \) and \( \gamma _2^2 = \delta _1^2 - \gamma _1^2 - \gamma _d^2 .\)

Choose \( V_1 (z_1) = \frac{1}{2}z_1^2\) and let \(z_2=x_2-\phi _1(z_1),\) where \(\phi _1(z_1)\) is the common stabilizing function to be designed.

Combining (42), Assumption 7 and the derivative of \(V_1(z_1)\) is given by

$$\begin{aligned} \dot{V}_1 \left( {z_1 } \right) \!+\!y^T y \!-\! \delta _1^2 \omega ^T \omega&= \Psi ' \left( \! {{x_1},a,b} \!\right) {z_1}\left[ \! {f_1^k}\left( \! {{z_1}} \!\right) \right. \nonumber \\&+\,\left. x_2+a_1^k\left( z_1 \right) \omega \right] \nonumber \\&+\, ( {1 + \frac{{\gamma _d^2 }}{{\gamma _1^2 }}} )h_k^T \left( {x _1 } \right) h_k \left( {x _1 } \right) \nonumber \\&-\, \gamma _2^2 \omega ^T \omega \nonumber \\&\le \Psi ' \left( {{x_1},a,b} \right) \bigg [ \left| {{z_1}{f_1^k}\left( {{z_1}} \right) } \right| \nonumber \\&+\, {z_1}\phi _1\left( {{z_1}} \right) + z_1z_2 \bigg ] \nonumber \\&+\, \frac{1}{{4\gamma _2^2}}\left( \! {\Psi ' \left( {{x_1},a,b} \right) z_1a_1^k\left( z_1 \right) }\!\right) ^2\nonumber \\&+\, \gamma _2^2 \omega ^T \omega +( {1 + \frac{{\gamma _d^2 }}{{\gamma _1^2 }}} )h_k^T \left( {x _1 } \right) \nonumber \\&\times \,h_k \left( {x _1 } \right) - \gamma _2^2 \omega ^T \omega \nonumber \\&\le \Psi ' \left( {{x_1},a,b} \right) \bigg [ \left| {{z_1}{f_1^k}\left( {{z_1}} \right) } \right| \nonumber \\&+\, {z_1}\phi _1\left( {{z_1}} \right) + z_1z_2 \bigg ] \nonumber \\&+\, z_1^2A_1(z_1)+z_1^2H(z_1), \end{aligned}$$
(43)

where \(A_1(z_1)\) and \(H(z_1)\) are smooth and satisfy \(A_1(z_1)\ge \frac{1}{{4\gamma _2^2}}\left( {\Psi ' \left( {{x_1},a,b} \right) a_1^k\left( z_1 \right) }\right) ^2\) and \(z_1^2H(z_1)\ge ( {1 + \frac{{\gamma _d^2 }}{{\gamma _1^2 }}} )h_k^T \left( {x _1 } \right) h_k \left( {x _1 } \right) , \forall k\in I_m\)

Using Assumption 4 and Assumption 7, it can be found that

$$\begin{aligned} \left| {f_1^k \left( {z_1 } \right) } \right| \le | {z_1 } |\hat{\mu }_1^k \left( { z_1 } \right) ,\forall k \in I_m, \end{aligned}$$
(44)

where \(\hat{\mu }_1^k \left( { z_1} \right) \) are a set of nonnegative smooth functions.

Then, we can get

$$\begin{aligned} \left| { z_1\Phi _1^k \left( { z_1 } \right) } \right| \le z_1^{2} \tilde{\varphi }_1^k \left( { z_1 } \right) ,\forall k \in I_m . \end{aligned}$$
(45)

where \(\Phi _1^k(z_1)=f_1^k ( z_1 ) \) and \(\tilde{\varphi }_1^k \left( { z_1 } \right) =\hat{\mu }_1^k \left( { z_1} \right) , k \in I_m \) are nonnegative smooth functions.

Then, it can be seen that

$$\begin{aligned}&\dot{V}_1 \left( {z_1 } \right) +y^T y - \delta _1^2 \omega ^T \omega \nonumber \\&\quad \le \Psi ' \left( {{x_1},a,b} \right) \bigg [ \left| {{z_1}\Phi _1^k\left( {{z_1}} \right) } \right| + {z_1}\phi _1\left( {{z_1}} \right) +{z_1}z_2 \bigg ]\nonumber \\&\qquad +\,z_1^2A_1(z_1)+z_1^2H(z_1)\nonumber \\&\quad \le \Psi ' \left( {{x_1},a,b} \right) \bigg [ z_1^{2}\tilde{\varphi }_{1,{max} }\left( {{z_1}} \right) + {z_1}\phi _1\left( {{z_1}} \right) +{z_1}z_2 \bigg ]\nonumber \\&\qquad +\,z_1^2A_1(z_1)+z_1^2H(z_1), \end{aligned}$$
(46)

where \(\tilde{\varphi }_{1,{max} } \left( { z_1 } \right) \ge \tilde{\varphi }_1^k \left( { z_1 } \right) \ge 0,\forall k \in I_m \) is a smooth function.

Design the common stabilizing function

$$\begin{aligned}&\phi _1 (z_1 ) =- z_1 [ \tilde{\varphi }_{1,{max} } \left( { z_1 } \right) \nonumber \\&\quad +\,\, z_1 + (n+z_1A_1(z_1)\nonumber \\&\quad +\,\, z_1H(z_1))/\Psi ' ({x_{1}},a,b)]. \end{aligned}$$
(47)

Substituting (47) into (46), one has

$$\begin{aligned}&\dot{V}_1 \left( {z_1 } \right) +y^T y - \delta _1^2 \omega ^T \omega \nonumber \\&\quad \le \Psi '\left( {{x_1},a,b} \right) \!\bigg [\!z_1^2\tilde{\varphi }_{1,{max} } \left( {{z_1}} \right) \!- z_1^2\tilde{\varphi }_{1,{max} }\left( {{z_1}} \right) \!- z_1^2 \nonumber \\&\qquad - n{{\Psi '}^{ - 1}}\left( {{x_1},a,b} \right) z_1^2 + {z_1}\left( {x_2 - \phi _1\left( {{z_1}} \right) } \right) \bigg ]\nonumber \\&\quad \le - nz_1^2 - \Psi '\left( {{x_1},a,b} \right) z_1^2 + \Psi '\left( {{x_1},a,b} \right) {z_1}z_2,\nonumber \\ \end{aligned}$$
(48)

where the coupling term \(\Psi '\left( {{x_1},a,b} \right) {z_1}z_2\) will be canceled in the subsequent step.

\(Step\,2.\) Let \(z_3 = x_3 -\phi _2(\bar{z}_2)\), where \(\phi _2(\bar{z}_2)\) is the common stabilizing function to be designed.

Choose \(\overline{V}_2 (\bar{z}_2)= V_1(z_1)+\frac{1}{{{2}}}z_2^{{2}}\), and then the time derivative of \(\overline{V}_2 (\bar{z}_2)\) is given by

$$\begin{aligned}&\dot{ \overline{V}}_2 \left( {\bar{z}_2 } \right) +y^T y - \delta _2^2 \omega ^T \omega \nonumber \\&\le - nz_1^2 - \Psi '\left( {{x_1},a,b} \right) z_1^2 + \Psi '\left( {{x_1},a,b} \right) {z_1}z_2\nonumber \\&\quad +\, z_2\left( {{\Phi _2^k}\left( {{{\bar{z}}_2}} \right) + \phi _2\left( {{{\bar{z}}_2}} \right) + z_3} \right) \nonumber \\&\quad -\,(\delta _2^2 -\delta _1^2)\omega ^T \omega +z_2A_2^k({\bar{z}_2})\omega \nonumber \\&\le \! - nz_1^2 - \Psi '\left( {{x_1},a,b} \right) z_1^2 + \Psi '\left( {{x_1},a,b} \right) |{z_1}z_2|\nonumber \\&\quad +\,|z_2 {\Phi _2^k}\left( {{{\bar{z}}_2}} \right) | + z_2\phi _2\left( {{{\bar{z}}_2}} \right) + z_2z_3\nonumber \\&\quad -\,\tau _2^2\omega ^T \omega +\,z_2A_2^k({\bar{z}_2})\omega , \end{aligned}$$
(49)

where \(\tau _2^2=\delta _2^2 -\delta _1^2,\delta _1<\delta _2<\Gamma ,\,\Phi _2^k \left( {\bar{z}_2 } \right) \,= f_2^k \left( {\bar{z}_2 }\right) - \frac{{\partial \phi _1 (z_1 )}}{{\partial z_1 }}\Gamma _1^k\left( {\bar{z}_2 } \right) , \Gamma _1^k \left( {\bar{z}_2 } \right) =\Psi '\left( {{x_1},a,b} \right) (f_1^k(z_1)+ (z_2 + \phi _1 (z_1 ))),A_2^k({\bar{z}_2})=a_2^k({\bar{z}_2}) - \frac{{\partial \phi ({z_1})}}{{\partial {z_1}}}\Psi '\left( {{x_1},a,b} \right) a_1^k({ z_1}),k\in I_m\)

Using Assumption 4 gives that

$$\begin{aligned} \left| { \Phi _2^k \left( {\bar{z}_2 } \right) } \right| \le \left( {{{\left| {{z_1}} \right| }} + {{\left| {{z_2}} \right| }}} \right) {\hat{\mu } _2^k}\left( {{{\bar{z}}_2}} \right) , \end{aligned}$$
(50)

where \( \hat{\mu }_2^k \left( {\bar{z}_2 } \right) \) are a set of nonnegative smooth functions.

Furthermore, according to Lemma 5 and (49)–(50), one can infer that

$$\begin{aligned}&\mathrm{{ - }}\tau _2^2{\omega ^\mathrm{{T}}}\omega + {z_2}A_2^k\left( {{{\bar{z}}_2}} \right) \omega \nonumber \\&\quad \le - {\left| {{\tau _2}\omega - \frac{1}{{2{\tau _2}}}{z_2}A_2^k\left( {{{\bar{z}}_2}} \right) } \right| ^2} + \frac{1}{{4\tau _2^2}}{\left( {{z_2}A_2^k\left( {{{\bar{z}}_2}} \right) } \right) ^2}\nonumber \\&\quad \le \frac{1}{{4\tau _2^2}}{\left( {{z_2}{A_2}\left( {{{\bar{z}}_2}} \right) } \right) ^2} \end{aligned}$$
(51)
$$\begin{aligned}&\left| z_1z_2 \right| \le z_1^{2} + z_2^{2}\tilde{\varphi }_2 \left( {{{\bar{z}}_2}} \right) , \end{aligned}$$
(52)
$$\begin{aligned}&\left| {z_2{\Phi _2^k}\left( {{{\bar{z}}_2}} \right) } \right| \le z_1^{2} + z_2^{2}\hat{\varphi }_2^k \left( {{{\bar{z}}_2}} \right) , \end{aligned}$$
(53)

where \( {A_2}\left( {{{\bar{z}}_2}} \right) \ge {A_2^k}\left( {{{\bar{z}}_2}} \right) ,\tilde{\varphi }_2 \left( {\bar{z}_2 } \right) \ge 0, \hat{\varphi } _2^k \left( {\bar{z}_2 } \right) \ge 0,k\in I_m \) are some smooth functions.

Thus, we obtain

$$\begin{aligned}&\dot{ \overline{V}}_2 \left( {\bar{z}_2 } \right) +y^T y - \delta _2^2 \omega ^T \omega \nonumber \\&\quad \le - nz_1^{2} - \Psi '\left( {{x_1},a,b} \right) z_1^{2} + \Psi '\left( {{x_1},a,b} \right) z_1^{2} \nonumber \\&\qquad + \Psi '\left( {{x_1},a,b} \right) z_2^{2}{{\tilde{\varphi }}_2}\left( {{{\bar{z}}_2}} \right) + z_1^{2}\!+\! z_2^{2} \hat{\varphi }_2^k \left( {{{\bar{z}}_2}} \right) \nonumber \\&\quad \quad +\frac{1}{{4\tau _2^2}}{\left( {{z_2}{A_2}\left( {{{\bar{z}}_2}} \right) } \right) ^2}\!+\!z_2\phi _2\left( {{{\bar{z}}_2}} \right) \!+\! z_2z_3 \nonumber \\&\quad \le - \left( {n \!-\! 1} \right) z_1^2 +\! \left( {\Psi '\left( {{x_1},a,b} \right) {{\tilde{\varphi }}_2}\left( {{{\bar{z}}_2}} \right) + \hat{\varphi }_2^k\left( {{{\bar{z}}_2}} \right) } \right) z_2^2 \nonumber \\&\quad \quad +\frac{1}{{4\tau _2^2}}{\left( {{z_2}{A_2}\left( {{{\bar{z}}_2}} \right) } \right) ^2}+ z_2\phi _2\left( {{{\bar{z}}_2}} \right) +z_2z_3 \nonumber \\&\quad \le - \left( {n - 1} \right) z_1^2 + z_2^2{\varphi _{2,max}}\left( {{{\bar{z}}_2}} \right) + z_2\phi _2\left( {{{\bar{z}}_2}} \right) \nonumber \\&\qquad +\frac{1}{{4\tau _2^2}}{\left( {{z_2}{A_2}\left( {{{\bar{z}}_2}} \right) } \right) ^2}+z_2z_3, \end{aligned}$$
(54)

where \(\varphi _{2,max} \ge \Psi ' ({x_{1d}},a,b) \tilde{\varphi }_2 \left( {\bar{z}_2 } \right) + \hat{\varphi } _2^k \left( {\bar{z}_2 } \right) \) is a smooth function.

Design the common stabilizing function

$$\begin{aligned} \phi _2 (\bar{z}_2 )&= -z_2 [ \varphi _{2,max} \left( {\bar{z}_2 } \right) + \frac{1}{{4\tau _2^2}}{\left( {{A_2}\left( {{{\bar{z}}_2}} \right) } \right) ^2}{z_2}\nonumber \\&\quad + (n - 1)]. \end{aligned}$$
(55)

Substituting (55) into (54) yields

$$\begin{aligned}&\dot{ \overline{V}}_2 \left( {\bar{z}_2 } \right) +y^T y - \delta _2^2 \omega ^T \omega \le - (n - 1)(z_1^{2} + z_2^2 )\nonumber \\&\quad + z_2^2z_3^2, \end{aligned}$$
(56)

where the coupling term \(z_2^2z_3^2\) will be canceled in the subsequent step.

\(Step\,i.\) Let \(z_{i+1} = x_{i+1 }- \phi _i(\bar{z}_i)\), where \( \phi _i(\bar{z}_i)\) is the common stabilizing function to be designed.

Assume that we have completed the first \(i - 1 (2 \le i \le n) \) steps, that is, for the following collection of auxiliary \((z_1, \ldots , z_{i-1})\)-equations:

$$\begin{aligned} \dot{z}_j&= \Phi _j^k (\bar{z}_j ) + x_{j + 1}+A_j^k\left( {{{\bar{z}}_j}} \right) \omega ,\,\nonumber \\&\quad j = 1, \ldots ,i - 1, \end{aligned}$$
(57)

where \( \Phi _j^k (\bar{z}_j ) = f_j^k(\bar{z}_j ) - \sum _{l = 1}^{j - 1} {\frac{{\partial \phi _{j-1} (\bar{z}_{j-1} )}}{{\partial z_l }}} \Gamma _l^k(\bar{z}_{l - 1} ),A_j^k\left( {{{\bar{z}}_j}} \right) = a_j^k\left( {{{\bar{z}}_j}} \right) - \frac{{\partial {\phi _{j - 1}}}}{{\partial {x_1}}}\Psi '({x_1},a,b)a_1^k\left( {{z_1}} \right) \omega -\sum _{l =2}^{j - 1} {\frac{{\partial {\phi _{j - 1}}}}{{\partial {x_l}}}} a_l^k\left( {{{\bar{z}}_l}} \right) \), we have had positive scalars \(\delta _1,\ldots ,\delta _i-1\) satisfying \({\gamma _d} < {\delta _1} < {\delta _2} < \ldots < {\delta _{i - 1}} < \gamma \), a set of common stabilizing functions (47), (55) and

$$\begin{aligned} \phi _j (\bar{z}_j )&= -z_j [ \varphi _{j,{\max } }\left( {\bar{z}_j } \right) +\frac{1}{{4\tau _j^2}}{\left( {{A_j}\left( {{{\bar{z}}_j}} \right) } \right) ^2}{z_j}\nonumber \\&\quad + (n - j + 1)], \end{aligned}$$
(58)

where \(3 \le j \le i -1\), such that there exists a CLF for the transform system (57),

$$\begin{aligned} \overline{V}_{i-1} (\bar{z}_{i-1})= V_1(z_1)+\sum \limits _{l = 2}^{i-1 }\frac{1}{2}{z_l^{2} } , \end{aligned}$$
(59)

and the time derivative of \(\overline{V}_{i-1} (\bar{z}_{i-1})\) satisfies \( \dot{\overline{V}}_{i - 1} \left( {\bar{z}_{i - 1} } \right) +y^T y - \delta _{i-1}^2 \omega ^T \omega \le - (n-i+2)(z_1^2 + \ldots + z_{i - 1}^2)\) \( + z_{i - 1}z_i.\)

Choose \( \overline{V}_{i} (\bar{z}_{i})=\overline{V}_{i-1} (\bar{z}_{i-1}) +\frac{1}{2}{z_i } , \) then one conclude

$$\begin{aligned}&\dot{\overline{V}}_i \left( {\bar{z}_i } \right) +y^T y -\delta _{i}^2{\omega ^{T}}\omega \nonumber \\&\quad \le \!- \left( {n \!- \!i \!+ \!2} \right) \left( {z_1^{2} \!+\! \ldots \!+\ z_{i - 1}^{2}} \right) \!+ z_{i - 1}z_i-\tau _{i}^2 \omega ^T \omega \nonumber \\&\quad \quad +\, z_i\left( {{\Phi _i^k}\left( {{{\bar{z}}_i}}\right) +A_i^k\left( {{{\bar{z}}_i}} \right) \omega + \phi _i^k\left( {{{\bar{z}}_i}} \right) + z_{i+1}} \right) \nonumber \\&\quad \le \!-\! \left( {n \!-\! i \!+\! 2} \right) \left( {z_1^{2} \!+\! \ldots \!+\! z_{i \!-\! 1}^{2}} \right) \!+\! |z_{i - 1}z_i|\!-\!\tau _{i}^2 \omega ^T \omega \nonumber \\&\quad \quad + \left| {z_i{\Phi _i^k} \left( {{{\bar{z}}_i}}\right) } \right| \!+\! z_i\phi _i^{{p_i}}\left( {{{\bar{z}}_i}} \right) \!+\! \left| {z_iA_i^k\left( {{{\bar{z}}_i}} \right) \omega } \right| \!+\! z_iz_{i+1},\nonumber \\ \end{aligned}$$
(60)

where \( \tau _{i}^2=\delta _{i}^2-\delta _{i-1}^2,\Phi _i^k \left( {\bar{z}_i } \right) = f_i^k \left( {\bar{z}_i } \right) - \sum \nolimits _{l = 1}^{i - 1} {\frac{{\partial \phi _{l - 1} (\bar{z}_{l - 1})}}{{\partial z_i }}\Gamma _l^k \left( {\bar{z}_{l-1} } \right) } ,\) \(A_i^k\left( {{{\bar{z}}_i}} \right) \) \(= a_i^k\left( {{{\bar{z}}_i}} \right) \) \(- \frac{{\partial {\phi _{i - 1}}}}{{\partial {x_1}}}\) \(\Psi '({x_1},a,b)\) \(a_1^k\left( {{z_1}} \right) \omega -\sum _{l =2}^{i- 1} {\frac{{\partial {\phi _{i - 1}}}}{{\partial {x_l}}}} a_l^k\left( {{{\bar{z}}_l}} \right) \).

Similarly to Step 2, one has \( \left| {z_{i - 1}z_i} \right| \le \frac{{z_1^2}}{{2}} + \ldots + \frac{{z_{i-1}^2}}{{2}} + z_i^2{{\tilde{\varphi }}_i}\left( {{{\bar{z}}_i}} \right) , \left| {z_i{\Phi _i}\left( {{{\bar{z}}_i}} \right) } \right| \le \frac{1}{2}z_1^{2} + \ldots + \frac{1}{2}z_{i - 1}^{2} + z_i^2{{\hat{\varphi }}_i^k}\left( {{{\bar{z}}_i}} \right) ,\mathrm{{ - }}\tau _{i}^2{\omega ^\mathrm{{T}}}\omega + \left| {{z_i}A_i^k\left( {{{\bar{z}}_i}} \right) \omega } \right| \le - \Big | {\tau _i}\omega - \frac{1}{{2{\tau _i}}}{z_i}A_i^k\left( {{{\bar{z}}_i}} \right) \Big |^2 + \frac{1}{{4\tau _i^2}}{\left( {{z_i}A_i^k\left( {{{\bar{z}}_i}} \right) } \right) ^2} \le \frac{1}{{4\tau _i^2}}{\left( {{z_i}{A_i}\left( {{{\bar{z}}_2}} \right) } \right) ^2}\) where \({{A_i}\left( {{{\bar{z}}_2}} \right) }\ge {A_i^k\left( {{{\bar{z}}_i}} \right) },\tilde{\varphi }_i \left( {\bar{z}_i } \right) \ge 0,\hat{\varphi }_i^k\left( {\bar{z}_i } \right) \ge 0,\forall i\in I_m\) are some smooth functions. Thus, one can get

$$\begin{aligned}&\dot{\overline{V}}_i \left( {\bar{z}_i } \right) +y^T y -\delta _{i}^2{\omega ^{T}}\omega \nonumber \\&\quad \le - \left( {n - i + 2} \right) \left( {z_1^{2} + \ldots + z_{i - 1}^{2}} \right) + z_1^{2} + \ldots \nonumber \\&\qquad +\, z_{i - 1}^{2} + \frac{1}{{4\tau _i^2}}{\left( {{z_i}{A_i}\left( {{{\bar{z}}_2}} \right) } \right) ^2}+\, {{\hat{\varphi }}_i^k}\left( {{{\bar{z}}_i}} \right) z_i^{2}\nonumber \\&\qquad +\, {{\tilde{\varphi }}_i}\left( {{{\bar{z}}_i}} \right) z_i^{2} + z_i\phi _i\left( {{{\bar{z}}_i}} \right) + z_iz_{i+1}\nonumber \\&\quad \le - \left( {n - i + 2} \right) \left( {z_1^{2} + \ldots + z_{i - 1}^{2}} \right) \nonumber \\&\qquad +\, z_1^{2} + \ldots + z_{i - 1}^{2} +\frac{1}{{4\tau _i^2}}{\left( {{z_i}{A_i}\left( {{{\bar{z}}_2}} \right) } \right) ^2} \nonumber \\&\qquad +\, {\varphi _{i,max}}\left( {{{\bar{z}}_i}} \right) z_i^{2} + z_i\phi _i\left( {{{\bar{z}}_i}} \right) + z_iz_{i+1},\nonumber \\ \end{aligned}$$
(61)

where \( \varphi _{i,max} \left( {\bar{z}_i } \right) \ge \tilde{\varphi }_{i} \left( {\bar{z}_i } \right) +\hat{\varphi }_i^k \left( {\bar{z}_i } \right) \) is a smooth functions.

Design the common stabilizing function

$$\begin{aligned} \phi _i (\bar{z}_i ) \!=\! -z_i [ \varphi _{i,max} \left( {\bar{z}_i } \right) \!+\!\frac{1}{{4\tau _i^2}}{\left( {{A_i}\left( {{{\bar{z}}_2}} \right) } \right) ^2}{z_i} \!+\! (n \!- i \!+\! 1)].\!\!\nonumber \\ \end{aligned}$$
(62)

Then, substituting (62) into (61) yields

$$\begin{aligned}&\dot{\overline{V}}_i \left( {\bar{z}_i } \right) +y^T y -\delta _{i} ^2{\omega ^{T}}\omega \nonumber \\&\quad \le - \left( {n - i + 1} \right) \left( {z_1^{2} + \ldots + z_{i - 1}^{2}} \right) \nonumber \\&\quad +\, {\varphi _{i,max}}\left( {{{\bar{z}}_i}} \right) z_i^{2} - {\varphi _{i,max}}\left( {{{\bar{z}}_i}} \right) z_i^{2} \nonumber \\&\quad - \left( {n - i + 1} \right) z_i^{2} + z_iz_{i+1},\nonumber \\&\quad =- \left( {n - i + 1} \right) \left( {z_1^{2} + \ldots + z_{i }^{2}} \right) +z_{i }z_{i+1 },\nonumber \\ \end{aligned}$$
(63)

where the coupling term \(z_iz_{i+1}\) will be canceled in the subsequent step.

\(Step\,n\). By repeating the inductive argument above, it is straightforward to see that at the final step, there exists a CLF of the system (31)

$$\begin{aligned} \overline{V}_{n} (\bar{z}_{n})= V_1(z_1)+\frac{1}{2}\sum \limits _{l = 2}^{n }{z_l^2 } . \end{aligned}$$
(64)

Then, we can explicitly design a smooth-state feedback controller as follows

$$\begin{aligned} u(\bar{z}_n )&= -z_n \left[ \varphi _{n,max} \left( {\bar{z}_n } \right) +\frac{1}{{4\tau _n^2}}{\left( {{A_n}\left( {{{\bar{z}}_n}} \right) } \right) ^2}{z_n} + 1\right] ,\nonumber \\&\quad \forall k \in I_m \end{aligned}$$
(65)

such that

$$\begin{aligned} \dot{\overline{V}}_n \left( {\bar{z}_n } \right) +y^T y -\gamma ^2{\omega ^{T}}\omega \le - (z_1^{2} + \cdots + z_n^{2} ) \end{aligned}$$
(66)

with \(\gamma ^2=\delta _{n}^2\).

For any \( \forall T \ge 0,\) we let \(t_k < T < t_{k + 1},\) \(t_0=0\), for any integer \(k \ge 0\). Taking integration over both sides of the above inequality from \(t = 0\) to \(T\) yields

$$\begin{aligned}&\int _0^T {{{\dot{\overline{V}}_n} + y^T y - \gamma ^2 \omega ^T \omega } dt} \nonumber \\&\quad = (\overline{V}_n \left( {t_1 } \right) - \overline{V}_n\left( {t_0 } \right) + \overline{V}_n\left( {t_2 } \right) - \overline{V}_n\left( {t_1 } \right) + \ldots \nonumber \\&\quad \quad +\, \overline{V}_n \left( T \right) - \overline{V} _n\left( {t_k } \right) + \int _0^T {y^T y - \gamma ^2 \omega ^\mathrm{{T}} \omega dt}\nonumber \\&\quad = \overline{V}_n \left( T \right) - \overline{V}_n \left( {t_0 } \right) + \int _0^T {y^T y - \gamma ^2 \omega ^\mathrm{{T}} \omega dt} . \end{aligned}$$
(67)

Furthermore, we have

$$\begin{aligned} \int _0^T {y^T (t)y(t)d} t \le \gamma ^2 \int _0^T {\omega ^T (t)\omega (t)dt} + \overline{V}_n (T).\nonumber \end{aligned}$$

When \(\omega \equiv 0,\) it follows from (66) that

$$\begin{aligned} \dot{\overline{V}}_n (\bar{z}_n ) \le - (z_1^{2} + \ldots + z_n^{2} ). \end{aligned}$$
(68)

Thus, asymptotical stability of the closed-loop system (31) in a domain without violation of the state constraint (38) can be found based on the proof of Theorem 1.

5 Illustrative examples

In this subsection, we present two illustrative examples to demonstrate the applicability and effectiveness of the proposed approach.

Example 1

Consider the following nonlinear switched system:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1 = f_1^{i} \left( {x_1 } \right) + x_2 , \\ \dot{x}_2 = f_2^{i} \left( {\bar{x}_2 } \right) + g^{i} \left( {\bar{x}_2 } \right) u,\quad i=1,2 , \\ y = x_1 ,\\ \end{array} \right. \end{aligned}$$
(69)

where \( f_1^1 (x_1 ) = 2x_1 - 0.8, f_2^1 (\bar{x}_2 ) = x_1 x_2 ( 3 +x_1 x_2 ), f_1^2 (x_1 ) = 0, f_2^2 = 2x_1^2 x_2^2 , g^1 (\bar{x}_2 ) = [ - 1.2x_1^2 x_2^2 ,1.6],\) \(g^2 = [ - \sin ^2( x_1 + x_2 ),1.3 - \cos (x_1^3 x_2^2 )]. \) The objective is for \(y\left( t \right) \) to track the desired trajectory \(y_d = 0.4\), subject to a symmetric constraint \( \underline{L}=\bar{L} = 0.2\).

First, in view of the symmetric system constraint \( \underline{L}=\bar{L} = 0.2\) and Remark 2, we choose \(z_1=\Psi ({x_{1d}},-0.2,0.2)=tan(\frac{5\pi }{2}(x_1-0.4))\) and \(V_1 (z_1 ) = \frac{1}{2}z_1^2\). Moreover, we can show that \(\phi _1 = - 3z_1\) is a common smooth stabilizing function for the auxiliary \(z_1\)- equations. In this case

$$\begin{aligned} d_1^1&= -\frac{5}{2}\pi sec^2\left( \frac{5}{2}\pi (x-0.4)\right) z_1^2 , d_1^2\nonumber \\&= -\frac{15}{2}\pi sec^2\left( \frac{5}{2}\pi (x-0.4)\right) z_1^2. \end{aligned}$$
(70)

Define \(z_2 = x_2 - \phi _1\). Then, \( V_2 (\bar{z}_2 ) = \frac{1}{2}z_1^2 + \frac{1}{2}z_2^2 \) is positive definite and radially unbounded. Thus, \(V_2 \) is a common Lyapunov function for the two subsystems in (69). For \(k = 1,2,\) let

$$\begin{aligned} a_k&= d_k^1 + z_2 \left[ {\frac{5}{2}} \pi sec^2\left( \frac{5}{2}\pi (x-0.4)\right) z_1 + f_2^k ( {\bar{x}_2 })\right. \nonumber \\&\quad \left. -\frac{{\partial \phi _1 }}{{\partial x_1 }} ( x_2 + f_1^k ( \bar{x}_1 ))\right] , \nonumber \\ b_k&= z_2 g^k \left( \bar{x}_2\right) . \end{aligned}$$
(71)

It is clear that \(M = \{ 2\} ,F = \{ 1\}\). From (24)–(26), we can obtain the following controller:

$$\begin{aligned} u = [u_1 ,u_2 ]^T \end{aligned}$$
(72)

with

$$\begin{aligned} u_1 = \left\{ \begin{array}{ll} \hbox {max}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,2} } \right\} ,&{} \quad \hbox {if} \quad z_2 \,>\, 0 ,\\ \hbox {min}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,2} } \right\} , &{} \quad \hbox {if} \quad z_2 \, <\, 0 ,\\ z_2 = 0, &{} \quad \hbox {if} \quad z_2 \, =\, 0, \\ \end{array} \right. \end{aligned}$$
(73)

and

$$\begin{aligned} u_2 = \left\{ \begin{array}{ll} \hbox {min}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,1} } \right\} ,&{} \quad \hbox {if} \quad z_2 \, > \,0, \\ \hbox {max}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,1} } \right\} ,&{} \quad \hbox {if} \quad z_2 \, <\, 0, \\ z_2 = 0, &{} \quad \hbox {if} \quad z_2\, =\, 0 ,\\ \end{array} \right. \end{aligned}$$
(74)

where

$$\begin{aligned} \begin{array}{l} p_k \left( {\bar{x}_2 ,\tilde{y}_{d_2 } } \right) = \left[ {p_{k,1} \left( {\bar{x}_2 ,\tilde{y}_{d_2 } } \right) p_{k,2} \left( {\bar{x}_2 ,\tilde{y}_{d_2 } } \right) } \right] \\ \quad = \left\{ \begin{array}{ll} - b_k^T \frac{{\max \left\{ {a_k + b_k b_k^T ,0} \right\} }}{{b_k b_k^T }},&{} \quad \hbox {if} \quad z_2 \, \ne \, 0, \\ 0, &{} \quad \hbox {if}\quad z_2 \,\ne \,0. \\ \end{array} \right. \\ \end{array} \end{aligned}$$
(75)

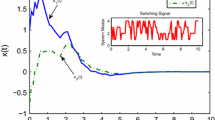
Let the initial values be \(x_1 \left( 0 \right) = 0.58,x_2 \left( 0 \right) = - 1.2\). Fig. 1 shows that asymptotic tracking performance is achieved under a random switching signal depicted in Fig. 2. Moreover, with various initial values of \(x_1\), Fig. 3 indicates that the error \(x_{1d}(t)\) converge to \(0\) while remaining in the set \((-0.2,0.2), \forall t\ge 0\).

Fig. 1
figure 1

Output tracking for the desired signal \(y_d=0.4\)

Full size image
Fig. 2
figure 2

The given switching signal for the system (69)

Full size image
Fig. 3
figure 3

Tracking error \(x_{1d}\) for various initial values satisfying \(\left| {x_1 \left( 0 \right) } \right| < 0.2\)

Full size image

Example 2

In this example, we will apply the proposed approach to the continuous stirred tank reactor (CSTR) with two modes feed stream (see Fig. 4), which is molded as a switched nonlinear system [16, 40]:

$$\begin{aligned} \dot{C}_A&= \frac{{q_\sigma }}{V}(C_{Af_\sigma } - C_A ) - a_0 e^{ - \frac{E}{{RT}}} C_A , \nonumber \\ \dot{T}&= \frac{{q_\sigma }}{V}(T_{f_\sigma } - T) - a_1 e^{ - \frac{E}{{RT}}} C_A \nonumber \\&+ \frac{{UA}}{{V_\rho C_p }}(T_c - T). \end{aligned}$$
(76)
Fig. 4
figure 4

Schematic diagram of the process

Full size image

The physical meaning of the parameters of this system can be found in [40]. Under a coordinate transformation and smooth feedback [40], the system can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1 = f_1^{\sigma \left( t \right) } + x_2 , \\ \dot{x}_2 = g^{\sigma \left( t \right) } u \\ \end{array} \right. \end{aligned}$$
(77)

with \( f_1^1 (x_1 ) = 0.5x_1 ,f_1^2 (x_1 ) = 2x_1 ,g^1 = g^2 = [1,1] \). From the point of view of engineering application, the objective is for \( y(t) \) to track desired trajectory \(y_d(t)\), subject to an asymmetric constraint \( \underline{L}=0.2,\bar{L} = 0.3\). For simplicity, we consider the system to be known for a stabilization task, i.e., \(y_d(t)\equiv 0.\)

First, defining \(z_1= \Psi ({x_1},0.2,0.3)=tan[\frac{\pi }{2}(2h(x,-0.2,0.3)-1)]-tan[\frac{\pi }{2}(2h(0,-0.2,0.3)-1)]\) as the \(p\)-times differentiable unbounded function candidate and with \(V_1 = \frac{1}{2} z_1^2 \), we can show that \( \phi _1 =- 2.5 z_1 \) is a dominating feedback law for the auxiliary first-order subsystems of (77). In this case

$$\begin{aligned}&d_1^1 \!=\! -2\Psi ' ({x_1},0.2,0.3) z_1^2 ,\nonumber \\&d_1^2=\! -0.5\Psi ' ({x_1},0.2,0.3) z_1^2. \end{aligned}$$
(78)

Furthermore, define \(z_2 = x_2 - \phi _1\), we further construct \(V_2(\bar{z}_2) = \frac{1}{2} z_1^2 +z_2^2.\) Thus, a common Lyapunov function for (77) is obtained by choosing \(V_2(\bar{z}_2)\). For \(k = 1,2,\) let

$$\begin{aligned} a_k&= d_k^1 + z_2 [ \Psi ' ({x_1},0.2,0.3)z_1 +f_2^k ( {\bar{x}_2 }) \nonumber \\&-\, \frac{{\partial \phi _1 }}{{\partial x_1 }}( x_2 + f_1^k ( \bar{x}_1 ))], \nonumber \\ b_k&= z_2 g^k \left( \bar{x}_2\right) . \end{aligned}$$
(79)

It is clear that \(M = \{ 1, 2\}\) and \(F\) is empty set. From (24)–(26), we can obtain the following controller:

$$\begin{aligned} u = [u_1 ,u_2 ]^T \end{aligned}$$
(80)

with

$$\begin{aligned} u_1 = \left\{ \begin{array}{ll} \hbox {min}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,1} } \right\} , &{} \quad \hbox {if} \quad z_2 \, >\, 0, \\ \hbox {max}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,1} } \right\} ,&{} \quad \hbox {if} \quad z_2 \, <\, 0, \\ z_2 = 0, &{} \quad \hbox {if} \quad z_2\, =\, 0 ,\\ \end{array} \right. \end{aligned}$$
(81)

and

$$\begin{aligned} u_2 = \left\{ \begin{array}{ll} \hbox {min}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,2} } \right\} , &{} \quad \hbox {if} \quad z_2\, >\, 0 ,\\ \hbox {max}_{i \in \left\{ {1,2} \right\} } \left\{ {p_{i,2} } \right\} , &{} \quad \hbox {if} \quad z_2 \, < \,0 ,\\ z_2 = 0, &{} \quad \hbox {if}\quad z_2\, = \,0, \\ \end{array} \right. \end{aligned}$$
(82)

where

$$\begin{aligned} \begin{array}{l} p_k \left( {\bar{x}_2 ,\tilde{y}_{d_2 } } \right) = \left[ {p_{k,1} \left( {\bar{x}_2 ,\tilde{y}_{d_2 } } \right) p_{k,2} \left( {\bar{x}_2 ,\tilde{y}_{d_2 } } \right) } \right] \\ = \left\{ \begin{array}{ll} - b_k^T \frac{{\max \left\{ {a_k + b_k b_k^T ,0} \right\} }}{{b_k b_k^T }},&{} \quad \hbox {if} \quad z_2\, \ne \,0, \\ 0,\quad &{} \quad \hbox {if}\quad z_2 \,\ne \, 0. \\ \end{array} \right. \end{array} \end{aligned}$$
(83)

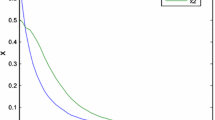
Given the initial values as \(x_1 \left( 0 \right) = -0.19,x_2 \left( 0 \right) = - 1.0\), Fig. 5 shows that asymptotic tracking performance is achieved, and we can see that the output stays strictly within the set (\(-\)0.2, 0.3). Furthermore, the random switching signal is demonstrated in Fig. 6.

Fig. 5
figure 5

The state response of the closed-loop system (77)

Full size image
Fig. 6
figure 6

The given switching signal for the system (77)

Full size image

6 Conclusions

In this paper, we have designed controller to deal with the problems of OCTC and SCHC of a class of switched nonlinear systems in a strict feedback form. In our approach, smooth or \(p\)-times differentiable unbouded functions are first introduced and incorporated in output tracking error (or the constrained state) transformations to convert the problem of controlling the systems with output tracking error constraints (or the constrained state) to a new problem of regulating the converted systems without a constraint but still in a strict feedback form. Then, the backstepping technique is employed to design controller for the transformed systems. Two illustrative examples of applications of the general results are presented at the end.