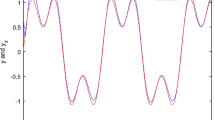Adaptive neural tracking control for a class of perturbed pure-feedback nonlinear systems

Abstract

This paper focuses on the problem of the adaptive neural control for a class of a perturbed pure-feedback nonlinear system. Based on radial basis function (RBF) neural networks’ universal approximation capability, an adaptive neural controller is developed via the backstepping technique. The proposed controller guarantees that all the signals in the closed-loop system are bounded and the tracking error eventually converges to a small neighborhood around the origin. The main advantage of this note lies in that a control strategy is presented for a class of pure-feedback nonlinear systems with external disturbances being bounded by functions of all state variables. A numerical example is provided to illustrate the effectiveness of the suggested approach.

1 Introduction

During the past decades, adaptive backstepping control has become one of the most popular design methods for nonlinear systems in triangular structure, and many significant results have been obtained; see, for instance [1–3] and the reference therein. These researches provide a systematic methodology of solving tracking or regulation control problems of nonlinear systems without satisfying the matching condition. However, it is assumed that an accurate model of the system is available and the unknown parameters appear linearly with respect to known nonlinear functions. This assumption is not sufficient for many practical situations, since it is a difficult work to precisely describe a nonlinear system by known nonlinear functions. Therefore, the investigation on the problem of controlling nonlinear systems with incomplete model knowledge is a meaningful issue.

In order to deal with highly uncertain nonlinear and complex systems, approximator-based adaptive control approaches have also been extensively studied in the past decades by using Lyapunov stability theory. In control design procedure, RBF neural networks (or fuzzy logic systems) are used to approximate uncertain nonlinear functions in dynamic systems because of their universal approximation capability, and then the backstepping technique is applied to construct an adaptive controller. Based on this idea, many interesting control schemes have been proposed for a large class of strict-feedback nonlinear system with uncertain nonlinear functions [5–24]. Using the universal approximation capability of fuzzy logic systems, Wang [4] first proposed a stable adaptive fuzzy control approach for a class of nonlinear systems with unknown functions. Then many adaptive fuzzy control schemes were obtained for uncertain nonlinear systems [7–17]. Alternatively, some adaptive control approaches were investigated for nonlinear systems based on RBF neural networks [5, 6, 18–24]. In the aforementioned papers, however, the research results are obtained under the condition that the considered systems are of affine nonlinear systems, in which the system inputs appear linearly in the state equation.

The nonaffine pure-feedback system stands for a more general class of triangular systems, which have no affine appearance of the variables to be utilized as virtual control inputs. In practice, many nonlinear systems are of nonaffine structure, such as mechanical systems [25], biochemical processes [3], and so on. Therefore, the control of nonaffine pure-feedback nonlinear systems is a meaningful issue and has received increasing attention in the control community in recent years [26–35]. In [26, 27], a class of much simpler pure-feedback systems where the last one or two equations were assumed to be affine were investigated. Using input-to-state stability analysis and the small gain theorem, an improved adaptive neural control approach was presented for a class of completely nonaffine pure-feedback systems [28]. Furthermore, many researchers further considered other types of pure-feedback nonlinear systems, such as pure-feedback systems with time-delay [32], with dead-zone [31], and discrete-time pure-feedback systems [34]. More recently, in [35], an novel observer-based adaptive fuzzy output-feedback control scheme is proposed for a class of MIMO pure-feedback nonlinear systems. Nevertheless, only a few results have been reported for the problem of adaptive control for pure-feedback nonlinear systems with external disturbance [31–33], in which the unknown external disturbance d _i (x,t) maybe the function of all states, but its bounding function must be the function of $\bar{x}_{i}=[x_{1}, x_{2}, \ldots, x_{i}]^{T}$, such as in [31, 32], or an unknown constant [33].

Motivated by the above observations, the problem of adaptive neural control for a class of pure-feedback nonlinear systems with external disturbance is investigated based on backstepping. It is shown that the proposed controller guarantees that all signals in the closed-loop systems remain bounded and the tracking error eventually converges to a small neighborhood around the origin. The main contributions of this paper lie in that (i) an adaptive neural control scheme is systematically derived to control a class of nonlinear pure-feedback systems with external disturbances bounded by functions of all system state variables which is more general than the existing ones; (ii) only one adaptive parameter is needed to be estimated online for n order nonlinear systems. As a result, computational burden is significantly alleviated, which might render this control design more suitable for practical application.

The remainder of this paper is organized as follows. The problem formulation and preliminaries are given in Sect. 2. A novel adaptive neural control scheme is presented in Sect. 3. The simulation examples are given in Sect. 4, followed by Sect. 5, which concludes the work.

2 Preliminaries and problem formulation

Consider a class of perturbed pure-feedback nonlinear system in the following form:

$$ \left \{ \begin{array}{l} \dot{x}_i=f_i(\bar{x}_i,x_{i+1})+\psi_i(x,t),\quad 1\leq i\leq n-1,\\[2pt] \dot{x}_n=f_n(\bar{x}_n, u)+\psi_n(x, t),\\[2pt] y=x_1, \end{array} \right . $$

(1)

where x=[x ₁,x ₂,…,x _n ]^T∈R ⁿ, u∈R, and y∈R are state variable, system input, and system output, respectively, $\bar{x}_{i}=[x_{1}, x_{2}, \ldots, x_{i}]^{T}\in R^{i}$; f _i (⋅): R ⁱ⁺¹→R with f _i (0)=0 are unknown, but smooth nonaffine nonlinear functions; ψ _i (⋅):R ⁿ→R with ψ _i (0)=0 can be viewed as model uncertainties or unknown external disturbance functions.

The control objective in this paper is to design an adaptive neural tracking controller u for the system (1), such that the system output y converges to a small neighborhood of the reference signal y _d , and all the signals in the closed-loop remain bounded.

For the control of pure-feedback system (1), define

(2)

with x _n+1=u.

Assumption 1

The signs of $g_{i}(\bar{x}_{i}, x_{i+1})$, i=1,2,…,n are known, and there exist constants b _m and b _M , such that for 1≤i≤n,

(3)

Remark 1

Assumption 1 implies that the unknown smooth functions $g_{i}(\bar{x}_{i+1})$, i=1,2,…,n, are strictly either positive or negative. Without loss of generality, it is assumed that $0<b_{m}\leq g_{i}(\bar{x}_{i+1})\leq b_{M}$, $\forall \bar{x}_{i+1}\in R^{i+1}$. Moreover, since the constants b _m and b _M are not used for controller design, their true values are not necessary to be known.

Assumption 2

For functions ψ _i (⋅)s in (1), there exist strict increasing smooth functions ϕ _i (⋅):R ⁺→R ⁺ with ϕ _i (0)=0 such that for i=1,2,…,n,

$$\bigl|\psi_i(x, t)\bigr|\leq \phi_i\bigl(\|x\|\bigr). $$

Remark 2

The increasing property of ϕ _i (⋅) means that if a _k ≥0, for k=1,2,…,n, then $\phi_{i}(\sum_{k=1}^{n}a_{k})\leq \sum_{k=1}^{n}\phi_{i}(na_{k})$. Note that ϕ _i (s) is a smooth function with ϕ _i (0)=0, so there exists a smooth function q _i (s) such that ϕ _i (s)=sq _i (s), which results in

$$ \phi_i\Biggl(\sum_{k=1}^na_k \Biggr)\leq \sum_{k=1}^n na_kq_i(na_k). $$

(4)

Assumption 3

The desired trajectory y _d (t) and its time derivatives up to the nth order $y_{d}^{(n)}(t)$ are continuous and bounded. It is further assumed that there exists a positive constant d ^∗ such that |y _d (t)|≤d ^∗.

Throughout this paper, the following RBF neural networks will be used to approximate any continuous function f(Z):R ⁿ→R,

(5)

where Z∈Ω _Z ⊂R ^q is the input vector with q being the neural networks input dimension, weight vector W=[w ₁,w ₂,…,w _l ]^T∈R ^l, l>1 is the neural networks node number, and S(Z)=[s ₁(Z),s ₂(Z),…,s _l (Z)]^T means the basis function vector with s _i (Z) being chosen as the commonly used Gaussian function of the form:

(6)

where μ _i =[μ _i1,μ _i2,…,μ _iq ]^T is the center of the receptive field and η _i is the width of the Gaussian function. In [36], it has been indicated that with sufficiently large node number l, the RBF neural networks (5) can approximate any continuous function f(Z) over a compact set Ω _Z ⊂R ^q to arbitrary any accuracy ε>0 as

$$ f(Z)={W^{*}}^{T}S(Z)+\delta (Z),\quad \forall z\in \varOmega_{z}\in R^{q}, $$

(7)

where W ^∗ is the ideal constant weight vector and defined as

$$W^{*}:=\arg \min_{W\in \bar{R}^{l}}\Bigl\{\sup_{Z\in \varOmega _{Z}}\bigl|f(Z)-W^{T}S(Z)\bigr| \Bigr\}, $$

where δ(Z) denotes the approximation error and satisfies |δ(Z)|≤ε.

Lemma 1

[37]

Consider the Gaussian RBF networks (5) and (6). Let $\rho:=\frac{1}{2}\min_{i\neq j}\|\mu_{i}-\mu_{j}\|$, then an upper bound of ∥S(Z)∥ is taken as

(8)

It has been shown in [28] that the constant s in Lemma 3 is a limited value and is independent of the variable Z and the dimension of neural weights l.

Lemma 2

[38]

For any η∈R and ϵ>0, the following inequality holds:

$$ 0\leq|\eta|-\eta\tanh\biggl(\frac{\eta}{\epsilon}\biggr)\leq \delta \epsilon,\quad \delta=0.2785. $$

(9)

In Sect. 3, an adaptive neural control via backstepping technique is proposed for perturbed pure-feedback nonlinear systems (1). The backstepping design with n steps is developed based on the following coordinate transformation:

(10)

where α ₀=y _d , $\bar{y}_{d}^{(i)}$ denotes the vector of y _d and up to its ith order time derivative and α _i is the virtual control law. $\hat{\theta}$ is the estimation of unknown constant θ which is specified as

$$ \theta=\max\biggl\{\frac{b_M^2}{b_m}\bigl\|W_i^*\bigr\|^2;i=1,2, \ldots,n\biggr\} $$

(11)

with b _m and b _M being defined in Assumption 1, and $W^{*}_{i}$ will be given later.

The adaptive neural controller and adaptive law will be constructed in the following forms:

(12)

(13)

where k _i , a _i , k ₀, and λ are positive design parameters, S _i (Z _i ) is the basis function vector with $Z_{i}=[\bar{x}_{i}^{T}, \hat{\theta}, \bar{y}_{d}^{(i)T}]^{T}\in \varOmega_{Z_{i}} \subset R^{2i+2}$ (i=2,…,n). Note that, when i=n, α _n is the actual control input u(t).

Remark 3

It is easy to prove from (13) that if initial condition $\hat{\theta}(0)\geq 0$, then $\hat{\theta}(t)\geq 0$ for all t≥0. In fact, it is always reasonable to choose $\hat{\theta}(0)\geq 0$ in a practical situation, as $\hat{\theta}$ is an estimation of θ. This property will be used in each design step.

Lemma 3

For the coordinate transformations z _i =x _i −α _i−1, i=1,2,…,n, the following result holds:

$$ \|x\|\leq \sum_{i=1}^n|z_i| \varphi_i( \hat{\theta})+d^* $$

(14)

with $\varphi_{i}(\hat{\theta})=(k_{i}+1)+\frac{1}{2a_{i}^{2}}s^{2}\hat{\theta}$, for i=1,2,…,n−1, and φ _n =1.

Proof

From α ₀=y _d , (10), (12), and Lemma 1, we have

 □

3 Adaptive neural tracking control

In the following, for simplicity, the time variable t will be omitted from the corresponding functions and let S _i (Z _i )=S _i .

Step 1. Let us consider the first differential equation of system (1). Noting z ₁=x ₁−y _d , its derivative is

$$ \dot{z}_1=f_1(x_1,x_2)- \dot{y}_d+ \psi_1(x, t). $$

(15)

To design a stabilization control law for (15), consider a Lyapunov function candidate as

$$ V_1=\frac{1}{2}z_1^2+\frac{b_m}{2\lambda} \tilde{\theta}^2, $$

(16)

where $\tilde{\theta}=\theta-\hat{\theta}$ is the parameter error. Then the time derivative of V ₁ along (15) is given by

$$ \dot{V}_1\leq z_1\bigl(f_1(x_1,x_2)- \dot{y}_d+\psi_1(x,t)\bigr) -\frac{b_m}{\lambda}\tilde{ \theta}\dot{\hat{\theta}}. $$

(17)

By using Assumption 2, (4), (14), and the completion of squares, the following result can be obtained easily:

(18)

where $\bar{\phi}^{2}_{1}(z_{l},\hat{\theta})=\frac{1}{2}{(n+1)^{2}} \varphi^{2}_{l}(\hat{\theta}) q^{2}_{1}({(n+1)}|z_{l}|\*\varphi_{l}(\hat{\theta}))$. Further, applying Lemma 2 to the last term on the right-hand side in (18) gives

(19)

Substituting (18) into (17) and using (19) yields

(20)

Define a new function $w_{1}=-\dot{y}_{d} +\phi_{1}((n+1)d^{*})\*\tanh(\frac{z_{1}\phi_{1}((n+1)d^{*})}{\epsilon_{1}}) +\frac{1}{2}(n+2)z_{1}+k_{1}z_{1}+ z_{1}\sum_{k=1}^{n-1}\sum_{j=1}^{k}\bar{\phi}^{2}_{j}(z_{1},\hat{\theta})$. Then (20) can be rewritten as

(21)

Considering that $\frac{\partial w_{1}}{\partial x_{2}}=0$, the following inequality based on Assumption 1 will be obtained:

(22)

According to Lemma 1 [6], for every value of x ₁ and w ₁, there exists a smooth ideal control input $x_{2}=\bar{\alpha}_{1}(x_{1}, w_{1})$ such that

(23)

Applying mean value theorem [39], there exists μ ₁ (0<μ ₁<1) such that

(24)

where $g_{\mu_{1}}:=g_{1}(x_{1}, x_{\mu_{1}})$, $x_{\mu_{1}}=\mu_{1}x_{2}+(1-\mu_{1})\bar{\alpha}_{1}$. Obviously, Assumption 1 on g ₁(x ₁,x ₂) is still valid for $g_{\mu_{1}}$.

Next, substituting (24) into (21) and using the fact of (23) produces

(25)

with z ₂=x ₂−α ₁ and α ₁ being virtual control signal which will be defined later.

Since $\bar{\alpha}_{1}$ contains unknown function w ₁, an RBF neural network $W_{1}^{T}S_{1}(Z_{1})$ is used to model $\bar{\alpha}_{1}$ such that

$$ \bar{\alpha}_1=W^{*T}_1S_1(Z_1)+ \delta_1(Z_1),\quad \bigl|\delta_1(Z_1)\bigr| \leq\varepsilon_1, $$

(26)

where δ ₁(Z ₁) refers to the approximation error and ε ₁ is a given constant.

Furthermore, the following inequality is true:

(27)

where θ has been defined in (11).

By constructing virtual control law α ₁ in (12) with i=1, and using the fact of $\hat{\theta}\geq 0$ and Assumption 1, the following result can be obtained:

(28)

Subsequently, by combining (25) together with (27) and (28), we have

(29)

where $\rho_{1}=\delta\epsilon_{1}+\frac{1}{2}a_{1}^{2} +\frac{1}{2}b_{M}^{2}\varepsilon_{1}^{2}$.

Step 2. The derivative of z ₂=x ₂−α ₁ is

$$ \dot{z}_2=f_2(\bar{x}_2, x_3)+ \psi_2(x,t)-\dot{\alpha}_1, $$

(30)

where

(31)

Choose the following Lyapunov function:

$$ V_2=V_1+\frac{1}{2}z_2^2. $$

(32)

The time derivative of V ₂ is

(33)

Following the same line as that used in (18) results in

(34)

(35)

where $\bar{\phi}^{2}_{j}(z_{l},\hat{\theta})=\frac{1}{2}{(n+1)^{2}}\varphi^{2}_{l}(\hat{\theta}) q^{2}_{j}({(n+1)}|z_{l}|\*\varphi_{l}(\hat{\theta}))$, j=1,2.

Let $U_{2}=|\frac{\partial \alpha_{1}}{\partial x_{1}}|\phi_{1}((n+1)d^{*})+\phi_{2}((n+1)d^{*})$. Then, applying Lemma 2, we obtain

$$ |z_2|U_2-z_2U_2\tanh\biggl( \frac{z_2U_2}{\epsilon_2}\biggr)\leq \delta\epsilon_2. $$

(36)

In addition, by applying the definition of $\dot{\hat{\theta}}$ in (13), one has

(37)

Furthermore, by substituting (29), (34), and (35) into (33) and using (36)–(37), we can rewrite (33) as

(38)

where

(39)

Noting the fact that $\frac{\partial w_{2}}{\partial x_{3}}=0$, the following inequality holds:

For every value of $\bar{x}_{2}$ and w ₂, there exists a smooth ideal virtual control input $x_{3}=\bar{\alpha}_{2}(\bar{x}_{2}, w_{2})$ such that

(40)

Using mean value theorem [39], there exists μ ₂ (0<μ ₂<1) such that

(41)

where $g_{\mu_{2}}:=g_{2}(\bar{x}_{2}, x_{\mu_{2}})$, $x_{\mu_{2}}=\mu_{2}x_{3}+(1-\mu_{2})\bar{\alpha}_{2}$. Apparently, Assumption 1 is still valid for $g_{\mu_{2}}$. Combining (38), (40), and (41), we have

(42)

By employing an RBF neural network $W^{*T}_{2}S_{2}(Z_{2})$ to approximate $\bar{\alpha}_{2}$, for any given constant ε ₂>0, $\bar{\alpha}_{2}$ can be expressed as

(43)

where the approximate error δ ₂(Z ₂) satisfies |δ ₂(Z ₂)|≤ε ₂. Repeating the method utilized in (27) gives

(44)

Then, by choosing virtual control signal α ₂ in (12) with i=2 and following the similar method to (28), we have

(45)

By adding and subtracting virtual control signal α ₂ in (42) and using (44)–(45), (42) can be rewritten as

(46)

where z ₂=x ₃−α ₂, $\rho_{j}=\delta\epsilon_{j}+\frac{1}{2}a_{j}^{2} +\frac{1}{2}b_{M}^{2}\varepsilon_{j}^{2}$, j=1,2.

Remark 4

The adaptive law $\dot{\hat{\theta}}$ in (13) is a function of all the error variables. So, unlike the conventional approximation-based adaptive control schemes, the term $\frac{\partial \alpha_{1}}{\partial\hat{\theta}}\dot{\hat{\theta}}$ in (31) cannot be approximated directly by the RBF neural networks $W^{*T}_{2}S_{2}(Z_{2})$. To solve this problem, in (37), $\frac{\partial \alpha_{1}}{\partial\hat{\theta}}\dot{\hat{\theta}}$ is decomposed into two parts. The first term on the right-hand side of (37) can be contained in $\bar{f}_{2}(Z_{2})$ modeled by $W^{*T}_{2}S_{2}(Z_{2})$, and the last one in (37), which is the function of the latter error variables, namely z _i , i=3,…,n, will be dealt with in the later design steps. This design idea will be repeated at the following steps.

Step i (3≤i≤n−1). For z _i =x _i+1−α _i , the time derivative of z _i is given by

(47)

where

(48)

Define the following Lyapunov function candidate:

$$ V_i=V_{i-1}+\frac{1}{2}z_i^2. $$

(49)

Then the derivative of V _i in (49) along with (47) can be expressed as

(50)

where the term $\dot{V}_{i-1}$ in (50) can be obtained in the below form by following the procedures outlined in Step 2:

(51)

Following the procedures outlined in Step 2, one can get the following two inequalities:

(52)

(53)

where $\bar{\phi}^{2}_{j}(z_{l},\hat{\theta})=\frac{1}{2}{(n+1)^{2}}\varphi^{2}_{l}(\hat{\theta}) q^{2}_{j}({(n+1)}|z_{l}|\*\varphi_{l}(\hat{\theta}))$, j=1,2,…,i. Furthermore, similar to (36), the following result is true:

$$ |z_i|U_i-z_iU_i\tanh\biggl( \frac{z_iU_i}{\epsilon_i}\biggr)\leq \delta\epsilon_i, $$

(54)

where $U_{i}=\sum_{j=1}^{i-1}|\frac{\partial \alpha_{i-1}}{\partial x_{j}}|\phi_{j}((n+1)d^{*})+\phi_{i}((n+1)d^{*})$.

For the term $\frac{\partial \alpha_{i-1}}{\partial \hat{\theta}}\dot{\hat{\theta}}$, by using (13), we have

(55)

Subsequently, combining (50) with (51)–(55) produces

(56)

where

(57)

Considering the fact that $\frac{\partial w_{i}}{\partial x_{i+1}}=0$, one has

According to Lemma 1 [6], by viewing x _i+1 as a virtual control input, for every value of $\bar{x}_{i}$ and w _i , there exists a smooth ideal control input $x_{i+1}=\bar{\alpha}_{i}(\bar{x}_{i}, w_{i})$ such that

(58)

Applying mean value theorem [39], there exists μ _i (0<μ _i <1) such that

(59)

where $g_{\mu_{i}}:=g_{i}(\bar{x}_{i}, x_{\mu_{i}})$, $x_{\mu_{i}}=\mu_{i}x_{i+1}+(1-\mu_{i})\bar{\alpha}_{i}$. Note that Assumption 1 is still valid for $g_{\mu_{2}}$.

Substituting (59) into (56) and using (58) results in

(60)

Next, using an RBF neural networks $W_{i}^{*T}S_{i}(Z_{i})$ to approximate $\bar{\alpha}_{i}$, then constructing virtual control signal α _i in (12) and following the same line as the procedures used from (43)–(46), one has

(61)

where z _i+1=x _i+1−α _i , $\rho_{j}=\delta\epsilon_{j}+\frac{1}{2}a_{j}^{2} +\frac{1}{2}b_{M}^{2}\varepsilon_{j}^{2}$, j=1,2,…,i.

Step n. This is the final step; the actual control input u will be constructed. For z _n =x _n −α _n−1, we have

$$ \dot{z}_n=f_n(\bar{x}_n, u)+ \psi_n(x,t)-\dot{\alpha}_{n-1}, $$

(62)

where $\dot{\alpha}_{n-1}$ is given in (48) with i=n Take the Lyapunov function as

$$ V_n=V_{n-1}+\frac{1}{2}z_n^2. $$

(63)

With the straightforward derivation similar to those employed in Step i, the derivative of V _n satisfies the following inequality:

(64)

where w _n is defined as

(65)

From (65), Assumption 1 and Lemma 1 [6], for every value $\bar{x}_{n}$ and w _n , there exists a smooth ideal control input $u=\bar{\alpha}_{n}(\bar{x}_{n}, w_{n})$ such that

(66)

Using mean value theorem [39], there exists μ _n (0<μ _n <1) such that

(67)

with $g_{\mu_{n}}:=g_{n}(\bar{x}_{n}, x_{\mu_{n}})$, $x_{\mu_{n}}=\mu_{n}u+(1-\mu_{n})\bar{\alpha}_{n}$. Assumption 1 is still valid for $g_{\mu_{n}}$.

By combining (64) together with (66) and (67), one has

(68)

Similarly, for any given positive constant ε _n , an RBF neural network $W_{n}^{*T}S_{n}(Z_{n})$ is utilized to approximate the unknown function $\bar{\alpha}_{n}$. Following the same line as used in (27), we have

(69)

Now, construct the actual control signal u in (12) with i=n, then the following inequality holds:

(70)

Further, substituting (69) and (70) into (68) and taking (13) into account result in

(71)

where the inequality $\frac{k_{0}b_{m}}{\lambda}\tilde{\theta}\hat{\theta}\leq-\frac{b_{m}}{2\lambda}k_{0}\tilde{\theta}^{2}+ \frac{b_{m}}{2\lambda}k_{0}\theta^{2}$ has been used in (71) and $\rho_{j}=\delta\epsilon_{j}+\frac{1}{2}a_{j}^{2} +\frac{1}{2}b_{M}^{2}\varepsilon_{j}^{2}$, j=1,2,…,n−1, $\rho_{n}=\frac{1}{2}a_{n}^{2} +\frac{1}{2}b_{M}^{2}\varepsilon_{n}^{2}+\frac{b_{m}}{2\lambda}k_{0}\theta^{2}$.

To date, the adaptive neural control design has been completed based on backstepping technique. The main result of this note will be summarized by the following theorem.

Theorem 1

Consider the pure-feedback nonlinear system (1), the controller (12), and the adaptive law (13) under Assumptions 1–3. Assume there exist sufficiently large compacts $\varOmega_{Z_{i}}$, i=1,2,…,n such that $Z_{i}\in\varOmega_{Z_{i}}$ for all t≥0. Then, for bounded initial conditions with $\hat{\theta}(0)\geq0$, all signals in the closed-loop system remain bounded and the following inequality holds:

$$ \lim_{t\rightarrow\infty}z_1^2\leq 2\frac{b_0}{a_0} $$

(72)

with a ₀=min{2(1+b _m )k _j ,k ₀,j=1,2,…,n} and $b_{0}=\sum_{j=1}^{n}\rho_{j}$.

Proof

For the stability analysis of the closed-loop system, choose the Lyapunov function as V=V _n . From (71), it follows

(73)

where a ₀=min{2(1+b _m )k _j ,k ₀,j=1,2,…,n} and $b_{0}=\sum_{j=1}^{n}\rho_{j}$.

Then the following result is true:

(74)

which implies that all the signals in the closed-loop system are bounded.

Especially, from definition of V, one has

As a result, (72) can be obtained immediately. The proof is thus completed. □

Remark 5

In this research, the external disturbance ψ _i (x,t) in (1) and its bounding function are assumed to be the function of all states. However, in many practical situations, the disturbance may be only the function of time, i.e., ψ _i (x,t)=d _i (t). In this case, a common restriction to external disturbance d _i (t) is that there exists a constant d _i such that |d _i (t)|≤d _i . Then, similar to the method proposed in [33], with a minor change of the virtual control signal (12), the similar result can be obtained by repeating the aforementioned procedures.

4 Simulation example

Example 1

To demonstrate the proposed control scheme, consider the following second-order pure-feedback nonlinear system:

where x ₁ and x ₂ are the state variables, y and u denote the system output, and the actual control input, respectively. The control objective is to design an adaptive neural controller such that all the signals in the closed-loop system remain bounded and the system output y follows the given reference signal y _d =0.5(sin(t)+sin(0.5t)). According to Theorem 1, the virtual control law, the actual control law, and the adaptive laws are designed as

where z ₁=x ₁−y _d ,z ₂=x ₂−α ₁ and $Z_{i}=[\bar{x}_{i}^{T}, \hat{\theta},\allowbreak \bar{y}_{d}^{(i)T}]^{T}$ (i=1,2), and the design parameters are taken as follows: k ₁=k ₂=5, a ₁=a ₂=2, k ₀=0.3, and λ=1. The simulation are run with the initial conditions [x ₁(0),x ₂(0)]^T=[0.2,0.1]^T, and $\hat{\theta}(0)=0$.

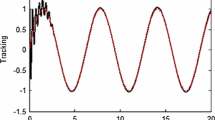
The simulation results are shown in Figs. 1–4. Figure 1 shows the system output y and the reference signal y _d . From Fig. 1, we can see that the good tracking performance has been achieved. Figure 2 shows that the state variable x ₂ is bounded. Figure 3 displays the control signal u. Figure 4 shows that the adaptive parameters $\hat{\theta}$ is bounded.

Fig. 1

System output y(t) and reference signal y _d (t)

Fig. 2

State variable x ₂

Fig. 3

The true control input u

Fig. 4

The adaptive parameter $\hat{\theta}$

5 Conclusion

In this paper, an adaptive neural control scheme has been proposed for a class of nonaffine pure-feedback nonlinear system with external disturbance. The developed adaptive neural tracking controller guarantees that all the signals involved are bounded, while the tracking error eventually converges to a small neighborhood of the origin. Moreover, the suggested controller contains only one adaptive parameter needed to be updated online. This makes our design scheme may be easily implemented in practical applications. Simulation results further illustrate the effectiveness of the proposed scheme.