Bifurcation-based micro-/nanoelectromechanical mass detection

Abstract

This paper investigates an alternative mass-sensing technique based on nonlinear micro-/nanoelectromechanical resonant sensors. The proposed approach takes advantage of multi-stability and bifurcations of the hysteretic frequency responses of the electrostatically actuated resonator. For this purpose, a reduced-order model is considered. Numerical results show that sudden jumps in amplitude make the detection of a very small mass possible. Moreover, the limit of detection can be set with the value of the operating frequency. However, when operating at fixed frequency, the study of basins of attraction indicates that this bifurcation-based mass detection does not exhibit the expected robustness. A possible improvement is proposed, based on the reinitialization of the system by a forced jump down on the hysteretic response curve. Using a frequency sweep which varies slowly in sinusoidal form solves the reinitialization problem and enables automatic real-time detection. Finally, the added mass is located on the beam by using the resonance at the first two natural frequencies.

1 Introduction

Measuring tiny masses is an important application of M/NEMS resonant sensors. Mass sensors are used in biologic environment for DNA hybridization, biomolecules, enzymes, proteins [1–3], chemical reactions [4], mercury’s vapor [5–7], gas concentration [8], explosives [9], etc.

Generally speaking, the principle of a resonant sensor is based on the forcing of a microbeam on its fundamental bending mode by means of an electrode that can also serve as a detection sensor of the frequency shift induced by an external perturbation (added mass, acceleration, Coriolis force [10]). The size of the sensor is conditioned by the mass to be detected. The dynamic range can theoretically be improved by downsizing the sensors. However, downsizing is limited by available manufacturing processes, by the need of detection surfaces as large as possible, and by the onset of undesirable nonlinear phenomena. A length of 150 nm associated with a forcing frequency of 2 GHz makes a 1.7 yg ($1\,\hbox {yg}=10^{-24}\,\hbox {g}$) mass detection possible, see Chaste et al. [11], while a length of 4 $\upmu$m limits the detection to a 0.4 ag ($1\,\hbox {ag} = 10^{-18}\,\hbox {g}$) [12]. Hanay et al. [13] studied the potential of NEMS-based mass spectrometry (NEMS-MS) by measuring the mass of an individual protein macromolecules in real time. Such a NEMS-MS system can access masses above 500 kDa (1 Da $=$ $1.66\times 10^{-27}\,\hbox {kg}$) and has a sensitivity of a single Dalton and an upper limit of detection of hundreds of MegaDaltons [14]. In [12], the theoretical and experimental fundamental frequency shifts are compared. It is shown that the relationship between frequency shift and added mass is linear, i.e., the smaller the added mass is, the smaller the frequency shift is.

Several techniques have been explored to enhance the sensitivity. The resonator can be driven in linear or nonlinear regime. In the linear regime [12], vibrations are limited to small amplitudes, which may not exceed thermomechanical noise, thus making the detection difficult. Exciting the microbeam in the nonlinear regime can improve the sensitivity of detection, as shown by Buks and Yurke [15] and Kacem et al. [16], but exposes the resonator to pull-in, namely the collapse of the moving structure onto the fixed electrode [17–19]. Another possibility consists in using higher modes. Narducci et al. [20] studied the first two modes of a beam and showed experimentally that the sensitivity is higher for the second resonance frequency than for the fundamental one. In [21], the sensitivity of detection is improved from 23 to 276 times when switching from the second to the fourth mode. However, exciting higher modes require much more energy than for the fundamental mode to obtain the same output signal amplitude. Using the first torsional mode of microcantilevers rather than the first bending mode can also improve the resolution by one order [22, 23]. Parametrically excited mechanical systems have also attracted attention [24]. Zhang et al. [25] and Zhang and Turner [26] concluded that if the resonator is parametrically excited, its sensitivity is highly increased. Similarly, Thomas et al. [27] achieved experimentally a quality factor enhancement by up to a factor 14 in air by means of parametric amplification.

Recent research has developed alternative sensing approaches exploiting inherent properties of the nonlinear behavior of MEMS like dynamic instabilities or bistability, and based on amplitude rather than frequency shifts. Khater et al. [28] showed that the sensitivity of electrostatically actuated MEMS is highly enhanced when the sensor is operated close to pull-in. They proposed a binary sensing mechanism in which the sensor goes to pull-in when the mass to detect exceeds a given threshold. Younis and Alsaleem [29] observed that exciting a electrostatically actuated microbeam close twice its fundamental frequency is very attractive as it provides a sharp transition from the no-mass to the added-mass response curve.

Very recently, Kumar et al. [30, 31] proposed a bifurcation-based mass-sensing technique and explained the use of amplitude jumps between multi-stable states close to a cyclic-fold/saddle-node bifurcation in the nonlinear frequency response. Harne and Wang [32] presented a bifurcation-based coupled linear-bistable system for mass-sensing, providing experimental results of bifurcations between multi-stable states. Guo and Fedder [33] introduced the use of hysteretic cycle in the frame of a bistate control of a parametric resonance.

In this paper, similar ideas are discussed and improved taking into account dynamical bifurcations and transient behaviors in hysteretic cycles. Strategies for detection, quantification, and localization of an added mass are proposed. Section 2 presents the model, Sect. 3 the principle of detection, Sect. 4 the quantification, and Sect. 5 the localization.

2 Model

To describe the principles of detection, quantification, and localization of a small added mass, a model of a clamped–clamped beam is studied with or without added mass. The model considered here permits developing orders of magnitude of realistic beams. These developments could be extended to other models.

2.1 Case without added mass

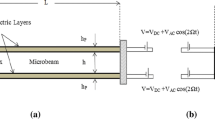
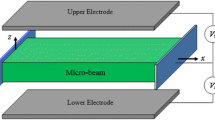
Let the clamped–clamped beam model sketched in Fig. 1 have its nonlinear behavior in bending governed by the integro-differential equation [34, 35]:

$$\begin{aligned}&EI \dfrac{\partial ^4 \tilde{w}( \tilde{x}, \tilde{t}) }{\partial \tilde{x}^4 } + \rho b h \dfrac{\partial ^2 \tilde{w}(\tilde{x}, \tilde{t}) }{\partial \tilde{t}^2 } + \tilde{c} \dfrac{\partial \tilde{w}(\tilde{x}, \tilde{t}) }{ \partial \tilde{t} } \nonumber \\&\qquad -\Big [\tilde{N}+ \dfrac{Ebh}{2l} \int _0^l \Big ( \dfrac{\partial \tilde{w}(\tilde{x}, \tilde{t}) }{ \partial \tilde{x} }\Big )^2 \, \hbox {d}\tilde{x} \Big ] \dfrac{ \partial ^2 \tilde{w}(\tilde{x},\tilde{t}) }{\partial \tilde{x}^2 } \nonumber \\&\quad =\dfrac{1}{2}\varepsilon _0 \dfrac{bC_n \big ( V_\mathrm{dc} + V_\mathrm{ac} \cos \tilde{\varOmega } \tilde{t} \big )^2}{\left( g-\tilde{w}(\tilde{x},\tilde{t})\right) ^2 }, \end{aligned}$$

(1)

with $\tilde{w}(\tilde{x},\tilde{t})$ the lateral deflexion of the beam along the axis Ox, $I,h,b$, and $l$ the moment of inertia, thickness, height, and length of the beam, respectively, $E$ and $\rho$ the modulus of elasticity and the mass density of the material, $\tilde{c}$ the viscous damping coefficient, $g$ the beam–electrode gap. The axial force $\tilde{N}$ is due to design and manufacturing, and the bias $V_\mathrm{dc}$ and alternative $V_\mathrm{ac}$ voltages to the electrode. The coefficient $C_n$ related to fringing field effect is computed in [36]. By using nondimensional variables, Eq. (1) becomes

$$\begin{aligned}&\dfrac{\partial ^4 w(x,t) }{\partial x^4} + \dfrac{\partial ^2 w(x,t)}{\partial t^2}+ c \dfrac{\partial w(x,t)}{\partial t} \nonumber \\&\qquad - \Big [ N+ \alpha _1 \int _0^1 \! \Big (\dfrac{\partial w(x,t)}{\partial x} \Big )^2 \, \hbox {d}x \Big ] \dfrac{\partial ^2 w(x,t)}{\partial x^2} \nonumber \\&\quad = \alpha _2 \dfrac{\big (V_\mathrm{dc}+V_\mathrm{ac} \cos \varOmega t \big )^2}{(1-w(x,t))^2}, \end{aligned}$$

(2)

where

$$\begin{aligned} \begin{aligned}&w= \frac{\tilde{w}}{g}, \quad x= \frac{\tilde{x}}{l}, \quad t= \frac{\tilde{t}}{\tau } \\&N= \dfrac{\tilde{N}l^2 }{EI}, \quad \alpha _1 = 6 \Big (\dfrac{g}{h}\Big )^2, \quad \alpha _2 = 6 C_n \dfrac{\varepsilon _0l^4}{Eh^3g^3} \\&\tau = \dfrac{2l^2}{h}\sqrt{ \dfrac{3\rho }{E} }; \, \varOmega = \tilde{\varOmega }; \, c=\dfrac{\tilde{c}l^4 }{EI \tau }; \,\tilde{c}=\rho b h \dfrac{\omega _1}{\tau Q} \end{aligned} \end{aligned}$$

(3)

$\omega _1$ and $Q$ are the fundamental frequency and its associated quality factor. The eigenmodes of the linear undamped and unloaded microbeam $\phi _k(x)$ are calculated, and the following Galerkin expansion is used for the displacement $w(x,t)$:

$$\begin{aligned} w(x,t)=\sum _{k=1}^{N_m} \phi _k(x) a_k(t), \end{aligned}$$

(4)

where $a_k(t)$ is the kth time-varying generalized coordinate. Then, Eq. (2) is multiplied by $(1-w(x,t))^2 \phi _i(x)$ for $i=1,\ldots ,N_m$ and integrated from 0 to 1, and the second-order differential equation in time is written in the form of the matrix equation:

$$\begin{aligned}&\big [ \mathbf{M}_0 + \mathbf{M}_1(\mathbf{a}) + \mathbf{M}_2(\mathbf{a})\big ] \ddot{\mathbf{a}} + \big [ \mathbf{C}_0 +\mathbf{C}_1(\mathbf{a})+\mathbf{C}_2(\mathbf{a}) \big ] \dot{\mathbf{a} } \nonumber \\&\quad +\,\big [ K_0 + \mathbf{K}_1(\mathbf{a}) + \mathbf{K}_2(\mathbf{a}) \big ]\mathbf{a} - \big (N+\alpha _1 T_2(\mathbf{a})\big )\big [ \mathbf{K}_T \nonumber \\&\quad +\,\mathbf{K}_{T1}(\mathbf{a})+ \mathbf{K}_{T2}(\mathbf{a}) \big ] \mathbf{a} = \alpha _2 \big ( V_\mathrm{dc} + V_\mathrm{ac} \cos \varOmega t \big )^2 \mathbf{F}.\nonumber \\ \end{aligned}$$

(5)

The matrices $\mathbf{M}_0,\,\mathbf{M}_1(\mathbf{a}),\,\mathbf{M}_2(\mathbf{a})$, $\mathbf{C}_0$, $\mathbf{C}_1(\mathbf{a})$, $\mathbf{C}_2(\mathbf{a})$, $\mathbf{K}_0$, $\mathbf{K}_1(\mathbf{a})$, $\mathbf{K}_2(\mathbf{a})$, $\mathbf{K}_T$, $\mathbf{K}_{T1}(\mathbf{a})$, $\mathbf{K}_{T2}(\mathbf{a})$, the vector $\mathbf{F}$ and the scalar $T_2(\mathbf{a})$ are defined in [35]. In this paper, the quasi-analytical averaging method as well as a numerical procedure based on the Harmonic Balance Method and the Asymptotic Numerical Method (ANM) [37] are used to solve Eq. (2) as explained in [35]. The results of the two methods are similar for small amplitude but the difference is significant for high-vibration amplitude vibration. This is due to the basic assumptions of the averaging method that limit its use to small nonlinearities. In [35], the influence of higher modes is also considered, and it is shown that for high-vibration amplitudes $(W_{\mathrm{max}}>0.5)$, the computation must be carried out with several modes.

Fig. 1

Schematic of the clamped–clamped microbeam-based electromechanical resonator

2.2 Case with added mass

Let the small and lumped added mass of mass $m_p$ and of tiny size fall onto the beam’s surface. The beam and the added mass constitute a continuum whose bending behavior is governed by the following equation applied to an infinitesimal volume $\hbox {d}\tilde{x}$, with $\delta _{\tilde{x}_0}(\tilde{x})$ the Dirac function:

$$\begin{aligned}&EI \dfrac{\partial ^4 \tilde{w}( \tilde{x}, \tilde{t}) }{\partial \tilde{x}^4 }\hbox {d}\tilde{x} +\rho bh \dfrac{\partial ^2 \tilde{w}(\tilde{x},\tilde{t}) }{\partial \tilde{t}^2 } \hbox {d}\tilde{x}\nonumber \\&\qquad +\, \delta _{\tilde{x}_0}(\tilde{x}) m_p \dfrac{\partial ^2 \tilde{w}(\tilde{x}, \tilde{t}) }{\partial \tilde{t}^2 } +\tilde{c} \dfrac{\partial \tilde{w}( \tilde{x}, \tilde{t}) }{\partial \tilde{t} } \hbox {d}\tilde{x}\nonumber \\&\qquad -\,\Big (\tilde{N}+ \dfrac{Ebh}{2l} \int _0^l \, \Big [ \dfrac{\partial \tilde{w}(\tilde{x},\tilde{t}) }{\partial \tilde{x}} \Big ]^2 \hbox {d}\tilde{x} \Big ) \dfrac{\partial ^2 \tilde{w}(\tilde{x},\tilde{t}) }{\partial \tilde{x}^2 }\hbox {d}\tilde{x}\nonumber \\&\quad = \dfrac{1}{2}\varepsilon _0 \dfrac{bC_n\big [V_\mathrm{dc} + V_\mathrm{ac} \cos \tilde{\varOmega } \tilde{t} \big ]^2 }{\big ( g- \tilde{w}( \tilde{x}, \tilde{t} \big )^2 } \! \hbox {d}\tilde{x}. \end{aligned}$$

(6)

By introducing the nondimensional variables (3), Eq. (6) is written in the form

$$\begin{aligned}&\dfrac{\partial ^4 w(x,t) }{\partial x^4 }\hbox {d}x + \dfrac{\partial ^2 w(x,t) }{\partial t^2 } \hbox {d}x + \delta _{x_0} (x) m \dfrac{\partial ^2 w(x,t) }{\partial t^2 } \nonumber \\&\quad +\,c \dfrac{\partial w(x,t)}{\partial t} \hbox {d}x-\Big (N+\alpha _1 \int _0^1 \, \Big [ \dfrac{\partial w(x,t)}{\partial x} \Big ]^2 \! \hbox {d}x \Big )\nonumber \\&\quad \dfrac{\partial ^2 w(x,t)}{\partial x^2} \hbox {d}x =\,\alpha _2 \dfrac{\big [V_\mathrm{dc}+V_\mathrm{ac} \cos \varOmega t \big ]^2}{(1-w(x,t))^2} \hbox {d}x,\quad \end{aligned}$$

(7)

with $m=\frac{m_p}{\rho b h l}$ the mass ratio. As in the case without added mass, the Galerkin expansion (4) is used and the new matrix equation contains the additional matrices $\varvec{\mu }_0, \varvec{\mu }_1(\mathbf{a}),\varvec{\mu }_2(\mathbf{a})$:

$$\begin{aligned}&\big [ \mathbf{M}_0 + \mathbf{M}_1(\mathbf{a}) + \mathbf{M}_2(\mathbf{a}) + \varvec{\mu }_0 + \varvec{\mu }_1(\mathbf{a}) + \varvec{\mu }_2(\mathbf{a}) \big ] \ddot{\mathbf{a}} \nonumber \\&\quad +\big [ \mathbf{C}_0 \!+\!\mathbf{C}_1(\mathbf{a})\!+\!\mathbf{C}_2(\mathbf{a}) \big ] \dot{\mathbf{a}} \!+\! \big [ K_0 \!+\! \mathbf{K}_1(\mathbf{a}) \!+\! \mathbf{K}_2(\mathbf{a}) \big ]\mathbf{a} \nonumber \\&\quad - \big (N+\alpha _1 T_2(\mathbf{a})\big )\big [ \mathbf{K}_T + \mathbf{K}_{T1}(\mathbf{a}) + \mathbf{K}_{T2}(\mathbf{a}) \big ] \mathbf{a} \nonumber \\&\quad = \alpha _2 \big ( V_\mathrm{dc} + V_\mathrm{ac} \cos \varOmega t \big )^2 \mathbf{F}. \end{aligned}$$

(8)

$\varvec{\mu }_0, \, \varvec{\mu }_1, \, \varvec{\mu }_2$ are determined as follows, with $1 \le i,j,k,l \le N_{m}$:

$$\begin{aligned} \mu _{0ij}&= m \phi _i(x_0) \phi _j (x_0 ), \end{aligned}$$

(9)

$$\begin{aligned} \mu _{1ij}&= -2m \sum _{k=1}^{N_m} \Big (\phi _i(x_0) \phi _j(x_0) \phi _k (x_0 ) \Big ) a_k(t), \end{aligned}$$

(10)

$$\begin{aligned} \mu _{2ij}\!&= \! m \sum _{k=1}^{N_m} \sum _{l=1}^{N_m} \Big ( \phi _i(x_0) \phi _j(x_0) \phi _k (x_0 ) \phi _l(x_0) \Big )a_k(t)a_l(t),\nonumber \\ \end{aligned}$$

(11)

In the following sections, two microbeam designs and three mass ratios (see Tables 1, 2) are tested. The location of the added mass is assumed to be known in the sections dedicated to the detection and to the quantification. The forced frequency–response curves are computed with the ANM.

Table 1 Designs 1 and 2 of the clamped–clamped microbeam

Table 2 Nondimensional and physical values of added mass

3 Detection of the presence of an added mass

3.1 Principle

The detection of added mass is based on the shift of the forced frequency responses. Two methods are possible. The first one is based on the frequency shift at the maximum of resonance: the presence of the added mass shifts down the forced frequency response, see Fig. 2, $\varDelta \varOmega$ being the resonant frequency shift. The second one focuses on the amplitude shift $\varDelta W_{\mathrm{max}}$, see Fig. 2. Unfortunately, at the maximum of resonance, this shift is too small for an accurate detection. In [31], the amplitude shift is measured close to a saddle-node bifurcation instead. This permits to take advantage of the nonlinear characteristics of the frequency response and results in a large amplitude jump, thus providing an efficient mass-sensing approach. This technique also simplifies the experimental implementation by eliminating the need for complex frequency-tracking hardware [30].

Fig. 2

Design 2: $V_\mathrm{dc}=100\,V_\mathrm{ac}=1.9\,\mathrm{V}$, without added mass (solid line), with added mass $m=5\times 10^{-5}$ (dashed line)

3.2 Softening behavior

Let us consider design 2 exhibiting a softening behavior. In order to identify the presence of the added mass, the beam is forced at an operating frequency $\varOmega _{\mathrm{op}}$ close to the bifurcation frequency $\varOmega _{\mathrm{bif}}$. In practice, the frequency is first increased from $\varOmega _1$ to $\varOmega _2$. When approaching the bifurcation point $\varOmega _\mathrm{bif}$, the frequency is fixed to $\varOmega _\mathrm{op}$. Then, as shown in Fig. 2, the sudden presence of the added mass induces a jump from point $A_1$ on the solid curve (without added mass) to point $A_2$ on the dashed curve (with added mass). Figure 3 shows the forced frequency responses due to two different added masses. A small added mass creates a large jump from $A_1$ to $A_3$ and a bigger mass, a smaller jump from $A_1$ to $A_2$. Therefore, the smaller the added mass is, the larger the amplitude shift will be.

Fig. 3

Design 2: $V_\mathrm{dc}=100V_\mathrm{ac}=1.9\,\mathrm{V}$, without added mass (solid line), with small added mass (dashed line), with bigger added mass (dotted line)

3.3 Hardening behavior

Let us consider design 1 exhibiting a hardening behavior (see Fig. 4). As for the softening behavior, when approaching the bifurcation frequency $\varOmega _{\mathrm{bif}}$, the response jumps from a large amplitude at $A_1$ (solid curve) to a small amplitude at $A_2$ (dashed curve) with the added mass. This mass is thus detected by the large jump $A_1 \rightarrow A_2$.

Fig. 4

Design 1: $V_\mathrm{dc}=10V_\mathrm{ac}=9\,\mathrm{V}$, without added mass (solid line), with added mass (dashed line)

3.4 Robustness and reinitialization of detection mechanism

For the softening behavior, with the added mass, the response stabilizes on the periodic limit cycle corresponding to $A_2$ (see Fig. 2). When the added mass leaves the microbeam, the solution escapes this limit cycle and, after some transient motion, reaches the limit cycle corresponding either to point A1 or to point A3, depending on the initial conditions. If it returns to $A_1$, the next added mass is easily detected. Conversely, if the solution jumps to the upper point $A_3$, the next small added mass will cause a small, difficult to detect, jump from $A_3$ to $A_2$. The value of the added mass defines a unique limit cycle, and the moment of its takeoff defines a unique point on this limit cycle and thus unique initial conditions for the escape from $A_2$. Establishing the basins of attraction of the microbeam without added mass, and identifying these initial conditions for several values of $m$ (indicated by red dots on Fig. 5a), permits to determine which point ($A_1$ or $A_3$) is reached. It can be shown that, depending on the moment when the solution escapes the periodic limit cycle, the basin of attraction and the initial conditions simply undergo a rotation and keep the same relative position. In other words, the jump down to $A_1$ or up to $A_3$ does not depend on the moment when the mass takes off. From the computations at $\varOmega _\mathrm{op}=22.3274$, it turns out that for mass ratios $m \le 5\times 10^{-4}$, i.e., for values $m_{p} \le 10^{-16}\,\hbox {kg}$, the jump always occurs toward the upper solution $A_3$ and consequently the bifurcation-based detection does not work anymore (see Fig. 5a).

Fig. 5

Basin of attraction of design 2 without added mass, $V_\mathrm{dc}=100V_\mathrm{ac}=1.9\,\mathrm{V}$. a $\varOmega _\mathrm{op}=22.3274$, b $\varOmega _\mathrm{op}=22.325$. Basin of attraction of point $A_1$ (yellow) and point $A_3$ (blue). (Color figure online)

In Fig. 5b, with the forcing frequency $\varOmega _\mathrm{op}=22.325$, the basin of attraction of the bottom stable solution is larger and $A_1$ is reached when $m>1.5\times 10^{-4}$, i.e., $m_{p} >3\times 10^{-17}\,\mathrm{kg}$. Since the masses of interest are much lower than this value, it can be concluded that the system never returns to its initial stable position, i.e., it is not reinitialized, and thus the bifurcation-based detection only works once.

A reinitialization solution, see Fig. 2, consists in first decreasing the operating frequency $\varOmega _{\mathrm{op}}$ until point $B_2$, then jumping down to point $B_1$, and finally, increasing the frequency again up to point $A_1$.

For the hardening behavior, the reinitialization is also presented in Fig. 4. After the takeoff of the added mass, the response arrives at $A_3$ (close to $A_2$) and it cannot return to $A_1$, see Fig. 4. Thus, the reinitialization is necessary to return to the operating point $A_1$. Firstly, the frequency is decreased from $\varOmega _{A_3}$ to $\varOmega _{B_1}$. Here, the response jumps to $B_2$ and then the frequency is increased up to the operating frequency $\varOmega _{A_1}$.

However, some drawbacks arise: because of the small jump from $A_2$ to $A_3$ (Figs. 2 or 4), the “takeoff” moment of the added mass is difficult to detect. So the moment when the reinitialization must be performed remains unknown.

3.5 Automatic reinitialization

The aforementioned problems of reinitialization can be overcome by using a slow time-varying frequency sweep such as

$$\begin{aligned} \varOmega (t)=\varOmega _\mathrm{op} + \delta \cos (\varepsilon \pi t+ \phi ) \end{aligned}$$

(12)

with the sweep velocity $\varepsilon \ll \varOmega _\mathrm{op}$. $\varOmega _{\mathrm{max}}=\varOmega _\mathrm{op}+\delta$ and $\varOmega _{\mathrm{min}}=\varOmega _\mathrm{op}-\delta$ are the frequency-sweep boundaries.

In Fig. 6a, several successive frequency sweep-up and sweep-down according to Eq. (12) are performed, and $W$ (respectively, $\varOmega$) is plotted versus nondimensional time $t$ (Fig. 6a, respectively b).

Fig. 6

Determination of the frequency-sweep response. a amplitude $W(t)$, b frequency $\varOmega (t)$, c frequency-sweep response

In Fig. 6a, variations in $W$ versus $t$ permit to distinguish some phases 1–2–3–4–5/1–2–3–4–5/...of the behavior, which are presented in Fig. 6c as a frequency–amplitude plot. This sequence of phases defines the hysteretic cycle obtained by a dynamical variation in $\varOmega$: in the limit case of quasi-static evolution of $\varOmega$ ($\varepsilon \rightarrow 0^+$), the hysteretic cycle corresponding to the theoretical response curve of Fig. 2 with added mass is obtained.

3.5.1 Frequency-sweep principle for the softening behavior

This subsection presents the principle of the frequency sweep for the softening behavior. It is illustrated with theoretical response curves determined by the ANM.

The frequency sweep $\varOmega (t)$ is illustrated in Fig. 7. $\varOmega _{\mathrm{bif}1}^0$ and $\varOmega _{\mathrm{bif}2}^0$ are the two bifurcation frequencies of the response without added mass, and the maximum and minimum frequencies $\varOmega _{\mathrm{min}}$ and $\varOmega _{\mathrm{max}}$ are set below $\varOmega _{\mathrm{bif}1}^0$ and $\varOmega _{\mathrm{bif}2}^0$, respectively. $\varDelta \varOmega =\varOmega _{\mathrm{bif}1}^0-\varOmega _{\mathrm{min}}$ defines the frequency shift of the maximal added mass to be detected. $\varOmega _{\mathrm{bif}1}^0-\varOmega _{\mathrm{max}}=\varDelta \varOmega -2 \delta$ defines the threshold of mass detection.

Fig. 7

Principle of frequency sweep without added mass. The response goes back-and-forth between points A and B

Figure 7 illustrates specifically the cycle without added mass. The response follows the curve between points A and B. There is no hysteretic cycle nor associated amplitude jump.

The detection of a mass variation, for instance a bioparticle falling on the microbeam, is illustrated in Fig. 8 where the frequency sweep defines hysteretic cycles corresponding to the two following cases:

• In the first case, shown in Fig. 8a, the particle falls at the moment (point 1) when the sweep frequency $\varOmega$ remains lower than $\varOmega _{\mathrm{bif}1}^m$. So the response goes through the hysteretic cycle according to the path joined by the succession of the following points: 1–2/3–4–5–6–7–8/3–4–5–6–7–8/..., there are amplitude jumps from 3 to 4 and from 6 to 7 in a cyclic manner.

• In the second case, shown in Fig. 8b, the particle falls at the moment (point 1) when the sweep frequency is between $\varOmega _{\mathrm{bif}1}^m$ and $\varOmega _{\mathrm{bif}}^0$. The response path is 1–2/3–4–5–6–7–8/3–4–5–6–7–8/.... When the particle falls on the beam, the amplitude first jumps from 1 to 2. Then, there are two amplitude jumps from 7 to 8 and from 4 to 5 in a cyclic manner.

Fig. 8

Responses with added mass. An added mass arrives when $\varOmega <\varOmega _{\mathrm{bif}1}^m$ (a) or when $\varOmega \ge \varOmega _{\mathrm{bif}1}^m$ (b). The response follows hysteretic cycles

When the particle takes off, the response is presented in Fig. 9. The two following cases are distinguished as:

• In the first case, shown in Fig. 9a, the particle takes off at the moment when the sweep frequency is lower than $\varOmega _{\mathrm{bif}2}^0$. The starting point is 1 or 1$'$ depending on whether the response starts from the top or the bottom of the curve $F_M$ and the response path is then 1 or 1$'$–2/A–B/A–B/.... After a jump to point 2, the response follows the curve $F_0$ between points A and B, i.e., the response curve without added mass of Fig. 7. There is no hysteretic cycle nor amplitude jump.

• In the second case, shown in Fig. 9b, the particle takes off at the moment when the sweep frequency is higher than $\varOmega _{\mathrm{bif}2}^0$: the starting point is 1 or 1$'$, and the response jumps to top point 2$'$ or bottom point 2. If there is a jump down to 2, the response path is then 1 or 1$'$–2/B–A/B–A/.... After a jump to point 2, the response is the part of the curve $F_0$ between points A and B. If there is a jump up to 2$'$, the response path is then 1 or 1$'$–2$'$–3$'$–4$'$–4/A–B/A–B/.... After two successive jumps up to 2$'$ and down to 4, the response also goes back-and-forth between A and B as in Fig. 7.

Fig. 9

Responses after mass takeoff triggered when $\varOmega <\varOmega _{\mathrm{bif}2}^0$ (a) or when $\varOmega \ge \varOmega _{\mathrm{bif}1}^m$ (b)

Hence when varying the frequency from $\varOmega _{\mathrm{min}}$ up to $\varOmega _{\mathrm{max}}$, the steady response path presents a maximum of amplitude $W_{\mathrm{max}} > 0.5$ with added mass (Fig. 8), whereas $W_{\mathrm{max}}<0.2$ without added mass (Fig. 7). The detection principle is based on this difference.

3.5.2 Numerical example of the frequency sweep for the softening behavior

In order to validate the frequency-sweep principle presented in Sect. 3.5.1, a numerical example with a given $\varepsilon$ is presented in what follows.

Let us consider design 2 and the following frequency sweep:

$$\begin{aligned} \varOmega (t)=22.317 + 0.01 \sin (10^{-5} \pi t), \end{aligned}$$

(13)

corresponding to the physical values:

$$\begin{aligned} \tilde{\varOmega }(\tilde{t})&= 8.1866 \times 10^{6} +\,3.67 \times 10^{3} \sin (23\pi \tilde{t})\, (\hbox {Hz}).\nonumber \\ \end{aligned}$$

(14)

Let the added mass remain on the beam during two sweep periods in such a way that no additional added mass falls on the beam in the mean time.

Figure 10a shows the evolution of $W_{\mathrm{max}}$ versus time for several periods of the frequency sweep. The following scenario is considered: from an initial position $P_0$, the microbeam vibrates without added mass. The steady-state regime is reached after transient regime from $P_0$ to $P_1$ (see Fig. 10b). Then, at point 1, the added mass $m_1$ falls on the microbeam (dashed line) and the response path is 1/2–3–4–5–6/2–3–4–5–6.... After two sweep periods, this added mass leaves the microbeam at point 7 and the beam continues to vibrate without added mass. Finally, the process is iterated from point 8, with another mass $m_2$.

Fig. 10

Frequency sweep for design 2. a response $W_{\mathrm{max}}- t$, b response $W_{\mathrm{max}}-\varOmega$. Without added mass (solid line), with small added mass (dashed line), and big added mass (dotted line)

In Fig. 10a, the time history response shows that in the presence of the added mass on the beam, the peaks are larger than 0.5 for two successive periods. Hence, for the softening behavior, the detection principle is based on amplitude jumps and on the change in maximum amplitude.

In Fig. 10b, the transient regime and the corresponding steady-state response curve are plotted, providing the hysteretic cycle described by the sequence of numbered points. This curve is used again in the next section to quantify the added mass.

3.5.3 Frequency-sweep principle for the hardening behavior

Similarly to Sect. 3.5.1, the frequency-sweep principle is illustrated with the theoretical response determined by the ANM.

The frequency varies slowly according to (12), with $\varOmega _{\mathrm{min}}<\varOmega _{\mathrm{bif}2}^0$ and $\varOmega _{\mathrm{max}}<\varOmega _{\mathrm{bif}1}^0$. Without added mass, the steady response is $A-B/A-B/\ldots$. When the particle falls on the beam, the two following cases are distinguished as:

• In the first case, shown in Fig. 11a, the particle arrives when the sweep frequency is lower than $\varOmega _{\mathrm{bif}1}^m$. The response path is 1–2/3–4–5–6–7–8/3–4–5–6–7–8/...or 1–2$'$/4–5–6–7–8–3/4–5–6–7–8–3/...

• In the second case, shown in Fig. 11b, the particle arrives when the sweep frequency is larger than $\varOmega _{\mathrm{bif}1}^m$. The response curve is 1–2/3–4–5–6–7–8/3–4–5–6–7–8/...

So, the response with added mass is the hysteretic cycle with two amplitude jumps at the bifurcation frequencies.

Fig. 11

Responses with an added mass arriving when $\varOmega < \varOmega _{\mathrm{bif}1}^m$ (a) or when $\varOmega \ge \varOmega _{\mathrm{bif}1}^m$ (b)

When the added mass takes off, the two following cases are distinguished as:

• In the first case, shown in Fig. 12a, the added mass takes off at the moment when the sweep frequency is lower than $\varOmega _{\mathrm{bif}2}^0$. The starting point is 1 or 1$'$ and the response path is then 1 or 1$'$–2/A–B/A–B/...

• In the second case, shown in Fig. 12b, the added mass takes off at the moment when the sweep frequency is larger than $\varOmega _{\mathrm{bif}2}^0$. The starting point is 1 or 1$'$. If jumping to 2, the response path is then 1 or 1$'$–2/3–4–4$'$/A–B/A–B/.... If jumping to 2$'$, the response path is then 1 or 1$'$–2$'$/B–A/B–A/...

Fig. 12

Responses after mass takeoff triggered when $\varOmega <\varOmega _{\mathrm{bif}2}^0$ (a) or when $\varOmega \ge \varOmega _{\mathrm{bif}1}^m$ (b)

Hence, when sweeping from $\varOmega _{\mathrm{min}}$ to $\varOmega _{\mathrm{max}}$, the steady-state response without added mass is the branch $A-B$, with no hysteretic cycle. So there is no amplitude jump, and the minimum amplitude is obtained at point A ($W_{\mathrm{max}}(A)$). The steady-state response with added mass follows the hysteretic cycle of Fig. 11, with two amplitude jumps. The minimum amplitude is very small. Its measurement could be difficult in the presence of noise.

3.5.4 Numerical example of the frequency sweep for the hardening behavior

Let us consider the following frequency sweep for design 1 exhibiting the hardening behavior

$$\begin{aligned} \varOmega (t)=22.3956 + 0.0256 \sin (5\times 10^{-5} \pi t), \end{aligned}$$

(15)

corresponding to the physical values

$$\begin{aligned} \tilde{\varOmega }(\tilde{t})=5.477 \times 10^{5} + 620 \sin (7.68\pi \tilde{t} )\, (\hbox {Hz}). \end{aligned}$$

(16)

In Fig. 13a, without added mass, the response (solid line) does not show any amplitude jump. Once the steady-state regime has been reached, the response is the branch $A-B$, see Fig. 13b with a change in amplitude from $W_{\mathrm{max}}=0.49$ at point B to $W_{\mathrm{max}}=0.14$ at point A. At moment $3$, an added mass $m_1=10^{-5}$ falls on the beam. The response (dashed line) jumps from a maximum amplitude $W_{\mathrm{max}}\simeq 0.49$ (point 4) to a minimum amplitude $W_{\mathrm{max}}\simeq 0.01$ (point 5). After two sweep periods, the added mass takes off at point 8, the response goes back to the branch $A-B$ with no jump. At point 9, another mass $m_2=10^{-4}$ arrives, and the response jumps from a maximum amplitude $W_{\mathrm{max}}\simeq 0.49$ (point 13) to a minimum amplitude $W_{\mathrm{max}}\simeq 0.01$ (point 10).

Fig. 13

Frequency sweep for design 1: without added mass (solid line), with small mass $m_1=10^{-5}$ (dashed line) and bigger mass $m_2=10^{-4}$ (dotted line). a response $W_{\mathrm{max}} \, - \, t$, b response $W_{\mathrm{max}}\, - \, \varOmega$

Hence, for the hardening behavior, the detection principle is based on amplitude jumps and on the change in minimum amplitude.

From a theoretical point of view, there is no real advantage in using either softening or hardening behavior for mass detection. The respective hysteretic cycles are basically reversed, with similar properties. As shown in Figs. 10a and 13a, an event is characterized by a clear change in the maximum/minimum amplitude in the case of softening/hardening behavior, respectively, and by large jumps in both cases.

3.6 Mass-detection threshold

Theoretically, if it is possible to set exactly $\varOmega _{\mathrm{max}}=\varOmega _{\mathrm{bif}1}^0$, then any mass without any lower limit will cause a jump in amplitude. However, in practice, this is either not possible because of the limited resolution of the instrumentation or not desirable in order to avoid unwanted jumps due to noise-related perturbations. As a consequence, $\varOmega _{\mathrm{max}}$ is set such that $\varOmega _{\mathrm{max}}<\varOmega _{\mathrm{bif}1}^0$, and the difference between $\varOmega _{\mathrm{max}}$ and $\varOmega _{\mathrm{bif}1}^0$ governs the threshold providing the minimal mass that can be detected.

For example, in Fig. 14, at $\varOmega _\mathrm{op}=22.325$, a large jump from $P_0$ ($W_{\mathrm{max}}=0.09$) to $P_2$ on the dotted line ($W_{\mathrm{max}}=0.42$) indicates the presence of masses $m\ge 9\times 10^{-5}$. For masses $m<9\times 10^{-5}$, for instance $m=8\times 10^{-5}$, there is only a small jump from $P_0$ to $P_1$ instead of the upper point near $P_2$, as confirmed by a study of the basin of attraction.

Fig. 14

Detection threshold of design 2 at $\varOmega _\mathrm{op}=22.325$ and $V_\mathrm{dc}=10V_\mathrm{ac}=9\,\mathrm{V}$, without added mass (solid line), $m=8\times 10^{-5}$ (dashed line), $m=9 \times 10^{-5}$ (dotted line)

4 Quantification of an added mass

4.1 Quantification via frequency shift

Let $x_0$ be the position of the added mass on the beam. If $\phi (x_0) \ne 0$, there is always a frequency shift of the response curve depending on the added mass. Hence, the frequency shift $\varDelta \varOmega$ is measured to identify the mass (see Fig. 15). Though it is commonly used in the linear regime, this type of quantification is even more interesting in the nonlinear regime since $W_{\mathrm{max}}$ is larger and easier to discriminate from the measurement noise. However, in both cases, the relationship between $\varDelta \varOmega$ and the added mass $m$ is linear; thus, the quantification becomes all the more difficult as the mass decreases.

Fig. 15

Design 2: quantification with frequency shift, for $V_\mathrm{dc}=100V_\mathrm{ac}=1.9\,\mathrm{V}$, without added mass (solid line), $m=5\times 10^{-4}$ (dashed line); $m=10^{-3}$ (dotted line)

4.2 Quantification via amplitude jumps

4.2.1 Using fixed frequency

For the hardening behavior, with a large or small added mass, there is always a jump from a large value to a small value of $W_{\mathrm{max}}$, see Figs. 11 and 13. The detection of the added mass is possible but its quantification is difficult with a fixed frequency $\varOmega _\mathrm{op}$ since the amplitude of the jump is almost the same whatever the value of the added mass.

For the softening behavior, at a fixed frequency $\varOmega _\mathrm{op}$, the amplitude of the jump depends on the value of the mass: a small mass induces a large jump and vice versa. Using only one fixed frequency is not sufficient to quantify a large range of added masses. Using several fixed frequencies changes the threshold of detection (see Sect. 3.6) and permits to improve this range of quantifiable masses or to set the upper and lower bounds of masses to be detected.

In Fig. 16, at $\varOmega _\mathrm{op}=22.317$, the masses $3.8\times 10^{-4} \le m \le 5\times 10^{-4}$ are quantified by jumps from $W_{\mathrm{max}}=0.02$ to $W_{\mathrm{max}}=0.25$ or 0.4. When $\varOmega _\mathrm{op}$ approaches $\varOmega _{\mathrm{bif}}$ more closely, i.e., $\varOmega _\mathrm{op}=22.325$, masses $9\times 10^{-5} \le m \le 2\times 10^{-4}$ are quantified by the jumps from 0.1 to 0.25 or 0.4.

Fig. 16

Design 2: quantification with amplitude jumps at two fixed frequencies. a $\varOmega =22.317$, b $\varOmega =22.325$

4.2.2 Quantification via frequency sweep and hysteretic cycles

In the case with added mass, for the softening behavior (respectively, for the hardening behavior), $\varDelta W$ and $\varDelta \varOmega$ are the amplitude and frequency differences between two points, one point having the maximal amplitude and other the maximal frequency $\varOmega _{\mathrm{max}}$ (respectively, the minimal frequency), as represented in Fig. 17.

Fig. 17

Quantification via frequency sweep for design 2 (softening behavior)

Similarly to Sects. 3.5.2 and 3.5.4, the frequency sweep can be used to quantify the added mass. In Fig. 10b, the quantification can be carried out using the values $\varDelta W_1,\,\varDelta W_2$ or $\varDelta \varOmega _1,\,\varDelta \varOmega _2$. So, in comparison with quantification at fixed frequency, the frequency sweep is more interesting: the added mass can fall at any moment and the quantification is automatic.

However, for the frequency sweep, the accuracy of the quantification depends on the nondimensional sweep velocity $\varepsilon$ of Eq. (12). Since the frequency sweep is essentially transient, numerical results are computed by means of a time integration scheme (Runge–Kutta). Two cases of frequency sweep with different sweep velocity $\varepsilon$ are compared with the reference steady-state response curve obtained with the ANM. In Fig. 18a, the response curve for $\varepsilon =5\times 10^{-6}$ and the ANM is similar. However, for a large $\varepsilon \, (\varepsilon =5\times 10^{-5})$, the response is strongly modulated (see Fig. 18b). The jumps are not vertical and do not coincide precisely with the bifurcation position $S_1$ and $S_2$. Choosing a small $\varepsilon$ is therefore required but $\varepsilon$ also decides the quantification time. If $\varepsilon$ is too small, the quantification time is very long; thus, there is a risk that the added mass takes off before the quantification end.

Fig. 18

Influence of $\varepsilon$ on the response. a For $\varepsilon =5\times 10^{-6}$ (solid line) and reference response with ANM (dashed-dotted line), b $\varepsilon =5\times 10^{-6}$ (solid line) and $\varepsilon =5\times 10^{-5}$ (dashed line)

5 Localization of an added mass

For a clamped–clamped microbeam, the frequency shift is determined by (see “Appendix”):

$$\begin{aligned} \varDelta _{f_i} = \frac{\omega _{i}-\omega _{i0}}{\omega _{i0}}\approx -\frac{1}{2} m \phi _i^2(x_0), \end{aligned}$$

(17)

with $x_0$ the position of the added mass, $\omega _{i0}$ and $\omega _i$ the resonant frequencies of the ith mode without and with the added mass, respectively. There are one equation and two unknowns; thus, the resonance at the frequency of another mode has to be considered. Due to the symmetry of the clamped–clamped beam, let the first and third mode shapes be selected. Considering the resonance at the frequencies of the first and third modes permits to determine $x_0$ and m:

$$\begin{aligned} {\left\{ \begin{array}{ll} \varDelta _{f1}\approx -\dfrac{1}{2}m\phi _1^2(x_0),\, \varDelta _{f3} \approx -\dfrac{1}{2} m \phi _3^2(x_0), \\ \Big (\dfrac{\phi _3(x_0)}{\phi _1(x_0)}\Big )^2=\dfrac{\varDelta _{f3}}{\varDelta _{f1}}. \end{array}\right. } \end{aligned}$$

(18)

The principle of localization is illustrated in Fig. 19. First, the frequency shifts $\varDelta _{f1}$ and $\varDelta _{f3}$ between curves with and without added mass are determined at the resonant frequency of the first and third modes. Then, the position of the added mass is located from the ratio $\sqrt{\varDelta _{f3}/\varDelta _{f1}}$.

Fig. 19

Principle of localization. Frequency shift at the a first and b third mode; without added mass (solid line), with added mass (dashed line). Ratio of the third and first mode shapes along the beam axis c

For example, let us consider design 1 (hardening behavior) with $V_{\mathrm{dc}1}=10V_{\mathrm{ac}1}=9\,\mathrm{V}$ at the resonant frequency of the first mode and $V_{\mathrm{ac}2}=1.5V_{\mathrm{dc}2}=67.5\,\mathrm{V}$ for the third mode. Several arbitrary values for $m_0,x_0$ are first used to generate the responses with added mass. Then, the principle of localization is used to identify the values of $m_0,x_0$ from the knowledge of these curves only. To this end, $\varDelta _{f1}$ and $\varDelta _{f3}$ are measured on the responses, and two couples of solutions $(m_{1},x_{1}),\,(m_{2},x_{2})$ are calculated from the system (18). Incorrect values $(m_{2},x_{2})$ can be eliminated by considering the resonance at the frequency of the higher mode. Table 3 shows that the localization is exact for positions close to the middle of the beam. For positions close to the ends of the beam, the deviation is large because $\phi _k(x_0)$ is small at these positions, yielding a small frequency shift.

Table 3 Design 1: example of localization. At $\varOmega \approx \omega _{10}, V_\mathrm{dc}=10V_\mathrm{ac}=9\,\mathrm{V}$; at $\varOmega \approx \omega _{30},\,V_\mathrm{ac}=1.5V_\mathrm{dc}=67.5\,\mathrm{V}$

This procedure only depends on the experimental measure of $\varDelta _{f1}$ and $\varDelta _{f3}$, and is therefore identical for both softening and hardening behaviors.

6 Conclusion

An alternative mass-sensing technique based on nonlinear micro-/nanoelectromechanical resonant sensors has been numerically investigated. The detection takes advantage of bistability and bifurcations of the hysteretic nonlinear responses of the electrostatically actuated resonator. Contrary to the classical detection based on the frequency shift induced by an additional mass, sudden jumps in amplitude make the detection of a very small mass possible. Another interesting feature lies in the fact that the limit of detection can be set with the value of the operating frequency. However, when operating at fixed frequency, it appears that this bifurcation-based mass detection does not exhibit the expected robustness. A possible improvement has been proposed, based on a frequency sweep that varies slowly in sinusoidal form around the resonance and automatically forces the reinitialization of the detection, thus enabling real-time ultrasensitive detection and quantification. The localization of an added mass is very satisfactory for positions far enough from clamped ends of the sensor. This bifurcation-based mass detection will be investigated experimentally in a near future in order to validate the numerical results presented in this paper. This single sensing device is a first step toward the use of NEMS arrays [38]. In the long term, it could lead to new mass measurement architectures and open prospect to miniaturized mass spectrometers with very high analysis rate. In this perspective, robustness to noise of the proposed bifurcation-based sensing technique will be of prime interest. Some works address the problem of noise sensitivity of the systems when one adds a small mass and consider noise-induced switching near bifurcation points [32, 39–44]. These developments will be needed but are beyond the goal of this paper.

Appendix

Let $m_p$ and $x_0$ be the physical mass and position of the added mass, and $\omega _i^m, \, \phi _i^m(x)$ and $\omega _i^0, \phi _i^0(x)$ the frequencies and eigenmodes corresponding to cases with and without added mass. The equation of motion for an infinitesimal volume $\hbox {d}\tilde{x}$ without excitation and damping force is

$$\begin{aligned} \dfrac{\partial }{\partial ^2 \tilde{x}^2} \Big ( EI \dfrac{\partial ^2 \tilde{w}}{\partial \tilde{x}^2} \Big ) \hbox {d} \tilde{x} + \rho S \dfrac{\partial ^2 \tilde{w} }{\partial \tilde{t}^2 } \hbox {d}\tilde{x} + m_p \delta _{\tilde{x}_0}(\tilde{x}) \dfrac{\partial ^2 \tilde{w}}{\partial \tilde{x}^2 } =0\nonumber \\ \end{aligned}$$

(19)

Using the nondimensional variables of Sect. 2, Eq. (19) becomes

$$\begin{aligned} \dfrac{\partial ^4 w}{\partial x^4}\hbox {d}x + \dfrac{\partial ^2 w}{\partial t^2}\hbox {d}x + \dfrac{m_p}{\rho b h l} \delta _{x_0}(x) \dfrac{\partial ^2 w }{\partial t^2} =0. \end{aligned}$$

(20)

Let $m={m_p}/{\rho b h l}$. Assuming that eigenmodes are unchanged with an added mass, then $\phi ^m(x)=\phi ^0(x)=\phi (x)$. Expressing the displacement as $w(x,t)=\phi ^m(x) a^m(t) = \phi (x) a^m(t)$, Eq. (20) becomes for the i$^{th}$ mode

$$\begin{aligned}&\dfrac{\hbox {d} x}{\hbox {d}x + m \delta _{x_0}(x)} \times \dfrac{1}{\phi _i(x)} \times \dfrac{\hbox {d}^4\phi _i(x)}{\hbox {d}x^4}\nonumber \\&\quad =- \dfrac{1}{a_i^m(t)} \dfrac{\hbox {d}^2a_i^m(t)}{\hbox {d}t^2}= (\omega _i^m)^2 \end{aligned}$$

(21)

So,

$$\begin{aligned} \phi _i^{(IV)}(x)\hbox {d}x \!-\! (\omega _i^m)^2 \phi _i(x) \hbox {d}x \!-\! m(\omega _i^m)^2 \delta _{x_0}(x) \phi _i(x)\!=\!0. \nonumber \\ \end{aligned}$$

(22)

Without added mass, let

$$\begin{aligned} \phi _i^{(IV)}(x)=(\omega _i^0)^2 \phi _i(x), \end{aligned}$$

(23)

be replaced in Eq. (22). Multiplying this equation by $\phi _i(x)$, integrating from $x=0$ to $x=1$, and using the normalization condition

$$\begin{aligned} \int _0^1 \, \phi _i(x)^2 \! \hbox {d} x = 1, \end{aligned}$$

(24)

we obtain

$$\begin{aligned} \dfrac{(\omega _i^0)^2 - (\omega _i^m)^2}{(\omega _i^m)^2} = m \phi _i(x_0)^2. \end{aligned}$$

(25)

This can be rewritten as follows by introducing $\varDelta \omega _i= \omega _i^m - \omega _i^0$:

$$\begin{aligned} \dfrac{\varDelta \omega _i}{\omega _i^0} = -\dfrac{1}{2} m \phi _i(x_0)^2 \end{aligned}$$

(26)