1 Introduction

Parametric excitation has drawn major interest in the MEMS community in recent years. Unlike excitation forces of the external excitation, which appears as inhomogeneous term in the differential equation governing the dynamics of a system, the force here appears as time-varying coefficients or parameters in the differential equation (Nayfeh and Mook 1979). Parametric excitation has fascinated scientists since the early 1800s when Faraday observed that the surface waves of fluid-filled cylinders exhibit periodic motion that is twice the vertical excitation frequency (Nayfeh and Mook 1979). Since then, many researchers have utilized the parametric excitation in their own works such as Turner et al. (1988), Ghaderi and Dick (2012), Rugar and Grutter (1991), Ibrahim and Barr (1978), Krylov et al. (2005). Zhang et al. (2007) presented an electrostatically actuated MEMS resonant sensor under two-frequency parametric and external excitations. They studied the responses and dynamics of the MEMS resonator to a combination resonance. The response of the steady-state conditions and their stability were investigated using the method of multiple scales. Krylov et al. (2008) investigated the parametric instability of double-clamped micro scale beams actuated by a time-varying distributed electrostatic force. The stability was performed by evaluating the sign of the largest Lyapunov exponent. Some researchers utilized parametric excitation to realize a mass sensor of amplified response (Zhang et al. 2002; Zhang and Turner 2005). Zhang et al. (2002) investigated the design of a highly sensitive mass sensor. They used in-plane parametrically resonant oscillator to show the effect of nonlinearities on the behavior of parametric resonance of a micro-machined oscillator. To drive the oscillator and catch the dynamic responses, they used either interdigitated or non-interdigitated comb fingers. Zhang and Turner (2005) proposed a mass sensing concept based on parametric resonance amplification. To create mass change to test the concept, a small volume of platinum (Pt) is deposited on the backbone using focused ion beam (FIB). Mass change could be detected by measuring frequency shift at the boundary of the first order parametric resonance ‘tongue’. The application of frequency shift at the boundary of the first order parametric resonance and parametric resonance amplification can be seen in other literature such as Turner and Zhang (2001), Raskin et al. (2000), Olkhovets et al. (2001), Bachels and Schafer (1998). Nowadays, piezoelectric materials are widely used in actuators and sensors as smart structures in MEMS (Rezaei Kivi et al. 2015; Mitrovic et al. 2001; Cattan et al. 1999; Irschik 2002; Zamanian et al. 2008; Rezaei Kivi and Azizi 2015a, b; Rezazadeh et al. 2009; Saeedi Vahdat et al. 2012). Piezoelectric sandwiched micro-beam were first proposed by Rezazadeh et al. (2006) to control the static pull-in instability of a MEM device, and later many researchers studied on similar model such as Zamanian et al. (2008), Rezaei Kivi and Azizi (2015a), Azizi et al. (2011, 2012a, b, 2013, 2014). Linear and nonlinear Mathieu equations have been numerously reported in the literatures such as Azizi et al. (2011), El-Dib (2001), Pandey et al. (2008), DeMartini et al. (2007), Ghazavi et al. (2010). Ghazavi et al. (2010) investigated the stability of a micro cantilever governed by linear Mathieu equation. They showed the effect of viscose damping and DC voltage on stability region of the problem. Azizi et al. (2011) investigated the stability of an electrostatically deflected clamped–clamped micro beam sandwiched by two piezoelectric layers undergoing a parametric excitation. The governing equation of the motion was linear Mathieu type equation in its damped form. They investigated the stable and unstable region of the linear Mathieu equation using Floquet theory.

In this paper, nonlinear dynamics of a parametrically excited clamped–clamped micro-beam sandwiched with two piezoelectric layers is investigated to measure the added mass. Added mass not only shifts the resonance frequency of the system but also activates the parametric resonance and pushes the system response inside the resonance region. Application of same DC and AC voltages to the upper and lower piezoelectric layers creates an axial force with steady and time-varying components. Time-varying axial load leads to time varying stiffness and accordingly activates the parametric resonance. The micro beam exhibits three qualitatively different responses including damped, periodic and parametrically resonated responses. The micro beam is set to operate in the damped region and once the mass is added the response is pushed inside the resonated region and the amplitude magnification is used to measure the added mass.

1.1 Modeling

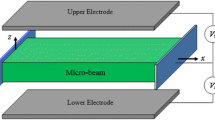
As illustrated in Fig. 1 the studied model is an isotropic micro-beam of length \( \ell \), width \( a \), thickness \( h \), density \( \rho \) Young’s modulus \( E \), sandwiched with two piezoelectric layers with thickness \( h_{P} \), density \( \rho_{P} \) throughout the micro-beam length. The Young’s modulus of the piezoelectric layers is denoted by \( E_{P} \) and the equivalent piezoelectric coefficient is \( \bar{e}_{31} \). Piezoelectric layers are actuated by a combination of a DC and an AC voltage denoted by \( V_{DC} \) and \( V_{AC} \), respectively; this voltages is applied along the height direction of the piezoelectric layers. The coordinate system as illustrated in Fig. 1, is attached to the middle of the left end of the micro-beam where \( x \) and \( z \) refer to a horizontal and vertical coordinates, respectively.

Fig. 1
figure 1

Schematic view of the proposed model. a Front view. b Side view

Full size image

The total potential strain energy of the micro-beam is due to the bending (\( U_{b} \)), axial force due to piezoelectric actuation (\( U_{P} \)), and axial force due to the mid-plane stretching (\( U_{a} \)).

The strain energy due to mechanical bending is expressed as:

$$ U_{b} = \frac{{(EI)_{eq} }}{2}\int_{x = 0}^{x = \ell } {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} dx} $$
(1)

where \( (EI)_{eq} \) is defined as follows (Saeedi Vahdat et al. 2012):

$$ (EI)_{Eq} = EI + E_{P} hah_{P} \left( {\frac{h}{2} + h_{P} } \right) $$
(2)

Due to the immovable edges, the extended length of the beam \( (\ell^{\prime}) \) becomes more than the initial length \( \ell \) and this leads to the introduction of an axial stress and accordingly an axial force denoted as (Azizi et al. 2013):

$$ F_{a} = \frac{{(EA)_{eq} }}{\ell }(\ell^{\prime} - \ell ) \approx \frac{{(EA)_{eq} }}{2\ell }\int\limits_{0}^{\ell } {\left( {\frac{\partial w}{\partial x}} \right)}^{2} dx $$
(3)

where \( (EA)_{eq} = Eah + 2E_{P} ah_{P} \) and \( U_{a} = {{F_{a} (\ell^{\prime} - \ell )} \mathord{\left/ {\vphantom {{F_{a} (\ell^{\prime} - \ell )} 2}} \right. \kern-0pt} 2} \) which is bending strain energy.

Piezoelectric actuation due to immovable boundary conditions leads to the generation of another axial force; based on constitutive equation of piezoelectricity, (Azizi et al. 2012a, b) and considering the direction of applied electrical field, the axial force due to the piezoelectric actuation is expressed as follows:

$$ F_{P} = - 2\frac{{V_{P} a}}{h}\int\limits_{0}^{{h_{P} }} {\bar{e}_{31} } dh $$
(4)

where \( \bar{e}_{31} \) is the corresponding piezoelectric voltage constant (\( Coulomb/m^{2} \)); considering the strain potential energy (\( U_{P} = F_{P} (\ell^{\prime} - \ell ) \)) due to the axial piezoelectric force, the total potential energy of the system reduces to:

$$ U = U_{b} + U_{a} + U_{P} $$
(5)

The kinetic energy of the micro beam is represented as:

$$ T = \frac{{(\rho ah)_{eq} }}{2}\int\limits_{0}^{\ell } {\left( {\frac{\partial w}{\partial t}} \right)^{2} } dx $$
(6)

where:

$$ (\rho ah)_{eq} = \rho ah + 2\rho_{P} ah_{P} $$
(7)

The governing partial differential equation of the motion is obtained by the minimization of the Hamiltonian as:

$$ \delta \int\limits_{0}^{t} {Hdt} = \delta \int\limits_{0}^{t} {(T - U)dt} = 0 $$
(8)

Introducing Eqs. (5) and (6) and into Eq. (8), reduces to:

$$ \begin{aligned} \delta \int\limits_{0}^{t} {Hdt} = \int\limits_{0}^{t} {\left\{ {\begin{array}{*{20}c} { - (EI)_{eq} w^{\prime\prime}\delta w^{\prime}\left| {_{0}^{\ell } } \right. + (EI)_{eq} w^{\prime\prime\prime}\delta w\left| {_{0}^{\ell } } \right. - (EI)_{eq} \int\limits_{0}^{\ell } {w^{IV} \delta wdx} } \\ { - F_{P} w^{\prime}\delta w\left| {_{0}^{\ell } } \right. + F_{P} w^{\prime\prime}\delta wdx - \frac{{(EA)_{eq} }}{2}\int\limits_{0}^{\ell } {w^{\prime 2} dxw^{\prime}\delta w\left| {_{0}^{\ell } } \right.} } \\ { + \frac{{(EA)_{eq} }}{2}\int\limits_{0}^{\ell } {w^{\prime 2} dx} \int\limits_{0}^{\ell } {w^{\prime\prime}\delta wdx} } \\ \end{array} } \right\}} dt \hfill \\ \int\limits_{0}^{t} {\left\{ {(\rho A)_{eq} \int\limits_{0}^{\ell } {\dot{w}\delta w} \left| {_{0}^{\ell } } \right. - (\rho A)_{eq} \int\limits_{0}^{t} {\textit{\"{w}}\delta wdt} } \right\}} dx = 0 \hfill \\ \end{aligned} $$
(9)

Including the effect of viscous damping, the governing equation and the corresponding boundary conditions reduce to (Azizi et al. 2013, 2014):

$$ \begin{aligned} & (EI)_{eq} \frac{{\partial^{4} w(x,t)}}{{\partial x^{4} }} + (\rho A)_{eq} \frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} \hfill \\ &- (F_{P} + \frac{{(EA)_{eq} }}{2\ell }\int\limits_{0}^{\ell } {\left( {\frac{\partial w}{\partial x}} \right)^{2} } dx)\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \frac{\partial w}{\partial t} = 0 \end{aligned}$$
(10)
$$ w(0,t) = w(\ell ,t) = 0,\;\frac{\partial w(0,t)}{\partial x} = \frac{\partial w(\ell ,t)}{\partial x} = 0 $$
(11)

where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) denotes the viscose damping per unit length of the micro-beam (Ghazavi et al. 2010).

To obtain the equation of the motion in non-dimensional form, the following non-dimensional parameters are introduced:

$$ \hat{w} = \frac{w}{\varGamma },\,\,\hat{x} = \frac{x}{\ell },\,\,\hat{t} = \frac{t}{{\tilde{t}}},\,\quad \varGamma = 2.75 \,\, \upmu {\text{m}} $$
(12)

where:

$$ \tilde{t} = \sqrt {\frac{{(\rho A)_{eq} \ell^{4} }}{{(EI)_{eq} }}} $$
(13)

Substituting Eq. (12) into Eq. (10) and dropping the hats the differential equation of the motion in non-dimensional form reduces to:

$$ \frac{{\partial^{4} w(x,t)}}{{\partial x^{4} }} + \frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} - (\alpha_{1} + 2\alpha_{2} \cos (2\varOmega t) + \alpha_{3} \varLambda (w,w))\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \alpha_{4} \frac{\partial w(x,t)}{\partial t} = 0 $$
(14)

Subjected to the following boundary conditions in non-dimensional form:

$$ w(0,t) = w(1,t) = 0,\,\,\,\,\,\frac{\partial w(0,t)}{\partial x} = \frac{\partial w(1,t)}{\partial x} = 0 $$
(15)

In Eq. (14), the function \( \varLambda \) and coefficients \( \alpha_{i} \) are defined as:

$$ \begin{aligned} & \varLambda (w,w) = \int\limits_{0}^{1} {\frac{\partial w}{\partial x}} \frac{\partial w}{\partial x}dx \\ & \alpha_{1} = \frac{{2ae_{31} \ell^{2} V_{DC} }}{{(EI)_{eq} }},\,\,\alpha_{2} = \frac{{ae_{31} \ell^{2} V_{AC} }}{{(EI)_{eq} }},\,\,\alpha_{3} = \frac{{(EA)_{eq} \varGamma^{2} }}{{2(EI)_{eq} }}, \hfill \\ & \alpha_{4} = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \ell^{2} }}{{2\sqrt {(\rho A)_{eq} (EI)_{eq} } }} \\ \end{aligned} $$
(16)

2 Numerical solution

There is no exact solution to Eq. (14) (Mohanta 2006); therefore an approximate solution is assumed to be in the following form:

$$ w(x,t) = \sum\limits_{j = 1}^{n} {\varphi_{j} (x)q_{j} (t)} $$
(17)

where \( \varphi_{j} (x) \) and \( q_{j} (t) \) refer to the shape functions of a clamped–clamped micro-beam and time dependent amplitudes, respectively. Substituting Eq. (17) in Eq. (14) results in:

$$ \begin{aligned} & \sum\limits_{j = 1}^{n} {\varphi_{j}^{IV} (x)q_{j} (t)} + \sum\limits_{j = 1}^{n} {\varphi_{j} (x)\textit{\"{q}}_{j} (t)} \hfill \\ & \quad \;\; - (\alpha_{1} + 2\alpha_{2} \cos (2\varOmega t))\sum\limits_{j = 1}^{n} {\varphi^{\prime\prime}_{j} (x)q_{j} (t)} \hfill \\ & \quad \;\; - \alpha_{3} \left(\int\limits_{0}^{\ell } {(\varphi^{\prime}_{j} (x))^{2} dx} \right) \\ & \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {q_{i} (t)q_{j} (t)q_{k} (t)} } } \varphi^{\prime\prime}_{j} (x) \hfill \\ & + \alpha_{4} \sum\limits_{j = 1}^{n} {\varphi_{j} (x)\dot{q}_{j} (t)} = residual \\ \end{aligned} $$
(18)

Multiplying the resultant in \( \varphi_{i} (x) \) and integrating the outcome over \( [0,1] \) yields:

$$ \begin{aligned} & \sum\limits_{j = 1}^{n} {q_{j} (t)} \int\limits_{0}^{1} {\varphi_{i} (x)\varphi_{j}^{IV} (x)} dx + \sum\limits_{j = 1}^{n} {\textit{\"{q}}_{j} (t)\int\limits_{0}^{1} {\varphi_{i} (x)\varphi_{j} (x)} } dx \\ & - \quad \;\; (\alpha_{1} + 2\alpha_{2} \cos (2\varOmega t))\sum\limits_{j = 1}^{n} {q_{j} (t)} \int\limits_{0}^{1} {\varphi_{i} (x)\varphi^{\prime\prime}_{j} (x)dx} \\ & \quad \;\; - \alpha_{3} \int\limits_{0}^{1} {(\varphi^{\prime}_{j} (x))^{2} } dx) \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {q_{i} (t)q_{j} (t)q_{k} (t)} } } \int\limits_{0}^{1} {\varphi_{i} (x)\varphi^{\prime\prime}_{j} (x)dx} \\ & \quad \;\; + \alpha_{4} \sum\limits_{j = 1}^{n} {\dot{q}_{j} (t)\int\limits_{0}^{1} {\varphi_{i} (x)\varphi_{j} (x)} } dx = 0 \\ \end{aligned} $$
(19)

Equation (19) is simplified to the following form:

$$ \sum\limits_{j = 1}^{n} {\textit{\"{q}}_{j} (t)M_{ij} } + \sum\limits_{j = 1}^{n} {\dot{q}_{j} (t)C_{ij} } + \sum\limits_{j = 1}^{n} {q_{j} (t)K_{{L_{ij} }} } + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {q_{i} (t)q_{j} (t)q_{k} (t)} k_{{nL_{ijkl} }} } } = 0 $$
(20)

where:

$$ \begin{aligned} M_{ij} & = \int\limits_{0}^{1} {\varphi_{i} (x)\varphi_{j} (x)} dx \\ C_{ij} & = \alpha_{4} \int\limits_{0}^{1} {\varphi_{i} (x)\varphi_{j} (x)} dx \\ K_{{L_{ij} }} & = \int\limits_{0}^{1} {\varphi_{i} (x)\varphi_{j}^{IV} (x)} dx - (\alpha_{1} + 2\alpha_{2} \cos (2\varOmega t))\int\limits_{0}^{1} {\varphi_{i} (x)\varphi^{\prime\prime}_{j} (x)} dx \\ K_{{nL_{ijkl} }} & = - \alpha_{3} \int\limits_{0}^{1} {(\varphi^{\prime}_{j} (x))^{2} dx} \int\limits_{0}^{1} {\varphi^{\prime\prime}_{j} (x)\varphi_{i} (x)dx} \\ \end{aligned} $$
(21)

Keeping the first mode in the modal expansion and introducing the transformation \( \tau = \varOmega t \) to Eq. (20), yields to nonlinear Mathieu equation as follows:

$$ \frac{{d^{2} q}}{{d\tau^{2} }} + C\frac{dq}{d\tau } + (\delta + 2\varepsilon \cos (2\tau ))q + \beta q^{3} = 0 $$
(22)

where:

$$ \begin{aligned} \delta & = \frac{ 5 0 0. 5 4 6 6 5 3 2}{{\varOmega^{2} }} - \frac{ 1 2. 3 0 6 4 9 2 6 6}{{\varOmega^{2} }}\alpha_{1} \\ \varepsilon & = - 6. 1 5 3 2 4 6 3 3 0\frac{{\alpha_{2} }}{{\varOmega^{2} }} \\ \beta & = - 1 5 6. 8 7 3 6 6 7 7\frac{{\alpha_{3} }}{{\varOmega^{2} }} \\ C & = \frac{{\alpha_{4} }}{\varOmega } \\ \end{aligned} $$
(23)

\( \delta \) is unvarying equivalent stiffness of the clamped–clamped micro-beam as a function of flexural rigidity and the applied DC voltage, and \( \varepsilon \) is time-varying equivalent stiffness as a function of AC voltage, and \( \beta \) is the nonlinear cubic stiffness term as a function of mechanical and geometrical characteristics of the micro beam.

3 Results and discussion

The geometrical and mechanical properties of the case study are represented in Table 1.

Table 1 Geometrical and material properties of the micro-beam and piezoelectric layers
Full size table

Figure 2a, b depict the bounded (stable) and unbounded (unstable) regions for (\( \beta = 0 \)) with different damping coefficients (\( C = 0 \) and \( C = 0.1 \)). The bounded and unbounded regions are separated via periodic solutions as the boundaries.

Fig. 2
figure 2

The boundaries of stable and unstable (shaded) region (periodic solutions) for \( \beta = 0 \) a \( C = 0 \) and b \( C = 0.1 \)

Full size image

As obvious, damping raises the unstable region, so a nonzero force is needed to trigger the instability. The larger is the value of \( C \), the higher the instability tongues are raised.

Figure 3 shows the boundaries of the stable and unstable (shaded) region accompanied with two pair of time histories for points “A” (outside) and “B” (inside) the tongue. As depicted in Fig. 3, the response of the system for a pair of \( (\delta ,\varepsilon ) \) located outside the instability tongue point “A” (\( \mu = 0.1,\;\,\delta = 1,\,\;\varepsilon = 0.1 \)) is stable. For a pair of \( (\delta ,\varepsilon ) \) inside the unstable region the scenario is completely different. In this case, the amplitude of the response for a definite initial condition due to the so-called parametric resonance suddenly increases and the system experiences unstable oscillations. Figure 3 shows time history of point “B” (\( C = 0.1,\,\;\delta = 1,\,\;\varepsilon = 0.5 \)) which is inside the unstable region. In the absence of nonlinear stiffness term damping does not cap the response (Nayfeh and Mook 1979; Saeedi Vahdat et al. 2012; Rezazadeh et al. 2006).

Fig. 3
figure 3

The boundaries of stable and unstable region (periodic solutions) for \( \beta = 0 \) and \( C = 0.1 \) accompanied with time histories corresponding to points “A” (\( C = 0.1,\,\delta = 1,\,\varepsilon = 0.1 \)) and “B” (\( C = 0.1,\,\delta = 1,\,\varepsilon = 0.5 \))

Full size image

Assuming (\( \beta \ne 0 \)), the geometric nonlinearity caps the response amplitude inside the tongue and makes it bounded. In this case, the response inside the tongue becomes significantly higher than that outside the tongue. Figure 4 illustrates the stability boundaries in the plane of \( (\delta ,\varepsilon ) \) with cubic nonlinearity (\( \beta = 1 \)) and damping coefficient \( (C = 0.1) \).

Fig. 4
figure 4

The boundaries of resonance region (periodic orbits) for (\( \beta = 1 \)) for \( C = 0.1 \)

Full size image

The responses of the micro beam corresponding to three different pairs of \( (\delta ,\varepsilon ) \) (“C”, “D”, and “E”) are depicted in following figures. In spite of the absence of cubic nonlinearity where the response is unbounded inside the tongue, the nonlinearity limits the response and leads to a bounded however considerably high amplitude response inside the tongue.

Figure 5 illustrates the temporal response and phase plane of point “D” on the boundary which exhibits a periodic solution. Figure 6 depicts the temporal response corresponding to point “C” and “E” outside and inside the tongue, respectively. On the boundary of the tongue, the response is periodic.

Fig. 5
figure 5

Temporal response and phase portrait of the point “D” on the tongue

Full size image
Fig. 6
figure 6

Temporal response of the points “C” outside and “E” inside the tongue

Full size image

As mentioned, to detect the added mass we took benefit of nonlinearity to amplify the response inside the tongue. Figure 7 shows the tongue of the system (\( \beta = 1,\,\;C = 0.1 \)) with two pair of points which has different \( \delta \) and the same \( \varepsilon \)(\( A:(1.47,0.41),\;\,B:(1.41,0.41) \)). To detect an added mass, the system is set to operate outside the tongue in the vicinity of the boarder say at point “A”. Once the added mass is deposited on the micro-beam, natural frequency and accordingly \( \delta \) decrease and this, in turn, pushes the response inside the tongue and subsequently parametrically resonates the response amplitude. The parametric resonance is qualitatively depicted in Fig. 7.

Fig. 7
figure 7

Time response of the system corresponding to points “A” (before adding mass) and “B” (after adding mass)

Full size image

It is worth mentioning, the higher we move on the boundaries of the tongue the less is the required mass to push the response inside the tongue. To put it more simply, for a higher pair of \( (\delta ,\varepsilon ) \) the sensitivity of the system is increased. To confirm our claim, the responses of the system with higher pair of \( (\delta ,\varepsilon ) \) are shown in Fig. 8 (\( C:(1.71,0.65),\,\;D:(1.57,0.65) \)) and Fig. 9 (\( E:(1.87,0.94),\,\;F:(1.84,0.94) \)).

Fig. 8
figure 8

Time response of the system corresponding to points “C” (before adding mass) and “D” (after adding mass)

Full size image
Fig. 9
figure 9

Time response of the system corresponding to points “E” (before adding mass) and “F” (after adding mass)

Full size image

The added mass to push the response from outside to inside the tongue is represented. Table 2 represents the required mass to move the response from outside to inside the instability tongue. The minimum detectable mass is compared with that reported by Zhang et al. (2005) in Table 3.

Table 2 The required mass to move the system from outside to inside the instability tongue
Full size table
Table 3 A comparison between the minimum detectable mass by authors and Zhang
Full size table

4 Conclusion

Nonlinear dynamics of a parametrically excited mass-sensor was studied. The proposed model is a clamped–clamped micro-beam sandwiched by two piezoelectric layers underlying throughout the length of the micro-beam. Piezoelectric layers were excited by a combination of a DC and an AC voltage. Applying AC voltage resulted in the generation of time-varying axial force. The governing partial differential equation of the motion was derived by minimization of the Hamiltonian and discretized to a single degree of freedom nonlinear damped Mathieu equation. The periodic solutions were captured using shooting method and the boundaries between damped and parametrically resonated regions were determined. The micro beam was excited nearby the periodic solutions outside the boundaries of the region of parametric resonance. Once the added was deposited on the micro beam the response was pushed inside the region of parametric resonance. The amplification of the response amplitude was used as a measure of added mass. The effect of governing parameters including piezoelectric DC and AC voltage on the mass detection sensitivity were also investigated.