1 Introduction

The dynamics on an attractor is said to be chaotic if there exists exponential sensitivity to initial conditions. For most cases involving differential equations, chaos usually occurs together with geometrical strangeness [1, 2]. In a BLDCM system, the chaotic behavior leads to the intermittent oscillation of torque and speed, irregular current noise of the system, and unstable control performance. Therefore, it intensively influences the stability of the system and safety as well [3]. The advantage of BLDCM is the elimination of the physical contact between the brushes and the commutators. Then, BLDCM is widely applied in direct-drive applications such as robotics [4] and aerospace [5].

For ameliorating the performance of the BLDCM system, a large amount of literatures and control methods have been attempted to apply in the motor drivers. For example, to speed up the error convergence rate, nonsingular fast terminal sliding-mode control (SMC) [6], which can reach finite-time stability, is applied. In Ref. [7], a high-order SMC method via backstepping is presented to attain finite-time tracking control regardless of mismatched disturbance. The Ott, Grebogi, and Yorke (OGY) method is a fundamental technology for controlling chaos [8, 9]; unfortunately, choosing an adjustable parameter usually becomes very difficult. The neural fuzzy control (NFC) approaches can also achieve self-learning; however, it is difficult for online learning real-time control [10, 11]. Chaos anti-control of three time scale brushless DC motors and chaos synchronization of different order systems are studied [12]. Anti-control of chaos of single time scale brushless DC motors and chaos synchronization of different order systems are proposed further [13]. However, neither of them considers the time delay, output constraint, and unknown parameters.

Recently, a barrier Lyapunov function (BLF) which is proposed for constraint handling in Brunovaky-type system and nonlinear systems in strict feedback form are introduced for the special property of approaching infinity whenever its arguments approach some limits [14, 15]. In addition, backstepping design method is an effective tool, which is often applied in nonlinear systems control with non-matching conditions, as well as systems with uncertain functions [16, 17]. However, it suffers from repetitive differentiations. To solve this problem, the DSC is used to successfully overcome the shortage of traditional backstepping, and its first-order low-pass filter is used to gain the derivative information of the virtual control at the design procedure [18, 19]. Control of chaos using the time-delay feedback control technology though is introduced to the real applications [20]. But it suffers from some problems as the control objective must be the equilibrium. Then, an adaptive DSC method is introduced to solve it for a class of uncertain time-delay nonlinear system with state constraint [21]. Using the high-gain observer, an adaptive fuzzy backstepping output feedback control approach is developed for a class of multiple-input and multiple-output (MIMO) nonlinear systems with time delays and immeasurable states [22]. For a class of MIMO stochastic nonlinear systems with immeasurable states, an adaptive fuzzy backstepping output feedback DSC approach is presented [23].

To the best of our knowledge, the combination among adaptive DSC, TBLF, and RBFNN has been seldom applied in the control of chaos for the BLDCM system yet. Further contribution includes the design of adaptive RBFNN DSC controller to handle uncertain time delays and parametric uncertainties. The proposed controller owns the suppression of the chaotic behavior, in addition to driving the system to the pre-defined trajectory with high precision and short response time. Meanwhile, the complexity of the designed controller is reduced, and the design procedure is much simpler than that of traditional backstepping. Simulation results show that control scheme is able to reduce chaos and effects of parameter variation. Similarly, the results are presented to show the effectiveness and robustness to control the BLDCM.

2 System descriptions and mathematical preliminaries

2.1 System descriptions

The brushless DC motor system considered here is illustrated in Fig. 1. It is an electromechanical system, and its equations of electrical and mechanical dynamics can be written in the following forms [12, 24]:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}\omega }{\mathrm{d}t}=\frac{n}{J}\left[ {k_\mathrm{t} i_\mathrm{q} +\left( {L_\mathrm{d} -L_\mathrm{q} } \right) i_\mathrm{q} i_\mathrm{d} } \right] -\frac{1}{J}\left( {b\omega +\bar{{T}}_\mathrm{L} } \right) \\ \frac{\mathrm{d}i_\mathrm{q} }{\mathrm{d}t}=\frac{1}{L_\mathrm{q} }\left[ {-Ri_\mathrm{q} -n\omega \left( {L_\mathrm{d} i_\mathrm{d} +k_\mathrm{t} } \right) +v_\mathrm{q} } \right] \\ \frac{\mathrm{d}i_\mathrm{d} }{\mathrm{d}t}=\frac{1}{L_\mathrm{d} }\left[ {-Ri_\mathrm{d} +nL_\mathrm{q} \omega i_\mathrm{q} +v_\mathrm{d} } \right] \\ \end{array}} \right. \end{aligned}$$
(1)

The denotations of the BLDCM system parameters are shown in Table 1. In order to reduce the number of parameters, a transformation is carried out in the next section. Suppose the multiple time scales \(\tau _{1},\,\tau _{2},\, \tau _{3}\) are defined as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _1 =JR/k_\mathrm{t}^2 \\ \tau _2 =L_\mathrm{q} /R \\ \tau _3 =L_\mathrm{d} /R \\ \end{array}} \right. , \end{aligned}$$
(2)

where \(\tau _{1},\, \tau _{2}\), and \(\tau _{3}\) denote the mechanical time constant, the first electrical time constant, and the second electrical time constant, respectively.

Fig. 1
figure 1

The brushless DC motor system and its commutation

Full size image
Table 1 The denotation of the BLDCM parameters
Full size table

Then, the new state space model for the BLDCM becomes

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _1 \frac{\mathrm{d}x_1 }{\mathrm{d}t}=\sigma x_2 +\rho x_2 x_3 -\eta x_1 -T_\mathrm{L} \\ \tau _2 \frac{\mathrm{d}x_2 }{\mathrm{d}t}=-x_2 -x_1 -x_1 x_3 +u_\mathrm{q} \\ \tau _3 \frac{\mathrm{d}x_3 }{\mathrm{d}t}=x_1 x_2 -x_3 +u_\mathrm{d} \\ \end{array}} \right. , \end{aligned}$$
(3)

where the non-dimensional variables are

$$\begin{aligned} x_1&= \frac{nL_\mathrm{q} }{R\sqrt{\delta }}\omega , \quad x_2 =\frac{L_\mathrm{q} }{k_\mathrm{t} \sqrt{\delta }}i_\mathrm{q} , \quad x_3 =\frac{L_\mathrm{q} }{k_\mathrm{t} \delta }i_\mathrm{d} ,\\ u_\mathrm{q}&= \frac{L_\mathrm{q} }{k_\mathrm{t} R\sqrt{\delta }}v_\mathrm{q} , \quad u_\mathrm{d} =\frac{L_\mathrm{q} }{k_\mathrm{t} R\delta }v_\mathrm{d} ,\quad \sigma =n^{2}, \\ \rho&= (1\!-\!\delta )n^{2},\quad \eta \!=\!\frac{Rb}{k_\mathrm{t}^2 },\quad T_\mathrm{L}\! =\!\frac{nL_\mathrm{q} }{k_\mathrm{t}^2 \sqrt{\delta }}\bar{{T}}_\mathrm{L} , \quad \delta \!=\!\frac{L_\mathrm{q} }{L_\mathrm{d} }. \end{aligned}$$

It can be easily seen that the mathematical model of BLDCM owns high nonlinearity because of the coupling between the speed and the currents. In Eq. (3), \(T_{\mathrm{L}}\) presents the normalized load torque; \(u_{\mathrm{q}}\) and \(u_{\mathrm{d}}\) denote the normalized quadrature-axis and direct-axis stator voltage, respectively; and \(\sigma ,\, \eta \), and \(\rho \) are unknown system parameters.

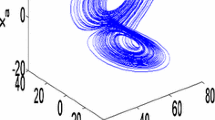
In order to show the computational results such as phase portrait, strange attractor, choose the parameters as \(u_{\mathrm{q}}=4.017\), \(u_{\mathrm{d}} =-15.305,\, \tau _{1}= 1,\, \tau _{2}=6.45,\, \tau _{3}=7.125,\, T_{\mathrm{L}}=2.678\), and select the true values of unknown parameters as \(\sigma =16,\, \rho =1.516\) for chaos condition. The initial conditions of the drive systems are \(x_{1}(0)=x_{2}(0)= x_{3}(0)=0\). Figure 2 illustrates the phase portrait of various \(\eta \). The motion is periodic in the situations of \(\eta =3.0,\, 2.36\). However, in the situations of \(\eta = 2.1,\, 1.6\), the motion appears chaotic behavior, and \(\eta = 2.34\) is a critical value. Figure 3 shows the strange attractor in BLDCM with parameter \(\eta =1.6\). Figure 4 shows the bifurcation diagram.

Fig. 2
figure 2

Phase portrait with different \(\eta \)

Full size image
Fig. 3
figure 3

Strange attractor with parameter \(\eta = 1.6\)

Full size image
Fig. 4
figure 4

Bifurcation diagram

Full size image

A time delay in the overall system can lead to voltage and current distortions due to the low-pass filter, hysteresis control inverter, microprocessor program computation time, and so on. Then, the mathematical model of BLDCM with uncertain nonlinear time delay is rewritten as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =\frac{1}{\tau _1 }\left[ {\sigma x_2 +\rho x_2 x_3 -\eta x_1 -T_\mathrm{L} +\Delta f_1 (x_1 (t-\tau _1 ))} \right] \\ \dot{x}_2 =\frac{1}{\tau _2 }\left[ {-x_2 -x_1 -x_1 x_3 +u_q +\Delta f_2 (\bar{{x}}_2 (t-\tau _2 ))} \right] \\ \dot{x}_3 =\frac{1}{\tau _1 }\left[ {x_1 x_2 -x_3 +u_\mathrm{d} +\Delta f_3 (x_3 (t-\tau _3 ))} \right] \\ \end{array}} \right. \!\!, \end{aligned}$$
(4)

where \(\bar{{x}}_2 (t)=[x_1 (t),x_2 (t)]^{T},\Delta f_i (x_i (t-\tau _i )),\, i=1, 2, 3\), denote the nonlinear time delay item, and \(\tau _i ,\, i=1, 2, 3\), stand for the time delay constant.

For any given continuous signal \(y_{\mathrm{r}}\), the dynamics surfaces are defined as

$$\begin{aligned} \left\{ {\begin{array}{l} S_1 \left( t \right) =x_1 -y_\mathrm{r} \\ S_2 \left( t \right) =x_2 -a_{2\mathrm{f}} \\ S_3 \left( t \right) =x_3 \\ \end{array}} \right. , \end{aligned}$$
(5)

where \(a_{2\mathrm{f}}\) is the filtered virtual controller.

Assumption 1

The nonlinear time delay items satisfy the following inequality:

$$\begin{aligned} \left\{ {\begin{array}{l} \left| {\Delta f_1 (x_1 (t-\tau _1 ))} \right| \le \left| {S_1 (t-\tau _1 )} \right| q_{11} (S_1 (t-\tau _1 )) \\ \left| {\Delta f_2 (\bar{{x}}_2 (t-\tau _2 ))} \right| \le \left| {S_1 (t-\tau _2 )} \right| q_{21} (S_1 (t-\tau _2 )) \\ \hbox { }+\left| {S_2 (t-\tau _2 )} \right| q_{22} (\bar{{S}}_2 (t-\tau _2 )) \\ \left| {\Delta f_3 (x_3 (t-\tau _3 ))} \right| \le \left| {S_3 (t-\tau _3 )} \right| q_{31} (S_3 (t-\tau _3 )) \\ \end{array}} \right. , \end{aligned}$$
(6)

where the nonlinear functions \(q_{11},\,q_{21},\,q_{22}\), and \(q_{31}\) are known, \(\bar{{S}}_2 (t)=[x_1 (t),x_2 (t)]^{T}\).

Assumption 2

The reference trajectory \(y_{\mathrm{r}}\) is bounded by \(-d\le y_{\mathrm{r}}\le d,\, (a > d > 0)\), and the time derivatives \(y_{\mathrm{r}}^{(1)},\, y_{\mathrm{r}}^{(2)}\) are bounded.

The constraints are not violated in the whole dynamic process. That is, \(x_{1}(t)\in (-a, a),\, \forall t > 0\), where the constant \(a> 0\).

2.2 Tangent barrier function

For the sake of ensuring that system state is bounded in a desired region, a tangent barrier function \(y\, \hbox {tan}(y)\) is employed in this paper, where \(\hbox {tan}(\cdot )\) stands for the tangent function. It is obvious that the tangent barrier function satisfies the characteristics listed as below:

$$\begin{aligned} +\infty >y\tan (y)\ge 0\,\hbox {for}\, y\in (-\pi /2, \pi /2). \end{aligned}$$
(7)

According to the above descriptions, we can formalize the results for general forms of tangent barrier function in Lyapunov synthesis satisfying \(y\hbox {tan}(y)\rightarrow \infty \) as \(y\rightarrow -\pi /2\) or \(y\rightarrow \,\pi /2\).

3 Design of chaos controller based on TBLF

3.1 RBFNN

For the continuous function \(f\left( {\theta ,z} \right) \)and bounded closed set \(\Omega \rightarrow R^{n}\), there is a RBFNN shown in Fig.5, which satisfies

$$\begin{aligned} f\left( {\theta ,z} \right) =\theta ^{T}\xi \left( z \right) +\varepsilon , \end{aligned}$$
(8)

where \(z\in \Omega \subset R^{n}\) is the input vector with \(n\) being the neural network input dimension, \(\Omega \) denotes some compact set in \(R^{n},\,\theta =[\theta _1 ,\theta _2 ,\cdots ,\theta _n ]^{T}\in R^{l}\) is the weight vector, and \(l>1\) is the node number of neuron.\(\varepsilon \) is the estimation error, and \(\xi \left( z \right) =[\xi _1 \left( z \right) ,\xi _2 \left( z \right) ,\cdots ,\xi _n \left( z \right) ]^{T}\in R^{l}\) is a basic function vector.

Fig. 5
figure 5

The structure of the RBFNN

Full size image

The Gaussian basis function is selected as

$$\begin{aligned} \xi _i \left( z \right) =\exp \left[ {-\frac{\left\| {z-\mu _i } \right\| ^{2}}{2\sigma _i^2 }} \right] ,i=1,2,\cdots ,l \end{aligned}$$
(9)

where \(\mu _i =\left[ {\mu _{i1} ,\mu _{i2} ,\cdots ,\mu _{in} } \right] ^{T}\) is the center of basic function \(\xi _i \left( z \right) ,\,\sigma _i \) is the width of \(\xi _i \left( z \right) \), and \(\left\| \cdot \right\| \) denotes the 2-norm of a vector.

Define the best weight vector as

$$\begin{aligned} \theta ^{{*}}=\arg \mathop {\min }\limits _{\theta \in R^{n}} \left\{ {\mathop {\sup }\limits _{z\in \Omega } \left\| {f\left( z \right) -{\mathop {\theta }\limits ^{\frown }}^{T}\xi \left( z \right) } \right\| } \right\} . \end{aligned}$$
(10)

Assumption 3

There is a positive constant \(\varepsilon _{M}\) which satisfies \(\left| {\varepsilon _i } \right| \le \varepsilon _{M} ,i=1,2,3\)

3.2 Controller design

Theorem 1

The special case of the Cauchy–Schwarz inequality in a Euclidean space is called Cauchy’s inequality. It is one of the most important inequalities in all of mathematics [25]. It is usually written as

$$\begin{aligned} \left( {\sum {r_i s_i } } \right) ^{2}\le \sum {r_i^2 } \sum {s_i^2 }, \end{aligned}$$
(11)

where all of \(r_{i}, \quad s_{i}\in R\).

According to the above-mentioned dynamics system, the whole design process consists of three phases. Then, the process of the design is given in detail.

Step 1: Calculate the derivative of \(S_{1}\)

$$\begin{aligned} \dot{S}_1 =\frac{1}{\tau _1 }\left[ {\sigma x_2 +f_1 +\Delta f_1 \left( {x_1 \left( {t-\tau _1 } \right) } \right) } \right] -\dot{y}_\mathrm{r}, \end{aligned}$$
(12)

where \(f_1 =\rho x_2 x_3 -\eta x_1 -T_\mathrm{L} \).

Based on the above description, \(\sigma ,\, \eta \) and \(\rho \) are unknown parameters of system. Then, it is not easy to construct the controller for traditional methods. To cope with this problem, adaptive technique is employed to deal with the unknown gain, and RBFNN is used to approximate the uncertain nonlinear function \(f_{1}\). Therefore, for any given \(\varepsilon { }_1\), there exists a RBFNN \(\theta _1^T \xi { }_1\) such that

$$\begin{aligned} f_1 =\theta _1^T \xi { }_1+\varepsilon _1, \end{aligned}$$
(13)

where \(\varepsilon { }_1\) is the approximation error and satisfies

$$\begin{aligned} \left| {\varepsilon { }_1} \right| \le \varepsilon { }_{M}. \end{aligned}$$

Substituting Eq. (13) into Eq. (12), it is obtained

$$\begin{aligned} \dot{S}_1 \!=\!\frac{1}{\tau _1 }\left[ {\sigma x_2 +\theta _1^T \xi { }_1\!+\!\Delta f_1 \left( {x_1 \left( {t\!-\!\tau _1 } \right) } \right) } \right] -\dot{y}_\mathrm{r}. \end{aligned}$$
(14)

Choose a TBLF candidate as

$$\begin{aligned}&V_1 =\tau _1 S_1 \left( t \right) \tan \left( {\frac{\pi }{2\beta }S_1 \left( t \right) } \right) \nonumber \\&\quad +\sum _{i=1}^2 {\int \limits _{t-\tau _i }^t\! {S_1^2 \left( t \right) q_{i1}^2 \left( {S_1 \left( t \right) } \right) } } \mathrm{d}\tau \!\!+\!\frac{1}{2\gamma { }_1}\tilde{\theta }_1^T \tilde{\theta }_1 \!+\!\frac{1}{2\Gamma { }_1}\tilde{\sigma }^{2}, \nonumber \\ \end{aligned}$$
(15)

where the design parameter \(\beta =a-d>0(a>d)\) denotes the constraint on \(S_{1}(t)\). That is, \(S_{1}(t)\in (- \beta ,\, \beta )\).

Then, the time derivative of \(V_{1}\) is calculated by

$$\begin{aligned}&\dot{V}_1 =\tau _1 \dot{S}_1 \left( t \right) \left[ {\begin{array}{l} \tan \left( {\frac{\pi }{2\beta }S_1 \left( t \right) } \right) +\frac{\pi }{2\beta }S_1 \left( t \right) \\ \sec ^{2}(\frac{\pi }{2\beta }S_1 \left( t \right) ) \nonumber \\ \end{array}} \right] \\&+\sum _{i=1}^2 {S_1^2 \left( t \right) q_{i1}^2 \left( {S_1 \left( t \right) } \right) } +\frac{1}{\gamma { }_1}\tilde{\theta }_1^T \dot{\mathop {\theta }\limits ^{\frown }}_1 +\frac{1}{\Gamma { }_1}\tilde{\sigma }\dot{\mathop {\sigma }\limits ^{\frown }} \nonumber \\&-\sum _{i=1}^2 {S_1^2 \left( {t-\tau _i } \right) q_{i1}^2 \left( {S_1 \left( {t-\tau _i } \right) } \right) } \nonumber \\&=\left[ {\sigma \left( {S_2 +y_2 +\alpha _2 } \right) +\theta _1^T \xi { }_1-\tau _1 \dot{y}_r } \right] M \nonumber \\&+\Delta f_1 \left( {x_1 \left( {t-\tau _1 } \right) } \right) M+\sum _{i=1}^2 {S_1^2 \left( t \right) q_{i1}^2 \left( {S_1 \left( t \right) } \right) } \nonumber \\&-\!\sum _{i=1}^2 {S_1^2 \left( {t\!-\!\tau _i } \right) q_{i1}^2 \left( {S_1 t\!-\!\tau _i } \right) } +\frac{1}{\gamma { }_1}\tilde{\theta }_1^T \dot{\mathop {\theta }\limits ^{\frown }}_1 +\frac{1}{\Gamma { }_1}\tilde{\sigma }\dot{\mathop {\sigma }\limits ^{\frown }}, \nonumber \\ \end{aligned}$$
(16)

where \(\hbox {tan}(\cdot )\) and \(\hbox {sec}(\cdot )\) stand for tangent function and secant function, respectively. \(M=\tan (\frac{\pi }{2\beta }S_1 (t))+\frac{\pi }{2\beta }S_1 (t)\sec ^{2}(\frac{\pi }{2\beta }S_1 (t))\) .

According to the Assumption1 and Young’s inequality, there exist

$$\begin{aligned} \left\{ {\begin{array}{lll} &{}&{}\Delta f_1 \left( {x_1 \left( {t-\tau _1 } \right) } \right) M\le \frac{1}{4}M^{2}+S_1^2 \left( {t-\tau _1 } \right) \\ &{}&{}\qquad q_{11}^2 \left( {S_1 \left( {t-\tau _1 } \right) } \right) \\ &{}&{}My_2 \le \frac{1}{2}M^{2}+\frac{1}{2}y_2^2 \\ \end{array}} \right. . \end{aligned}$$
(17)

Therefore,

$$\begin{aligned} \begin{array}{l} \dot{V}_1 \le \left[ {\sigma S_2 +\sigma \alpha _2 +\frac{1}{2}\sigma M+\frac{1}{4}M+\theta _1^T \xi { }_1-\tau _1 \dot{y}_\mathrm{r} } \right] \\ \quad M+\frac{1}{2}\sigma y_2^2 +D_1 +\sum \limits _{i=1}^2 {S_1^2 (t)q_{i1}^2 (S_1 (t))} \\ \quad +\frac{1}{\gamma { }_1}\tilde{\theta }_1^T \dot{\mathop {\theta }\limits ^{\frown }}_1 +\frac{1}{\Gamma { }_1}\tilde{\sigma }\dot{\mathop {\sigma }\limits ^{\frown }}, \\ \end{array} \end{aligned}$$
(18)

where \(D_1 =S_1^2 \left( {t-\tau _1 } \right) q_{11}^2 \left( {S_1 \left( {t-\tau _1 } \right) } \right) -\sum _{i=1}^2 {S_1^2 \left( {t-\tau _i } \right) q_{i1}^2 \left( {S_1 \left( {t-\tau _i } \right) } \right) } \).

The virtual control and adaptive laws are designed as below:

$$\begin{aligned} \alpha _2&= \frac{\mathop {\sigma }\limits ^{\frown }}{{\mathop {\sigma }\limits ^{\frown }}^{2}+\eta _1 }\left( \begin{array}{l} \left( -k_1 -\frac{1}{4}-\frac{1}{2}{\mathop {\sigma }\limits ^{\frown }} \right) M-{\mathop {\theta }\limits ^{\frown }} _1^T \xi { }_1+ \\ \tau _1 \dot{y}_\mathrm{r} -\frac{2\beta }{\pi }\sum \limits _{i=1}^2 {S_1 \left( t \right) q_{i1}^2 \left( {S_1 (t)} \right) } \\ \end{array} \right) \end{aligned}$$
(19)
$$\begin{aligned} \dot{\mathop {\theta }\limits ^{\frown }}_1&= \gamma { }_1\left( \xi { }_1M-m{ }_1{\mathop {\theta }\limits ^{\frown }} _1 \right) \end{aligned}$$
(20)
$$\begin{aligned} \dot{\mathop {\sigma }\limits ^{\frown }}&= \Gamma _1 \left( M\alpha _2 -c_1 \mathop {\sigma }\limits ^{\frown } \right) , \end{aligned}$$
(21)

where \(k_{1},\, m_{1},\,\gamma _{1},c_{1}\), and \(\hbox {a}_{1}\) are the design constants, and \(\eta _{1}\) is a small positive constant.

Remark 1

The estimation errors are given as \(\tilde{\theta }_1 =\mathop {\theta }\limits ^{\frown } _1 -\theta _1\) and \(\tilde{\sigma }=\mathop {\sigma }\limits ^{\frown } -\sigma \), and \(\hat{{\theta }}_1 ,\,\mathop {\sigma }\limits ^{\frown }\) are the estimation of vector \(\theta _{1},\, \mathop {\sigma }\limits ^{\frown }\), respectively.

From the Eq. (19–21), it obtains that

$$\begin{aligned}&\dot{V}_1 \le \left\{ {\begin{array}{l} \sigma S_2 \!-\!\tilde{\sigma }\alpha _2 -\frac{\eta _1 }{{\mathop {\sigma }\limits ^{\frown }} ^{2}+\eta _1 }\left[ {\begin{array}{l} \left( -k_1 \!-\!\frac{1}{4}-\frac{1}{2}\mathop {\sigma }\limits ^{\frown } \right) M-{\mathop {\theta }\limits ^{\frown }}_1^T \xi { }_1 \\ +\tau _1 \dot{y}_\mathrm{r}\! -\!\frac{2\beta }{\pi }\displaystyle \sum _{i=1}^2 {S_1 (t)q_{i1}^2 (S_1 (t))} \\ \end{array}} \right] \nonumber \\ -\left( {k_1 M+\frac{2\beta }{\pi }\displaystyle \sum _{i=1}^2 {S_1 (t)q_{i1}^2 (} S_1 (t))+\frac{1}{2}\tilde{\sigma }M+\tilde{\theta }_1^T \xi { }_1} \right) \\ \end{array}} \right\} \nonumber \\&M+\frac{1}{2}\sigma y_2^2 +D_1 +\sum _{i=1}^2 {S_1^2 (t)q_{i1}^2 (S_1 (t))} +\tilde{\theta }_1^T \xi { }_1M+\tilde{\sigma }M\alpha _2 \nonumber \\&-m{ }_1\tilde{\theta }_1^T{ \mathop {\theta }\limits ^{\frown }} _1 -c_1 \tilde{\sigma }\mathop {\sigma }\limits ^{\frown } \nonumber \\&\le \sigma MS_2 -k_1 M^{2}-\frac{1}{2}\tilde{\sigma }M^{2}+\frac{1}{2}\sigma y_2^2 +D_1 -c_1 \tilde{\sigma }\mathop {\sigma }\limits ^{\frown } \nonumber \\&+\sum _{i=1}^2 {\left[ {S_1^2 (t)-\frac{2\beta }{\pi }S_1 (t)M} \right] q_{i1}^2 (S_1 (t))} -m{ }_1\tilde{\theta }_1^T {\mathop {\theta }\limits ^{\frown }} _1 \nonumber \\&\le \sigma MS_2 -k_1 M^{2}-\frac{1}{2}\tilde{\sigma }M^{2}+\frac{1}{2}\sigma y_2^2 \nonumber \\&+D_1 -\frac{1}{2}m{ }_1\tilde{\theta }_1^2 -\frac{1}{2}c_1 \tilde{\sigma }^{2}+\frac{1}{2}m{ }_1\theta _1^2 +\frac{1}{2}c_1 \sigma ^{2}. \nonumber \\ \end{aligned}$$
(22)

Remark 2

\(-m{ }_1\tilde{\theta }_1 \mathop {\theta }\limits ^{\frown } _1 \le -\frac{1}{2}m{ }_1\tilde{\theta }_1^2 +\frac{1}{2}m{ }_1\theta _1^2 ,\, -c_1 \tilde{\sigma }\mathop {\sigma }\limits ^{\frown } \le -\frac{1}{2}c_1 \tilde{\sigma }^{2}+\frac{1}{2}c_1 \sigma ^{2},\,S_1^2 (t)-\frac{2\beta }{\pi }S_1 (t)M\le S_1^2 (t)\left( {1-\sec ^{2}\left( {\frac{\pi }{2\beta }S_1 (t)} \right) } \right) \le 0\).

Step 2: Filter \(\alpha _{2}\) through the following first-order filter with a time constant \(\tau _{2}\):

$$\begin{aligned} \tau _2 \dot{\alpha }_{2\mathrm{f}} +\alpha _{2\mathrm{f}} =\alpha _2 ,\alpha _{2\mathrm{f}} (0)=\alpha _2 (0). \end{aligned}$$
(23)

Then, one has

$$\begin{aligned} \dot{\alpha }_{2\mathrm{f}} =-\frac{y_2 }{\tau _2 }. \end{aligned}$$
(24)

Define the filter error of the first-order subsystem: \(y_{2} =\alpha _{2\mathrm{f}}-\alpha _{2}\). Take the time derivative of \(y_{2}\), and obtain

$$\begin{aligned} \left| {\dot{y}_2 +\frac{y_2 }{\tau _2 }} \right| \le B_2 \left( {M,S_1 ,S_2 ,y_2 ,\mathop {\theta }\limits ^{\frown } ,\mathop {\sigma }\limits ^{\frown } ,q_{11} ,q_{21} ,y_\mathrm{r} ,\dot{y}_\mathrm{r} ,\ddot{y}_\mathrm{r} } \right) .\nonumber \\ \end{aligned}$$
(25)

Consequently, a calculation produces the following inequality:

$$\begin{aligned} y_2 \dot{y}_2 \le -\frac{y_2^2 }{\tau _2 }+y_2^2 +\frac{1}{4}B_2^2, \end{aligned}$$
(26)

where \(B_{2}\) is the continuous function.

Then, the derivative of \(S_{2}\) is presented as below:

$$\begin{aligned} \dot{S}_2 =\frac{1}{\tau _2 }\left[ {f_2 +u_\mathrm{q} +\Delta f_2 \left( {\bar{{x}}_2 \left( {t-\tau _2 } \right) } \right) } \right] -\dot{\alpha }_{2\mathrm{f}}, \end{aligned}$$
(27)

where \(f_2 =-x_2 -x_1 -x_1 x_3\).

To facilitate its application in engineering, the RBFNN is used to approximate the nonlinear function \(f_{2}\) again. So there exists a RBFNN system such that

$$\begin{aligned} f_2 =\theta _2^T \xi { }_2+\varepsilon _2, \end{aligned}$$
(28)

where \(\varepsilon { }_2\) is the approximation error and satisfies \(\left| {\varepsilon { }_2} \right| \le \varepsilon { }_\mathrm{M}\).

Substituting Eq. (28) into Eq. (27), it yields

$$\begin{aligned} \dot{S}_2 =\frac{1}{\tau _2 }\left[ {\theta _2^T \xi { }_2+u_\mathrm{q} +\Delta f_2 (\bar{{x}}_2 (t-\tau _2 ))} \right] -\dot{\alpha }_{2\mathrm{f}}. \end{aligned}$$
(29)

Choose the Lyapunov function candidate as below:

$$\begin{aligned} \begin{array}{l} V_2 =V_1 +\frac{1}{2}\tau _2 S_2^2 +\frac{1}{2}y_2^2 +\frac{1}{2\gamma _2 }\tilde{\theta }_2^T \tilde{\theta }_2 \\ \hbox { }+\int \limits _{t-\tau _2 }^t {S_2^2 (\tau )q_{22}^2 (\bar{{S}}_2 (\tau ))} d\tau . \\ \end{array} \end{aligned}$$
(30)

The time derivative of \(V_{2}\) is given as below:

$$\begin{aligned}&\dot{V}_2 \le \dot{V}_1 +S_2 \left( {\theta _2^T \xi { }_2+u_\mathrm{q} -\tau _2 \dot{\alpha }_{2\mathrm{f}} } \right) \nonumber \\&\quad +S_2 \Delta f_2 \left( {\bar{{x}}_2 \left( {t-\tau _2 } \right) } \right) +\left( {1-\frac{1}{\tau _2 }} \right) y_2^2 +\frac{1}{4}B_2^2\nonumber \\&\quad +\frac{1}{\gamma _2 }\tilde{\theta }_2^T \dot{\mathop {\theta }\limits ^{\frown }}_2 +S_2^2 \left( t \right) q_{22}^2 \left( {\bar{{S}}_2 \left( t \right) } \right) \nonumber \\&\quad -S_2^2 \left( {t-\tau _2 } \right) q_{22}^2 \left( {\bar{{S}}_2 \left( {t-\tau _2 } \right) } \right) . \end{aligned}$$
(31)

Note the following inequality:

$$\begin{aligned}&S_2 \Delta f_2 (\bar{{x}}_2 (t\!-\!\tau _2 ))\le \frac{1}{4}S_2^2 \!+\!S_1^2 (t\!-\!\tau _2 )q_{21}^2 (S_1 (t-\tau _2 )) \nonumber \\&\quad \hbox { }+S_2^2 (t-\tau _2 )q_{22}^2 (\bar{{S}}_2 (t-\tau _2 )). \end{aligned}$$
(32)

Substituting Eq. (32) into Eq. (31), the equation can be rewritten as

$$\begin{aligned}&\dot{V}_2 \le -k_1 M^{2}-\frac{1}{2}\tilde{\sigma }M^{2}+\frac{1}{2}\sigma y_2^2 +D_1 -\frac{1}{2}m{ }_1\tilde{\theta }_1^2 \nonumber \\&-\frac{1}{2}c_1 \tilde{\sigma }^{2}+\frac{1}{2}m{ }_1\theta _1^2 +\frac{1}{2}c_1 \sigma ^{2}+S_2 \left[ {\theta _2^T \xi { }_2+} \right. \nonumber \\&\sigma M\left. {+u_\mathrm{q} -\tau _2 \dot{\alpha }_{2\mathrm{f}} +\frac{1}{4}S_2 +S_2 (t)q_{22}^2 (\bar{{S}}_2 (t))} \right] \nonumber \\&+D_2 +\left( {1-\frac{1}{\tau _2 }} \right) y_2^2 +\frac{1}{4}B_2^2 +\frac{1}{\gamma _2 }\tilde{\theta }_2^T \dot{\mathop {\theta }\limits ^{\frown }}_2, \end{aligned}$$
(33)

where \(D_2 =S_1^2 (t-\tau _2 )q_{21}^2 (S_1 (t-\tau _2 ))\).

In the same way, the control law and adaptive law are given as the following forms:

$$\begin{aligned} u_\mathrm{q}&= -\, k_2 S_2 -\sigma M-{\mathop {\theta }\limits ^{\frown }} _2^T \xi { }_2+\tau _2 \dot{\alpha }_{2\mathrm{f}} -\frac{1}{4}S_2\nonumber \\&\quad -S_2 (t)q_{22}^2 (\bar{{S}}_2 (t))\end{aligned}$$
(34)
$$\begin{aligned} \dot{\mathop {\theta }\limits ^{\frown }}_2&= \gamma { }_2\left( {\xi { }_2S{ }_2-m{ }_2{\mathop {\theta }\limits ^{\frown }} _2 } \right) , \end{aligned}$$
(35)

where \(k_{2},m_{2}\) and \(\gamma _{2}\) are the design constant.

With Eq. (34) and Eq. (35), Eq. (33) is written as follows:

$$\begin{aligned}&\dot{V}_2 \le -\left( {k_1 +\frac{1}{2}\tilde{\sigma }} \right) M^{2}+\left( {1+\frac{1}{2}\sigma -\frac{1}{\tau _2 }} \right) \nonumber \\&\quad -S_2 \mathop {\sigma }\limits ^{\frown } My_2^2 -k_2 S_2^2 +\sum _{i=1}^2 {D_i } +\frac{1}{4}B_2^2 -\frac{1}{2}c_1 \tilde{\sigma }^{2} \nonumber \\&\quad -\frac{1}{2}\sum _{i=1}^2 {m{ }_i\tilde{\theta }_i^2 } +\frac{1}{2}c_1 \sigma ^{2}+\frac{1}{2}\sum _{i=1}^2 {m{ }_i\theta _i^2 }. \end{aligned}$$
(36)

Remark 3

The estimation error is written as \(\tilde{\theta }_2 =\mathop {\theta }\limits ^{\frown } _2 -\theta _2 \), and \(\hat{{\theta }}_2\) is the estimation of vector \(\theta _{2},\,-m{ }_2\tilde{\theta }_2 \mathop {\theta }\limits ^{\frown } _2 \le -\frac{1}{2}m{ }_2\tilde{\theta }_2^2 +\frac{1}{2}m{ }_2\theta _2^2 \).

Step 3: The time derivative of \(S_{3}\) is obtained as

$$\begin{aligned} \dot{S}_3&= \frac{1}{\tau _1 }\left[ {x_1 x_2 -x_3 +u_\mathrm{d} +\Delta f_3 (x_3 (t-\tau _3 ))} \right] \nonumber \\&= \frac{1}{\tau _1 }\left[ {f_3 +u_\mathrm{d} +\Delta f_3 (x_3 (t-\tau _3 ))} \right] , \end{aligned}$$
(37)

where \(f_3 =x_1 x_2 -x_3 \).

Similarly, for simplicity, there exists a RBFNN system such that

$$\begin{aligned} f_3 =\theta _3^T \xi { }_3+\varepsilon _3, \end{aligned}$$
(38)

where \(\varepsilon { }_3\) is the approximation error and satisfies

$$\begin{aligned} \left| {\varepsilon { }_3} \right| \le \varepsilon { }_{M}. \end{aligned}$$

Choose the Lyapunov function candidate as

$$\begin{aligned} V_3 \!=\!V_2 \!+\!\frac{1}{2}\tau _3 S_3^2 \!+\!\frac{1}{2\gamma _3 }\tilde{\theta }_3^T \tilde{\theta }_3 \!+\!\int _{t-\tau _3 }^t {S_3^2 (\tau )q_{31}^2 (S_3 (\tau ))} d\tau .\nonumber \\ \end{aligned}$$
(39)

Then, the derivative of \(V_{3}\) is calculated as below:

$$\begin{aligned} \dot{V}_3&= \dot{V}_2 +S_3 \left( {\theta _3^T \xi { }_3+u_\mathrm{d} } \right) +S_3 \Delta f_3 \left( {x_3 (t-\tau _3 )} \right) +\frac{1}{\gamma _3 }\tilde{\theta }_3^T \nonumber \\&\dot{\mathop {\theta }\limits ^{\frown }}_3 +S_3^2 (t)q_{31}^2 \left( {S_3 (t)} \right) +S_3^2 (t-\tau _3 )q_{31}^2 \left( {S_3 (t-\tau _3 )} \right) .\nonumber \\ \end{aligned}$$
(40)

According to Eq. (6), the following inequality yields:

$$\begin{aligned} S_3 \Delta f_3 (x_3 (t\!-\!\tau _3 ))\!\le \! \frac{1}{4}S_3^2 \!+\!S_3^2 (t\!-\!\tau _3 )q_{31}^2 (S_3 (t\!-\!\tau _3 )).\nonumber \\ \end{aligned}$$
(41)

Substituting Eq. (41) into Eq. (40), the equation can be rewritten as

$$\begin{aligned}&\dot{V}_3 =-\left( {k_1 +\frac{1}{2}\tilde{\sigma }} \right) M^{2}+\left( {1+\frac{1}{2}\sigma -\frac{1}{\tau _2 }} \right) y_2^2 \nonumber \\&\quad -\, k_2 S_2^2 +\sum _{i=1}^2 {D_i } +\frac{1}{4}B_2^2 -\frac{1}{2}\sum _{i=1}^2 {m{ }_i\tilde{\theta }_i^2 }\nonumber \\&\quad +\, S_3 \left( {\theta _3^T \xi { }_3+u_\mathrm{d} +S{ }_3(t)q_{31}^2 (S_3 (t))+\frac{1}{4}S{ }_3} \right) \nonumber \\&\quad -\frac{1}{2}c_1 \tilde{\sigma }^{2}+\frac{1}{2}c_1 \sigma ^{2}+\frac{1}{2}\sum _{i=1}^2 {m{ }_i\theta _i^2 } +\frac{1}{\gamma _3 }\tilde{\theta }_3^T \dot{\mathop {\theta }\limits ^{\frown }}_3. \end{aligned}$$
(42)

At the current stage, the control input is chosen as

$$\begin{aligned} u_\mathrm{d} =-k_3 S_3 -{\mathop {\theta }\limits ^{\frown }}_3^T \xi { }_3-\frac{1}{4}S_3-S_3(t)q_{31}^2 (S_3 (t)), \end{aligned}$$
(43)

where \(k_{3}\) is the positive constant.

In addition, the update law is chosen as follows:

$$\begin{aligned} \dot{\mathop {\theta }\limits ^{\frown }}_3 =\gamma { }_3\left( {\xi { }_3S{ }_3-m{ }_3\mathop {\theta }\limits ^{\frown }} \right) , \end{aligned}$$
(44)

where \(m_{3}\) and \(\gamma _{3}\) are the design constant.

Substituting Eq. (43–44) into Eq. (42), the time derivative of \(V_{3}\) is rewritten as follows:

$$\begin{aligned} \dot{V}_3&= -\left( {k_1 +\frac{1}{2}\tilde{\sigma }} \right) M^{2}+\left( {1+\frac{1}{2}\sigma -\frac{1}{\tau _2 }} \right) y_2^2 \nonumber \\&\quad -\, k_2 S_2^2 -k_3 S_3^2 +\sum _{i=1}^2 {D_i } -\frac{1}{2}\sum _{i=1}^3 {m{ }_i\tilde{\theta }_i^2 } \nonumber \\&\quad +\, \frac{1}{4}B_2^2 \!-\!\frac{1}{2}c_1 \tilde{\sigma }^{2}\!+\!\frac{1}{2}c_1 \sigma ^{2}+\frac{1}{2}\sum _{i=1}^3 {m{ }_i\theta _i^2 }. \end{aligned}$$
(45)

Remark 4

The estimation error is expressed as \(\tilde{\theta }_3 ={\mathop {\theta }\limits ^{\frown }}_3 -\theta _3 \), and \(\hat{{\theta }}_3\) is the estimation of vector \(\theta _{3},\, -m{ }_3\tilde{\theta }_3 {\mathop {\theta }\limits ^{\frown }} _3 \le -\frac{1}{2}m{ }_3\tilde{\theta }_3^2 +\frac{1}{2}m{ }_3\theta _3^2 \).

Up to now, the whole design process of the controller of BLDCM is completed. The schematic plan of proposed control method is depicted in Fig. 6.

Fig. 6
figure 6

Control schematic of BLDCM

Full size image

4 Stability analysis

For any given \(p>\)0, the closed sets can be defined as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \Pi _1 =\left\{ {\begin{array}{l} (M,S_1 ,\mathop {\theta }\limits ^{\frown } _1 ,\mathop {\sigma }\limits ^{\frown } ,q_{11} ,q_{12} ):M^{2}+\frac{1}{\gamma { }_1}\tilde{\theta }_1^2 +\frac{1}{\Gamma { }_1}\tilde{\sigma }^{2} \\ +2\sum \limits _{i=1}^2 {\int \limits _{t-\tau _i }^t {S_1^2 (\tau )q_{i1}^2 (S_1 (\tau ))} } d\tau \le 2p \\ \end{array}} \right\} \\ \Pi _2 =\left\{ {\begin{array}{l} (M,S_1 ,S_2 ,{\mathop {\theta }\limits ^{\frown }} _1 ,{\mathop {\theta }\limits ^{\frown }} _2 ,\mathop {\sigma }\limits ^{\frown } ,y_2 ,q_{11} ,q_{12} ,q_{22} ):M^{2}+S_2^2 +y_2^2 \\ +\sum \limits _{i=1}^2 {\frac{1}{\gamma { }_i}\tilde{\theta }_i^2 } +\frac{1}{\Gamma { }_1}\tilde{\sigma }^{2}+2\int \limits _{t-\tau _2 }^t {S_2^2 (\tau )q_{22}^2 (\bar{{S}}_2 (\tau ))} d\tau \le 2p \\ \end{array}} \right\} \\ \Pi _3 =\left\{ {\begin{array}{l} (M,S_1 ,S_2 ,S_3 ,{\mathop {\theta }\limits ^{\frown }} _1 ,\cdots ,{\mathop {\theta }\limits ^{\frown }} _3 ,{\mathop {\sigma }\limits ^{\frown }} ,y_2 ,q_{11} ,q_{12} ,q_{22} ,q_{31} ):M^{2} \\ +\sum \limits _{i=2}^3 {S_i^2 } +y_2^2 +\sum \limits _{i=1}^3 {\frac{1}{\gamma { }_i}\tilde{\theta }_i^2 } +\frac{1}{\Gamma { }_1}\tilde{\sigma }^{2}+2\int \limits _{t-\tau _3 }^t {S_3^2 (\tau )q_{31}^2 (S_3 (\tau ))} d\tau \le 2p \\ \end{array}} \right\} \\ \end{array}} \right. . \end{aligned}$$
(46)

Theorem 2

Suppose that the dynamic surface controllers Eq. (34) and (43) with adaptive laws Eq. (20),(21) (35), and (44) are applied to the BLDCM system with the uncertain time delays described by Eq. (4), by selecting the proper parameters like \(k_{i},\, \gamma _{i},\, m_{i},\, \Gamma _{1}, \eta _{1},\, \tau _{2}\), and \(\hbox {c}_{1}\), then the \(S_{1}\hbox {(t)}\) is asymptotically tracking stability in the sense of uniformly ultimate boundedness when the initial conditions satisfy the \(\Pi _i\) and \(x_{1}(0)\in (-a+d+y_{\mathrm{r}} (0),\, a-d+ y_{\mathrm{r}} (0))\). Furthermore, the state \(x_{1}(t)\) can keep in the set \(\Omega := \{x_{1}\, \hbox {(t)} \in \quad R: {\vert } x_{1}\, (t){\vert } < a\}\) and error state \(S_{1}(t)\in (-\beta ,\, \beta )\) for \(\forall t > \quad 0\).

Proof

First, calculate the derivative of the Lyapunov function candidate as

$$\begin{aligned} \begin{array}{l} \dot{V}=\dot{V}_3 =-\left( {k_1 +\frac{1}{2}\tilde{\sigma }} \right) M^{2}-k_2 S_2^2 -k_3 S_3^2 \\ \hbox { }+\left( {1+\frac{1}{2}\sigma -\frac{1}{\tau _2 }} \right) y_2^2 -\frac{1}{2}\sum _{i=1}^3 {m{ }_i\tilde{\theta }_i^2 } -\frac{1}{2}c_1 \\ \hbox { }\tilde{\sigma }^{2}+\sum _{i=1}^2 {D_i } +\frac{1}{4}B_2^2 +\frac{1}{2}c_1 \sigma ^{2}+\frac{1}{2}\sum _{i=1}^3 {m{ }_i\theta _i^2 }. \\ \end{array} \end{aligned}$$
(47)

If \(V=p\), taking those pre-mentioned into account, then there exists

$$\begin{aligned} \dot{V}\le -2a_0 V+\mu , \end{aligned}$$
(48)

where \(\mu =\sum _{i=1}^2 {D_i } +\frac{1}{4}B_2^2 +\frac{1}{2}c_1 \sigma ^{2}+\frac{1}{2}\sum _{i=1}^3 {m{ }_i\theta _i^2 } \).

If \(V=p\) and \(a_0 >\mu /p\), then \(\dot{V}\le 0\). As the initial condition \(V(0)\le p\), one has \(V(t)\le \,p,\,\forall t\ge 0\).

Let Eq.(48) be compute the integral on [0 \(t\)], then

$$\begin{aligned} 0\le V(t)\le \frac{\mu }{a_0 }+(V(0)-\frac{\mu }{a_0 })e^{-2a_0 t}. \end{aligned}$$
(49)

Second, note the fact that \(S_{1}\hbox {(t)}\, \hbox {tan}((\pi /2 \beta )\times S_{1}\hbox {(t)})\rightarrow \infty \) as \(S_{1}\hbox {(t)}\rightarrow \beta \) or - \(\beta \). Since \(S_{1}\hbox {(t)}\) and \(S_{1}\hbox {(t)}\, \hbox {tan}((\pi /2 \beta )\times S_{1}\hbox {(t)})\) is uniformly ultimately bounded, there exists \(S_{1}\hbox {(t)} \ne -\beta \) and \(S_{1}\hbox {(t)} \ne \beta \). Let give initial condition \(S_{1}\hbox {(t)}\in (-\beta ,\, \beta )\), it can be concluded that \(S_{1}\hbox {(t)}\) remains in the region \((-\beta ,\, \beta )\) for \(\forall t > 0\). Furthermore, owing to the fact \(\beta = a -d\), the following relations hold:

$$\begin{aligned}&- a +d < S_{1}\hbox {(t)} < a-d \Leftrightarrow -a +d \nonumber \\&\qquad \qquad +\, y_{\mathrm{r}} < x_{1}(t) < a-d +y_{\mathrm{r}}. \end{aligned}$$
(50)

Then, with the fact \(d +y_{\mathrm{r}} \quad \ge 0\) and \(-d +y_{\mathrm{r}} \le 0\), it is obtained that \(-a < x_{1}\hbox {(t)} < a\). Up to now, the proof is completed.

5 Performance evaluation

In this section, the numerical simulations are conducted in order to validate the feasibility and effectiveness of the proposed method. Meanwhile, it is mainly utilized to verify the performance of the BLDCM with chaotic behavior and parameter variation.

Taking into account uncertain time delay, the relative equations can be described by

$$\begin{aligned}&\Delta f_1 (x_1 (t-\tau _1 ))=\sin (x_1 (t-\tau _1 )),\nonumber \\&\Delta f_2 (\bar{{x}}_2 (t-\tau _2 ))=x_1 (t-\tau _2 )x_2 (t-\tau _2 ),\nonumber \\&\Delta f_3 (x(t-\tau _3 ))=\sin (x_3 (t-\tau _3 )). \end{aligned}$$
(51)

The part of system parameters are given as \(q_{11} = 1,q_{21} =1-\sqrt{2-S_1^2},\, q_{22} = {\vert }S_{2}{\vert }, q_{31} = 0,\, \tau _{1}= 0.4,\, \tau _{2} = 0.5,\, \tau _{3}= 0.6\), and the rest are the same as ones mentioned before.

Suppose that the state is required to constraint \({\vert }\hbox {x}_{1}(t){\vert } <1.2\), and the reference signal is \(-1.0\le y_{\mathrm{r}}=0.7^{*}\hbox {sin}(4t) +0.2^{*}\hbox {cos}(2t+0.3)\le 1.0\); meanwhile, the corresponding design parameter is chosen as \(\beta ={\vert }x_{1}{\vert }-{\vert }y_{\mathrm{r}}{\vert }=0.2\). The simulations are done with initial conditions \(x_{1}(0) =0\in (-0.2,0.2),\, x_{2}(0)=0.45,\, x_{3}(0)=0.4\). The design parameters of controller are chosen as \(k_{1}\!=\!k_{2} \!=\!1,\, k_{3} \!=\! 3,\,\gamma _{1} \!=\!\gamma _{2} \!=\! \gamma _{3} \!=\! 12,\, m_{1}\!=\!m_{2}\!=\!m_{3} \!=\! 0.5,\, c_{1} \!=\! 0.8,\,r_{1} = 0.2,\, \sigma (0) = 35,\, \eta _{1}= 0.001,\, \tau _{2}= 0.01\). In addition, the center of neural network \(\mu _{i}\) is uniformly distributed in the field of [\(-\)5,5], and its width \(\sigma _{i}\) is equal to 2.

5.1 Trajectory tracking analysis

Figure 7 shows that the steady-state error of velocity is equal to \(\pm 0.01\, \hbox {Rad/s}\) with little time. On the other hand, it can be seen clearly that the system tracks the desired trajectory perfectly within 0.1s. The state \({\vert }x_{1}(t){\vert }<1.2\) is ensured by the fact that tracking error \(\hbox {S}_{1}(t)\in (-0. 2, 0. 2)\) when the TBLF is used.

Fig. 7
figure 7

The trajectory tracking with parameter \(\eta =1.6\). a The rotor velocity tracking, b the rotor velocity tracking error

Full size image

5.2 Robustness analysis

Figure 8 shows the results of the BLDCM control performance when disturbance of the system parameters \(\sigma \) and \(\rho \) occurs, i.e., \(\sigma =16,\, \rho =1.516,\, \sigma =17,\, \rho = 1.416,\, \sigma =18,\, \rho =1.316\). When the system parameters add or reduce the value a bit, the three kinds of indicator curves of BLDCM can basically coincide. That is, the proposed controller owns good robustness for disturbance in whole process.

Fig. 8
figure 8

The robustness analysis with parameter variation. a The rotor velocity tracking error, b d axis voltage

Full size image

5.3 Chaos suppression analysis

Comparing with the result mentioned above, it can be seen clearly that BLDCM system successfully escapes from the chaotic behavior which can cause some irreparable losses on the local power system in the Fig. 9.

Fig. 9
figure 9

Phase portrait with different \(\eta \)

Full size image

6 Conclusion

An adaptive RBFNN-based DSC strategy is presented for the chaotic BLDCM with uncertain time delays in detail. The controller based on the adaptive DSC, TBLF, and RBFNN is applied to prevent the motor drive system from chaos when systemic parameters are falling into a special area. Both the unknown BLDCM parameters and uncertain time delays are considered. At the same time, the state constraint is satisfied using TBLF. In addition, the stability analysis is derived to verify the system reliability by the Lyapunov theory. Finally, the simulation results are demonstrated to show the effectiveness and robustness of the proposed approach by choosing appropriate design parameters.