1 Introduction

Chaos, hyperchaos, multistability, extreme multistability, antimonotonicity and so on (Pisarchik 2001) have been reported in many fields of engineering including electronic circuits (Linsay 1981), mechanical systems (Thompson and Stewart 2002), biological systems (Hans et al. 2013), electrical machine systems (Cabrera et al. 2015; Bruno et al. 2006; Chau and Wang 2011a; Chen et al. 2001) and so on. Hemati (1994) reported for the first time the chaotic behavior in BLDCM. BLDCM is the good candidate for manufacturing applications due to their high power density, good speed–torque characteristics, high efficiency, wide speed ranges and low maintenance. BLDCMs have been used in industrial engineering such as linear motors, servomotors, actuators for industrial robots, extruder drive motors and feed drives for DC machine tools (Xia 2012). Computer peripherals (disk drives, printers), handheld power tools (Melkote and Khorrami 1999; Prasetyo et al. 2016) and vehicles ranging from model aircraft to automobiles (Santiago et al. 2012; Hwang et al. 2012; Praveen et al. 2012) are places where you can find BLDCMs.

Unfortunately, chaotic behavior and coexisting attractors in BLDCM are source of instability, unpredictable disturbance (Chau and Wang 2011; Wang et al. 2016). It is therefore important to control chaos behavior and coexisting attractors in this system. Some recent works were focused on controlling chaos used many schemes to achieve the objectives. The global exponential stabilization for the chaotic BLDCM is illustrated in Wan et al. (2014). The sliding mode control scheme of single time-scale BLDCM was investigated in Uyaroğlu and Cevher (2013). Ping et al. 2015 used the stabilization of the fractional-order chaotic BLDCM system via single input; based on the generalized Gronwall inequality, the Mittag–Leffler function was studied. Other studies of anti-control of chaos in BLDCM are investigated (Ge et al. 2004, 2006a, 2006c). As a result, these control strategies require heavy computational effort and are difficult to implement in real engineering applications.

As far as the authors knowledge, no study on the control of coexisting attractors in BLDCM has been carried out in the literature. So, the objective of this work is twofold: (1) to use a weak harmonic modulation of a parameter of the BLDCM in order to destroy the coexistence between period-1-oscillations and chaotic oscillations and transform BLDCM to period-1-oscillations. (2) To develop two single controllers based on the principle of Lyapunov’s method for asymptotic global stability to control chaos in BLDCM. The single control method is simple, concise and easy to implement. Therefore, the control of coexisting and chaotic attractors in BLDCM is analytically, numerically and electronically analyzed in this paper. The structure of this paper is organized as follows: The control of coexisting attractor in BLDCM using a weak harmonic modulation of a parameter of the BLDCM is performed in Sect. 2. It is followed by the chaos control in BLDCM using single controller in Sect. 3. In Sect. 4, the electronic circuits are implemented to check the existence of chaotic and coexisting attractors found in BLDCM and the effectiveness of the two proposed single controllers. The sensitivity of each control strategy to parametric errors is investigated in Sect. 5. Some concluding remarks are given in Sect. 6.

2 Control of Coexisting Attractors in Brushless Direct Current Motor

The dimensionless form of the mathematical model of the BLDCM without loading conditions is given by Hemati (1994), Ge and Chang (2004), and Ge et al. (2006a, 2006b) as:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = - x - yz + \rho z, $$
(1a)
$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y + xz, $$
(1b)
$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = \sigma \left( {x - z} \right) + \eta xy, $$
(1c)

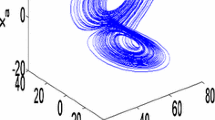
where \(x\,,\,\,y,\,z\,\) denote quadrature–direct-axis current of the motor and angle speed, respectively. The parameters \(\,\rho ,\,\delta ,\sigma \,\) and \(\,\eta \,\) are the parameters of BLDCM. For specific value of the parameters \(\,\sigma ,\,\,\eta\) and \(\,\rho\), system (1) can exhibit chaotic and coexisting attractors as shown in Fig. 1.

Fig. 1
figure 1

Phase portraits of chaotic and coexisting attractors for specific value of the parameter \(\,\delta\): a\(\,\delta = 0.4\,\) and b \(\,\delta = 0.016\). In panels a and b1, the initial conditions are (x(0), y(0), z(0)) = (0.01, 0.01, 0.01), while in panel b2, the initial conditions are (x(0), y(0), z(0)) = (1.25, 58.79, 0.0). The other parameter values are \(\,\eta = 0.26,\,\) \(\sigma = 4.55\,\) and \(\rho = 60\)

Full size image

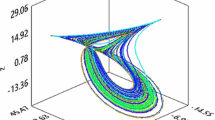
System (1) displays double-scroll chaotic attractor in Fig. 1a, while in Fig. 1b, system (1) exhibits double-scroll chaotic attractor or periodic attractor as a function of the initial conditions. The basin of attraction of system (1) in the plane \(\,z = 0\,\) for \(\,\delta = 0.016\) is presented in Fig. 2.

Fig. 2
figure 2

(Color online) Cross section of the basin of attraction of system (1) in the \(\,\left( {x,\,y} \right)\,\) plane at \(\,z = 0\,\) for \(\,\delta = 0.016\), \(\,\eta = 0.26,\,\) \(\sigma = 4.55\,\) and \(\rho = 60\)

Full size image

In Fig. 2, the initial conditions in the cyan regions lead to the periodic attractor and those in the red region lead to the chaotic attractor. The control of this phenomenon is discussed by using a weak harmonic modulation control scheme (Pisarchik and Feudel 2014; Ainamon et al. 2019) because of the inconveniences of multistability behavior in many nonlinear systems as well as in BLDCM (Pisarchik 2001; Hemati 1993). Therefore, a weak harmonic modulation is used to replace the parameter \(\,\delta \,\) of system (1) as \(\,\delta = \delta_{0} + \delta_{c} \sin \left( {2\pi f_{c} t} \right)\,\) where \(\,\delta_{0}\) is the initial value of the parameter in the uncontrolled system, \(\delta_{c}\) and \(\,f_{c} \,\)(\(f_{c} \ll f_{0} = {{\sqrt {\delta_{0} } } \mathord{\left/ {\vphantom {{\sqrt {\delta_{0} } } {2\pi }}} \right. \kern-\nulldelimiterspace} {2\pi }}\)) are the amplitude and frequency of the control modulation, respectively. The bifurcation diagram depicting the local extrema of variable \(\,y\left( t \right)\,\) versus the control amplitude parameter \(\,\delta_{c} \,\) is plotted in Fig. 3 in order to check the control of coexisting attractors.

Fig. 3
figure 3

(Color online) Bifurcation diagram depicting the local extrema of \(\,y\left( t \right)\,\) with respect to the control amplitude parameter \(\,\delta_{c} \,\) for \(\,\delta_{0} = 0.016\), \(\,f_{c} = 10^{ - 8}\), \(\,\eta = 0.26,\,\) \(\sigma = 4.55\,\) and \(\rho = 60\). The upward (downward) bifurcations are indicated by black (red) dots for local maxima and gray (blue) dot for local minima, respectively

Full size image

The coexistence between chaotic and periodic attractors is shown in Fig. 3 for \(\,\delta_{c} \le 7.02\). While for \(\,\delta_{c} > 7.02\), this coexistence between chaotic and periodic attractors is converted to periodic attractors. Therefore, the weak harmonic modulation transforms the multistable attractors to monostable one in system (1). The coexisting attractors in system (1) can be clearly see by plotting the phase portraits as shown in Fig. 4 for specific value of control amplitude parameter \(\,\delta_{c}\).

Fig. 4
figure 4

Phase portraits of system (1) for specific value of control amplitude parameter \(\,\delta_{c}\): a \(\,\delta_{c} = 5\,\) and b \(\,\delta_{c} = 14\). The curves in black are obtained using the initial conditions: (x(0), y(0), z(0)) = (0.01, 0.01, 0.01), while the curves in gray are obtained using the initial conditions: (x(0), y(0), z(0)) = (1.25, 58.79, 0.0). The others parameter values are \(\,\delta_{0} = 0.016\), \(\,f_{c} = 10^{ - 8}\), \(\,\eta = 0.26,\,\) \(\sigma = 4.55\,\) and \(\rho = 60\)

Full size image

System (1) displays the coexistence between chaotic oscillations and period-1-oscillations for \(\,\delta_{c} = 5\) in Fig. 4a. While in Fig. 4b1, b2 where \(\,\delta_{c} = 14\), the system (1) is actually monostable and the coexisting attractors are converted to period-1-oscillations because of a weak harmonic modulation to parameter \(\,\delta\).

3 Chaos Control of Brushless Direct Current Motor Using Single Controller

A single controller is used in this section to control the chaotic behavior found in BLDCM. Therefore, two simple and single controllers are mathematically designed by using the principle of Lyapunov’s method for asymptotic global stability.

3.1 Proposed controller 1

In this subsection, the controller \(\,u_{1} \,\) is added to the first equation of system (1):

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = - x - yz + \rho z + u_{1} , $$
(2a)
$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y + xz, $$
(2b)
$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = \sigma \left( {x - z} \right) + \eta xy, $$
(2c)

where \(\,u_{1} = z\left( {y - \rho } \right)\). By substituting the expression of the controller \(\,u_{1} \,\) into the controlled system (2), it becomes:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = - x, $$
(3a)
$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y + xz, $$
(3b)
$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = \sigma \left( {x - z} \right) + \eta xy. $$
(3c)

The solution of Eq. (3a) is \(\,x\left( t \right) = x\left( 0 \right)e^{ - t}\). That is yield \(\lim_{t \to \infty } x\left( t \right) = 0\). Thus, system (3) can be reduced as follows:

$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y, $$
(4a)
$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = - \sigma z, $$
(4b)

The solution of system (4) can be rewritten as follows:

$$ \,y\left( t \right) = y\left( 0 \right)e^{ - \delta t} , $$
(5a)
$$ \,z\left( t \right) = z\left( 0 \right)e^{ - \sigma t} . $$
(5b)

That is yield \(\lim_{t \to \infty } y\left( t \right) = 0\) and \(\lim_{t \to \infty } z\left( t \right) = 0\). Thereafter, the following theorem is given:

Theorem 1

The chaotic behavior found in the BLDCM can be controlled using the controller \(\,u_{1} = z\left( {y - \rho } \right)\).

Proof

The proof is obvious, so leave it out.□

The time series of the state responses and the output of the controller are shown in Fig. 5.

Fig. 5
figure 5

Time series of \(\,x,\,\,y,\,\,z\) and the output of the controller \(\,u_{1} \,\) for \(\,\sigma = 4.55,\,\) \(\rho = 60,\,\) \(\delta = 0.4\,\) and \(\,\eta = 0.26\). The initial conditions are (x(0), y(0), z(0)) = (0.01, 0.01, 0.01)

Full size image

In Fig. 5, the controller \(\,u_{1} \,\) is activated at \(\,t \ge 1400\). It is noted that theorem 1 is effective.

3.2 Proposed controller 2

In this subsection, the controller \(\,u_{2} \,\) is added to the third equation of system (1):

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = - x - yz + \rho z, $$
(6a)
$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y + xz, $$
(6b)
$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = \sigma \left( {x - z} \right) + \eta xy + u_{2} , $$
(6c)

where \(\,u_{2} = - x\left( {\eta y + \sigma } \right)\). By substituting the expression of the controller \(\,u_{2} \,\) into the controlled system (6), it becomes:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = - x - yz + \rho z, $$
(7a)
$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y + xz, $$
(7b)
$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = - \sigma z. $$
(7c)

The solution of Eq. (7c) is \(\,z\left( t \right) = z\left( 0 \right)e^{ - \sigma t}\). That is yield \(\lim_{t \to \infty } z\left( t \right) = 0\). Thus, system (7) can be reduced as follows:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = - x, $$
(8a)
$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - \delta y. $$
(8b)

The solution of system (8) is given by:

$$ \,x\left( t \right) = x\left( 0 \right)e^{ - t} , $$
(9a)
$$ \,y\left( t \right) = y\left( 0 \right)e^{ - \delta t} . $$
(9b)

That is yield \(\lim_{t \to \infty } x\left( t \right) = 0\) and \(\lim_{t \to \infty } y\left( t \right) = 0\). Thereafter, the following theorem is given:

Theorem 2

The chaotic behavior found in the BLDCM can be controlled using the controller \(\,u_{2} = - x\left( {\eta y + \sigma } \right)\).

Proof

The proof is obvious, so leave it out. □

The time series of the state responses and the output of the controller are shown in Fig. 6.

Fig. 6
figure 6

Time series of \(\,x,\,\,y,\,\,z\) and the output of the controller \(\,u_{2} \,\) for \(\,\sigma = 4.55,\,\) \(\rho = 60,\,\) \(\delta = 0.4\,\) and \(\,\eta = 0.26\). The initial conditions are (x(0), y(0), z(0)) = (0.01, 0.01, 0.01)

Full size image

In Fig. 6, the controller \(\,u_{2} \,\) is activated at \(\,t \ge 1400\). It is noted that theorem 2 is effective.

4 Circuit Implementation

The analogue circuitry of system (1) is shown in Fig. 7.

Fig. 7
figure 7

The electronic circuit of the BLDCM described by system (1)

Full size image

The circuit of Fig. 7 is built by using the operational amplifier working in their linear regime, the ideal multipliers, the resistors and the capacitors. Using the following values of parameters:\(C_{1} = C_{2} = C_{3} = 10\,{\text{nF}}\), \(R_{\eta } = 384.615\,{\text{k}}\Omega\) (for \(\eta = 0.26\)), \(R_{\rho } = 1.667\,{\text{k}}\Omega\) (for \(\rho = 60\)), \(R_{\sigma } = 21.978\,{\text{k}}\Omega\) (for \(\sigma = 4.55\)),\(R_{1} = R_{2} = R_{3} = R_{4} = R_{5} = R_{6} = R_{7} = 100\,{\text{k}}\Omega\), the phase portraits of chaotic and coexisting attractors found in BLDCM generated from circuit diagram of Fig. 7 are shown in Fig. 8.

Fig. 8
figure 8

(Color online) The phase portraits of the chaotic attractor a with \(\,R_{\eta } = 250\,k\Omega \,\) and coexisting attractors b with \(\,R_{\eta } = 6250\,k\Omega \,\) in planes \(\,\left( {V_{x} ,\,V_{y} } \right)\),\(\,\left( {V_{y} ,\,V_{z} } \right)\) and \(\,\left( {V_{x} ,\,V_{z} } \right)\) observed on the PSpice oscilloscope. The initial conditions are \(V_{x} (0) = V_{y} (0) = V_{z} (0) = 0.01\,V\) in panels a and b1, while in panel b2, the initial conditions are \(V_{x} (0) = 0.0125\,V\),\(V_{y} (0) = 5.879\,V\) and \(\,V_{z} (0) = 0\,V\)

Full size image

The existence of the double-scroll chaotic and coexisting attractors found in BLDCM during the numerical simulations (Fig. 1) can be clearly seen from Fig. 8. The analogue circuitries of the controlled systems (3) and (7) are shown in Fig. 9.

Fig. 9
figure 9

The electronic circuits of the controlled systems: a controlled systems (3) and b controlled systems (7)

Full size image

The circuits of Fig. 9 are built by using the operational amplifier working in their linear regime, the ideal multipliers, the resistors, the capacitors and the switches. The switch K of each schematic diagram of the controlled systems (3) and (7) is closed after 1400 ms. The time series of the state responses and the output of the single controller 1 generated from the circuit diagram of Fig. 9a are shown in Fig. 10.

Fig. 10
figure 10

(Color online) Time series of \(\,V_{x} ,\,V_{y} ,V_{z} ,V_{{u_{1} }} \,\) of chaos suppression in BLDCM observed on the PSpice oscilloscope

Full size image

In Fig. 10, the matching of PSpice results with the numerical simulation results of Fig. 5 signifies the feasibility of the proposed single controller 1. The time series of the state responses and the output of the single controller 2 generated from the circuit diagram of Fig. 9b are shown in Fig. 11.

Fig. 11
figure 11

(Color online) Time series of \(\,V_{x} ,\,V_{y} ,V_{z} ,V_{{u_{2} }} \,\) of chaos suppression in the BLDCM observed on the PSpice oscilloscope

Full size image

In Fig. 11, the matching of PSpice results with the numerical simulations results of Fig. 6 signifies the feasibility of the proposed single controller 2.

5 Control of Coexisting and Chaotic Attractors in the Presence of Parametric Errors

In this section, the sensitivity of the three proposed controllers to parametric errors is investigated because in real process the parameters used in the control may contain parametric errors (Peruzzi et al. 2016; Balthazar et al. 2012; Avanço et al. 2018). To consider the effects of parametric errors uncertainties on the performance of the three proposed controllers, the parameters used in each control will be considered to have a random error of \(\, \pm \,20\,\)% (Nozaki et al. 2013; Tusset et al. 2015). Figure 12 presents the controller of coexisting attractors without and with variation in parameters of \(\,\overline{\delta }_{c} = 14 + 7r\left( t \right)\,\) and \(\,\overline{f}_{c} = 10^{ - 8} + 5 \times 10^{ - 9} r\left( t \right)\,\) where \(\,r\left( t \right)\,\) is the normally distributed random function.

Fig. 12
figure 12

Coexisting attractors of the BLDCM converted into monostable periodic attractor considering the control without a and with b uncertainties in parameters: \(\,\delta_{c} \,\) and \(\,f_{c}\). The initial conditions are (x(0), y(0), z(0)) = (1.25, 58.79, 0.0). The other parameter values are \(\,\delta_{0} = 0.016\), \(\,\eta = 0.26,\,\) \(\sigma = 4.55\,\) and \(\rho = 60\)

Full size image

The results of Fig. 12 demonstrate that the controller of coexisting attractors is robust to parametric errors. Figure 13 depicts the two proposed chaos controllers without and with variation in parameters of \(\,\overline{\rho } = 60 + 30r\left( t \right)\), \(\,\overline{\eta } = 0.26 + 0.13r\left( t \right)\,\) and \(\,\overline{\sigma } = 4.55 + 2.275r\left( t \right)\,\) where \(\,r\left( t \right)\,\) is the normally distributed random function.

Fig. 13
figure 13

Time series of \(\,x,\,\,y,\,\,z\,\) considering the control without (black lines) and with (gray lines) uncertainties in parameters: a \(\,\rho \,\)(proposed controller 1) and b \(\,\eta ,\,\sigma \,\)(proposed controller 2). The initial conditions are (x(0), y(0), z(0)) = (0.01, 0.01, 0.01). The other parameter value is \(\,\delta = 0.4\)

Full size image

It is clear from Fig. 13 that the two proposed chaos controllers are robust to parametric errors.

6 Conclusion

The development of three controllers to suppress the coexisting attractors and chaos found in brushless direct current motor was performed in this paper. The coexisting of attractors found in brushless direct current motor was controlled to a desired trajectory by using a weak harmonic modulation. Moreover, the two proposed single controllers were designed to suppress the chaotic behavior in brushless direct current motor. In order to access the physical feasibility of the two proposed single controllers and the existence of chaotic and coexisting attractors in brushless direct current motor, electronic circuits were implemented and tested on OrCAD-PSpice software. It was revealed that OrCAD-PSpice validated the numerical simulation results. Thanks to numerical simulations, it was demonstrated that the three proposed controllers are more robust to parametric uncertainties.