1 Introduction

In this paper, we consider the following \(n\)-order nonlinear systems

(1)

where \(x=(x_1,\ldots ,x_n)^T\in R^n\) is the system state, \(u\) is the control law to be designed, \(a(t)\) is uncertain time-varying parameter, \(f(t,x_1,\ldots ,x_n)\) is unknown time-varying nonlinear perturbation, and \(d(t)\) is time-varying external disturbance. The control objective is to design a control law such that the state of system (1) can track the reference signal in a finite time.

Since many practical individual systems, especially mechanical systems, are of high-order dynamics, it is significative and necessary to study control problem for the high-order nonlinear systems. Compared to the conventionally asymptotic tracking control, the closed-loop system with finite-time convergence usually demonstrates faster convergence rates, higher accuracies, better disturbance rejection properties, and robustness against uncertainties [1–4]. Although the finite-time control has these advantages, the stability analysis and controller design for finite-time control systems are very difficult due to the non-smoothness of finite-time controller. In other words, the closed-loop system with finite-time convergence does not satisfy Lipschitz continuity. Although the design of finite-time controller for different dynamic systems is difficult and challenging, there are still some results in the literature, such as finite-time stabilization by state feedback [1, 5–11] and output feedback [12–14], etc.

However, the previous listed finite-time control results cannot solve the finite-time tracking problem for nonlinear system (1) due to the uncertain time-varying control coefficients and unknown external disturbance. This certainly limits the application of finite-time control algorithm in the control practice where exist many nonlinear systems with uncertain time-varying control coefficients and unknown nonlinear perturbations. For example, to design a finite-time control algorithm for the roll angle of BTT (bank-to-turn) missile (see Sect. 4), uncertain time-varying aerodynamic parameters will need to be addressed. It is well-known that in the literature, the terminal sliding mode method [15, 16] can be used to design finite-time controller in the presence of uncertainties and external disturbances. However, as pointed out in [17, 18], there usually is a singularity problem in the terminal sliding mode controller when the order of system is larger than three. Because of such reasons, this paper will employ the technique of adding a power integrator [19] to develop a non-singular high-order finite-time control algorithm for the high-order nonlinear system (1). The design procedure is divided into two steps. First, the technique of adding a power integrator [19] is employed to construct a finite-time tracking control algorithm. Then, based on the variable structure control method, a variable structure finite-time controller is proposed. Rigorous theoretic analysis shows that under the proposed controller the system’s state can reach the desired signal in a finite time.

2 Preliminaries and problem formulation

2.1 Problem formulation

Let \(x^d=(x_1^d,\ldots ,x_n^d)^T\) denote the desired reference state and satisfy

$$\begin{aligned} \dot{x}_1^d=x_2^d, \quad \dot{x}_2^d=x_3^d,\ldots ,\dot{x}_{n-1}^d=x_n^d,\quad \dot{x}_n^d=u^d.\qquad \end{aligned}$$
(2)

Without loss of generality, assume \(u^d(t)\) is bounded, i.e., \(| u^d(t)|\le L_1<+\infty \), where \(L_1\) is a known constant. The control objective is to design a control law such that the desired state in system (2) can be tracked by the real state of system (1) in a finite time.

In addition, we need to impose the following assumption conditions for the considered system:

Assumption 1

There are known positive constants \(\underline{a},\overline{a},L_2\), and function \(F(x_1,\ldots ,x_n)\) such that

  1. (i)

    \(\underline{a}\le a(t) \le \overline{a}\),

  2. (ii)

    \(|f(t,x_1,\ldots ,x_n)|\le F(x_1,\ldots ,x_n)\),

  3. (iii)

    \(|d(t)|\le L_2\).

Remark 1

It should be pointed out that the considered system (1) in this paper is more general than the double integrators model which is commonly studied in the literature, see for example [3, 5, 12]. First, in practice, the system parameters might not be precisely known due to the lack of detailed knowledge of system specifications. In some cases, the parameters are even varying caused by various reasons such as mechanical wears, model errors, environments changes, etc. A specific example is that the BTT missile model [20, 21] has time-varying aerodynamic parameters, which is shown in Example part. Second, there usually are unknown nonlinear perturbations and external disturbance in the control channel, e.g., the model of BTT missile. Hence, in this paper we consider the systems with unknown parameters and perturbations to encompass more practical systems included BTT missile in applications. In addition, although the problem of finite-time stabilization for double-integrators system has been solved in [3], the proposed method is not available here for system (1) due to the unknown parameters and perturbations.

2.2 Some lemmas

Lemma 1

[1] Consider system \(\dot{x}=f(x), f(0)=0, x\in R^n, \) where \(f(\cdot ):{R}^n\rightarrow {R}^n\) is a continuous vector function. Suppose there exists a continuous, positive definite function \(V(x): U\rightarrow R\) defined on an open neighborhood \(U\) of the origin such that \(\dot{V}(x)+c(V(x))^\alpha \le 0\) on \(U\setminus \{0\}\) for some \(c>0\) and \(\alpha \in (0,1)\). Then, the origin is a finite-time stable equilibrium of system \(\dot{x}=f(x)\) and the finite settling time \(T \) satisfies \(T\le \frac{V(x(0))^{1-\alpha }}{c(1-\alpha )}\).

Lemma 2

[19] If \(0<p=p_1/p_2\le 1,\) where \(p_1>0,p_2>0\) are positive odd integers, then

$$\begin{aligned} |x^p-y^p| \le 2^{1-p}|x-y|^p. \end{aligned}$$

Lemma 3

[19] For \(x\in R, y\in R,\) \(c>0,d>0\), then

$$\begin{aligned}|x|^c|y|^d\le \frac{c}{c+d}|x|^{c+d}+\frac{d}{c+d}|y|^{c+d}. \end{aligned}$$

Lemma 4

[22] For \(x_i\in R,i=1,\ldots ,n,\) and a real number \(0< p \le 1\), then

$$\begin{aligned} (|x_1|+\cdots +|x_n|)^{p} \le |x_1|^{p}+\cdots +|x_n|^{p}. \end{aligned}$$

3 Main result

In this section, it will be shown that the problem of finite-time tracking control of nonlinear system (1) is solvable. To solve this problem, a recursive design method is employed. To construct such a finite-time control law, we first define

$$\begin{aligned} r_i=1+(i-1)\tau ,i=1,\ldots ,n+1, \end{aligned}$$
(3)

with a constant \(\tau \in (-1/n,0)\). For simplicity of statement, in this paper, we assume \(\tau =-{q}/{p}\) with a positive even integer \(q\) and a positive odd integer \(p\). Based on this, \(r_i, i=1,\ldots ,n+1\), will be odd in both denominator and numerator, which will simplify the notation of the controller since \(s^{r_i}=\mathrm{sign}(s)\cdot |s|^{r_i}\) for any \(s\in R\). In the case when \(\tau \) cannot be represented as an even/odd ratio, a similar proof can be obtained for any real number \(\tau \) by defining \([s]^{r_i/{r_j}}=\mathrm{sign}(s)\cdot |s|^{r_i/{r_j}}\) as shown in [23].

Now, we present our main result.

Theorem 1

For the nonlinear system (1) under Assumption 1, if the control law \(u\) is designed as

$$\begin{aligned} u&= -\frac{\beta _n}{\underline{a}}s^{r_n+\tau }- \frac{F(x_1,\ldots ,x_n)+L_1+L_2}{\underline{a}}\mathrm{sign}(s), \nonumber \\ s&= \ \left( x_{n}-x_n^d \right) ^{\frac{1}{r_{n}}}+\beta _{n-1}^{\frac{1}{r_n}} \Big [\left( x_{n-1}-x_{n-1}^d \right) ^{\frac{1}{r_{n-1}}}+ \cdots \nonumber \\&+\, \beta _2^{\frac{1}{r_3}}\Big [\left( x_{2}-x_2^d \right) ^{\frac{1}{r_2}}+ \beta _1^{\frac{1}{r_2}}\left( x_{1}-x_{1}^d \right) \Big ]\cdots \Big ],\nonumber \\ \end{aligned}$$
(4)

where \(\beta _1,\ldots ,\beta _n\) are appropriate gains, then system’s state will track the desired state (i.e., the state of system (2)) in a finite time, i.e., \(x(t)\rightarrow x_d\) in a finite time.

Proof

Define

$$\begin{aligned} e_1=x_1-x_1^d, \quad e_2=x_2-x_2^d,\ldots , e_n=x_n-x_n^d \end{aligned}$$

as the tracking error, then it follows from system (1) and (2) that the error system’s dynamic is

$$\begin{aligned} \dot{e}_1&= e_2,\quad \dot{e}_2 =e_3, \ldots , \dot{e}_n= a(t)u+f(t,x_1,\ldots ,x_n)\nonumber \\&+\, d(t)-\dot{x}_n^d. \end{aligned}$$
(5)

The finite-time controller design is based on a recursive argument.

Step 1: Construct a Lyapunov candidate

$$\begin{aligned} V_1=\frac{1}{2}e_1^2. \end{aligned}$$
(6)

which yields

$$\begin{aligned} \dot{V}_1= e_1e_2. \end{aligned}$$
(7)

Denote \(\xi _1=e_1\) and choose the virtual controller

$$\begin{aligned} e_{2}^*=-\beta _{1} \xi _{1}^{r_2} ~~\mathrm{with ~constant}~~ \beta _{1}= {n},~~ \end{aligned}$$
(8)

which renders

$$\begin{aligned} \dot{V}_1 \le -n\xi _{1}^{2+\tau }+\xi _{1}\left( e_{2}-e_{2}^* \right) . \end{aligned}$$
(9)

Step 2: Denote \(\xi _{2}=e_{2}^{1/{r_2}}-{e_{2}^*}^{1/{r_2}}\) and construct the Lyapunov function

$$\begin{aligned} V_2=V_{1}+ \int \limits _{e_{2}^*}^{e_{2}}\left( \mu ^{1/r_2}-{e_{2}^*}^{1/r_2} \right) ^{{2-r_2}}d\mu . \end{aligned}$$
(10)

We first prove that this Lyapunov function is positive definite. By Lemma 2, we have

$$\begin{aligned} |\mu -e_2^{*}|&= |\left( \mu ^{1/{r_2}}\right) ^{{r_2}}-\left( {e_2^{*1/{r_2}}} \right) ^{r_2}|\nonumber \\&\le 2^{1-r_2}|\mu ^{1/{r_2}}-e_2^{*1/{r_2}}|^{r_2}, \end{aligned}$$
(11)

then

$$\begin{aligned} |\mu ^{1/r_2}-e_2^{*1/r_2}|\ge \left( 2^{r_2-1}|\mu -e_2^{*}|\right) ^{1/{r_2}}. \end{aligned}$$
(12)

If \( e_2\ge e_2^*\), by (12) we have

$$\begin{aligned}&\!\!\!\!\int \limits _{e_{2}^*}^{e_{2}}\left( \mu ^{1/{r_2}}-{e_{2}^*}^{1/{r_2}} \right) ^{{2-r_2}}d\mu \nonumber \\&\quad \ge \int \limits _{e_2^*}^{e_2}\left( 2^{r_2-1}(\mu -e_2^{*})\right) ^{2/{r_2}-1}d\mu \nonumber \\&\quad =\frac{\left( 2^{r_2-1} \right) ^{2/{r_2}-1}}{2/{r_2}}\left. (\mu -e_2^{*})^{2/{r_2}}\right| _{e_2^{*}}^{e_2}\nonumber \\&\quad = r_22^{2-r_2-2/{r_2}}\left( e_2-e_2^{*} \right) ^{2/{r_2}}. \end{aligned}$$
(13)

In the case of \( e_2< e_2^*\), the proof is similar and (13) is still true. Based on the definition of \(V_1\), we conclude that \(V_2\) is positive definite.

Together with (9), the derivative of \(V_2\) along system (5) is

$$\begin{aligned}&\dot{V}_2 \le -n\xi _{1}^{2+\tau }+\xi _{1}\left( e_{2}-e_{2}^* \right) +\xi _{2}^{{2\!-\!r_{2}\!}}e_{3}\nonumber \\&\quad +\, \frac{d \left[ -{e_{2}^*}^{1/r_2} \right] }{dt}\int \limits _{e_{2}^*}^{{e_{2}}} \left( \mu ^{1/r_2}-{e_{2}} ^{*1/r_2} \right) ^{{1-r_2}}d\mu . \end{aligned}$$
(14)

Using Lemma 2 and Lemma 3 results in

$$\begin{aligned}&\Big |\xi _{1}\left( e_{2}-e_{2}^* \right) \Big |\le |\xi _{1}|\cdot \left| \left( e_{2}^{1/{r_2}} \right) ^{r_2}-\left( e_{2}^{*1/{r_2}} \right) ^{r_2}\right| \nonumber \\&\quad \le 2^{1-r_2}|\xi _{1}||\xi _{2}|^{r_2} \le \frac{1}{2}\xi _{1}^{2+\tau } + c_1\xi _{2}^{2+\tau } \end{aligned}$$
(15)

where \(c_1\) is a positive constant.

Note that

$$\begin{aligned} \frac{d\left[ -{e_{2}^*}^{1/r_2} \right] }{dt}= \beta _{1}^{1/r_2}{\dot{\xi }_{1}}{}= \beta _{1}^{1/r_2}{ e_{2}}. \end{aligned}$$
(16)

Since \(|e_{2}|=\Big |\xi _{2}+{e_{2}^*}^{1/{r_2}}\Big |^{r_2}\), it follows from Lemma 4 that

$$\begin{aligned} |e_{2}|\le |\xi _{2}|^{{r_2}} +|{e_{2}^*}|^{{}{}} =|\xi _{2}|^{r_2}+\beta _{1}|{\xi _{1}}|^{r_2}. \end{aligned}$$
(17)

In addition, by Lemma 2, we have

$$\begin{aligned}&\!\!\!\!\Big |\int \limits _{e_{2}^*}^{{e_{2}}}\left( \mu ^{1/r_2}-{e_{2}} ^{*1/r_2} \right) ^{{1-r_2}}ds\Big | \le |\xi _{2}|^{1-r_2}|e_{2}-e_{2}^*|\nonumber \\&\le 2^{1-r_2}|\xi _{2}|^{1-r_2}|\xi _{2}|^{r_2} = 2^{1-r_2}|\xi _{2}|. \end{aligned}$$
(18)

Together (18) with (16), (17) and since \(r_2=1+\tau \), it follows from Lemma 3 that

$$\begin{aligned}&\!\!\!\!\Big |\frac{d\left[ -{e_{2}^*}^{1/r_2} \right] }{dt}\int \limits _{e_{2}^*}^{{e_{2}}}\left( \mu ^{1/r_2}-{e_{2}} ^{*1/r_2} \right) ^{{1-r_2}}d\mu \Big |\nonumber \\&\le c_2|\xi _{2}|^{2+\tau }+\frac{1}{2}|{\xi _{1}}|^{2+\tau } \end{aligned}$$
(19)

for a positive constant \(c_2\).

Substituting (15) and (19) into (14) gives

$$\begin{aligned} \dot{V}_2 \le&-(n-1)\xi _{1}^{2+\tau }+[c_1+c_2]\xi _{2}^{2+\tau } +\xi _{2}^{{2\!-\!r_{2}\!}}e_{3}. \end{aligned}$$
(20)

Thus, a virtual controller of the form

$$\begin{aligned} e_{3}^*=-\xi _{2}^{r_3}[n-1+c_1+c_2]:=-\xi _{2}^{r_3}\beta _{2} \end{aligned}$$
(21)

is such that

$$\begin{aligned} \dot{V}_2 \le -(n-1)\Big (\xi _{1}^{2+\tau }+\xi _{2}^{2+\tau }\Big )+ \xi _{2}^{{2\!-\!r_{2}\!}}[e_{3}-e_{3}^*]. \end{aligned}$$
(22)

Inductive Step: Suppose at step \(k-1\), there are a set of virtual controllers \(e_{1}^{*},\ldots ,e_{k}^{*}\), defined by

$$\begin{aligned} \begin{array}{l@{\quad }l} e_{1}^*=0, &{} \xi _{1}=e_{1},\\ e_{2}^*=-\xi _{1}^{r_2}\beta _{1},&{}\xi _{2}=e_{2}^{1/{r_2}}-{e_{2}^*}^{1/{r_2}},\\ e_{3}^*=-\xi _{2}^{r_3}\beta _{2},&{}\xi _{3}=e_{3}^{1/{r_3}}-{e_{3}^*}^{1/{r_3}},\\ \vdots &{}\vdots \\ e_{k}^*=-\xi _{{k-1}}^{r_k}\beta _{k-1},&{}\xi _{k}=e_{k}^{1/{r_k}}-{e_{k}^*}^{1/{r_k}}, \end{array} \end{aligned}$$
(23)

with positive constants \(\beta _{1},\ldots ,\beta _{k-1}\), and a \(\mathcal {C}^1\) Lyapunov function

$$\begin{aligned} V_{k-1}&= V_{1}+\int \limits _{e_{2}^*}^{e_{2}}\left( \mu ^{1/r_2}-{e_{2}^*} ^{1/r_2} \right) ^{{2-r_2}}d\mu \cdots \nonumber \\&+\int \limits _{e_{k-1}^*}^{e_{k-1}}\left( \mu ^{1/r_{k-1}} -{e_{k-1}^*}^{1/r_{k-1}} \right) ^{{2-r_{k-1}}}d\mu \end{aligned}$$
(24)

such that

$$\begin{aligned}&\dot{V}_{k-1} \le -(n-k+2)\Big (\xi _{1}^{2+\tau }+\xi _{2}^{2+\tau }+ \cdots +\xi _{k-1}^{2+\tau }\Big )\nonumber \\&\quad +\,\xi _{k-1}^{{2\!-\!r_{k-1}\!}}\left[ e_{k}-e_{k}^* \right] . \end{aligned}$$
(25)

In the sequel, we will show that (25) also holds at step \(k\). To prove this issue, consider the following \(\mathcal {C}^1\) Lyapunov function

$$\begin{aligned} V_k=V_{k-1}+ \int \limits _{e_{k}^*}^{e_{k}}\left( \mu ^{1/r_k}-{e_{k}^*}^{1/r_k} \right) ^{{2-r_k}}d\mu . \end{aligned}$$
(26)

Together with (25), the derivative of \(V_k\) along system (1) is

$$\begin{aligned} \dot{V}_k&\le -(n-k+2)\Big (\xi _{1}^{2+\tau }+\xi _{2}^{2+ \tau }+\cdots +\xi _{k-1}^{2+\tau }\Big )\nonumber \\&\quad +\,\xi _{k-1}^{{2\!-\!r_{k-1}\!}}\left[ e_{k}-e_{k}^* \right] +\xi _{k}^{{2\!-\!r_{k} \!}}e_{k+1}\nonumber \\&\quad +\frac{d \left[ -{e_{k}}^{*1/r_k} \right] }{dt}\int \limits _{e_{k}^*}^{{e_{k}}} \left( \mu ^{1/r_k}\!-\!{e_{k}}^{*1/r_k} \right) ^{{1-r_k}}ds.\qquad \nonumber \\ \end{aligned}$$
(27)

A similar proof as that in Step 2 leads to

$$\begin{aligned} \dot{V}_k&\le -(n-k+1)\Big (\xi _{1}^{2+\tau }+\xi _{2}^{2+\tau }+ \cdots +\xi _{k-1}^{2+\tau }\Big )\nonumber \\&\quad +\,c_k\xi _{k}^{2+\tau }+\xi _{k}^{{2\!-\!r_{k}\!}}e_{k+1}. \end{aligned}$$
(28)

for a positive constant \(c_k\). Clearly, we can choose a virtual controller in the form of

$$\begin{aligned} e_{k+1}^*=-\xi _{k}^{r_{k+1}}[n-k+1+c_k]:=-\xi _{k}^{r_{k+1}}\beta _{k} \end{aligned}$$
(29)

such that

$$\begin{aligned} \dot{V}_k&\le -(n-k+1)\Big (\xi _{1}^{2+\tau }+\cdots +\xi _{k}^{2+\tau }\Big )\nonumber \\&\quad +\,\xi _{k}^{{2\!-\!r_{k}\!}}[e_{k+1}-e_{k+1}^*] \end{aligned}$$
(30)

which completes the inductive proof.

From the above inductive proof, at step \(n\), we can find series of gains \(\beta _1,\cdots ,\beta _{n-1}\) such that

$$\begin{aligned} \dot{V}_{n}&\le -\Big (\xi _{1}^{2+\tau }+\xi _{2}^{2+ \tau }+\cdots +\xi _{n-1}^{2+\tau }\Big )+c_n\xi _{n}^{2+\tau }\nonumber \\&\quad +\,\xi _{n}^{{2\!-\!r_{n}\!}}[a(t)u+f(t,x_1,\cdots ,x_n)+d(t)-\dot{x}_n^d].\nonumber \\ \end{aligned}$$
(31)

where \(c_n\) is a positive constant and

$$\begin{aligned} V_{n}&= V_{1}+\int \limits _{e_{2}^*}^{e_{2}}\left( \mu ^{1/r_2}-{e_{2}^*}^{1/r_2} \right) ^ {{2-r_2}}d\mu +\cdots \nonumber \\&\quad +\int \limits _{e_{n}^*}^{e_{n}}\left( \mu ^{1/r_{n}}-{e_{n}^*}^{1/r_{n}} \right) ^{{2-r_{n}}}d\mu . \end{aligned}$$
(32)

Let

$$\begin{aligned} s=\xi _n, \quad \beta _n=c_n+1 \end{aligned}$$
(33)

and design \(u\) as

$$\begin{aligned} u&= -\frac{\beta _n}{\underline{a}}s^{r_n+\tau }\nonumber \\&- \frac{F(t,x_1, \ldots ,x_n)+L_1+L_2}{\underline{a}}\mathrm{sign}(s). \end{aligned}$$
(34)

Under Assumption 1 and control law (34), it follows from (31) that

$$\begin{aligned} \dot{V}_{n} \le&-\Big (\xi _{1}^{2+\tau }+\xi _{2}^{2+\tau }+\cdots +\xi _{n}^{2+\tau }\Big ). \end{aligned}$$
(35)

Finally, it will be shown that \(V_n\) will reach zero in finite time. Based on the definition of \(V_n\) in (32), and by Lemma 2, we have for \(i=2,\ldots ,n\),

$$\begin{aligned}&\!\!\!\!\Big |\int \limits _{e_{i}^*}^{{e_{i}}} \left( \mu ^{1/r_i}-{e_{i}} ^{*1/r_i} \right) ^{{2-r_i}}d\mu \Big |\le |\xi _{i}|^{2-r_i}|e_{i}-e_{i}^*| \nonumber \\&\le 2^{1-r_i}\xi _{i}^2, \end{aligned}$$
(36)

which implies that there is a constant \(\rho >0\) such that

$$\begin{aligned} {V}_{n} \le \rho \Big (\xi _{1}^{2}+\xi _{2}^{2}+\cdots +\xi _{n}^{2}\Big ). \end{aligned}$$
(37)

With (35) and (37) in mind, it follows from Lemma 4 that

$$\begin{aligned} \dot{V}_n+\rho ^{-\frac{2+\tau }{2}}V_n^{\frac{2+\tau }{2}} \le 0. \end{aligned}$$
(38)

Noticing \(\tau <0\), by Lemma 1, we conclude that \(V_n\) reaches zero in a finite time, which implies there exists a time \(T <+\infty \), such that \(V_n(t)\equiv 0, \forall t \ge T\), i.e., \(e_i(t)=0,i=1,\cdots ,n\), \(\forall t \ge T\). Thus, the proof is completed. \(\square \)

Remark 2

In the literature, in order to achieve finite-time control for nonlinear systems, an available method is to employ the terminal sliding mode method [15]. Nevertheless, as pointed out in [17, 18], there is a singularity problem in the terminal sliding mode controller when the system is high-order case. However, it should be pointed out that in our proposed finite-time controller (4) which is based on the technique of adding a power integrator [19], there is not any singularity problem.

Remark 3

Note that the discontinues control in the proposed finite-time controller (4) may lead to a chattering phenomenon in practice. To avoid this problem, it is often to use a continuous saturation function \(\mathrm{sat}(\frac{x}{\varepsilon })\) with a small positive constant \(\varepsilon \) instead of the discontinuous function \(\mathrm{sign}(x)\). The modified finite-time control law is given as:

$$\begin{aligned} u&= {-}\frac{\beta _n}{\underline{a}}s^{r_n+\tau } {-} \frac{F\left( x_1,\cdots ,x_n \right) +L_1+L_2}{\underline{a}}\mathrm{sat}\left( \frac{s}{\varepsilon } \right) ,\nonumber \\ s&= \left( x_{n}-x_n^d \right) ^{\frac{1}{r_{n}}}+\beta _{n-1}^{\frac{1}{r_n}} \Big [\left( x_{n-1}-x_{n-1}^d \right) ^{\frac{1}{r_{n-1}}}+ \cdots \nonumber \\&+\,\beta _2^{\frac{1}{r_3}}\Big [\left( x_{2}-x_2^d \right) ^{\frac{1}{r_2}}+ \beta _1^{\frac{1}{r_2}}\left( x_{1}-x_{1}^d \right) \Big ]\cdots \Big ],\nonumber \\ \end{aligned}$$
(39)

where \(\varepsilon >0\) and the other parameters are the same as that of Theorem 1. Simulation results will demonstrate this case.

4 Example

In this section, we will use one example to illustrate the efficiency of the proposed theoretic result.

Consider the problem of finite-time attitude control of roll channel of bank-to-turn (BTT) missile. From [20, 21], the mathematical model for BTT missile is described as

$$\begin{aligned} \dot{\gamma }&= \omega \nonumber \\ \dot{\omega }&= -a(t)\omega -c(t)\delta +d(t), \end{aligned}$$
(40)

where \(\gamma \) and \(\omega \) are the roll angle and roll rate, respectively, \(\delta \) is roll control deflection angle, to be designed. Coefficients \(a(t)\) and \(c(t)\) are time-varying aerodynamic parameters of the missile system. \(d(t)\) is time-varying bounded external disturbance. By [20], we know that the parameters \(a(t)\) and \(c(t)\) are usually bounded and satisfy \(a(t)\in [0.491,1.673],c(t)\in [584.220,3045.292]\), which means Assumption 1 holds. Assume the desired signal of the roll angle for the missile is \(\gamma _d(t)=10-\sin (t)\).

According to Theorem 1, we can design finite-time attitude tracking controller in the form of

$$\begin{aligned} \delta&= \frac{\beta _2}{\underline{c}}s^{r_2+\tau }+ \frac{\overline{a}|\omega |+L_1+L_2}{\underline{c}}\mathrm{sign}(s), \nonumber \\ s&= (\omega -\dot{\gamma }_d)^{\frac{1}{r_2}}+\beta _1^{\frac{1}{r_2}}(\gamma -\gamma _d), \end{aligned}$$
(41)

where \(\beta _1,\beta _2\) are appropriate gains.

In simulation, as shown in [24], to simulate the time-varying aerodynamic parameters, the time-varying parameters are given as follows:

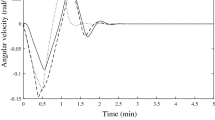
$$\begin{aligned} a(t){=}\!\left\{ \!\! \begin{array}{lll} a(t_1), &{} 0\le \hbox {t}\le \hbox {t}_1;&{}\nonumber \\ a(t_{j-1}) +\frac{a(t_j)-a(t_{j-1})}{t_j-t_{j-1}}, (t-t_{j-1}), &{} \,j=2,\ldots ,7, (t-t_{j-1}),\nonumber \end{array} \right. \nonumber \\ \end{aligned}$$
(42)

where \(a(t_j)\) is the parameter’s value at different operation points given in Table 1. The time-varying parameter \(c(t)\) is given by the same way. In addition, the external disturbance is given as: \(d(t)=1.1\mathrm{sin}(8t-1),\) which implies \(L_2\) can be selected as \(L_2=1.1.\) By a careful calculation, the controller gains can be chosen as \(\beta _2=20,\beta _1=10, \; \mathrm{and} \; \tau =-2/5\). Under the proposed finite-time controller (4), the response curves of the closed-loop systems (41, 40) are shown in Fig. 1, respectively, where the initial conditions are chosen as \(\gamma (0)=20,\omega (0)=0\). It is easy to see that the roll angle will track the reference signal.

Fig. 1
figure 1

The response curves of the BTT missile under the proposed finite-time controller (41)

Full size image
Table 1 Model parameters for different operation points [20]
Full size table

In addition, from the control response curves, i.e., Fig. 1, it can be found that there is a chatting phenomenon in the finite-time controller (41). To this end, we use the modified finite-time control law (39) with \(\varepsilon =0.1\). The response curves of closed-loop systems (39, 40) are shown in Fig. 2. It is clear that the chatting phenomenon can be avoided.

Fig. 2
figure 2

The response curves of the BTT missile under the modified finite-time control law (39)

Full size image

5 Conclusions

In this paper, we have studied the problem of finite-time tracking control for a class of high-order nonlinear systems. Rigorous theoretic analysis shows that the proposed finite-time algorithm can deal with the case with uncertain time-varying control coefficient and unknown nonlinear perturbations. Future works include how to extend the result of this paper to output feedback case.