New Class of Attitude Controllers Guaranteed to Converge within Specified Finite-Time

Abstract

This paper introduces a new class of finite-time feedback controllers for rigid-body attitude dynamics subject to full actuation. The control structure is Lyapunov-based and is designed to regulate the configuration from an arbitrary initial state to any prescribed final state within user-specified finite transfer-time. A salient feature here is that the synthesis of the control structure is explicit, i.e., given the transfer-time time, the feedback-gains are explicitly stated to satisfy the convergence specifications. A major contrast between this work and others in the literature is that instead of resorting to feedback-linearization (to get to the so-called normal form), our approach efficiently marries the process of designing time-varying feedback gains with the logarithmic Lyapunov function for attitude kinematics based on the Modified Rodrigues Parameters representation. Saliently, this finite-time solution extends nicely for accommodating trajectory tracking objectives and possesses robustness with respect to bounded external disturbance torques. Numerical simulations are performed to test and validate the performance and robustness features of the new control designs.

Introduction

This work introduces a finite-time feedback controller for fully actuated rigid-body attitude dynamics. We make use of Lyapunov’s Direct Method to design a feedback law that regulates the configuration from an arbitrary initial state to any final state within a desired finite transfer-time t_f. The control synthesis is explicit, i.e., given the transfer-time time t_f, the feedback-gains are explicitly stated to satisfy the convergence specifications, even in the presence of bounded disturbances.

Several recent papers in literature address finite-time regulation problems for fully-controllable systems that are diffeomorphic to the so-called normal form representation. Some of these methods stem from non-smooth feedback, such as bang-bang [1], fractional-order systems, and/or sliding-mode controllers. These methods usually introduce discontinuous dynamics through feedback, which can lead to chattering and excitation of undesired frequencies [2]. Other methods are built on top of the “Lyapunov differential inequality” [3], and many recent results stem from this methodology (see Ref. [4] and references therein). Whereas many of existing methods provide results for finite-time control algorithms, the explicit synthesis of such feedback schemes is far from being fully resolved, especially when applied to nonlinear systems such as the attitude control problem.

In this work, we introduce a feedback control law whose feedback gains are time-varying and grow unbounded towards the terminal time t_f. Although the notion of using unbounded feedback gains can be unsettling at a first glance, such an approach has certain strong theoretical underpinnings that are based upon variational calculus. Specifically, finite-horizon optimal control problems with terminal state constraints are known to produce unbounded feedback gains [5].

The major contributions of this paper are as follows. Our formulation introduces a feedback structure that is closely related to Ref. [4]. However, a major contrast is that our work does not seek to arbitrarily cancel out nonlinearities including those associated with the non-working terms within Euler’s rotational dynamics equations. Thus, instead of resorting to the traditional approach of feedback-linearization, our approach utilizes the unbounded gains in conjunction with the logarithmic Lyapunov function presented by Ref. [6] for the attitude kinematics based on the Modified Rodrigues Parameters (MRPs) representation.

This paper is structured along these following lines: Section “Control Design” presents our control design for attitude stabilization around the origin, while Section “Tracking Control” extends the result for trajectory tracking problems (such as slew maneuvers). Section “Practical Considerations” introduces some practical considerations for the implementation of the designed controller. Section “Simulation Results” presents numerical simulation results and Section “Conclusion” summarizes the paper by drawing some concluding remarks.

Control Design

Assume a rotation of an angle $\psi \in \left (\begin {array}{llll}-2\pi , 2\pi \end {array}\right )$ rad around a unit-norm axis $\hat {\boldsymbol {e}} \in \mathbb {R}^{3}$. The three-parameter MRP (Modified Rodrigues Parameters) representation $\boldsymbol {\sigma } \in \mathbb {R}^{3}$ for the same rotation is defined as:

$$ \boldsymbol{\sigma} \triangleq \hat{\boldsymbol{e}}\tan{\frac{\psi}{4}}. $$

(1)

The kinematics of MRPs [7] is given by

$$ \dot{\boldsymbol{\sigma}}(t) = \frac{1}{4}\boldsymbol{B}\left( \begin{array}{llll}\boldsymbol{\sigma}(t) \end{array}\right)\boldsymbol{\omega}(t), $$

(2)

where $\boldsymbol {\omega }(t) \in \mathbb {R}^{3}$ is the angular velocity expressed in a body-fixed frame, and

$$ \boldsymbol{B}\left( \begin{array}{llll}\boldsymbol{\sigma}(t) \end{array}\right) = (1-\boldsymbol{\sigma}^{T}\boldsymbol{\sigma})\boldsymbol{I}_{3} + 2\boldsymbol{\sigma}^{*} + 2\boldsymbol{\sigma}\boldsymbol{\sigma}^{T}, $$

(3)

where we denote v^∗ as the skew-symmetric matrix associated with a vector $\boldsymbol {v} \in \mathbb {R}^{3}$.

It should be noticed that the product σ^TB(σ) satisfies the property:

$$ \boldsymbol{\sigma}^{T}\boldsymbol{B}(\boldsymbol{\sigma}) = (1-\boldsymbol{\sigma}^{T}\boldsymbol{\sigma})\boldsymbol{\sigma}^{T} + 2\boldsymbol{\sigma}^{T}\boldsymbol{\sigma}\boldsymbol{\sigma}^{T} = (1+\boldsymbol{\sigma}^{T}\boldsymbol{\sigma})\boldsymbol{\sigma}^{T}. $$

(4)

The composition rule between the MRPs σ₁ and σ₂ is given by [8]:

$$ \boldsymbol{\sigma}_{3} \triangleq \boldsymbol{\sigma}_{1} \otimes \boldsymbol{\sigma}_{2} = \frac{(1-||\boldsymbol{\sigma}_{1}||^{2})\boldsymbol{\sigma}_{2} + (1 - ||\boldsymbol{\sigma}_{2}||^{2})\boldsymbol{\sigma}_{1} + 2\boldsymbol{\sigma}_{2}^{*} \boldsymbol{\sigma}_{1}}{1 + ||\boldsymbol{\sigma}_{1}||^{2}||\boldsymbol{\sigma}_{2}||^{2} - 2\boldsymbol{\sigma}_{1}^{T}\boldsymbol{\sigma}_{2}}. $$

(5)

The direction cosine matrix associated with an MRP σ can be obtained by:

$$ \boldsymbol{C}(\boldsymbol{\sigma}) = \boldsymbol{I} + \frac{8(\boldsymbol{\sigma}^{*})^{2} - 4(1-\boldsymbol{\sigma}^{T}\boldsymbol{\sigma})\boldsymbol{\sigma}^{*}}{(1 + \boldsymbol{\sigma}^{T}\boldsymbol{\sigma})^{2}} $$

(6)

Defining the MRP inverse σ^− 1 as the parameterization for the rotation matrix C(σ^− 1) = C^T(σ), then the relation between σ^− 1 and σ is given by:

$$ \boldsymbol{\sigma}^{-1} = -\boldsymbol{\sigma}. $$

(7)

The body angular velocity ω(t) evolves according with Euler’s rotation equation:

$$ \boldsymbol{J}\dot{\boldsymbol{\omega}}(t) = -\boldsymbol{\omega}^{*}(t) \boldsymbol{J}\boldsymbol{\omega}(t) + \boldsymbol{u}(t) + \boldsymbol{d}(t), $$

(8)

where J = J^T > 0 is the inertia tensor expressed in the body-fixed frame, u(t) is an input torque, and d(t) is an unknown bounded disturbance torque.

The goal of this work is to find a control law for u(t),t ∈ [0,t_f), such that σ(t_f) = ω(t_f) = 0, for some specified final time 0 < t_f < ∞, even in the presence of non-zero disturbance torques. We accomplish this through a backstepping design: first, we assume that ω(t) = ω_r(t) is an “input” to Eq. 2. We find a Lyapunov candidate function that stabilizes the MRP in finite time (i.e., σ(t_f) = 0) by applying the control law ω_r(t),t ∈ [0,t_f). Then, we use ω_r(t) to find a new control law u that stabilizes both σ(t) and ω(t).

Section “MRP Stabilization” presents the procedure for stabilizing (2) assuming input ω(t) = ω_r(t). Section “Attitude Stabilization” presents the backstepping formulation for designing the feedback law u(t) that stabilizes both (2) and (8).

MRP Stabilization

Assume that ω_r(t) is the input to

$$ \dot{\boldsymbol{\sigma}}(t) = \frac{1}{4}\boldsymbol{B}\left( \begin{array}{llll}\boldsymbol{\sigma}(t) \end{array}\right)\boldsymbol{\omega}_{r}(t), \quad t \in [0, t_{f}). $$

(9)

Next, define the function μ(t) as:

$$ \mu(t) \triangleq \frac{t_{f}}{t_{f} - t}, \quad t \in [0, t_{f}). $$

(10)

One should note that μ(0) = 1, μ(t) > 1,∀t ∈ (0,t_f), and $\lim _{t \to t_{f}}\mu (t) = \infty$. In addition, the derivative of μ(t) with respect to time is given by:

$$ \dot{\mu}(t) = \frac{t_{f}}{(t_{f} - t)^{2}} = \frac{1}{t_{f}} \left( \begin{array}{llll} \frac{t_{f}}{t_{f} - t} \end{array}\right)^{2} = \frac{1}{t_{f}}\mu^{2}(t), \quad t \in [0, t_{f}). $$

(11)

The integral of μ²(t) with respect to time is given by:

$$ {\int_{0}^{t}} \mu^{2}(\beta) d\beta = \frac{{t_{f}^{2}}}{t_{f}-t}|_{0}^{t} = t_{f} \mu(t)|_{0}^{t} = t_{f} (\mu(t) - 1 ) = t_{f} \bar{\mu}(t), $$

(12)

where $\bar {\mu }(t) \triangleq \mu (t) - 1$. The signal $\bar {\mu }(t)$ satisfies the properties $\bar {\mu }(0) = 0$, $\bar {\mu }(t) > 0, \forall t \in (0, t_{f})$, $\lim _{t \to t_{f}}\bar {\mu }(t) = \infty$, and $\dot {\bar {\mu }}(t) = \dot {\mu }(t)$.

We define the following Lyapunov candidate function:

$$ V_{0}(t) = \mu^{\lambda}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right), \quad t \in [0, t_{f}), $$

(13)

for some $\lambda \in \mathbb {R}_{>0}$. Clearly, V (t) = 0 ⇔ ||σ(t)|| = 0, and V (t) > 0,∀t ∈ [0,t_f), if ||σ(t)||≠ 0.

The time derivative of Eq. 13 is given by:

$$ \begin{array}{@{}rcl@{}} \dot{V}_{0}(t) &=& \frac{\partial V_{0}}{\partial \mu} \dot{\mu}(t) + \frac{\partial V_{0}}{\partial \boldsymbol{\sigma}} \dot{\boldsymbol{\sigma}}(t) \\ &=& \lambda\mu^{\lambda-1}\dot{\mu}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) + \frac{1}{4}\frac{\partial V_{0}}{\partial \boldsymbol{\sigma}}\boldsymbol{B}(\boldsymbol{\sigma}(t)) \boldsymbol{\omega}_{r}(t) \\ &=& \frac{\lambda}{t_{f}}\mu^{\lambda+1}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) + \frac{\mu^{\lambda}(t)}{2}\cdot\frac{\boldsymbol{\sigma}^{T}(t)}{1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t)}\boldsymbol{B} (\boldsymbol{\sigma}(t)) \boldsymbol{\omega}_{r}(t) \\ &=& \frac{\lambda}{t_{f}}\mu^{\lambda+1}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) + \frac{\mu^{\lambda}(t)}{2}\cdot\frac{\boldsymbol{\sigma}^{T}(t)\boldsymbol{B}(\boldsymbol{\sigma}(t))}{1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t)} \boldsymbol{\omega}_{r}(t). \end{array} $$

(14)

Using the property from Eq. 4 into Eq. 14 leads to:

$$ \dot{V}_{0}(t) = \frac{\lambda}{t_{f}}\mu^{\lambda+1}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) + \frac{\mu^{\lambda}(t)}{2} \boldsymbol{\sigma}^{T}(t)\boldsymbol{\omega}_{r}(t). $$

(15)

Since ln(1 + η) ≤ η,∀η ≥ 0, then:

$$ \dot{V}_{0}(t) \leq \frac{\lambda}{t_{f}}\mu^{\lambda+1}(t) \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) + \frac{\mu^{\lambda}(t)}{2} \boldsymbol{\sigma}^{T}(t)\boldsymbol{\omega}_{r}(t) $$

(16)

In addition, μ^λ+ 1(t)σ^T(t)σ(t) ≤ μ^λ+ 2(t)σ^T(t)σ(t),t ∈ [0,t_f), leading to:

$$ \begin{array}{@{}rcl@{}} \dot{V}_{0}(t) &\leq& \frac{\lambda}{t_{f}}\mu^{\lambda+2}(t) \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) + \frac{\mu^{\lambda}(t)}{2} \boldsymbol{\sigma}^{T}(t)\boldsymbol{\omega}_{r}(t) \\ &= & \mu^{\lambda}(t)\boldsymbol{\sigma}^{T}(t) \left( \begin{array}{llll} \frac{\lambda}{t_{f}}\mu^{2}(t)\boldsymbol{\sigma}(t) + \frac{1}{2} \boldsymbol{\omega}_{r}(t) \end{array}\right) \end{array} $$

(17)

We can choose the control law:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\omega}_{r}(t) &=& -2 \left( \begin{array}{llll} \frac{\lambda}{t_{f}}\mu^{2}(t)\boldsymbol{\sigma}(t) + k \mu^{2}(t)\boldsymbol{\sigma}(t) \end{array}\right) \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} &=& -2 \left( \begin{array}{llll} \frac{\lambda}{t_{f}} + k \end{array}\right)\mu^{2}(t) \boldsymbol{\sigma}(t), \end{array} $$

(19)

$$ \begin{array}{@{}rcl@{}} &=& -\phi \mu^{2}(t) \boldsymbol{\sigma}(t), \end{array} $$

(20)

for some constant gain k > 0, $\phi \triangleq 2 \left (\begin {array}{llll} \frac {\lambda }{t_{f}} + k \end {array}\right ) > 0$ and t ∈ [0,t_f), leading to:

$$ \dot{V}_{0}(t) \leq -k\mu^{\lambda+2}(t)\boldsymbol{\sigma}^{T}(t)\boldsymbol{\sigma}(t). $$

(21)

Noticing again that − ln(1 + η) ≥−η,∀η ≥ 0, then:

$$ \begin{array}{@{}rcl@{}} \dot{V}_{0}(t) &\leq& -k\mu^{\lambda+2}(t)\ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) \\ &=& -k\mu^{2}(t)V_{0}. \end{array} $$

(22)

Invoking the Comparison Lemma [9], we have that:

$$ V_{0}(t) \leq V_{0}(0)\exp \left[\begin{array}{llll} -k {\int_{0}^{t}} \mu^{2}(\gamma) d\gamma \end{array}\right]. $$

(23)

Using Eq. 12, we get:

$$ \begin{array}{@{}rcl@{}} V_{0}(t)& \leq&V_{0}(0)\exp \left[\begin{array}{llll} -kt_{f}\cdot\bar{\mu}(t) \end{array}\right] \\ \mu^{\lambda}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) &\leq& V_{0}(0)\exp \left[\begin{array}{llll} -kt_{f}\cdot\bar{\mu}(t) \end{array}\right]. \end{array} $$

(24)

Observing that $\lim _{t \to t_{f}}\exp \left [\begin {array}{llll} -kt_{f}\cdot \bar {\mu }(t) \end {array}\right ] = 0$, then:

$$ \lim\limits_{t \to t_{f}}V_{0}(t) \leq 0 \implies \lim\limits_{t \to t_{f}}V_{0}(t) = 0 \implies \lim\limits_{t \to t_{f}} \boldsymbol{\sigma}(t) = 0. $$

(25)

Therefore, if the control law in Eq. 20 is realizable (i.e. ω_r ∈ L_∞), then we have finite time convergence of σ to the origin. Also, it is desirable that $\lim _{t \to t_{f}}\boldsymbol {\omega }_{r}(t) = 0$, which would imply that once the state σ reaches zero at t = t_f, it will remain there for t > t_f (i.e., soft-landing).

Taking the two-norm of the control law from Eq. 20, we get that:

$$ ||\boldsymbol{\omega}_{r}(t)|| = \phi||\mu^{2}(t) \boldsymbol{\sigma}(t)|| $$

(26)

Therefore, it is sufficient to say that if the product μ²σ ∈ L_∞, then ω_r ∈ L_∞, implying that the control law is realizable. Appendix A proves that if Eq. 24 holds true, then $\mu ^{\alpha _{1}} \boldsymbol {\sigma } \in L_{\infty }, \forall \alpha _{1} \in \mathbb {R}$, implying that:

$$ \exists \alpha_{2} \in \mathbb{R} s.t. ||\mu^{\alpha_{1}}(t) \boldsymbol{\sigma}(t)|| \leq \alpha_{2}, \forall t \in [0, t_{f}) \implies ||\mu^{\alpha_{1}-1}(t) \boldsymbol{\sigma}(t)|| \leq \frac{\alpha_{2}}{\mu^{2}(t)} \forall t \in [0, t_{f}). $$

(27)

Choosing α₁ = 3, we have that:

$$ \lim\limits_{t \to t_{f}}||\mu^{2}(t) \boldsymbol{\sigma}(t)|| \leq \lim\limits_{t \to t_{f}} \frac{\alpha_{2}}{\mu^{2}(t)} = 0. $$

(28)

Therefore, from Eq. 26 we get that $\lim _{t \to t_{f}}||\mu ^{2}(t) \boldsymbol {\sigma }(t)|| = 0 \implies \lim _{t \to t_{f}}||\boldsymbol {\omega }_{r}(t)|| = 0$.

Attitude Stabilization

In the previous subsection, the variable ω(t) = ω_r(t) was assumed to be a control variable. Now, we employ a backstepping design to stabilize σ(t) and ω(t) in finite time. The equations of motion are given by:

$$ \left\{\begin{array}{llll} \dot{\boldsymbol{\sigma}}(t) = \boldsymbol{g}(\sigma)\boldsymbol{\omega}(t) \\ \boldsymbol{J}\dot{\boldsymbol{\omega}}(t) = -\boldsymbol{\omega}^{*}(t) \boldsymbol{J}\boldsymbol{\omega}(t) + \boldsymbol{u}(t) + \boldsymbol{d}(t) \end{array}\right., $$

(29)

where $\boldsymbol {g}(\sigma ) \triangleq \frac {1}{4}\boldsymbol {B}\left (\begin {array}{llll}\boldsymbol {\sigma }(t) \end {array}\right )$, and d(t) is a bounded disturbance input with $||\boldsymbol {d}(t)|| \leq \bar {d}$.

The goal is to design u(t) such that u ∈ L_∞ and $\lim _{t \to t_{f}}[\boldsymbol {\sigma }(t), \boldsymbol {\omega }(t)] = 0$.

We rewrite (2) as:

$$ \begin{array}{@{}rcl@{}} \dot{\boldsymbol{\sigma}}(t) &=& \boldsymbol{g}(\sigma)\boldsymbol{\omega}(t) + \boldsymbol{g}(\sigma)\boldsymbol{\omega}_{r}(t) - \boldsymbol{g}(\sigma)\boldsymbol{\omega}_{r}(t) \\ &=& \boldsymbol{g}(\sigma)\boldsymbol{\omega}_{r}(t) + \boldsymbol{g}(\sigma)\left( \begin{array}{llll} \boldsymbol{\omega}(t) - \boldsymbol{\omega}_{r}(t) \end{array}\right) \\ &=& \boldsymbol{g}(\sigma)\boldsymbol{\omega}_{r}(t) + \boldsymbol{g}(\sigma)\boldsymbol{\omega}_{e}(t), \end{array} $$

(30)

where $\boldsymbol {\omega }_{e}(t) \triangleq \boldsymbol {\omega }(t) - \boldsymbol {\omega }_{r}(t)$.

Then, we construct a new Lyapunov candidate function $V:[0, t_{f})\to \mathbb {R}^{+}$:

$$ \begin{array}{@{}rcl@{}} V(t) &=& V_{0}(t) + \frac{1}{2}\mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t), \\ &=& \mu^{\lambda}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) + \frac{1}{2}\mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t). \end{array} $$

(31)

The time derivative of Eq. 31 is given by:

$$ \begin{array}{@{}rcl@{}} \dot{V}(t)& =& \frac{\partial V_{0}}{\partial \boldsymbol{\mu}} \dot{\boldsymbol{\mu}}(t) + \frac{\partial V_{0}}{\partial \boldsymbol{\sigma}} \dot{\boldsymbol{\sigma}}(t) + 2\mu^{3}(t)\dot{\mu}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) + \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\dot{\boldsymbol{\omega}}_{e} \\ &=& \frac{\partial V_{0}}{\partial \boldsymbol{\mu}} \dot{\boldsymbol{\mu}}(t) + \frac{\partial V_{0}}{\partial \boldsymbol{\sigma}}\boldsymbol{g}(\boldsymbol{\sigma}) \boldsymbol{\omega}_{r}(t) + \frac{\partial V_{0}}{\partial \boldsymbol{\sigma}}\boldsymbol{g}(\boldsymbol{\sigma}) \boldsymbol{\omega}_{e}(t) + \frac{2}{t_{f}}\mu^{5}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) \\ & &+ \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t) \left[\begin{array}{llll} \boldsymbol{u}(t) + \boldsymbol{d}(t) - \boldsymbol{\omega}^{*}(t)\boldsymbol{J}\boldsymbol{\omega}(t) - \boldsymbol{J}\dot{\boldsymbol{\omega}}_{r}(t) \end{array}\right]. \end{array} $$

From Eqs. 14–22 in the previous section, it follows that:

$$ \frac{\partial V_{0}}{\partial \boldsymbol{\mu}} \dot{\boldsymbol{\mu}}(t) + \frac{\partial V_{0}}{\partial \boldsymbol{\sigma}}\boldsymbol{g}(\boldsymbol{\sigma}) \boldsymbol{\omega}_{r}(t) \leq -k\mu^{2}(t)V_{0}(t), $$

(32)

for some k > 0 and ω_r(t) given by Eq. 20. Using Eq. 32 together with the property from Eq. 4, we get:

$$ \begin{array}{@{}rcl@{}} \dot{V}(t) &\leq& -k\mu^{2}(t)V_{0}(t) + \frac{\mu^{\lambda}(t)}{2}\boldsymbol{\sigma}^{T}(t) \boldsymbol{\omega}_{e}(t) + \frac{2}{t_{f}}\mu^{5}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) \\ &&+ \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t) \left[\begin{array}{llll} \boldsymbol{u}(t) - \boldsymbol{\omega}^{*}(t)\boldsymbol{J}\boldsymbol{\omega}(t) - \boldsymbol{J}\dot{\boldsymbol{\omega}}_{r}(t) \end{array}\right] + \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{d}(t). \end{array} $$

Focusing on the disturbance term, we have that:¹

$$ \begin{array}{@{}rcl@{}} \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{d}(t) &=& \mu^{2}(t) \left( \begin{array}{llll} \mu^{2}(t)\boldsymbol{\omega}_{e}^{T}(t) \end{array}\right)\boldsymbol{d}(t) \\ &\leq& \frac{1}{2} \mu^{2}(t) \left[\begin{array}{llll} \mu^{4}(t) ||\boldsymbol{\omega}_{e}(t)||^{2} + ||\boldsymbol{d}(t)||^{2} \end{array}\right]\\ &\leq& \frac{1}{2} \mu^{6}(t) ||\boldsymbol{\omega}_{e}(t)||^{2} + \frac{1}{2}\mu^{2}(t)\bar{d}^{2}. \end{array} $$

(33)

In addition, using the fact $\mu ^{5}(t)\boldsymbol {\omega }_{e}^{T}(t)\boldsymbol {J}\boldsymbol {\omega }_{e}(t) \leq \mu ^{6}(t)\boldsymbol {\omega }_{e}^{T}(t)\boldsymbol {J}\boldsymbol {\omega }_{e}(t)$, we get that:

$$ \begin{array}{@{}rcl@{}} \dot{V}(t) &\leq& -k\mu^{2}(t)V_{0}(t) + \frac{\mu^{\lambda}(t)}{2}\boldsymbol{\sigma}^{T}(t) \boldsymbol{\omega}_{e}(t) + \frac{2}{t_{f}}\mu^{6}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) \\ &&+ \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t) \left[\begin{array}{llll} \boldsymbol{u}(t) + \frac{\mu^{2}(t)}{2}\boldsymbol{\omega}_{e}(t) - \boldsymbol{\omega}^{*}(t)\boldsymbol{J}\boldsymbol{\omega}(t) - \boldsymbol{J}\dot{\boldsymbol{\omega}}_{r}(t) \end{array}\right] + \frac{1}{2}\mu^{2}(t)\bar{d}^{2} \\ &\leq& -k\mu^{2}(t)V_{0}(t) + \frac{1}{2}\mu^{2}(t)\bar{d}^{2} \\ &&\!+ \mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t) \left[\begin{array}{llll} \boldsymbol{u}(t) \!+\!\mu^{2}(t)\left( \begin{array}{llll} \frac{1}{2}\boldsymbol{I} \!+\! \frac{2}{t_{f}}\boldsymbol{J} \end{array}\right)\boldsymbol{\omega}_{e}(t) \!-\! \boldsymbol{\omega}^{*}(t)\boldsymbol{J}\boldsymbol{\omega}(t) \!-\! \boldsymbol{J}\dot{\boldsymbol{\omega}}_{r}(t) + \frac{1}{2}\mu^{\lambda-4}(t)\boldsymbol{\sigma}(t) \end{array}\right]. \end{array} $$

(34)

We can choose the control law:

$$ \boldsymbol{u}(t) = -\left( \begin{array}{llll} \frac{1}{2}k\boldsymbol{J} + \frac{2}{t_{f}}\boldsymbol{J} + \frac{1}{2}\boldsymbol{I} \end{array}\right) \mu^{2}(t)\boldsymbol{\omega}_{e}(t) - \frac{1}{2}\mu^{\lambda-4}(t)\boldsymbol{\sigma}(t) + \boldsymbol{\omega}^{*}(t)\boldsymbol{J}\boldsymbol{\omega}(t) + \boldsymbol{J}\dot{\boldsymbol{\omega}}_{r}(t), $$

(35)

where $\dot {\boldsymbol {\omega }}_{r}(t)$ can be obtained by differentiating Eq. 20:

$$ \begin{array}{@{}rcl@{}} \dot{\boldsymbol{\omega}}_{r}(t) &=& -\phi \mu^{2}(t) \left[\begin{array}{llll} \frac{2}{t_{f}}\mu(t) \boldsymbol{\sigma}(t) + \boldsymbol{g}(\boldsymbol{\sigma})\boldsymbol{\omega}(t) \end{array}\right] \\ &=& - \frac{2}{t_{f}}\phi\mu^{3}(t)\boldsymbol{\sigma}(t) - \phi\boldsymbol{g}(\boldsymbol{\sigma})\mu^{2}(t)\boldsymbol{\omega}_{e}(t) - \phi\boldsymbol{g}(\boldsymbol{\sigma})\mu^{2}(t)\boldsymbol{\omega}_{r}(t) \\ &=& - \frac{2}{t_{f}}\phi\mu^{3}(t)\boldsymbol{\sigma}(t) - \phi\boldsymbol{g}(\boldsymbol{\sigma})\mu^{2}(t)\boldsymbol{\omega}_{e}(t) + \phi^{2}\boldsymbol{g}(\boldsymbol{\sigma})\mu^{4}(t)\boldsymbol{\sigma}(t) . \end{array} $$

(36)

Substituting Eq. 35 into Eq. 34 leads to:

$$ \begin{array}{@{}rcl@{}} \dot{V}(t) &\leq& -k\mu^{2}(t)V_{0}(t) -\frac{1}{2}k\mu^{6}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) + \frac{1}{2}\mu^{2}(t)\bar{d}^{2} \\ &\leq& -k\mu^{2}(t)\left( \begin{array}{llll} V_{0}(t) + \frac{1}{2}\mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) \end{array}\right) + \frac{1}{2}\mu^{2}(t)\bar{d}^{2} \\ &\leq& -k\mu^{2}(t) V(t) + \frac{1}{2}\mu^{2}(t)\bar{d}^{2}. \end{array} $$

(37)

Once again, invoking the Comparison lemma leads to:

$$ V(t) \leq {\Phi}(t,0)V(0) + {\Phi}(t,0) {\int_{0}^{t}} {\Phi}(0,\tau) \frac{1}{2}\mu^{2}(t)\bar{d}^{2} d\tau, $$

(38)

where ${\Phi }(t_{1},t_{2}) = \exp \left [\begin {array}{llll} -k t_{f} \left (\begin {array}{llll} \mu (t_{1}) - \mu (t_{2}) \end {array}\right ) \end {array}\right ]$. Solving the integral in Eq. 38, we can show that:

$$ V(t) \leq V(0)\exp \left[\begin{array}{llll} -k t_{f} \cdot \bar{\mu}(t) \end{array}\right] + \frac{\bar{d}^{2}}{2k} \left( \begin{array}{llll} 1 - \exp \left[\begin{array}{llll} -k t_{f} \cdot \bar{\mu}(t) \end{array}\right] \end{array}\right) $$

(39)

We provide the analysis for the disturbance free case in Section “Disturbance-Free Analysis” and the analysis for the case with non-zero disturbance torques in Section “Disturbance Analysis”. We demonstrate that the control objectives are reached in the disturbance-free case for any λ > 0, while we require λ = 8 to satisfy complete disturbance rejection at terminal time t_f.

Disturbance-Free Analysis

In the absence of disturbances, $\bar {d} = 0$ and the following holds:

$$ \begin{array}{@{}rcl@{}} V(t) \leq V(0)\exp \left[\begin{array}{llll} -k t_{f} \cdot \bar{\mu}(t) \end{array}\right] \implies \left\{\begin{array}{llll} \frac{1}{2}\mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) \leq V(0)\exp \left[\begin{array}{llll} -k t_{f} \cdot \bar{\mu}(t) \end{array}\right] \\ \mu^{\lambda}\ln(1 + \boldsymbol{\sigma}^{T}\boldsymbol{\sigma}) \leq V(0)\exp \left[\begin{array}{llll} -k t_{f} \cdot \bar{\mu}(t) \end{array}\right] \end{array}\right. \end{array} $$

(40)

$$ \begin{array}{@{}rcl@{}} \lim\limits_{t \to t_{f}}V(t) \leq 0 \implies \lim\limits_{t \to t_{f}}V(t) = 0 \implies \left\{\begin{array}{llll} \lim\limits_{t \to t_{f}}||\mu^{2}(t)\boldsymbol{\omega}_{e}(t)||^{2} = 0 \\ \lim\limits_{t \to t_{f}}||\boldsymbol{\sigma}(t)||^{2} = 0 \end{array}\right.. \end{array} $$

(41)

Since $\lim _{t \to t_{f}}\boldsymbol {\omega }_{e}(t) = 0$ and $\lim _{t \to t_{f}}\boldsymbol {\omega }_{r}(t) = 0$ (See Eqs. 26 and 28), then $\lim _{t \to t_{f}}\boldsymbol {\omega }(t) = 0$. Also, the right-hand side of Eq. 39 is a bounded function, for t ∈ [0,t_f), implying that:

$$ V \in L_{\infty} \implies \boldsymbol{\omega}_{e} \in L_{\infty} \implies \boldsymbol{\omega} \in L_{\infty}, $$

(42)

where the last implication above holds true given that ω_r = −ϕμ²σ ∈ L_∞ (See Appendix A).

We need to ensure that the control torque u(t) is bounded. According with Eqs. 40 and 41, μ²ω_e ∈ L_∞, σ ∈ L_∞, $\lim _{t \to t_{f}}||\mu ^{2}(t)\boldsymbol {\omega }_{e}(t)|| = 0$, and $\lim _{t \to t_{f}}||\boldsymbol {\sigma }(t)|| = 0$. Given that Eq. 40 holds, Appendix A shows that μ³σ ∈ L_∞, $\lim _{t \to t_{f}}||\mu ^{3}(t)\boldsymbol {\sigma }(t)|| = 0$, μ⁴σ ∈ L_∞, $\lim _{t \to t_{f}}||\mu ^{4}(t)\boldsymbol {\sigma }(t)|| = 0$. Since σ ∈ L_∞, then g(σ) ∈ L_∞.

Therefore, u(t) is composed as a sum of bounded signals, which implies that u ∈ L_∞. In addition, since $\lim _{t \to t_{f}}||\mu ^{2}(t)\boldsymbol {\omega }_{e}(t)|| = 0$, $\lim _{t \to t_{f}}||\boldsymbol {\sigma }(t)|| = 0$, $\lim _{t \to t_{f}}||\mu ^{3}(t)\boldsymbol {\sigma }(t)|| = 0$ and $\lim _{t \to t_{f}}||\mu ^{4}(t)\boldsymbol {\sigma }(t)|| = 0$, then $\lim _{t \to t_{f}}\boldsymbol {u}(t) = \boldsymbol {0}$.

Disturbance Analysis

Equation 39 can be upper bounded as:

$$ V(t) \leq V(0) + \frac{\bar{d}^{2}}{2k}. $$

(43)

Defining the constant $\bar {V} \triangleq V(0) + \frac {\bar {d}^{2}}{2k}$, if follows that:

$$ \begin{array}{@{}rcl@{}} \mu^{\lambda}(t)\ln(1 + \boldsymbol{\sigma}^{T}(t)\boldsymbol{\sigma}(t)) &\leq& \bar{V} \end{array} $$

(44)

$$ \begin{array}{@{}rcl@{}} \frac{1}{2}\mu^{4}(t)\boldsymbol{\omega}_{e}^{T}(t)\boldsymbol{J}\boldsymbol{\omega}_{e}(t) &\leq& \bar{V}. \end{array} $$

(45)

Starting from Eq. 44, it is possible to show that μ^λ/2σ ∈ L_∞ and that $\lim _{t \to t_{f}}\mu ^{\rho }(t)\boldsymbol {\sigma }(t) = 0, \forall \rho < \lambda /2$ (See Appendix B), which implies that $\lim _{t \to t_{f}}\boldsymbol {\sigma }(t) = 0$, if λ > 0.

Given that the control law of Eq. 35 is function of $\dot {\boldsymbol {\omega }}_{r}(t)$, which depends on μ⁴(t)σ(t) (see Eq. 36), then we need that λ/2 ≥ 4 ⇒ λ ≥ 8 to satisfy μ⁴σ ∈ L_∞. Additionally, the control law of Eq. 35 depends on μ^λ− 4(t)σ(t), implying that we need λ − 4 ≤ λ/2 ⇒ λ ≤ 8. Therefore, λ = 8 satisfies both μ⁴σ ∈ L_∞ and μ^λ− 4σ ∈ L_∞.

Equation 45 implies that μ²ω_e ∈ L_∞. Also, since $\boldsymbol {\omega }_{e}^{T}(t)\boldsymbol {J}\boldsymbol {\omega }_{e}(t) \leq \mu ^{-4}(t)\bar {V}$, then $\lim _{t \to t_{f}}\boldsymbol {\omega }_{e}^{T}(t)\boldsymbol {J}\boldsymbol {\omega }_{e}(t) = 0 \implies \lim _{t \to t_{f}}\boldsymbol {\omega }_{e}(t) = 0$.

Given that $\lim _{t \to t_{f}}\boldsymbol {\omega }_{e}(t) = 0$ and $\lim _{t \to t_{f}}\boldsymbol {\omega }_{r}(t) = \lim _{t \to t_{f}}-\phi \mu ^{2}(t)\boldsymbol {\sigma }(t) = 0$ (for λ = 8), then $\lim _{t \to t_{f}}\boldsymbol {\omega }(t) = \lim _{t \to t_{f}}\boldsymbol {\omega }_{e}(t) + \lim _{t \to t_{f}}\boldsymbol {\omega }_{r}(t) = 0$.

Therefore, by choosing λ = 8 we have that the control law of Eq. 35 is a sum of bounded terms, implying that u ∈ L_∞. In addition, $\lim _{t \to t_{f}}\boldsymbol {\sigma }(t) = 0$ and $\lim _{t \to t_{f}}\boldsymbol {\omega }(t) = 0$, accomplishing the desired control objectives. One should also note that there are no guarantees that $\lim _{t \to t_{f}}\boldsymbol {u}(t) = 0$, as is the case for the disturbance-free control.

Tracking Control

In the previous section, we developed a stabilizing controller that takes the system to the origin. In this section, we generalize the solution for tracking a desired trajectory.

Assume a desired trajectory given by a desired orientation signal σ_d(t) and a desired angular velocity signal ω_d(t). The objective is to reach the desired trajectory at time t = t_f, i.e., δσ(t_f) = 0 and δω(t_f) = 0, where $\delta \boldsymbol {\sigma }(t) \triangleq \boldsymbol {\sigma }(t) \otimes \boldsymbol {\sigma }_{d}^{-1}(t)$ is the reference attitude error and $\delta \boldsymbol {\omega }(t) \triangleq \boldsymbol {\omega }(t) - \boldsymbol {C}(\delta \boldsymbol {\sigma })\boldsymbol {\omega }_{d}(t)$ is the angular velocity error expressed in the true orientation’s frame of reference. The matrix C(δσ) is the direction cosine matrix equivalent to the rotation δσ (see Eq. 6) and satisfies $\dot {\boldsymbol {C}}(\delta \boldsymbol {\sigma }) = -\delta \boldsymbol {\omega }^{*}\boldsymbol {C}(\delta \boldsymbol {\sigma })$. We assume that the quantities σ_d(t), ω_d(t), and $\dot {\boldsymbol {\omega }}_{d}(t)$ are fully specified as part of the tracking control objective.

As in the previous section, we first assume that the error dynamics for $\delta \dot {\boldsymbol {\sigma }}(t)$ is driven by a signal δω_r(t) as follows:

$$ \delta \dot{\boldsymbol{\sigma}}(t) = \boldsymbol{g}(\delta \boldsymbol{\sigma})\delta \boldsymbol{\omega}_{r}(t), $$

(46)

where $\boldsymbol {g}(\delta \boldsymbol {\sigma }) \triangleq \frac {1}{4}\boldsymbol {B}(\delta \boldsymbol {\sigma })$.

We can choose the control law

$$ \delta \boldsymbol{\omega}_{r}(t) = -\phi\mu^{2}(t)\delta \boldsymbol{\sigma}(t), $$

(47)

which was already shown to lead to $\lim _{t \to t_{f}} \delta \boldsymbol {\sigma }(t) = 0$. Also, we’ve already proven that the control law given by Eq.47 is realizable and that $\lim _{t \to t_{f}} \delta \boldsymbol {\omega }_{r}(t) = 0$.

In order to control the tracking error dynamics, we need to stabilize the equations of motion below:

$$ \left\{\begin{array}{llll} \delta \dot{\boldsymbol{\sigma}}(t) = \boldsymbol{g}(\delta \boldsymbol{\sigma})\delta\boldsymbol{\omega}(t) \\ \boldsymbol{J}\dot{\boldsymbol{\omega}}(t) = -\boldsymbol{\omega}^{*}(t) \boldsymbol{J}\boldsymbol{\omega}(t) + \boldsymbol{u}(t) + \boldsymbol{d}(t) \end{array}\right.. $$

(48)

In order to achieve stability, we define the angular velocity error signal $\delta \boldsymbol {\omega }_{e}(t) \triangleq \delta \boldsymbol {\omega }(t) - \delta \boldsymbol {\omega }_{r}(t)$. The derivative of Jδω_e(t) is given by:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{J}\delta\dot{\boldsymbol{\omega}}_{e}(t) &=& \boldsymbol{J}\delta\dot{\boldsymbol{\omega}}(t) - \boldsymbol{J}\delta\dot{\boldsymbol{\omega}}_{r}(t) \\ &=& \boldsymbol{J}\dot{\boldsymbol{\omega}}(t) - \boldsymbol{J}\dot{\boldsymbol{C}}(\delta\boldsymbol{\sigma})\boldsymbol{\omega}_{d}(t) - \boldsymbol{J}\boldsymbol{C}(\delta\boldsymbol{\sigma})\dot{\boldsymbol{\omega}}_{d}(t) - \boldsymbol{J}\delta\dot{\boldsymbol{\omega}}_{r}(t) \\ &=& -\boldsymbol{\omega}^{*}(t) \boldsymbol{J}\boldsymbol{\omega}(t) + \boldsymbol{u}(t) + \boldsymbol{d}(t) + \boldsymbol{J}\delta\boldsymbol{\omega}^{*}(t)\boldsymbol{C}(\delta\boldsymbol{\sigma})\boldsymbol{\omega}_{d}(t) - \boldsymbol{J}\boldsymbol{C}(\delta\boldsymbol{\sigma})\dot{\boldsymbol{\omega}}_{d}(t) - \boldsymbol{J}\delta\dot{\boldsymbol{\omega}}_{r}(t), \end{array} $$

(49)

where $\delta \dot {\boldsymbol {\omega }}_{r}(t)$ can be obtained by differentiating Eq. 47:

$$ \delta\dot{\boldsymbol{\omega}}_{r}(t) = -\phi \mu^{2}(t) \left[\begin{array}{llll} \frac{2}{t_{f}}\mu(t)\delta \boldsymbol{\sigma}(t) + \boldsymbol{g}(\delta \boldsymbol{\sigma})\delta\boldsymbol{\omega}(t) \end{array}\right]. $$

(50)

We choose the control law:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{u}(t) &=& -\left( \begin{array}{llll} \frac{1}{2}k\boldsymbol{J} + \frac{2}{t_{f}}\boldsymbol{J} + \frac{1}{2}\boldsymbol{I} \end{array}\right) \mu^{2}(t)\delta\boldsymbol{\omega}_{e}(t) - \frac{1}{2}\mu^{\lambda - 4}(t)\boldsymbol{\sigma}(t) + \boldsymbol{\omega}^{*}(t)\boldsymbol{J}\boldsymbol{\omega}(t) + \boldsymbol{J}\dot{\boldsymbol{\omega}}_{r}(t) \\ &&- \boldsymbol{J}\delta\boldsymbol{\omega}^{*}(t)\boldsymbol{C}(\delta\boldsymbol{\sigma})\boldsymbol{\omega}_{d}(t) + \boldsymbol{J}\boldsymbol{C}(\delta\boldsymbol{\sigma})\dot{\boldsymbol{\omega}}_{d}(t). \end{array} $$

(51)

Replicating the same analysis as in the stabilization case, it is possible to show that the tracking error converges to zero: $\lim _{t \to t_{f}}\delta \boldsymbol {\sigma }(t) = 0$ and $\lim _{t \to t_{f}}\delta \boldsymbol {\omega }(t) = 0$. In addition, it is possible to use the same arguments as before to show that the control law from Eq. 51 is realizable (both in the presence and absence of disturbances).

Practical Considerations

We have proven in the previous sections that the control laws Eqs. 35 and 51 are bounded even in the presence of disturbances. Still, there are some practical aspects that have to be considered when utilizing these controller designs.

An important matter that arises in any real implementation concerns the feedback control using noisy measurements. Assuming a measurement model with zero-mean additive noise, the designed control laws cannot guarantee to drive the system to the origin anymore. As t approaches t_f, μ(t) increases unboundedly and amplifies the measurement noise that is introduced into the system through Eqs. 35 or 51. Instead of being driven to the origin, the system states converge to a time-varying residual set whose extent changes as a function of μ(t).

A simple saturation heuristic that can be used to remedy the noise amplification is to bound μ(t) as follows:

$$ \mu(t) = \left\{\begin{array}{llll} \frac{t_{f}}{t_{f} - t}, \quad t \in [0, \kappa t_{f}) \\ \frac{t_{f}}{t_{f} - \kappa t_{f}}, \quad t \in [\kappa t_{f}, \infty) \end{array}\right., $$

(52)

for some user-chosen κ ∈ (0,1). This heuristic avoids μ(t) from becoming unbounded and thereby eliminating the possibility of increasingly amplifying the measurement noise.

A judicious choice of κ in Eq. 52 depends on the measurement noise characteristics, as well as the final time t_f. As κ approaches 0, the risk is that the system might not reach an acceptably small residual set within the prescribed finite time. Alternatively, as κ approaches 1, the noise amplification might be too high, demanding too much on the actuators. Therefore, a rational choice of κ would be one that caps the signal μ(t) as soon as the system reaches to within a small enough residual set.

In order to identify whether or not the system trajectories are within the residual set, one can perform a rigorous analysis to characterize the measure of the residual set as a function of noise variance, initial states and final time. Alternatively, our experience based on extensive numerical simulations of the control laws Eqs. 35 and 51 shows that it is possible to determine whether the system has reached the residual set by analyzing the Fast Fourier Transform (FFT) of the measured angular velocity ω (δω for the tracking case) and identifying the instant when the high-frequencies (mostly noise) dominates the measured signal.

Finite-time (or even infinite time) convergence to the origin in the presence of noise is unattainable, given that the controller attempts to converge to a measured zero, which is not the true zero. Once the system states reach within a residual set, we cannot really claim that there is any advantage in using the control law from Eqs. 35 or 51 with respect to other works in the literature, including non-finite controllers. This means that one can run the finite-time controller until the system reaches the residual set, then switch to some other classical control law, such as a Proportional-Derivative controller [6, 10, 11] tuned with optimal feedback gains (minimizing actuation energy or residual set measure).

Simulation Results

This section presents some simulation results for the designed control laws. In the absence of measurement noise, we show that the designed control laws drive the system to zero error as expected. Section “Perfect Measurements” presents results for the control being applied in the absence of measurement noise, while Section “Noise Corrupted Measurements” shows the results for the control law with noisy measurements. Our simulations are performed for final time t_f = 30s.

For all simulations, the initial orientation is given by a rotation of ψ(0) = π around the axis $\hat {\boldsymbol {e}}(0) = 1/\sqrt {3}\left [\begin {array}{llll}1, & 1, & 1 \end {array}\right ]^{T}$, and the initial angular velocity is given by $\boldsymbol {\omega }(0) = \left [\begin {array}{llll} -0.03, & 0.04, & -0.05 \end {array}\right ]^{T}$. The inertia matrix is given by:

$$ \boldsymbol{J} = \left[\begin{array}{llll} 95 & -0.69 & 0.18 \\ -0.69 & 190 & 0.12 \\ 0.18 & 0.12 & 142.5 \end{array}\right] $$

(53)

Perfect Measurements

This section presents simulation results for attitude stabilization using noise-free measurements. We are able to demonstrate that the system converges to arbitrary final configurations for arbitrary initial conditions. We implement μ(t) with saturation as in Eq. 52 with κ = 0.995, avoiding the singularity at t = t_f.

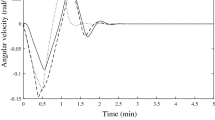
Figure 1 shows the result for the stabilization of the system to the origin using the control law from Eq. 35. Values below 2.20 ⋅ 10^− 16 are considered zero and are not shown on the log plot. We can see that the system is being driven towards the origin increasingly faster until the machine zero is reached. Notice that the states (ω(t) and σ(t)) and the inputs (u(t)) all converge to zero. The log plots fade after 20 seconds, but one should have in mind that this is the double precision zero, not the mathematical zero. The mathematical zero should only happen at exactly t = t_f as per our proofs.

Fig. 1

Time histories of state trajectories for the set-point regulation case with perfect measurements

Figure 2 shows the result for the stabilization of a perturbed system to the origin using the control law from Eq. 35 with λ = 8. The disturbance is constant and given by $d(t) = \left [\begin {array}{llll} 1, & 1, & 1 \end {array}\right ]^{T}$. The angular velocity ω(t) reaches zero before the terminal time, while ||σ(t_f)|| = 3.62 ⋅ 10^− 12. In steady state, the input torque compensates the disturbance signal $\boldsymbol {u}(t) \to \left [\begin {array}{llll} -1, & -1, & -1 \end {array}\right ]^{T}$.

Fig. 2

Time histories of state trajectories for the set-point regulation case with perfect measurements and applied disturbances

Figure 3 shows a result for the stabilization of the system to a tumbling configuration, using the control law from Eq. 51. The desired trajectory follows the differential equation:

$$ \left\{\begin{array}{llll} \dot{\boldsymbol{\sigma}}_{d}(t) = \boldsymbol{g}(\boldsymbol{\sigma}_{d})\boldsymbol{\omega}_{d}(t) \\ \boldsymbol{J}\dot{\boldsymbol{\omega}_{d}}(t) = -\boldsymbol{\omega}_{d}^{*}(t) \boldsymbol{J}\boldsymbol{\omega}_{d}(t) \end{array}\right., $$

(54)

with $\boldsymbol {\sigma }_{d}(0) = -1/\sqrt {3}\left [\begin {array}{llll}1, & 1, & 1 \end {array}\right ]^{T}$, $\boldsymbol {\omega }_{d}(0) = \left [\begin {array}{llll}0.01, & 0.01, & 0.01 \end {array}\right ]^{T}$. We can see that, for this scenario, the states of the error dynamics converge to “machine-zero” sometime after about 20s. The states (ω(t) and σ(t)) and the input torques u(t) all converge to zero.

Fig. 3

Time histories of state trajectory errors for the trajectory tracking case with perfect measurements

Noise Corrupted Measurements

In order to test the presented algorithm in presence of noise, we add measurement noise that is typical for a spacecraft with a star tracker, a gyroscope, and is executing an onboard state estimation algorithm. We assume that the state estimator is executing at a rate of 100Hz, and that it produces angular velocity measurements with standard deviation σ_ω = 0.002rad/s and attitude measurements with angular orientation error having standard deviation of σ_ϕ = 2arcsec= 9.7 ⋅ 10^− 6rad (in fact, commercial star tracker standard deviation is typically below 1.5arcsec [12]).

Figure 4 shows a result for the stabilization of the system to the origin using the two heuristics described in Section “Practical Considerations” for measurement noise accommodation. The blue plot implements μ(t) as in Eq. 52 with a fixed value of κ = 0.85 (Fixed Kappa Method - FKM). The red plot implements the FFT heuristic described in Section “Practical Considerations” by analyzing the FFT of ||ω|| over a window of 256 measurements, and tracking the instant at which frequencies above 10Hz dominate over frequencies below 10Hz.

Fig. 4

System convergence to the origin with noisy measurements. The blue plot shows the controller that caps μ(t) at κ = 0.85, while the red plot shows the controller that detects the switching time through the FFT method

We can see in the blue plot of Fig. 4 that even though the state errors reach a residual set sometime after 13s, the controller gains keep increasing until t = 25.5s. Because of this, the FKM controller demands more control torque on average than the one using the FFT method, which capped the value of μ(t) at t = 12.22s. In average, the FKM results get to a narrower residual set for δσ than the FFT results, but the residual set for δω is larger in the FKM results than it is in FFT one.

Conclusion

In this paper, we have introduced a finite-time controller for fully-actuated rigid-body attitude dynamics. The feedback control law is stablished using Lyapunov’s direct method, regulating the system’s configuration from any arbitrary initial state to any final one within user-specified finite transfer time t_f even in the presence of disturbances. In order to achieve finite-time regulation, the feedback gain grows unbounded as time approaches t_f.

We have presented simulation results, demonstrating the efficacy of the controller in reaching the desired configuration within finite time. In presence of noise, the system trajectories are shown to converge within a residual set and we propose mechanisms to avoid unnecessary amplification of noise.

An interesting avenue for further work would be seeking the design of a finite-time controller for attitude dynamics without going through the backstepping process, as in the current work. An obvious downside of the backstepping design is that the designed control laws (35 and 51) are algebraically heavy due to the fact that they partially compensate for the “non-working” gyroscopic terms in the attitude dynamics equations (for example, the ω^∗Jω term). On the other hand, the literature for asymptotic attitude stabilization (not finite-time) is abundant with control designs that can be obtained without gyroscopic compensation [6, 10].

Appendices

Appendix A

In this section, we prove that if:

$$ \mu^{\lambda}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) \leq V_{0}(0)\exp \left[\begin{array}{llll} -kt_{f}\cdot\bar{\mu}(t) \end{array}\right], $$

(55)

then $\mu ^{\alpha _{1}} \boldsymbol {\sigma } \in L_{\infty }, \forall \alpha _{1} \in \mathbb {R}$.

Starting from Eq. 55, we use the definition $\bar {\mu }(t) \triangleq \mu (t) - 1$ to get:

$$ \begin{array}{@{}rcl@{}} \mu^{\lambda}(t) \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) &\leq& V_{0}(0)\exp \left[\begin{array}{llll} -kt_{f}\cdot(\mu(t) - 1) \end{array}\right] \\ &= &V_{0}(0)e^{kt_{f}} \exp \left[\begin{array}{llll} -kt_{f} \cdot \mu(t) \end{array}\right] \\ &= &\alpha_{2} \exp \left[\begin{array}{llll} -kt_{f} \cdot \mu(t) \end{array}\right], \end{array} $$

(56)

where $\alpha _{2} \triangleq V_{0}(0)e^{kt_{f}} > 0$.

Defining $\beta (t) \triangleq \exp \left [\begin {array}{llll} -kt_{f}\cdot \mu (t) \end {array}\right ]$, it follows that:

$$ \begin{array}{@{}rcl@{}} \mu^{\lambda}(t)\ln\left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) &\leq& \alpha_{2} \beta(t) \\ \ln \left( \begin{array}{llll} 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) \end{array}\right) &\leq& \alpha_{2} \mu^{-\lambda}(t)\beta(t) \\ 1 + \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) &\leq& \exp \left[\begin{array}{llll} \alpha_{2} \mu^{-\lambda}(t)\beta(t) \end{array}\right] \\ \boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) &\leq &\exp \left[\begin{array}{llll} \alpha_{2} \mu^{-\lambda}(t)\beta(t) \end{array}\right] - 1 \\ \mu^{2\alpha_{1}}(t)\boldsymbol{\sigma}^{T}(t) \boldsymbol{\sigma}(t) &\leq& \mu^{2\alpha_{1}}(t) \left[\begin{array}{llll} \exp \left[\begin{array}{llll} \alpha_{2} \mu^{-\lambda}(t)\beta(t) \end{array}\right] - 1 \end{array}\right] \\ ||\mu^{\alpha_{1}}(t)\boldsymbol{\sigma}(t)||^{2} &\leq& \frac{\exp \left[\begin{array}{llll} \alpha_{2} \mu^{-\lambda}(t)\beta(t) \end{array}\right] - 1} {\mu^{-2\alpha_{1}}(t)}. \end{array} $$

(57)

In order to show that the signal $f(t) \triangleq ||\mu ^{\alpha _{1}}(t)\boldsymbol {\sigma }(t)||^{2}$ is bounded, we need to evaluate the limit as t → t_f. Taking the limit on both sides:

$$ \lim\limits_{t \to t_{f}}f(t) \leq \lim\limits_{t \to t_{f}}\frac{\exp \left[\begin{array}{llll} \alpha_{2} \mu^{-\lambda}(t)\beta(t) \end{array}\right] - 1} {\mu^{-2\alpha_{1}}(t)}. $$

(58)

The above limit can be rewritten as:

$$ \lim\limits_{t \to t_{f}}f(t) \leq \lim\limits_{\mu \to \infty}\frac{\exp \left[\begin{array}{llll} \alpha_{2} \mu^{-\lambda} \exp \left[\begin{array}{llll} -k\cdot t_{f}\cdot\mu \end{array}\right] \end{array}\right] - 1} {\mu^{-2\alpha_{1}}}. $$

(59)

Assuming that λ < 2α₁, Lemmas 1 and 2 are used to prove that the right-hand side of Eq. 59 is equal to zero, implying that $||\mu ^{\alpha _{1}}(t)\boldsymbol {\sigma }(t)||^{2} \in L_{\infty }, \forall \alpha _{1} > \lambda /2$. In addition, since $||\mu ^{\eta _{1}}(t)\boldsymbol {\sigma }(t)||^{2} \leq ||\mu ^{\eta _{2}}(t)\boldsymbol {\sigma }(t)||^{2}$, for η₁ ≤ η₂, then $||\mu ^{\alpha _{1}}(t)\boldsymbol {\sigma }(t)||^{2} \in L_{\infty }, \forall \alpha _{1} \in \mathbb {R}$.

Lemma 1

For any finite real constantsα₁≠ 0,α₂ > 0,γ₁ > 0,γ₂ > 0, then:

$$ \lim\limits_{x \to 0+} \alpha_{1} x^{-\gamma_{1}}exp\left[\begin{array}{llll} -\alpha_{2} x^{-\gamma_{2}} \end{array}\right] = 0. $$

(60)

Proof

Making the substitution $y = x^{-\gamma _{2}}$, then:

$$ \lim\limits_{x \to 0+} \alpha_{1} x^{-\gamma_{1}}exp\left[\begin{array}{llll} -\alpha_{2} x^{-\gamma_{2}} \end{array}\right] = \lim\limits_{y \to \infty} \alpha_{1} y^{\gamma_{3} + \gamma_{4}}e^{-\alpha_{2} y}, $$

(61)

where $\gamma _{3} \in \mathbb {N} \triangleq \lfloor \gamma _{1}/\gamma _{2} \rfloor$ and $\gamma _{4} \in [0, 1) \triangleq \gamma _{1}/\gamma _{2} - \gamma _{3}$.

One can notice that the limit in Eq. 61 is a product of zero with ∞, which can be solved for by using L’Hospital’s rule. Defining $\gamma _{5} \triangleq \gamma _{3} + \gamma _{4}$, we apply L’Hospital’s rule γ₃ times, leading to:

$$ \begin{array}{@{}rcl@{}} \lim_{y \to \infty} \alpha_{1} y^{\gamma_{5}}e^{-\alpha_{2} y} &= &\lim\limits_{y \to \infty} -\alpha_{1} \alpha_{2} \gamma_{5} y^{\gamma_{5}-1}e^{-\alpha_{2} y} \\ &= &\lim\limits_{y \to \infty} \alpha_{1} {\alpha_{2}^{2}} \gamma_{5}(\gamma_{5}-1) y^{\gamma_{5}-2}e^{-\alpha_{2} y} \\ &= &\cdots \\ &= &\lim\limits_{y \to \infty} (-1)^{\gamma_{3}}\alpha_{1} \alpha_{2}^{\gamma_{3}} \gamma_{5}(\gamma_{5}-1)\cdots(\gamma_{5}-\gamma_{3}) y^{\gamma_{4}}e^{-\alpha_{2} y}. \end{array} $$

(62)

If γ₄ = 0, then the proof is complete. However, if γ₄ ∈ (0, 1), then we need to use L’Hospital’s rule one more time:

$$ \begin{array}{@{}rcl@{}} \lim\limits_{y \to \infty} \alpha_{1} y^{\gamma_{5}}e^{-\alpha_{2} y} &= &\lim\limits_{y \to \infty} (-1)^{\gamma_{3}+1}\alpha_{1} \alpha_{2}^{\gamma_{3}+1} \gamma_{5}(\gamma_{5}-1)\cdots(\gamma_{5}-\gamma_{3})\gamma_{4} y^{\gamma_{4}-1}e^{-\alpha_{2} y} = 0. \end{array} $$

(63)

Lemma 2

For any finite real constantsα₁ > 0,α₂ > 0, and0 < γ₁ ≤ γ₂ < γ₃,then$\lim _{x \to \infty }f(x) = 0$,where:

$$ f(x) = \frac{\exp \left[\begin{array}{llll} \alpha_{1} x^{-\gamma_{2}}\exp\left[\begin{array}{llll} -\alpha_{2} x^{\gamma_{1}} \end{array}\right] \end{array}\right] - 1} {x^{-\gamma3}}. $$

(64)

Proof

Defining $y \triangleq x^{-\gamma _{3}}$, we have that $y^{-\gamma _{4}} = x^{\gamma _{1}}$, and $y^{\gamma _{5}} = x^{-\gamma _{2}}$, where $\gamma _{4} \triangleq \frac {\gamma _{1}}{\gamma _{3}}$ and $\gamma _{5} \triangleq \frac {\gamma _{2}}{\gamma _{3}}$. Since 0 < γ₁ ≤ γ₂ < γ₃, then 0 < γ₄ ≤ γ₅ < 1. The limit can be rewritten as:

$$ \lim\limits_{x \to \infty}f(x) = \lim\limits_{y \to 0^{+}}f(y) = \frac{\exp \left[\begin{array}{llll} \alpha_{1} y^{\gamma_{5}}\exp\left[\begin{array}{llll} -\alpha_{2} y^{-\gamma_{4}} \end{array}\right] \end{array}\right] - 1} {y}. $$

(65)

For notation simplicity, we define $\beta (y) \triangleq \exp \left [\begin {array}{llll} -\alpha _{2} y^{-\gamma _{4}} \end {array}\right ]$, leading to:

$$ \lim\limits_{y \to 0^{+}}f(y) = \lim\limits_{y \to 0^{+}}\frac{\exp \left[\begin{array}{llll} \alpha_{1} y^{\gamma_{5}} \beta(y) \end{array}\right] - 1} {y}. $$

(66)

It is straightforward to see that $\lim _{y \to 0^{+}}\beta (y) = 0$ and that $\lim _{y \to 0^{+}}e^{\alpha _{1} y^{\gamma _{5}} \beta (y)} = 1$. Since this limit is a ratio of zero with zero, we can use L’Hospital’s rule to show that the right-hand side of Eq. 66 converges to zero as y → 0⁺. We define the numerator signal as:

$$ n(y) \triangleq e^{\alpha_{1} y^{\gamma_{5}}\beta(y)} - 1. $$

(67)

Clearly, it is sufficient to prove that if $\lim _{y \to 0^{+}}\frac {dn(y)}{dy} = 0$, then

$$ \lim\limits_{y \to 0^{+}}\frac{e^{\alpha_{1} y^{\gamma_{5}}\beta(y)} - 1} {y} = 0, $$

(68)

implying that $\lim _{y \to 0^{+}}f(y) = 0$. Using the notation $f^{\prime } \triangleq \frac {\partial f}{\partial y}$ the derivative of n(y) is given by:

$$ n^{\prime}(y) = \alpha_{1} \left( \begin{array}{llll} \frac{\gamma_{5}}{y^{\gamma_{6}}}\beta(y) + y^{\gamma_{5}}\beta^{\prime}(y) \end{array}\right)e^{\alpha_{1} y^{\gamma_{5}}\beta(y)}, $$

(69)

where γ₆ > 0 is defined as $\gamma _{6} \triangleq 1 - \gamma _{5}$. Given that

$$ \beta^{\prime}(y) = \alpha_{2} \gamma_{4} y^{-\gamma_{4} - 1}\exp \left[\begin{array}{llll} -\alpha_{2} y^{-\gamma_{4}} \end{array}\right] = \frac{\alpha_{2} \gamma_{4}}{y^{\gamma_{7}}}\beta(y), $$

(70)

for $\gamma _{7} \triangleq 1 + \gamma _{4} > 1$, we can substitute Eq. 70 into Eq. 69:

$$ n^{\prime}(y) = \alpha_{1} \left( \begin{array}{llll} \frac{\gamma_{5}}{y^{\gamma_{6}}}\beta(y) + \frac{\alpha_{2} \gamma_{4}}{y^{\gamma_{7} - \gamma_{5}}}\beta(y) \end{array}\right)e^{\alpha_{1} y^{\gamma_{5}}\beta(y)}. $$

(71)

One should note that since γ₇ > 1 and 0 < γ₅ < 1, then γ₇ − γ₅ > 0. Using Lemma 1 and the definition $\beta (y) \triangleq \exp \left [\begin {array}{llll} -\alpha _{2} y^{-\gamma _{4}} \end {array}\right ]$, then:

$$ \left\{\begin{array}{llll} \lim_{\xi \to 0^{+}} \frac{\gamma_{5}}{y^{\gamma_{6}}}\beta(y) = 0, \\ \lim_{\xi \to 0^{+}} \frac{\alpha_{2} \gamma_{4}}{y^{\gamma_{7} - \gamma_{5}}}\beta(y) = 0 \end{array}\right.. $$

(72)

Remembering that $\lim _{y \to 0^{+}}\beta (y) = 0$, and that $\lim _{y \to 0^{+}}e^{\alpha _{1} y^{\gamma _{5}}\beta (y)} = 1$, then $\lim _{y \to 0^{+}} n^{\prime }(y) = 0$, which implies that $\lim _{x \to \infty }f(x) = 0$.

Appendix B

In this section, we show that the inequality

$$ \mu^{\lambda}(t)\ln(1 + \boldsymbol{\sigma}^{T}(t)\boldsymbol{\sigma}(t)) \leq \bar{V}, $$

(73)

for a constant $\bar {V} > 0$, implies that μ^λ/2σ ∈ L_∞ and that $\lim _{t \to t_{f}}\mu ^{\rho }(t)\boldsymbol {\sigma }(t) = 0, \forall \rho < \lambda /2$.

Starting from Eq. 73, we have that:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\sigma}^{T}(t)\boldsymbol{\sigma}(t) &\leq& \exp \left[\begin{array}{llll} \bar{V}\mu^{-\lambda}(t) \end{array}\right] - 1 \end{array} $$

(74)

$$ \begin{array}{@{}rcl@{}} \mu^{\lambda}(t)\boldsymbol{\sigma}^{T}(t)\boldsymbol{\sigma}(t) &\leq& \mu^{\lambda}(t) \left[\begin{array}{llll} \exp \left[\begin{array}{llll} \bar{V}\mu^{-\lambda}(t) \end{array}\right] - 1 \end{array}\right] \end{array} $$

(75)

$$ \begin{array}{@{}rcl@{}} ||\mu^{\lambda/2}(t)\boldsymbol{\sigma}(t)||^{2} &\leq& \frac{\exp \left[\begin{array}{llll} \bar{V}\mu^{-\lambda}(t) \end{array}\right] - 1}{\mu^{-\lambda}(t)}. \end{array} $$

(76)

In order to show that the signal $f(t) \triangleq ||\mu ^{\lambda /2}(t)\boldsymbol {\sigma }(t)||^{2}$ is bounded, we need to evaluate the limit as t → t_f. Taking the limit on both sides:

$$ \lim\limits_{t \to t_{f}}f(t) \leq \lim\limits_{t \to t_{f}} \frac{\exp \left[\begin{array}{llll} \bar{V}\mu^{-\lambda}(t) \end{array}\right] - 1}{\mu^{-\lambda}(t)}. $$

(77)

Assuming λ > 0, the above limit can be rewritten as:

$$ \lim\limits_{t \to t_{f}}f(t) \leq \lim\limits_{\mu \to \infty} \frac{\exp \left[\begin{array}{llll} \bar{V}\mu^{-\lambda} \end{array}\right] - 1}{\mu^{-\lambda}}. $$

(78)

Defining $\xi (t) \triangleq \mu ^{-\lambda }(t)$, we have that:

$$ \lim\limits_{t \to t_{f}}f(t) \leq \lim\limits_{\xi \to 0^{+}} \frac{\exp \left[\begin{array}{llll} \bar{V}\xi \end{array}\right] - 1}{\xi}. $$

(79)

Since the above limit is a ratio of zero with zero, we can use L’Hospital’s rule:

$$ \begin{array}{@{}rcl@{}} \lim\limits_{t \to t_{f}}f(t) &\leq& \lim\limits_{\xi \to 0^{+}} \frac{\frac{d}{d\xi} \left[\begin{array}{llll} \exp \left[\begin{array}{llll} \bar{V}\xi \end{array}\right] - 1 \end{array}\right]}{\frac{d}{d\xi}\xi} \end{array} $$

(80)

$$ \begin{array}{@{}rcl@{}} &=& \lim\limits_{\xi \to 0^{+}} \bar{V} \exp \left[\begin{array}{llll} \bar{V}\xi \end{array}\right] \end{array} $$

(81)

$$ \begin{array}{@{}rcl@{}} &=& \bar{V} \end{array} $$

(82)

Therefore, $f(t) \triangleq ||\mu ^{\lambda /2}(t)\boldsymbol {\sigma }(t)||^{2}$ is bounded, i.e., μ^λ/2σ ∈ L_∞. Also, since $||\mu ^{\lambda /2}(t)\boldsymbol {\sigma }(t)||^{2} \leq \bar {V}$, then for any 𝜖 > 0 and constant ρ such that 2𝜖 + ρ = λ/2 we have that $||\mu ^{\rho }\boldsymbol {\sigma }(t)||^{2} \leq \mu ^{-\epsilon }(t)\bar {V}$, implying that $\lim _{t \to t_{f}} ||\mu ^{\rho }\boldsymbol {\sigma }(t)||^{2} = 0$.