1 Introduction

Chaotic dynamical systems are very complex nonlinear systems that display unpredictable and irregular behaviors. The main special feature of the chaotic systems is that a tiny change in the initial conditions and the system parameters leads to an enormous difference in the long-term behavior of the system. Since the pioneering work by Ott, Grebogi and Yorke in 1990 [1], chaos control and synchronization of autonomous chaotic and dynamical systems has received considerable attention in recent years [2–11]. On the other hand, with introducing some non-autonomous chaotic systems in engineering sciences and physics, chaos suppression of non-autonomous chaotic systems has received significant interest among many researchers and various control techniques for chaos suppression and synchronization of non-autonomous chaotic systems have been developed, which include adaptive control [12, 13], active control [14], sinusoidal state error feedback control [15], nonlinear control [16], fuzzy control [17], variable substitution control [18] and so on.

The centrifugal flywheel governor [19] is one of the most interesting and attractive rotational machine systems. It is a mechanical device that automatically controls the speed of an engine and avoids the damage caused by abrupt change of load torque. The centrifugal flywheel governors have found useful applications in many practical systems such as diesel engine, steam engine, gas turbine and so on. Recent research has recognized different kinds of the centrifugal flywheel governor systems with a rich variety of nonlinear behavior. Furthermore, it has been shown that these systems display a diverse range of dynamic behavior including regular and chaotic motions [20–28]. On the other hand, if a rotational machine system operates chaotically, the subsequently large broadband vibration may increase the likelihood of fatigue failure and shorten the system lifetime. Therefore, designing a controller to suppress the chaotic behavior of the rotational machine systems is an important issue.

In recent years, complex dynamics, chaos control, anti-control and synchronization of the centrifugal flywheel governor systems have been studied by researchers. In [20], the nonlinear dynamics of a non-autonomous centrifugal flywheel governor system and its synchronization have been studied. Regular and chaotic dynamics of both autonomous and non-autonomous rotational machines with a centrifugal governor subjected to an external disturbance have been studied in [21]. Zhang et al. [22] have studied complex dynamical behaviors of a class of centrifugal flywheel governor systems and have proposed a parametric open-plus-closed-loop approach for controlling their chaos. By numerically integrating the Lagrangian equations of motion, bifurcation and chaos of a non-autonomous centrifugal flywheel governor system have been investigated in [23]. Sotomayor et al. [24] have studied the Lyapunov stability and the Hopf bifurcation in a system coupling a hexagonal centrifugal governor with a steam engine. Ge and Jhuang [25] have investigated the chaos, its control and synchronization for a fractional-order rotational machine system with a centrifugal governor. Nonlinear dynamics and chaos control of a rotational machine with a hexagonal centrifugal governor and a spring considering the effects of external disturbances have been addressed in [26]. Chaos anti-control and synchronization of an autonomous rotational machine system with a hexagonal centrifugal governor have been reported in [27]. Ge and Lee [28] have studied the chaotic behavior of an autonomous rotational machine system with a hexagonal centrifugal governor and spring. They have considered the effects of time-delay and have proposed linear feedback control and adaptive control algorithms to suppress the chaos of the system.

However, all of the above-mentioned methods and control strategies have been proposed to suppress/synchronize chaos of the rotational machine systems asymptotically. In other words, these studies have guaranteed that the state trajectories of the system can converge to zero as time goes infinite. Nevertheless, from a practical engineering point of view, it is more valuable to control chaos of the centrifugal flywheel governor system in a finite time rather than merely asymptotically. To achieve faster convergence speed in control systems, the finite-time control method is an effective technique. Finite-time control means the optimality in settling time. Moreover, the finite-time control techniques have demonstrated better robustness and disturbance rejection properties [29]. On the other hand, in real world applications, the parameters of the chaotic systems are inevitably disturbed by external inartificial factors, such as temperature, voltage oscillation and mutual interfere among components, etc., and cannot be exactly known in advance. Since chaotic systems are very sensitive to any system parameter variations, the effects of unknown parameters may cause to instability of the chaotic system. Therefore, the effects of the unknown parameters should not be neglected in the chaos suppression of the centrifugal flywheel governor systems. However, to the best knowledge of the authors there is little result in the literature about the problem of finite-time chaos suppression of non-autonomous centrifugal flywheel governor systems with fully unknown parameters.

Based on the above discussion, in this paper the problem of finite-time chaos suppression of non-autonomous chaotic centrifugal flywheel governor systems with completely unknown parameters is investigated. To tackle the unknown parameters of the system, suitable adaptation laws are introduced. On the basis of the adaptation laws and finite-time control technique, an adaptive controller is designed to suppress the chaos of the uncertain non-autonomous centrifugal flywheel governor system in a given finite time. The finite-time stability and convergence of the closed-loop system are analytically proven. A numerical simulation is given to illustrate the robustness and applicability of the proposed technique and to validate the theoretical results of the paper.

2 Description of the system and problem formulation

In this section, first a brief description of a non-autonomous chaotic centrifugal flywheel governor system is given. Then, the problem of robust finite-time chaos suppression of the centrifugal flywheel governor with fully unknown parameters is formulated and the precise definition of the finite-time stability is presented.

2.1 Centrifugal flywheel governor system description

The mechanical centrifugal flywheel governor system [19] is schematically depicted in Fig. 1. The motor drives the flywheel to rotate with angular velocity ω. The flywheel is joined to the axis through a gear case, so the axis rotates with angular velocity nω. Rods 1 and 2 have length 1 and are joined to a hinge at the end of the axis. Both rods are also attached to a ball of mass m. The balls are also connected to a sleeve over the axis by rods 3 and 4. A linear spring of stiffness k is attached to the sleeve, covering the upper portion of the axis. The vapor’s flux Q into the engine is adjusted by a mechanical governor on the sleeve, which is set to make the flywheel rotate at a certain angular velocity ω 0. When Δω=ω−ω 0≠0, the balls will move outward or inward, and the sleeve will slide up or down [20].

Fig. 1
figure 1

Physical model of a mechanical centrifugal flywheel governor [20]

Full size image

With some assumptions, the motion of the mechanical non-autonomous centrifugal flywheel governor is given by [20]:

(1)

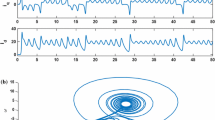
where φ is the angle between the rotational axis and the rods and n=3, l=1.5, a=0.8, w=1, e=0.3, b=0.4, I=1.2, α=0.611, F=0.3, g=9.8 are system parameters. For the above-mentioned parameters values the system (1) exhibits chaotic behavior [20]. The strange attractors of this system are illustrated in Fig. 2.

Fig. 2
figure 2

Strange attractors of the chaotic centrifugal flywheel governor system

Full size image

2.2 Formulation of finite-time chaos suppression problem

Defining \(x_{1} = \varphi, x_{2} = \dot{\varphi} , x_{3} = \omega\), one can rewrite the non-autonomous centrifugal flywheel governor system (1) with fully unknown parameters and control inputs as follows:

(2)

where x=[x 1,x 2,x 3]T is the state vector of the system and u(t)=[u 1(t),u 2(t)]T is the vector of control inputs.

Assume that the parameters n,l,a,w,e,b,I,α,F, and g are unknown in advance and consider θ=[θ 1,θ 2,θ 3,θ 4]T=[e,n 2,e+g/l,b]T and ψ=[ψ 1,ψ 2]T=[α/I,F/I+a]T as the vectors of the unknown parameters of the system (2). Then, the following assumption is made.

Assumption 1

It is assumed that the unknown vector parameters θ and ψ are bounded by

(3)

where ∥.∥ denotes the Euclidean norm in ℜn, and Θ and Ψ are known positive constants.

Definition 1

Consider the non-autonomous centrifugal flywheel governor system described by (2). If there exists a constant T=T(x(0))>0, such that

(4)

and ∥x(t)∥≡0 if t≥T, then the chaos suppression of the non-autonomous centrifugal flywheel governor system (2) is achieved in a finite time.

The main objective of this paper is that for the non-autonomous centrifugal flywheel governor system (2) with unknown parameters an adaptive control law u(t) is designed such that the chaos of the system is suppressed in finite time.

3 Design procedure of adaptive finite-time control scheme

In this section, an adaptive finite-time controller is designed to suppress the chaos of the chaotic non-autonomous centrifugal flywheel governor system (2) with unknown parameters. First, appropriate adaptation laws are derived to estimate the unknown parameters. Then, suitable adaptive control laws are proposed to stabilize the closed-loop system in a given finite time. Finally, the finite-time convergence and stability of the proposed control scheme are proved via the Lyapunov stability theory.

Lemma 1

([30]) Assume that a continuous, positive-definite function V(t) satisfies the following differential inequality:

(5)

where c>0,0<ξ<1 are two constants. Then, for any given t 0,V(t) satisfies the following inequality:

(6)

and V(t)≡0,∀t≥t 1 with t 1 given by

(7)

Lemma 2

For a 1,a 2,…,a n ∈ℜ, the following inequality holds:

(8)

This result is quite straightforward and the proof is omitted here.

In order to guarantee the finite-time chaos suppression of the chaotic non-autonomous centrifugal flywheel governor system (2), suitable control laws are proposed as follows:

(9)

where \(\hat{\theta} = [\hat{\theta}_{1}, \hat{\theta}_{2},\hat{\theta}_{3}, \hat{\theta}_{4}]^{T}\) and \(\hat{\psi} = [\hat{\psi}_{1}, \hat{\psi}_{2}]^{T}\) are estimations for unknown parameters θ and ψ, respectively, μ=min{η i }, i=1,2,3, η i >0, i=1,2,3 is a constant gain,  sgn(.) is the sign function, if x 2(t)=0 then \(\frac{x_{1}^{2}}{x_{2}\| x \|^{2}} = 0\) and if x(t)=0 then \(\frac{x_{3}}{\| x \|^{2}} = \frac{x_{2}}{\| x \|^{2}} = 0\).

To tackle the unknown parameters, the following adaptation laws are proposed:

(10)

where \(\hat{\theta}_{10}, \hat{\theta}_{20}, \hat{\theta}_{30},\hat{\theta}_{40}, \hat{\psi}_{10}\) and \(\hat{\psi}_{20}\) are the initial values of the adaptation parameters \(\hat{\theta}_{1},\hat{\theta}_{2}, \hat{\theta}_{3}, \hat{\theta}_{4}, \hat{\psi}_{1}\) and \(\hat{\psi}_{2}\), respectively.

Theorem 1

If the non-autonomous centrifugal flywheel governor system (2) with fully unknown parameters is controlled by the control laws (9) with the adaptation laws (10), then the system trajectories will converge to zero in finite time and the chaotic behavior of the system will be suppressed.

Proof

Choose a positive-definite Lyapunov function in the form of

(11)

Taking the time derivative of V(t), one has

(12)

Inserting \(\dot{x}_{i}\) from (2) into the above equation, yields

(13)

Knowing that all the parameters of the centrifugal flywheel governor system are positive [20], one obtains

(14)

Using \(\theta^{T}\dot{\hat{\theta}} = ex_{2}\sin x_{1}\cos x_{1} +n^{2}x_{2}x_{3}^{2}\sin x_{1}\cos x_{1} - (e + g/l)x_{2}\sin x_{1} -bx_{2}^{2}\) and \(\psi^{T}\dot{\hat{\psi}} = ax_{3}\cos x_{1}/I + (F/l +a)| x_{3} |\), we have

(15)

Introducing control inputs u 1(t) and u 2(t) from (9) into the right-hand side of the above inequality, one has

(16)

Using \(\hat{\theta}^{T}\dot{\hat{\theta}} = \hat{\theta}_{1}x_{2}\sin x_{1}\cos x_{1} + \hat{\theta}_{2}x_{2}x_{3}^{2}\sin x_{1}\*\cos x_{1} -\hat{\theta}_{3}x_{2}\sin x_{1} - \hat{\theta}_{4}x_{2}^{2},\hat{\psi}^{T}\dot{\hat{\psi}} = \hat{\psi}_{1}x_{3}\cos x_{1} +\hat{\psi}_{2}| x_{3} |\), \(( \frac{x_{1}^{2}}{\| x \|^{2}} ) + (\frac{x_{2}^{2}}{\| x \|^{2}} ) + ( \frac{x_{3}^{2}}{\| x \|^{2}} ) =1\) and x sgn(x)=|x|, one can obtain

(17)

Based on Lemma 2, we have

(18)

By Lemma 2, Assumption 1 and since \(\| \hat{\theta} - \theta\| \le\|\hat{\theta} \| + \| \theta\| \le\| \hat{\theta} \| + \varTheta\) and \(\|\hat{\psi} - \psi\| \le\| \hat{\psi} \| + \| \psi\| \le \| \hat{\psi} \|+ \varPsi\) are always satisfied, we have

(19)

Therefore, from Lemma 1, the system trajectories x(t) will converge to zero in the finite time \(T = \frac{\sqrt{2}}{\mu} ( \frac{1}{2}( \|x(0) \|^{2} + \| \hat{\theta} (0) - \theta\|^{2} + \| \hat{\psi} (0) -\psi\|^{2} ) )^{\frac{1}{2}}\). Hence the chaotic behavior of the non-autonomous centrifugal flywheel governor system (2) will be suppressed in finite time. Thus the proof is achieved completely. □

4 Numerical simulations

In this section, some numerical simulations are presented to validate the robustness and feasibility of the proposed finite-time controller in chaos suppression of the uncertain chaotic non-autonomous centrifugal flywheel governor system. The simulations are done using the MATLAB software. The parameters n=3, l=1.5, a=0.8, w=1, e=0.3, b=0.4, I=1.2, α=0.611, F=0.3 and g=9.8 are selected in the simulation to ensure the existence of chaos for the centrifugal flywheel governor system [20]. The parameters’ bounds Θ and Ψ are chosen equal to 10 and 2, respectively. The initial values of the system are chosen as x 1(0)=0.6, x 2(0)=0.7 and x 3(0)=0.15. The initial values of both adaptation vector parameters \(\hat{\theta}\) and \(\hat{\psi}\) are all set to 1. All the constant gains η 1, η 2 and η 3 are chosen equal to 1.

State trajectories of the uncertain chaotic non-autonomous centrifugal flywheel governor system (2) are depicted in Fig. 3, where the control inputs are activated at t=5 s. It can be seen that the system trajectories converge to zero quickly. This means that with applying the proposed adaptive controller, the non-autonomous centrifugal flywheel governor system (2) with unknown parameters is stabilized in a finite time and the closed-loop system is not chaotic anymore, and, therefore, there is no strange attractor. The time histories of the adaptation vector parameters \(\hat{\theta}\) and \(\hat{\psi}\) are shown in Figs. 4 and 5, respectively. Obviously, all adaptation parameters converge to some constants.

Fig. 3
figure 3

State trajectories of the controlled centrifugal flywheel governor system

Full size image
Fig. 4
figure 4

Time responses of the adaptation vector parameter \(\hat{\theta}\)

Full size image
Fig. 5
figure 5

Time responses of the adaptation vector parameter \(\hat{\psi}\)

Full size image

5 Conclusions

The problem of finite-time chaos suppression of rotational machine systems is studied in this paper. It is assumed that the parameters of the system are completely unknown in advance. To tackle the system unknown parameters, proper adaptation laws are designed. Using the Lyapunov stability theory and adaptation parameters, a finite-time adaptive controller is proposed. Numerical simulations reveal that the proposed controller works well for the finite-time chaos suppression of the chaotic non-autonomous centrifugal flywheel governor system, even when the system parameters are fully unknown. To note, the results of this paper are of practical utility to designers of rotational machines.