1 Introduction

Fractional calculus has been attracting the attention of scientists and engineers from 300 years ago. Since the nineties of the last century, fractional calculus has been rediscovered and applied in an increasing number of fields, namely in several areas of physics, control engineering, signal processing, and system modelling [1].

Since Hartley et al. have shown that there are chaotic solutions in fractional-order systems [2], there has been a surge of interest in control and synchronization of fractional-order chaotic systems. For example, control and synchronization of fractional-order Modified Van der Pol-Duffing systems is presented by Matouk in [3] using the active control method. Synchronization of different fractional-order chaotic systems via active control is studied in [4]. Synchronization of fractional-order Genesio–Tesi systems via active control and sliding mode control is reported by Faieghi and Delavari in [5]. Control of fractional Liu systems via the fuzzy fractional-order sliding mode is studied in [6]. In [7], synchronization of fractional chaotic systems with non-identical fractional orders is investigated. The authors used a compensation controller to make error dynamics dependent on the order of the response system and then derive an active control law to realize synchronization. Design of a sliding mode controller for a class of fractional-order chaotic systems is presented in [8], and in [9] an adaptive fuzzy approach is proposed for H∞ synchronization of uncertain fractional chaotic systems.

Most of the control methods proposed in the literature tackling with suppression and synchronization of fractional-order chaotic systems are nonlinear. For example, the active control law contains nonlinear terms used to cancel nonlinearities in the control systems. The sliding mode control method results a nonlinear control law integrated with a switching control law. The fuzzy-based methods are obviously nonlinear. Nonlinear controllers have complicated structure. Despite their high performance, from practical point of view, usually, implementation of nonlinear controllers is not suitable due to the complicated structure. Thus, it is desired to make the controllers simpler while maintaining their consistent performance. Linear controllers have much simpler structure than nonlinear controllers. Moreover, since chaotic systems are highly nonlinear and the stability theory of fractional-order nonlinear systems is still considered as an open problem, the stability problem of closed-loop fractional chaotic systems in the presence of a linear controller is a challenging problem. Note that most of existing methods rely on transforming the chaotic systems to linear ones by utilizing some form of nonlinear controllers. After that, a stability theory of fractional-order linear systems is applied; see, for example, [3, 4, 7].

In this paper, we employ a simple feedback controller to control of fractional chaotic systems. The control law is multivariable, but it is set to be linear and decoupling, which ease the implementation. Here, a decoupling control law means that each control input depends on only a single state. We consider a class of fractional chaotic systems and introduce a feedback controller. Since the chaotic systems are dissipative, it can be concluded that all the chaotic trajectories are bounded. Having this in mind, we treat with fractional-order chaotic systems as fractional-order LTI interval systems which their interval uncertainty can be determined readily by the bounds of chaotic states. Based on the theory of stabilization of interval LTI systems [10], the control problem is summarized to solving a LMI. Existence of a feasible solution for the LMI results in asymptotic stability of fractional-order LTI interval systems, which implies that the chaotic trajectories will be brought to the origin eventually. Moreover, the solution of LMI will give us appropriate values for the feedback gains. The idea is originally brought from [11] and in this present paper we extend the results to a class of chaotic systems, which several chaotic systems belongs to this class. The prominent feature of this controller is its simplicity and guarantee of closed-loop stability.

This paper is organized as follows: Mathematical preliminaries are presented in Sect. 2. Main results are included in Sect. 3. Numerical simulations are presented in Sect. 4, and concluding remarks are given in Sect. 5.

2 Mathematical preliminaries

2.1 Basic definitions

A fractional-order differentiator can be denoted by a general fundamental operator as a generalization of differential and integral operators. It is defined as follows:

$$ {}_{a}D_{t}^{q} = \left \{ \begin{array}{l@{\quad}l} \frac{d^{q}}{dt^{q}},& q > 0 \\ 1,& q = 0 \\ \int_{a}^{t} (d\tau)^{ - q},& q < 0 \end{array} \right . $$
(1)

where q is the fractional order, the constants a and t are the bounds of the operation. The three common definitions used for the general fractional differintegral are the Grünwald–Letnikov (GL) definition, the Riemann–Liouville (RL), and the Caputo definition. Let q be a rational number and n be the first integer which is not less than q, i.e. n−1<q<n.

Definition 1

The GL definition of q-th order of fractional derivative is given by

(2)

Definition 2

The RL definition q-th order of fractional derivative is given by

$$ {}_{a}D_{t}^{q}f(t) = \frac{1}{\Gamma (n - q)}\frac{d^{n}}{dt^{n}}\int_{0}^{t} (t - \tau)^{n - q - 1}f(\tau)\,d\tau $$
(3)

where n is the first integer which is not less than q, i.e. n−1<q<n and Γ is a Gamma function.

Definition 3

The Caputo definition q-th order of fractional derivative is given by

$$ {}_{a}D_{t}^{q}f(t) = \frac{1}{\Gamma (n - q)}\int_{a}^{t} (t - \tau)^{n - q - 1}f^{(n)} (\tau)\,d\tau $$
(4)

An in-depth discussion can be found in [1].

2.2 Fractional-order LTI interval system

A fractional-order LTI interval system is described as [10]

$$ D^{q}x = \breve{\mathrm{A}} x + \breve{\mathrm{B}} u $$
(5)

where the system matrices Ă and \(\breve{\mathrm{B}}\) are interval uncertain satisfying

(6)
(7)

The following notations are used in the following theorem:

(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)

where \(e_{i}^{p}\) is the p-column vector with the ith element being 1 and all the other being 0.

Theorem 1

[10] The interval system (5) with input u=Kx and 0<q<1 is asymptotically stablizable if there are a m×n real matrix X, a symmetric positive-definite real matrix Q, and four real positive scalars α 1,α 2,β 1, and β 2 such that

$$ \left [ \begin{array}{c@{\quad}c} \Gamma_{11} & \Gamma_{12} \\ \Gamma_{12} & \Gamma_{22} \end{array} \right ] < 0 $$
(16)

where

(17)
(18)
$$ \Gamma_{22} = - \mathit{diag}( \alpha_{1},\alpha_{2}, \beta_{1},\beta_{2} ) \otimes I_{2n} $$
(19)
(20)
(21)
(22)
(23)
(24)
(25)

and ⊗ denotes the Kronecker product. Moreover, a stabilization feedback gain matrix is given by

$$ K = XQ^{ - 1} $$
(26)

Note that the condition (16) given in the theorem is a LMI in X,Q,α 1,α 2,β 1,β 2, and it can be easily solved by various LMI solvers such as MATLAB’s Robust Control Toolbox.

2.3 Numerical methods for fractional-order differential equations

Since most of the fractional-order differential equations do not have exact analytic solutions, approximation and numerical techniques must be used. Several analytical and numerical methods have been proposed to solve the fractional-order differential equations. In [12], it is declared that frequency domain methods are not suitable for chaos recognizing. Hence, in the simulations of this paper, we employ an Adams-type predictor-corrector method proposed in [13–15]. To give the approximate solution of nonlinear fractional-order differential equations by means of this algorithm, consider the following differential equation:

(27)

This differential equation is equivalent to the Volterra integral equation

$$ y(t) = \sum_{k = 0}^{ \lceil q \rceil - 1} y_{0}^{(k)} \frac{t^{k}}{k!} + \frac{1}{\Gamma (q)}\int_{0}^{t} (t - s)^{q - 1}r\bigl(s,y(s)\bigr)\,ds $$
(28)

Now, set h=T/N,t n =nh(n=0,1,2,…,N). Then (28) can be discretized as follows:

(29)

where the predicted value y h (t n+1) is determined by

(30)

in which

$$ a_{j,n + 1} = \left\{ \begin{array}{l@{\quad}l} n^{q + 1} - (n - q)(n + 1)^{q},& j = 0 \\ (n - j + 2)^{q + 1} + (n - j)^{q + 1}\\ \quad{} - 2(n - j + 1)^{q + 1},& 1 \le j \le n \\ 1,& j = n + 1 \end{array} \right . $$

and

$$ b_{j,n + 1} = \frac{h^{q}}{q}\bigl( (n + 1 - j)^{q} - (n - j)^{q} \bigr). $$

In the simulations of this paper, we set the step size h=0.001.

3 Main results

Consider the following class of fractional-order differential equations:

(31)

where f(.),g(.),h(.) , and Φ(.) are smooth nonlinear functions. Many fractional-order chaotic systems belong to this class (see Table 1). In order to suppress the chaos governed by (31), let us introduce a multivariable control strategy with three control inputs as follows:

(32a)

or

(32b)
Table 1 Some of the chaotic systems which belongs to the proposed class
Full size table

We want to determine a simple linear control law to suppress the chaos. Here, we propose a decoupling control structure as follows:

$$ u_{1} = k_{1}x,\qquad u_{2} = k_{2}y,\qquad u_{3} = k_{3}z $$
(33)

This simple and decoupling structure ease in implementation. It is worth to notice that the chaotic systems are dissipative. This means that all the system orbits will ultimately be confined to a specific subset of zero volume and the asymptotic motion settles onto an attractor. As a result, all the states have bounded amplitude. This implies that, in a particular time t there are some positive constants c i ,i=1,…,4 such that the following boundness conditions hold:

(34)

Therefore, the system (32a), (32b) can be written in the form (5) with

(35)

By assuming that there exist X,Q,α 1,α 2,β 1,β 2 fulfilling the condition (16) in Theorem 1, the controller u=Kx,K=XQ −1, asymptotically suppresses the chaotic behavior of the fractional-order chaotic system (31) as desired. Moreover, in order to achieve the proposed decoupling control structure, we constrain X and Q being diagonal matrices.

4 Numerical simulations

Two fractional-order chaotic systems from the class of the chaotic systems (31) are employed as illustrative examples. They are fractional-order Liu system and fractional-order Lorenz system.

First, let us consider the fractional-order Liu system [6]

(36)

where a=e=1,b=2.5,c=5 , and k=m=4. It is obvious that the system (36) belongs to the class of chaotic systems (31) by choosing α=a,f(x,y,z)=−ey,β=−b,g(x,y,z)=−kz,γ=c,h(x,y,z)=mx, and Φ(x,y,z)=0. Thus, by adding three control inputs to the system, we can write (36) in the form of (32a), (32b) as follows:

(37)

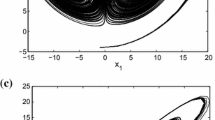
Next step is to determine the bounds of Ă and \(\breve{\mathrm{B}}\) for the system (37). Numerical simulations can be used here to determine these bounds. A set of the state trajectories of the system are shown in Fig. 1 for q=0.98 starting from various initial conditions. From the simulation curves, we found −8<x<5,−8<y<7, and −6<z<8. Thus, one can define the upper and lower bounds of the above functions as c 1=8,c 2=32,c 3=32, and c 4=0. Solving the LMI for the system (37) yields

$$Q = \left [ \begin{array}{c@{\quad}c@{\quad}c} 0.1666e + 8 & 0 & 0 \\ 0 & 0.1653e + 8 & 0 \\ 0 & 0 & 1.4055e + 8 \end{array} \right ] $$
$$X = \left [ \begin{array}{c@{\quad}c@{\quad}c} - 3.5598e + 8 & 0 & 0 \\ 0 & - 9.0719e + 8 & 0 \\ 0 & 0 & - 0.2610e + 8 \\\end{array} \right ] $$

and

$$K = \left [ \begin{array}{c@{\quad}c@{\quad}c} - 21.3707 & 0 & 0 \\ 0 & - 54.8760 & 0 \\ 0 & 0 & - 0.1857 \\\end{array} \right ] $$

Therefore, the control inputs are

(38)

In order to verify the effectiveness of the obtained controller, simulations have been carried out and the results are depicted in Fig. 2. It is shown that controller is capable to bring the chaotic trajectories to the origin magnificently.

Fig. 1
figure 1

State trajectories of fractional-order Liu system for various initial conditions

Full size image
Fig. 2
figure 2

State trajectories of fractional-order Liu system with the controller

Full size image

As another example, let us consider the stabilization problem of the fractional-order Lorenz system [8]

(39)

where a=10,b=28 and c=8/3 yield chaotic trajectory. By setting α=a,f(x,y,z)=a, β=1, g(x,y,z)=b−z, γ=c, h(x,y,z)=x and Φ(x,y,z)=0, it can be concluded that the system (39) is in the form of (31). Thus, by adding three control inputs to the system, we can write (38) in the form of (32a), (32b) as follows:

(40)

The bounds of uncertainty can be determined by observation of state trajectories of the fractional-order Lorenz system. Starting from various initial conditions with q=0.993 the state trajectories are depicted in Fig. 3. In order to find feasible solution for LMI we set −20<x<30,−25<y<30 and 0<z<50. Thus, one can define the upper and lower bounds of the above functions as c 1=10,c 2=78,c 3=30, and c 4=0. Solving the LMI for the system (40) yields

and

$$K = \left [ \begin{array}{c@{\quad}c@{\quad}c} - 36.6974 & 0 & 0 \\ 0 & - 97.7525 & 0 \\ 0 & 0 & - 0.3325 \\\end{array} \right ] $$

Therefore, the control laws become as follows:

(41)

Simulation results for the closed-loop system are depicted in Fig. 4. It is shown that the controller suppress the chaotic trajectories with a fast response.

Fig. 3
figure 3

State trajectories of fractional-order Lorenz system for various initial conditions

Full size image
Fig. 4
figure 4

State trajectories of fractional-order Lorenz system with the controller

Full size image

We have clarified the design procedure by giving two illustrative examples. The same procedure can be used for other chaotic systems belong to this class. Moreover, the method might be used for other chaotic systems, which do not belong to this class just by some modifications. The concept of dissipativity and the idea of considering fractional-order chaotic systems as fractional-order LTI interval systems can be used for all chaotic systems, however, the LMI problem formulation might change according to the structure of the systems.

5 Conclusion

In this paper, a simple linear controller is proposed for stabilization of a class of fractional-order chaotic systems. The main idea is to consider the chaotic systems as fractional-order LTI interval systems due to attractiveness of chaotic attractors. This allows us to employ the theory of stabilization of interval systems to suppress the chaotic trajectories. In this manner, the stabilization problem of fractional-order chaotic systems is converted to solving a LMI. The solution will also give us appropriate values for the feedback gains. Two illustrative examples are given for the fractional-order Liu system and fractional-order Lorenz system, which shows the effectiveness of the proposed method.