1 Introduction

In the past several decades, chaotic systems and their synchronization problem have attracted the attention of many researchers due to their powerful potential applications in various practical areas such as chemical reactions, biological systems, information processing, and secure communication [1–6]. In the literature, a number of various techniques of chaos synchronization and their applications have been extensively studied [7–13]. In [7], the phase synchronization scheme was developed for two coupled chaotic neurons. Synchronization of weighted networks and complex synchronized regions were studied in [8]. In [9], the robust adaptive neural network synchronization control was developed for a class of time delay uncertain chaotic systems. The control and synchronization problem was investigated for chaotic and hyperchaotic systems via linear feedback control in [10]. In [11], the regulation and controlled synchronization was studied for complex dynamical systems. Synchronization problem was investigated for small-world dynamical networks in [12]. In [13], chaotic synchronization and control were developed for nonlinear-coupled Hindmarsh–Rose neural systems.

Note that nonlinearity, modeling error, external disturbance, and uncertainty usually exist in a chaotic system. Thus, the robust adaptive synchronization control of uncertain chaotic systems has been widely developed to enhance the synchronous performance [14–21]. In [14], H ∞ synchronization control was designed for uncertain chaotic systems using neural networks. Chaotic synchronization in the presence of disturbances was studied based on an orthogonal function neural network in [15]. In [16], the robust synchronization problem was investigated via internal model approach. Adaptive synchronization was studied for uncertain coupled stochastic complex networks in [17]. In [18], adaptive sliding mode observer-based synchronization was investigated for uncertain chaotic systems. Adaptive control and synchronization were developed for chaotic systems with parametric uncertainties in [19]. In [20], adaptive sliding mode control was proposed for chaotic dynamical systems with application to synchronization. Chaos synchronization of two uncertain chaotic nonlinear gyros was presented using fuzzy sliding mode control in [21]. In general, various approximators can be adopted to estimate the unknown uncertainty in chaotic system [22–31]. However, the time-varying external disturbance of the chaotic systems need to be efficiently tackled to obtain good synchronous performance. To improve the anti-disturbance ability of synchronization error, the disturbance observer is employed to design the synchronous control scheme in our paper.

In recent years, lots of different design methods have been intensively developed for disturbance observers to explore the information about the characteristic of external disturbances [32, 33]. In this literature, the disturbance observers were adopted to approximate the external disturbance, and robust control were designed based on the output of disturbance observers. The general framework was given for nonlinear systems subject to disturbances using disturbance observer based control (DOBC) techniques [32]. The nonlinear PID predictive control was proposed based on disturbance observers in [33]. In [34], nonlinear-disturbance observer was proposed for multivariable minimum-phase systems with arbitrary relative degrees. The nonlinear disturbance observer for robotic manipulators was developed in [35]. In [36], composite disturbance-observer-based control and terminal sliding mode control were investigated for uncertain structural systems. In [37], nonlinear disturbance observer-based approach was proposed for longitudinal dynamics of a missile. The disturbance attenuation and rejection problem was investigated for a class of multi-input and multi-output (MIMO) nonlinear systems using DOBC framework in [38]. In [39], composite DOBC and H ∞ control were proposed for complex continuous models. Composite DOBC and terminal sliding mode control (TSMC) were studied for nonlinear systems with disturbances in [40]. In [41], sliding mode synchronization control was proposed for uncertain chaotic systems using disturbance observer. Sliding mode control was developed for a class of uncertain nonlinear systems based disturbance observer in [42]. In [43], robust DOBC was presented for time delay uncertain systems. However, the disturbance observer should be further developed for the synchronization control of uncertain chaotic systems with the bounded control input. The reason is that the saturation is the most important non-smooth nonlinearity of the control input.

Now, there are a few results of the robust synchronization control design in which the control input saturation has been considered. If ignored the effect of control input constraint, the synchronous performance may be severely degraded. Thus, input saturation should be explicitly considered in the synchronization control design to guarantee the synchronous performance. In [44–51], the analysis and design of control systems with input saturation constraints have been studied. The robust adaptive neural network control was proposed for a class of uncertain MIMO nonlinear systems with input nonlinearities [44]. In [45], neural network tracking control was developed for ocean surface vessels with input saturation. Hover control was studied for an unmanned aerial vehicle (UAV) with backstepping design including input saturations in [46]. In [47], robust stability analysis and fuzzy-scheduling control were developed for nonlinear systems subject to actuator saturation. Globally stable adaptive control was presented for minimum phase single-input and single-output (SISO) plants with input saturation [48]. Nonlinear control was proposed to achieve the attitude maneuver of a three-axis stabilized flexible spacecraft with control input nonlinearity [49]. However, robust constrained synchronization control need to be further developed for uncertain chaotic systems to guarantee the synchronous performance [52].

This work is motivated by the robust constrained synchronization control of chaotic systems with system uncertainties and unknown external disturbance [53, 54]. The synchronization control objective is that the robust synchronization control scheme is developed to obtain the good synchronization performance in the presence of systems uncertainties, the time varying disturbances and unknown non-symmetric input constraints. The organization of the paper is as follows. The problem statement is given in Sect. 2. Section 3 describes the design of nonlinear disturbance observer and the design of robust constrained synchronization control based on disturbance observer. Simulation results are given to demonstrate the effectiveness of our proposed synchronization control approach in Sect. 4, followed by some concluding remarks in Sect. 5.

2 Problem formulation

Considering the uncertain chaotic systems are described as

(1)
(2)

where x∈R n, y∈R n are states of uncertain chaotic systems (1) and (2); A∈R n×n is a known constant matrix with proper dimension; ΔA 1 and ΔA 2 are parametric uncertainties of chaotic systems; f(⋅) and g(⋅) are known smooth nonlinear function vectors; Δf(⋅) and Δg(⋅) are unknown nonlinear function vectors which denote function uncertainties of chaotic systems (1) and (2); d 1(t) and d 2(t) are the external disturbances of chaotic systems (1) and (2); u∈R n is the control input vector of the uncertain chaotic system (1) which is constrained by

(3)

where v i is the designed synchronization control input command. u imin and u imax are the unknown parameters of non-symmetric input saturation.

In this paper, the synchronization control objective is to develop the robust synchronization control v=[v 1,v 2,…,v n ]T to ensure that the synchronization error asymptotically converges in the presence of uncertainties, control input saturation, and the time-varying external disturbances based on the disturbance observer.

To develop the disturbance-observer-based synchronous control for the uncertain chaotic system (1) and the uncertain chaotic system (2), the following assumption and lemmas are required:

Assumption 1

The parameter uncertainties of the uncertain chaotic system (1) and the uncertain chaotic system (2) are assumed to be of the form

(4)

where E, D 1, and D 2 are constant matrices with corresponding dimensions which denote the system structure uncertainty. F(t) is an unknown, real and possibly time-varying matrix with Lebesgue-measurable elements satisfying

(5)

where ∥⋅∥ denotes the Euclidean norm.

Lemma 1

[55]

For bounded initial conditions, if there exists a C 1-continuous and positive definite Lyapunov function V(x) satisfying π 1(∥x∥)≤V(x)≤π 2(∥x∥) such that \(\dot{V}(x)\leq -\kappa V(x)+c\), where π 1,π 2:R n→R are class K functions and c is a positive constant, then the solution x(t) is uniformly bounded.

Lemma 2

[56]

For appropriate dimension vectors or matrices X and Y, by choosing a constant α>0, the following inequality always holds:

(6)

Define e=x−y. It is apparent that the uncertain chaotic system (1) and the uncertain chaotic system (2) are synchronous if lim t→∞ e(t)=0.

Considering uncertain chaotic systems (1) and (2), the derivative of e is given by

(7)

Defining

(8)

the synchronous error system (7) can be reexpressed as

(9)

To facilitate the robust synchronization control design, we further define

(10)

Invoking (10), the synchronous error system (9) can be rewritten as

(11)

Since Δf(x), Δg(y), Δu, d 1(t), and d 2(t) are unknown, D(x,y,u,t) is also unknown which can be treated as the compound disturbance of the synchronous error system (11). In this paper, the disturbance observer is adopted to estimate D(x,y,u,t) and design the robust synchronization controller to render chaotic systems (1) and (2) synchronous by using the output of the presented nonlinear disturbance observer.

Considering Assumption 1, the synchronous error system (9) can be expressed as

(12)

3 Robust synchronization control based on disturbance observer

In this section, we develop a constrained robust synchronization control scheme for the uncertain chaotic system (1) and the uncertain chaotic system (2) using the developed disturbance observer. The block diagram of the proposed robust synchronization control based on disturbance observer is shown in Fig. 1.

Fig. 1
figure 1

Structure of synchronization control based on nonlinear disturbance observer

Full size image

For the unknown compounded disturbance D(x,y,u,t) shown in (12), it cannot be directly used to design the synchronization control scheme. It is apparent that the compound D(x,y,u,t) is bounded. However, the boundary is unknown. Hence, we design the nonlinear disturbance observer to estimate it [32–43]. To design the nonlinear disturbance observer, an auxiliary variable is defined as

(13)

where K=K T>0 is a design constant matrix.

For the unknown time-varying compounded disturbance D(x,y,u,t), without loss of generality, we assume that the derivative of D(x,y,u,t) satisfies

(14)

where δ is an unknown positive constant.

Considering (12) and (13), the time derivative of η can be written as

(15)

To design the nonlinear disturbance observer, the estimate of the intermediate variable η is proposed as

(16)

where \(\hat{\eta}\) is the estimate of η.

In accordance with (13), the estimate of disturbance D can be obtained as follows:

(17)

Define

(18)

Differentiating (18) and considering (15) and (16), we obtain

(19)

To analyze the convergent ability of disturbance estimate error \(\tilde{D}\), the Lyapunov function candidate is chosen as

(20)

Considering (19), the derivative of V o is

(21)

Invoking (21), Assumption 1 and Lemma 2, we obtain

(22)

For the synchronous error system (12), the robust synchronization control based on the output of the disturbance observer is designed as

(23)

where

\(A_{0}=A_{0}^{T}>0\) is an aforehand design matrix. ε is a small positive design parameter. If ∥e∥<ε is satisfied, then the synchronization control objective is achieved. Thus, we only need to analyze the closed-loop system stability when ∥e∥≥ε.

Substituting (23) into (12), we obtain

(24)

The above design procedure can be summarized in the following theorem which contains the results of disturbance-observer-based synchronization control for the unknown chaotic systems with the time-varying external disturbance.

Theorem 1

Consider uncertain chaotic systems (1) and (2), and the unknown compound disturbance is approximated using the disturbance observer (16) and (17). Then, all closed-loop system signals are semi-globally uniformly stable under the proposed robust synchronization control (23) based on the nonlinear disturbance observer. Furthermore, the synchronous error e and the disturbance approximation error \(\tilde{D}\) remain within the compact sets Ω e and \(\varOmega_{\tilde{D}}\) respectively defined by

where \(\varOmega_{1}=2(V(0)+\frac{C}{\kappa})\) with C and κ as defined in (29).

Proof

Let the Lyapunov function candidate be given by

(25)

Considering (22) and (24), the time derivative of V is

(26)

Invoking Lemma 2, we obtain

(27)

Substituting v 0 into (27), we have

(28)

where

(29)

To ensure the closed-loop stability, the corresponding design parameters A 0 and K should be chosen to make A 0−1.5I n×n >0 and K−2.0I m×m >0. According to (29) and Lemma 1, it can be directly shown that the signals \(\tilde{D}\) and e are semi-globally uniformly bounded. For conciseness, the details of the proof are omitted here. This concludes the proof. □

Remark 1

Since the chaotic error system possesses the unknown time-varying compound disturbance, the nonlinear disturbance observer is adopted to estimate the compound disturbance in this paper. To develop the disturbance observer, assumption (14) is introduced. This assumption means that the derivative of the compound disturbance is bounded. According to (10), we can see that the compounded disturbance consists of d 1(t), Δf(x), Δg(y), d 2(t), and Δu. Since d 1(t) and d 2(t) are the external disturbances of uncertain chaotic systems (1) and (2) which are bounded, the derivatives of d 1(t) and d 2(t) are bounded. Similarly, the derivatives of Δf(x) and Δg(y) are bounded. On the other hand, the difference Δu between the control input command and the actual control input should be bounded in accordance with the controllability requirement of the practical control system. Thus, this assumption given in (14) is reasonable for the compounded disturbance.

Remark 2

As for the proposed disturbance observer, we can see that the approximation error with suitable transient performance can be obtained by felicitously adjusting design parameter matrix K. For example, the approximation error could be decreased by increasing the value of K. Therefore, caution must be exercised in the choice of the design parameters, due to the fact that there are some trade-offs between the disturbance approximation performance and other issues.

Remark 3

In this paper, the upper boundary of the external disturbance is not required in the design of the robust synchronization control (23) owing to the use of the nonlinear disturbance observer. Thus, the proposed disturbance-observer-based robust synchronization control scheme can fully explore the dynamic characteristic of the time-varying disturbances. Furthermore, to the best of our knowledge, it is the first time in the literature that the unknown non-symmetric input saturation is considered in the synchronization control design which is different from the existing results.

4 Simulation results

Simulation results are given in this section to illustrate the effectiveness of the proposed constrained synchronous control technique. Let us consider a model Hindmarsh–Rose neuron described by the following equations of motion [13]:

(30)

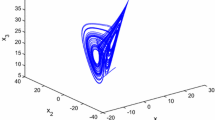
where x 1 is the membrane potential, x 2 is a recovery variable associated with fast current, x 3 is a slowly changing adaptation current. Here a=1.0, b=3.0, c=1.0, d=5.0, S=4.0, r=0.006, \(\bar{x}=-1.56\), and I ext is the external current input. When I ext=3.0 and the initial state is chosen as x=[x 1,x 2,x 3]T=[0.2,−0.2,0.5]T, this system exhibits a multi-time scaled burst-spike chaotic behavior as shown in Fig. 2.

Fig. 2
figure 2

Chaotic trajectory of the model Hindmarsh–Rose neuron

Full size image

Below the extensive simulation is presented to demonstrate the effectiveness of the proposed robust constrained synchronization control based on the disturbance observer. To illustrate the synchronous control performance, the chaotic system (30) is treated as the slave chaotic system and the chaotic system (30) with uncertainties and disturbances is treated as the master chaotic system. Thus, the master chaotic system and the slave chaotic system are written as

(31)
(32)

The chaotic trajectory of the model Hindmarsh–Rose neuron (31) with uncertainties and disturbances is shown in Fig. 3. From Fig. 3, we know that the uncertain chaotic system (31) processes a chaotic phenomenon.

Fig. 3
figure 3

Chaotic trajectory of the model Hindmarsh–Rose neuron with uncertainties and disturbances

Full size image

To proceed with the design of nonlinear disturbance observer and robust constrained synchronization control scheme, design parameters are chosen as K=200I 3×3 and A 0=5I 3×3. The initial state condition of chaotic systems are arbitrarily given by x=[0.2,−0.2,0.5]T and y=[−0.2,0.2,−0.5]T. The initial state condition of the disturbance observer is arbitrarily chosen as \(\hat{D}=[0.1,0,0]^{T}\). From (32), we obtain

Here, we do not consider the control input saturation first. Namely, we have u=v and Δu=0. The nonlinear disturbance observer and the robust synchronization control are designed as in (16), (17), and (23). Under the proposed disturbance-observer-based robust synchronization control, the synchronization error and the synchronization control input are shown in Figs. 4 and 5. From Fig. 4, we can observe that the synchronization error is satisfactory. According to Fig. 5, we can see that the synchronization control input is bounded and convergent. Based on these simulation results, we can obtain that the proposed disturbance-observer-based robust synchronization control is valid for the uncertain chaotic systems.

Fig. 4
figure 4

Synchronization error

Full size image
Fig. 5
figure 5

Synchronous control input

Full size image

To illustrate the effectiveness of the proposed constrained robust synchronization control, the control input saturation values are given by u 1max=5.5, u 1min=−2.0, u 2max=7.0, u 2min=−5.0, u 3max=7.0, and u 3min=−5.0 in this simulation study. The nonlinear disturbance observer and the robust synchronization controller are still designed as in (16), (17), and (23). Under the proposed constrained robust synchronization controller, the synchronization error and the synchronization control input are presented in Fig. 6 and Fig. 7. Although there exist the non-symmetric input saturation and the time-varying external disturbance, the synchronization error is still satisfactory as shown in Fig. 6. The non-symmetric input saturation of the synchronization control input signal is observed from Fig. 7.

Fig. 6
figure 6

Synchronization error under the constrained control

Full size image
Fig. 7
figure 7

Constrained synchronous control input

Full size image

From simulation results of the two cases, we obtain that the designed robust synchronization control scheme based on disturbance observer is valid for the synchronization control of uncertain chaotic systems. On the other hand, the proposed disturbance-observer-based synchronization control scheme can be applied to synchronize other chaotic systems.

5 Conclusion

In this paper, the disturbance-observer-based synchronization control has been proposed for uncertain chaotic systems. To improve the ability of the disturbance attenuation and synchronous control performance, the nonlinear disturbance observer has been adopted to approximate the compound disturbance of the synchronous error system. Using the output of the disturbance observer, the disturbance-observer-based synchronous control has been presented for uncertain chaotic systems considering the non-symmetric input constraints. The stability of the closed-loop system has been proved using rigorous Lyapunov analysis. Finally, simulation results have been used to illustrate the effectiveness of the proposed robust synchronization control scheme.