1 Introduction

Controlling chaos and synchronization is a significant issue in the control community. In nature, chaos systems exhibit complicated behavior, including very sensitive dependence on initial conditions and parameter variations. In 1990, Pecora and Carroll were the first to introduce synchronization, and research on chaos control and chaos synchronization has advanced over the past two decades. Synchronization is an important phenomenon and closely connected to chaos (Alfi 2012; Pereira-Pinto et al. 2004). Generally, there are two methods of coupling synchronization, unidirectional coupling and bidirectional coupling, which may have different synchronized states. Unidirectional coupling synchronization, such as communication with chaos, considers a drive (master) system and a response (slave) system, which may generally be chaotic but not necessarily identical. However, bidirectional coupling synchronization can be achieved by introducing the state of a system to another system, where each system can be considered as a response system (Bhaskar et al. 2021; Jia 2008; Korneev et al. 2021). In chaotic synchronization, two chaotic systems with appropriate coupling create similar oscillations. The chaotic synchronization issue implies that, depending on various initial conditions between the master and slave systems, it is feasible to develop a mechanism to bring the states of the systems into synchrony. Several master–slave synchronization techniques have been introduced. The key challenge in chaotic applications is chaos control and chaotic system synchronization. Regardless of their potential applicability in science and technology, chaotic systems may be controlled and synchronized. For the robust stability of disturbed nonlinear systems, a new barrier function-based adaptive non-singular terminal sliding mode control (SMC) technique with application to two chaotic systems has been proposed (Mobayen et al. 2022).

Research on the earth’s geomagnetic fields has a long history, and geophysicists have traditionally placed a premium on these readily visible features. Throughout geological history, the earth’s dipole has reverted to its original polarity several times. A well-known mechanical model for analyzing reversals of the earth’s magnetic fields consists of two-disk dynamo systems proposed by Japanese geophysicist Rikitake (Pang et al. 2020). Many studies have investigated the Rikitake system, including chaos control and synchronization secure communications (Vafamand and Khorshidi 2018; Mata-Machuca et al. 2012), SMC (Xu et al. 2021), time delay (Wang et al. 2019), fractional-order system (Aghayan and Alfi 2023), and many others.

The issue of actuator saturation is a significant challenge in real control systems. Input saturation is a common and unavoidable design issue (Li et al. 2018; Benzaouia et al. 2014). If designers fail to consider the actuator saturation issue, it may lead to performance deterioration or even cases of instability in the closed-loop system. Despite the reason for actuator saturation, analyzing and designing a system with saturated actuators is an essential topic. This issue is not only difficult from a theoretical standpoint, but also significant from a practical perspective. There are two main approaches to dealing with actuator saturation. The first technique is to disregard saturation during the first phase of control design and subsequently implement solutions to reduce the negative consequences of saturation (Guo and Yue 2012; Naseri and Asemani 2018). This work aims to analyze and investigate fuzzy control systems with actuator saturation scenarios. The fundamental concept behind these strategies is to offer composite nonlinear feedback (CNF) (Amiri et al. 2022a) to ensure that the actuator remains within its limitations. In the face of a variety of challenges, including uncertainty, disturbance, time delay, and the saturation of the actuator, a CNF controller is used to investigate the issue of robust tracking in uncertain nonlinear time-delay systems (Ghaffari et al. 2022). The integral sliding mode control (ISMC) technique combined with CNF control is discussed in Hu et al. (2022) for time-delay uncertain systems, taking into account challenges such as time-varying delays, actuator saturation, and external disturbances. Hence, the tracking issue is addressed subject to constraints, and the controller settings may be obtained by means of a solution for linear matrix inequality (LMI).

SMC is a distinct kind of variable structure control developed by Emel’yanov and coworkers. SMC has evolved into a mature approach for developing robust controllers for a diverse range of systems, including nonlinear, uncertain, and time-delay systems. SMC algorithms have been used extensively for synchronous control to increase the control accuracy of synchronization due to their simple design and high robustness. To ensure satisfactory performance and robustness within a closed-loop system and to maximize the reaching phase, ISMC has been considered (Chang et al. 2022; Kumar et al. 2022).

Takagi–Sugeno (TS) fuzzy models are well established as a universal approximation approach, and a large class of nonlinear systems may be precisely described as TS systems. Various techniques exist for constructing a fuzzy representation or approximation of a nonlinear system. The sector nonlinearity (SN) approach is used to obtain a TS model of a system. Furthermore, the TS approach is a convex combination of linear models that facilitates stability analysis, modeling of complicated systems, controller design, and other related concepts within the framework of LMIs (Feng 2018; Zhao et al. 2021). ISMC methodologies combined with TS systems have been broadly utilized over the past decade. It has been recognized that TS fuzzy control and the ISMC are synergistic, since fuzzy control contains a vigorous framework for representing expert knowledge (Farbood et al. 2021; Soltanian and Shasadeghi 2022). In some publications, the well-known TS fuzzy model has been extended to chaos control and synchronization to describe chaotic models in state space. However, some parameters of a chaotic system cannot be precisely determined in advance. If only a component of a chaotic system is available, i.e., if its dynamics are known but some or all of its parameters are unknown, then a synchronization method based on a precise model of chaotic systems may be infeasible (Haris et al. 2021; Aghababa and Aghababa 2011). Adaptive strategies for a number of chaotic systems have been suggested to address the issue of chaotic synchronization with undetermined parameters. A high-gain observer-based adaptive output feedback design was investigated by Yang and Xu (2022) for the output synchronization issue of an uncertain nonlinear system. The suggested scheme for heterogeneous multi-agent systems concurrently takes into account the input saturation and output constraint. It was demonstrated that the proposed scheme is capable of ensuring the boundedness of entire closed-loop signals. In Giap et al. (2020), by transforming the control synchronization of two nonidentical chaotic systems into a TS fuzzy system, a new TS fuzzy system was constructed. The time-varying disturbance elements were eliminated, and the proposed disturbance observer’s convergence was shown to be perfect. Zhao et al. (2018) provided an adaptive control scheme for the \(H\infty\) synchronization of a fuzzy coronary artery system when the input is nonlinear and the parameters are perturbed.

Although the ISMC problem for TS fuzzy systems has been studied extensively and a number of significant advances have been published, the use of the adaptive fuzzy composite nonlinear feedback integral sliding mode (AFCNFISM) controller for synchronizing chaotic Rikitake systems with actuator saturation is not well studied in the published literature.

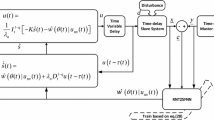
In this study, we propose a control strategy based on AFCNFISM for the synchronization of chaotic systems with exogenous disturbances and uncertainties pertaining to actuator saturation. The TS fuzzy model is employed for modeling the nonlinear chaotic Rikitake system. On the basis of this fuzzy model, synchronization error dynamics are deduced, and the stability of the entire synchronization system is investigated. The subject of setting restrictions on the magnitude of the control signal is evaluated, and an ISMC-based controller is developed. By employing Lyapunov’s theory of stability and employing an AFCNFISM controller against uncertainties and exogenous disturbances, the stability of the Rikitake system is ensured, and its chaos synchronization errors converge to zero. The uniformly ultimate boundedness (UUB) (Amiri et al. 2022b) of the closed-loop system of the Rikitake system is recast as an LMI problem during stability analysis.

The remaining sections of this work are organized as follows. Section 2 is devoted to the TS fuzzy modeling of the Rikitake system. The proposed scheme for ISMC and AFCNFISM is presented in Sect. 3. In Sect. 4, the limited specifications of the input signal are considered. The results of the simulation are presented and discussed in Sect. 5, and Section 6 contains the paper’s conclusion.

Notations: The following notation is employed in this paper. The inverse and transpose of the matrix are indicated by the superscripts “−1” and “T,” respectively. \(\parallel P\parallel\) signifies the 2-norm of the matrix \(P\). \(\mathrm{sym}\{P\}\) indicates \(P+{P}^{T}\), and \(P>0\). \(I\) stands for the identity matrix in the proper dimensions. \({\lambda }_{\mathrm{min}}(P)\) symbolizes the lowest eigenvalue of the matrix \(P\). The sign and saturation functions are shown below:

$$\mathrm{sign}(s)=\left\{\begin{array}{ll}-1& \mathrm{if} s<0\\ 0& \mathrm{if }s=0\\ 1& \mathrm{if }\, s>0\\ & \end{array}\right. \mathrm{sat}({u}_{i})=\left\{\begin{array}{ll}\stackrel{*}{u}& \mathrm{if} \, {u}_{i}<-\stackrel{*}{u}\\ u& \mathrm{if} \, -\stackrel{*}{u}\le {u}_{i}\le \stackrel{*}{u}\\ \stackrel{*}{u}& \mathrm{if} \, {u}_{i}>\stackrel{*}{u}\\ & \end{array}\right.$$

2 Problem Description and Preliminaries

In 1958, the Japanese geophysicist Rikitake discovered the Rikitake dynamo system (Llibre and Messias 2009). As seen in Fig. 1, the Rikitake system consists of two conductive spinning disks that are joined into two coils. Each circuit is rotated with an angular velocity by applying an external constant mechanical torque to the axis. By Faraday’s law, a magnetic field traversing a disk creates an electromagnetic field between the disk’s center and edge, causing an induced inner current to flow in the opposite direction, thereby cancelling out the initial current. Thus, the mathematical model is as follows:

$$\left\{\begin{array}{l}{\dot{x}}_{1}(t)=-\mu {x}_{1}(t)+{x}_{2}(t){x}_{3}(t)\\ {\dot{x}}_{2}(t)=-\mu {x}_{2}(t)-a{x}_{1}(t)+{x}_{1}(t){x}_{3}(t)\\ {\dot{x}}_{3}(t)=1-{x}_{1}(t){x}_{2}(t)\end{array}\right.$$
(1)

where \(x = \left( {x_{1} ,x_{2} ,x_{3} } \right) \in {\mathbb{R}}^{3}\) are state variables, and \(\mu\) and a are positive parameters. As can be seen, this system for \(\mu =2\) and \(a=5\) with initial condition \((\mathrm{0.2,0.3,0.5})\) has a chaotic behavior, which is shown in Figs. 1, 2, 3, and 4.

Fig. 1
figure 1

The Rikitake two-disk dynamo

Full size image
Fig. 2
figure 2

The Rikitake chaotic attractor in (1), in the \({x}_{1}-{x}_{2}\) space

Full size image
Fig. 3
figure 3

The Rikitake chaotic attractor in (1), in the \({x}_{2}-{x}_{3}\) space

Full size image
Fig. 4
figure 4

The Rikitake chaotic attractor in (1), in the \({x}_{1}-{x}_{2}-{x}_{3}\) space

Full size image

To construct the TS fuzzy model of the Rikitake system (1), the SN approach is presented. This approach is one of the most frequently utilized approaches for constructing TS models for fuzzy control design, as it can achieve an exact fuzzy representation of very complex or chaotic systems. Considering this feature, the SN approach can be employed for the Rikitake systems. For the purpose of simplicity, the state space representation of system (1) can be stated as follows:

$$\dot{x}(t)=Ax(t)+C$$
(2)

where \(x\left( t \right) = x\_1\left( t \right)x\_2\left( t \right)x\_3\left( t \right)^{T} \in {\mathbb{R}}^{3}\)

$$A = \left[ {\begin{array}{*{20}l} { - \mu } \hfill & 0 \hfill & {x_{2} \left( t \right)} \hfill \\ {x_{3} \left( t \right) - a} \hfill & { - \mu } \hfill & 0 \hfill \\ { - x_{2} \left( t \right)} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],~~C = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{array} } \right]$$

Define \({\varkappa }_{1}(t)={x}_{2}(t)\) and \({\varkappa }_{2}(t)={x}_{3}(t)\) for the nonlinear terms. Then we have

$$A = \left[ {\begin{array}{*{20}l} { - \mu } \hfill & 0 \hfill & {{\varkappa }_{1} \left( t \right)} \hfill \\ {{\varkappa }_{2} \left( t \right) - a} \hfill & { - \mu } \hfill & 0 \hfill \\ { - {\varkappa }_{1} \left( t \right)} \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right], C = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{array} } \right]$$

Then, compute the minimum and maximum values of \({\varkappa }_{1} \left( t \right)\) and \({\varkappa }_{2} \left( t \right)\) under \(x_{2} \left( t \right) \in \left[ { - 1,1} \right]\) and \(x_{3} \left( t \right) \in \left[ { - 1,1} \right]\). These values are of the form \({\text{max}}{\varkappa }_{1} \left( t \right) = 1\), \({\text{min}}{\varkappa }_{1} \left( t \right) = - 1\), \({\text{max}}{\varkappa }_{2} \left( t \right) = 1\), and \({\text{min}}{\varkappa }_{2} \left( t \right) = - 1\). From the maximum and minimum values, \({\varkappa }_{1} \left( t \right)\) and \({\varkappa }_{2} \left( t \right)\) can be represented by

$${\varkappa }_{1} \left( t \right) = x_{2} \left( t \right) = M_{11} \left( {{\varkappa }_{1} \left( t \right)} \right).1 + M_{21} \left( {{\varkappa }_{1} \left( t \right)} \right).\left( { - 1} \right)$$
$${\varkappa }_{2} \left( t \right) = x_{3} \left( t \right) = M_{12} \left( {{\varkappa }_{2} \left( t \right)} \right).1 + M_{22} \left( {{\varkappa }_{2} \left( t \right)} \right).\left( { - 1} \right)$$

where

$$M_{11} \left( {{\varkappa }_{1} \left( t \right)} \right) + M_{21} \left( {{\varkappa }_{1} \left( t \right)} \right) = 1$$
$$M_{12} \left( {{\varkappa }_{2} \left( t \right)} \right) + M_{22} \left( {{\varkappa }_{2} \left( t \right)} \right) = 1$$

Hence, the membership functions can be computed as

$$M_{11} \left( {{\varkappa }_{1} \left( t \right)} \right) = \frac{1}{2}\left( {1 + x_{2} \left( t \right)} \right)$$
$$M_{21} \left( {{\varkappa }_{1} \left( t \right)} \right) = \frac{1}{2}\left( {1 - x_{2} \left( t \right)} \right)$$
$$M_{12} \left( {{\varkappa }_{2} \left( t \right)} \right) = \frac{1}{2}\left( {1 + x_{3} \left( t \right)} \right)$$
$$M_{22} \left( {{\varkappa }_{2} \left( t \right)} \right) = \frac{1}{2}\left( {1 - x_{3} \left( t \right)} \right)$$

By employing four membership functions \(M_{11}\), \(M_{21}\), \(M_{12}\) and \(M_{22}\), the nonlinear system (1) with control input \(u\left( t \right)\) is represented by the following TS model:

$$R_{i} :{\text{IF}}\;{\varkappa }_{1} \left( t \right) \;{\text{is}}\;M_{i1} ,\;{\varkappa }_{2} \left( t \right)\; {\text{is}}\;M_{i2} , \ldots , {\text{and}}\;{\varkappa }_{p} \left( t \right)\;{\text{is}}\;M_{ip} ,\;{\text{THEN}}\;\dot{x}\left( t \right) = A_{i} x\left( t \right) + B_{i} {\text{sat}}\left( {u\left( t \right)} \right) + C_{i}$$

where \(i \in {\mathbb{C}} = \left\{ {1,2,3,4} \right\}\) and \(j \in {\mathbb{D}} = \left\{ {1,2,3,4} \right\}\) represent the number of fuzzy rules and premise variables, respectively. \(M_{ij}\) are fuzzy sets. \(x\left( t \right) \in {\mathbb{R}}^{3 \times 1}\) and \(u\left( t \right) \in {\mathbb{R}}^{3 \times 1}\) are the state variable and control input, respectively. \({\varkappa }_{i} \left( t \right)\) denotes the premise variable, and \(M_{ij}\) is a fuzzy set. \(A_{i} \in {\mathbb{R}}^{3 \times 3}\) and \(B_{i} \in {\mathbb{R}}^{3 \times 3}\) are system matrices, and \(C_{i}\) is known with the proper dimension.

\({R}_{1}\): IF \({\varkappa }_{1} \left( t \right)\) is \({M}_{11}\) and \({\varkappa }_{2} \left( t \right)\) is \({M}_{12}\), THEN

$$\dot{x}(t)={A}_{1}x(t)+{B}_{1}\mathrm{sat}(u(t))+{C}_{1}$$

\({R}_{2}\): IF \({\varkappa }_{1} \left( t \right)\) is \({M}_{11}\) and \({\varkappa }_{2} \left( t \right)\) is \({M}_{22}\), THEN

$$\dot{x}(t)={A}_{2}x(t)+{B}_{2}\mathrm{sat}(u(t))+{C}_{2}$$

\({R}_{3}\): IF \({\varkappa }_{1} \left( t \right)\) is \({M}_{21}\) and \({\varkappa }_{2} \left( t \right)\) is \({M}_{12}\), THEN

$$\dot{x}(t)={A}_{3}x(t)+{B}_{3}\mathrm{sat}(u(t))+{C}_{3}$$

\({R}_{4}\): IF \({\varkappa }_{1} \left( t \right)\) is \({M}_{21}\) and \({\varkappa }_{2} \left( t \right)\) is \({M}_{22}\) , THEN

$$\dot{x}(t)={A}_{4}x(t)+{B}_{4}\mathrm{sat}(u(t))+{C}_{4}$$

Then

$${A}_{1}=\left[\begin{array}{lll}-\mu & 0& 1\\ 1-a& -\mu & 0\\ -1& 0& 0\end{array}\right]{A}_{2}=\left[\begin{array}{lll}-\mu & 0& 1\\ -1-a& -\mu & 0\\ -1& 0& 0\end{array}\right]$$
$${A}_{3}=\left[\begin{array}{lll}-\mu & 0& -1\\ 1-a& -\mu & 0\\ 1& 0& 0\end{array}\right]{A}_{4}=\left[\begin{array}{lll}-\mu & 0& -1\\ -1-a& -\mu & 0\\ 1& 0& 0\end{array}\right]$$
$${B}_{1}={B}_{2}={B}_{3}={B}_{4}=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
$${C}_{1}={C}_{2}={C}_{3}={C}_{4}=\left[\begin{array}{l}0\\ 0\\ 1\end{array}\right]$$

By utilizing the center-average defuzzifier, the overall fuzzy model of the Rikitake system (1) is created by fuzzy blending as follows:

$$\dot{x}(t)=\sum_{i=1}^{r}{\lambda }_{i}(\varkappa (t))({A}_{i}x(t)+{B}_{i}\mathrm{sat}(u(t))+{C}_{i})$$
(3)

where \(\lambda_{i} \left( {{\varkappa } \left( t \right)} \right) = \frac{{w_{i} \left( {{\varkappa } \left( t \right)} \right)}}{{\mathop \sum \nolimits_{i = 1}^{r} w_{i} \left( {{\varkappa } \left( t \right)} \right)}}\) and \(w_{i} \left( {{\varkappa } \left( t \right)} \right) = \mathop \prod \nolimits_{j = 1}^{p} M_{ij} \left( {{\varkappa }_{j} \left( t \right)} \right)\). \(\lambda_{i} \left( {{\varkappa } \left( t \right)} \right)\) is denoted as the normalized weight of the if–then rules which satisfies

$$\left\{ {\begin{array}{*{20}l} {\sum\nolimits_{i = 1}^{r} {\lambda_{i} \left( {{\varkappa } \left( t \right)} \right) = 1} } \hfill \\ {\lambda_{i} \left( {{\varkappa } \left( t \right)} \right) \ge 0} \hfill \\ \end{array} } \right.$$

and

$$\lambda_{1} \left( {{\varkappa } \left( t \right)} \right) = M_{11} \left( {{\varkappa }_{1} \left( t \right)} \right)M_{12} \left( {{\varkappa }_{2} \left( t \right)} \right)$$
$$\lambda_{2} \left( {{\varkappa } \left( t \right)} \right) = M_{11} \left( {{\varkappa }_{1} \left( t \right)} \right)M_{22} \left( {{\varkappa }_{2} \left( t \right)} \right)$$
$$\lambda_{3} \left( {{\varkappa } \left( t \right)} \right) = M_{21} \left( {{\varkappa }_{1} \left( t \right)} \right)M_{12} \left( {{\varkappa }_{2} \left( t \right)} \right)$$
$$\lambda_{4} \left( {\left( t \right)} \right) = M_{21} \left( {_{1} \left( t \right)} \right)M_{22} \left( {_{2} \left( t \right)} \right)$$

This fuzzy model precisely illustrates the dynamics of the nonlinear Rikitake system (1) under \(-1\le {x}_{2}(t)\le 1\) and \(-1\le {x}_{3}(t)\le 1\). By employing the master–slave concept, the dynamic equation of the TS fuzzy system (master system) is given as

$$\dot{x}\left( t \right) = \mathop \sum \limits_{i = 1}^{r} \lambda_{i} \left( {{\varkappa } \left( t \right)} \right)\left( {A_{i} x\left( t \right) + C_{i} } \right)$$
(4)

The slave system (response system) of the TS fuzzy Rikitake system is as follows:

$$\dot{y}\left( t \right) = \sum\limits_{i = 1}^{r} {\lambda_{i} (\hat{{\varkappa } }(t))\left\{ {A_{i} y(t) + B_{i} {\text{sat(u(t)) + }}F_{i} \varpi (t) + C_{i} } \right\}}$$
(5)

where \(y(t)=[{y}_{1}(t) {y}_{2}(t) {y}_{3}(t){]}^{T}\in {\mathbb{R}}^{3}\) is the state vector, \(u\) is the control input, and \({{F}}_{i}\) and \({C}_{i}\) are disturbance and known constant matrices, respectively. \(\varpi (t)\) is an exogenous disturbance with an uncertain structure which is unknown but bounded and satisfied by a looser constraint:

$$\parallel \varpi (t)\parallel \le {\mu }_{1}+{\mu }_{2}\parallel e(t)\parallel$$
(6)

In constraint (6), \({\mu }_{1}\) and \({\mu }_{2}\) are both unknown parameters that are determined based on the structure of \(\varpi (t)\) and \(e(t)\). It should be noted that premise variables are also used in fuzzy models for outputs. Therefore, the premise variables in the TS fuzzy model of master system are similar to the slave, namely \(\lambda_{i} \left( {\hat{{\varkappa } }\left( t \right)} \right) = \lambda_{i} \left( {\hat{{\varkappa } }\left( t \right)} \right)\). In consequence, the synchronization error is determined as

$$\begin{array}{ll}\dot{e}(t)& =\dot{y}(t)-\dot{x}(t)\\ & =\sum_{i=1}^{r}{\lambda }_{i}(\varkappa (t))\{{A}_{i}e(t)+{B}_{i}\mathrm{sat}(u(t))+{{F}}_{i}\varpi (t)\}\end{array}$$
(7)

3 Main Results

This section will cover the method of developing the fuzzy surface and AFCNFISM controller for the chaotic synchronization in (7). According to the Lyapunov stability criteria, the stability and reachability criteria are evaluated.

3.1 Synchronization of the Chaotic Rikitake System

In accordance with the structure of (7), the fuzzy surface is selected as follows:

$$\eta \left( t \right) = \Im e\left( t \right) - \int\limits_{0}^{t} {\sum\limits_{i = 1}^{r} {\sum\limits_{j = 1}^{r} {\lambda_{i} ({\varkappa } (0))\lambda_{j} ({\varkappa } (0))\Im (A_{i} + B_{i} K_{j} )e(\theta ){\text{d}}(\theta ) - \Im e(0)} } }$$
(8)

Remark 1

Regarding the ISMC design of system (7), we take into consideration the system matrices \(F_{i}\) and \(B_{i}\) with two cases, namely the \(F_{i} = B_{i}\) case and the \(F_{i} \ne B_{i}\) case. Hence, in the following sections, we will investigate the stability of the sliding-motion dynamic based on the fuzzy surface (8) in two distinct cases.

In (8), \(\Im \in {\mathbb{R}}^{1 \times 3}\) is non-singular, and the matrix \(K_{j} \in {\mathbb{R}}^{3 \times 3}\). It should be emphasized that, in contrast to classic SMC, ISMC enhances transient performance in uncertain and chaotic conditions. The purpose of ISMC is to drive sliding motion on \(\eta \left( t \right) = 0\); therefore, using the derivative of fuzzy surface (8) and system (7), we have:

$$\dot{\eta }\left( t \right) = \sum\limits_{i = 1}^{r} {\sum\limits_{j = 1}^{r} {\lambda_{i} \left( {{\varkappa } \left( \theta \right)} \right)\lambda_{j} \left( {{\varkappa } \left( \theta \right)} \right)GB_{i} \left\{ {{\text{sat}}\left( {u\left( t \right)} \right) + \varpi \left( t \right) - K_{j} e\left( t \right)} \right\}} }$$
(9)

Based on the definition of equivalent control (Zhang et al. 2022), the state trajectory of (7) enters the sliding motion, i.e., \(\eta (t)=0\) and \(\dot{\eta }(t)=0\) for the case \({{F}}_{i}={B}_{i}\), the equivalent control can be stated as

$$\mathrm{sat}(u(t))={K}_{j}e(t)-\varpi (t)$$
(10)

By substituting (10) into (7), the dynamic of sliding motion can be obtained:

$$\dot{e}\left( t \right) = \mathop \sum \limits_{i = 1}^{r} \mathop \sum \limits_{j = 1}^{r} \lambda_{i} \left( {{\varkappa } \left( t \right)} \right)\lambda_{j} \left( {{\varkappa } \left( t \right)} \right)\left( {A_{i} + B_{i} K_{j} } \right)e\left( t \right)$$
(11)

Remark 2

There are various control and estimating issues that can be characterized as a "double sum negative" problem as follows:

$$\mathop \sum \limits_{i = 1}^{r} \mathop \sum \limits_{j = 1}^{r} \lambda_{i} \left( {\varkappa } \right)\lambda_{j} \left( {\varkappa } \right)\Lambda_{ij} \left( z \right)$$
(12)

While the nonlinear functions \(\lambda_{i} \left( {\varkappa } \right)\) satisfy the convex sum property, namely, \(\sum\nolimits_{i = 1}^{r} {\lambda_{i} ({\varkappa } ) = 1} \;{\text{and}}\;\lambda_{i} ({\varkappa } ) \ge 1\), the symmetric matrices \({\Lambda }_{ij} \left( z \right)\) are affinely dependent on the unknown variables \(z \in {\mathbb{R}}^{3}\). By relying only on the convex sum criterion for the nonlinear functions \(\lambda_{i} \left( {\varkappa } \right)\), the objective is to determine the least conservative criteria on \({\Lambda }_{ij} \left( z \right)\) such that (13) is fulfilled.

Theorem 1

(Palanimuthu et al. 2022) The synchronization error of the system (11) is globally asymptotically stable if there exist symmetric positive definite matrices \({X}_{i}\) and \({Y}_{i}\) such that

$$\left\{\begin{array}{l}{\Lambda }_{ii}<0\\ \frac{2}{r-1}{\Lambda }_{ii}+{\Lambda }_{ij}+{\Lambda }_{ji}<00\le i\in {\mathbb{C}}\ne j\in {\mathbb{D}}\le r\\ {\Lambda }_{ij}={A}_{i}X+{B}_{i}{Y}_{j}+({A}_{i}X+{B}_{i}{Y}_{j}{)}^{T}\end{array}\right.$$
(13)

Proof

Consider the Lyapunov function \(V(e(t))={e}^{T}(t)Pe(t)\), which satisfies \({P}^{T}=P\) for sliding motion (11). The time derivative of the Lyapunov function yields

$$\begin{aligned} \dot{V}(e(t)) & = \{ \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))(A_{i} + B_{i} K_{j} )e(t)\} ^{T} Pe(t) \\ & \quad + e^{T} (t)P\{ \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))(A_{i} + B_{i} K_{j} )e(t)\} \\ & = \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))e^{T} (t)\{ A_{i}^{T} P + PA_{i} + PB_{i} K_{j} + K_{j}^{T} B_{i}^{T} P\} e(t) \\ \end{aligned}$$
(14)

Consequently, \(\dot{V}(e(t))<0\) is guaranteed if Remark 2 is fulfilled, namely

$$\sum_{i=1}^{r}\sum_{j=1}^{r}{\lambda }_{i}(\varkappa (t)){\lambda }_{j}(\varkappa (t))\{{A}_{i}^{T}P+P{A}_{i}+P{B}_{i}{K}_{j}+{K}_{j}^{T}{B}_{i}^{T}P\}<0$$
(15)

where

$$\left\{\begin{array}{l}{A}_{i}^{T}P+P{A}_{i}+P{B}_{i}{K}_{i}+{K}_{i}^{T}{B}_{i}^{T}P<0\\ \frac{2}{r-1}({A}_{i}^{T}P+P{A}_{i}+P{B}_{i}{K}_{i}+{K}_{i}^{T}{B}_{i}^{T}P)+({A}_{i}^{T}P+P{A}_{i}+P{B}_{i}{K}_{j}+{K}_{j}^{T}{B}_{i}^{T}P)\\ +({A}_{j}^{T}P+P{A}_{j}+P{B}_{j}{K}_{i}+{K}_{i}^{T}{B}_{j}^{T}P)<0, \le i\in {\mathbb{C}}\ne j\in \end{array}\right.$$
(16)

To realize the LMI conditions, change the variables as follows: \(X={P}^{-1}\), \({K}_{j}={Y}_{j}{X}^{-1}\). The matrix inequalities (16) are identical to the linear matrix inequalities (13), which completes the proof of Theorem 1.

3.2 Robust Synchronization of the Uncertain Chaotic Rikitake System

Real-world systems frequently exhibit parameter uncertainties due to inaccurate modeling or environmental changes. Consequently, parameter uncertainty must be taken into account in the master–slave synchronization strategy. In this subsection, we aim to design an AFCNFISM controller for an uncertain model of the Rikitake system, which was inspired by the preceding section. The uncertain TS model of the Rikitake system is structured as follows:

$$\dot{e}(t)=\sum_{i=1}^{r}{\lambda }_{i}(\varkappa (t))\{({A}_{i}+\Delta {A}_{i}(t))e(t)+{B}_{i}\mathrm{sat}(u(t))+{{F}}_{i}\varpi (t)\}$$
(17)

In accordance with the feature of (17), the fuzzy surface is defined as

$$\eta (t)=\mathfrak{I}e(t)-{\int }_{0}^{t}\sum_{i=1}^{r}\sum_{j=1}^{r}{\lambda }_{i}(\varkappa (\theta )){\lambda }_{j}(\varkappa (\theta ))\mathfrak{I}({A}_{i}+\Delta {A}_{i}(t)+{B}_{i}{K}_{j})e(\theta )d(\theta )-\mathfrak{I}e(0)$$
(18)

From (18) and (17), the derivative of the fuzzy surface for the \({B}_{i}\ne {{F}}_{i}\) case by setting \(\mathfrak{I}{{F}}_{i}=0\) is obtained as

$$\dot{\eta }(t)=\sum_{i=1}^{r}\sum_{j=1}^{r}{\lambda }_{i}(\varkappa (t)){\lambda }_{j}(\varkappa (t))\mathfrak{I}{B}_{i}\{sat(u(t))-{K}_{j}e(t)\}$$
(19)

Remark 3

Since \(\Delta {A}_{i}(t)={T}_{i}{D}_{i}(t){L}_{i}\), \({T}_{i}\) and \({L}_{i}\) are real known constant matrices with appropriate dimensions, and \({D}_{i}(t)\) is a vague time-varying matrix with Lebesgue-measurable elements and fulfilling \({D}_{i}^{T}(t){D}_{i}(t)\le I\), the parameter uncertainties mentioned here are norm-bounded (Phu et al. 2020).

The following dynamic of the sliding motion can be determined as

$$\dot{e}(t)=\sum_{i=1}^{r}\sum_{j=1}^{r}{\lambda }_{i}(\varkappa (t)){\lambda }_{j}(\varkappa (t))\{({A}_{i}+\Delta {A}_{i}(t)+{B}_{i}{K}_{j})e(t)+{{F}}_{i}\varpi (t)\}$$
(20)

where

$${\overline{A} }_{ij}=({A}_{i}+\Delta {A}_{i}(t)+{B}_{i}{K}_{j})$$

Under the sliding motion defined by (20), the succeeding Definition 1 and Theorem 2 present the bounded stability criterion of (20).

Definition 1

Take into consideration the system (20), where \(x(t)\in \mathfrak{R}\triangleq \{\mathrm{\eth }:\parallel \mathrm{\eth }\parallel \le {\gamma }_{1},\mathrm{\eth }\in {\mathbb{R}}^{n}\}\) for constrained variable \({\gamma }_{1}\ge 0\), \({\gamma }_{1}\in {\mathbb{R}}\) and \(t\ge 0\). If \({\mathrm{lim}}_{x\to \infty }x(t)=0\) is fulfilled, for all \(x(t)\in \mathrm{\eth }\), the system in (20) is said to be boundedly stable.

Theorem 2

System (20) is considered boundedly stable for a symmetric positive definite matrix \({\zeta }_{ij}\) if there exists a feasible solution \((P,{K}_{j})\) with positive definite matrices \(P={P}^{T}\in {\mathbb{R}}^{n\times n}\) and \({K}_{j}^{m\times n}\) meeting the following criteria:

$$\left\{\begin{array}{l}2{\mu }_{2}\parallel P{{F}}_{i}\parallel -{\lambda }_{\mathrm{min}}({\zeta }_{ij})<0\\ {\zeta }_{ij}\triangleq -{\overline{A} }_{ij}^{T}P-P{\overline{A} }_{ij}\end{array}\right.$$
(21)

Proof

By specifying a candidate for the Lyapunov function as \(V(e(t))={e}^{T}(t)Pe(t)\), we have

$$\begin{aligned} \dot{V}(t) & = \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))\{ \bar{A}_{{ij}} + F_{i} \varpi (t)\} ^{T} Px(t) \\ & \quad + x^{T} (t)P\sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))\{ \bar{A}_{{ij}} + F_{i} \varpi (t)\} \\ & = \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))\{ x^{T} (t)(\bar{A}_{{ij}}^{T} P + P\bar{A}_{{ij}} )x(t) \\ & \quad + \varpi ^{T} (t)F_{i}^{T} Px(t) + x^{T} (t)PF_{i} \varpi (t)\} \\ & \le \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))\{ 2(\mu _{1} + \mu _{2} \parallel x(t)\parallel )\parallel PF_{i} \parallel \parallel x(t)\parallel - \lambda _{{{\text{min}}}} (\zeta _{{ij}} )\parallel x(t)\parallel ^{2} \} \\ & = \sum\limits_{{i = 1}}^{r} {\sum\limits_{{j = 1}}^{r} {\lambda _{i} } } ((t))\lambda _{j} ((t))\{ - (\lambda _{{{\text{min}}}} (\zeta _{{ij}} ) - 2\mu _{2} \parallel PF_{i} \parallel )\parallel x(t)\parallel ^{2} + 2\mu _{1} \parallel PF_{i} \parallel \parallel x(t)\parallel \} \\ \end{aligned}$$
(22)

Thus, \(\dot{V}<0\) is achieved if the condition in (21) holds, and then the system (20) is boundedly stable.

Remark 4

For the proposed sliding surface in (18), when \({B}_{i}\ne {{F}}_{i}\), the appropriate matrix \({K}_{j}\) can be obtained by solving the condition in (21). In addition, the selected matrix \(\mathfrak{I}\) satisfies \(\mathfrak{I}{{F}}_{i}=0\) when \({B}_{i}\ne {{F}}_{i}\), and \(\mathfrak{I}{{F}}_{i}\) is non-singular, which is essential for the subsequent adaptive CNF-based fuzzy sliding mode controller synthesis process.

3.3 AFCNFISM Controller Design

This novel AFCNFISM controller is suggested to be appropriate for the TS fuzzy model in (7) and (17). The objective of the AFCNFISM controller is to propel the state trajectory of the system (7) and (17) into the fuzzy surface (8) and (18), and thereafter to preserve them within the fuzzy surface regardless of disturbances or uncertainties. Indeed, the AFCNFISM controller modifies the values of the sliding parameters. In other words, the attractiveness of the fuzzy surface is enhanced by imposing criteria on the controller that make it reachable. This control structure consists of four terms. The first term is developed using the parallel distribution compensation (PDC) technique. The second term, which we refer to as the adjusted term, is any arbitrary nonlinear function of the error that has the features described in Remark 5. The third term is designed using the adaptive mechanism, which is defined by the parameters \({\widetilde{\mu }}_{1}(t)={\widehat{\mu }}_{1}(t)-{\mu }_{1}\) and \({\widetilde{\mu }}_{2}(t)={\widehat{\mu }}_{2}(t)-{\mu }_{2}\) to estimate known parameters \({\widehat{\mu }}_{1}(t)\) and \({\widehat{\mu }}_{2}(t)\) to the system’s unknown parameters \({\mu }_{1}\) and \({\mu }_{2}\), respectively. The structure of the fourth term is based on the well-known SMC.

Theorem 3

Let the system (7) with the constraints (6) hold. The fuzzy surface (8) can be reached in a limited time, the closed-loop system (7) and the fuzzy surface \(\eta (t)\) under the AFCNFISM controller is UUB.

We define

$$\left\{\begin{array}{l}K=\sum_{j=1}^{r}{\lambda }_{j}(\varkappa (t)){K}_{j}\\ \hslash (t)={\widehat{\mu }}_{1}(t)+{\widehat{\mu }}_{2}(t)\parallel e(t)\parallel \\ {u}_{N}=\sum_{i=1}^{r}{\lambda }_{i}(\varkappa (t))\xi (e(t))\mathfrak{I}{B}_{i}e(t)\\ {\mathrm{\eth }}_{ij}(t)=\sum_{i=1}^{r}\sum_{j=1}^{r}{\lambda }_{i}(\varkappa (t)){\lambda }_{j}(\varkappa (t))\mathfrak{I}{B}_{i}\\ \end{array}\right.$$
(23)

Remark 5

In the development of the CNF control law, the choice of the negative nonlinear function \(\xi (e(t))\) is a crucial step. This nonlinear function provides anti-overshoot characteristics and dampens response overshoot (Jafari and Binazadeh 2019).

The AFCNFISM controller is designed in the following manner:

$$u(t)=\left\{\begin{array}{l}{u}_{N}-\frac{\eta (t){\mathrm{\eth }}_{ij}(t)}{\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel }\hslash (t)-\varphi sign(\eta (t){\mathrm{\eth }}_{ij}(t))+Ke(t)\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel \ne 0\\ \\ Ke(t)+{u}_{N} \parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel =0\end{array}\right.$$
(24)

where adaptive laws are defined as follows:

$$\left\{\begin{array}{l}{\dot{\widehat{\mu }}}_{1}(t)={\xi }_{1}(\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel -{\varepsilon }_{1}{\widehat{\mu }}_{1}(t))\\ {\dot{\widehat{\mu }}}_{2}(t)=({\xi }_{2}-1)({\varepsilon }_{2}{\widehat{\mu }}_{2}(t)-\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel \parallel e(t)\parallel )\end{array}\right.$$
(25)

where \({\xi }_{1}\), \({\xi }_{2}\), \({\varepsilon }_{1}\), \({\varepsilon }_{2}\), and \(\varphi\) are designed positive scalars.

Proof

Define the Lyapunov function for the closed-loop system:

$$V(t)=\frac{1}{2}{\eta }^{T}(t)\eta (t)+\frac{1}{2{\xi }_{1}}{\widetilde{\mu }}_{1}^{2}(t)+\frac{1}{2(1-{\xi }_{2})}{\widetilde{\mu }}_{2}^{2}(t)$$
(26)

In consideration of the nature of the control signal, the stability analysis of saturated and unsaturated scenarios is expressed. Hence, based on (8) and the control law stated in (24), the derivative of the Lyapunov function with respect to time is computed as follows:

$$\dot{V}(t)={\eta }^{T}(t)\{{\mathrm{\eth }}_{ij}(t)(sat(u(t))+\varpi (t)-Ke(t))\} +\frac{1}{{\xi }_{1}}{\widetilde{\mu }}_{1}(t){\dot{\widehat{\mu }}}_{1}(t)+\frac{1}{2(1-{\xi }_{2})}{\widetilde{\mu }}_{2}(t){\dot{\widehat{\mu }}}_{2}(t)$$
(27)

Scenario 1

None of the input signals are saturated, i.e. \(|u(t)|<\stackrel{*}{u}\); therefore, utilizing (25)–(27), the following results can be acquired:

$$\begin{aligned}\dot{V}\left( t \right) &= \eta ^{T} \left( t \right)\left\{ {_{{ij}} \left( t \right)\left( {u\left( t \right) + \varpi \left( t \right) - Ke\left( t \right)} \right)} \right\}~~ + \frac{1}{{\xi _{1} }}\tilde{\mu }_{1} \left( t \right) {\dot{\hat{\mu }}} \left( t \right) + \frac{1}{{2\left( {1 - \xi _{2} } \right)}}\tilde{\mu }_{2} \left( t \right) \dot{\hat{\mu }}_{2} \left( t \right)\\ & = \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\left\{ {u\left( t \right) + \varpi \left( t \right) - Ke\left( t \right)} \right\} + \tilde{\mu }_{1} \left( t \right)\left( {\parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel - \varepsilon _{1} \hat{\mu }_{1} \left( t \right)} \right)\\ &\quad + \tilde{\mu }_{2} \left( t \right)\left( {\left\| {\eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)} \right\|\left\| {e\left( t \right)} \right\| - \varepsilon _{2} \hat{\mu }_{2} \left( t \right)} \right) \\ &\quad \le \left\| {\eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)} \right\|\{ - \frac{{\eta \left( t \right){\text{}}_{{ij}} \left( t \right)}}{{\left\| {\eta \left( t \right){\text{}}_{{ij}} \left( t \right)} \right\|}}\left( {\hat{\mu }_{1} \left( t \right) + \hat{\mu }_{2} \left( t \right)\left\| {e\left( t \right)} \right\|} \right) - \varphi sign\left( {\eta \left( t \right){\text{}}_{{ij}} \left( t \right)} \right) \\ & \quad + \mu _{1} + \mu _{2} \left\| {e\left( t \right)} \right\|\} + \left( {\tilde{\mu }_{1} \left( t \right) + \tilde{\mu }_{2} \left( t \right)\left\| {e\left( t \right)} \right\|} \right)\left\| {\eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)} \right\| - \varepsilon _{1} \hat{\mu }_{1} \left( t \right)\left( {\hat{\mu }_{1} \left( t \right) - \mu _{1} } \right) \\ & \quad - \varepsilon _{2} \hat{\mu }_{2} \left( t \right)\left( {\hat{\mu }_{2} \left( t \right) - \mu _{2} } \right) \\ & = - \varphi \left\| {\eta \left( t \right){\text{}}_{{ij}} \left( t \right)} \right\|_{1} - \varepsilon _{1} (\hat{\mu }_{1} \left( t \right) - \frac{1}{2}\mu _{1} )^{2} - \varepsilon _{2} (\hat{\mu }_{2} \left( t \right) - \frac{1}{2}\mu _{2} )^{2} + \frac{1}{4}\left( {\varepsilon _{1} \mu _{1}^{2} + \varepsilon _{2} \mu _{2}^{2} } \right) \\ & \quad \le - \varphi \left\| {\eta \left( t \right){\text{}}_{{ij}} \left( t \right)} \right\|_{1} + \frac{1}{4}\left( {\varepsilon _{1} \mu _{1}^{2} + \varepsilon _{2} \mu _{2}^{2} } \right) \end{aligned}$$
(28)

Scenario 2

All input signals transcend their upper limits, which means \(u(t)>\stackrel{*}{u}\).

$$u(t)=Ke(t)+{u}_{N}-\frac{\eta (t){\mathrm{\eth }}_{ij}(t)}{\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel }\hslash (t)-\varphi \mathrm{sign}(\eta (t){\mathrm{\eth }}_{ij}(t))\ge \stackrel{*}{u}$$
(29)

In this scenario, one can reveal that if \({u}_{i}>\stackrel{*}{u}\) is established, then one has \(\stackrel{*}{u}-{\sum }_{j=1}^{r}{\lambda }_{j}(\varkappa (t)){K}_{j}e(t)\ge 0\). Based on the definition of saturation function, \(\mathrm{sat}(u(t))=\stackrel{*}{u}\), and from (29), the following is obtained:

$$\dot{V}\left( t \right) = \eta^{T} \left( t \right)\left\{ {_{ij} \left( t \right)\left( {\mathop u\limits^{*} + \varpi \left( t \right) - Ke\left( t \right)} \right)} \right\} + \frac{1}{{\xi_{1} }}\tilde{\mu }_{1} \left( t \right)\mathop {\hat{\mu }}\limits_{1} \left( t \right) + \frac{1}{{2\left( {1 - \xi_{2} } \right)}}\tilde{\mu }_{2} \left( t \right)\mathop {\hat{\mu }}\limits_{2} \left( t \right)$$
(30)

where (29) and (30) result in

$${u}_{N}-\frac{\eta (t){\mathrm{\eth }}_{ij}(t)}{\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel }\hslash (t)-\varphi \mathrm{sign}(\eta (t){\mathrm{\eth }}_{ij}(t))\ge \stackrel{*}{u}-Ke(t)\ge 0$$
(31)

Thus, we acquire via (30) and (31):

$$\begin{aligned} \dot{V}\left( t \right) & = \eta ^{T} \left( t \right)\left\{ {{\text{}}_{{ij}} \left( t \right)\left( {\mathop u\limits^{{\text{*}}} + \varpi \left( t \right) - Ke\left( t \right)} \right)} \right\}~~ + \frac{1}{{\xi _{1} }}\tilde{\mu }_{1} \left( t \right)\dot{\hat{\mu }}_{1} \left( t \right) + \frac{1}{{2\left( {1 - \xi _{2} } \right)}}\tilde{\mu }_{2} \left( t \right)\dot{\hat{\mu }}_{2} \left( t \right) \\ & \le \parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel \{ u_{N} - \frac{{\eta \left( t \right){\text{}}_{{ij}} \left( t \right)}}{{\parallel \eta \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel }}\left( {\hat{\mu }_{1} \left( t \right) + \hat{\mu }_{2} \left( t \right)\parallel e\left( t \right)\parallel } \right) - \varphi sign\left( {\eta \left( t \right){\text{}}_{{ij}} \left( t \right)} \right) \\ & + \mu _{1} + \mu _{2} \parallel e\left( t \right)\parallel \} + \tilde{\mu }_{1} \left( t \right)\left( {\parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel - \varepsilon _{1} \hat{\mu }_{1} \left( t \right)} \right) \\ & + \tilde{\mu }_{2} \left( t \right)\left( {\parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel \parallel e\left( t \right)\parallel - \varepsilon _{2} \hat{\mu }_{2} \left( t \right)} \right) \\ & \le - \varphi \parallel \eta \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel _{1} + \frac{1}{4}\left( {\varepsilon _{1} \mu _{1}^{2} + \varepsilon _{2} \mu _{2}^{2} } \right) \\ \end{aligned}$$
(32)

Scenario 3

All input signals transcend their lower limits, which implies \(u(t)\le -\stackrel{*}{u}\).

$$Ke(t)+{u}_{N}-\frac{\eta (t){\mathrm{\eth }}_{ij}(t)}{\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel }\hslash (t)-\varphi \mathrm{sign}(\eta (t){\mathrm{\eth }}_{ij}(t))\le -\stackrel{*}{u}$$
(33)

In this scenario, one can indicate that if \({u}_{i}<-\stackrel{*}{u}\) is determined, then one has \(\stackrel{*}{u}+{\sum }_{j=1}^{r}{\lambda }_{j}(\varkappa (t)){K}_{j}e(t)\ge 0\). From (33) and the definition of the saturation function, it can be determine that

$${u}_{N}-\frac{\eta (t){\mathrm{\eth }}_{ij}(t)}{\parallel \eta (t){\mathrm{\eth }}_{ij}(t)\parallel }\hslash (t)-\varphi \mathrm{sign}(\eta (t){\mathrm{\eth }}_{ij}(t))\ge -\stackrel{*}{u}-Ke(t)$$
(34)

Lastly, (27) and (34) denote that

$$\begin{aligned} \dot{V}\left( t \right) & = \eta ^{T} \left( t \right)\left\{ {{\text{}}_{{ij}} \left( t \right)\left( { - \mathop u\limits^{{\text{*}}} + \varpi \left( t \right) - Ke\left( t \right)} \right)} \right\}~~ + \frac{1}{{\xi _{1} }}\tilde{\mu }_{1} \left( t \right)\mathop {\hat{\mu }}\limits^{} _{1} \left( t \right) + \frac{1}{{2\left( {1 - \xi _{2} } \right)}}\tilde{\mu }_{2} \left( t \right)\mathop {\hat{\mu }}\limits^{} _{2} \left( t \right) \\ & \le \parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel \{ u_{N} - \frac{{\eta \left( t \right){\text{}}_{{ij}} \left( t \right)}}{{\parallel \eta \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel }}\left( {\hat{\mu }_{1} \left( t \right) + \hat{\mu }_{2} \left( t \right)\parallel e\left( t \right)\parallel } \right) - \varphi sign\left( {\eta \left( t \right){\text{}}_{{ij}} \left( t \right)} \right) \\ & + \mu _{1} + \mu _{2} \parallel e\left( t \right)\parallel \} + \tilde{\mu }_{1} \left( t \right)\left( {\parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel - \varepsilon _{1} \hat{\mu }_{1} \left( t \right)} \right) \\ & + \tilde{\mu }_{2} \left( t \right)\left( {\parallel \eta ^{T} \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel \parallel e\left( t \right)\parallel - \varepsilon _{2} \hat{\mu }_{2} \left( t \right)} \right) \\ & \le - \varphi \parallel \eta \left( t \right){\text{}}_{{ij}} \left( t \right)\parallel _{1} + \frac{1}{4}\left( {\varepsilon _{1} \mu _{1}^{2} + \varepsilon _{2} \mu _{2}^{2} } \right) \\ \end{aligned}$$
(35)

Therefore, based on (26) and (27), and in accordance with Theorem 3, the UUB of the system (7) for three scenarios can be obtained. The UUB of the system (17) is identical to that of (7), then it is eliminated.

4 Constrained Control Performance Specifications

The mathematical framework based on LMI constraints is set to the control signal for the simulation to demonstrate good behavior. To obtain an efficient and robust control, the LMI constraints are introduced to the Rikitake system’s control signal. Assume that the initial state \(x\left( 0 \right)\) is known, and that the quantity of the \({\Psi }\) boundaries is the maximum value permitted for the control signal’s 2-norm (\(\parallel u\left( t \right)\parallel_{2} \le \psi\)).

$$\left[ {\begin{array}{*{20}l} 1 \hfill & {x(0)^{T} } \hfill \\ {x\left( 0 \right)} \hfill & X \hfill \\ \end{array} } \right] \ge 0,\quad \left[ {\begin{array}{*{20}l} X \hfill & {W_{i}^{T} } \hfill \\ {W_{i} } \hfill & {{\Psi }^{2} I} \hfill \\ \end{array} } \right] \ge 0$$
(36)

where \(W_{i} = K_{i} X\) and \(X = P^{ - 1}\).

The following phases offer a concise summary of the proposed strategy:

Algorithm 1 (Fuzzy SMC phases).

  • Phase 1. Specify nonlinear variables in (1) in terms of \({\varkappa }_{1} \left( t \right)\) and \({\varkappa }_{2} \left( t \right)\).

  • Phase 2. Achieve the maximum and minimum variables in (1).

  • Phase 3. The normalized firing strengths \(\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,\) and \(\lambda_{4}\) are determined using membership functions \(M_{11}\), \(M_{12}\), \(M_{21}\), and \(M_{22}\).

  • Phase 4. Specify the fuzzy rules.

  • Phase 5. Specify the state matrices \(A_{1}\), \(A_{2}\), \(A_{3}\), and \(A_{4}\) using the minimum and maximum values of the \({\varkappa }_{1} \left( t \right)\) and \({\varkappa }_{2} \left( t \right)\) as well as fuzzy rules.

  • Phase 6. There are two scenarios taken into account for the TS model in (13): matrices with \(E_{i} = B_{i}\) and matrices with \(E_{i} \ne B_{i}\).

  • Phase 7. Design the AFCNFISM controller in (24) as the control law.

  • Phase 8. Determine the sliding surface matrix \(K_{j}\) in two cases from a feasible solution of (13) for the case \(E_{i} = B_{i}\) and a feasible solution of inequality (21) for the case \(E_{i} \ne B_{i}\) which is represented in Examples 1 and 2.

  • Phase 9. Determine the values for the design parameters \(\xi_{1}\),\(\xi_{2}\),\(\varphi\),\(\varepsilon_{1}\), \(\varepsilon_{2}\), \(\hat{\mu }_{1} \left( 0 \right)\), and \(\hat{\mu }_{2} \left( 0 \right)\) that are provided in (24) and (25).

  • Phase 10. Apply the designed control law with the constrained (36) and unconstrained control law in the system (7) and the uncertain chaotic Rikitake system in (17).

5 Illustrative Examples

Example 1

This part is presented to verify the effectiveness and advantages of the proposed fuzzy model and control scheme. Applying the designed AFCNFISM controller in (19) for the unsaturated TS fuzzy control of the Rikitake system in (7), we select \(\varphi = 5.5\), \(\xi_{1} = 0.01\), \(\xi_{2} = 0.01\), \(\varepsilon_{1} = 0.04\), \(\varepsilon_{2} = 0.03\), and \({\Psi } = 5\). The adaptive parameters are given as \(\hat{\mu }_{1} \left( 0 \right) = 0.1\) and \(\hat{\mu }_{2} \left( 0 \right) = 0.2\). Then, matrix \({\Im }\) is selected as \(\Im = 0 \, 0.01 \, 0.1\). By utilizing a feasible solution of (13) and considering Theorem 1, the fuzzy surface is selected as follows:

$$\eta \left( t \right) = \Im e\left( t \right) - \Im e\left( 0 \right) - \mathop \int \limits_{0}^{t} \mathop \sum \limits_{i = 1}^{4} \mathop \sum \limits_{j = 1}^{4} \lambda_{i} \left( {{\varkappa } \left( \theta \right)} \right)\lambda_{j} \left( {{\varkappa } \left( \theta \right)} \right)\Im \left( {A_{i} + B_{i} K_{j} } \right)e\left( \theta \right)d\left( \theta \right)$$
(37)

All the nonlinear simulations are implemented entirely in the MATLAB software/SeDuMi solver, where the initial condition is \(e\left( 0 \right) = \begin{array}{*{20}c} {0.0{1}} & {0.0{1}} & {0.0{1}} \\ \end{array}^{T}\), and \(\varpi \left( t \right) = 0.4 + 0.3{\text{sin}}\left( t \right)\) is an exogenous disturbance. The unconstrained gain \(K_{j}\) is calculated as follows:

$$K_{1} = \left[ {\begin{array}{*{20}l} {1.7375} \hfill & {2.0002} \hfill & {0.0002} \hfill \\ {2.0001} \hfill & {1.7389} \hfill & {0.0002} \hfill \\ { - 0.0001} \hfill & { - 0.0001} \hfill & { - 0.2621} \hfill \\ \end{array} } \right], \quad K_{2} = \left[ {\begin{array}{*{20}l} {1.7633} \hfill & {3.0003} \hfill & {1.0003} \hfill \\ {3.0001} \hfill & {1.7658} \hfill & {0.0002} \hfill \\ {0.9997} \hfill & { - 0.0007} \hfill & { - 0.2355} \hfill \\ \end{array} } \right]$$
$$K_{3} = \left[ {\begin{array}{*{20}l} {1.7183} \hfill & {2.0002} \hfill & {0.0000} \hfill \\ {2.0001} \hfill & {1.7201} \hfill & { - 0.0002} \hfill \\ { - 0.0003} \hfill & { - 0.0006} \hfill & { - 0.2806} \hfill \\ \end{array} } \right], \quad K_{4} = \left[ {\begin{array}{*{20}l} {1.7287} \hfill & {3.0003} \hfill & {0.0000} \hfill \\ {3.0001} \hfill & {1.7314} \hfill & { - 0.0002} \hfill \\ { - 0.0003} \hfill & { - 0.0007} \hfill & { - 0.2697} \hfill \\ \end{array} } \right]$$
$$P = \left[ {\begin{array}{*{20}l} {0.9995} \hfill & { - 0.0004} \hfill & {0.0002} \hfill \\ { - 0.0004} \hfill & {0.9995} \hfill & { - 0.0000} \hfill \\ {0.0002} \hfill & { - 0.0000} \hfill & {0.9997} \hfill \\ \end{array} } \right]$$

After applying new LMI conditions (24) on the control signal (19), the matrix \(K_{j}\) is obtained as

$$K_{1} = \left[ {\begin{array}{*{20}l} {0.6990} \hfill & {0.3766} \hfill & { - 0.2307} \hfill \\ {0.6942} \hfill & {0.4119} \hfill & { - 0.1121} \hfill \\ { - 1.3249} \hfill & { - 0.5583} \hfill & { - 0.5189} \hfill \\ \end{array} } \right], \quad K_{2} = \left[ {\begin{array}{*{20}l} {0.6722} \hfill & {0.6918} \hfill & {0.4781} \hfill \\ {1.2830} \hfill & {0.1147} \hfill & { - 0.2201} \hfill \\ {1.3653} \hfill & {0.0135} \hfill & { - 0.3794} \hfill \\ \end{array} } \right]$$
$$K_{3} = \left[ {\begin{array}{*{20}l} {0.4551} \hfill & {0.3284} \hfill & {0.2681} \hfill \\ {0.7894} \hfill & {0.4145} \hfill & {0.0279} \hfill \\ {0.8917} \hfill & {0.2415} \hfill & { - 0.3223} \hfill \\ \end{array} } \right],\quad K_{4} = \left[ {\begin{array}{*{20}l} {0.5785} \hfill & {0.6658} \hfill & {0.2459} \hfill \\ {1.2438} \hfill & {0.0132} \hfill & { - 0.0097} \hfill \\ {0.7135} \hfill & {0.1033} \hfill & { - 0.3321} \hfill \\ \end{array} } \right]$$
$$P = \left[ {\begin{array}{*{20}l} {0.6094} \hfill & {0.1721} \hfill & {0.0324} \hfill \\ {0.1721} \hfill & {0.2467} \hfill & {0.0070} \hfill \\ {0.0324} \hfill & {0.0070} \hfill & {0.1541} \hfill \\ \end{array} } \right]$$

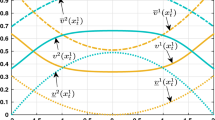
Thus, Figs. 5a and 6a depict the behavior of synchronization errors of the Rikitake system: unconstrained and constrained, respectively. Clearly, the state trajectories in Fig. 6a almost reach zero after 2 s with minimum transient oscillations with the short time in comparison to the Fig. 5a. This implies that the stabilization objective is met despite primary transient oscillations in the states. It is observed that the amplitude of the control signals in Fig. 6b is less than that in Fig. 5b, and chattering has been significantly reduced. The fuzzy surfaces are represented in Figs. 5c and 6c.

Fig. 5
figure 5

a The unconstrained responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image
Fig. 6
figure 6

a The constrained responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image

Example 2

This section considers the uncertain unsaturated TS Rikitake disturbed system in (17). In (23), the parameters \(\varphi = 10.5\), \(\xi_{1} = 0.02\), \(\xi_{2} = 0.03\), \(\varepsilon_{1} = 0.05\), \(\varepsilon_{2} = 0.02\), \(\mu_{1} \left( 0 \right) = 0.2\), \(\mu_{2} \left( 0 \right) = 0.3\), and \({\Psi } = 5\) are selected for the designed AFCNFISM controller. Then, the matrix \({\Im }\) is selected as \(\Im = 0 \, 0.{1 }0\). Using a feasible solution of (21) and taking into account Theorem 2, the fuzzy surface is chosen as follows:

$$\eta \left( t \right) = \Im e\left( t \right) - \mathop \int \limits_{0}^{t} \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\lambda_{i} \left( {{\varkappa } \left( \theta \right)} \right)\lambda_{j} \left( {{\varkappa } \left( \theta \right)} \right)\Im \left( {A_{i} + \Delta A_{i} \left( t \right) + B_{i} K_{j} } \right)e\left( \theta \right){\text{d}}\left( \theta \right) - \Im e\left( 0 \right)} }$$
(38)
$$L_{1} = \left[ {\begin{array}{*{20}l} {0.1} \hfill & 0 \hfill & 0 \hfill \\ { - 0.1} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\quad L_{2} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - 0.1} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$
$$L_{3} = \left[ {\begin{array}{*{20}l} { - 0.1} \hfill & 0 \hfill & 0 \hfill \\ {0.1} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\quad L_{4} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {0.1} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$
$$T_{1} = \left[ {\begin{array}{*{20}l} {0.01} \hfill & 0 \hfill & 0 \hfill \\ { - 0.01} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\quad T_{2} = \left[ {\begin{array}{*{20}l} {0.01} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - 0.01} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$
$$T_{3} = \left[ {\begin{array}{*{20}l} { - 0.01} \hfill & 0 \hfill & 0 \hfill \\ {0.01} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\quad T_{4} = \left[ {\begin{array}{*{20}l} { - 0.01} \hfill & 0 \hfill & 0 \hfill \\ {0.01} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$
$$\begin{aligned} & D_{1} \left( t \right) = D_{2} \left( t \right) = D_{3} \left( t \right) = D_{4} \left( t \right) = \\ & {\text{sin}}\left( t \right){\text{The}}\;{\text{unconstrained}}\;{\text{gain}}\;K_{j} \;{\text{is}}\;{\text{computed}}\;{\text{as}}\;{\text{follows:}} \\ & K_{1} = \left[ {\begin{array}{*{20}l} {1.6624} \hfill & {1.5499} \hfill & {0.0507} \hfill \\ {1.4714} \hfill & {2.2534} \hfill & {0.4331} \hfill \\ { - 0.0000} \hfill & {0.5000} \hfill & { - 0.0375} \hfill \\ \end{array} } \right], \quad K_{2} = \left[ {\begin{array}{*{20}l} {1.6417} \hfill & {1.5556} \hfill & { - 0.0507} \hfill \\ {1.4768} \hfill & {2.2357} \hfill & { - 0.4331} \hfill \\ { - 0.0000} \hfill & { - 0.5000} \hfill & { - 0.0525} \hfill \\ \end{array} } \right]. \\ \end{aligned}$$
$$K_{3} = \left[ {\begin{array}{*{20}l} {1.6826} \hfill & {3.5468} \hfill & {0.0507} \hfill \\ {3.4557} \hfill & {2.2744} \hfill & {0.4331} \hfill \\ {0.0000} \hfill & {0.5000} \hfill & { - 0.0263} \hfill \\ \end{array} } \right],\quad K_{4} = \left[ {\begin{array}{*{20}l} {1.6635} \hfill & {3.5596} \hfill & { - 0.0507} \hfill \\ {3.4670} \hfill & {2.2680} \hfill & { - 0.4331} \hfill \\ {0.0000} \hfill & { - 0.5000} \hfill & { - 0.0325} \hfill \\ \end{array} } \right]$$
$$P = \left[ {\begin{array}{*{20}l} {0.0135} \hfill & { - 0.0016} \hfill & { - 0.0000} \hfill \\ { - 0.0016} \hfill & {0.0136} \hfill & { - 0.0000} \hfill \\ { - 0.0000} \hfill & { - 0.0000} \hfill & {0.0116} \hfill \\ \end{array} } \right]$$

The matrix \(K_{j}\) is derived as follows after applying new LMI conditions to the control signal (18):

$$\begin{array}{*{20}c} {K_{1} = \left[ {\begin{array}{*{20}l} {1.3257} \hfill & {8.2545} \hfill & { - 0.0000} \hfill \\ {1.6986} \hfill & { - 7.8034} \hfill & {0.0000} \hfill \\ {0.0037} \hfill & {0.5538} \hfill & { - 0.0000} \hfill \\ \end{array} } \right],\quad K_{2} = \left[ {\begin{array}{*{20}l} {1.0666} \hfill & {8.2411} \hfill & { - 0.0000} \hfill \\ {1.7003} \hfill & { - 7.8131} \hfill & { - 0.0000} \hfill \\ {0.0036} \hfill & { - 0.4462} \hfill & { - 0.0000} \hfill \\ \end{array} } \right]} \\ {K_{3} = \left[ {\begin{array}{*{20}l} {1.6050} \hfill & {13.6811} \hfill & { - 0.0000} \hfill \\ {2.9227} \hfill & { - 7.8617} \hfill & {0.0000} \hfill \\ {0.0075} \hfill & {0.5734} \hfill & { - 0.0000} \hfill \\ \end{array} } \right],\quad K_{4} = \left[ {\begin{array}{*{20}l} {1.4541} \hfill & {13.6889} \hfill & { - 0.0000} \hfill \\ {3.5954} \hfill & {27.3827} \hfill & { - 0.0000} \hfill \\ {0.0076} \hfill & { - 0.4266} \hfill & { - 0.0000} \hfill \\ \end{array} } \right]} \\ \end{array}$$
$$P = \left[ {\begin{array}{*{20}l} {1.4564} \hfill & {0.1218} \hfill & { - 0.0000} \hfill \\ {0.1218} \hfill & {6.4230} \hfill & { - 0.0000} \hfill \\ { - 0.0000} \hfill & { - 0.0000} \hfill & {0.0000} \hfill \\ \end{array} } \right]$$

Consequently, Figs. 7a and 8a illustrate the unconstrained and constrained responses of synchronization errors in the Rikitake system, respectively. Evidently, in comparison to Fig. 7a, the state trajectories in Fig. 8a nearly approach zero after 3 s with minimal transient oscillations and a short UUB time. This indicates that despite transient oscillations in the states, the UUB aim of stabilizing and decreasing synchronization errors is fulfilled. The control signals in Fig. 8b have a lower amplitude than Fig. 7b, and chattering has been reduced considerably. The fuzzy surfaces are shown in Figs. 7c and 8c.

Fig. 7
figure 7

a The unconstrained uncertain responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image
Fig. 8
figure 8

a The constrained uncertain responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image

A chattering-free control signal must be constructed to guarantee that the system is robust against uncertainties and external disturbances with unknown bounds after providing control signals. Due to the nature of the control signal (18), the existence of the chattering phenomenon and its non-convergence to zero is inevitable. A frequent solution to this control chattering issue is the boundary layer design, which replaces the discontinuous switching function \({\text{sign}}\left( \eta \right) = \frac{\eta }{\left| \eta \right|}\) with a continuous approximation function \(\frac{\eta }{\left| \eta \right| + \tau }\), in which \(\tau\) is a small positive constant.

Therefore, the responses of synchronization errors, control signals, and fuzzy surface for the unconstrained and constrained approximation cases are shown in Figs. 9 and 10. As compared to Figs. 5a and 6a, in both the unconstrained and constrained cases, the rate of convergence errors in Figs. 9a and 10a are faster and smoother. The unconstrained approximation control effort in Fig. 9b and particularly in 10b are small relative to the unconstrained and constrained control effort in Figs. 5b and 6b. The chattering and oscillations illustrated in Figs. 9b and 10b are significantly reduced in comparison to the preceding cases depicted in Figs. 5b and 6b. The fuzzy surfaces shown in Figs. 9c and 10c have less chattering than Figs. 5c and 6c.

Fig. 9
figure 9

a The unconstrained approximation responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image
Fig. 10
figure 10

a The constrained approximation responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image

Figures 11 and 12 illustrate the behavior of synchronization errors, control signals, and the fuzzy surface in the unconstrained and constrained uncertain approximation cases. In comparison to Figs. 7 and 8, the rate of convergence errors in Figs. 11 and 12 is quicker and smoother in both unconstrained and constrained uncertain cases. The unconstrained uncertain approximation control effort shown in Fig. 11b and, more specifically, in Fig. 12b has low activity compared to the unconstrained and constrained uncertain control effort depicted in Figs. 7b and 8b. Figures 11c and 12c exhibit less chattering than Figs. 7c and 8c.

Fig. 11
figure 11

a The unconstrained uncertain approximation responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image
Fig. 12
figure 12

a The constrained uncertain approximation responses of the synchronization error. b Control signals. c Fuzzy surface

Full size image

6 Conclusion

In this paper, we have investigated the Takagi–Sugeno fuzzy approach for modeling the chaos synchronization of the nonlinear Rikitake system subject to actuator saturation. By employing this method, the nonlinear components of a system can be represented by linear subsystems, and the findings can be structured in the form of a simpler model with uncomplicated dynamics. Meanwhile, to achieve efficient control, an LMI constraint is added to the Rikitake system’s control signal. By establishing the Lyapunov function and appropriate fuzzy sliding surface and designing the AFCNFISM controller, the controlled systems are UUB, and the synchronization error of the chaotic Rikitake system in the presence of external disturbances and uncertainties converges to zero. Sufficient conditions have been set to ensure the synchronization of the controlled system with respect to LMIs. Compared with the unconstrained control, the constrained control yields better performance in the face of uncertainty and exterior disturbances.

Future research is planned to implement the higher-order sliding mode (HOSM) control approach to chaotic synchronization of a nonlinear time-delay system with asymmetric actuator saturation.