1 Introduction

Since the pioneering work of Strogatz and Barabasi, complex networks have been prosperous greatly in various fields of sciences and engineering over the past decades [1, 2]. As we all know, complex networks exist in many natural and man-made systems, such as neural networks, cellular and metabolic networks, biological networks, computer networks, the World Wide Web, coauthorship and citation networks, social networks, etc.

In fact, synchronization is a kind of typical collective behavior exhibited in many natural systems. It has been demonstrated that many real-world problems have close relationships with network synchronization. Recently, this kind of synchronization of complex dynamical networks has been extensively studied in various fields of science and engineering [3–9]. Wu et al. explored the synchronization of random directed networks [8]. Lü and Chen studied the synchronization of time-varying complex dynamical networks [9]. Zhou and Chen studied the synchronization criteria of coupled neural network systems with time delays [10]. Lately, some researchers investigated the synchronization of complex networks with pinning controllers [11–13]. Zhang and Lu proposed some adaptive feedback criteria for the synchronization of complex networks with delayed nodes [14]. Tang and Chen studied the adaptive synchronization between two complex networks with nonidentical topology [15]. Then the adaptive synchronization of uncertain complex dynamical networks was further studied by Lü et al. [16] and Zhang et al. [17]. Recently, based on the adaptive method, Zhou et al. studied the synchronization of networks with uncertain topology [18], Wu and Liu et al. investigated the structure identification of uncertain complex networks with time delays [19, 20].

In fact, many practical systems such as signal processing systems, computer networks, automatic control systems and telecommunications, impulsive effects are common phenomena due to instantaneous perturbations at certain moments. Therefore, the study of the complex dynamical networks with impulsive effects is important for understanding the dynamical behaviors of the most real-world complex networks. The impulsive synchronization of complex dynamical networks of identical nodes and nonidentical nodes was discussed in [21, 22]. Sun et al. and Zhou et al. studied the impulsive synchronization of delayed complex networks [23, 24]. Very recently, Wang and Wu analyzed the synchronization criteria for impulsive complex dynamical networks with time-varying delay [25], and Yang et al. studied the synchronization of impulsively coupled complex switched networks with parametric uncertainties and time-varying delays [26].

The adaptive-impulsive synchronization has only been lightly covered in References [27, 28]. To the best of our knowledge, most of existing works are dealing with the network problems with known dynamical properties and topology in a prior. However, few work has done for the synchronization and parameter tracking of uncertain networks. As an interesting and challenging topic, there are many questions in need to be paid more attention. It is a challenge to give further sights to such kinds of complex network.

Motivated by the above reasons, in this paper, we consider a general complex dynamical network with some uncertain parameters. Based on the adaptive feedback and impulsive control method, several novel criteria for the networks consisting of the nonidentical nodes and identical nodes have been obtained by constructing a suitable drive network and an impulsively controlled slave network. They guarantee that the unknown parameters are identified when the synchronization occurs between complex dynamical networks.

This paper is organized as follows. Section 2 introduces a general complex dynamical network several useful hypotheses. A set of novel adaptive-impulsive laws and synchronization criteria are given in Sect. 3. Section 4 uses a simple example to show the effectiveness of the proposed synchronization criteria. Some concluding remarks are given in Sect. 5.

2 Problem formulation and preliminaries

Consider a class of n-dimensional dynamical system, which is described by the following form of the differential equation:

$$ \dot{x}_i(t)=F_i\bigl(t,x_i(t), \varTheta_i\bigr), $$
(1)

in which x i (t)=(x i1(t),x i2(t),…,x in (t))T∈R n, Θ i ∈R p is the parameter vector. Further, it can be rewritten as

$$ \dot{x}_i(t)=f_i\bigl(t,x_i(t) \bigr)+g_i\bigl(t,x_i(t)\bigr)\cdot\varTheta_i, $$
(2)

where f i (t,x i (t)):R +×R n→R n is the continuous nonlinear function vector without unknown parameters and g i (t,x i (t)):R +×R n→R n×p is a continuous function matrix, Θ i ∈R p is the unknown parameter vector.

Throughout this paper, we always assume that the vector-valued function F i (t,x i (t),Θ i ) satisfies the uniform Lipschitz condition with respect to Θ i , that is,

Assumption 1

For any x i (t)=(x i1(t),x i2(t),…,x in (t))T and y i (t)=(y i1(t),y i2(t),…,y in (t))T, there exists a positive constant L i >0, such that

In fact, this assumption is very loose under the condition that the solution of Eq. (1) is bounded.

Now, we consider a general complex network consisting of N dynamical nodes. Each isolate node of the network is an n-dimensional dynamical system satisfies the above-mentioned assumption. Then the drive network is described by

(3)

where x i (t)=(x i1(t),x i2(t),…,x in (t))T ∈R n are the state variables of node i, and C=(c ij ) N×N is the weighted configuration matrix. If there is a directed coupling from node i to j(j≠i), then c ij ≠0 and c ij is the weight; otherwise, c ij =0. The matrix A=(a ij ) n×n ∈R n×n is the inner connecting matrix of each node.

Remark 1

In the network (3), the outer-coupling matrix C is not necessarily to be symmetric and the elements c ij are not assumed to be only 0 or 1. Moreover, there is not any constraint on the inner-coupling matrix A.

Remark 2

The network model (3) is more popular and generous because it is composed with N different node dynamics. If there are some kinds of the same nodes, it degenerates into the cluster network. If all the nodes have the same dynamics, it simplified to the general network in Refs. [3–8].

3 Parameter identification and synchronization by adaptive and impulsive controllers

In order to focus on the insights of the unknown dynamical parameters of the general complex networks, another impulsively controlled slave network is designed as

$$ \left \{\begin{array}{l} \dot{y}_i(t)=F_i(t,y_i(t), \hat{\varTheta}_i)+\sum_{j=1}^N {c}_{ij}Ay_ j(t)+U_i,\\[6pt] \quad t\neq t_k\\[6pt] \Delta y_i(t^+)=B_{ik}e_i(t),\quad t=t_k, \ k=1,2,\ldots\\[6pt] y_i(t_0^+)=y_{i0}, \end{array} \right . $$
(4)

where y i (t)=(y i1(t),y i2(t),…,y in (t))T ∈R n are the response state variables of node i, and \(\hat{\varTheta}_{i}\) is the estimation of the unknown Θ i . B ik is the feedback matrix of node i received at impulsive moment t k , U i is the adaptive controller received by the ith node. Moreover, \(\Delta y_{i}(t_{k}^{+})=y_{i}(t_{k}^{+})-y_{i}(t_{k}^{-})\), \(y_{i}(t_{k}^{+})=\lim_{t\rightarrow t_{k}^{+}}y_{i}(t)\) and any solution of (4) is left continuous at each t k , i.e. \(y_{i}(t_{k}^{-})=y_{i}(t_{k})\). The moments of impulse satisfy t 1<t 2<⋯<t k <t k+1<⋯ and lim k→∞ t k =∞, τ k =t k −t k−1<∞.

In the following, the main goal is to design appropriate adaptive controllers U i and the corresponding updating laws which make the impulsively controlled network (4) and (3) be asymptotically synchronous.

Define error vectors as

(5)

where i=1,2,…,N. According to equation (2) and the controlled network (4) and (3), the error systems are described by

(6)

and

(7)

where I is the identical matrix with the same dimension as B ik .

Theorem 1

Suppose that Assumption 1 holds. Let λ be the largest eigenvalue of (C⊗A)+(C⊗A)T, if

$$ \beta_{ik}=\lambda_{\max}\bigl[(I+B_{ik})^T(I+B_{ik}) \bigr]<1 $$
(8)

and there exists a constant ξ>1 such that

$$ 2\alpha\tau_k+\ln (\xi)<0 $$
(9)

under the following restriction conditions:

(10)

where k i are positive constants. Then, the impulsively controlled network (4) and (3) is asymptotically synchronous. Moreover,

$$ \hat{\varTheta}_i\rightarrow\varTheta_i, \quad i=1,2,\ldots,N. $$
(11)

Proof

Construct the Lyapunov function as follows:

(12)

where \(d_{i}^{\ast}(1\leq i\leq N)\) are some positive constants.

Then

along with Eq. (6) and Assumption 1, we have

Denote \(E(t)=(e_{1}^{T}(t),e_{2}^{T}(t),\ldots,e_{N}^{T}(t))^{T}\), and L=max i {L i }, substitute Eq. (10) into the above equality, we further have

where \(d^{\ast}=\min_{i}\{d_{i}^{\ast}\}>0\).

So

where \(\alpha=L+\frac{1}{2}\lambda-d^{\ast}\).

This implies that

$$ V(t)\leq V\bigl(t_{k-1}^+\bigr)e^{2\alpha(t-t_{k-1})},\quad t\in (t_{k-1},t_k] $$
(13)

For t=t k , from Eq. (7), we have

(14)

because of β ik =λ max[(I+B ik )T(I+B ik )]<1.

Thus, let k=1 in the inequality (13), for any t∈(t 0,t 1], we have

$$V(t)\leq V\bigl(t_0^+\bigr)e^{2\alpha(t-t_0)}, $$

which leads to

$$V(t_1)\leq V\bigl(t_0^+\bigr)e^{2\alpha(t_1-t_0)}. $$

Then from (14), there is

$$V\bigl(t_1^+\bigr)\leq V(t_1)\leq V \bigl(t_0^+\bigr)e^{2\alpha(t_1-t_0)}. $$

Therefore, for t∈(t 1,t 2],

$$V(t)\leq V\bigl(t_1^+\bigr)e^{2\alpha(t-t_1)}\leq V \bigl(t_0^+\bigr)e^{2\alpha(t-t_0)}. $$

Repeating the same process, for t∈(t k ,t k+1],

$$ V(t)\leq V\bigl(t_0^+\bigr)e^{2\alpha(t-t_0)}. $$
(15)

In virtue of the inequality (9) given in Theorem 1, we know that

$$e^{2\alpha\tau_k}<\frac{1}{\xi},\quad k=1,2,\ldots $$

Notice that t−t 0=(t−t k )+(t k −t k−1)+(t k−1−t k−2)⋯+(t 2−t 1)+(t 1−t 0)=(t−t k )+τ k +τ k−1+⋯+τ 2+τ 1. Thus, the inequality (15) can be further rewritten as

(16)

therefore V(t)→0 as k→∞ because of ξ>1, which implies that all the errors e i (t)→0 and \(\hat{\varTheta}_{i}\rightarrow \varTheta_{i}, d_{i}\rightarrow d_{i}^{\ast}(i=1,2,\ldots,N)\). So the synchronization between the impulsively controlled complex network (4) and network (3) is realized and the unknown system parameters are identified simultaneously. □

Corollary 1

If a complex network consists of N identical nodes, which can be described by

(17)

then unknown system parameters Θ can be identified by using the estimated values \(\hat{\varTheta}\) with the following impulsively controlled response network:

$$ \left \{\begin{array}{l} \dot{y}_i(t)=f(t,y_i(t))+g(t,y_i(t))\cdot\hat{\varTheta}\\[3pt] \phantom{\dot{y}_i(t)=}+\sum_{j=1}^N {c}_{ij}Ay_ j(t)+U_i,\quad t\neq t_k\\[6pt] \Delta y_i(t^+)=B_{ik}e_i(t),\quad t=t_k, \ k=1,2,\ldots\\[6pt] y_i(t_0^+)=y_{i0},\\[6pt] U_i=-d_i(t)e_i(t), \end{array} \right . $$
(18)

if

$$ 2\alpha\tau_k+\ln (\xi)<0 $$
(19)

and

(20)

where λ is the largest eigenvalue of (C⊗A)+(C⊗A)T, constant ξ>1 and α is the same defined in Theorem 1.

4 A simulation example

In the foregoing section, Theorems 1 and Corollary 1 essentially provide the criteria for synchronization and unknown system parameters identification between impulsively controlled uncertain complex networks. Here, we use a simple example to illustrate how these results can be applied in complex networks with identical nodes.

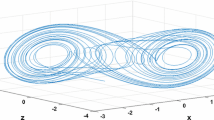
Consider a simple network with five identical nodes. The chaotic Lorenz system is taken as the node’s dynamical function in this example, which is given by

(21)

where the parameters a=10,b=8/3,c=28,Θ=(a,b,c)T.

Then

$$f\bigl(t,x_i(t)\bigr)=\left ( \begin{array}{c} 0 \\ -x_{i1}x_{i3}-x_{i2} \\ x_{i1}x_{i2} \end{array} \right ), $$

and

$$g\bigl(t,x_i(t)\bigr)=\left ( \begin{array}{c@{\quad}c@{\quad}c} x_{i2}-x_{i1} & 0 & 0 \\ 0 & 0 & x_{i1} \\ 0 & -x_{i3} & 0 \end{array} \right ). $$

Here, we assume that the inner matrix A=I 3 and these nodes are connected with weighted zero-row-sum. For example, the weighed outer-coupling configuration matrix is given by

$$C=\left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -4 & 1 & 1 & 2 & 0 \\ 1 & -7 & 4 & 0 & 2 \\ 1 & 4 & -6 & 2 & -1 \\ 2 & 0 & 2 & -7 & 3 \\ 0 & 2 & -1 & 3 & -4 \end{array} \right ), $$

and Fig. 1 shows the topology connection between these five nodes.

Fig. 1
figure 1

Topological structure of an uncertain complex network in the example

Full size image

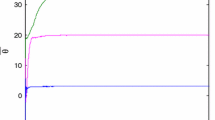
We assume that all the parameters a,b,c are unknown in prior. Let B ik =diag{−0.5,−0.5,−0.5}, τ k =0.2,k i =10∗i(i=1,2,…,5). Figure 2 shows the synchronization errors of e i1(t),e i2(t)e i3(t) under the updating laws (10). Clearly, all synchronization errors are rapidly converging to zero. From Figs. 3 and 4, one can see that the system parameters tracking is realized and all the adaptive feedback gain d i (t) converge to zero at the same time.

Fig. 2
figure 2

Synchronization errors e i (t) (1≤i≤5)

Full size image
Fig. 3
figure 3

Identification of system parameters

Full size image
Fig. 4
figure 4

The adaptive feedback d i (t)

Full size image

5 Conclusion

The adaptive-impulsive synchronization and parameter identification of unknown general complex dynamical networks has been studied in this paper. Specifically, some uncertain factors are taken into account in this network, such as some unknown system parameters. By constructing another suitable impulsively controlled slave network, several novel adaptive laws and synchronization criteria are derived. These criteria are very useful for understanding the mechanism of synchronization in complex networks. Moreover, the hypotheses and the resulting adaptive controllers for achieving network synchronization are expressed in simple forms that can be readily applied in practical situations. Finally, numerical simulations have been presented to demonstrate the effectiveness of the proposed synchronization criteria.