1 Introduction

Over the past decade, complex networks have gained extensive attention from various fields of engineering and applications, including social networks, biological systems and global economic markets [1, 2]. Synchronization of complex networks is one of the most important issues in this field. Recently, large variety of theoretical methods are presented for synchronizing complex networks and dynamics such as adaptive control [3–5], time delay feedback control [6] and sampled data [7]. More recently, impulsive control theory and pinning control have received increasingly attention due to their efficiency in synchronization of complex networks and networks of networks [8–12]. In [13, 14], it has been shown that sampled-data systems can be modeled by impulsive systems.

Impulsive control theory is a discrete method based on impulsive differential equation, and there is a tendency of synchronizing complex networks with it. It is one of the most efficient methods of synchronizing nonlinear dynamics and complex networks with uncertainty. In this method, response network receives small impulses from drive network in discrete impulse instants, which considerably lowers the bandwidth needed for transmitting data. This is the outstanding attribute of impulsive control method, which distinguishes it over other methods. This property reduces the transmitted information intensively and increases robustness of network against disturbances [15, 16].

In the literature, “synchronization of complex networks” refers to two concepts: inner and outer synchronization. The majority of recent works are focused on inner synchronization, which concerns with synchronization of nodes with each others [17, 18]. The outer synchronization refers to the synchronization of two or more complex networks [19–21], which is more important in real world to be realized.

Projective synchronization is one of the most useful issues in which complex network tracks target network, using a scaling constant in definition of tracking error. This paper mainly investigates outer projective and lag synchronization due to their efficient applications. In addition, projective and lag synchronization between complex networks with delay in both coupled and uncoupled terms are a challenge, which is not considered yet. These are considered in the current work. Recently, some other methods are used to achieve synchronization between networks with nonidentical nodes (like [22] and [23]); however, in almost all of the existing researches which are concerned with using impulsive criteria as a method for synchronization, all nodes of the network are assumed to be identical ([24–28] to name a few). Here in this paper, different dynamics for each node is considered. This is more realistic because nodes have different dynamical behaviors in practical cases [29, 30].

Recently, in some chaotic systems hidden attractors were discovered, and it is shown that the existence of hidden attractors may complicate the analysis of the systems and significantly affect the synchronization [31–33]. One more contribution provided in the current work lies in the type of stability (or synchronization). Unlike most of reports such as [8] and [25], in which some sufficient conditions are proposed in order to prove local synchronization, we have investigated the problem of globally exponentially stability. This paper is organized as follows: in Sect. 2, some preliminaries and the complex dynamical network model are presented. Section 3 has two parts, first part is devoted to the projective synchronization of the presented networks and second one is devoted to lag synchronization. For this, some new sufficient conditions based on impulsive control theory are derived. In Sect. 4, the effectiveness of results is illustrated via simulation on complex networks composed of chaotic Lur’e and Chua systems. In this Sect. 2 examples are considered: in first one, Chua system has been considered with parameters that lead to existence of self-excited attractor in it, and in second one, we have considered Lur’e system’s parameters in a way that hidden attractor appears. Some conclusions are drawn in Sect. 5.

2 Preliminaries and model description

In this paper, we consider a complex dynamical network with N nodes. Each node is n-dimensional dynamic system composed of linear and nonlinear terms with multiple time-varying delays and uncertainties. The state equation of the drive network is described by the following differential equation

$$\begin{aligned} \dot{x}_{i}= & {} (A_{i}+\Delta A_{i} ) x_{i} (t)+f_{i} (t,x_{i} (t),x_{i} (t-r_{1} (t) ),\nonumber \\&\ldots ,x_{i} (t-r_{m} (t) ) )\nonumber \\&+\,\Delta f_{i} (t,x_{i} (t),x_{i} (t-r_{1} (t) ),\ldots ,x_{i} (t-r_{m} (t) ) )\nonumber \\&+\sum _{j=1,j\ne i}^{N} g_{ij} (t,x_{j} (t),x_{j} (t-r_{1} (t) ),\ldots , \nonumber \\&\quad x_{j} (t-r_{m} (t) ) ) \end{aligned}$$
(1)

and the corresponding response network dynamic is given by

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\tilde{x}}_{i} =\left( {A_{i} +\Delta A_{i}^{\prime } } \right) \tilde{x}_{i} \left( t \right) \\ \qquad +f_{i} \left( {t,\tilde{x}_{i} \left( t \right) ,\tilde{x}_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots , \tilde{x}_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) \\ \qquad +\Delta f_{i}^{\prime } \left( {t,\tilde{x}_{i} \left( t \right) ,\,\tilde{x}_{i} \left( {t-r_{1} \left( t \right) } \right) ,\,\ldots ,\,\tilde{x}_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) \\ \qquad +\mathop \sum \nolimits _{j=1,j\ne i}^{N} g_{ij} \left( t,\tilde{x}_{j} \left( t \right) ,\tilde{x}_{j} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,\right. \\ \qquad \left. \tilde{x}_{j} \left( {t-r_{m} \left( t \right) } \right) \right) ,\quad t\ne t_{k} \\ \Delta \tilde{x}_{i} \left( t \right) =B_{ik} e\left( {t_{k}^- } \right) ,\quad t=t_{k} \\ \tilde{x}_{i}\left( t \right) =\emptyset _{i}(t),\quad -\mathop {\max }\limits _{1<l<m} \tau _{l} \le t\le 0 \\ \end{array}\right. \end{aligned}$$
(2)

where \(i,j=1,2,\ldots ,N\) and N is the number of network nodes. \(x_{i} =\left[ {x_{i1} ,x_{i2} , \ldots ,x_{in} } \right] ^{T},\tilde{x}_{i} =\left[ {\tilde{x}_{i1} , \tilde{x}_{i2} ,\ldots ,\tilde{x}_{in} } \right] ^{T}\in R^{n}\) are the vectors of state variables of the ith node, \(\Delta A_{i},\Delta A_{i}^{\prime } \in {\mathbb {R}}^{n\times n}\) represent uncertainties in the linear parts and \(\Delta f_{i} =\left[ {\Delta f_{i1} ,\Delta f_{i2} ,\ldots ,\Delta f_{in}}\right] \), \(\Delta f_{i}^{\prime } =\left[ \Delta f_{i1}^{\prime },\Delta f_{i2}^{\prime },\ldots ,\right. \left. \Delta f_{in}^{\prime }\right] :{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) represent uncertainties in the nonlinear parts of the drive and response network systems, respectively.

\(f_{i} {=}\left[ {f_{i1} ,f_{i2} ,\ldots ,f_{in} } \right] ,g_{ij} {=}\left[ {g_{ij1} ,g_{ij2} ,\ldots ,g_{ijn} } \right] :{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) and \(A_{i} \in {\mathbb {R}}^{n\times n}\) are constant functions and matrices. The time delays \(r_{i} \) may be unknown and time-varying but assumed to be bounded by known constant, i.e., \(0\le r_{l} \left( t \right) \le \tau _{l} \), (\(\tau _{l} \) are positive constants). \(\Delta \tilde{x}_{i} \left( {t^{+}} \right) =\mathop {\lim }\nolimits _{t\rightarrow t_{k}^+ } \tilde{x}_{i} \left( t \right) \) .\(\mathop {\lim }\nolimits _{h\rightarrow 0^{+}} x\left( {t_{k} +h} \right) =\tilde{x}\left( {t_{k}^+ } \right) =\tilde{x}\left( {t_{k}^- } \right) \) and \(\mathop {\lim }\nolimits _{h\rightarrow 0^{+}} \tilde{x}\left( {t_{k} -h} \right) =\tilde{x}\left( {t_{k} } \right) \) imply that \(\tilde{x}\left( t\right) \) is right continuous at \(t=t_{k} \). Thus, by considering equation (1),(2) and \(x\left( {t_{k}^+} \right) =x\left( {t_{k}^- } \right) \) the error network can be obtained as follows.

Remark 1

The time delays being considered in network synchronization could be generated due to the various reasons. Propagation delay is the one in signal propagation between nodes within finite time period. In addition, processing delay, as another type of it, is caused by intrinsic response delay or processing delay to external forcing, such as autapse connected to neurons [34, 35].

Remark 2

In practice, components of drive and response complex networks are different. This fact is considered in just few researches like [36]. Here, it is considered in presented complex network models (1) and (2) by taking \(\Delta A_{i}^{\prime }\) other than \({\Delta }A_{i} \) and \(\Delta f_{i}^{\prime } \) other than \({\Delta }f_{i}\).

Remark 3

Chaotic signals are considered to be bounded by a positive constant \(\chi \), \(\left\| x_{i}\right\| \le \chi \).

Remark 4

It is assumed that uncertainties in (1) and (2) do not destroy chaotic behavior of complex network.

Note that the origin is not equilibrium point of the following error dynamics, which implies that it is impossible to achieve complete synchronization between systems (1) and (2). Indeed, in some chaotic dynamics such as Lorenz systems, complete synchronization could be realized [37]. However, it should be noted that complete synchronization may not be necessarily satisfied in all conditions. As a result, we can employ specific error bound, which is less restrictive than complete synchronization but more realistic.

In this context, the goal is to derive some sufficient conditions in order to find the impulsive controller gain \(B_{ik}\) and impulse distances \(t_{k}\) such that drive and corresponding response complex networks synchronize.

3 Main results

3.1 Exponentially impulsive projective synchronization of between uncertain complex networks

Definition 1

In projective synchronization, the error of each node is defined as follows

$$\begin{aligned} e_{i} \left( t \right) ={\tilde{x}} _{i} \left( t \right) -\sigma x_{i} \left( t \right) \end{aligned}$$

in which \(\sigma \ne 0\) is a scaling constant. If \(\mathop {\lim }\nolimits _{t\rightarrow \infty } e_{i} \left( t \right) =0\), then projective synchronization is achieved. In special cases, anti-synchronization and complete synchronization are resulted with \(\sigma =-1\) and \(\sigma =1\), respectively.

Assumption 1

We assume that for each \(\sigma \) the following terms are being satisfied

$$\begin{aligned}&\left\| {f_{iz} \left( {t,\tilde{x}_{i} \left( t \right) ,\tilde{x}_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,\tilde{x}_{i} \left( {t-r_{m} \left( t\right) } \right) } \right) }\right. \nonumber \\&\qquad \left. -\,\sigma f_{iz} \left( {t,x_{i} \left( t \right) ,x_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) \right\| \nonumber \\&\quad \le k_{iz} \left\| {e_{i} \left( t \right) }\right\| +\mathop \sum \limits _{l=1}^{m} k_{izl} \left\| {e_{il} \left( {t-r_{l} \left( t \right) } \right) }\right\| \end{aligned}$$
(3)
$$\begin{aligned}&\left\| {g_{ijz} \left( {t,\tilde{x}_{i} \left( t \right) ,\tilde{x}_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,\tilde{x}_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) }\right. \nonumber \\&\qquad \left. {-\,\sigma g_{ijz} \left( {t,x_{i} \left( t \right) ,x_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) }\right\| \nonumber \\&\quad \le w_{ijz} \left\| {e_{i} \left( t \right) }\right\| +\mathop \sum \limits _{l=1}^{m} w_{ijzl} \left\| {e_{il} \left( {t-r_{l} \left( t \right) } \right) }\right\| \end{aligned}$$
(4)

and

$$\begin{aligned}&\left\| {\Delta f_{iz}^{\prime } \left( {t,\tilde{x}_{i} \left( t \right) ,\tilde{x}_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,\tilde{x}_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) }\right. \nonumber \\&\qquad \left. {-\,\sigma \Delta f_{iz}^{\prime } \left( {t,x_{i} \left( t \right) ,x_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) }\right\| \nonumber \\&\quad \le q_{iz} \left\| {e_{i} \left( t \right) }\right\| +\mathop \sum \limits _{l=1}^{m} q_{izl} \left\| {e_{il} \left( {t-r_{l} \left( t \right) } \right) }\right\| \end{aligned}$$
(5)

also the following term is considered

$$\begin{aligned}&\left\| {\Delta f_{iz}^{\prime } \left( {t,x_{i} \left( t \right) ,x_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) }\right. \nonumber \\&\qquad \left. {-\Delta f_{iz} \left( {t,x_{i} \left( t \right) ,x_{i} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x_{i} \left( {t-r_{m} \left( t \right) } \right) } \right) }\right\| \nonumber \\&\quad \le q_{iz}^{\prime } \left\| {x_{i} \left( t \right) }\right\| +\mathop \sum \limits _{l=1}^{m} q_{izl}^{\prime } \left\| {x_{il} \left( {t-r_{l} \left( t \right) } \right) }\right\| \end{aligned}$$
(6)

where \(k_{iz} ,k_{izl} ,\,w_{ijz} ,w_{ijzl} ,q_{iz} ,q_{izl} ,q_{iz}^{\prime } ,q_{izl}^{\prime } >0\) for any \(x\left( t \right) ,\,\,x\left( {t-r_{i} \left( t \right) } \right) ,\,\,e\left( t \right) ,\,e\left( {t-r_{i} \left( t \right) } \right) \in R^{n}\) and\(,1\le z\le n\,,1\le l\le m\).

Remark 5

In order to achieve less conservative constraints in following theorems, we considered Lipschitz constant for each state of each node separately.

Lemma 1

(see [11]) The following inequality satisfies for any real matrices \(X_{1} \), \(X_{2} \) and \(\mho =\mho ^{T}>0:\)

$$\begin{aligned} X_{1} ^{T}X_{2} +X_{2} ^{T}X_{1} \le X_{1} ^{T}\mho X_{1} +X_{1}^{T}\mho ^{-1}X_{1} \end{aligned}$$

Lemma 2

(see [15]) Let \(0\le r_{l} \left( t \right) \le \tau \), \(\mathfrak {I}\left( {t,u,u\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,u\left( {t-r_{m} \left( t \right) } \right) } \right) :{\mathbb {R}}^{+}\times \overbrace{{\mathbb {R}}\times \ldots \times {\mathbb {R}}}^{m+1}\rightarrow {\mathbb {R}}\) be nondecreasing in \(\bar{u}_{l} \) for each fixed \(\left( {t,u,\bar{u} _{1} ,\ldots ,\bar{u} _{m} } \right) ,l=1,2,\ldots ,m\) and \(\varpi _{k} :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be nondecreasing in u. Suppose that \(v\left( t \right) ,u\left( t \right) \in \hbox {PC}\left[ {\left[ {-\tau ,\infty } \right) ,{\mathbb {R}}} \right] \) satisfy

$$\begin{aligned}&\left\{ {{\begin{array}{l} {D^{+}u\left( t \right) \le \mathfrak {I}\left( {t,u\left( t \right) ,u\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,u\left( {t-r_{m} \left( t \right) } \right) } \right) ,\,\,t\ge 0} \\ {u\left( {t_{k} } \right) \le \varpi _{k} \left( {u\left( {t_{k}^- } \right) } \right) ,\quad k\in {\mathbb {N}}} \\ \end{array} }} \right. \\&\left\{ {{\begin{array}{l} {D^{+}v\left( t \right) \ge \mathfrak {I}\left( {t,v\left( t \right) ,v\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,v\left( {t-r_{m} \left( t \right) } \right) } \right) ,\,\,t\ge 0} \\ {v\left( {t_{k} } \right) \ge \varpi _{k} \left( {v\left( {t_{k}^- } \right) } \right) ,\quad k\in {\mathbb {N}}} \\ \end{array} }} \right. \end{aligned}$$

Then \(u\left( t \right) \le v\left( t \right) \), for \(-\tau \le t\le 0\) implies \(u\left( t \right) \le v\left( t \right) \), for \(t\ge 0.\)

Definition 2

The impulsive control input for synchronization of drive and response complex networks is considered as follows;

$$\begin{aligned} u\left( t \right)= & {} \mathop \sum \limits _{k=1}^\infty B_{k} e\left( {t_{k}^- } \right) =\mathop \sum \limits _{k=1}^\infty I_{N} \otimes B_{ki} e\left( {t_{k}^- } \right) ,\quad t=t_{k} ,\nonumber \\&0<t_{k} -t_{k-1} <\infty , \quad k =1,\ldots ,\infty \end{aligned}$$
(7)

One can rewrite impulsive networks (1), (2) in the following Kronecker product form, respectively

$$\begin{aligned} \dot{x}= & {} (A+\Delta A)x(t)+F\left( t,x_{i} (t),x_{i} (t-r_{1} (t) ),\right. \nonumber \\&\left. \ldots ,x_{i} (t-r_{m} (t) ) \right) \nonumber \\&+\,\Delta F(t,x_{i} (t),x_{i} (t-r_{1} (t) ),\ldots ,x_{i} (t-r_{m} (t) ) )\nonumber \\&+\,G(t,x_{j} (t),x_{j} (t-r_{1} (t) ),\ldots , x_{j} (t-r_{m} (t) ) ) \end{aligned}$$
(8)
$$\begin{aligned}&\left\{ \begin{array}{l} \dot{\tilde{x}}=(A+\Delta A^{'} ) {\tilde{x}}(t)+F(t,{\tilde{x}}_{i} (t),{\tilde{x}}_{i} (t-r_{1} (t) ),\\ \qquad \quad \ldots ,{\tilde{x}}_{i} (t-r_{m} (t) ) )\\ \qquad \quad +\,\Delta F^{'} (t,{\tilde{x}}_{i} (t),{\tilde{x}}_{i} (t-r_{1} (t) ),\ldots ,{\tilde{x}}_{i} (t-r_{m} (t) ) ) \\ \qquad \quad +\,G(t,{\tilde{x}}_{j} (t),{\tilde{x}}_{j} (t-r_{1} (t) ),\ldots ,{\tilde{x}}_{j} (t-r_{m} (t) ) ),\quad t\ne t_{k} \\ {\tilde{x}}(t)=B_{k} e(t_{k}^- )=(I_{N}\otimes B_{ki} )e(t_{k}^- ), \quad t=t_{k} \\ {\tilde{x}}(t)=\emptyset (t), -\mathop {\max }\limits _{1<l<m} \tau _{l} \le t\le 0 \end{array}\right. \nonumber \\ \end{aligned}$$
(9)

where

$$\begin{aligned}&x\left( t \right) =\left[ {x_{1}^{T} \left( t \right) ,x_{2}^{T} \left( t \right) ,\ldots ,x_{N}^{T} \left( t \right) } \right] ^{T}\\&\tilde{x}\left( t \right) =\left[ {\tilde{x}_{1}^{T} \left( t \right) ,\tilde{x}_{2}^{T} \left( t \right) ,\ldots ,\tilde{x}_{N}^{T} \left( t \right) } \right] ^{T}\\&A=diag\,\left\{ {A_{1} ,A_{2} ,\ldots ,A_{N} } \right\} \\&\Delta A=diag\,\left\{ {\Delta A_{1} ,\Delta A_{2} ,\ldots ,\Delta A_{N} } \right\} \\&\Delta A^{{\prime }}=diag\,\left\{ {\Delta A_{1}^{\prime } ,\Delta A_{2}^{\prime } ,\ldots ,\Delta _{N}^{\prime } } \right\} \\&F\left( \ldots \right) =\left[ {f_{1}^{T} \left( \ldots \right) ,f_{2}^{T} \left( \ldots \right) ,\ldots ,f_{N}^{T} \left( \ldots \right) } \right] ^{T}\\&\Delta F\left( \ldots \right) =\left[ {\Delta f_{1} ^{T}\left( \ldots \right) ,\Delta f_{2} ^{T}\left( \ldots \right) ,\ldots ,\Delta f_{N} ^{T}\left( \ldots \right) } \right] ^{T}\\&G\left( \ldots \right) =\left[ \left( {\mathop \sum \limits _{j=1}^{N} g_{1j} \left( \ldots \right) } \right) ^{T},\left( {\mathop \sum \limits _{j=1}^{N} g_{2j} \left( \ldots \right) } \right) ^{T},\right. \\&\qquad \left. \ldots ,\left( {\mathop \sum \limits _{j=1}^{N} g_{Nj} \left( \ldots \right) } \right) ^{T} \right] ^{T}\\&\Delta F^{'} (\dots )=[\Delta f_{1}^{'T} (\ldots ),\Delta f_{2}^{'T} (\ldots ),\ldots ,\Delta f_{N}^{'T} (\ldots )]^{T} \end{aligned}$$

\(\emptyset \left( t \right) =\left[ {\emptyset _{1}^{\prime T}\left( t \right) ,\emptyset _{2}^{\prime T}\left( t \right) ,\ldots ,\emptyset _{N}^{\prime T}\left( t \right) } \right] ^{T}\) By considering equation (8),(9) and the fact that \(x\left( {t_{k}^+ } \right) =x\left( {t_{k}^- } \right) \) the error network can be obtain as follows

$$\begin{aligned} \left\{ \begin{array}{l} \dot{e}(t)=(A+\Delta A^{'} )e(t)+\sigma (\Delta A^{'}-\Delta A)x(t)\\ \quad \qquad +E_{1}+E_{2}+E_{3}+E_{4} ,\quad t\ne t_{k}\\ \Delta e=B_{k} e(t_{k}^- )=(I_{N} \otimes B_{ki} )e(t_{k}^- ), \quad t=t_{k}\\ e(t)=\emptyset (t)-{\max }_{1<l<m}\tau _{l} \le t\le 0\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(10)

where

$$\begin{aligned}&e\left( t \right) =\left[ {e_{1}^{T} \left( t \right) ,e_{2}^{T} \left( t \right) ,\ldots ,e_{N}^{T} \left( t \right) } \right] ^{T}\\&E_{1} =\left[ F\left( {t,{\tilde{x}} \left( t \right) ,{\tilde{x}} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,{\tilde{x}} \left( {t-r_{m} \left( t \right) } \right) } \right) \right. \\&\qquad \quad \left. -\,\sigma F\left( {t,x\left( t \right) ,x\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x\left( {t-r_{m} \left( t \right) } \right) } \right) \right] \\&E_{2}=\left[ \Delta F^{'} (t,{\tilde{x}} (t),{\tilde{x}} (t-r_{1} (t) ),\ldots ,{\tilde{x}} (t-r_{m} (t) ),\ldots )\right. \\&\qquad \quad \left. -\,\sigma \Delta F^{'} (t,x(t),x(t-r_{1} (t) ),\ldots ,x(t-r_{m} (t) ) )\right] \\&E_{3} =\left[ G\left( {t,\tilde{x}\left( t \right) ,\tilde{x}\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,\tilde{x}\left( {t-r_{m} \left( t \right) } \right) } \right) \right. \\&\quad \qquad \left. -\,\sigma G\left( {t,x\left( t \right) ,x\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x\left( {t-r_{m} \left( t \right) } \right) } \right) \, \right] \\&E_{4} =\sigma \left[ \Delta F^{{\prime }}\left( {t,x\left( t \right) ,x\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x\left( {t-r_{m} \left( t \right) } \right) } \right) \right. \\&\qquad \quad \left. -\,\Delta F\left( {t,x\left( t \right) ,x\left( {t-r_{1} \left( t \right) } \right) ,\ldots ,x\left( {t-r_{m} \left( t \right) } \right) } \right) \right] \end{aligned}$$

Theorem 1

Let \(\delta =\mathop {\max }\nolimits _{k\in {\mathbb {N}}} t_{k} -t_{k-1} \)The impulsive distance and control gain are defined as (7). Positive symmetric matrix \(\mho \) is considered such that the following conditions hold:

$$\begin{aligned}&\left\| {1+B_{k} }\right\| \le \alpha ,\quad 0<\alpha <1,\quad k\in {\mathbb {N}} \end{aligned}$$
(11)
$$\begin{aligned}&\frac{ln\, \alpha }{\delta }+\kappa +\mathop \sum \limits _{l=1}^{m} \frac{\kappa _{l} }{\alpha }<0 \end{aligned}$$
(12)

Then, the origin of error system (10) is globally exponentially stable in the following sense

$$\begin{aligned} \left\| {e\left( t \right) }\right\| \le \alpha ^{-1}e^{\frac{-\lambda }{2}t}sup_{-\tau \le s\le 0} \left( {\left\| {\phi \left( s \right) }\right\| } \right) ,\,\,t\ge 0 \end{aligned}$$
(13)

in which \(\lambda >0\) is a unique solution of

$$\begin{aligned} \lambda -a-\mathop \sum \limits _{l=1}^{m} b_{l} e^{\lambda \tau _{l} }=0 \end{aligned}$$
(14)

where

$$\begin{aligned} \kappa= & {} \left\| \left( {A+\Delta A^{{\prime }}} \right) +\left( {A+\Delta A^{{\prime }}} \right) ^{T}\right. \\&\left. +\,2\left( {K+W_{j} +Q} \right) +2\chi d\xi \,^{-1}I+m\mho ^{-1}\right\| \\ \kappa _{l}= & {} \left\| \left( {K_{l} +W_{jl} +Q_{l} } \right) ^{T}\mho \left( {K_{l} +W_{jl} +Q_{l} } \right) \right\| \\ b_{l}= & {} \frac{\kappa _{l} }{\alpha ^{2}}\\ a= & {} \frac{-2\,ln\, \alpha }{\delta }-2\kappa ;\\ d= & {} \left( {\left\| Q^{'}+\sum _{l=1}^{m}Q_{l}^{'} \right\| }\right) Q_{l}^{\prime } +\left\| \Delta A^{{\prime }}-\Delta A\right\| \end{aligned}$$

Proof

Let \(V=e^{T}\left( t \right) e\left( t \right) \) be a candidate Lyapunov function. Its derivative along the solution of (10) yields

$$\begin{aligned} D^{+}V= & {} e^{T}\left( t \right) ((A+\Delta A^{'} )+(A+\Delta A^{'} )^{T} )e(t)\\&+\,2\sigma e^{T} (t)(\Delta A^{'}-\Delta A)x(t)\\&+\,2e^{T}\left( t \right) \left( E_{1} +E_{2} +E_{3} \right) +2e^{T}\left( t \right) E_{4} \\ \end{aligned}$$

In the case that \(\Vert e\Vert \ge \xi \,\), then \(\Vert e\Vert \le \xi \,^{-1}e^{T}e\). From (3)–(6) and Lemma 1, it yields

$$\begin{aligned} D^+ V\le & {} e^{T} (t)\left( \left( A+\Delta A^{'} \right) +\left( A+\Delta A^{'} \right) ^{T} \right) e(t)\\&+2e^{T} (t)\left[ (K+W_{j}+Q)e(t)\right. \\&\left. +\sum _{l=1}^{m}(K_{l}+W_{jl}+Q_{l} ) e_{l} (t-r_{l} (t) ) \right] \\&+2\left\| {e}\right\| \left( \chi |\sigma |\left( \left\| {Q^{'}+\sum _{l=1}^{m}}Q_{l}^{'}\right\| \right. \right. \\&\left. \left. +\left\| {\Delta A^{'}-\Delta A}\right\| \right) \right) \\\le & {} e^{T} (t)[(A+\Delta A^{'} )+(A+\Delta A^{'} )^{T}\\&+2(K+W_{j}+Q)\\&+2\chi d\xi ^{-1} I+m\mho ^{-1} ] e(t)\\&+\sum _{l=1}^{m} e_{l} (t-r_{l} (t))^{T} (K_{l}+W_{jl}+Q_{l} )^{T}\\&\mho (K_{l}+W_{jl} +Q_{l} ) e_{l} (t-r_{l} (t) )\\= & {} \kappa V(t,e(t) )+\sum _{l=1}^{m} \kappa _{l} V(t-r_{l} (t) ) \end{aligned}$$

where

$$\begin{aligned} K= & {} diag\left\{ k_{11} ,k_{12} ,\ldots ,k_{1n} ,k_{21} ,k_{22} ,\ldots ,k_{2n} ,\right. \\&\left. \ldots ,k_{N1} ,k_{N2} ,\ldots ,k_{Nn} \right\} \\ K_{l}= & {} diag\left\{ k_{11l} ,k_{12l} ,\ldots ,k_{1nl} ,k_{21l} ,k_{22l} ,\ldots ,k_{2nl} ,\right. \\&\left. \ldots ,k_{N1l} ,k_{N2l} ,\ldots ,k_{Nnl} \right\} \\ W_{j}= & {} diag\left\{ w_{1j1} ,w_{1j2} ,\ldots ,w_{1jn} ,w_{2j1} ,w_{2j2} ,\right. \\&\left. \ldots ,w_{2jn} ,\ldots ,w_{Nj1} ,w_{Nj2} ,\ldots ,w_{Njn} \right\} \\ W_{jl}= & {} diag\left\{ w_{1j1l} ,w_{1j2l} ,\ldots ,w_{1jnl} ,w_{2j1l} ,w_{2j2l} ,\right. \\&\left. \ldots ,w_{2jn} ,\ldots ,w_{Nj1} ,w_{Nj2} ,\ldots ,w_{Njn} \right\} \\ Q= & {} diag\left\{ q_{11} ,q_{12} ,\ldots ,q_{1n} ,q_{21} ,q_{22} ,\ldots ,\right. \\&\left. q_{2n} ,\ldots ,q_{N1} ,q_{N2} ,\ldots ,q_{Nn} \right\} \\ Q_{l}= & {} diag\left\{ q_{11l} ,q_{12l} ,\ldots ,q_{1nl} ,q_{21l} ,q_{22l} ,\ldots ,q_{2nl} ,\right. \\&\left. \ldots ,q_{N1l} ,q_{N2l} ,\ldots ,q_{Nnl} \right\} \\ Q^{'}= & {} diag \left\{ q_{11}^{'},q_{12}^{'},\ldots ,q_{1n}^{'},q_{21}^{'},q_{22}^{'},\ldots ,q_{2n}^{'},\right. \\&\left. \ldots ,q_{N1}^{'},q_{N2}^{'},\ldots ,q_{Nn}^{'} \right\} \\ Q_{l}^{\prime }= & {} diag\left\{ q_{11l}^{\prime } ,q_{12l}^{\prime } ,\ldots ,q_{1nl}^{\prime } ,\right. \\&q_{21l}^{\prime } ,q_{22l}^{\prime } ,\ldots ,q_{2nl}^{\prime } ,\ldots ,q_{N1l}^{\prime } ,\\&\left. q_{N2l}^{\prime } ,\ldots ,q_{Nnl}^{\prime } \right\} \end{aligned}$$

Also

$$\begin{aligned} V\left( {t_{k}^+ } \right)= & {} e^{T}\left( {t_{k}^- } \right) \left( {I+B_{k} } \right) ^{T}\left( {I+B_{k} } \right) e^{T}(t_{k}^- )\nonumber \\\le & {} \left\| \left( {I+B_{k} } \right) \right\| ^{2}e^{T}\left( {t_{k}^- } \right) e^{T}(t_{k}^- )\nonumber \\\le & {} \alpha ^{2}V\left( {t_{k}^- } \right) ,\quad t=t_{k} ,\quad k\in {\mathbb {N}} \end{aligned}$$
(15)

For any \(\varepsilon >0\), let \(v\left( t \right) \) be a unique solution of the following impulsive delayed system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{v}=\kappa v\left( {t,e\left( t \right) }\right) +\mathop \sum \nolimits _{l=1}^{m} \kappa _{l} v\left( {t-r_{l} \left( t \right) }\right) \\ \quad +\,\varepsilon ,\,\, t\ge 0,\,\, t\ne t_{k} \\ v(t_{k})=\alpha ^{2}v\left( {t_{k}^- }\right) ,t=t_{k}\\ v(t)=\left\| {\emptyset (t)}\right\| ^{2}, -\mathop {\max }\nolimits _{1<l<m}\tau _{l} \le t\le 0\\ \end{array}\right. \end{aligned}$$
(16)

Lemma 2 and the fact that \(V\left( t \right) =\left\| {\emptyset \left( t \right) }\right\| ^{2}\) for \(-\mathop {\max }\nolimits _{1<l<m} \tau _{l} \le t\le 0\) implies

$$\begin{aligned} V\left( t \right) \le v\left( t \right) ,\quad t\ge 0 \end{aligned}$$

Ref [38] solved (16) as follows

$$\begin{aligned} v\left( t \right)= & {} W\left( {t,0} \right) v\left( 0 \right) \nonumber \\&+\int _{0}^{t} W\left( {t,s} \right) \left( {\mathop \sum \limits _{l=1}^{m} \kappa _{l} v\left( {s-r_{l} \left( s \right) } \right) +\varepsilon } \right) ds\nonumber \\ \end{aligned}$$
(17)

where \(W\left( {t,s} \right) ,0\le s\le t\) is the Cauchy matrix of the following linear system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\vartheta }(t)=\kappa \vartheta ( t ),\quad t\ne t_{k} \\ \vartheta (t_{k}^+)=\alpha ^{2}\vartheta \left( {t_{k}^- }\right) ,\quad k\in {\mathbb {N}}\, \end{array}\right. \end{aligned}$$
(18)

Considering the corresponding Cauchy matrix, since \(0<\alpha <1\) and \(\delta \ge t_{k} -t_{k-1} \), thus

$$\begin{aligned} W\left( {t,s} \right)= & {} e^{\kappa \left( {t-s} \right) }\mathop \prod \limits _{s<t_{k} <t} \alpha ^{2}\le e^{\left( {-a-\frac{2\,ln \,\alpha }{\delta }} \right) \left( {t-s} \right) }\alpha ^{2\left( {\frac{t-s}{\delta }-1} \right) }\,\,\nonumber \\= & {} \alpha ^{-2}e^{-a\left( {t-s} \right) },\quad \mathrm{for}\; t\ge s\ge 0 \end{aligned}$$
(19)

Let \( \Omega =\alpha ^{-2}\hbox {sup}_{-\mathop {\max }\limits _{1<l<m} \tau _{l} \le s\le 0} \left\| \phi \left( t \right) \right\| ^{2}\). It obtains from (17) and (19),

$$\begin{aligned} v\left( t \right)\le & {} \alpha ^{-2}e^{-at}\left\| {\phi \left( 0 \right) }\right\| ^{2}\nonumber \\&+\int _{0}^{t} {\alpha ^{-2}e^{-a\left( {t-s} \right) }\left( {\mathop \sum \limits _{l=1}^{m} \kappa _{l} v\left( {s-r_{l} \left( s \right) } \right) +\varepsilon } \right) \mathrm{d}s} \nonumber \\\le & {} {\varOmega }e^{-at}+\int _{0}^{t} e^{-a\left( {t-s} \right) }\left( \mathop \sum \limits _{l=1}^{m} b_{l} v\left( {t-r_{l} \left( t \right) } \right) \right. \nonumber \\&\left. +\,\frac{\varepsilon }{\alpha ^{2}} \right) \mathrm{d}s ,\quad t>0 \end{aligned}$$
(20)

Since \(\varepsilon >0\), \(\lambda >0\), \(a-\mathop \sum \nolimits _{l=1}^{m} b_{l} >0\) [from (16)] and \(0<\alpha <1\), for \(-\mathop {\max }\nolimits _{1<l<m} \tau _{l} \le t\le 0\), we have

$$\begin{aligned}&v\left( {t} \right) <{\varOmega }{e}^{-\lambda t}\nonumber \\&\quad +\frac{{\varepsilon }}{\left( {{a}-\mathop \sum \nolimits _{{l}=1}^{m} {b}_{l} } \right) {\alpha }^{2}},\quad \hbox {for} \;0\ge {t}\ge -\mathop {\max }\limits _{{1<l<}m} {\tau }_{l}\nonumber \\ \end{aligned}$$
(21)

We need to prove that (21) holds for \(t>0\). If it is not true, then there is \(t^{'}>0\) that satisfying the following inequalities

$$\begin{aligned} v\left( {{t}'} \right)\ge & {} {\varOmega }e^{-\lambda {t}'}+\frac{\varepsilon }{\left( {a-\mathop \sum \nolimits _{l=1}^{m} b_{l} } \right) \alpha ^{2}} \end{aligned}$$
(22)
$$\begin{aligned} v\left( t \right)< & {} {\varOmega }e^{-\lambda t}+\frac{\varepsilon }{\left( {a-\mathop \sum \nolimits _{l=1}^{m} b_{l} } \right) \alpha ^{2}},\quad t<{t}' \end{aligned}$$
(23)
$$\begin{aligned} v(t)\le & {} {\varOmega }e^{-a{t^{'}}}\nonumber \\&+\,\int _{0}^{t} e^{-a({t^{'}}-s)} \left( \sum _{l=1}^{m} b_{l} v(s-r_{l} (s))+\frac{\varepsilon }{\alpha ^{2}} \right) \mathrm{d}s\nonumber \\< & {} e^{-a{{t^{'}}}} \left[ {\varOmega }+\frac{\varepsilon }{\left( a-\sum _{l=1}^{m} b_{l}\right) \alpha ^{2} }\right. \nonumber \\&+\,\int _{0}^{t^{'}} e^{as} \left( \sum _{l=1}^{m} b_{l} {\varOmega }e^{-\lambda (s-r_{l} (s))}\right. \nonumber \\&\left. \left. + \frac{\varepsilon \sum _{i=1}^{m} b_{i}}{\left( a-\sum _{l=1}^{m} b_{l} \right) \alpha ^{2}} +\frac{\varepsilon }{\alpha ^{2}} \right) \mathrm{d}s \right] \nonumber \\\le & {} e^{-a{t^{'}}}\left[ {\varOmega }+\frac{\varepsilon }{\left( a-\sum _{l=1}^{m} b_{l} \right) \alpha ^{2}}\right. \nonumber \\&+\,\left( \sum _{i=1}^{m} b_{l} {\varOmega }e^{\lambda {\tau _{i}}} \int _{0}^{t^{'}} e^{(a-\lambda ) s} \mathrm{d}s\right. \nonumber \\&\left. \left. +\frac{a\varepsilon }{\left( a-\sum _{l=1}^{m} b_{l} \right) \alpha ^{2} } \int _{0}^{t^{'}} e^{as} \mathrm{d}s\right) \right] \nonumber \\= & {} {\varOmega }e^{-\lambda {t^{'}} }+\frac{\varepsilon }{\left( a-\sum _{l=1}^{m} b_{l} \right) \alpha ^{2} } \end{aligned}$$
(24)

By (14), (20) and (23), we have

Obviously, (28) is in conflict with (26), so that (25) holds for \(t>0\). Letting \(\varepsilon \rightarrow 0,\) then we have

$$\begin{aligned} V\left( t \right) \le v\left( t \right) \le {\varOmega }e^{-\lambda t},\,t\ge 0. \end{aligned}$$

3.2 Exponentially impulsive lag synchronization between uncertain complex networks

Definition 3

In lag synchronization, the error of each node is defined as follows

$$\begin{aligned} {e}_{i} \left( {t} \right) ={\tilde{{x}}} _{i} \left( {t} \right) -{x}_{i} \left( {{t}-\mathcal{L}} \right) \end{aligned}$$

in which \(\mathcal{L}\ge 0\) is a time delay. If \( \mathop {\lim }\nolimits _{t\rightarrow \infty } e_{i} \left( t \right) =0\), then lag synchronization is achieved.

Assumption 2

We assume that for each \(\sigma \) the following terms are being satisfied

$$\begin{aligned}&\left\| {f_{iz} \left( t,{\tilde{x}}_{i} (t),{\tilde{x}}_{i} (t-r_{1} (t) ),\ldots ,{\tilde{x}}_{i} (t-r_{m} (t) ) \right) }\right. \nonumber \\&\qquad -f_{iz} \left( t-{\mathcal {L}},x_{i} (t-{\mathcal {L}}),x_{i} (t-{\mathcal {L}}-r_{1} (t-{\mathcal {L}}) ),\right. \nonumber \\&\qquad \left. \left. \ldots ,x_{i}(t-{\mathcal {L}}-r_{m} (t-{\mathcal {L}}) ) \right) \right\| \nonumber \\&\quad \le k_{iz}^* \left\| {e_{i} (t) }\right\| +\sum _{l=1}^{m} k_{izl}^* \left\| {e_{il} (t-r_{l} (t)) }\right\| \end{aligned}$$
(25)
$$\begin{aligned}&\left\| g_{ijz} (t,{\tilde{x}}_{i} (t),{\tilde{x}}_{i} (t-r_{1} (t) ),\ldots ,{\tilde{x}}_{i} (t-r_{m} (t) ) )\right. \nonumber \\&\qquad \left. -g_{ijz} (t-{\mathcal {L}},x_{i} (t-{\mathcal {L}}),x_{i} (t-r_{1} (t-{\mathcal {L}}) ),\right. \nonumber \\&\qquad \left. \ldots ,x_{i} (t-{\mathcal {L}}-r_{m} (t-{\mathcal {L}}) ) )\right\| \nonumber \\&\quad \le w_{ijz}^* \left\| {e_{i} (t) }\right\| \nonumber \\&\qquad +\sum _{l=1}^{m} w_{ijzl}^* \left\| {e_{il} (t-r_{l} (t) ) }\right\| \end{aligned}$$
(26)

and

$$\begin{aligned}&\left\| {\Delta f_{iz}^{'} (t,{\tilde{x}}_{i} (t),{\tilde{x}}_{i} (t-r_{1} (t)),\ldots ,{\tilde{x}}_{i} (t-r_{m} (t) ) )}\right. \nonumber \\&\qquad \left. -\Delta f_{iz}^{'} (t-{\mathcal {L}},x_{i} (t-{\mathcal {L}}),x_{i} (t-{\mathcal {L}}-r_{1} (t-{\mathcal {L}}) ),\right. \nonumber \\&\qquad \left. \ldots ,x_{i} (t-{\mathcal {L}}-r_{m} (t-{\mathcal {L}}) ) )\right\| \nonumber \\&\quad \le p_{iz} \left\| {e_{i} (t)}\right\| +\sum _{l=1}^{m} p_{izl} \left\| {e_{il} (t-r_{l} (t) )}\right\| \end{aligned}$$
(27)

also the following term is considered

$$\begin{aligned}&\left\| \Delta f_{iz}^{'} \left( t-{{{\mathcal {L}}}},x_{i} (t-{{{\mathcal {L}}}}),x_{i} (t-{\mathcal {L}}-r_{1} (t-{\mathcal {L}}) ),\right. \right. \nonumber \\&\qquad \left. \ldots ,x_{i} \left( t-{{{\mathcal {L}}}}-r_{m} (t-{{{\mathcal {L}}}}) \right) \right) -\Delta f_{iz} \left( t\right. \nonumber \\&\qquad -{{{\mathcal {L}}}},x_{i} (t-{{{\mathcal {L}}}}),x_{i} \left( t-r_{1} (t-{{{\mathcal {L}}}}) \right) ,\nonumber \\&\qquad \left. \left. \ldots ,x_{i} (t-{{{\mathcal {L}}}}-r_{m} (t-{{{\mathcal {L}}}}) ) \right) \right\| \nonumber \\&\quad \le p_{iz}^{'} \left\| {x_{i} (t-{{{\mathcal {L}}}}) }\right\| +\sum _{l=1}^{m} p_{izl}^{'} \left\| x_{il} (t\right. \nonumber \\&\qquad \left. -{\mathcal {L}}-r_{l} (t-{\mathcal {L}}) ) \right\| \end{aligned}$$
(28)

where \(k_{iz}^*,k_{izl}^*,\,w_{ijz}^*,w_{ijzl}^*,p_{iz} ,p_{izl} ,p_{iz}^{\prime } ,p_{izl}^{\prime } >0\) for any \(x\left( t \right) ,\,\,x\left( {t-r_{i} \left( t \right) } \right) ,\,\,e\left( t\right) ,{\,}e\left( {t-r_{i} \left( t \right) } \right) \in R^{n}\) and \(,1\le z\le n\,,1\le l\le m\).

By considering Eqs. (8) and (9), error network can be obtained as follows

$$\begin{aligned} \left\{ \begin{array}{l} \dot{e}(t)=(A+\Delta A^{'})e(t)\\ \quad \qquad +\,(\Delta A^{'}-\Delta A)x(t-\!{{{\mathcal {L}}}})\nonumber \\ \quad \qquad +\,E_{1}^*+E_{2}^*+E_{3}^* +E_{4}^* ,\quad t\ne t_{k}\\ \Delta e=B_{k} e(t_{k}^- )=(I_{N}\otimes B_{ki} )e(t_{k}^- ), \quad t=t_{k}\\ e(t)=\emptyset (t) \quad -\underset{1<l<m}{\max } \tau _{l} \le t\le 0\\ \end{array}\right. \nonumber \\ \end{aligned}$$
(29)

where

$$\begin{aligned}&e\left( t \right) =\left[ {e_{1}^{T} \left( t \right) ,e_{2}^{T} \left( t \right) ,\ldots ,e_{N}^{T} \left( t \right) } \right] ^{T}\\&E_{1}^*=\left[ F\left( {t,{\tilde{x}} \left( t \right) ,{\tilde{x}} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,{\tilde{x}} \left( {t-r_{m} \left( t \right) } \right) } \right) \right. \nonumber \\&\qquad \qquad -\,F\left( t-{{\mathcal {L}}},x\left( {t-{{\mathcal {L}}}} \right) ,x\left( {t-{{\mathcal {L}}}-r_{1} \left( {t-{{\mathcal {L}}}} \right) } \right) ,\right. \nonumber \\&\qquad \qquad \left. \left. \ldots ,x\left( {t-{{\mathcal {L}}}-r_{m} \left( {t-{{\mathcal {L}}}} \right) } \right) \right) \right] \\&E_{2}^*=\left[ \Delta F^{'} (t,{\tilde{x}}(t),{\tilde{x}}(t-r_{1} (t) ),\right. \nonumber \\&\qquad \qquad \ldots ,{\tilde{x}}(t-r_{m} (t) ),\ldots )-\Delta F^{'} (t-{{\mathcal {L}}},\nonumber \\&\qquad \qquad x(t-{\mathcal {L}}),x(t-{\mathcal {L}}-r_{1} (t-{\mathcal {L}}) ),\nonumber \\&\qquad \qquad \left. \ldots ,x(t-{\mathcal {L}}-r_{m} (t-{\mathcal {L}}) ) ) \right] \\&E_{3}^*=\left[ G\left( t,{\tilde{x}} \left( t \right) ,\right. \right. \nonumber \\&\qquad \quad \left. \quad {\tilde{x}} \left( {t-r_{1} \left( t \right) } \right) ,\ldots ,{\tilde{x}} \left( {t-r_{m} \left( t \right) } \right) \right) \nonumber \\&\qquad \qquad -\,G\left( t-{{\mathcal {L}}},x\left( {t-{{\mathcal {L}}}} \right) ,x\left( {t-r_{1} \left( {t-{{\mathcal {L}}}} \right) } \right) ,\right. \nonumber \\&\qquad \qquad \left. \left. \ldots ,x\left( {t-{{\mathcal {L}}}-r_{m} \left( {t-{{\mathcal {L}}}} \right) } \right) \right) \, \right] \\&E_{4}^*=\left[ \Delta F^{{\prime }}\left( t-{{\mathcal {L}}},x\left( {t-{{\mathcal {L}}}} \right) ,x\left( {t-{{\mathcal {L}}}-r_{1} \left( {t-{{\mathcal {L}}}} \right) } \right) ,\right. \right. \nonumber \\&\qquad \qquad \left. \ldots ,x\left( {t-{{\mathcal {L}}}-r_{m} \left( {t-{{\mathcal {L}}}} \right) } \right) \right) -\Delta F\left( t\right. \nonumber \\&\qquad \qquad -\,{{\mathcal {L}}},x\left( {t-{{\mathcal {L}}}} \right) ,x\left( {t-{{\mathcal {L}}}-r_{1} \left( {t-{{\mathcal {L}}}} \right) } \right) ,\nonumber \\&\qquad \qquad \left. \left. \ldots ,x\left( {t-{{\mathcal {L}}}-r_{m} \left( {t-{{\mathcal {L}}}} \right) } \right) \right) \right] . \end{aligned}$$
Fig. 1
figure 1

Phase portrait of Lur’e system \(x(0)=-0.2,\,y(0)=-0.3,\,\,z\left( 0\right) =0.2\)

Full size image

Theorem 2

The impulsive distance and control gain are defined as (7). Positive symmetric matrix \(\mho ^{*}\) is considered such that the following conditions hold:

$$\begin{aligned} \left\| {1+B_{k} }\right\| \le \alpha , \quad 0<\alpha <1,\quad k \in {\mathbb {N}} \end{aligned}$$
(30)
$$\begin{aligned} \frac{ln\,\alpha }{\delta }+\kappa ^*+\sum _{l=1}^{m} \frac{\kappa _{{L}}^*}{\alpha }<0 \end{aligned}$$
(31)

Then, the origin of error system (29) is globally exponentially stable in the following sense

$$\begin{aligned} \left\| {e(t)}\right\| \le \alpha ^{-1} e^{\frac{-\lambda }{2} t} sup_{-\tau \le s\le 0} (\left\| {\phi (s)}\right\| ),\quad t\ge 0 \end{aligned}$$
(32)

in which \(\lambda >0\) is a unique solution of

$$\begin{aligned} \lambda -a-\sum \limits _{l=1}^{m} b_{l} e^{\lambda \tau _{l}}=0 \end{aligned}$$
(33)

where

$$\begin{aligned} \kappa ^{*}= & {} \left\| {\left( {{A}+\Delta {A}^{{\prime }}} \right) +\left( {{A}+\Delta {A}^{{\prime }}} \right) ^{{T}}}\right. \nonumber \\&\left. +\,{2\left( {{K}^{{*}}+{W}_{j}^{*} +{P}} \right) +2{\chi {d}\xi \,}^{-1}{I}+{m}\mho ^{{*-1}}} \right\| \\ \kappa _{l}^{*}= & {} \left\| { {\left( {{K}_\mathrm{l}^{*} +{W}_{{jl}}^{*} +{P}_{l} } \right) ^{{T}}\mho ^{*}\left( {{K}_{l}^{*} +{W}_{{jl}}^{*} +{P}_{l} } \right) } }\right\| \\ {b}_{l}^{*}= & {} \frac{{\kappa }_{l}^{*} }{{\alpha }^{2}}\\ {a}= & {} \frac{-2\,ln\, \alpha }{{\delta }}-2{\kappa }^{{*}};\\ {d}= & {} \left( {\left\| P'+\sum _{l=1}^{m}P_{l}^{'} \right\| {P}_{l}^{\prime }} +\left\| \Delta {A}^{{\prime }}-\Delta {A}\right\| \right) \end{aligned}$$

Proof

Let \(V=e^{T}\left( t \right) e\left( t \right) \) be a candidate Lyapunov function. Its derivative along the solution of (29) yields

$$\begin{aligned} D^+ V= & {} e^T (t)((A+\Delta A^{'} )+(A+\Delta A^{'} )^T )e(t)\\&+\,2\sigma e^T (t)(\Delta A^{'}-\Delta A)x(t-{\mathcal {L}})\\&+\,2e^T (t)(E_1^*+E_2^*+E_3^* )+2e^T (t) E_4^* \end{aligned}$$

In the case that \(\Vert e\Vert \ge \xi \,\), considering (25)–(28) and Lemma 1 it yields

$$\begin{aligned} D^+ V\le & {} e^{T} (t)((A+\Delta A^{'} )+(A+\Delta A^{'} )^{T} )e(t)\\&+\,2e^{T} (t)\left[ (K^*+W_{j}^*+P)e(t)\right. \\&\left. +\sum _{l=1}^{m} (K_{l}^*+W_{jl}^*+P_{l} ) e_{l} (t-r_{l} (t) ) \right] \\&+\,2\left\| {e(t)}\right\| \left( \chi \left( \left\| {P^{'}+\sum _{l=1}^{m} P_{l}^{'}}\right\| +\left\| {\Delta A^{'}-\Delta A}\right\| \right) \right) \\\le & {} e^{T} (t)\left[ (A+\Delta A^{'} )+(A+\Delta A^{'} )^{T}\right. \\&\left. +\,2(K^*+W_{j}^*+P)+2\chi d \xi ^{-1} I+m\mho ^{*-1} \right] e(t)\\&+\,\sum _{l=1}^{m} e_{l} (t-r_{l} (t))^{T} (K_{l}^*+W_{jl}^*+P_{l} )^{T}\mho (K_{l}^*\\&+\,W_{jl}^*+P_{l} ) e_{l} (t-r_{l} (t) )\\= & {} \kappa ^* V(t,e(t) )+\sum _{l=1}^{m}\kappa _{l}^* V(t-r_{l} (t) ) \end{aligned}$$

where

$$\begin{aligned}&K^{*}=diag\left\{ k_{11}^*,k_{12}^*,\ldots ,k_{1n}^*,k_{21}^*,k_{22}^*,\right. \\&\qquad \quad \left. \ldots ,k_{2n}^*,\ldots ,k_{N1}^*,k_{N2}^*,\ldots ,k_{Nn}^*\right\} \\&K_{l}^*=diag\left\{ k_{11l}^*,k_{12l}^*,\ldots ,k_{1nl}^*,k_{21l}^*,k_{22l}^*,\right. \\&\qquad \quad \left. \ldots ,k_{2nl}^*,\ldots ,k_{N1l}^*,k_{N2l}^*,\ldots ,k_{Nnl}^*\right\} \\&W_{j}^*=diag\left\{ w_{1j1}^*,w_{1j2}^*,\ldots ,w_{1jn}^*,w_{2j1}^*,w_{2j2}^*,\right. \\&\qquad \quad \left. \ldots ,w_{2jn}^*,\ldots ,w_{Nj1}^*,w_{Nj2}^*,\ldots ,w_{Njn}^*\right\} \\&W_{jl}^*=diag\left\{ w_{1j1l}^*,w_{1j2l}^*,\ldots ,w_{1jnl}^*,w_{2j1l}^*,w_{2j2l}^*,\right. \\&\qquad \quad \left. \ldots ,w_{2jnl}^*,\ldots ,w_{Nj1l}^*,w_{Nj2l}^*,\ldots ,w_{Njnl}^*\right\} \\&P = diag\left\{ p_{11} ,p_{12} ,\ldots ,p_{1n} ,p_{21} ,p_{22} ,\ldots ,p_{2n} ,\ldots , \right. \nonumber \\&\qquad \quad \left. p_{N1} ,p_{N2} ,\ldots ,p_{Nn} \right\} \\&P_{l} =diag\left\{ p_{11l} ,p_{12l} ,\ldots ,p_{1nl} ,p_{21l} ,p_{22l} ,\right. \\&\qquad \quad \left. \ldots ,p_{2nl} ,\ldots ,p_{N1l} ,p_{N2l} ,\ldots ,p_{Nnl} \right\} \\&P^{'}=diag \left\{ p_{11}^{'},p_{12}^{'},\ldots ,p_{1n}^{'},p_{21}^{'},p_{22}^{'},\ldots ,p_{2n}^{'},\right. \\&\qquad \quad \left. \ldots ,p_{N1}^{'},p_{N2}^{'},\ldots ,p_{Nn}^{'} \right\} \\&P_{l}^{\prime } =diag\left\{ p_{11l}^{\prime } ,p_{12l}^{\prime } ,\ldots ,p_{1nl}^{\prime } ,p_{21l}^{\prime } ,p_{22l}^{\prime } ,\right. \\&\qquad \quad \ldots \left. p_{2nl}^{\prime } ,\ldots ,p_{N1l}^{\prime } ,p_{N2l}^{\prime } ,\ldots ,p_{Nnl}^{\prime } \right\} \end{aligned}$$

Similar to proof Theorem 1, we can obtain Theorem 2. In order to avoid the repetition, here we omit its complete proof.

Fig. 2
figure 2

Phase portrait of Chua’s system with time-varying time delays \(x\left( 0 \right) =-0.2,y\left( 0 \right) =-0.3,\,z\left( 0 \right) =0.2\)

Full size image

4 Numerical simulation

In this section, in order to demonstrate the effectiveness of obtained conditions, numerical simulation for synchronizing complex networks is presented.

Example 1

Two 100-node complex networks, composed of Lur’e [6] and Chua’s [39, 40] systems, are considered in which coupled terms have nonlinear dynamics. Moreover, there are time-varying delays in both coupled and uncoupled terms as well as different uncertainties.

Dynamics of Lur’e system is given by (Fig. 1)

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t)=a(y(t)-h(x(t)))\\ \dot{y}(t)=x(t)-y(t)+z(t)\\ \dot{z}(t)=-by(t)\\ \end{array} \right. \end{aligned}$$
(34)

and dynamics of Chua’s system with time-varying delays is represented by (Fig. 2)

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t)=a(y(t)-h(x(t)))-cx(t-\tau _{1})\\ \dot{y}(t)=x(t)-y(t)+z(t)-cx(t-\tau _{2})\\ \dot{z}(t)=-by(t)+c\left( 2x(t-\tau _{3}))-y(t-\tau _{3})\right) \\ \end{array} \right. \end{aligned}$$
(35)

with nonlinear characteristics:

$$\begin{aligned} h\left( {x\left( t \right) } \right)= & {} m_{1} x\left( t \right) +1/2\left( {m_{0} -m_{1} } \right) \\&\quad \left( {\left| {x\left( t \right) +1} \right| -\left| {x\left( t \right) -1} \right| } \right) \end{aligned}$$

numerical parameters are considered as \(m_{0} =-\frac{1}{7},m_{1} =\frac{2}{7},a=9,b=14.28,c=.1\) and \(\tau _{1} =.25\left( {\sin t+1} \right) ,\tau _{2} =.2\left( {\sin t+1} \right) ,\tau _{3} =.4\left( {\sin t+1} \right) .\)

Consider complex networks containing 40 Lur’e dynamic nodes \(\left( {f_{1} \left( \ldots \right) ,f_{2} \left( \ldots \right) ,\ldots ,f_{40} \left( \ldots \right) } \right) \) and 60 Chua’s dynamic nodes \(\left( f_{60} \left( \ldots \right) ,f_{61} \left( \ldots \right) ,,\ldots \right. \left. ,\,f_{100} \left( \ldots \right) \right) \) . We assumed coupling dynamics and uncertainties as follows

$$\begin{aligned}&\sum \limits _{{j}=1}^{{N}} {g}_{{ij}}\\&\quad =\left[ {{\begin{array}{l} {.01{x}_{\left( {{i}+20} \right) 2} \left( {t} \right) {x}_{\left( {{i}+20} \right) 2} \left( {t} \right) } \\ 0\\ {.1{x}_{\left( {{i}+20} \right) 4} \left( {{t}-{r}_{3} } \right) } \\ \end{array} }} \right] \,\quad \mathrm{for}\;1\le {i}<20,\\&\sum \limits _{{j}=1}^{{N}} {g}_{{ij}}\\&\quad =\left[ {{\begin{array}{l} {.01{x}_{\left( {{i}+20} \right) 1} \left( {t} \right) {x}_{\left( {{i}+20} \right) 1} \left( {t} \right) } \\ {.1sin\left( {{x}_{\left( {{i}+20} \right) 1} \left( {t} \right) } \right) } \\ 0 \\ \end{array} }} \right] \,\quad \mathrm{for}\; 20\le {i}<40,\\ \end{aligned}$$
$$\begin{aligned}&\sum \limits _{{j}=1}^{{N}} {g}_{{ij}}=\left[ {{\begin{array}{l} {.1\left( {{x}_{\left( {{i}+20} \right) 2} \left( {t} \right) {x}_{{i}2} \left( {t} \right) +{sin}\left( {{x}_{\left( {{i}+20} \right) 4} \left( {{t}-{r}_{1} } \right) } \right) } \right) } \\ 0 \\ 0 \\ \end{array} }} \right] \,\quad \mathrm{for}\; 40\le {i}<60, \end{aligned}$$
$$\begin{aligned}&\sum \limits _{{j}=1}^{{N}} {g}_{{ij}}\\&\quad =\left[ {{\begin{array}{l} {.01{x}_{\left( {{i}+20} \right) 2} \left( {t} \right) {x}_{{i}2} \left( {t} \right) } \\ 0 \\ {.1{x}_{\left( {{i}+20} \right) 4} \left( {{t}-{r}_{2} } \right) } \\ \end{array} }} \right] \,\quad \mathrm{for}\; 60\le {i}<80,\\&\sum \limits _{{j}=1}^{{N}} {g}_{{ij}}\\&\quad =\left[ {{\begin{array}{l} {-.1sin\left( {{x}_{\left( {{i}-20} \right) 2} \left( {t} \right) } \right) } \\ 0 \\ {.1{x}_{\left( {{i}-20} \right) 2} \left( {t} \right) sin\left( {{x}_{{i}2} \left( {t} \right) } \right) } \\ \end{array} }} \right] \quad \mathrm{for}\;80\le {i}\le 100 \end{aligned}$$
$$\begin{aligned} \Delta {f}_{i}= & {} \left[ {{\begin{array}{l} {.9m{x}_{{i}1} \left( {t} \right) } \\ {.1m\left( {{x}_{{i}1} \left( {t} \right) -{x}_{{i}1} \left( {t} \right) +{x}_{{i}1} \left( {t} \right) } \right) } \\ 0 \\ \end{array} }} \right] \quad \mathrm{for}\; 1\le {i}<20,\\ \Delta {f}_{i}= & {} \left[ {{\begin{array}{l} {.9m{x}_{{i}1} \left( {t} \right) +.1mh\left( {{x}_{{i}1} \left( {t} \right) } \right) } \\ 0 \\ {1.428m{x}_{{i}2} \left( {t} \right) } \\ \end{array} }} \right] \,\quad \mathrm{for}\; 20\le {i}<40,\\ \Delta {f}_{i}= & {} \left[ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ \end{array} }} \right] \,\quad \mathrm{for}\; 40\le {i}<60,\\ \Delta {f}_{i}= & {} \left[ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ \end{array} }} \right] \,\quad \mathrm{for}\; 60\le {i}<80,\\[5pc] \Delta {f}_{i}= & {} \left[ {{\begin{array}{l} 0 \\ {.01m{x}_{{i}3} \left( {{t}-{r}_{4} } \right) } \\ 0 \\ \end{array} }} \right] \,\quad \mathrm{for}\; 80\le {i}\le 100 \end{aligned}$$
Fig. 3
figure 3

Error evolution between drive and response networks, \(\sigma =1\)

Full size image
Fig. 4
figure 4

Lag synchronization errors \((\mathcal{L}=0.004)\)

Full size image

where \(,r_{1} ,\,r_{2} ,\,r_{3} ,\,r_{4} =1/2(\sin t+1)\). Considering \(\delta =0.01,\,\,B_{k} =-0.9I\,\), by simple computation clearly conditions (11) and (12) are satisfied. Response network’s uncertainties are similar to uncertainties in derive network, except in \(r_{1} ,\,r_{2} ,\,r_{3} ,\,r_{4} =.3(\sin t+1).\)

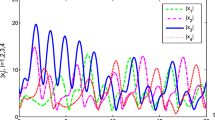
Figure 3 shows the error evolution between drive and corresponding response networks. The initial conditions are chosen randomly between \(-\)1 and 1. It is demonstrated that states of drive network are similar to states of response network. We observe that synchronization error converges to a neighborhood of zero and their magnitude is smaller than \(\xi =0.1\), and it is impossible to achieve complete synchronization due to differences of networks structure. Because of time delays, synchronization error starts to converge to zero after 1 s.

Fig. 5
figure 5

Hidden chaotic attractor

Full size image
Fig. 6
figure 6

Error evolution between drive and response networks

Full size image

Similarly, the error evolution between drive and corresponding response networks when \({{\mathcal {L}}}=0.004\) is shown in Fig. 4; synchronization errors converge to smaller than \(\xi =0.1\). It is seen that lag synchronization is realized.

Example 2

In this Example 2, two 100-node complex networks, composed of Chua’s systems (36) and Chua’s systems with time-varying delay, are considered in which coupled terms have nonlinear dynamics as Example 1. Moreover, in this example we have considered Chua’s systems parameters in a way that hidden attractor appears (Fig. 5).

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{x}(t)=a(y(t)-{x}(t)-h(x(t)))\\ \dot{y}(t)=x(t)-y(t)+z(t)\\ \dot{z}(t)=-by(t)-\gamma z(t)\\ \end{array}\right. \nonumber \\&h\left( {x\left( t \right) } \right) =m_{1} x\left( t \right) +1/2\left( {m_{0} -m_{1} } \right) \left( \left| x\left( t \right) \right. \right. \nonumber \\&\qquad \qquad \qquad \left. \left. +\,1 \right| -\left| {x\left( t \right) -1} \right| \right) \end{aligned}$$
(36)

Numerical parameters for Chua’s systems are considered as the same as the parameters considered in [33]. \(m_{0} =-0.1768,m_{1} =-1.1468,a=8.4562,b=12.0732,\,\gamma =0.0052\) and \(\sum \nolimits _{j=1}^{N} g_{ij} =\Delta f_{i} =0\) for \(for\,1\le i<40.\)

Figure 6 shows the error evolution between drive and corresponding response networks for Example 2. The initial conditions are chosen like Example 1. It is demonstrated that states of drive network are similar to states of response network; it shows the effectiveness of this approach for synchronization of systems with hidden attractor. We observe that synchronization error converges to a neighborhood of zero and their magnitude is smaller than \(\xi =0.1\).

5 Conclusion and outlook

This correspondence has investigated the issue of impulsive projective and lag synchronization of uncertain complex networks with time-varying delays in both coupled and uncoupled terms. Due to differences in structures of drive and response networks and other mismatches, considered uncertainties in model definition for drive network are different from response network uncertainties. However, both coupled and uncoupled terms are taken under the circumstance of multiple time-varying delays. In contrast to conventional models, nodes vary in terms of dynamical behavior. Based on impulsive differential equation, some new sufficient conditions are derived in order to globally exponentially synchronization of drive and response complex networks. Less conservative conditions need to be developed in future researches. Furthermore, “factor of synchronization” can be calculated by selecting the statistical function to detect the synchronization [41, 42] in future researches. At the end, two examples are given to verify the effectiveness of this approach for systems with hidden attractor or self-excited one.