1 Introduction

In recent years, much active research effort has been focused on nonlinear Rossby waves that have emerged in the atmospheric and oceanic circulation dynamics [1–8]. It has been shown that Rossby waves represent a fundamental component of planetary scale oceanic and atmospheric motion. Forcing factors such as topography play very important roles in fluid motion. There has been a lot of research on the effect of topographic forcing on Rossby waves, in most of which is involved the stable topography, such as concave, convex or Gaussian topography and so on [9–15]. It seems that very few on unstable topography are available up to now. On the other hand, as everyone knows that the real oceanic and atmospheric motion is dissipative, otherwise the motion would grow explosively because of the constant injecting of the external forcing energy. But in many researches dissipation effect is ignored.

In the paper, we will first derive a forced dissipative Boussinesq equation by using a perturbation method from the geostrophic potential vorticity equation with dissipation and topography effect. Especially, here we restrict ourselves to consider the effect of unstable topography and dissipation on Rossby waves. It is great different from the previous papers. In fact, people had noticed the instability of submarine topography in the late 19th century and made a lot of research. People found that sediment transport, the shaking of the platform in ocean engineering and the strong earthquake and so on can cause the seabed instability [16–18]. Furthermore, waves are also regarded as the main outer factor to induce the topography to change [19]. So it has important theoretical and practical meaning to study the effect of unstable topography on Rossby waves. Then, we will discuss conservation laws and give an approximate analytic solution of the dissipative Boussinesq equation by using modified Jacobi elliptic function expansion method [20]. Finally, numerical simulation of the forced dissipative Boussinesq equation is presented by using the pseudo-spectral method [21]. By comparing the waterfall plots, we discuss the differences of the solitary Rossby waves under the influence of stable topography and unstable topography.

2 Model and forced dissipative Boussinesq equation

The theoretical basis is found in the paper of Pedlosky [1] treating shallow fluid model on a beta plane. In this model, the vorticity equation governing the inviscid, quasi-geostrophic fluid motion is, in non-dimensional form, given by

(1)

where the topography effect and dissipation is considered, β effect is a nonlinear function of latitudinal variable y, φ represents the geostrophic stream function, ∇2 φ expresses the vorticity dissipation which is caused by the Ekman boundary layer, μ 0 is a dissipation coefficient and 0≤μ 0≪1. Especially, the distribution function of topography is taken as h(x,t), i.e. the topography is unstable. We specify the non-dimensional rigid-wall boundary conditions:

(2)

In order to consider weakly nonlinear perturbations on a zonal flow, we assume that the solution of Eq. (1) has an asymptotic expression of the form

(3)

where ε≪1 is a small parameter characterizing the smallness of terms which measures the weakness of the nonlinearity and O(α)=1, which is a measure of the proximity of the system to a resonate state, and may be referred to as a detuning parameter. c 0 is a constant, which is regarded as a Rossby wave phase speed. In order to achieve a balance between nonlinearity and dispersion, we introduce the following slow scales:

(4)

and in order to balance topography, turbulent dissipation and nonlinearity, we assume

(5)

Substituting Eq. (3), Eq. (4), and Eq. (5) into Eq. (1) and Eq. (2) yields

(6)

with the boundary conditions \(\frac{\partial\varphi_{i}}{\partial X}=0\) y=0, 1 i=0,1,2, where \(J[a,b]=\frac{\partial a}{\partial x}\frac{\partial b}{\partial y}-\frac{\partial a}{\partial y}\frac{\partial b}{\partial x}\) is a Jacobi operator.

For ε 0, assuming φ 0=A(X,T)ϕ 0(y), then we have

(7)

Equation (7) is a variable coefficient eigenvalue problem and describes the space structure of the wave along direction. A(X,T) is the unknown amplitude in the order O(ε 0), which needs higher order equations to determine. For \(\varepsilon^{\frac{1}{2}}\), by analysis, we deduce that \(\frac{\partial \varphi_{1}}{\partial X}=\frac{\partial A}{\partial T}\phi_{1}(y)\), where ϕ 1(y) satisfies the following equation:

(8)

To get the mathematical model of the Rossby waves’ amplitude, we need to solve higher order equations. Based on φ 0=A(X,T)ϕ 0(y), \(\frac{\partial \varphi_{1}}{\partial X}=\frac{\partial A}{\partial T}\phi_{1}(y)\) and Eq. (6), we get

(9)

Finally, utilizing the solvability condition of Eq. (9), we obtain an equation which governs the evolution of the amplitude A:

(10)

where

(11)

In Eq. (10), the term \(\frac{\partial A}{\partial X}\) expresses the dissipation effect. In the absence of dissipation and topographic forcing, Eq. (10) degenerates to the standard Boussinesq equation, so we call Eq. (10) forced dissipative Boussinesq equation.

3 Solitary-wave-like solution of dissipative Boussinesq equation

In this section, we will take into account the evolutional characters of Rossby waves under the influence of dissipation. Mathematically, we should note that the standard Boussinesq equation is completely integrable [22] and this kind of equation can be solved by many methods, such as the Wronskian technique [23], Bäcklund transformation [24], the inverse scattering method and so on. Especially very recently, the linear superposition principle was also presented to generate exact soliton solutions to bilinear differential equations [25]. In additional to the exact solution, some remarkable properties such as Painlevé property, Lax representation, approximate Group Analysis, an infinite number of conservation laws were studied in [26–31]. Based on the above research, it is easy to obtain the clock shape solitary-wave solution of standard Boussinesq equation:

(12)

where N 0 expresses the maximum amplitude at initial moment, \(\nu=\sqrt{-(a_{2}+\frac{2a_{3}N_{0}}{3})}\) expresses the moving speed of the solitary waves, \(\sqrt{6a_{1}/a_{3}N_{0}}\) expresses the width of the solitary waves. It is obvious that the amplitude and speed of the solitary waves remain constant during propagation without dissipation and topographic forcing.

In the presence of dissipation, the standard Boussinesq model becomes the so-called dissipative Boussinesq equation:

(13)

which is not known to be integrable and cannot be solved by the inverse scattering. Here we will derive the analytic solutions to Eq. (13) by the modified Jacobi elliptic function expansion method. The Jacobi elliptic function expansion method is a powerful method and has been applied to atmospheric and oceanic dynamics and many classical PDEs [20, 32–35].

In order to illustrate the basic idea of the modified Jacobi elliptic function expansion method, we consider first the nonlinear equation of the following form:

(14)

introducing a complex variation ξ defined as ξ=f(T)X+b(T). The modified Jacobi elliptic function expansion method is very simple and straightforward, it is based on the assumption that traveling wave solutions can be expressed in the following form:

(15)

By choosing suitable n, we balance the derivative term of highest order in Eq. (14) with the highest order nonlinear term. By simple calculation, the coefficients g j (T) are determined and then the solutions to Eq. (14) are obtained. Furthermore, sn 2 ξ+cn 2 ξ=1, when m→1, \(cn\xi\rightarrow \mathop{\mathrm{sech}}\nolimits \xi\), Eq. (15) degenerates to

(16)

then we get the solitary-wave-like solutions.

Next, we apply the above method to solve Eq. (13). Assuming the solution can be expressed in the form of Eq. (15), balancing the derivative term of highest order in Eq. (13) with the highest order nonlinear term, we obtain the solution in the following form:

(17)

Substituting Eq. (17) into Eq. (13), assuming μa 4≪a 3, vanishing the coefficients of the various powers of elliptic functions, by direct computations, we easily get

So the solution of Eq. (13) reads

(18)

When m→1, we obtain a solitary-wave-like solution:

(19)

In order to simplify the calculation and to focus on the variation of amplitude A(X,T) with time T and dissipation coefficient μ, let the former term of A(X,T) equal zero, then Eq. (18) becomes

(20)

From Fig. 1, we find that when the dissipative coefficient μ=0, the amplitude of solitary waves is the largest, while the width of the solitary waves is the smallest. The amplitude decreases and the width increases with the increasing of the dissipative coefficient μ. Figure 2 shows that the amplitude of the solitary waves becomes smaller and smaller with time T, while the width of the solitary waves becomes larger and larger with time T. It is obvious that the dissipation effect causes the amplitude of the solitary waves to decrease and the width of the solitary waves to increase.

Fig. 1
figure 1

Variation of amplitude and width according to the dissipative coefficient μ (a 1=5, a 2=−10, a 3=5, a 4=1, T=50)

Full size image
Fig. 2
figure 2

Solitary-waves evolution in the presence of dissipation

Full size image

4 Numerical simulation and discussion

In Sect. 3, we study the dissipation effect on the solitary Rossby waves and get the conclusion that the dissipation effect causes the amplitude of the solitary waves decrease and the width of the solitary waves increase. But what the solitary Rossby waves happen under the influence of dissipation and topography? Specially what happens with the solitary Rossby waves under the influence of dissipation and the unstable topography? In this section, we will take into account the problem.

In fact, in Sect. 2, we have obtain Eq. (10) which governs the evolution of the amplitude of the solitary waves under the influence of dissipation and topography. But there is no analytic solution for Eq. (10), here we will look for the numerical solution of Eq. (10) by using the pseudo-spectral method. First, let us simply introduce the method.

This method will be described for Eq. (10). It also can be written as

(21)

This is a pseudo-spectral method, which uses a Fourier transform treatment of the space dependence together with a leap-forg scheme in time. For ease of presentation the spatial period is normalized to [0,2π]. This intervals is divided into 2N points, then ΔT=π/N. The function A(X,T) can be transformed to the Fourier space by

(22)

The inversion formula is

(23)

These transformations can use Fast Fourier Transform algorithm to efficiently perform.

With this scheme, \(\frac{\partial A}{\partial X}\) can be evaluated as F −1{ivFA}, \(\frac{\partial^{2} A}{\partial X^{2}}\) as −F −1{v 2 FA}, \(\frac{\partial^{4} A}{\partial X^{4}}\) as F −1{v 4 FA}, \(\frac{\partial^{2} H}{\partial X^{2}}\) as −F −1{v 2 FH} and so on. Combined with a leap-frog time step, Eq. (21) would be approximated by

(24)

The computational cost for Eq. (24) is six fast Fourier transforms per time step.

For a given zonal flow u(y), β-plane approximation function β(y) and topographic forcing function H(X,T) as well the dissipative coefficient μ, it is easy to find the coefficients of Eq. (10) by using Eq. (7) and Eq. (8). In order to simplify the calculation and to focus attention on the time evolution of the solitary waves under the influence of dissipation and topographic forcing, we take a 1=10, a 2=−20, a 3=1, a 4=1, a 5=1. As an initial condition, we take A(X,T)=0, T=0. The bottom topography, as a forcing for wave generation, used for the present numerical computations is

where M is a measure for rate of topography vary with time. In order to compare the effect of stable topography and unstable topography, we will consider the case of M=0 and M=−0.3. Meanwhile, in order to study the dissipation effect, we take μ=0 and μ=0.01, respectively. The simulated results are shown in Figs. 3 and 4.

Fig. 3
figure 3

Wavetrains excited by topography in the absence of dissipation (μ=0), (a) M=0; (b) M=−0.3

Full size image
Fig. 4
figure 4

Wavetrains excited by topography in the presence of dissipation (μ=0.01), (a) M=0; (b) M=−0.3

Full size image

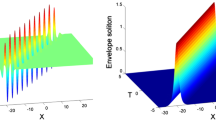
From Fig. 3, it is easy to find that a solitary wave is generated in the topographic forcing region. Two symmetric modulated wavetrains propagating toward both upstream and downstream are generated. It is very different from the modulated wavetrains expressed with the forced KdV equation and mKdV equation [13, 14]. This is because the topographic forcing term in Eq. (10) is the second order derivative with respect to X, the forcing term remains the original symmetric feature of the topography. By comparison of Figs. 3(a) and 3(b), it is not difficult to find that the solitary wave in stable topographic forcing region is excited and its amplitude increases rapidly and then remains invariant with time T. While the solitary wave in unstable topographic forcing region is also excited, but its amplitude increases rapidly and then decreases slowly with time T. At the end of the calculation time, the amplitude in Fig. 3(b) is much less than the amplitude in Fig. 3(a). The amplitudes of the modulated wavetrains excited in upstream and downstream increase with time T both in Figs. 3(a) and 3(b), the variation of M has almost no effect on the propagation speed and quantity of the modulated wavetrains, but make the amplitudes of the modulated wavetrains vary slowly. Additionally, between the solitary wave and the modulated wavetrains, there exists a buffer region. The buffer region located in the horizontal plane and is steady in Fig. 3(a), while it is unsteady and there is a convex above the horizontal plane in Fig. 3(b).

By comparing Figs. 3 and 4, we will find that the dissipation effect makes the amplitude of the solitary wave, the modulated wavetrains in the upstream and downstream, the buffer region between the solitary wave and the modulated wavetrains change. First, the dissipation effect makes the amplitude of the solitary wave in the forcing region decrease. From Fig. 4, we see that the solitary wave in stable topographic forcing region is excited and its amplitude increases rapidly and then decreases slowly with time T. The amplitude in Fig. 4 is less than the amplitude in Fig. 3. Especially, the solitary wave in Fig. 4(b) almost disappears at the end of the calculation time under the influence of dissipation and unstable topographic forcing. Because of dissipation effect, the symmetric feature of modulated wavetrains in upstream and downstream is destroyed. Two asymmetric modulated wavetrains propagating toward both upstream and downstream are generated. The amplitudes of modulated wavetrains in upstream region increase slowly with time T, the buffer region between the solitary wave and modulated wavetrains in upstream region lies a concave below the horizontal plane. On the contrary, the amplitudes of modulated wavetrains in downstream region increase quickly with time T, the buffer region between the solitary wave and modulated wavetrains in downstream region lies a convex above the horizontal plane.

In conclusion, by comparing Figs. 3 and 4, we will find that the dissipation effect and topographic forcing have great effect on the solitary wave and the modulated wavetrains.

5 Conclusions

In the paper, the effects of topographic forcing and dissipation on solitary Rossby waves are studied. Special attention is given to solitary Rossby waves excited by unstable topography. The dissipative Boussinesq equation which is derived by the perturbation method is solved by using the modified Jacobi elliptic function expansion method and pseudo-spectral method. By analyzing the plots, we obtain the following conclusions.

  1. (1)

    The dissipation effect causes the amplitude of the solitary waves decrease and the width of the solitary waves increase in the absence of topographic forcing.

  2. (2)

    The solitary wave in stable topographic forcing region is excited and its amplitude increases rapidly and then remains invariant with time T; While the solitary wave in unstable topographic forcing region is also excited, but its amplitude increases rapidly and then decreases slowly with time T in the absence of dissipation.

  3. (3)

    The unstable topography has almost no effect on the propagate speed and quantity of the modulated wavetrains, but make the amplitude of the modulated wavetrains and the buffer region between the solitary wave and the modulated wavetrains vary slowly.

  4. (4)

    Because of dissipation effect, the symmetric feature of modulated wavetrains in upstream and downstream which excited by topography is destroyed.