Nonlinear Schrödinger equation for envelope Rossby waves with complete Coriolis force and its solution

Abstract

The physical features of the equatorial envelope Rossby waves including with complete Coriolis force and dissipation are investigated analytically. Staring with a potential vorticity equation, the wave amplitude evolution of equatorial envelope Rossby waves is described as a nonlinear Schrödinger equation by employing multiple scale analysis and perturbation expansions. The equation is more suitable for describing envelope Rossby solitary waves when the horizontal component of Coriolis force is stronger near the equator. Then, based on the Jacobi elliptic function expansion method and trial function method, the classical Rossby solitary wave solution and the corresponding stream function of the envelope Rossby solitary waves are obtained, respectively. With the help of these solutions, the effect of dissipation and the horizontal component of Coriolis parameter are discussed in detail by graphical presentations. The results reveal the effect of the horizontal component of Coriolis force and dissipation on the classical Rossby solitary waves.

1 Introduction

In recent years, equatorial Rossby wave theory has been an important research subject in the atmospheric and oceanic dynamics (Boyd 2018; Ching et al. 2015; Puy et al. 2016). In 1834, Russell first observed solitary wave. Since then, Rossby waves have attracted much more attention as a branch of solitary waves, and many mathematical models are constructed to study the generation and evolution of Rossby solitary waves, such as the Korteweg-de Vries (KdV), the modified KdV (mKdV) equation, the Zakharov–Kuznetsov equation, the nonlinear Schrödinger equation (NLS), and so on. Meanwhile, some natural phenomena related to Rossby waves were explained better with the help of these mathematical models.

The KdV equation was firstly obtained by Long (1964) in barotropic fluid, which is a famous soliton wave equation. Later, Redekopp (1977) discussed the general theory of solitary waves in zonal planetary shear flow and obtained mKdV equation. After these pioneer work, the classical Rossby solitary waves theory was formed step by step (Boyd 1980; Wadati 1973; Yang et al. 2014). However, the disadvantages of the KdV-type solitons must be satisfied the long-wave approximation. For the envelope Rossby solitary waves depicted by the NLS equation, it is not need to satisfy the long-wave approximation. Therefore, it is more appropriate to describe the Rossby waves contrast to the KdV or mKdV solitary wave models. The equation was firstly obtained by Benney (1979) in atmospheric dynamics for describing the envelope Rossby solitary waves. Then, Luo (1991) used the NLS equation to explain atmospheric vortex pair blocking in the mid-high latitudes. Tan and Boyd (2000) derived the dissipative NLS equation and studied the effects of forcing and dissipation on the collision interaction of two envelope Rossby solitary waves. Demiray (2003) sought a traveling wave solution to the dissipative NLS equation by using of the hyperbolic tangent method. Barletti et al. (2018) used the Hamiltonian Boundary Value Methods for solving the NLS equation. Fu et al. (2018) derived the time–space fractional (2 + 1)-dimensional NLS equation to describe the envelope gravity waves by using the multiple scale and obtained the solution of the equation. Recently, a new ZK-BO equation and ZK–ILW equation are derived to describe the evolution of Rossby solitary waves by Yang et al. (2018) and Guo et al. (2018). However, looking at the above results, none of them considered the effects of the horizontal component of Coriolis parameter. It is discarded in the usual shallow water equation. The simplifications are known as the ‘traditional approximation’ which involves the neglect of the locally horizontal components of the Earth’s rotation vector (Hua et al. 1997).

For the traditional approximation, it is valid when the vertical length scales are small compared with the horizontal length scales. However, it becomes increasingly controversial questions from the dynamical perspective (Kasahara 2003; Philips 1968; Veronis 1968; Wangsness 1970) and many researchers indicated that the horizontal component of Coriolis parameter neglected has significant effects under the specific circumstances (Raymond 2000). Meanwhile, White and Bromley (1995) gave a set of “quasi-hydrostatic” models and examined the importance of the cosine Coriolis terms. They pointed out that the cosine Coriolis terms are not neglected in planetary-scale motion and in tropical synoptic-scale motion. Dellar and Salmon (2005) derived a conserved potential vorticity equation including with complete Coriolis force by variational method. In 2010, Stewart and Dellar (2010) extended this work and described the flow of multiple superposed layers of inviscid, incompressible fluids in a rotating frame. Stewart and Dellar (2012) investigated the behavior of linear plane waves with the complete Coriolis force in multilayer shallow water equations. Recently, Lu et al. (2018) constructed time-fractional Boussinesq equation to describe Rossby solitary waves from the quasi-geostrophic vorticity equation with dissipation and complete Coriolis force in stratified fluid.

On the other hand, the solutions of solitary wave models have been extensively investigated and many powerful methods have been proposed to solve nonlinear partial differential equations; for example, traveling wave solutions (Zayed and Gepreel 2009), Jacobi elliptic function expansion methods (Liu et al. 2001; Liu and Fan 2005), Bäcklund transformations (Quispel et al. 1984), trial function methods (Belytschko et al. 1994), homotopy perturbation methods (He 2003), new homotopy perturbation methods (Biazar and Eslami 2013; Eslami 2014; Eslami and Mirzazadeh 2014), sine–cosine expansion methods (Triki and Wazwaz 2011, 2014), and so on. In the present paper, we give asymptotic solutions of the new NLS equation including with complete Coriolis force and dissipation by using Jacobi elliptic function expansion methods and trial function methods.

Considering all of the above discussions, this paper is organized as follows. From conserved potential vorticity equation including with complete Coriolis force and dissipation, we derive a NLS equation by multiple scale analysis and perturbation expansions in Sect. 2. In Sect. 3, the classical Rossby solitary wave solution and the stream function of the envelope Rossby solitary waves are obtained by using Jacobi elliptic function expansion methods and trial function methods, respectively. Then, graphical presentations are presented, and the effects of the dissipation and the horizontal component of Coriolis parameter are discussed. Finally, some conclusions are given in Sect. 4.

2 Basic mathematical model

Based on the potential vorticity equation near the equator with complete Coriolis force and turbulent dissipation, it can be written as follows:

$$ \left( {\frac{\partial }{\partial t} - \frac{\partial \psi }{\partial y}\frac{\partial }{\partial x} + \frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}} \right)\left[ {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + f - f_{H} \frac{\partial B}{\partial y}} \right] = - \mu \nabla^{2} \psi + Q, $$

(1)

where $\psi (x,y)$ is the total stream function; $f = \beta (y)y$ is the vertical component of Coriolis parameter; $f_{H}$ is the horizontal component of Coriolis parameter, it is constant; $B(x,y)$ is the bottom topography; $\mu$ is the turbulent dissipation parameter; $Q$ denotes the external heating source due to the tropical ocean; $\nabla^{2}$ is the two-dimensional Laplace operator.

The boundary conditions are defined by the following:

$$ \frac{\partial \psi }{\partial x} = 0,\,\;y = y_{1} ,\;y = y_{2} . $$

(2)

Here, $y = y_{1} ,\,\,y = y_{2}$ denote the southern and northern edges of the zonal flow.

Introducing the dimensionless as

$$ \left( {x,y} \right) = L_{0} (x^{*} ,y^{*} ),t = \frac{{L_{0} }}{{U_{0} }}t^{*} ,\psi = L_{0} U_{0} \psi^{*} ,B = \frac{{U_{0} H}}{{f_{H} L_{0} }}B^{*} ,\beta = \frac{{U_{0} }}{{L_{0}^{2} }}\beta^{ \bullet } ,\mu_{0} = \frac{{U_{0} }}{{L_{0} }}\mu^{*} ,Q = \frac{{U_{0}^{2} }}{{L_{0}^{2} }}Q^{*} , $$

(3)

where dimensionless variables are marked by an asterisk.$L_{0}$ is the zonal characteristic length of the mean zonal flow, and $H$ is a vertical characteristic length, respectively; $U_{0}$ is the characteristic velocity.

Substituting of (3) into (1) and (2) gets

$$ \left( {\frac{\partial }{\partial t} - \frac{\partial \psi }{\partial y}\frac{\partial }{\partial x} + \frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}} \right)\left[ {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \beta (y)y - \delta^{\prime}\frac{\partial B}{\partial y}} \right] = - \mu \nabla^{2} \psi + Q(x,y,t), $$

(4)

and the boundary conditions of nondimensional form is as follows:

$$ \frac{\partial \psi }{\partial x} = 0,\;y = 0,\;y = 1. $$

(5)

Here, the subscript asterisks have been dropped for simplicity. $\delta^{\prime} = {\raise0.7ex\hbox{$H$} \!\mathord{\left/ {\vphantom {H {L_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${L_{0} }$}}$ represents factors of the aspect ratio. To balance the external source and nonlinearity, we introduce a new small parameter $\delta ,$

$$ \delta^{\prime} = \varepsilon \delta . $$

(6)

Here, $\varepsilon$ is a small parameter characterizing the weakness of the nonlinearity.

Assuming that the total stream function can be decomposed as follows:

$$ \psi (x,y,t) = - \int_{0}^{y} {[U(s)} - c_{0} ]{\text{d}}s + \varepsilon \psi^{'} (x,y,t), $$

(7)

where $c_{0}$ is a constant, $U(s)$ is the basic flow, and the external source balances the diffusion of the basic flow (Caillol and Grimshaw 2008). Substituting of (6) and (7) into (4) yields:

$$ \left[ {\frac{\partial }{\partial t} + \left( {U - c_{0} } \right)\frac{\partial }{\partial x}} \right]\nabla^{2} \psi^{'} + p\left( y \right)\frac{{\partial \psi^{'} }}{\partial x} + \varepsilon J(\psi^{'} ,\nabla^{2} \psi^{'} ) - \varepsilon \delta J\left( {\psi^{'} ,\frac{\partial B}{\partial y}} \right) - \delta \left( {U - c_{0} } \right)\frac{\partial }{\partial x}\left( {\frac{\partial B}{\partial y}} \right) = - \mu \nabla^{2} \psi^{'} , $$

(8)

where $p(y) = \frac{{{\text{d}}(\beta (y)y)}}{{{\text{d}}y}} - U^{''} ,J\left( {A,B} \right) = \frac{\partial A}{\partial x}\frac{\partial B}{\partial y} - \frac{\partial A}{\partial y}\frac{\partial B}{\partial x},\;Q = - \mu \frac{{{\text{d}}U}}{{{\text{d}}y}}.$

Introducing the slow time and space variables:

$$ T_{1} = \varepsilon t,T_{2} = \varepsilon^{2} t;X_{1} = \varepsilon x,X_{2} = \varepsilon^{2} x. $$

(9)

The derivative transformations are as follows:

$$ \frac{\partial }{\partial t} \to \frac{\partial }{\partial t} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial T_{2} }};\;\frac{\partial }{\partial x} \to \frac{\partial }{\partial x} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial X_{2} }}, $$

(10)

By adopting the transformation, the Eq. (8) becomes

$$\begin{aligned} & \left[ {\left( {\frac{\partial }{{\partial t}} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial T_{2} }}} \right) + (U - c_{0} )\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)} \right]\left[ {\nabla ^{2} \psi ^{'} + 2\varepsilon \frac{{\partial ^{2} \psi ^{'} }}{{\partial x\partial X_{1} }} + \varepsilon ^{2} \left( {\frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{1} ^{2} }} + 2\frac{{\partial ^{2} \psi ^{'} }}{{\partial x\partial X_{2} }}} \right)} \right. \\ & \quad \left. { + 2\varepsilon ^{3} \frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{1} \partial X_{2} }} + \varepsilon ^{4} \frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{2} ^{2} }}} \right] + \varepsilon \left[ {\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)\psi ^{'} \left( {\frac{\partial }{{\partial y}}} \right) - \frac{{\partial \psi ^{'} }}{{\partial y}}\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)} \right] \\ & \quad \times \left[ {\nabla ^{2} \psi ^{'} + 2\varepsilon \frac{{\partial ^{2} \psi ^{'} }}{{\partial x\partial X_{1} }} + \varepsilon ^{2} \left( {\frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{1} ^{2} }} + 2\frac{{\partial ^{2} \psi ^{'} }}{{\partial x\partial X_{2} }}} \right) + 2\varepsilon ^{3} \frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{1} \partial X_{2} }} + \varepsilon ^{4} \frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{2} ^{2} }}} \right] - \varepsilon \delta \left[ {\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }}} \right.} \right. \\ & \quad \left. {\left. { + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)\psi ^{'} \frac{\partial }{{\partial y}}\left( {\frac{{\partial B}}{{\partial y}}} \right) - \frac{{\partial \psi ^{'} }}{{\partial y}}\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)\left( {\frac{{\partial B}}{{\partial y}}} \right)} \right] + p(y)\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)\psi ^{'} \\ & \quad - \delta (U - c_{0} )\left( {\frac{\partial }{{\partial x}} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon ^{2} \frac{\partial }{{\partial X_{2} }}} \right)\frac{{\partial B}}{{\partial y}} = - \varepsilon ^{2} \lambda \left[ {\nabla ^{2} \psi ^{'} + 2\varepsilon \frac{{\partial ^{2} \psi ^{'} }}{{\partial x\partial X_{1} }} + \varepsilon ^{2} \left( {\frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{1} ^{2} }} + 2\frac{{\partial ^{2} \psi ^{'} }}{{\partial x\partial X_{2} }}} \right)} \right. \\ & \quad \left. { + 2\varepsilon ^{3} \frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{1} \partial X_{2} }} + \varepsilon ^{4} \frac{{\partial ^{2} \psi ^{'} }}{{\partial X_{2} ^{2} }}} \right]. \\ \end{aligned}$$

(11)

In Eq. (11), further assumptions are as follows:

$$ \frac{\partial B}{\partial y} = \varepsilon D(y),\mu = \varepsilon^{2} \lambda . $$

(12)

Assuming the disturbance stream function can be expanded as follows:

$$ \psi^{'} = \psi_{0} (x,y,t;X_{1} ,X_{2} ;T_{1} ,T_{2} ) + \varepsilon \psi_{1} (x,y,t;X_{1} ,X_{2} ;T_{1} ,T_{2} ) + \varepsilon^{2} \psi_{2} (x,y,t;X_{1} ,X_{2} ;T_{1} ,T_{2} ) + \cdots $$

(13)

Substituting of (13) into (11), the lowest order equation is as follows:

$$ o(\varepsilon^{0} ):\left[ {\frac{\partial }{\partial t} + (U - c_{0} )\frac{\partial }{\partial x}} \right]\nabla^{2} \psi_{0} + p(y)\frac{{\partial \psi_{0} }}{\partial x} = 0. $$

(14)

Assuming that the solution of Eq. (14) is as follows:

$$ \psi_{0} = A(X_{1} ,X_{2} ;T_{1} ,T_{2} )\varPhi_{0} (y){\text{e}}^{i(kx - wt)} + {\text{c}} . {\text{c}} . , $$

(15)

where $A$ is a slowly varying envelope amplitude, $k$ is the zonal wave number, $\omega$ is the frequency of Rossby waves, and ${\text{c}} . {\text{c}} .$ denotes the complex conjugate of the preceding term.

When $U - c_{0} - c \ne 0,$$\varPhi_{0}$ satisfies the following equation:

$$ \varPhi_{0}^{''} + \left( {\frac{p(y)}{{U - c_{0} - c}} - k^{2} } \right)\varPhi_{0} = 0, $$

(16)

$$ \varPhi_{0} (0) = \varPhi_{0} (1) = 0, $$

(17)

where $c$ is the really constant. For the $o(\varepsilon ),$ we get the following:

$$ \left[ {\frac{\partial }{\partial t} + (U - c_{0} )\frac{\partial }{\partial x}} \right]\nabla^{2} \psi_{1} + p(y)\frac{{\partial \psi_{1} }}{\partial x} \equiv F_{1} , $$

(18)

$$ \varPhi_{1} (0) = \varPhi_{1} (1) = 0, $$

(19)

where $F_{I}$ being defined as follows:

$$ F_{1} = - \left\{ {\left[ {\frac{\partial }{{\partial T_{1} }} + \left( {U - c_{0} } \right)\frac{\partial }{{\partial X_{1} }}} \right]\nabla^{2} \psi_{0} + p(y)\frac{{\partial \psi_{0} }}{{\partial X_{1} }} + J\left( {\psi_{0} ,\nabla^{2} \psi_{0} } \right) + 2\left[ {\frac{\partial }{\partial t} + (U - c_{0} )\frac{\partial }{\partial x}} \right]\frac{{\partial^{2} \psi_{0} }}{{\partial x\partial X_{1} }}} \right\}. $$

(20)

Equation (20) becomes

$$ F_{1} = \frac{{p(y)\varPhi_{0} }}{{U - c_{0} - c}}\left( {\frac{\partial A}{{\partial T_{1} }} + c_{1} \frac{\partial A}{{\partial X_{1} }}} \right){\text{e}}^{i(kx - \omega t)} + ik\left( {\frac{p(y)}{{U - c_{0} - c}}} \right)_{y} \varPhi_{0}^{2} A^{2} {\text{e}}^{2i(kx - \omega t)} + {\text{c}} . {\text{c}} . , $$

(21)

with $c_{1} = c + \frac{{2k^{2} (U - c_{0} - c)^{2} }}{p(y)}.$By eliminating these secular terms, we get the following:

$$ \frac{\partial A}{{\partial T_{1} }} + c_{\text{g}} \frac{\partial A}{{\partial X_{1} }} = 0, $$

(22)

where

$$ c_{\text{g}} = c + \frac{{I_{1} }}{I},I_{1} = \int_{0}^{1} {2k^{2} } \varPhi_{0}^{2} {\text{d}}y,I = \int_{0}^{1} {\frac{{p(y)\varPhi_{0}^{2} }}{{(U - c_{0} - c)^{2} }}} {\text{d}}y, $$

(23)

where $c_{\text{g}}$ is the group velocity of Rossby wave. Equation (18) then reduces to

$$ \left[ {\frac{\partial }{\partial t} + (U - c_{0} )\frac{\partial }{\partial x}} \right]\nabla^{2} \psi_{1} + p(y)\frac{{\partial \psi_{1} }}{\partial x} \equiv ikA^{2} Q(y){\text{e}}^{2i(kx - \omega t)} + {\text{c}} . {\text{c}}. $$

(24)

Here, $Q(y) = \left( {\frac{p(y)}{{U - c_{0} - c}}} \right)_{y} \varPhi_{0}^{2} .$

Assuming that the solution of Eq. (24) is as follows:

$$ \psi_{1} = B\left( {X_{1} ,X_{2} ;T_{1} ,T_{2} } \right)\varPhi_{1} {\text{e}}^{{2i\left( {kx - \omega t} \right)}} + {\text{c}} . {\text{c}}. $$

(25)

By combining (24) with (25), get

$$ \left[ {\varPhi_{1}^{''} - 4k^{2} \varPhi_{1} + \frac{p\left( y \right)}{{U - c - c_{0} }}\varPhi_{1} } \right]B = A^{2} Q(y)\frac{1}{{2(U - c - c_{0} )}}. $$

(26)

In Eq. (26),$A$ and $B$ are not two independent variables. For simplification, $B$ will be taken into the following forms, namely

$$ \psi_{1} = A^{2} \varPhi_{1} {\text{e}}^{{2i\left( {kx - \omega t} \right)}} + {\text{c}} . {\text{c}}. $$

(27)

For

$$ o\left( {\varepsilon^{2} } \right):\left[ {\frac{\partial }{\partial t} + \left( {U - c_{0} } \right)\frac{\partial }{\partial x}} \right]\nabla^{2} \psi_{2} + p\left( y \right)\frac{{\partial \psi_{2} }}{\partial x} = F_{2} , $$

(28)

With

$$ \begin{aligned} F_{2} & = - \left\{ {\left( {\frac{\partial }{\partial t} + \left( {U - c_{0} } \right)\frac{\partial }{\partial x}} \right)\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial X_{1}^{2} }} + 2\frac{{\partial^{2} \psi_{0} }}{{\partial x\partial X_{2} }}} \right) + \left( {\frac{\partial }{{\partial T_{1} }} + \left( {U - c_{0} } \right)\frac{\partial }{{\partial X_{1} }}} \right)\nabla^{2} \psi_{1} + \left( {\frac{\partial }{{\partial T_{1} }} + \left( {U - c_{0} } \right)\frac{\partial }{{\partial X_{1} }}} \right)2\frac{{\partial^{2} \psi_{0} }}{{\partial x\partial X_{1} }}} \right. \\ & \quad + \left( {\frac{\partial }{\partial t} + \left( {U - c_{0} } \right)\frac{\partial }{\partial x}} \right)\left( {2\frac{{\partial^{2} \psi_{1} }}{{\partial x\partial X_{1} }}} \right) + \left( {\frac{\partial }{{\partial T_{2} }} + \left( {U - c_{0} } \right)\frac{\partial }{{\partial X_{2} }}} \right)\nabla^{2} \psi_{0} + \frac{{\partial \psi_{0} }}{\partial x}\frac{\partial }{\partial y}\nabla^{2} \psi_{1} + \frac{{\partial \psi_{0} }}{\partial x}\frac{\partial }{\partial y}\left( {2\frac{{\partial^{2} \psi_{0} }}{{\partial x\partial X_{1} }}} \right) \\ & \quad + \frac{{\partial \psi_{0} }}{{\partial X_{1} }}\frac{\partial }{\partial y}\nabla^{2} \psi_{0} + \frac{{\partial \psi_{1} }}{\partial x}\frac{\partial }{\partial y}\nabla^{2} \psi_{0} - \frac{{\partial \psi_{0} }}{\partial y}\frac{\partial }{\partial x}\nabla^{2} \psi_{1} - \frac{{\partial \psi_{0} }}{\partial y}\frac{\partial }{\partial x}\left( {2\varepsilon \frac{{\partial^{2} \psi_{0} }}{{\partial x\partial X_{1} }}} \right) - \frac{{\partial \psi_{0} }}{\partial y}\frac{\partial }{{\partial X_{1} }}\nabla^{2} \psi_{0} - \frac{{\partial \psi_{1} }}{\partial y}\frac{\partial }{\partial x}\nabla^{2} \psi_{0} \\ & \quad \left. {+ p\left( y \right)\frac{{\partial \psi_{1} }}{{\partial X_{1} }} + p\left( y \right)\frac{{\partial \psi_{0} }}{{\partial X_{2} }} - \delta \frac{{\partial \psi_{0} }}{\partial x}\frac{\partial }{\partial y}D\left( y \right) + \lambda \left( {\frac{{\partial^{2} \psi_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)} \right\}. \\ \end{aligned} $$

(29)

Next, Eq. (29) becomes

$$ \begin{aligned} F_{2} =\, & \frac{{p(y)\varPhi_{0} }}{{U - c - c_{0} }}\left[ {\frac{\partial A}{{\partial T_{2} }} + c_{1} \frac{\partial A}{{\partial X_{2} }} + ik\frac{{U - c - c_{0} }}{p\left( y \right)}\left( {c + 2c_{g} - 3(U - c_{0} )} \right)\frac{{\partial^{2} A}}{{\partial X_{1}^{2} }} +\, ik\delta \frac{{U - c - c_{0} }}{p\left( y \right)}D^{\prime}\left( y \right)A - \lambda A} \right]{\text{e}}^{{i\left( {kx - wt} \right)}} \\ & - \,ik\left| A \right|^{2} A\left[ {\varPhi_{0} \left( {\varPhi_{1}^{\prime \prime } - 4k^{2} \varPhi_{1} } \right)^{\prime } } \right. + 2\varPhi_{0}^{\prime } \left( {\varPhi_{1}^{\prime \prime } - 4k^{2} \varPhi_{1} } \right) + 2\varPhi_{1} \left( {\varPhi_{0}^{\prime \prime } - k^{2} \varPhi_{0} } \right)^{\prime } \\ & \left. { +\, \varPhi_{1} \left( {\varPhi_{0}^{\prime \prime } - k^{2} \varPhi_{0} } \right)} \right]{\text{e}}^{{i\left( {kx - \omega t} \right)}} + {\text{c}} . {\text{c}} .+ \square , \\ \end{aligned} $$

(30)

where $\square$ for other items related to the ${\text{e}}^{{ \pm 2i\left( {kx - \omega t} \right)}} ,$ and ${\text{e}}^{{ \pm 3i\left( {kx - \omega t} \right)}}$.

Eliminating these secular terms $\int_{0}^{1} {\frac{{\varPhi_{0} }}{{U - c - c_{0} }}} F_{2} {\text{d}}y = 0,$ we get the following:

$$ \begin{aligned} & \int_{0}^{1} {\frac{p(y)}{{\left( {U - c - c_{0} } \right)^{2} }}} \varPhi_{0}^{2} {\text{d}}y\left( {\frac{\partial A}{{\partial T_{2} }} + c_{1} \frac{\partial A}{{\partial X_{2} }}} \right) + ik\int_{0}^{1} {\frac{{c + 2c_{g} - 3(U - c_{0} )}}{{U - c - c_{0} }}} \varPhi_{0} {\text{d}}y\frac{{\partial^{2} A}}{{\partial X_{1}^{2} }} + ik\delta \int_{0}^{1} {\frac{{\varPhi_{0}^{2} }}{{U - c - c_{0} }}} D^{\prime}(y){\text{d}}yA - \lambda A \\ & \int_{0}^{1} {\frac{{p(y)\varPhi_{0}^{2} }}{{(U - c - c_{0} )^{2} }}{\text{d}}y} + ik\left| A \right|^{2} A\int_{0}^{1} {\frac{{\varPhi_{0} }}{{U - c - c_{0} }}} \left[ {\frac{{\varPhi_{0} }}{2}\left( {\frac{Q(y)}{{U - c - c_{0} }}} \right)_{y} + \varPhi_{0} \varPhi_{1} \left( {\frac{p(y)}{{U - c - c_{0} }}} \right)_{y} + \frac{Q(y)}{{U - c - c_{0} }}\frac{{d\varPhi_{0} }}{dy}} \right]{\text{d}}y = 0. \\ \end{aligned} $$

(31)

Set

$$ \alpha = \frac{{I_{1} }}{I},\lambda = \frac{{I_{2} }}{I},\gamma = \frac{{I_{3} }}{I},\eta = \frac{{I_{4} }}{I}, $$

(32)

where

$$ \begin{aligned} I = & \int_{0}^{1} {\frac{p(y)}{{(U - c - c_{0} )^{2} }}} \varPhi_{0}^{2} {\text{d}}y, I_{1} = k\int_{0}^{1} {\frac{{c + 2c_{g} - 3(U - c_{0} )}}{{U - c - c_{0} }}} \varPhi_{0} {\text{d}}y, I_{2} =\, \delta k\int_{0}^{1} {\frac{{\varPhi_{0}^{2} }}{{U - c - c_{0} }}} D^{\prime}(y){\text{d}}y, \,I_{4} = - \lambda \int_{0}^{1} {\frac{{p(y)\varPhi_{0}^{2} }}{{(U - c - c_{0} )^{2} }}{\text{d}}y} . \\ I_{3} = & k\int_{0}^{1} {\frac{{\varPhi_{0} }}{{U - c - c_{0} }}\left[ {\frac{{\varPhi_{0} }}{2}\left( {\frac{Q\left( y \right)}{{U - c - c_{0} }}} \right)_{y} + \varPhi_{0} \varPhi_{1} \left( {\frac{p(y)}{{U - c - c_{0} }}} \right)_{y} + \frac{Q\left( y \right)}{{U - c - c_{0} }}\frac{{d\varPhi_{0} }}{dy}} \right]} {\text{d}}y. \\ \end{aligned} $$

Equation (32) can be rewritten as follows;

$$ i\left( {\frac{\partial A}{{\partial T_{2} }} + c_{1} \frac{\partial A}{{\partial X_{2} }}} \right) + \alpha \frac{{\partial^{2} A}}{{\partial X_{1}^{2} }} + \lambda A + \gamma \left| A \right|^{2} A + i\eta A = 0. $$

(33)

Equation (33) is a nonlinear Schrödinger equation with the horizontal component of Coriolis parameter and dissipation. The coefficients $\alpha ,$ $\gamma$ are the dispersion coefficient and the Landau number which are related to the shear basic flow and generalized beta effect, respectively. The term with coefficient $\eta$ represents the dissipation effect. The term with coefficient $\lambda$ denotes that the horizontal components of Coriolis parameter and bottom topography are interacting with the equatorial envelop Rossby waves. When the horizontal component of the Coriolis parameter is neglected, namely $\lambda = 0,$ the equation deduces to the results of Demiray (2003).

3 Asymptotic solution

3.1 Solutions of NLS equation with the horizontal components of Coriolis parameter

In this section, we will consider the effects of the horizontal component of the Coriolis parameter. For Eq. (33), by adopting the axis transform by Jeffrey and Kawahara (1982) as follows:

$$ T = T_{2} ,X = \frac{1}{\varepsilon }(X_{2} - c_{\text{g}} T_{2} ) = X_{1} - c_{\text{g}} T_{1} . $$

(34)

Equation (33) can be rewritten as follows:

$$ i\frac{\partial A}{\partial T} + \alpha \frac{{\partial^{2} A}}{{\partial X^{2} }} + \lambda A + \gamma \left| A \right|^{2} A + i\eta A = 0. $$

(35)

In Eq. (35), when the coefficient $\lambda = 0,\eta = 0,$ the equation becomes a standard NLS equation obtained by Benney and Newell (1967):

$$ i\frac{\partial A}{\partial T} + \alpha \frac{{\partial^{2} A}}{{\partial X^{2} }} + \gamma \left| A \right|^{2} A = 0. $$

(36)

The single envelope Rossby solitary wave solution of Eq. (36) is as follows:

$$ A_{0} (X,T) = \sqrt {\frac{2\alpha }{\gamma }} M\,\text{sech} \,M(X - 2\alpha k_{0} T)\exp \left\{ {i[k_{0} X - \alpha (k_{0}^{2} } \right. - M^{2} )T]\} , $$

(37)

which the parameter $M$ is the amplitude and $k_{0}$ is the moving speed of the envelope Rossby solitary waves, whose value is determined by the original state of $A_{0} (X,T).$

Substituting of (37) and (13) into (7) yields

$$ \psi_{0} = - \int_{{}}^{y} {[U(s) - c_{0} ]} {\text{d}}s + \varepsilon \sqrt {\frac{2\alpha }{\gamma }} M\,\text{sech} \,\varepsilon M(x - V_{0} t)\varPhi_{0} (y)\exp \{ i[K_{0} x - \varOmega_{0} ]t\} , $$

(38)

where

$$ V_{0} = c_{\text{g}} + 2\varepsilon \alpha k_{0} ,K_{0} = k + \varepsilon k_{0} ,\varOmega_{0} = \omega + \varepsilon k_{0} c_{\text{g}} + \varepsilon^{2} \alpha (k_{0}^{2} - M^{2} ). $$

(39)

In the following discussion, we suppose $\lambda \ne 0,\eta = 0.$ Equation (35) becomes

$$ i\frac{\partial A}{\partial T} + \alpha \frac{{\partial^{2} A}}{{\partial X^{2} }} + \lambda A + \gamma \left| A \right|^{2} A = 0; $$

(40)

taking the following transformation:

$$ A = B\exp \{ i\lambda T\} . $$

(41)

Substituting of (41) into (40), we get the following:

$$ i\frac{\partial B}{\partial T} + \alpha \frac{{\partial^{2} B}}{{\partial X^{2} }} + \gamma \left| B \right|^{2} B = 0. $$

(42)

Based on the above discussion, the envelope Rossby solitary wave solution of Eq. (40) is as follows:

$$ A_{1} (X,T) = \sqrt {\frac{2\alpha }{\gamma }} M\,\text{sech} \,M(X - 2\alpha k_{0} T)\exp \left\{ {i[k_{0} X - [\alpha (k_{0}^{2} } \right. - M^{2} )]T + \lambda T]\} . $$

(43)

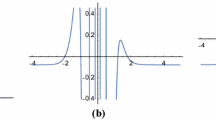
The behavior of function A(X,T) defined by Eq. (43) is given in Figs. 1 and 2. Figure 1 describes the evolution of Rossby solitary wave amplitude $A(X,T)$ changing with time and spatial when the dissipation is absent. The amplitude of Rossby solitary waves is not changed with time; it is the idealized solitary wave. Then, we discuss the effects of the horizontal component of Coriolis parameter $\lambda$ on the amplitude of solitary wave in the absent of dissipation in Figs. 2 and 3; we find that with increasing of the Coriolis parameter $\lambda$, the amplitude of solitary wave decreases when the latitude $X = 0.5$ and $X = 1,$ and it means that it is more beneficial to form the large amplitude solitary wave when the Coriolis parameter $\lambda$ is smaller.

Fig. 1

The real part and envelope of the solution (43) with parameters chosen as: $\alpha = 1,$ $\gamma = 1,M = 1,k_{0} = 2,$ and $\lambda = 1$

Fig. 2

The real part of the solution (43) with different parameters chosen as: a $\alpha = 1,$ $\gamma = 1,M = 1,k_{0} = 2,$ and $\lambda = 0;$ b $\alpha = 1,$$\gamma = 1,M = 1,k_{0} = 2,$ and $\lambda = 2$

Fig. 3

The effects of $\lambda$ on the amplitude of Rossby solitary waves when $X = 1$ and $X = 0.5$

The stream function of envelope Rossby solitary waves in Eq. (40) is as follows:

$$ \psi_{1} = - \int_{{}}^{y} {[U(s) - c_{0} ]} {\text{d}}s + \varepsilon \sqrt {\frac{2\alpha }{\gamma }} M\,\text{sech} \,M\varepsilon (x - V_{1} t)\varPhi_{0} (y)\exp \{ i[K_{1} x - \varOmega_{1} t]\} , $$

(44)

where

$$ V_{1} = c_{\text{g}} + 2\varepsilon \alpha k_{0} ,K_{1} = k + \varepsilon k_{0} ,\varOmega_{1} = \omega + \varepsilon k_{0} c_{\text{g}} + \varepsilon^{2} \alpha (k_{0}^{2} - M^{2} ) - \varepsilon^{2} \lambda . $$

(45)

Comparing with Eqs. (39) and (45), we find that the carrier frequency $\varOmega_{1}$ is based on $\varOmega_{0}$ plus a small correction $\varepsilon^{2} \lambda$, but the propagation velocity and the carrier wave number have nothing to do with the Coriolis parameter. It means that the horizontal component of the Coriolis parameter can amend the carrier frequency.

3.2 Solutions of NLS equation with the horizontal components and dissipation

In this section, we mainly find asymptotic solution of Eq. (35) and analyze the dissipation effects on the evolution of Rossby solitary waves. We assume the coefficient $\lambda \ne 0,\eta \ne 0,$ and $\eta < < 1$, taking the following transformation:

$$ A = \left[ {a_{0} (T) + a_{1} (T)cn\xi } \right]{\text{e}}^{i(k(T) - \omega (T))} ,\xi = f(T)(X - g(T)). $$

(46)

Substituting of (46) into (35) get

$$ \begin{aligned} & ( - \gamma a_{1}^{3} + 2\alpha a_{1} f^{2} m^{2} )sn^{2} \xi cn\xi + \left[ {i\left( {\eta a_{1} + \frac{{{\text{d}}a_{1} }}{{{\text{d}}T}}} \right) + \left( { - \frac{{{\text{d}}k}}{{{\text{d}}T}}a_{1} X - \alpha k^{2} a_{1} + 3\gamma a_{0}^{2} a_{1} + \frac{{{\text{d}}\omega }}{{{\text{d}}T}}a_{1} + \gamma a_{1}^{3} - \alpha a_{1} f^{2} + \lambda a_{1} } \right)} \right] \\ & \quad \times cn\xi + i\left( { - a_{1} \frac{{{\text{d}}f}}{{{\text{d}}T}}X + a_{1} \frac{{{\text{d}}f}}{{{\text{d}}T}}g - 2\alpha ka_{1} f + a_{1} f\frac{{{\text{d}}g}}{{{\text{d}}T}}} \right)sn\xi {\text{d}}n\xi - 3\gamma a_{0} a_{1}^{2} sn^{2} \xi + i\left( {\frac{{{\text{d}}a_{0} }}{{{\text{d}}T}} + \eta a_{0} } \right) + \left( { - \frac{{{\text{d}}k}}{{{\text{d}}T}}a_{0} X} \right. \\ & \quad \left. { + 3\gamma a_{0} a_{1}^{2} + \gamma a_{0}^{3} + \frac{{{\text{d}}\omega }}{{{\text{d}}T}}a_{0} - \alpha k^{2} a_{0} + \lambda a_{0} } \right) = 0. \\ \end{aligned} $$

(47)

Therefore

$$ \begin{aligned} & - \gamma a_{1}^{3} + 2\alpha a_{1} f^{2} m^{2} = 0,\eta a_{1} + \frac{{{\text{d}}a_{1} }}{{{\text{d}}T}} = 0, - \frac{{{\text{d}}k}}{{{\text{d}}T}}a_{1} X - \alpha k^{2} a_{1} + 3\gamma a_{0}^{2} a_{1} + \frac{{{\text{d}}\omega }}{{{\text{d}}T}}a_{1} + \gamma a_{1}^{3} - \alpha a_{1} f^{2} + \lambda a_{1} = 0 \\ & - a_{1} \frac{{{\text{d}}f}}{{{\text{d}}T}}X + a_{1} \frac{{{\text{d}}f}}{{{\text{d}}T}}g - 2\alpha ka_{1} f + a_{1} f\frac{{{\text{d}}g}}{{{\text{d}}T}} = 0, - 3\gamma a_{0} a_{1}^{2} = 0,\frac{{{\text{d}}a_{0} }}{{{\text{d}}T}} + \eta a_{0} = 0, \\ & - \frac{{{\text{d}}k}}{{{\text{d}}T}}a_{0} X + 3\gamma a_{0} a_{1}^{2} + \gamma a_{0}^{3} + \frac{{{\text{d}}\omega }}{{{\text{d}}T}}a_{0} - \alpha k^{2} a_{0} + \lambda a_{0} = 0. \\ \end{aligned} $$

(48)

By solving Eq. (48), we obtain the following:

$$ a_{0} = 0,a_{1} = \sqrt {\frac{2\alpha }{\gamma }} h{\text{e}}^{ - \eta T} ,f = \frac{h}{m}{\text{e}}^{ - \eta T} ,k(T) = k_{0} ,\omega = \alpha \left[ {\left( {k_{0}^{2} - \frac{\lambda }{\alpha }} \right)T + \frac{{h^{2} (2m^{2} - 1)}}{{2\eta m^{2} }}{\text{e}}^{ - 2\eta T} } \right]; $$

(49)

substituting of (49) into (48), we get

$$ \eta (X - g(T)) + \left( {\frac{{{\text{d}}g}}{{{\text{d}}T}} - 2\alpha k(T)} \right) = 0. $$

(50)

Because of $\eta < < 1$, the item of $\eta (X - g(T))$ can be omitted in Eq. (50); therefore

$$ g(T) = 2\alpha k_{0} T. $$

(51)

The solution of the Eq. (35) is given by the following:

$$ A(X,T) = \sqrt {\frac{2\alpha }{\gamma }} h{\text{e}}^{ - \eta T} cn\left( {\frac{h}{m}{\text{e}}^{ - \eta T} (X - 2\alpha k_{0} T)} \right)\exp \left\{ {i\left[ {k_{0} X - \alpha \left( {\left( {k_{0}^{2} - \frac{\lambda }{\alpha }} \right)T + \frac{{(2m^{2} - 1)h^{2} }}{{2\eta m^{2} }}{\text{e}}^{ - 2\eta T} } \right)} \right]} \right\}. $$

(52)

For $m \to 1,$ the solution is degenerated as follows:

$$ A = \sqrt {\frac{2\alpha }{\gamma }} h{\text{e}}^{ - \eta T} \,\text{sech} \,[h{\text{e}}^{ - \eta T} (X - 2\alpha k_{0} T)]\exp \left\{ {i\left[ {k_{0} X - \alpha \left( {\left( {k_{0}^{2} - \frac{\lambda }{\alpha }} \right)T + \frac{{h^{2} }}{2\eta }{\text{e}}^{ - 2\eta T} } \right)} \right]} \right\}. $$

(53)

The behavior of function $A(X,T)$ defined by (53) is given in Figs. 4 and 5.

Fig. 4

The real part and envelope of the solution (54) with parameters chosen as: $\alpha = 1\;\gamma = 1\; h = 1\; \eta = 0.15\; k_{0} = 2\; \lambda = 1$

Fig. 5

The real part of the solution (54) with parameters chosen as: $\alpha = 1\; \gamma = 1\; h = 1\; \eta = 0.15$ and $k_{0} = 2$

Figures 4 and 5 show the effects of the horizontal component of Coriolis parameter $\lambda$ and the dissipation on the amplitude of solitary waves, and we can obtain the following conclusions. When the dissipation is exist, the wave amplitude is decreasing with time as $h{\text{e}}^{ - \eta T}$, where $h$ is the initial amplitude. This is different from the previous results. From Figs. 4 and 5, with the increasing the Coriolis parameter $\lambda ,$, the amplitude of the solitary waves will accelerate decay. There is obvious difference in the absence of the dissipation (Fig. 6).

Fig. 6

The effects of $\lambda$ on the amplitude of Rossby waves when $X = 1$ and $X = 0.5$

Corresponding, the stream function of equatorial envelope Rossby solitary waves is as follows:

$$ \psi_{0} = - \int_{{}}^{y} {[U(s) - c_{0} ]} {\text{d}}s + \varepsilon \sqrt {\frac{2\alpha }{\gamma }} h{\text{e}}^{{ - \eta \varepsilon^{2} t}} \,\text{sech} \,[\varepsilon h{\text{e}}^{{ - \eta \varepsilon^{2} t}} (x - V_{2} t)]\varPhi_{0} (y)\exp \{ i[K_{2} x - \varOmega_{2} ]\} ; $$

(54)

here

$$ V_{2} = c_{\text{g}} + 2\varepsilon \alpha k_{0} ,K_{2} = k + \varepsilon k_{0} ,\varOmega_{2} = (\omega + \varepsilon k_{0} c_{\text{g}} + \varepsilon^{2} \alpha k_{0}^{2} - \varepsilon^{2} \lambda )t + \frac{{h^{2} }}{2\eta }{\text{e}}^{{ - 2\eta \varepsilon t^{2} }} . $$

(55)

Comparing with Eqs. (45) and (55), it shows that the dissipation has no effect on the propagation velocity and the carrier wave number, but it has certain influence on the carrier frequency of equatorial envelope Rossby solitary waves. This conclusion was also obtained by Yun-Long et al. (2015)but they have not considered the horizontal component of Coriolis parameter. In addition, Eq. (55) reveals that the carrier frequency is equal to frequency of linear Rossby waves plus three small corrections, which are related to dispersion and the Coriolis horizontal component.

4 Conclusion

In this paper, we investigate the evolution of equatorial envelope Rossby solitary waves with complete Coriolis force and dissipation. The evolution of Rossby solitary waves is described by a nonlinear Schrödinger equation by means of multiple scale analysis and perturbation methods, it is more suitable for describing the equatorial envelope solitary Rossby waves. Then, based on Jacobi elliptic function expansion methods and trial function methods, the asymptotic solutions of the dissipative NLS equation are obtained. With the help of these solutions, the effect of dissipation and the horizontal component of Coriolis parameter on the evolution of envelope Rossby solitary waves are investigated, respectively. The results indicate that the dissipations influence on the carrier frequency of equatorial envelope Rossby solitary waves and accelerate the fragmentation of wave amplitude, while it has no effect on the propagation speed.

On the other hand, the wave amplitude is also affected by the horizontal component of Coriolis parameter. With the increasing the Coriolis parameter $\lambda ,$ the amplitude of Rossby solitary waves will accelerate decay. The Coriolis parameter also makes a correction to the wave frequency. However, the propagation velocity and the carrier wave number have nothing to do with the Coriolis parameter.