Existence and Stability of Pseudo Almost Periodic Solution for Neutral Type High-Order Hopfield Neural Networks with Delays in Leakage Terms on Time Scales

Abstract

Using the exponential dichotomy of linear dynamic equations on time scales, a fixed point theorem and the theory of calculus on time scales, we obtain some sufficient conditions for the existence and global exponential stability of pseudo almost periodic solutions for a class of neutral type high-order Hopfield neural networks with delays in leakage terms on time scales. Our results show that the continuous-time neural network and its discrete-time analogue have the same dynamical behaviors. Finally, we give a numerical example and simulation to illustrate the feasibility of our results. Results of this paper are completely new even if the time scale $\mathbb {T}=\mathbb {R}$ or $\mathbb {Z}$.

1 Introduction

Neural networks are widely applied in signal processing, pattern recognition, static image processing, associative memory, and combinatorial optimization. In such applications, it is major importance to ensure that the designed neural network is stable [1, 2]. Since high-order Hopfield neural networks (HHNNs) have stronger approximation property, faster convergence rate, great stronger capacity and higher fault tolerance, HHNNs have been extensively applied in psychophysics, robotics, adaptive pattern recognition and image processing. Hence, HHNNs have been widely studied in recent years. For instance, in [3–6], authors studied the absolute stability, robust stability, global asymptotic stability and exponential stability of HHNNs, respectively; in [7], by using coincidence degree theory and Lyapunov functional, authors studied the existence and global exponential stability of periodic solutions for delayed HHNNs, respectively; in [8], the author obtained sufficient conditions on the existence and exponential stability of anti-periodic solutions for HHNNs; in [9, 10], by using a fixed point theorem, Lyapunov functional method and differential inequality techniques, authors obtained sufficient conditions on the existence and exponential stability of almost periodic solutions for HHNNs.

In fact, it is natural and important that systems will contain some information about the derivative of the past state to further describe and model the dynamics for such complex neural reactions [11], many authors investigated the dynamical behaviors of neutral type neural networks. For example, authors in [12–17] studied the stability for different classes of neutral type neural networks; authors in [18] obtained some sufficient conditions for the existence of periodic solutions for neutral type cellular neural networks with delays; authors in [19–21] studied almost periodic solutions of several classes of neural networks with neutral delays.

On the other hand, very recently, a leakage delay, which is the time delay in the leakage term of the systems and a considerable factor affecting dynamics for the worse in the systems, is being put to use in the problem of stability for neural networks (see [22, 23]). Such time delays in the leakage term are difficult to handle but has great impact on the dynamical behavior of neural networks. Therefore, it is meaningful to consider neural networks with time delays in leakage terms. For example, authors of [24–27] studied the stability of some classes of neural networks with leakage delays; authors of [28] studied the equilibrium point of two classes fuzzy neural networks with delays in leakage terms; authors of [29] studied the global attractive periodic solutions of BAM neural networks with continuously distributed delays in the leakage term; authors of [30, 31] studied almost periodic solutions of a classes of neural networks with leakage delays.

Also, as we all know that both continuous time and discrete time neural networks have equal importance in various applications. But it is troublesome to study the dynamical properties for continuous and discrete time systems, respectively. Hence, the theory of time scales, which was initialed by Hilger [32] in his Ph.D. thesis to contain both difference and differential calculus in a consistent way, has recently received a lot of attention from many scholars. By choosing the time scale to be the set of real numbers and the set of integers, results on time scales yield results concerning with differential equations and difference equations, respectively. Besides, results on time scales can also be extended to other types of equations, for example, q-difference equations. Therefore, it is significant to study the dynamical behaviors of neural networks on time scales. For instance, in [33], authors studied periodic solutions of BAM neural networks on time scales; in [34], authors studied almost periodic solutions of neural networks on time scales.

In reality, almost periodicity is much universal than periodicity. And the concept of the pseudo-almost periodicity on time scales, which is the central question in this paper, was introduced by Li and Wang [35] in 2012, as a natural generalization of the well-known almost periodicity. However, to the best of our knowledge, there is no paper published on the pseudo almost periodic of high-order Hopfield neural networks with variable delays in leakage terms on time scales.

Motivated by the above, in this paper, we consider the following neutral type high-order Hopfield neural networks with variable delays on time scales:

$$\begin{aligned} x_{i}^{\Delta }(t)= & {} -c_i(t)x_i(t-\tau _i(t))+ \sum ^n_{j=1}a_{ij}(t)f_j(x_j^\Delta (t-\delta _{ij}(t)))\nonumber \\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(t)g_j(x_j(t-\sigma _{ijl}(t)))g_l(x_l(t-\zeta _{ijl}(t))) +I_i(t),\,\,t\in \mathbb {T}, \end{aligned}$$

(1.1)

where $\mathbb {T}$ is an almost periodic time scale, $i=1,2,\ldots ,n$, n corresponds to the number of units in a neural network; $x_i(t)$ corresponds to the state vector of the ith unit at the time t; $c_i(t)$ represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs; $a_{ij}(t)$ and $b_{ijl}(t)$ are the first-order and second-order connection weights of the neural network; $\tau _i(t)>0$ with $t-\tau _i(t)\in \mathbb {T}$ denotes time delay in the leakage term; $\delta _{ij}(t)\ge 0, \sigma _{ijl}(t)\ge 0$, $\zeta _{ijl}(t)\ge 0$ correspond to the transmission delays and satisfy $t-\delta _{ij}(t)\in \mathbb {T}, t-\sigma _{ijl}(t)\in \mathbb {T}$, $t-\zeta _{ijl}(t)\in \mathbb {T}$; $I_i(t)$ denote the external inputs at time t; $f_j$ and $g_j$ are the activation functions of signal transmission, $j=1,2,\ldots ,n$.

Remark 1.1

If we take $\mathbb {T}=\mathbb {R}$, then (1.1) reduces to the following form

$$\begin{aligned} x{^\prime }_{i}(t)= & {} -c_i(t)x_i(t-\tau _i(t))+ \sum ^n_{j=1}a_{ij}(t)f_j(x{^\prime }_j(t-\delta _{ij}(t)))\nonumber \\&\,+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(t)g_j(x_j(t-\sigma _{ijl}(t)))g_l(x_l(t-\zeta _{ijl}(t)))\nonumber \\&+\,I_i(t),\quad i=1,2,\ldots ,n,\quad t\in \mathbb {R}; \end{aligned}$$

(1.2)

if we take $\mathbb {T}=\mathbb {Z}$, then (1.1) reduces to the following form

$$\begin{aligned} x_{i}(k+1)-x_{i}(k)= & {} -\,c_i(k)x_i(k-\tau _i(k))+ \sum ^n_{j=1}a_{ij}(k)f_j(x_j(k+1-\delta _{ij}(k+1))\nonumber \\&\,-\,x_j(k-\delta _{ij}(k)))\nonumber \\&\,+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(k)g_j(x_j(k-\sigma _{ijl}(k)))g_l(x_l(k-\zeta _{ijl}(k)))\nonumber \\&\,+\,I_i(k),\quad i=1,2,\ldots ,n,\quad k\in \mathbb {Z}. \end{aligned}$$

(1.3)

To the best of our knowledge, there is no paper published on the existence and exponential stability of pseudo almost periodic solutions for (1.2) and (1.3).

Our main purpose of this paper is to study the existence and global exponential stability of pseudo almost periodic solutions for (1.1). Our results of this paper are completely new even if the time scale $\mathbb {T}=\mathbb {R}$ or $\mathbb {Z}$. Our results show that the existence and exponential stability of almost periodic solutions for system (1.1) not only depends on the delays in the leakage term, but also depends on the neutral terms in the network. Our results also show that the continuous-time neural network (1.2) and its discrete-time analogue (1.3) have the same dynamical behaviors, which provides a theoretical basis for the numerical simulation of continuous-time neural network system (1.2).

For convenience, we denote $[a,b]_\mathbb {T}=\{t| t\in [a, b]\cap \mathbb {T}\}$. For a bounded function $f:\mathbb {T}\rightarrow \mathbb {R}$, denote $f^+=\sup \limits _{t\in \mathbb {T}}|f(t)|, f^-=\inf \limits _{t\in \mathbb {T}}|f(t)|$. We denote by $\mathbb {R}$ the set of real numbers, by $\mathbb {R}^+$ the set of positive real numbers, by $\mathbb {E}^n$ a real Banach space with the norm $||\cdot ||$, by D a subset of $\mathbb {E}^n$ and by $BC(\mathbb {T}\times D,\mathbb {E}^n)$ the set of all $\mathbb {E}^n$-valued bounded continuous functions.

The initial condition of (1.1) is the following

$$\begin{aligned} x_{i}(s)=\varphi _{i}(s),\quad x_{i}^\Delta (s)=\varphi _{i}^\Delta (s),\quad s\in [-\theta ,0]_\mathbb {T},\,\, \end{aligned}$$

where $\theta = \max \big \{\max \limits _{1\le i\le n}\tau _i^+, \max \limits _{(i,j)}\{\delta _{ij}^+, \sigma _{ijl}^+, \zeta _{ijl}^+\}\big \}$, $\varphi _i\in C^1([-\theta ,0]_{\mathbb {T}}, \mathbb {R})$, $i=1,2,\ldots ,n$.

This paper is organized as follows: In Sect. 2, we introduce some notations and definitions and state some preliminary results which are needed in later sections. In Sect. 3, we establish some sufficient conditions for the existence of pseudo almost periodic solutions of (1.1) and prove that the pseudo almost periodic solution is globally exponentially stable. In Sect. 4, we give an example to illustrate the feasibility of our results obtained in previous sections.

2 Preliminaries

In this section, we introduce some definitions and state some preliminary results.

Definition 2.1

[36] Let $\mathbb {T}$ be a nonempty closed subset (time scale) of $\mathbb {R}$. The forward and backward jump operators $\sigma , \rho :\mathbb {T}\rightarrow \mathbb {T}$ and the graininess $\mu :\mathbb {T}\rightarrow \mathbb {R}_+$ are defined, respectively, by

$$\begin{aligned} \sigma (t)=\inf \{s\in \mathbb {T}:s>t\},\,\,\,\, \rho (t)=\sup \{s\in \mathbb {T}:s<t\}\,\,\,\,\mathrm{and}\,\,\,\,\mu (t)=\sigma (t)-t. \end{aligned}$$

Lemma 2.1

[36] Assume that $p,q:\mathbb {T}\rightarrow \mathbb {R}$ are two regressive functions, then

(i):

$e_0(t,s)\equiv 1$ and $e_p(t,t)\equiv 1$;

(ii):

$e_p(t,s)=\frac{1}{e_p(s,t)}=e_{\ominus p}(s,t)$;

(iii):

$e_p(t,s)e_p(s,r)=e_p(t,r)$;

(iv):

$(e_{p}(t,s))^\Delta =p(t)e_{p}(t,s)$.

Lemma 2.2

[36] Let f, g be $\Delta$-differentiable functions on T, then

(i):

$(\nu _{1} f+\nu _{2} g)^{\Delta }=\nu _{1} f^{\Delta }+\nu _{2} g^{\Delta }$, for any constants $\nu _{1},\nu _{2}$;

(ii):

$(fg)^{\Delta }(t)=f^{\Delta }(t)g(t)+f(\sigma (t))g^{\Delta }(t) =f(t)g^{\Delta }(t)+f^{\Delta }(t)g(\sigma (t))$;

Lemma 2.3

[36] Assume that $p(t)\ge 0$ for $t\ge s$, then $e_{p}(t,s)\ge 1$.

Definition 2.2

[36] A function $p: \mathbb {T}\rightarrow \mathbb {R}$ is called regressive provided $1+\mu (t)p(t)\ne 0$ for all $t\in \mathbb {T}^k$; $p: \mathbb {T}\rightarrow \mathbb {R}$ is called positively regressive provided $1+\mu (t)p(t)>0$ for all $t\in \mathbb {T}^k$. The set of all regressive and rd-continuous functions $p:\mathbb {T} \rightarrow \mathbb {R}$ will be denoted by $\mathcal {R}=\mathcal {R}(\mathbb {T}, \mathbb {R})$ and the set of all positively regressive functions and rd-continuous functions will be denoted by $\mathcal {R}^+=\mathcal {R}^+(\mathbb {T}, \mathbb {R})$.

Lemma 2.4

[36] Suppose that $p\in \mathcal {R}^{+}$, then

(i):

$e_{p}(t,s)>0$,   for all $t,s\in \mathbb {T}$;

(ii):

if $p(t)\le q(t)$    for all $t\ge s, t,s\in \mathbb {T}$, then $e_{p}(t,s)\le e_{q}(t,s)$ for all $t \ge s$.

Lemma 2.5

([36]) If $p\in \mathcal {R}$ and $a,b,c\in \mathbb {T}$, then

$$\begin{aligned}{}[e_p(c,\cdot )]^{\Delta }=-p[e_p(c,\cdot )]^{\sigma } \end{aligned}$$

and

$$\begin{aligned} \int _a^{b}p(t)e_p(c,\sigma (t))\Delta t=e_p(c,a)-e_p(c,b). \end{aligned}$$

Lemma 2.6

[36] Let $a\in \mathbb {T}^{k}, b\in \mathbb {T}$ and assume that $f:\mathbb {T}\times \mathbb {T}^k\rightarrow \mathbb {R}$ is continuous at (t, t), where $t\in \mathbb {T}^k$ with $t>a$. Also assume that $f^\Delta (t,\cdot )$ is rd-continuous on $[a, \sigma (t)]$. Suppose that for each $\varepsilon >0$, there exists a neighborhood U of $\tau \in [a, \sigma (t)]$ such that

$$\begin{aligned} |f(\sigma (t),\tau )-f(s,\tau )-f^\Delta (t,\tau )(\sigma (t)-s)|\le \varepsilon |\sigma (t)-s|,\quad \forall s\in U, \end{aligned}$$

where $f^\Delta$ denotes the derivative of f with respect to the first variable. Then

(i):

$g(t):=\int _a^tf(t,\tau )\Delta \tau$ implies $g^\Delta (t):=\int _a^tf^\Delta (t,\tau )\Delta \tau +f(\sigma (t),t)$;

(ii):

$h(t):=\int _t^bf(t,\tau )\Delta \tau$ implies $h^\Delta (t):=\int _t^bf^\Delta (t,\tau )\Delta \tau -f(\sigma (t),t)$.

In the following, we recall some definitions, notations and basic results of almost periodicity and pseudo almost periodicity on time scales. For more details, we refer the reader to [35, 37].

Definition 2.3

[37] A time scale $\mathbb {T}$ is called an almost periodic time scale if

$$\begin{aligned} \Pi :=\big \{\tau \in \mathbb {R}: t\pm \tau \in \mathbb {T},\,\forall t\in \mathbb {T}\big \}\ne \{0\}. \end{aligned}$$

In this paper, we restrict our discussion on almost periodic time scales.

Definition 2.4

[37] Let $\mathbb {T}$ be an almost periodic time scale. A function $f(t):\mathbb {T}\rightarrow \mathbb {R}^{n}$ is said to be almost periodic on $\mathbb {T}$, if for any $\varepsilon >0$, the set

$$\begin{aligned} E(\varepsilon ,f)=\{\tau \in \Pi :|f(t+\tau )-f(t)|<\varepsilon , \,\forall \, t\in \mathbb {T}\} \end{aligned}$$

is relatively dense, that is, for any $\varepsilon >0$, there exists a constant $l(\varepsilon )>0$ such that each interval of length $l(\varepsilon )$ contains at least one $\tau \in E(\varepsilon ,f)$ such that

$$\begin{aligned} |f(t+\tau )-f(t)|<\varepsilon , \quad \forall \, t\in \mathbb {T}. \end{aligned}$$

The set $E(\varepsilon ,f)$ is called the $\varepsilon$-translation set of f(t), $\tau$ is called the $\varepsilon$-translation number of f(t), and $l(\varepsilon )$ is called the inclusion of $E(\varepsilon ,f)$.

Definition 2.5

[37] Let $\mathbb {T}$ be an almost periodic time scale. A function $f\in C(\mathbb {T}\times D,\mathbb {E}^n)$ is said to be almost periodic in t uniformly for $x\in D$, if for any $\varepsilon >0$ and for each compact subset $S\subset D$, there exists a constant $l(\varepsilon )>0$ such that each interval of length $l(\varepsilon )$ contains at least one $\tau \in E(\varepsilon ,f)$ such that

$$\begin{aligned} |f(t+\tau , x)-f(t, x)|<\varepsilon , \qquad \forall \, t\in \mathbb {T},\quad x\in S. \end{aligned}$$

In the following, we introduce some notations

$$\begin{aligned} AP(\mathbb {T}\times D)_{n}= & {} \{f\in C(\mathbb {T}\times D,\mathbb {E}^{n}):\,\,f \text { is almost periodic in } t \text { uniformly for } x\in D\},\\ AP(\mathbb {T})_{n}= & {} \{f\in C(\mathbb {T},\mathbb {E}^{n}):\,\,f \text { is almost periodic}\},\\ PAP_{0}(\mathbb {T})_{n}= & {} \bigg \{f\in BC(\mathbb {T},\mathbb {E}^{n}): f \text { is } \Delta -\text { measurable such that}\\&\lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}|f(s)|\Delta s=0, \text {where} \,\,t_{0}\in \mathbb {T},r\in \Pi \bigg \},\\ PAP_{0}(\mathbb {T}\times D)_{n}= & {} \bigg \{f\in BC(\mathbb {T}\times D,\mathbb {E}^{n}): \,f(\cdot ,x)\in PAP_{0}(\mathbb {T})\,\text {for each}\,\,x\in D\,\text {and }\\&\lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}\Vert f(s,x)\Vert \Delta s=0\,\text {uniformly for }\,x\in D,\\&\text {where}\,\,t_{0}\in \mathbb {T},r\in \Pi \bigg \}. \end{aligned}$$

Definition 2.6

[35] Let $\mathbb {T}$ be an almost periodic time scale. A function $f\in C(\mathbb {T}\times D,\mathbb {E}^n)$ is said to be pseudo almost periodic in t uniformly for $x\in D$, if $f=g+\varphi$, where $g\in AP(\mathbb {T}\times D)_{n}$ and $\varphi \in PAP_{0}(\mathbb {T}\times D)_{n}$. We denote by $PAP(\mathbb {T}\times D)_{n}$ the set of all such functions.

Definition 2.7

[35] Let $\mathbb {T}$ be an almost periodic time scale. A function $f\in C(\mathbb {T},\mathbb {E}^n)$ is said to be pseudo almost periodic, if $f=g+\varphi$, where $g\in AP(\mathbb {T})_{n}$ and $\varphi \in PAP_{0}(\mathbb {T})_{n}$. We denote by $PAP(\mathbb {T})_{n}$ the set of all such functions.

Definition 2.8

[35] Let $X\in \mathbb {R}^{n}$ and A(t) be a $n\times n$ matrix-valued function on $\mathbb {T}$, the linear system

$$\begin{aligned} X^{\Delta }(t)=A(t)X(t),\,\,\,t\in \mathbb {T} \end{aligned}$$

(2.1)

is said to admit an exponential dichotomy on $\mathbb {T}$ if there exist positive constants $k_i,\alpha _i,i=1,2$, projection P and the fundamental solution matrix X(t) of (2.1) satisfying

$$\begin{aligned} \displaystyle&|X(t)PX^{-1}(s)|\le k_1e_{\ominus \alpha _1}(t,s),\qquad s,\; t\in \mathbb {T}, \; t\ge s,\\ \displaystyle&|X(t)(I-P)X^{-1}(s)|\le k_2e_{\ominus \alpha _2}(s,t),\qquad s,\; t\in \mathbb {T}, \; t\le s, \end{aligned}$$

where $|\cdot |$ is a matrix norm on $\mathbb {T}$, that is, if $A=(a_{ij})_{n\times m},$, then we can take $|A|=\big (\sum \limits _{i=1}^n\sum \limits _{j=1}^m|a_{ij}|^2\big )^{\frac{1}{2}}$.

Lemma 2.7

[35] Suppose that A(t) is almost periodic and $g\in PAP(\mathbb {T})_n$, (2.1) admits an exponential dichotomy, then the following system:

$$\begin{aligned} X^{\Delta }(t)=A(t)X(t)+g(t) \end{aligned}$$

has a unique bounded solution $X\in PAP(\mathbb {T})_n$ and X(t) is expressed as follows

$$\begin{aligned} X(t)=\int _{-\infty }^{t}X(t)PX^{-1}(\sigma (s))g(s)\Delta s-\int ^{+\infty }_{t}X(t)(I-P)X^{-1}(\sigma (s))g(s)\Delta s, \end{aligned}$$

where X(t) is the fundamental solution matrix of (2.1).

Lemma 2.8

[37] Let $c_i(t)>0$ and $-c_i(t)\in \mathcal {R}^+$, $\forall \ t\in \mathbb {T}$. If

$$\begin{aligned} \min \limits _{1\le i\le n}\big \{\inf \limits _{t\in \mathbb {T}}c_i(t)\big \}=\widetilde{m}>0, \end{aligned}$$

then the linear system

$$\begin{aligned} x^\Delta (t)=\mathrm{diag}\big (- c_1(t),- c_2(t),\ldots ,- c_n(t)\big )x(t) \end{aligned}$$

(2.2)

admits an exponential dichotomy on $\mathbb {T}$.

Definition 2.9

Let $x^*(t)=(x_1^*(t), x_2^*(t), \ldots , x_n^*(t))^T$ be a pseudo almost periodic solution of (1.1) with initial value $\varphi ^*(s)=(\varphi _1^*(s), \varphi _2^*(s), \ldots , \varphi _n^*(s))^T$. If there exist positive constants $\lambda$ with $\ominus \lambda \in \mathcal {R}^{+}$ and $M>1$ such that such that for an arbitrary solution $x(t)=(x_1(t), x_2(t), \ldots , x_n(t))^T$ of (1.1) with initial value $\varphi (s)=(\varphi _1(s), \varphi _2(s), \ldots , \varphi _n(s))^T$ satisfies

$$\begin{aligned} ||x-x^*||\le M||\varphi -\varphi ^*||e_{\ominus \lambda }(t,t_0),\quad t_0\in [-\theta ,\infty )_{\mathbb {T}},\,t\ge t_0. \end{aligned}$$

Then the solution $x^*(t)$ is said to be globally exponentially stable.

3 Main Results

In this section, we state and prove our main results.

Let $\mathbb {X}^*=\{f| f, f^\Delta \in PAP(\mathbb {T}, \mathbb {R}^n) \}$ with the norm $||f||_{\mathbb {X}^*}=\max \{|f|_1, |f^\Delta |_1\}$, where $|f|_1=\max \limits _{1\le i\le n}f_i^+, |f^\Delta |_1=\max \limits _{1\le i\le n}(f_i^\Delta )^+$. Then $\mathbb {X}^*$ is a Banach space. Let $\varphi ^0(t)=(\varphi _1^0(t),\varphi _2^0(t),\ldots , \varphi _n^0(t))^T$, where $\varphi _{i}^0(t)$ $=\int _{-\infty }^te_{-a_i}(t,\sigma (s))I_i(s)\Delta s,$ $i=1,2,\ldots ,n$ and L be a constant satisfying $L\ge \max \big \{||\varphi ^0||_{\mathbb {X}^*}, \max \limits _{1\!\le \! j\le n}\{|f_j(0)|\}, \max \limits _{1\le j\le n}\{|h_j(0)|\}, \max \limits _{1\le j\le n}\{|g_j(0)|\}\big \}$.

Theorem 3.1

Suppose that

$(H_1)$ :

$c_i\in C(\mathbb {T},\mathbb {R}^+)$ with $-c_{i}\in \mathcal {R}^{+}$ is almost periodic and $a_{ij},\,b_{ijl},\,I_i\in C(\mathbb {T},\mathbb {R})$, $\tau _i,\,\delta _{ij},\, \sigma _{ijl},\,\zeta _{ijl}\in C(\mathbb {T},\mathbb {R}^+)$ are pseudo almost periodic, where $i,j,l=1,2,\ldots ,n$;

$(H_2)$ :

$f_j, g_j\in C(\mathbb {R},\mathbb {R})$ and there exist positive constants $N_j,\,L_j,\,H_j$ such that $|g_j(u)|\le N_j$, $|f_j(u)-f_j(v)|\le L_j|u-v|,\,|g_j(u)-g_j(v)|\le H_j|u-v|$, where $u, v\in \mathbb {R}, j=1,2,\ldots ,n$;

$(H_3)$ :

$\max \limits _{1\le i\le n}\big \{\frac{\theta _i}{c_i^-}, \big (1+\frac{c_i^+}{c_i^-}\big )\theta _i\big \}\le \frac{1}{2}$, $\max \limits _{1\le i\le n}\big \{\frac{\gamma _i}{c_i^-}, \big (1+\frac{c_i^+}{c_i^-}\big )\gamma _i\big \}<1$, where $\theta _i=c_i^+\tau _i^++\sum \limits ^n_{j=1}\Big (a_{ij}^+(L_j$ $+\frac{1}{2})+\sum \limits _{l=1}^{n}b_{ijl}^+N_l(H_j+\frac{1}{2})\Big )$, $\gamma _i=c_i^+\tau _i^++\sum \limits ^n_{j=1}\Big (a_{ij}^+L_j+\sum \limits _{l=1}^{n}b_{ijl}^+(N_jH_l+H_jN_l)\Big )$, $i=1,2,\ldots ,n$,

then (1.1) has a unique pseudo almost periodic solution in $\mathbb {X}_0=\big \{\varphi \in \mathbb {X}^*\big |\, ||\varphi -\varphi ^0||_{\mathbb {X}^*}\le L\big \}$.

Proof

For any given $\varphi \in \mathbb {X}^*$, we consider the following system:

$$\begin{aligned} x_{i}^{\Delta }(t)=-c_i(t)x_i(t)+F_i(t, \varphi ) +I_i(t), \end{aligned}$$

(3.1)

where

$$\begin{aligned} F_i(t, \varphi )= & {} c_i(t)\int _{t-\tau _i(t)}^t\varphi _i^\Delta (s)\Delta s+\sum ^n_{j=1}a_{ij}(t)f_j(\varphi _j^\Delta (t-\delta _{ij}(t)))\\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(t)g_j(\varphi _j(t-\sigma _{ijl}(t)))g_l(\varphi _l(t-\zeta _{ijl}(t))),\quad i=1,2,\ldots ,n. \end{aligned}$$

Since $\min \limits _{1\le i\le n}\big \{\inf c_{i}(t)\big \}>0, t\in \mathbb {T}$, it follows from Lemma 2.8 that the linear system

$$\begin{aligned} x_{i}^{\Delta }(t)=-c_{i}(t)x_{i}(t),\quad i=1,2,\ldots ,n \end{aligned}$$

admits an exponential dichotomy on $\mathbb {T}$. Thus, by Lemma 2.7, we obtain that system (3.1) has exactly one pseudo almost periodic solution as follows

$$\begin{aligned} x^{\varphi }_i(t)= & {} \int _{-\infty }^{t}e_{-c_{i}}(t,\sigma (s))\big (F_i(s, \varphi )+I_i(s)\big )\Delta s, \quad i=1,2,\ldots ,n. \end{aligned}$$

For $\varphi \in \mathbb {X}^*$, then $||\varphi ||_{\mathbb {X}^*}\le ||\varphi -\varphi _0||_{\mathbb {X}^*}+||\varphi _0||_{\mathbb {X}^*}\le 2L$. Define the following operator

$$\begin{aligned} \Phi : \mathbb {X}^*\rightarrow \mathbb {X}^*, \,\,(\varphi _1, \varphi _2, \ldots , \varphi _n)^T\rightarrow (x_1^\varphi , x_2^\varphi ,\ldots , x_n^\varphi )^T. \end{aligned}$$

First we show that for any $\varphi \in \mathbb {X}^*$, we have $\Phi \varphi \in \mathbb {X}^*$. Note that

$$\begin{aligned} |F_i(s,\varphi )|= & {} \Bigg |c_i(s)\int _{s-\tau _i(s)}^s\varphi _i^\Delta (\vartheta )\Delta \vartheta +\sum ^n_{j=1}a_{ij}(s)f_j(\varphi _j^\Delta (s-\delta _{ij}(s)))\\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(s)g_j(\varphi _j(s-\sigma _{ijl}(s)))g_l(\varphi _l(s-\zeta _{ijl}(s)))\Bigg |\nonumber \\\le & {} c_i^+\tau _i^+||\varphi ||_{\mathbb {X}^*}+ \sum ^n_{j=1}a_{ij}^+\Bigg (\big |f_j(\varphi _j^\Delta (s-\delta _{ij}(s)))-f_j(0)\big |+\left| f_j(0)\right| \Bigg )\\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}^+N_l\Big (\big |g_j(\varphi _j(s-\sigma _{ijl}(s)))-g_j(0)\big |+\big |g_j(0)\big |\Big ) \\\le & {} \Big (c_i^+\tau _i^++\sum ^n_{j=1}a_{ij}^+L_j\Big )||\varphi ||_{\mathbb {X}^*} +\sum ^n_{j=1}a_{ij}^+\big |f_j(0)\big |\\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}^+N_lH_j||\varphi ||_{\mathbb {X}^*}+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}^+N_l|g_j(0)| \\\le & {} 2L\Bigg [c_i^+\tau _i^++\sum ^n_{j=1}\Bigg (a_{ij}^ +\left( L_j+\frac{1}{2}\right) +\sum _{l=1}^{n}b_{ijl}^+N_l\left( H_j+\frac{1}{2}\right) \Bigg )\Bigg ]. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \big |\big (\Phi (\varphi -\varphi ^0)\big )_i(t)\big |= & {} \Big |\int _{-\infty }^te_{-c_i}(t,\sigma (s))F_i(s,\varphi )\Delta s\Big |\\\le & {} \int _{-\infty }^te_{-c_i}(t,\sigma (s))|F_i(s,\varphi )|\Delta s\\\le & {} 2L\int _{-\infty }^te_{-c_i^-}(t,\sigma (s))\sum ^n_{j=1}\Bigg [c_i^+\tau _i^+ +\sum ^n_{j=1}\Bigg (a_{ij}^+\bigg (L_j+\frac{1}{2}\bigg )\\&+\sum _{l=1}^{n}b_{ijl}^+N_l\bigg (H_j+\frac{1}{2}\bigg )\Bigg )\Bigg ]\Delta s\\\le & {} \frac{2L\theta _i}{c_i^-},\quad i=1,2,\ldots ,n. \end{aligned}$$

On the other hand, for $i=1,2,\ldots ,n$, we have

$$\begin{aligned} \bigg |\bigg (\Phi \bigg (\varphi -\varphi ^0\bigg )\bigg )^\Delta _i(t)\bigg |= & {} \Bigg |\bigg (\int _{-\infty }^te_{-c_i}(t,\sigma (s))F_i(s,\varphi )\Delta s\bigg )^\Delta _t\Big |\\= & {} \Bigg |F_i(t,\varphi )-c_i(t)\int _{-\infty }^te_{-c_i}(t,\sigma (s))F_i(s,\varphi )\Delta s\Bigg |\\\le & {} |F_i(t,\varphi )|+|c_i(t)| \int _{-\infty }^te_{-c_i}(t,\sigma (s))|F_i(s,\varphi )|\Delta s\\\le & {} 2L\theta _i\bigg (1+\frac{c_i^+}{c_i^-}\bigg ). \end{aligned}$$

In view of $(H_3)$, we have

$$\begin{aligned} ||\Phi \varphi -\varphi ^0||_{\mathbb {X}^*}\le & {} 2L\max \limits _{1\le i\le n}\bigg \{\frac{\theta _i}{c_i^-}, \bigg (1+\frac{c_i^+}{c_i^-}\bigg )\theta _i\bigg \}\le L, \end{aligned}$$

that is, $\Phi \phi \in \mathbb {X}_0$. Next, we show that $\Phi$ is a contraction. For $\varphi =(\varphi _1, \varphi _2, \ldots , \varphi _n)^T$, $\psi =(\psi _1, \psi _2, \ldots , \psi _n)^T \in \mathbb {X}_0$, for $i=1,2,\ldots ,n$, denote by

$$\begin{aligned} G_i(s,\varphi ,\psi )= & {} c_i(s)\int _{s-\tau _i(s)}^s\big (\varphi ^\Delta (\theta )-\psi ^\Delta (\theta )\big )\Delta \theta \\&+\sum ^n_{j=1}a_{ij}(s)\big (f_j(\varphi ^\Delta _j(s-\delta _{ij}(s))) -f_j(\psi ^\Delta _j(s-\delta _{ij}(s)))\big ) \end{aligned}$$

and

$$\begin{aligned} K_i(s,\varphi ,\psi )= & {} \sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(s)\big (g_j(\varphi _j(s-\sigma _{ijl}(s)))g_l(\varphi _l(s-\zeta _{ijl}(s)))\\&-\,g_j(\psi _j(s-\sigma _{ijl}(s)))g_l(\psi _l(s-\zeta _{ijl}(s)))\big ). \end{aligned}$$

Note that, for $i=1,2,\ldots ,n$,

$$\begin{aligned} |G_i(s,\varphi ,\psi )|= & {} \bigg |c_i(s)\int _{s-\tau _i(s)}^s\big (\varphi ^\Delta (\theta )-\psi ^\Delta (\theta )\big )\Delta \theta \\&+\sum ^n_{j=1}a_{ij}(s)\big (f_j(\varphi ^\Delta _j(s-\delta _{ij}(s))) -f_j(\psi ^\Delta _j(s-\delta _{ij}(s)))\big )\bigg |\\\le & {} \left( c_i^+\tau _i^++\sum ^n_{j=1}a_{ij}^+L_j\right) ||\varphi -\psi ||_{\mathbb {X}^*} \end{aligned}$$

and

$$\begin{aligned} |K_i(s,\varphi ,\psi )|= & {} \left| \sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(s)\big (g_j(\varphi _j(s-\sigma _{ijl}(s)))g_l(\varphi _l(s-\zeta _{ijl}(s)))\right. \\&\left. \,-\,g_j(\psi _j(s-\sigma _{ijl}(s)))g_l(\psi _l(s-\zeta _{ijl}(s)))\big )\right| \nonumber \\\le & {} \sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}^+\bigg [\big |g_j(\varphi _j(s{-}\sigma _{ijl}(s)))\big |\big |g_l(\varphi _l(s{-}\zeta _{ijl}(s))) -\,g_l(\psi _l(s-\zeta _{ijl}(s)))\big |\\&+\,\big |g_j(\varphi _j(s-\sigma _{ijl}(s)))-g_j(\psi _j(s-\sigma _{ijl}(s)))\big |\big |g_l(\psi _l(s-\zeta _{ijl}(s)))\big |\bigg ]\\\le & {} \sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}^+\big (N_jH_l+H_jN_l\big )||\varphi -\psi ||_{\mathbb {X}^*}. \end{aligned}$$

Then, we have

$$\begin{aligned} \big |(\Phi \varphi -\Phi \psi )_i(t)\big |= & {} \Bigg |\int _{-\infty }^te_{-c_i}(t,\sigma (s))\big (G_i(s,\varphi ,\psi )+K_i(s,\varphi ,\psi )\big )\Delta s\Bigg |\\\le & {} \int _{-\infty }^te_{-c_i}(t,\sigma (s)) \Bigg (c_i^+\tau _i^++\sum \limits ^n_{j=1}\big (a_{ij}^+L_j\nonumber \\&+\sum \limits _{l=1}^{n}b_{ijl}^+(N_jH_l+H_jN_l)\big )\Bigg )\Delta s||\varphi -\psi ||_{\mathbb {X}^*}\\\le & {} \frac{\gamma _i}{c_i^-}||\varphi -\psi ||_{\mathbb {X}^*},\quad i=1,2,\ldots ,n \end{aligned}$$

and

$$\begin{aligned} \big |(\Phi \phi -\Phi \zeta )^\Delta _i(t)\big |= & {} \Bigg |\Bigg (\int _{-\infty }^te_{-c_i}(t,\sigma (s)) \big (G_i(s,\varphi ,\psi )+K_i(s,\varphi ,\psi )\big )^\Delta _t \Bigg )\Bigg |\\= & {} \Bigg |G_i(t,\varphi ,\psi )+K_i(t,\varphi ,\psi )\\&-\,c_i(t)\int _{-\infty }^te_{-c_i}(t,\sigma (s))\big (G_i(s,\varphi ,\psi )+K_i(s,\varphi ,\psi )\big )\Delta s\Bigg |\\\le & {} |G_i(t,\varphi ,\psi )|+|K_i(t,\varphi ,\psi )|\\&+\,|c_i(t)|\int _{-\infty }^te_{-c_i}(t,\sigma (s))\big |G_i(s,\varphi ,\psi )+K_i(s,\varphi ,\psi )\big |\Delta s\\\le & {} \bigg (1+\frac{c_i^+}{c_i^-}\bigg )\gamma _i||\varphi -\psi ||_{\mathbb {X}^*}, \quad i=1,2,\ldots ,n. \end{aligned}$$

By $(H_3)$, we have that $||\Phi \varphi -\Phi \psi ||<||\varphi -\psi ||$. Hence, $\Phi$ is a contraction. Therefore, $\Phi$ has a fixed point in $\mathbb {X}_0$, that is, (1.1) has a unique pseudo almost periodic solution in $\mathbb {X}_0$. This completes the proof of Theorem 3.1. $\square$

Theorem 3.2

Let $(H_1)$-$(H_3)$ hold. Then the pseudo almost periodic solution of system (1.1) is globally exponentially stable.

Proof

According to Theorem 3.1, we know that (1.1) has a pseudo almost periodic solution $x(t)=\big (x_1(t),x_2(t),\ldots ,x_n(t)\big )^T$ with the initial condition $\varphi (s)=(\varphi _1(s), \varphi _2(s), \ldots , \varphi _n(s))^T$. Suppose that $y(t)=\big (y_1(t), y_2(t),\ldots ,y_n(t)\big )^T$ is an arbitrary solution of (1.1) with the initial condition $\psi (s)=(\psi _1(s), \psi _2(s), \ldots , \psi _n(s))^T$. Denote $u(t)=(u_1(t),u_2(t),\ldots ,u_n(t))^T$, where $u_i(t)=y_i(t)-x_i(t)$, $i=1,2,\ldots ,n$. Then it follows from (1.1) that

$$\begin{aligned} u_i^\Delta (t)= & {} -c_i(t)u_i(t-\tau _i(t))+\sum ^n_{j=1}a_{ij}(t)\big (f_j(y_j^\Delta (t-\delta _{ij}(t)))-f_j(x_j^\Delta (t-\delta _{ij}(t)))\big )\nonumber \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(t)\big (g_j(y_j(t-\sigma _{ijl}(t)))g_l(y_l(t-\zeta _{ijl}(t)))\nonumber \\&\,-\,g_j(x_j(t-\sigma _{ijl}(t)))g_l(x_l(t-\zeta _{ijl}(t)))\big ),\,i=1,2,\ldots ,n. \end{aligned}$$

(3.2)

The initial condition of (3.2) is

$$\begin{aligned} \psi _i(s)=\varphi _i(s)-\psi _i(s),\,\psi ^\Delta _i(s)=\varphi ^\Delta _i(s)-\psi _i^\Delta (s),\,s\in [-\theta ,0]_\mathbb {T},\quad i=1,2,\ldots ,n. \end{aligned}$$

Rewrite (3.2) in the form

$$\begin{aligned} u_i^\Delta (t)= & {} -c_i(t)u_i(t)+c_i(t)\int _{t-\tau _i(t))}^tu_i^\Delta (s)\Delta s\nonumber \\&+\sum ^n_{j=1}a_{ij}(t)\big (f_j(y_j^\Delta (t-\delta _{ij}(t)))-f_j(x_j^\Delta (t-\delta _{ij}(t)))\big )\nonumber \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(t)\big (g_j(y_j(t-\sigma _{ijl}(t)))g_l(y_l(t-\zeta _{ijl}(t))) \nonumber \\&\,-\,g_j(x_j(t-\sigma _{ijl}(t)))g_l(x_l(t-\zeta _{ijl}(t)))\big ),\quad i=1,2,\ldots ,n. \end{aligned}$$

(3.3)

Then, for $i=1,2,\ldots ,n$ and $t\ge t_0, t_0\in [-\theta ,0]_\mathbb {T}$, we have

$$\begin{aligned} u_i(t)= & {} u_i(t_0)e_{-c_i}(t,t_0)+\int _{t_0}^{t}e_{-c_i}(t,\sigma (s))\Bigg \{c_i(s)\int _{s-\tau _i(s))}^su_i^\Delta (\vartheta )\Delta \vartheta \nonumber \\&+\,\sum ^n_{j=1}a_{ij}(s)\big (f_j(y_j^\Delta (s-\delta _{ij}(s)))-f_j(x_j^\Delta (s-\delta _{ij}(s)))\big )\nonumber \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{ijl}(s)\big (g_j(y_j(s-\sigma _{ijl}(s)))g_l(y_l(s-\zeta _{ijl}(s))) \nonumber \\&\,-\,g_j(x_j(s-\sigma _{ijl}(s)))g_l(x_l(s-\zeta _{ijl}(s)))\big )\Bigg \}\Delta s. \end{aligned}$$

(3.4)

For $\omega \in \mathbb {R}$, let $\Gamma _{i}(\omega )$ and $\Theta _{i}(\omega )$ be defined by

$$\begin{aligned} \Gamma _{i}(\omega )= & {} c_{i}^{-}-\omega -\exp \{\omega \sup \limits _{s\in \mathbb {T}}\mu (s)\}\Bigg (c_{i}^{+}\tau _{i}^{+}\exp \{\omega \tau _{i}^{+}\}+\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} \exp \{\omega \delta _{ij}^{+}\}\\&+\,\sum \limits _{j=1}^{n}b_{ijl}^{+}N_lH_{j} \exp \{\omega \sigma _{ijl}^{+}\}+\sum \limits _{j=1}^{n}b_{ijl}^{+}N_jH_{l} \exp \{\omega \zeta _{ijl}^{+}\}\Bigg ) \end{aligned}$$

and

$$\begin{aligned} \Theta _{i}(\omega )= & {} c_{i}^{-}-\omega -\bigg (c_{i}^{+}\exp \{\omega \sup \limits _{s\in \mathbb {T}}\mu (s)\}+c_{i}^{-}-\omega \big )\bigg (c_{i}^{+}\tau _{i}^{+}\exp \{\omega \tau _{i}^{+}\}\\&+\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} \exp \{\omega \delta _{ij}^{+}\}+\sum \limits _{j=1}^{n}b_{ijl}^{+}N_lH_{j} \exp \{\omega \sigma _{ijl}^{+}\}+\sum \limits _{j=1}^{n}b_{ijl}^{+}N_jH_{l} \exp \{\omega \zeta _{ijl}^{+}\}\bigg ), \end{aligned}$$

where $i=1,2,\ldots ,n$. In view of $(H_{3})$, for $i=1,2,\ldots ,n$, we have

$$\begin{aligned} \Gamma _{i}(0)=c_{i}^{-}-\Bigg (c_{i}^{+}\tau _{i}^{+}+\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} +\sum \limits _{j=1}^{n}b_{ijl}^{+}(N_lH_{j}+N_jH_{l})\Bigg )> 0, \end{aligned}$$

and

$$\begin{aligned} \Theta _{i}(0)=c_{i}^{-}-(c_{i}^{+}+c_{i}^{-})\Bigg (c_{i}^{+}\tau _{i}^{+}+\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} +\sum \limits _{j=1}^{n}b_{ijl}^{+}(N_lH_{j}+N_jH_{l})\Bigg )>0. \end{aligned}$$

Since $\Gamma _{i}(\omega ), \Theta _{i}(\omega )$ are continuous on $[0,+\infty )$ and $\Gamma _{i}(\omega ), \Theta _{i}(\omega ) \rightarrow -\infty$, as $\omega \rightarrow +\infty$, so there exist $\omega _{i}, \omega _{i}^{*} > 0$ such that $\Gamma _{i}(\omega _{i})=\Theta _{i}(\omega _{i}^{*})=0$ and $\Gamma _{i}(\omega )> 0$ for $\omega \in (0,\omega _{i})$, $\Theta _{i}(\omega )> 0$ for $\omega \in (0,\omega _{i}^{*}), i=1,2,\ldots ,n$. By choosing a positive constant $a=\min \big \{\omega _{1},\omega _{2},\ldots ,\omega _{n},\omega _{1}^{*},\omega _{2}^{*},\ldots ,\omega _{n}^{*}\big \}$, we have $\Gamma _{i}(a)\ge 0, \Theta _{i}(a)\ge 0, i=1,2,\ldots ,n.$ Hence, we can choose a positive constant $0< \alpha < \min \big \{a,\min \limits _{1\le i \le n}\{c_{i}^{-}\}\big \}$ such that

$$\begin{aligned} \Gamma _{i}(\alpha )>0,\,\,\Theta _{i}(\alpha )>0,\quad i=1,2,\ldots ,n, \end{aligned}$$

which implies that

$$\begin{aligned}&\frac{\exp \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\}}{c_{i}^{-}-\alpha }\bigg (c_{i}^{+}\tau _{i}^{+}\exp \{\alpha \tau _{i}^{+}\} +\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} \exp \{\alpha \delta _{ij}^{+}\}\\&\quad +\sum \limits _{j=1}^{n}b_{ijl}^{+}\big (N_lH_{j} \exp \{\alpha \sigma _{ijl}^{+}\}+N_jH_{l} \exp \{\alpha \zeta _{ijl}^{+}\}\big )\bigg )< 1 \end{aligned}$$

and

$$\begin{aligned}&\left( 1+\frac{c_{i}^{+}\exp \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\}}{c_{i}^{-}-\alpha }\right) \Bigg (c_{i}^{+}\tau _{i}^{+}\exp \{\alpha \tau _{i}^{+}\} +\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} \exp \{\alpha \delta _{ij}^{+}\}\\&\quad +\sum \limits _{j=1}^{n}b_{ijl}^{+}N_lH_{j} \exp \{\alpha \sigma _{ijl}^{+}\}+\sum \limits _{j=1}^{n}b_{ijl}^{+}N_jH_{l} \exp \{\alpha \zeta _{ijl}^{+}\}\Bigg )< 1, \end{aligned}$$

where $i=1,2,\ldots ,n$. Let

$$\begin{aligned} M=\max \limits _{1\le i \le n}\left\{ \frac{c_{i}^{-}}{{c_i^+\tau _i^++\sum \limits ^n_{j=1}\Big (a_{ij}^+L_j +\sum \limits _{l=1}^{n}b_{ijl}^+(N_jH_l+H_jN_l)\Big )}}\right\} . \end{aligned}$$

It follows from $(H_{3})$ that $M>1$. Thus, we can obtain that

$$\begin{aligned} \frac{1}{M}< & {} \frac{\exp \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\}}{c_{i}^{-}-\alpha }\bigg (c_{i}^{+}\tau _{i}^{+}\exp \{\alpha \tau _{i}^{+}\} +\sum \limits _{j=1}^{n}a_{ij}^{+}L_{j} \exp \{\alpha \delta _{ij}^{+}\}\\&+\sum \limits _{j=1}^{n}b_{ijl}^{+}\big (N_lH_{j} \exp \{\alpha \sigma _{ijl}^{+}\}+N_jH_{l} \exp \{\alpha \zeta _{ijl}^{+}\}\big )\bigg ). \end{aligned}$$

Moreover, we have that $e_{\ominus \alpha }(t,t_0)>1$, where $t\in [-\theta ,t_0]_{\mathbb {T}}$. Hence, it is obvious that

$$\begin{aligned} ||u||_{\mathbb {X}^*}\le M e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\quad \forall t\in [-\theta ,t_0]_{\mathbb {T}}. \end{aligned}$$

We claim that

$$\begin{aligned} ||u||_{\mathbb {X}^*}\le M e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\quad \forall t\in (t_0,+\infty )_{\mathbb {T}}. \end{aligned}$$

(3.5)

To prove this claim, we show that for any $p>1$, the following inequality holds

$$\begin{aligned} ||u||_{\mathbb {X}^*}< pM e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\quad \forall t\in (t_0,+\infty )_{\mathbb {T}}, \end{aligned}$$

(3.6)

which implies that, for $i=1,2,\ldots ,n$, we have

$$\begin{aligned} |u_i(t)|< pM e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\quad \forall t\in (t_0,+\infty )_{\mathbb {T}} \end{aligned}$$

(3.7)

and

$$\begin{aligned} |u_i^\Delta (t)|< pM e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\quad \forall t\in (t_0,+\infty )_{\mathbb {T}}. \end{aligned}$$

(3.8)

By way of contradiction, assume that (3.6) does not hold. Firstly, we consider the following two cases.

Case 1 (3.7) is not true and (3.8) is true. Then there exists $t_1\in (t_0,+\infty )_{\mathbb {T}}$ and $i_0\in \{1,2,\ldots ,n\}$ such that

$$\begin{aligned}&|u_{i_0}(t_1)|\ge pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}, \,\,|u_{i_0}(t)|<pM e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\,\, t\in (t_0,t_1)_{\mathbb {T}},\\&|u_{k}(t)|<pM e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\,\,\mathrm {for} \, k\ne i_0,\, \,t\in (t_0,t_1]_{\mathbb {T}}, k=1,2,\dots ,n. \end{aligned}$$

Therefore, there must be a constant $\alpha _1\ge 1$ such that

$$\begin{aligned}&|u_{i_0}(t_1)|= \alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}, \,\,|u_{i_0}(t)|<\alpha _1pM e_{\ominus \alpha }(t,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\,\,\\&\quad t\in (t_0,t_1)_{\mathbb {T}},\\&|u_{k}(t)|<\alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*},\quad \mathrm {for} \, k\ne i_0,\, \,t\in (t_0,t_1]_{\mathbb {T}}, k=1,2,\dots ,n. \end{aligned}$$

Note that, in view of (3.4), we have

$$\begin{aligned} |u_{i_0}(t_1)|= & {} \bigg |u_{i_0}(t_0)e_{-c_{i_0}}(t_1,t_0) +\int _{t_0}^{t_1}e_{-c_{i_0}}(t_1,\sigma (s))\Bigg \{c_{i_0}^+\int _{s-\tau _{i_0}(s))}^su_{i_0}^\Delta (\vartheta )\Delta \vartheta \\&+\sum ^n_{j=1}a_{{i_0}j}(s)\big (f_j(y_j^\Delta (s-\delta _{{i_0}j}(s)))-f_j(x_j^\Delta (s-\delta _{{i_0}j}(s)))\big ) \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}(s)\big (g_j(y_j(s-\sigma _{{i_0}jl}(s)))g_l(y_l(s-\zeta _{{i_0}jl}(s))) \\&-\,g_j(x_j(s-\sigma _{{i_0}jl}(s)))g_l(x_l(s-\zeta _{{i_0}jl}(s)))\big )\Bigg \}\Delta s\bigg |\nonumber \\\le & {} e_{-c_{i_0}}(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}+\alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\\&\times \Bigg |\int _{t_0}^{t_1}e_{-c_{i_0}}(t_1,\sigma (s))e_{\alpha }(t_{1},\sigma (s)) \bigg \{c_{i_0}^+\int _{s-\tau _{i_0}(s))}^se_{\alpha }(\sigma (s),\vartheta )\Delta \vartheta \\&+\,\sum ^n_{j=1}a_{{i_0}j}^+L_je_{\alpha }(\sigma (s),s-\delta _{{i_0}j}(s)) +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_le_{\alpha }(\sigma (s),s-\zeta _{{i_0}j}(s))\\&+\,N_lH_je_{\alpha }(\sigma (s),s-\sigma _{{i_0}j}(s))|\Big ) \bigg \}\Delta s\Bigg |\\\le & {} e_{-c_{i_0}}(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}+\alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\\&\times \,\Bigg |\int _{t_0}^{t_1}e_{-c_{i_0}\oplus \alpha }(t_1,\sigma (s)) \bigg \{c_{i_0}^+\tau _{i_0}^+e_{\alpha }(\sigma (s),s-\tau _{i_0}(s))\\&+\,\sum ^n_{j=1}a_{{i_0}j}^+L_je_{\alpha }(\sigma (s),s-\delta _{{i_0}j}(s)) +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_le_{\alpha }(\sigma (s),s-\zeta _{{i_0}j}(s)) \\&\,+\,N_lH_je_{\alpha }(\sigma (s),s-\sigma _{{i_0}j}(s))|\Big ) \bigg \}\Delta s\Bigg | \end{aligned}$$

$$\begin{aligned}\le & {} e_{-c_{i_0}}(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}+\alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg |\int _{t_0}^{t_1}e_{-c_{i_0}\oplus \alpha }(t_1,\sigma (s))\\&\times \bigg \{c_{i_0}^+\tau _{i_0}^+\exp \big \{\alpha (\tau _{i_0}^++\sup \limits _{s\in \mathbb {T}}\mu (s))\big \} +\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha (\delta _{{i_0}j}^++\sup \limits _{s\in \mathbb {T}}\mu (s))\big \}\\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_l\exp \big \{\alpha (\zeta _{{i_0}j}^++\sup \limits _{s\in \mathbb {T}}\mu (s))\big \}\\&+\,N_lH_j\exp \big \{\alpha (\sigma _{{i_0}j}^++\sup \limits _{s\in \mathbb {T}}\mu (s))\big \}\Big ) \bigg \}\Delta s\Bigg |\\= & {} \alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg \{\frac{1}{\alpha _1pM}e_{-c_{i_0}\oplus \alpha }(t_1,t_0) +\exp \big \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\big \}\\&\times \bigg [c_{i_0}^+\tau _{i_0}^+ \exp \big \{\alpha \tau _{i_0}^+\big \} +\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha \delta _{{i_0}j}^+\big \} +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_l\exp \big \{\alpha \zeta _{{i_0}j}^+\big \}\\&\,+N_lH_j\exp \big \{\alpha \sigma _{{i_0}j}^+\big \}\Big ) \int _{t_0}^{t_1}e_{-c_{i_0}\oplus \alpha }(t_1,\sigma (s))\Delta s\bigg ]\Bigg \}\\< & {} \alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg \{\frac{1}{M}e_{-(c_{i_0}-\alpha )}(t_1,t_0)\\&+\exp \big \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\big \}\bigg [c_{i_0}^+\tau _{i_0}^+ \exp \big \{\alpha \tau _{i_0}^+\big \} +\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha \delta _{{i_0}j}^+\big \}\\&+\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_l\exp \big \{\alpha \zeta _{{i_0}j}^+\big \}\\&\,+N_lH_j\exp \big \{\alpha \sigma _{{i_0}j}^+\big \}\Big ) \frac{1}{-(c_{i_0}-\alpha )}\int _{t_0}^{t_1}\big (-(c_{i_0}-\alpha )\big )e_{-(c_{i_0}-\alpha )}(t_1,\sigma (s))\Delta s\bigg ]\Bigg \}\\= & {} \alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg \{\bigg [\frac{1}{M} -\frac{\exp \big \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\big \}}{c_{i_0}^--\alpha } \bigg (c_{i_0}^+\tau _{i_0}^+\exp \big \{\alpha \tau _{i_0}^+\bigg \}\nonumber \\&+\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha \delta _{{i_0}j}^+\big \} +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Bigg (N_jH_l\exp \big \{\alpha \zeta _{{i_0}j}^+\big \} \\&+\,N_lH_j\exp \big \{\alpha \sigma _{{i_0}j}^+\big \}\Bigg )\bigg )\bigg ]e_{-(c_{i_0}-\alpha )}(t_1,t_0)\\&+\, \frac{\exp \big \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\big \}}{c_{i_0}-\alpha } \bigg (c_{i_0}^+\tau _{i_0}^+\exp \big \{\alpha \tau _{i_0}^+\big \} +\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha \delta _{{i_0}j}^+\big \}\\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Bigg (N_jH_l\exp \big \{\alpha \zeta _{{i_0}j}^+\big \} +\,N_lH_j\exp \big \{\alpha \sigma _{{i_0}j}^+\big \}\Bigg )\bigg )\Bigg \}\\< & {} \alpha _1pM e_{\ominus \alpha }(t_1,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}, \end{aligned}$$

which is a contradiction.

Case 2 (3.8) is not true and (3.7) is true. Then there exists $t_2\in (t_0,+\infty )_{\mathbb {T}}$ and $i_1\in \{1,2,\ldots ,n\}$ such that

$$\begin{aligned}&|u_{i_1}^\Delta (t_2)|\!\ge \! pM e_{\ominus \alpha }(t_2,t_0)||\varphi -\psi ||_{\mathbb {X}^*}, \,\,|u_{i_1}^\Delta (t)|\!<\!pM e_{\ominus \alpha }(t,t_0)||\varphi -\psi ||_{\mathbb {X}^*},\,\, t\in (t_0,t_2)_{\mathbb {T}},\\&|u_{k}^\Delta (t)|<pM e_{\ominus \alpha }(t,t_0)||\varphi -\psi ||_{\mathbb {X}^*},\,\,\mathrm {for} \, k\ne i_1,\, \,t\in (t_0,t_2]_{\mathbb {T}}, k=1,2,\dots ,n. \end{aligned}$$

Hence, there must be a constant $\alpha _2\ge 1$ such that

$$\begin{aligned}&|u_{i_1}^\Delta (t_2)|=\alpha _2pM e_{\ominus \alpha }(t_2,t_0)||\varphi -\psi ||_{\mathbb {X}^*}, \,\,|u_{i_1}^\Delta (t)|<\alpha _2pM e_{\ominus \alpha }(t,t_0)||\varphi -\psi ||_{\mathbb {X}^*},\,\, \\&\quad t\in (t_0,t_2)_{\mathbb {T}},\\&|u_{k}^\Delta (t)|<\alpha _2pM e_{\ominus \alpha }(t,t_0)||\varphi -\psi ||_{\mathbb {X}^*},\quad \mathrm {for} \, k\ne i_1,\, \,t\in (t_0,t_2]_{\mathbb {T}}, k=1,2,\dots ,n. \end{aligned}$$

Note that, in view of (3.4), we have

$$\begin{aligned} |u_{i_1}^\Delta (t_2)|= & {} \bigg |-c_{i_1}(t_2)u_{i_1}(t_0)e_{-c_{i_1}}(t_2,t_0)+c_{i_1}(t_2)\int _{t_2-\tau _{i_1}(t_2)}^{t_2}u_{i_1}^\Delta (s)\Delta s\\&+\,\sum ^n_{j=1}a_{{i_1}j}(t_2)\big (f_j(y_j^\Delta (t_2-\delta _{{i_1}j}(t_2)))-f_j(x_j^\Delta (t_2-\delta _{{i_1}j}(t_2)))\big )\nonumber \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}(t_2)\big (g_j(y_j(t_2-\sigma _{{i_1}jl}(t_2)))g_l(y_l(t_2-\zeta _{{i_1}jl}(t_2))) \\&\,-\,g_j(x_j(t_2-\sigma _{{i_1}jl}(t_2)))g_l(x_l(t_2-\zeta _{{i_1}jl}(t_2)))\big )\\&-\,c_{i_1}(t_2)\int _{t_0}^{t_2}e_{-c_{i_1}}(t_2,\sigma (s))\Bigg \{c_{i_1}(s)\int _{s-\tau _{i_1}(s))}^su_{i_1}^\Delta (\vartheta )\Delta \vartheta \\&\,+\,\sum ^n_{j=1}a_{{i_1}j}(s)\big (f_j(y_j^\Delta (s-\delta _{{i_1}j}(s)))-f_j(x_j^\Delta (s-\delta _{{i_1}j}(s)))\big )\nonumber \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}(s)\big (g_j(y_j(s-\sigma _{{i_1}jl}(s)))g_l(y_l(s-\zeta _{{i_1}jl}(s))) \\&-\,g_j(x_j(s-\sigma _{{i_1}jl}(s)))g_l(x_l(s-\zeta _{{i_1}jl}(s)))\big )\Bigg \}\Delta s\bigg |\\\le & {} c_{i_1}^+ e_{-c_{i_1}}(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\\&\,+\,\alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg (c_{i_1}^+\int _{s-\tau _{i_1}(s))}^se_{\alpha }(\sigma (s),\vartheta )\Delta \vartheta \\&+\,\sum ^n_{j=1}a_{{i_1}j}^+L_je_{\alpha }(\sigma (t_2),t_2-\delta _{{i_1}j}(t_2)) \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}^+\Big (N_jH_le_{\alpha }(\sigma (t_2),t_2-\zeta _{{i_1}j}(t_2)) +N_lH_je_{\alpha }(\sigma (t_2),t_2-\sigma _{{i_1}j}(t_2))\Big )\Bigg )\\&\,+c_{i_1}^+\alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg \{\int _{t_0}^{t_2}e_{-c_{i_1}}(t_2,\sigma (s)) e_{\alpha }(t_2,\sigma (s))\\&\times \bigg [c_{i_1}^+\int _{s-\tau _{i_1}(s)}^se_{\alpha }(\sigma (s),\theta )\Delta \theta +\sum ^n_{j=1}a_{{i_1}j}^+L_je_{\alpha }(\sigma (s),s-\delta _{{i_1}j}(s))\\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}^+\Big (N_jH_le_{\alpha }(\sigma (s),s\!-\!\zeta _{{i_1}j}(s)) \!+\!N_lH_je_{\alpha }(\sigma (s),s-\sigma _{{i_1}j}(s))|\Big ) \bigg ]\Delta s\Bigg \} \end{aligned}$$

$$\begin{aligned}\le & {} c_{i_1}^+ e_{-c_{i_1}}(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\\&+\,\alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg (c_{i_1}^+\tau _{i_1}^+e_{\alpha }(t_2,t_2-\tau _{i_1}(t_2)) \\&+\,\sum ^n_{j=1}a_{{i_1}j}^+L_je_{\alpha }(\sigma (t_2),t_2-\delta _{{i_1}j}(t_2)) \\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}^+\Big (N_jH_le_{\alpha }(\sigma (t_2),t_2-\zeta _{{i_1}j}(t_2)) +N_lH_je_{\alpha }(\sigma (t_2),t_2-\sigma _{{i_1}j}(t_2))\Big )\Bigg )\\&+\,c_{i_1}^+\alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg \{\int _{t_0}^{t_2}e_{-c_{i_1}\oplus \alpha }(t_2,\sigma (s))\\&\times \bigg [c_{i_1}^+\tau _{i_1}^+e_{\alpha }(\sigma (s),s-\tau _{i_1}(s)) +\sum ^n_{j=1}a_{{i_1}j}^+L_je_{\alpha }(\sigma (s),s-\delta _{{i_1}j}(s))\\&+\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}^+\Big (N_jH_le_{\alpha }(\sigma (s),s-\zeta _{{i_1}j}(s)) +N_lH_je_{\alpha }(\sigma (s),s-\sigma _{{i_1}j}(s))|\Big ) \bigg ]\Delta s\Bigg \}\\\le & {} c_{i_1}^+ e_{-c_{i_1}}(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}+\alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg (c_{i_1}^+\tau _{i_1}^+\exp \{\alpha \tau _{i_1}^+\}\\&+\,\sum ^n_{j=1}a_{{i_1}j}^+L_j\exp \{\alpha \delta _{{i_1}j}^+\} +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}^+\Big (N_jH_l\exp \{\alpha \zeta _{{i_1}j}^+\} +N_lH_j\exp \{\alpha \sigma _{{i_1}j}^+\}\Big )\Bigg )\\&\times \Bigg (1+c_{i_1}^+\exp \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s))\}\int _{t_0}^{t_2}e_{-c_{i_1}\oplus \alpha }(t_2,\sigma (s))\Delta s\Bigg )\\< & {} \alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\Bigg \{ \frac{c_{i_1}^+}{M} e_{-c_{i_1}\oplus \alpha }(t_2,t_0)+\Bigg (c_{i_1}^+\tau _{i_1}^+\exp \{\alpha \tau _{i_1}^+\}\\&+\,\sum ^n_{j=1}a_{{i_1}j}^+L_j\exp \{\alpha \delta _{{i_1}j}^+\} +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_1}jl}^+\Big (N_jH_l\exp \{\alpha \zeta _{{i_1}j}^+\} +N_lH_j\exp \{\alpha \sigma _{{i_1}j}^+\}\Big )\Bigg )\\&\times \Bigg (1+c_{i_1}^+\exp \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s))\}\int _{t_0}^{t_2}e_{-c_{i_1}\oplus \alpha }(t_2,\sigma (s))\Delta s\Bigg )\Bigg \} \end{aligned}$$

$$\begin{aligned}\le & {} \alpha _2pM e_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}\left\{ \left[ \frac{1}{M} -\frac{\exp \big \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\big \}}{c_{i_0}^--\alpha } \bigg (c_{i_0}^+\tau _{i_0}^+\exp \big \{\alpha \tau _{i_0}^+\big \}\right. \right. \\&\left. \left. +\,\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha \delta _{{i_0}j}^+\big \} +\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_l\exp \big \{\alpha \zeta _{{i_0}j}^+\big \}\right. \right. \\&\left. \left. +\,N_lH_j\exp \big \{\alpha \sigma _{{i_0}j}^+\big \}\Big )\bigg )\right] c_{i_1^+}e_{-(c_{i_0}-\alpha )}(t_2,t_0)\right. \\&\left. +\, \bigg (1+\frac{c_{i_1^+}\exp \big \{\alpha \sup \limits _{s\in \mathbb {T}}\mu (s)\big \}}{c_{i_0}-\alpha }\bigg ) \bigg (c_{i_0}^+\tau _{i_0}^+\exp \big \{\alpha \tau _{i_0}^+\big \} +\sum ^n_{j=1}a_{{i_0}j}^+L_j\exp \big \{\alpha \delta _{{i_0}j}^+\big \}\right. \\&\left. +\,\sum \limits ^n_{j=1}\sum _{l=1}^{n}b_{{i_0}jl}^+\Big (N_jH_l\exp \big \{\alpha \zeta _{{i_0}j}^+\big \} +N_lH_j\exp \big \{\alpha \sigma _{{i_0}j}^+\big \}\Big )\bigg )\right\} \\< & {} \alpha _2pMe_{\ominus \alpha }(t_2,t_0)\Vert \varphi -\psi \Vert _{\mathbb {X}^*}, \end{aligned}$$

which is also a contradiction. By above two cases, for other cases of negative proposition of (3.6), we can obtain a contradiction. Therefore, (3.6) holds. Let $p\rightarrow 1$, then (3.5) holds. We can take $\ominus \lambda =\ominus \alpha$, then $\lambda >0$ and $\ominus \lambda \in \mathcal {R}^+$. Hence, we have

$$\begin{aligned} ||u||_{\mathbb {X}^*}\le M\Vert \varphi -\psi \Vert _{\mathbb {X}^*}e_{\ominus \lambda }(t,t_0),\,\, t\in [-\theta ,\infty )_{\mathbb {T}},\,t\ge t_0, \end{aligned}$$

which means that, the pseudo almost periodic solution x(t) of (1.1) is globally exponentially stable. This completes the proof of Theorem 3.2. $\square$

Remark 3.1

According to $(H_3)$, we see that the existence and exponential stability of almost periodic solutions for system (1.1) not only depends on the delays in the leakage term, but also depends on the neutral terms in the network.

Remark 3.2

Since conditions $(H_1)$–$(H_4)$ do not impose any further restrictions on time scale $\mathbb {T}$ except that $\mathbb {T}$ is an almost periodic time scale, our results show that under conditions $(H_1)$–$(H_4)$ the continuous time network (1.2) and its corresponding discrete time network (1.3) have the same dynamical behaviors.

4 Numerical Example

In this section, we present an example to illustrate the feasibility of our results obtained in Sect. 3.

Example 4.1

Let $n=3$. Consider the following neural networks system on almost periodic time scale $\mathbb {T}$:

$$\begin{aligned} x_{i}^{\Delta }(t)= & {} -c_i(t)x_i(t-\tau _i(t))+ \sum ^3_{j=1}a_{ij}(t)f_j(x_j^\Delta (t-\delta _{ij}(t)))\nonumber \\&+\sum \limits ^3_{j=1}\sum _{l=1}^{3}b_{ijl}(t)g_j(x_j(t-\sigma _{ijl}(t)))g_l(x_l(t-\zeta _{ijl}(t))) +I_i(t),\,\,t\in \mathbb {T}, i=1,2,3 \nonumber \\ \end{aligned}$$

(4.1)

where

By calculating, we have

$$\begin{aligned} L_1= & {} H_1=N_1=0.25,\quad L_2=H_2=N_2=0.1,\quad L_3=H_3=N_3=0.15,\\ a_{11}^+= & {} 0.15,\quad a_{12}^+=0.26,\quad a_{13}^+=0.16,\quad a_{21}^+=0.05,\quad a_{22}^+=0.07,\quad a_{23}^+=0.07,\\ a_{31}^+= & {} 0.06,\quad a_{32}^+=0.06,\quad a_{33}^+=0.07,\quad I_1^+=0.05,\quad I_2^+=0.05,\quad I_3^+=0.04,\\ c_1^+= & {} 0.05,\quad c_1^-=0.03, \quad c_2^+=0.25, c_2^-=0.21,\quad c_3^+=0.28,\quad c_3^-=0.22,\\ b_{111}^+= & {} b_{222}^+=b_{333}^+=b_{123}^+=0.13,\quad b_{112}^+=b_{212}^+=b_{312}^+=b_{313}^+=0.3,\\ b_{113}^+= & {} b_{213}^+=b_{323}^+=b_{331}^+=0.17,\quad b_{121}^+=b_{122}^+=b_{131}^+=b_{132}^+=0.16,\\ b_{133}^+= & {} b_{211}^+=b_{311}^+=b_{221}^+=0.4,\quad b_{231}^+=b_{232}^+=b_{322}^+=b_{332}^+=0.16,\\ b_{223}^+= & {} b_{233}^+=b_{321}^+=0.4,\quad \tau _1^+=0.04,\quad \tau _2^+=0.05,\quad \tau _3^+=0.06. \end{aligned}$$

We can verify that all assumptions in Theorem 1 and Theorem 2 are satisfied. Therefore, we have that (4.1) has a pseudo almost periodic solution, which is globally exponentially stable.

Fig. 1

Responds of continuous situation

Fig. 2

Responds of discrete situation

Remark 4.1

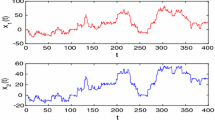
Our results about system (4.1) can not be obtained from previously known results in literatures. Especially, for both the cases of $\mathbb {T}=\mathbb {R}$ and $\mathbb {T}=\mathbb {Z}$, (4.1) always has a pseudo almost periodic solution, which is globally exponentially stable (see Figures 1,2).