1 Introduction

Memory is a crucial term which goes side to side with Artificial Neural Networks (ANN). Besides, natural neural networks are usually connected in more complex structures, like recurrent synaptic connections. Unfortunately, Feed Forward Networks (FFNs) lack of dynamic memory required for certain non-linear tasks. On the other hand, in addition to feed forward links, Recurrent ANNs are featured by feedback connections between their layers Ref. [27].

So, Recurrent Neural Networks (RNN) were originally developed as a way of extending neural networks to sequential data. The addition of recurrent connections allows RNNs to make use of previous context, as well as making them more robust and suited for dynamical systems modeling. The rich dynamics created by the recurrent connections enable signals to be spread in the different layers. Hence, the capability of RNN to hold non-linear systems behavior is revealed.

With regard to practical exploits, RNN have excelled in tasks that require good or working memory, for example for time series prediction used in financial dataset to predict the future stock market price or vertical position of a levitated magnet [14], or for short-Term power production of hydropower plants [21]. RNN were also used for path planning for autonomous robot [9] or for the estimation of the bipeds next position at each time and to achieve a human-like natural walking [2].

Therefore, RNN are an important class of computational models inspired from the brain structure. Hence, diverse types of RNNs can be distinguished such as Hopfield, Elman, Long short-term memory (LSTM), Echo State Network (ESN) and Bidirectional Associative Memory (BAM).

The BAM neural network models have been extensively analysed and studied as a key class of RNN (see Fig. 1). They were first introduced by Kosko [20]. The BAM neural network is composed of neurons arranged in two layers, the \(X-\)layer and \(Y-\)layer.

The neurons in one layer are fully interconnected to the neurons in the other layer. Through iterations of forward and backward information flows between the two layer, it performs a two-way associative search for stored bipolar vector pairs and generalize the single-layer autoassociative Hebbian correlation to a two-layer pattern-matched heteroassociative circuit. Therefore, this class of networks possesses good application prospects in the area of pattern recognition, signal and image processing, robotics, etc (see [5] and [26]).

Bidirectional recurrent neural networks (BRNN) can offer an elegant solution for classification and time series prediction (see [17] and [28]). The basic idea of BRNNs is to present each training sequence forwards and backwards to two separate recurrent hidden layers, both of them are connected to the same output layer.

This structure provides the output layer with complete past and future context for every point in the input sequence. BRNNs have previously given improved results in various domains, notably protein secondary structure prediction (see [17] and [34]) and speech processing [28]. Besides, we notice that the proposed algorithm for BAM architecture clearly outperforms the Multilayered feed-forward neural network (MLFNN) architectures [30].

Fig. 1
figure 1

General architecture of a BAM network with mixed delays

Full size image

The stability of BAM neural networks with delays has been extensively studied; interested readers may refer to the works of Chen, Li, Liao and Shaohong (see [11, 22, 23] and [29]).

It is well-known, that there exist time delays in the information processing of neurons due to various reasons. In neural networks, time delays make the dynamic behaviors more sophisticated, and may destabilize the equilibria and admit periodic oscillations, bifurcation and chaos. Although delays arise frequently in practical applications. But, it is difficult to measure them precisely.

Liao et al. [23] study the dynamical characteristics of hybrid BAM neural networks with constant transmission delays. They employed the Lyapunov function and Halanay-type inequalities to derive the delay-independent sufficient conditions. They have, also, investigated the exponential stability associated with temporally uniform external inputs. Li et al. [22] deal with a class of memristor-based BAM neural networks with time-varying delays.

To the best of our knowledge, few authors have considered oscillatory solutions for BAM networks with both discrete and continuously delays. Hence, the main purpose of this paper is to study the existence and uniqueness for the Weighted Pseudo-Almost Periodic (WPAP) solution of BAM networks with delays. Based on a fixed point theorem and analysis technique, several novel sufficient conditions are obtained ensuring the existence and uniqueness of the WPAP solution.

Obviously, our results improve and extend works in which authors investigate the periodic and almost periodic solutions of BAM (see [11, 25, 29] and [35]). In addition, the method used here is also different to that in the work of Arik in Ref. [4] and the main results are new and complement previously known results.

The outline of the paper is divided into seven sections. In Sect. 2, we introduce some necessary definitions and the basic properties of the continuous functions and the weighted pseudo-almost periodicity. In Sect. 3, the new BAM model with time-varying weights and continuously distributed delays is explained and will be be used later. The existence and uniqueness of the WPAP of Eq. (1) in the suitable convex set of \(PAP(\mathbb {R},\mathbb {R}^{k},\varrho )\) are proved in Sect. 4. Numerical examples are given in Sect. 5 to illustrate the effectiveness of our results. In Sect. 6, a comparative study with previous works is discussed. Finally, we draw conclusions in Sect. 7.

2 Preliminaries: The Functions Spaces

\(\forall k\in \mathbb {N}\), let \(BC(\mathbb {R},\mathbb {R}^{k})\) denote the collection of bounded continuous functions.

Definition 1

Let \(k\in \mathbb {N}.\) A function \(f:\mathbb {R}\longrightarrow \mathbb {R}^{k}\) is continuous,

if \(\forall \varepsilon >0,\) it exists \(l_{\epsilon }>0\) such that

$$\begin{aligned} \ \ \ \forall \alpha \in \mathbb {R},\ \ \exists \delta \in \left[ \alpha ,\alpha +l_{\varepsilon }\right] ,\ \left\| f\left( \delta +\cdot \right) -f\left( \cdot \right) \right\| \le \varepsilon . \end{aligned}$$

In this work, \(AP(\mathbb {R},\mathbb {R}^{k})\) will denote the set of all Almost Periodic (AP) \(\mathbb {R}^{k}\)-valued functions. It is well-known that the set \(AP(\mathbb {R},\mathbb {R}^{k})\) is a Banach space with the supremum norm. We refer the reader to Ref. [12] and [15] for the basic theory of almost periodic functions and their applications.

In order to construct new spaces and new generalizations of the concept of almost periodicity, the idea consists of enlarging the so-called ergodic component, with the help of a weighted measure \(d\mu \left( x\right) =\varrho \left( x\right) dx\), where \(\varrho :{\mathbb {R}}\) \(\longrightarrow \left] 0,+\infty \right[ \) is a locally integrable function over \({\mathbb {R} }\), which is commonly called weight. Roughly speaking, let \(\mathbb {U}\) denote the collection of all functions (weights) \(\varrho :{\mathbb {R}}\) \( \longrightarrow \left] 0,+\infty \right[ \) which are locally integrable over \({\mathbb {R}}\) such \(\varrho \left( x\right) >0\) for almost each \(x\in { \mathbb {R}}\). For \(\varrho \in \mathbb {U}\) and for \(r>0,\) we set

$$\begin{aligned} m(r,\varrho ):=\int \limits _{-r}^{r}\rho (x)dx \end{aligned}$$

Notice that if \(\varrho \left( x\right) =1,\) then

$$\begin{aligned} m(r,\varrho ):=\int \limits _{-r}^{r}\rho (x)dx=2r \end{aligned}$$

Throughout this paper , the sets of weights \(\mathbb {U}_{\infty }\) and \( \mathbb {U}_{B}\) stand respectively for

$$\begin{aligned} \mathbb {U}_{\infty }:=\left\{ \varrho \in \mathbb {U},\lim _{r\rightarrow \infty }m(r,\varrho )=+\,\infty \right\} \end{aligned}$$

and

$$\begin{aligned} \mathbb {U}_{B}:=\left\{ \varrho \in \mathbb {U},\quad \varrho \text { is bounded and } \inf \limits _{x\in \mathbb {R}}\varrho (x)>0\right\} . \end{aligned}$$

Obviously, \(\mathbb {U}_{B}\subset \mathbb {U}_{\infty }\subset \mathbb {U}\), with strict inclusions. To introduce those weighted pseudo-almost periodic functions, we need to define the “weighted ergodic” space \(\ PAP_{0}\left( \mathbb {R},\mathbb {R} ^{k},\varrho \right) .\) Hence, WPAP functions will then appear as perturbations of almost periodic functions by elements of \(PAP_{0}\left( \mathbb {R},\mathbb {R}^{k},\varrho \right) .\) More precisely, for a fixed \(\varrho \) in \(\mathbb {U}_{\infty }\) let define

$$\begin{aligned} PAP_{0}\left( \mathbb {R},\mathbb {R}^{k},\varrho \right) =\left\{ f\in BC\left( \mathbb {R},\mathbb {R}^{k}\right) ,\lim _{T\rightarrow +\infty }\frac{ 1}{m(T,\varrho )}\int \limits _{-T}^{T}\left\| f(t)\right\| \varrho \left( t\right) dt=0\right\} . \end{aligned}$$

Notice that

$$\begin{aligned} PAP_{0}\left( \mathbb {R},\mathbb {R}^{k}\right) =\left\{ f\in BC\left( \mathbb {R},\mathbb {R}^{k}\right) /\lim \limits _{L\rightarrow +\infty }\frac{1 }{2L}\int \limits _{-L}^{L}\left\| f(t)\right\| dt=0\right\} \end{aligned}$$

So,

$$\begin{aligned} PAP_{0}\left( \mathbb {R},\mathbb {R}^{k},1\right) =PAP_{0}\left( \mathbb {R},\mathbb {R} ^{k}\right) . \end{aligned}$$

Clearly, we have the following hierarchy

$$\begin{aligned} AP\left( \mathbb {R},\mathbb {R}^{k}\right) \varsubsetneq PAP\left( \mathbb {R}, \mathbb {R}^{k}\right) \varsubsetneq PAP\left( \mathbb {R},\mathbb {R} ^{k},\varrho \right) . \end{aligned}$$

Definition 2

Let \(\varrho \in \mathbb {U}_{\infty }.\) A function \(f\in BC \left( \mathbb {R},\mathbb {R}^{k}\right) \) is called WPAP if it can be expressed as \(f=g+\phi \), where \(g\in AP\left( \mathbb {R},\mathbb {R}^{k}\right) \) and \(\phi \in \) \(PAP_{0}\left( \mathbb {R},\mathbb {R}^{k},\varrho \right) \). The collection of such functions will be denoted by \(PAP\left( \mathbb {R},\mathbb {R}^{k},\varrho \right) .\) The functions g and \(\phi \) appearing above are respectively called the almost periodic and the weighted ergodic perturbation components of f.

Notice that the space \(PAP\left( \mathbb {R},\mathbb {R}^{k},\varrho \right) \) is a closed subspace of \(\left( BC\left( \mathbb {R},\mathbb {R}^{k}\right) ,\left\| \cdot \right\| _{\infty }\right) \) and consequently \(PAP\left( \mathbb {R},\mathbb {R}^{k},\varrho \right) \) is a Banach space (For more details see [12] and [18]).

3 The Model

Let us consider the following new model for (BAM) neural networks

$$\begin{aligned} \displaystyle \overset{\cdot }{x_{i}}\left( t\right)= & {} -\,a_{i}x_{i}(t)+\sum \limits _{j=1}^{m}c_{ij}(t)f_{j}(y_{j}\left( t-\tau _{ji}\right) ) +\sum \limits _{j=1}^{m}d_{ij}(t) \nonumber \\&\quad \displaystyle \int \limits _{-\infty }^{t}K_{ij}\left( t-s\right) f_{j}(y_{j}(s))ds+I_{i}\left( t\right) , \nonumber \\ \displaystyle \overset{\cdot }{y_{j}}\left( t\right)= & {} -\,b_{j}y_{j}(t)+\sum \limits _{i=1}^{n}w_{ji}\left( t\right) g_{i}(x_{i}\left( t-\sigma _{ij}\right) ) +\sum \limits _{i=1}^{n}\alpha _{ji}(t) \nonumber \\&\quad \displaystyle \int \limits _{-\infty }^{t}N_{ji}\left( t-s\right) g_{i}(x_{i}(s))ds+J_{j}\left( t\right) \end{aligned}$$
(1)

where \(i=1,...,n\) and \(j=1,...,m\) correspond to the number of neurons in X -layer and Y-layer, respectively, \(x_{i}\) \(\left( \cdot \right) \), \( y_{j}\left( \cdot \right) \), are the activation of the i-th and j-th neurons respectively \(c_{ij}\left( \cdot \right) ,d_{ij}\left( \cdot \right) ,\alpha _{ji}\left( \cdot \right) \). \(f_{j}(y_{j}\left( t-\tau _{ji}\right) )\) and \(f_{j}(y_{j}(s))\) are respectively the activation functions of j-th neuron at time t with dicrete delay \(\tau \) and without delay.

\(g_{i}(x_{i}\left( t-\sigma _{ij}\right) )\) and \(g_{i}(x_{i}(s))\) are respectively the activation functions of i-th neuron at time t with dicrete delay and without delay.

\(w_{ji}\left( t \right) \) are connection weights at the time t,  and \(I_{i}\left( t \right) \) and \( J_{j}\left( t \right) \) denote the external inputs at time t. \(a_{i}\left( t \right) \) \( \left( i\in \left\{ 1,\cdots ,n\right\} \right) ,b_{j}\left( t \right) \) \(\left( j\in \left\{ 1,\cdots ,m\right\} \right) \) represent the rate with which the i-th neuron and j-th neuron will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time t, respectively.

\(K_{ij}\left( \cdot \right) \) and \(N_{ji}\left( \cdot \right) \) denoted the refractoriness of the i-th neuron and j-th neuron after they have fired or responded.

Pose \(\tau =\max _{\begin{array}{c} 1\le i\le n \\ 1\le j\le m \end{array}}\left( \tau _{ji},\sigma _{ij}\right) \), let the initial conditions associated with Eq. (1) be of the form

$$\begin{aligned} \displaystyle \left\{ \begin{array}{cc} x_{i}(t)=\varphi _{i}(t) &{} t\in \left[ -\tau ,0\right] \\ \displaystyle y_{j}(t)=\psi _{j}(t) &{} t\in \left[ -\tau ,0\right] \end{array} \right. \end{aligned}$$

where \(\varphi _{i}\left( \cdot \right) \) and \(\psi _{j}\left( \cdot \right) \) are assumed to be weighted pseudo-almost periodic functions on \(\mathbb {R}\). For arbitrary vector:

$$\begin{aligned} (x(t),y(t)):=(x_{1}(t),\cdots ,x_{n}(t),y_{1}(t),\cdots ,y_{m}(t))^{T}\in \mathbb {R}^{n+m} \end{aligned}$$

define the norm: \(\left\| (x,y)\right\| \) \(=\) \(\left\| x\right\| +\left\| y\right\| \) where,

$$\begin{aligned} \left\| x\right\| =\sup _{t\in \mathbb {R}}\max _{1\le i\le n}\left\{ \left| x_{i}(t)\right| \right\} \end{aligned}$$

and

$$\begin{aligned} \displaystyle \left\| y\right\| =\sup _{t\in \mathbb {R}}\max _{1\le j\le m}\left\{ \left| y_{j}(t)\right| \right\} . \end{aligned}$$

Let us consider the following assumptions:

  • \(({{\varvec{H}}}_\mathbf{1 })\) \(\forall \) i, j; \(b_{j}>0\).

  • \(({{\varvec{H}}}_\mathbf{2 })\) \(\forall \) i, j; the following functions: \(I_{i}\left( .\right) ,J_{j}\left( .\right) , c_{ij}\left( .\right) , d_{ij}\left( .\right) , w_{ji}\left( .\right) , \alpha _{ji}\left( .\right) \) are weighted pseudo-almost periodic.

  • \(({{\varvec{H}}}_\mathbf{3 })\) \(\forall i, j\); there exist positive constant numbers \(L_{j}^{f},\) \(\ L_{i}^{g}\) \(>0\) such that \(\forall \) \(x,y\in \mathbb {R}\)

    $$\begin{aligned} \displaystyle \left| f_{j}(x)-f_{j}(y)\right|<L_{j}^{f}\left| x-y\right| ,\ \ \left| g_{i}(x)-g_{i}(y)\right| <L_{i}^{g}\left| x-y\right| . \end{aligned}$$

    Furthermore, we suppose that \(f_{j}(0)=g_{i}\left( 0\right) =0\), \(\forall \) i, j.

  • \(\left( {{\varvec{H}}}_\mathbf{4 }\right) \) \(\forall \) i, j; the delay kernels \(K_{ij}:[ 0,+\,\infty [ \longrightarrow [ 0,+\,\infty [ \) and \(N_{ji}:[ 0,+\,\infty [ \longrightarrow [ 0,+\,\infty [ \) are continuous, integrable and there exist non negative constants \(k_{ij},n_{ji}\) such that

    $$\begin{aligned} \displaystyle \int \limits _{0}^{+\infty }K_{ij}\left( s\right) ds\le k_{ij} \ and \ \int \limits _{0}^{+\infty }N_{ji}\left( s\right) ds\le n_{ji}. \end{aligned}$$

  • \(\left( {{\varvec{H}}}_\mathbf{5 }\right) \) Let \(\varrho \in \) \(U_{\infty }\) and assume that for each \(\tau \in \mathbb {R}\) the functions

    $$\begin{aligned} \displaystyle s\longmapsto \left( \frac{\varrho \left( s+\tau \right) }{ \varrho \left( s\right) }\right)<\infty \text { and }s\longmapsto \left( \frac{m\left( s+\tau ,\varrho \right) }{m(s,\varrho )}\right) <\infty \text { } \end{aligned}$$

    are bounded.

4 Existence and Uniqueness of the WPAP Solution

Here, we study the existence and uniqueness of the weighted pseudo-almost periodic solution of Eq. (1). Following along the same proof of [1] and [13] it follows that:

Lemma 1

Under \(\left( H_{5}\right) \) the space \(PAP\left( \mathbb {R},\mathbb {R} ^{k},\varrho \right) \) is translation invariant.

Lemma 2

If \(\varphi ,\psi \) \(\in \) \(PAP(\mathbb {R},\mathbb {R},\varrho )\), then \( \varphi \times \psi \in PAP(\mathbb {R},\mathbb {R},\varrho )\).

Theorem 1

Suppose that assumptions \((H_{3})--(H_{5})\) hold and

\(\forall \) i, j;  \(x_{i}(\cdot ), y_{j}(\cdot )\in \) \(PAP(\mathbb {R},\mathbb {R},\varrho )\)

$$\begin{aligned} \displaystyle \phi _{ij}:t\longmapsto \int \limits _{-\infty }^{t}K_{ij}\left( t-s\right) f_{j}(y_{j}(s))ds\text { belongs to }PAP(\mathbb {R},\mathbb {R} ,\varrho ) \end{aligned}$$

and

$$\begin{aligned} \displaystyle \psi _{ji}:t\longmapsto \int \limits _{-\infty }^{t}N_{ji}\left( t-s\right) g_{i}(x_{i}(s))ds\text { belongs to }PAP(\mathbb {R},\mathbb {R} ,\varrho ). \end{aligned}$$

Theorem 2

Suppose that assumptions \((H_{1})--(H_{5})\) hold and

$$\begin{aligned}&\displaystyle r=\max \\&\displaystyle \left( \max _{1\le i\le n}\left( \frac{\sum \nolimits _{j=1}^{m}\left( \left| c_{ij}\right| +\left| d_{ij}\right| k_{ij}\right) L_{j}^{f}}{\left| a_{i}\right| }\right) ,\max _{1\le j\le m}\left( \frac{\sum \nolimits _{i=1}^{n}\left( \left| w_{ji}\right| +\left| \alpha _{ji}\right| n_{ji}\right) L_{i}^{g}}{\left| b_{j}\right| }\right) \right) <1. \end{aligned}$$

Then, the BAM neural network of Eq. \(\left( 1\right) \) has a unique weighted pseudo-almost periodic solution in the convex set.

$$\begin{aligned} \displaystyle \mathcal {B}= & {} B(\left( x_{0},y_{0}\right) ,R) \\ \displaystyle= & {} \left\{ \left( x,y\right) \in PAP(\mathbb {R},\mathbb {R} ^{n+m},\varrho ),\left\| \left( x,y\right) -\left( x_{0},y_{0}\right) \right\| \le R\right\} , \end{aligned}$$

where

$$\begin{aligned} \displaystyle \left( x_{0},y_{0}\right) =\left( \begin{array}{c} \displaystyle \int \limits _{-\infty }^{t}e^{-\left( t-s\right) a_{1}}I_{1}\left( s\right) ds \\ \vdots \\ \displaystyle \int \limits _{-\infty }^{t}e^{-\left( t-s\right) a_{n}}I_{n}\left( s\right) ds \\ \displaystyle \int \limits _{-\infty }^{t}e^{-\left( t-s\right) b_{1}}J_{1}\left( s\right) ds \\ \vdots \\ \displaystyle \int \limits _{-\infty }^{t}e^{-\left( t-s\right) b_{m}}J_{m}\left( s\right) ds \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} \displaystyle R=\frac{\left( \max \nolimits _{1\le i\le n}\left\{ \frac{ \left| I_{i}\right| _{\infty }}{a_{i}}\right\} +\max \nolimits _{1\le j\le m}\left\{ \frac{\left| J_{j}\right| _{\infty }}{b_{j}}\right\} \right) r}{\left( 1-r\right) }. \end{aligned}$$

Proof

It is clear that,

$$\begin{aligned} \displaystyle \left| \int \limits _{-\infty }^{t}e^{-\left( t-s\right) a_{i}}I_{i}\left( \theta \right) d\theta \right| = \max _{1\le i\le n}\left\{ \frac{\left| I_{i}\right| _{\infty }}{ a_{i}}\right\} \end{aligned}$$

and

$$\begin{aligned} \displaystyle \left| \int \limits _{-\infty }^{t}e^{-\left( t-s\right) b_{j}}J_{j}\left( \theta \right) d\theta \right| =\max _{1\le j\le m}\left\{ \frac{\left| J_{j}\right| _{\infty }}{b_{j}}\right\} . \end{aligned}$$

Therefore,

$$\begin{aligned} \displaystyle \left\| \left( x_{0},y_{0}\right) \right\| =\max _{1\le i\le n}\left\{ \frac{\left| I_{i}\right| _{\infty }}{a_{i}}\right\} +\max _{1\le j\le m}\left\{ \frac{\left| J_{j}\right| _{\infty }}{ b_{j}}\right\} \end{aligned}$$

and

$$\begin{aligned} \displaystyle \left\| (x,y)\right\| \le \left( \left\| (x,y)-\left( x_{0},y_{0}\right) \right\| +\left\| \left( x_{0},y_{0}\right) \right\| \right) . \end{aligned}$$

Now, let us consider the operator \(\varGamma :\mathbb {R}^{n+m}\longrightarrow \mathbb {R}^{n+m}\) defined by

$$\begin{aligned} \displaystyle \varGamma \left( x,y\right) =\left( \begin{array}{c} \displaystyle \int \limits _{-{\infty }}^{t}e^{-\left( t-\xi \right) a_{1}}F_{1}\left( \xi \right) d\xi \\ \vdots \\ \displaystyle \int \limits _{-{\infty }}^{t}e^{-\left( t-\xi \right) a_{n}}F_{n}\left( \xi \right) d\xi \\ \displaystyle \int \limits _{-{\infty }}^{t}e^{-\left( t-\xi \right) b_{1}}G_{1}\left( \xi \right) d\xi \\ \vdots \\ \displaystyle \int \limits _{-{\infty }}^{t}e^{-\left( t-\xi \right) b_{m}}G_{m}\left( \xi \right) d\xi \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} \displaystyle F_{i}\left( \xi \right) =\sum \limits _{j=1}^{m}c_{ij}f_{j}(y_{j}\left( \xi -\tau _{ij}\right) )+\sum \limits _{j=1}^{m}d_{ij}\int \limits _{-\infty }^{\xi }K_{ij}\left( t-\theta \right) f_{j}(y_{j}(\theta ))d\theta +I_{i}\left( \xi \right) \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} \displaystyle G_{j}\left( \xi \right) =\sum \limits _{i=1}^{n}w_{ji}g_{i}(x_{i}\left( \xi -\sigma _{ji}\right) )+\sum \limits _{i=1}^{n}\alpha _{ji}\int \limits _{-\infty }^{\xi }N_{ji}\left( t-\theta \right) g_{i}(x_{i}(\theta ))d\theta +J_{j}\left( \xi \right) . \end{array} \end{aligned}$$

First, we shall prove that the operator \(\varGamma \) is a self-mapping from \( \mathcal {B}\) to \(\mathcal {B}\). In fact, for any \((x,y)\in \mathcal {B}\), we have

$$\begin{aligned}&\displaystyle \left\| \varGamma (x,y)-\left( x_{0},y_{0}\right) \right\| = \sup \limits _{t\in \mathbb {R}}\max \limits _{1\le i\le n}\\&\quad \displaystyle \int \limits _{-\infty }^{t}\left| e^{-\left( t-s\right) a_{i}}\left( \sum \limits _{j=1}^{m}c_{ij}f_{j}(y_{j}\left( \xi -\tau _{ji}\right) )\right. \right. \displaystyle \left. \left. +\sum \limits _{j=1}^{m}d_{ij}\int \limits _{-\infty }^{\xi }K_{ij}\left( t-\theta \right) f_{j}(y_{j}(\theta ))d\theta \right) d\xi \right| \\&\quad \displaystyle +\sup \limits _{t\in \mathbb {R}}\max \limits _{1\le j\le m}\\&\quad \displaystyle \int \limits _{-T}^{t}\left| e^{-\left( t-s\right) b_{j}}\left( \sum \limits _{i=1}^{n}w_{ji}g_{i}(x_{i}\left( \xi -\sigma _{ij}\right) )\right. \right. \displaystyle \left. \left. +\sum \limits _{i=1}^{n}\alpha _{ji}\int \limits _{-\infty }^{\xi }N_{ji}\left( t-\theta \right) g_{i}(x_{i}(s))ds\right) d\xi \right| \\&\quad \displaystyle \le r\left[ \frac{r\left( \max \nolimits _{1\le i\le n}\left\{ \frac{\left| I_{i}\right| _{\infty }}{a_{i}}\right\} +\max \nolimits _{1\le j\le m}\left\{ \frac{\left| J_{j}\right| _{\infty }}{b_{j}}\right\} \right) }{\left( 1-r\right) }\right. \left. +\max \limits _{1\le i\le n}\left\{ \frac{\left| I_{i}\right| _{\infty }}{a_{i}}\right\} +\max \limits _{1\le j\le m}\left\{ \frac{ \left| J_{j}\right| _{\infty }}{b_{j}}\right\} \right] \\&\quad \displaystyle \le \frac{\left( \max \nolimits _{1\le i\le n}\left\{ \frac{ \left| I_{i}\right| _{\infty }}{a_{i}}\right\} +\max \nolimits _{1\le j\le m}\left\{ \frac{\left| J_{j}\right| _{\infty }}{b_{j}}\right\} \right) r}{\left( 1-r\right) }=R. \end{aligned}$$

In view of \((H_{3})\), for any \(X=(x,y),U=(u,v) \in \mathbb {R}^{n+m}\), we have

$$\begin{aligned}&\displaystyle \left\| \varGamma (X)-\varGamma (U)\right\| \le \\&\quad \displaystyle \sup \limits _{t\in \mathbb {R}}\max \limits _{1\le i\le n}\int \limits _{-\infty }^{t}\left| e^{-\left( t-\xi \right) a_{i}}\left( \sum \limits _{j=1}^{m}c_{ij}\left( f_{j}(y_{j}\left( \xi -\tau _{j}\right) )-f_{j}(v_{j}\left( \xi -\tau _{j}\right) )\right) \right. \right. \\&\quad \displaystyle \left. \left. +\sum \limits _{j=1}^{m}d_{ij}\left( \int \limits _{-\infty }^{\xi }K_{ij}\left( \xi -\theta \right) \left( f_{j}(x_{j}(\theta ))-f_{j}(u_{j}(\theta ))\right) d\theta \right) \right) \right| d\xi \\&\quad \displaystyle +\sup \limits _{t\in \mathbb {R}}\max \limits _{1\le j\le m}\int \limits _{-\infty }^{t}\left| e^{-\left( t-\xi \right) b_{j}}\left( \sum \limits _{i=1}^{n}w_{ji}\left( g_{i}(y_{i}\left( \xi -\tau _{i}\right) )-g_{i}(v_{i}\left( \xi -\tau _{i}\right) )\right) \right. \right. \\&\quad \displaystyle \left. \left. +\sum \limits _{i=1}^{n}w_{i1}\left( \int \limits _{-\infty }^{\xi }N_{ji}\left( \xi -\theta \right) \left( g_{i}(x_{i}(\theta ))-g_{i}(x_{i}(\theta ))\right) d\theta \right) \right) \right| d\xi \\&\quad \displaystyle \le \max \limits _{1\le i\le n}\left( \frac{ \sum \nolimits _{j=1}^{m}\left( \left| c_{ij}\right| +\left| d_{ij}\right| k_{ij}\right) L_{j}^{f}}{\left| a_{i}\right| } \right) \left\| y-v\right\| \\&\quad \displaystyle +\max \limits _{1\le j\le m}\frac{\left( \sum \nolimits _{i=1}^{n}\left| w_{ji}\right| +\left| \alpha _{ji}\right| n_{ji}\right) L_{i}^{g}}{\left| b_{j}\right| } \left\| x-u\right\| \\&\quad \displaystyle < r\left\| X-U\right\| , \end{aligned}$$

which proves that \(\varGamma \) is a contraction mapping. Then, in virtue of the Banach fixed point theorem, \(\varGamma \) has a unique fixed point which is corresponding to the solution of Eq. (1) in \(\mathcal {B\subset }PAP( \mathbb {R},\mathbb {R}^{n+m},\varrho )\).

5 Numerical Examples

Example 1

Let \(\varrho \left( t\right) =e^{t}.\) Consider the model of Eq.  (1) with n = m = 2 where

$$\begin{aligned} a_{1}= & {} 0.01, a_{2}=0.05, b_{1}=0.05, b_{2}=0.02.\\ c_{ij}\left( t\right)= & {} \left( \begin{array}{cc} 0.1\left( \cos \pi t+e^{-t}\right) &{} 0.1\left( \cos t+\cos \sqrt{2}t\right) \\ 0.05\left( \sin t+\sin \sqrt{2}t\right) &{} 0.1\left( \cos t+e^{-t}\right) \\ \end{array}\right) \\ d_{ij}\left( t\right)= & {} \left( \begin{array}{cc} 0.05\left( 1+e^{-t}\right) &{} 0.1\cos \sqrt{2}t \\ 0.02\left( \sin t+\sin \sqrt{2}t\right) &{} 0.05\left( \cos t+e^{-t}\right) \\ \end{array}\right) \\ w_{ji}\left( t\right)= & {} \left( \begin{array}{cc} 0.1+0.1e^{-t} &{} 0.1\left( \cos t+\cos \sqrt{2}t\right) \\ 0.1\left( \sin t+\sin \sqrt{2}t\right) &{} 0.1\left( \cos t+e^{-t}\right) \\ \end{array}\right) \\ \alpha _{ji}\left( t\right)= & {} \left( \begin{array}{cc} 0.05\left( 1+e^{-t}\right) &{} 0.1\cos \sqrt{2}t \\ 0.02\left( \sin t+\sin \sqrt{2}t\right) &{} 0.05\left( \cos t+e^{-t}\right) \\ \end{array} \right) \end{aligned}$$

and \(\forall \) \(x\in \mathbb {R},\)

$$\begin{aligned} \displaystyle f_{j}(x)=g_{i}(x)=\frac{\left| x+1\right| -\left| x-1\right| }{2}. \end{aligned}$$

Then, \(L_{j}^{f}=L_{i}^{g}=1\) and

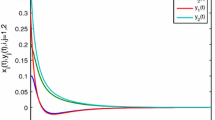
$$\begin{aligned} r=\max \left( \max _{1\le i\le 2}\left( \frac{\sum \nolimits _{j=1}^{2}\left( \left| c_{ij}\right| +\left| d_{ij}\right| k_{ij}\right) }{\left| a_{i}\right| }\right) ,\max _{1\le j\le 2}\left( \frac{\sum \nolimits _{i=1}^{2}\left( \left| w_{ji}\right| +\left| \alpha _{ji}\right| n_{ji}\right) }{\left| b_{j}\right| }\right) \right) <1 \end{aligned}$$

Therefore, all conditions of Theorem 2 are satisfied, then the model of example 1 has a unique WPAP solution (see Fig. 2).

Fig. 2
figure 2

Curves of the weighted pseudo-almost periodic solution for BAM networks with time-varying coefficients and mixed delays a (\(\tau =2, a_1=0.01,\) and \(a_2=0.05\)), b (\(\tau =2, b_1=0.05\) and \(b_2=0.02\) )

Full size image

Example 2

Let us consider the model of Eq. (1) with n = m = 3 where \(\left( a_{1},a_{2},a_{3}\right) ^{T}=\left( 3,5,4\right) ,\ \ \left( b_{1},b_{2},b_{3}\right) ^{T}=\left( 7,3,5\right) .\)

$$\begin{aligned} c_{ij}{(1\le i,j\le 3)}= & {} \left( \begin{array}{ccc} 0.5 &{} 0.6 &{} 0.1 \\ 0.2 &{} 0.2 &{} 0.1 \\ 0.3 &{} 0.2 &{} 0.1 \end{array} \right) ,\\ d_{ij}{(1\le i,j\le 3)}= & {} \left( \begin{array}{ccc} 0.5 &{} 0.6 &{} 0.1 \\ 0.3 &{} 0.3 &{} 0.1 \\ 0.2 &{} 0.3 &{} 0.1 \end{array} \right) ,\\ w_{ji}{(1\le i,j\le 3)}= & {} \left( \begin{array}{ccc} 0.2 &{} 0.1 &{} 0.3 \\ 0.2 &{} 0.2 &{} 0.3 \\ 0.5 &{} 0.2 &{} 0.2 \end{array} \right) ,\\ \alpha _{ji}{(1\le i,j\le 3)}= & {} \left( \begin{array}{ccc} 0.5 &{} 0.1 &{} 0.3 \\ 0.2 &{} 0.3 &{} 0.3 \\ 0.5 &{} 0.2 &{} 0.2 \end{array} \right) \end{aligned}$$

and \(\forall \) \(x\in \mathbb {R},\)

$$\begin{aligned} f_{j}(x)=g_{i}(x)=\frac{\left| x+1\right| -\left| x-1\right| }{2}. \end{aligned}$$

Clearly, \(L_{j}^{f}=L_{i}^{g}=1\) and

$$\begin{aligned} r=\max \left( \max _{1\le i\le 3}\left( \frac{\sum \nolimits _{j=1}^{3}\left( \left| c_{ij}\right| +\left| d_{ij}\right| k_{ij}\right) }{\left| a_{i}\right| }\right) ,\max _{1\le j\le 3}\left( \frac{\sum \nolimits _{i=1}^{3}\left( \left| w_{ji}\right| +\left| \alpha _{ji}\right| n_{ji}\right) }{\left| b_{j}\right| }\right) \right) \end{aligned}$$

\(r=max(max(\frac{1.2+1.2}{3},\frac{0.5+0.7}{5}, \frac{0.6+0.6}{4}),max(\frac{0.6+0.9}{7},\frac{0.7+0.8}{3},\frac{0.9+0.9}{5}))\) \(r=max(0.8,0.5)=0.8 <1.\)

Thus, it follows from Theorem 2 that the model of example 2 has a unique WPAP solution (see Fig. 3).

Fig. 3
figure 3

Curves of the weighted pseudo-almost periodic solution for BAM networks with time-varying coefficients and mixed delays (a) (\(\tau =2, a_1=2, a_2=5\) and \(a_3=4\)) (b)(\(\tau =2, a_1=7, a_2=3\) and \(a_3=5\))

Full size image

6 Comparison and Discussion

In previous papers ([1] and [8]) a single-layer recurrent neural networks with delays was studied by the authors. In particular, the attractivity and exponential stability of the PAP solution of RNNs are established and discussed. But, from the viewpoint of applications, the study on the dynamics such as stability and almost periodicity for the recurrent neural networks cannot be replaced by the study on dynamics for BAM neural networks.

First, it should be mentioned that the method used in the proof of this paper is original and essentially new since this class of functions is seldom considered for neural networks.

One can remark that our results need only the activations functions \(f_{j}\) and \(g_{j}\) satisfy the hypothesis \((H_{2})\), that is the Lipschitz condition, not requiring the functions \(f_{j}\) and \(g_{j}\) to be bounded and monotone nondecreasing. Therefore, our results are novel and have some significance in theories as well as in applications of almost-periodic oscillatory neural networks.

When \(\forall \) i, j,  \(c_{ij}=w_{ji}=0\) system (1) can be reduced to the model of Ref. [24], and when \(\forall \) i, j,  \(d_{ij}=\alpha _{ji}=0\) system (1) degenerates to the model investigated by Chen (see Ref. [10] and [11]).

On the other hand, if \(\forall \) \(i, j, \tau _{ij}=\sigma _{ij}=0\) system (1) degenerates to the model studied by Song and Cao [31]. Besides, our condition \(\left( H_{4}\right) \) dealing with the kernel is weaker than \(\left( H_{2}\right) \) in Ref. [31]. Further, our results can be seen as a generalization and improvement of [24] since their model assumes that \(d_{ij}\left( \cdot \right) =\alpha _{ji}\left( \cdot \right) =0\) and the results of the previous papers ([24] and [25]) considered the periodic and almost periodic case with periodic environment. In [10], system (1.1) is considered and two sufficient conditions guaranteeing the existence and the attractivity of the solution are derived. Compared with the results obtained in Ref. [10], our conditions in Theorem 1 is less restrictive than those in Ref. [10]. In fact, in Theorem 2, we do not require the condition in Ref. [10]: In addition, the method used here is also different to that in [10]. Finally, it should be interesting to adapt the technics of this paper to the BAM neural networks models of Xu et al. [32] and [33].

7 Conclusion

In this paper, a generalized model of (BAM) neural networks with mixed delays have been studied. Some new sufficient conditions for the existence and uniqueness of weighted pseudo-almost periodic solution of a class of two-layer (BAM) neural networks are given. Note that we just require that the activation function is globally Lipschitz continuous, which is less conservative and less restrictive than the monotonic assumption in previous results. The method is very concise and the obtained results are new and they complement previously known results. Finally, examples are given to illustrate our theory. The results obtained in this paper are completely new and complement the previously known works of (Ref. [1, 3] and [7]). Besides, the study of the stability (asymptotic, exponential, ...) of the solution of the Theorem 2 would be an excited subject. We are starting to took closely at this issue via new methods.