Analytical design methods for directional Gaussian 2D FIR filters

Abstract

This paper proposes two analytical design methods in the frequency domain for directional Gaussian 2D FIR filters, with a straight directional or an elliptically-shaped frequency response and with a specified selectivity and orientation in the frequency plane. One method relies on the substitution of a frequency mapping into the factored polynomial approximation of the Gaussian, while the other one is based on decomposing the frequency response into Gaussian components along three properly chosen directions in the frequency plane. The frequency response of the 2D directional filter results directly in a factored form, which is a major advantage in implementation. The filters are accurate, efficient and they eliminate the necessity of interpolation. With the mapping substitution method, they result also adjustable in orientation and aspect ratio. Several design examples are given for various specifications, and simulation results of directional filtering on test images are provided, to prove their applicability in image processing.

1 Introduction

The field of two-dimensional filters has known a steady development, and their design methods are well founded Najim (2006). Various aspects of two-dimensional IIR or FIR filter design have been approached by many authors. Most of the analytical design methods rely on 1D prototype low-pass filters and spectral transformations from s to z plane via bilinear approximation, in order to obtain 2D filters with desired frequency response, as approached in early papers like Harn and Shenoi (1986). A convenient tool for 2D FIR filter design is also the McClellan transform Chen and Lee (1994), Yeung and Chan (2002). Many authors have approached design methods based on numerical optimization techniques like least squares Zhu et al. (1999) and also genetic algorithms Tzeng (2004).

Gaussian filters have been widely used in image processing and computer vision for image smoothing and noise reduction. They are especially useful in tasks like image segmentation and edge detection. In particular, anisotropic filters performing directional blurring are commonly used in various image processing tasks.

In Nguyen and Swamy (1986) an approximation technique is developed for computing the McClellan transform for elliptically-shaped filters with arbitrary orientation. A reference paper for IIR Gaussian filter implementation is Young and Vliet (1995). In papers like Geusebroek et al. (2003), Lam and Shi (2007), Lampert and Wirjadi (2006), Lampert and Wirjadi (2006), efficient designs for anisotropic Gaussian filters are approached, some using directional decomposition along frequency axes. Gaussian 2D filters are useful as well in edge detection from noisy images Hsiao et al. (2006), remote sensing applications like directional smoothing of weather images Lakshmanan (2004), or phase noise reduction in synthetic aperture radar interferometry Wang et al. (2006). Some efficient designs and implementation of directional Gaussian smoothing filters are proposed in Charalampidis (2009) and Joginipelly et al. (2012).

An interesting application of such filters in stereoscopic image generation is developed in Horng and Tseng (2010), while a bilateral filter with a locally-controlled kernel for directional edge-preserving smoothing is approached in Venkatesh and Seelamantula (2015).

As proven in some papers, any 2D Gaussian filter can be decomposed into a cascade of 1D Gaussian filters along orthogonal axes. Next, each 1D Gaussian can be implemented using efficient recursive approximations Geusebroek et al. (2003).

As highlighted in Lam and Shi (2007), anisotropic Gaussians oriented along the x or y axes are $x-y$ separable. For anisotropic Gaussians with arbitrary orientation, the two orthogonal axes are not aligned with the image grid Lam and Shi (2007). In order to implement 1D Gaussians along these axes, interpolation is required, which increases the amount of computation and may cause the convolution kernels to be spatially non-uniform Lam and Shi (2007). A solution which partially avoids interpolation was given in Geusebroek et al. (2003). The necessity for interpolation is completely eliminated in Lam and Shi (2007) by decomposing the 2D Gaussian into a cascade of three one-dimensional Gaussians.

In Matei (2013), the author proposed an analytical design method in the frequency domain for directional Gaussian IIR filters, using a frequency response decomposition along the two frequency axes and the diagonal axis. The designed 2D filters are adjustable, as their transfer functions depend explicitly on the parameters specifying the orientation and bandwidth, so the design does not have to be repeated every time again from the start for various specifications. In Matei and Ungureanu (2009), 2D zero-phase maximally-flat IIR filters with elliptically-shaped support were designed in the frequency domain.

In this work, two analytical design methods are proposed for 2D Gaussian directional FIR (non-recursive) filters. They are based on specific frequency transformations applied to a Gaussian prototype filter with imposed selectivity, in order to obtain a 2D Gaussian oriented filter. The design is achieved in the frequency domain, yielding the desired frequency response which can be factored, and the filter large size kernel results as a convolution of smaller matrices.

The paper is organized as follows. In Sect. 2, the 1D Gaussian prototype filter used in design is presented, and its accurate polynomial approximation is found using the Chebyshev series. Section 3 introduces the frequency transformations applied in the design of two types of Gaussian orientation-selective filters, namely straight directional and elliptically-shaped. The two methods are presented in Sect. 4, where several design examples are provided. Section 4 also includes a distortion analysis of the designed filters and a comparative discussion regarding their advantages. In Sect. 5, simulation results are given for directional filtering of test images.

2 1D Gaussian prototype filters

Zero-phase filters (both FIR and IIR), in particular Gaussian filters are frequently used in image processing because they do not introduce any phase distortions in the filtered image. Furthermore, the 2D Gaussian is separable, so it can be implemented as a cascade of 1D filters. The Gaussian function in spatial frequency $\omega$ has the following expression:

$$\begin{aligned} H_G \left( \omega \right) =\exp \left( {-{\sigma ^{2}\omega ^{2}}/2} \right) \end{aligned}$$

(1)

which is the Fourier transform of the Gaussian function in the continuous spatial variable x:

$$\begin{aligned} g(x)=\left( {1/{\sqrt{2\pi }\sigma }} \right) \cdot \exp \left( {{-x^{2}}/{2\sigma ^{2}}} \right) \end{aligned}$$

(2)

where $\sigma$ represents the standard deviation. We look for a series expansion of the function $H_G (\omega )$ which has to be an approximation as accurate as possible on the frequency range $[-\pi ,\pi ]$. The most convenient for our purpose is the Chebyshev series expansion, because it yields an efficient and uniform approximation of a function on a desired interval. The Chebyshev series can be easily calculated using a symbolic computation software like MAPLE. Generally, a 1D function $H_P (\omega )$ can be approximated to a specified precision on a given frequency interval by a polynomial function $H_a (\omega )$ of order N:

$$\begin{aligned} H_P (\omega )\cong H_a (\omega )=\sum _{j=0}^N {a_j } \cdot \omega ^{ j} \end{aligned}$$

(3)

The order N of polynomial $H_a (\omega )$ depends on the filter selectivity, the imposed precision of approximation and the length of frequency interval. For simplicity, instead of (1), we use the expression $H_P(\omega )=\exp (-k\omega ^{2})$ for a Gaussian, with $k={\sigma ^{2}}/2$, where k has the role of a selectivity parameter; the larger the value of k, the narrower is the Gaussian function. Generally, the polynomial $H_P (\omega )$ will be factored as follows:

$$\begin{aligned} H_P (\omega )=\alpha \cdot \prod _{i=1}^{N_1 } {(\omega ^{2}-a_i )\cdot \prod _{j=1}^{N_2 } {(\omega ^{4}-b_j \cdot \omega ^{2}+c_j )}} \end{aligned}$$

(4)

where $2N_1 +4N_2 =N$ is the order of polynomial approximation and $\alpha$ is a constant.

Example 2.1

The Gaussian function $H_{P1} (\omega )=\exp (-\omega ^{2})$ is approximated by the following factored polynomial:

$$\begin{aligned} H_{P1} (\omega )\cong & {} \alpha \cdot \left( {\omega ^{2}-5.79682} \right) \left( {\omega ^{2}-6.59157} \right) \left( {\omega ^{2}-8.74311} \right) \left( {\omega ^{2}-9.72355} \right) \nonumber \\&\left( {\omega ^{4}-5.510944\cdot \omega ^{2}+13.360031} \right) =H_{G1} (\omega ) \end{aligned}$$

(5)

where the constant is $\alpha =0.229375\cdot 10^{-4}$. The polynomial $H_{G1} (\omega )$ is an accurate approximation of the Gaussian $H_P (\omega )=\exp (-\omega ^{2})$ on the frequency range $[-\pi ,\pi ]$, although it diverges outside this interval.

Fig. 1

The Gaussian function and its polynomial approximation on the frequency interval $[-\pi ,\pi ]$ for the functions: a $H_{P1} (\omega )=\exp (-\omega ^{2})$; b $H_{P2} (\omega )=\exp (-4\omega ^{2})$

Example 2.2

The Gaussian $H_{P2} (\omega )=\exp (-4\omega ^{2})$ is approximated by the factored polynomial $H_{G2} (\omega )$:

$$\begin{aligned} H_{P2} (\omega )\cong & {} \beta \cdot \left( {\omega ^{2}-2.0516} \right) \left( {\omega ^{2}-3.28931} \right) \left( {\omega ^{2}-4.68917} \right) \left( {\omega ^{2}-6.11946} \right) \nonumber \\&\quad \left( {\omega ^{2}-7.45535} \right) \cdot \left( {\omega ^{2}-8.5736} \right) \left( {\omega ^{2}-9.38604} \right) \left( {\omega ^{2}-9.8045} \right) \nonumber \\&\quad \left( {\omega ^{4}-1.89305\cdot \omega ^{2}+1.00547} \right) =H_{G2} (\omega ) \end{aligned}$$

(6)

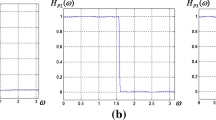
where the constant is $\beta =0.85705\cdot 10^{-6}$. The Gaussians $H_{P1} (\omega ), H_{P2} (\omega )$ and their accurate approximations $H_{G1} (\omega ), H_{G2} (\omega )$ are plotted in Fig.1a, b. The functions $H_{G1} (\omega ), H_{G2} (\omega )$ have a small amplitude ripple, depending on the approximation order.

3 Frequency mappings for 2D orientation-selective filters

In this work two types of orientation-selective 2D filters are approached. They result from a given 1D prototype by applying two different 1D to 2D frequency transformations. Both types of oriented filters discussed here have a Gaussian shape in vertical section along their longitudinal axis. However, in horizontal section, as the contour plots will show, one type of filter has a straight, directional shape, while the other has an elliptical shape. Both types of anisotropic filters can find useful applications in image processing. Next the two types of 2D oriented filters and the corresponding frequency mappings for obtaining the desired filter shape will be defined.

3.1 Straight directional filter

From a 1D prototype $H_P (\omega )$, a 2D oriented filter may be obtained by rotating the axes of the frequency plane $(\omega _1 ,\omega _2 )$ with an angle $\varphi$. The rotation is also defined by the following linear transformation, where $\omega _{ 1}, \omega _{2}$ are the original frequency variables and $\bar{{\omega }}_{ 1}, \bar{{\omega }}_{2}$ the new ones:

$$\begin{aligned} \left[ {{\begin{array}{l} {\bar{{\omega }}_{ 1} } \\ {\bar{{\omega }}_{2} } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {\;\; \cos \varphi }&{} {\sin \varphi } \\ {-\sin \varphi }&{} {\cos \varphi } \\ \end{array} }} \right] \cdot \left[ {{\begin{array}{l} {\omega _{ 1} } \\ {\omega _{2} } \\ \end{array} }} \right] \end{aligned}$$

(7)

The rotation by an angle $\varphi$ about $\omega _{ 1}$ axis is defined by the following 1D to 2D frequency mapping:

$$\begin{aligned} \omega \rightarrow \omega _1 \cos \varphi +\omega _2 \sin \varphi \end{aligned}$$

(8)

Applying this frequency transformation by simple substitution to the Gaussian prototype $H_P (\omega )=\exp (-k\omega ^{2})$, the following 2D frequency response $H_D (\omega _{1},\omega _2 )$ results, where the subscript D stands for directional:

$$\begin{aligned} H_D (\omega _{1},\omega _2 )=\exp \left( {-k (\omega _{1} \cos \varphi +\omega _2 \sin \varphi )^{2}} \right) \end{aligned}$$

(9)

3.2 Elliptically-shaped orientation-selective filter

The other type of orientation-selective 2D filters approached here are filters with elliptically-shaped support in the frequency plane. They are specified by the values of the semi-axes of the ellipse, while the orientation is given by the angle of the major axis with respect to $\omega _{ 1}$ axis. Starting from the same Gaussian prototype $H_P (\omega )$, a 2D orientation-selective filter with elliptically-shaped support results by applying the frequency transformation:

$$\begin{aligned} \omega ^{2}\rightarrow \Phi (\omega _{ 1},\omega _{ 2} )= & {} \omega _{ 1}^2 \left( {\frac{\cos ^{2}\varphi }{E^{2}}+\frac{\sin ^{2}\varphi }{F^{2}}} \right) +\omega _{2}^2 \left( {\frac{\sin ^{2}\varphi }{E^{2}}+\frac{\cos ^{2}\varphi }{F^{2}}} \right) \nonumber \\&+\,\omega _{ 1} \omega _{2} \sin (2\varphi )\left( {\frac{1}{F^{2}}-\frac{1}{E^{2}}} \right) \nonumber \\= & {} p_1 \cdot \omega _{ 1}^2 +p_2 \cdot \omega _{2}^2 +p_{12} \cdot \omega _{ 1} \omega _{2} \end{aligned}$$

(10)

where $p_1, p_2$ and $p_{12}$ result by identification. In (10), E and F are the values of major and minor semi-axes of the ellipse. The elliptically-shaped filter derives from a circular filter through the linear transformation:

$$\begin{aligned} \left[ {{\begin{array}{l} {\bar{{\omega }}_{ 1} } \\ {\bar{{\omega }}_{2} } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} E&{} 0 \\ 0&{} F \\ \end{array} }} \right] \cdot \left[ {{\begin{array}{ll} {\cos \varphi }&{} {-\sin \varphi } \\ {\sin \varphi }&{} {\;\;\cos \varphi } \\ \end{array} }} \right] \cdot \left[ {{\begin{array}{l} {\omega _{ 1} } \\ {\omega _{2} } \\ \end{array} }} \right] \end{aligned}$$

(11)

where $\bar{{\omega }}_{ 1}, \bar{{\omega }}_{2}$ are the current variables and $\omega _{ 1}, \omega _{2}$ are the former variables. Geometrically, the unit circle is stretched along the axes $\omega _{ 1}$ and $\omega _{ 2}$ with factors E and F, then counter-clockwise rotated with an angle $\varphi$, becoming an oriented ellipse. Thus, starting from the 1D Gaussian filter (1), we obtain a 2D filter with an elliptical support, specified by parameters E, F and $\varphi$ which impose the shape and orientation through substitution (10).

Applying the mapping (10) to the prototype $H_P (\omega )=\exp (-k\omega ^{2})$, with $k=1$, the 2D frequency response results:

$$\begin{aligned} H_E (\omega _{ 1},\omega _2 )=\exp \left( {-\left( {p_1 \omega _{ 1}^2 +p_2 \omega _2^2 +p_{12} \omega _{ 1} \omega _2 } \right) } \right) \end{aligned}$$

(12)

where $p_1, p_2$ and $p_{12}$ are determined from (10) and the subscript E comes from elliptical.

The mappings (8) and (10) can be generally applied to any prototype of a desired shape, not only Gaussian. For instance, using a maximally-flat prototype, 2D oriented filters with flat characteristics can be obtained. As a rule, the 2D filter will inherit the properties of its prototype (selectivity, flatness, sharpness etc.) and its cross section will have the shape of its prototype. Next the above mappings will be applied to a Gaussian prototype with imposed selectivity.

3.3 Examples of ideal Gaussian oriented filters

Before approaching the actual design method, two examples of ideal 2D oriented filters are given.

Example 3.1

Let us consider a straight directional filter with orientation angle $\varphi =\pi /6$, based on the Gaussian prototype $H_{P2} (\omega )=\exp (-4\omega ^{2})$. Using (9), the following 2D frequency response results:

$$\begin{aligned} H_{DI} (\omega _{1},\omega _2 )=\exp \left( {-(1.73205\cdot \omega _{1} +\omega _2 )^{2}} \right) \end{aligned}$$

(13)

This ideal frequency response $H_{DI} (\omega _{ 1},\omega _2 )$ is displayed in Fig. 2a and its corresponding contour plot in Fig. 2b. The 2D oriented filter $H_{DI} (\omega _1,\omega _2 )$ has the cross section along the line $\omega _1 \cos \varphi +\omega _2 \sin \varphi =0$ identical with the prototype $H_{P2} (\omega )$, and is constant along the line $\omega _1 \sin \varphi -\omega _2 \cos \varphi =0$, which is the filter longitudinal axis.

Example 3.2

Let us consider the orientation angle $\varphi =\pi /6$ and the ellipse semi-axes $E=4,F=1.4$. Based on (12), the following elliptically-shaped frequency response results:

$$\begin{aligned} H_{EI} (\omega _{1},\omega _2 )=\exp \left( {-\left( {0.174426\cdot \omega _{ 1}^2 +0.398278\cdot \omega _2^2 +0.387723\cdot \omega _{ 1} \omega _2 } \right) } \right) \end{aligned}$$

(14)

The 2D ideal oriented filter frequency response $H_{EI} (\omega _{1} ,\omega _2 )$ is displayed in Fig. 2c and its contour plot in Fig. 2d.

Fig. 2

Ideal frequency response (a) and contour plot (b) for a straight oriented filter with $\varphi =\pi /6$; ideal frequency response (c) and contour plot (d) for a Gaussian elliptically-shaped oriented filter with $\varphi =\pi /6$

3.4 Orientation selective filter design using Gaussian separability

For the Gaussian prototype introduced in Sect. 2, we obtain the ideal frequency responses of the oriented filters given by (9) and (12). Next we will exploit the useful property of the 2D Gaussian function to be separable into two or three Gaussians, along particular directions in the frequency plane.

In this design approach the 2D Gaussian filter will be decomposed into three 1D Gaussian filters. Let us first use the directions $\omega _{ 1}, \omega _2$ and $\omega _{ 1} +\omega _2$ (the two frequency axes and one diagonal of the frequency plane). Generally, a two-variable function $F(\omega _{ 1},\omega _2 )$ is said to be separable if it can be written as a product of functions of each variable:

$$\begin{aligned} F(\omega _{ 1},\omega _2 )=F_1 (\omega _{ 1} )\cdot F_2 (\omega _2 ) \end{aligned}$$

(15)

By extension, such a function may be named partially separable if it can be written, for instance:

$$\begin{aligned} F(\omega _{1},\omega _{2} )=F_{ 1} (\omega _{ 1} )\cdot F_{2} (\omega _{2} )\cdot F_{ 12} (\omega _{ 1} +\omega _{2} ) \end{aligned}$$

(16)

as a product of functions in variables $\omega _{ 1}, \omega _{2}$ and $\omega _{ 1} +\omega _2$ or even other linear combinations, as shown in Sect. 4. Let us consider now the decomposition given by (16). Denoting by $\Phi (\omega _{ 1},\omega _2 )$ the unsigned exponent of the 2D oriented Gaussian function, either (9) or (12), it can be written:

$$\begin{aligned} \Phi (\omega _{ 1},\omega _2 )=\Phi _1 (\omega _{ 1} )+\Phi _2 (\omega _2 )+\Phi _{12} (\omega _{ 1} +\omega _2 )=a \omega _{ 1}^2 +b \omega _2^2 +c\left( {\omega _{ 1} +\omega _2 } \right) ^{2} \end{aligned}$$

(17)

The coefficients a, b and c are determined separately for the two types of filters. Expanding the expression (9) and using the identity $\omega _{ 1} \omega _{2} =0.5\cdot \left( {(\omega _{ 1} +\omega _{2} )^{2}-\omega _{ 1}^2 -\omega _{2}^2 } \right)$, then identifying coefficients from (17), the following set results:

$$\begin{aligned} a= & {} 0.5 k (1+\cos 2\varphi -\sin 2\varphi ) \nonumber \\ b= & {} 0.5 k (1-\cos 2\varphi -\sin 2\varphi ) \nonumber \\ c= & {} 0.5 k \sin 2\varphi \end{aligned}$$

(18)

For the straight directional filter, as results from (18), the coefficients depend on the orientation angle $\varphi$ and the selectivity factor k. Likewise, in the case of a filter with elliptically-shaped support, comparing (10) and (17), we get:

$$\begin{aligned} a= & {} 0.5\left( {p+q} \right) +0.5\cdot \left( {p-q} \right) (\sin 2\varphi +\cos 2\varphi ) \nonumber \\ b= & {} 0.5\left( {p+q} \right) +0.5\cdot \left( {p-q} \right) (\sin 2\varphi -\cos 2\varphi ) \nonumber \\ c= & {} 0.5\cdot \left( {q-p} \right) \sin (2\varphi ) \end{aligned}$$

(19)

where for simplicity we denoted $p=1/{E^{2}}$ and $q=1/{F^{2}}$. So for the elliptically-shaped filter the coefficients depend on the orientation angle $\varphi$ and the ellipse parameters E and F.

4 Analytical design methods for 2D orientation-selective filters

In this work two analytical design methods are proposed for 2D FIR filters with orientation-selective frequency response. The first uses the factored polynomial approximation of a Gaussian with specified selectivity, in which each factor is substituted with its corresponding counterpart given by a specific mapping. The second version consists in decomposing the 2D Gaussian along three axes, properly selected to obtain efficient oriented filters (of minimum order). The design is entirely achieved in the frequency domain and both methods lead to a frequency response of a 2D zero-phase filter of the general form:

$$\begin{aligned} H_G (\omega _{ 1},\omega _2 )=\sum _{m=0}^{N_1 } \sum _{n=0}^{N_2 } {a(m,n)\cdot } \cos \left( {m\omega _{ 1} +n\omega _2 } \right) \end{aligned}$$

(20)

which is the two-variable Discrete Fourier Transform (2D DFT) of the filter convolution kernel. Since the 2D filters discussed here are zero-phase, their frequency responses are real and symmetric about the origin in the frequency plane (as shown in Fig. 2) and their convolution kernels will be centrally-symmetric square matrices.

4.1 Method based on mapping substitution into the factored prototype

The zero-phase 1D prototype filter function, in our case a Gaussian $H_P (\omega )$ is approximated by a polynomial on the range of interest, namely $\omega \in [-\pi ,\pi ]$, as shown in Sect. 2. This can be done either using a Taylor series expansion around zero, or a Chebyshev series approximation for $\omega \in [-\pi ,\pi ]$. While the Taylor series gives a better approximation around the expansion point, the Chebyshev series yields a uniform approximation over the entire specified range.

Example 4.1

The Gaussian $H_{P2} (\omega )=\exp (-4\omega ^{2})$ is approximated by a polynomial as shown in Sect. 2, with the factored expression (6). In order to obtain a 2D straight directional filter, the frequency transformation (8) is applied. The following substitution will be made, for $k=4$, where a, b and c are given by (18):

$$\begin{aligned} \omega ^{2}\rightarrow \omega _{ 1}^2 (\cos \varphi )^{2}+\omega _{2}^2 (\sin \varphi )^{2}+\omega _{1} \omega _2 \sin 2\varphi =a\cdot \omega _{ 1}^2 +b\cdot \omega _{2}^2 +c\cdot (\omega _{1} +\omega _2 )^{2} \end{aligned}$$

(21)

The next step is to find a convenient approximation of $\omega ^{2}$, as a cosine series. While the Chebyshev series expansion is generally more convenient, in this case we do not need a precise approximation of $\omega ^{2}$ on the entire range $[-\pi ,\pi ]$, but rather around zero. In order to achieve this, the change of variable $\omega =\arccos x\;\leftrightarrow x=\cos \omega$ is used. We find a suitable expansion of $(\arccos x)^{2}$ as a Taylor series around $x=1$, truncated to the second-order term as $(\arccos x)^{2}\cong -2(x-1)+(1/3)\cdot (x-1)^{2}={7/3}-(8/3)\cdot x+(1/3)\cdot x^{2}$. Substituting back $x=\cos \omega$ and using trigonometric identities, the following simple approximation is found:

$$\begin{aligned} \omega ^{2}\cong 2.5-2.66667\cdot \cos \omega +0.166667\cdot \cos 2\omega \end{aligned}$$

(22)

This approximation (curve 2 in Fig. 3a) is very accurate around zero but diverges towards the limits of the range $[-\pi ,\pi ]$ with a large error compared to the function $\omega ^{2}$ (curve 1). However, by substituting back expression (22) into each factor of $H_{G2} (\omega )$ given by (6), these marginal errors cancel out and the overall approximation is quite accurate, as shown in Fig. 3b where $H_{P2} (\omega )$ and its approximation are practically superposed. Therefore, the resulted 2D oriented filter will also be very close to its ideal version. Thus a uniform approximation on $[-\pi ,\pi ]$ is not necessary. The advantage is the low order of approximation, which finally leads to a more efficient, low-order 2D filter, convenient for implementation. Replacing in (22) the variable $\omega$ by $\omega _{1}, \omega _{ 2}$ and $\omega _{ 1} +\omega _{ 2}$, the following relations along three frequency axes are derived:

$$\begin{aligned} \omega _{ 1}^2\cong & {} 2.5-2.66667\cdot \cos \omega _{ 1} +0.166667\cdot \cos 2\omega _{ 1}\end{aligned}$$

(23)

$$\begin{aligned} \omega _2^2\cong & {} 2.5-2.66667\cdot \cos \omega _2 +0.166667\cdot \cos 2\omega _2\end{aligned}$$

(24)

$$\begin{aligned} (\omega _{ 1} +\omega _2 )^{2}\cong & {} 2.5-2.66667\cdot \cos (\omega _{ 1} +\omega _2 )+0.166667\cdot \cos (2\omega _{ 1} +2\omega _2 ) \end{aligned}$$

(25)

Fig. 3

a The function $\omega ^{2}$ and its approximation using Taylor series; b prototype $H_{P2} (\omega )$ and its approximation

Next, substituting the expressions (23)–(25) into (21) and replacing $\cos \omega _{ 1}, \cos \omega _{ 2}$ and $\cos (\omega _{ 1} +\omega _{ 2} )$ by ${(z_1 +z_1^{-1} )}/2, {(z_2 +z_2^{-1} )}/2$ and ${(z_1 z_2 +z_1^{-1} z_2^{-1} )}/2$ respectively, we finally obtain the following mapping expressed in matrix form:

$$\begin{aligned} \omega ^{2}\rightarrow F(z_1,z_2 )=\mathbf{z}_\mathbf{1} \times \mathbf{M}_\varphi \times \mathbf{z}_\mathbf{2}^T \end{aligned}$$

(26)

Here the vectors are $\mathbf{z}_\mathbf{1} =\left[ {{\begin{array}{lllll} {z_1^{-2} }&{} {z_1^{-1} }&{} 1&{} {z_1 }&{} {z_1^2 } \\ \end{array} }} \right]$ and $\mathbf{z}_\mathbf{2} =\left[ {{\begin{array}{lllll} {z_2^{-2} }&{} {z_2^{-1} }&{} 1&{} {z_2 }&{} {z_2^2 } \\ \end{array} }} \right]$, where $z_1 =\exp (j\omega _{ 1} )$ and $z_2 =\exp (j\omega _{ 2} )$ are the complex frequency variables in 2D Z-transform and $\mathbf{M}_\varphi$ is a $5\times 5$ matrix whose elements depend on the orientation angle $\varphi$ according to (18):

$$\begin{aligned} \mathbf{M}_\varphi =\left[ {{\begin{array}{ccccc} {0.083334 c}&{} 0&{} {0.083334 a}&{} 0&{} 0 \\ 0&{} {-1.3334 c}&{} {-1.3334 a}&{} 0&{} 0 \\ {0.083334 b}&{} {-1.3334 b}&{} {2.5\,(a+b+c)}&{} {-1.3334 b}&{} {0.083334 b} \\ 0&{} 0&{} {-1.3334 a}&{} {-1.3334 c}&{} 0 \\ 0&{} 0&{} {0.083334 a}&{} 0&{} {0.083334 c} \\ \end{array} }} \right] \end{aligned}$$

(27)

Example 4.2

For an orientation angle $\varphi =\pi /6$, we obtain from (18) the coefficients $a=0.316987, b=-0.183013, c=0.433013$ and the matrix $\mathbf{M}_\varphi$ will be:

$$\begin{aligned} \mathbf{M}_\varphi =\left[ {{\begin{array}{ccccc} { 0.03608}&{} 0&{} {0.026416}&{} 0&{} 0 \\ 0&{} {-0.57738}&{} {-0.42267}&{} 0&{} 0 \\ {-0.01525}&{} { 0.24403}&{} {1.417468}&{} { 0.24403}&{} {-0.01525} \\ 0&{} 0&{} {-0.42267}&{} {-0.57738}&{} 0 \\ 0&{} 0&{} {0.026416}&{} 0&{} { 0.03608} \\ \end{array} }} \right] \end{aligned}$$

(28)

The last design step is to substitute the mapping (26) into each factor of the prototype approximation given by (4). According to (26), each second order factor of the form $H_{P1i} (\omega )=(\omega ^{2}-a_i )$ from (4) will correspond to a convolution kernel given by $\mathbf{A}_i =\mathbf{M}_\varphi -a_i \cdot \mathbf{P}_0$, where by $\mathbf{P}_0$ we denote a matrix of size $5\times 5$ with all elements equal to zero, except the central element which is 1. The fourth order factor of the general form:

$$\begin{aligned} H_{P2j} (\omega )=(\omega ^{4}-b_j \cdot \omega ^{2}+c_j ) \end{aligned}$$

(29)

corresponds to a convolution kernel of size $9\times 9$ given by the expression:

$$\begin{aligned} \mathbf{B}_j =\mathbf{M}_\varphi {*}{} \mathbf{M}_\varphi -b_j \cdot \mathbf{P}_1 +c_j \cdot \mathbf{P}_2 \end{aligned}$$

(30)

where the symbol ${*}$ stands for matrix convolution and the matrix $\mathbf{P}_1$ is a $9\times 9$ matrix obtained by padding matrix $\mathbf{M}_\varphi$ (of size $5\times 5)$ with zeros up to size $9\times 9$, such that $\mathbf{P}_1 (3:7,3:7)=\mathbf{M}_\varphi$. The matrix $\mathbf{P}_2$ is a matrix of size $9\times 9$ with all elements equal to zero, except the central element which is equal to 1.

The component matrices $\mathbf{A}_i,\mathbf{B}_j$ with $i=1 \ldots N_1, j=1 \ldots N_2$ obtained as above, corresponding to the factors of polynomial (4), can be considered elementary convolution kernels of size $5\times 5$ and $9\times 9$. The overall convolution kernel of the designed 2D oriented filter, which is a square matrix G of size $L\times L$, with $L=5N_1 +9N_2 -1$, results as the convolution of these elementary kernels:

$$\begin{aligned} \mathbf{G}=\alpha \cdot \mathbf{A}_1 {*}{} \mathbf{A}_2 {*}\ldots {*}{} \mathbf{A}_{\mathrm{N1}} {*}{} \mathbf{B}_1 {*} \ldots {*}\mathbf{B}_{\mathrm{N2}} \end{aligned}$$

(31)

For the 2D filter previously discussed, based on factored prototype (6), we obtain $N_1 =8$ kernels of size $5\times 5$ and only one kernel of size $9\times 9$. Therefore, using this first method, the large kernel of the designed 2D filter results directly decomposed into smaller size kernels; thus, the 2D filter will be implemented as a cascade of its component filters, which is an important advantage. As can be noticed in Fig. 4a, the frequency response of the straight directional filter with parameters specified above has a very good linearity along the longitudinal axis, there is practically no visible shape distortion. The pass region along the filter axis is wide enough, compared to the ideal filter in Fig. 2a, b. The characteristic in longitudinal view is remarkably flat, due to the accurate approximation of the Gaussian around zero. Also the contour plot in Fig. 4b shows a good linearity of its shape in the frequency plane.

In the case of a 2D Gaussian elliptically-shaped filter, the same frequency mapping (26) is used, and the $5\times 5$ matrix $\mathbf{M}_\varphi$ has the same general form (27), only the parameters a, b and c are different, having the expressions (19).

Fig. 4

Frequency response (a) and contour plot (b) for a straight oriented filter with $\varphi =\pi /6$; frequency response (c) and contour plot (d) for a Gaussian elliptically-shaped oriented filter with $\varphi =\pi /6$

Example 4.3

For the same orientation $\varphi =\pi /6$ and semi-axes $E=4, F=1.5$ the following values result from (19):$a=0.183571, b=-0.0074, c=0.165386$; substituting them into (27), we obtain the matrix $\mathbf{M}_\varphi$ in this case. The frequency response and contour plot of the Gaussian elliptically-shaped filter are shown in Fig. 4c, d. Their shapes look very similar to the ones of the ideal filter, given in Fig. 2c, d.

4.2 Method based on three-axis decomposition of oriented Gaussian

The second design method uses the idea to decompose the two types of 2D oriented Gaussian filters - the straight directional filter (9) and the elliptically-shaped filter (12), into three 1D Gaussian filters oriented along various directions in the frequency plane. Thus the frequency response $H_G (\omega _1,\omega _2 )$ results as a product of three Gaussians:

$$\begin{aligned} H_G (\omega _1,\omega _2 )=H_{G1} (\omega _1,\omega _2 )\cdot H_{G2} (\omega _1,\omega _2 )\cdot H_{G3} (\omega _1,\omega _2 ) \end{aligned}$$

(32)

In the proposed design method, for simplicity, we actually design oriented filters with orientation angles between 0 and $\pi /4$, comprised in the gray-shaded region delimited by the triangle AOB, in Fig. 5a. Any other filter with an arbitrary orientation angle $\varphi$ can be reduced to this sector through symmetries. A generic orientation angle $\prec AOP=\varphi \in [0, \pi /4]$ is formed by the filter longitudinal axis $\hbox {P}\hbox {P}_{ 1}$ with the axis $\hbox {A}\hbox {A}_{ 1}$ (frequency axis $\omega _{1}$).

Other possible angles marked on the diagram are: $\prec AOQ\in [\pi /{4,} \pi /2], \prec AOR\in [\pi /{2,} {3\pi }/4], \prec AOS\in [{3\pi }/{4,} \pi ]$. Due to the symmetry of an oriented filter with respect to the frequency plane origin, a filter with $\varphi >\pi$ is identical to the same filter oriented at $\varphi -\pi$. For filters with $\varphi \in [ \pi /{4, \pi }]$, we simply design a filter with $\varphi \in [0, \pi /4]$ and then through a mirroring about frequency axes and a rotation, we find the desired frequency response, as detailed below.

Fig. 5

a Various orientation angles in the frequency plane; three-axis decomposition in the frequency plane, along the directions: b $\omega _{1}, 2\omega _{1} +\omega _{2}$ and $\omega _{1} +\omega _{2}$; c $\omega _{1} +\omega _{2}, 2\omega _{1} +\omega _{2}$ and $\omega _{1} +2\omega _{2}$; d $\omega _{1}, 2\omega _{1} -\omega _{2}$ and $2\omega _{1} -\omega _{2}$

For a desired angle $\varphi _1 \in [\pi /{4,} \pi /2]$ (for instance $\prec AOQ$ in Fig. 5a), we design the filter with $\varphi =\pi /2-\varphi _1$, obtaining its transfer function $H_\varphi (z_1,z_2 )$. Then we make a mirroring (left-right flip) about axis $\hbox {A}\hbox {A}_{ 1}$ followed by a rotation to the right by $\pi /2$; these operations imply the frequency variable change: $\omega _1 \rightarrow \omega _2, \omega _2 \rightarrow \omega _1$, which in Z-transform are written $z_1 \rightarrow z_2,z_2 \rightarrow z_1$. Therefore, the filter transfer function will be $H_{\varphi 1} (z_1,z_2 )=H_\varphi (z_2,z_1 )$, so the complex frequency variables are interchanged. For the other two cases (orientation angles $\prec AOR, \prec AOS$) we get similar results. All these equivalences using symmetry are summarized in Table 1.

Table 1 Filter transfer functions derived using symmetry for various orientation angles

The method described in this subsection will be applied on the two types of Gaussian oriented filters and several design examples will be further presented.

4.2.1 Gaussian oriented filters with straight section

The simplest three-axis decomposition, which leads to an efficient 2D Gaussian oriented filter, is achieved along the frequency axes $\omega _1, \omega _2$ and $\omega _1 +\omega _2$ and was already briefly discussed in Sect. 3. The coefficients a, b and c are obtained, with expressions (18). Their variation on the angular range $\varphi \in [0,{ \pi }/4]$ is represented in Fig. 6a. It can be noticed that while a and c are positive within the given range, the parameter b is negative.

Example 4.4

For the orientation angle $\varphi =\pi /6$ and $k=4$, using (18), the following factored 2D frequency response is obtained for $H_{P2} (\omega )=\exp (-4\omega ^{2})$:

$$\begin{aligned} H_G (\omega _1,\omega _2 )= & {} H_{G1} (\omega _1 )\cdot H_{G2} (\omega _2 )\cdot H_{12} (\omega _1 +\omega _2 )\nonumber \\= & {} \exp \left( {-1.2679\cdot \omega _1^2} \right) \cdot \exp \left( {0.73205\cdot \omega _2^2 } \right) \cdot \exp \left( {-1.73205\cdot (\omega _1 +\omega _2 )^{2}} \right) \nonumber \\ \end{aligned}$$

(33)

The second exponential in (33) results with a positive exponent. Since in the expression of $H_G (\omega _1,\omega _2)$ the parameter k gives the directional selectivity, we may have to approximate a function $H_P (\omega )=\exp (k\omega ^{2})$ with positive values of k. This can be conveniently done for smaller values of k (usually $k<1)$, while for larger values of k the function diverges too much from its polynomial approximation. In order to obtain a more convenient implementation, we will consider a decomposition along other directions of the frequency plane. Other two possible axes from the first quadrant $(\varphi \in [0,{ \pi }/2])$ are $2\omega _{ 1} +\omega _2$ and $\omega _{ 1} +2\omega _2$. Depending on the angle $\varphi$, we can choose three possible axes closer to the given direction. As the filter characteristics will show, if a 2D Gaussian is decomposed along three close directions, the resulted 2D filter has a larger longitudinal bandwidth and higher directional selectivity.

For angle values in the sector $\varphi \in [0,\pi /4]$, a convenient decomposition would be along the axes $\omega _{ 1}, \omega _{1} +\omega _2$ and $2\omega _1 +\omega _2$; these directions are shown in Fig. 5b. We look for a decomposition of the form:

$$\begin{aligned} \omega ^{2}\rightarrow a\cdot \omega _{ 1}^2 +b\cdot \left( {\omega _{ 1} +\omega _2 } \right) ^{2}+c\cdot \left( {2\omega _{ 1} +\omega _2 } \right) ^{2} \end{aligned}$$

(34)

and the coefficients a, b, c are identified by comparing relations (34) and (9):

$$\begin{aligned} a= & {} 0.5 k\left( {3-\cos (2\varphi )-3\sin (2\varphi )} \right) \nonumber \\ b= & {} 0.5 k\left( {2-2\cos (2\varphi )-\sin (2\varphi )} \right) \nonumber \\ c= & {} 0.5 k\left( {-1+\cos (2\varphi )+\sin (2\varphi )} \right) \end{aligned}$$

(35)

The variation of the coefficients a, b, c given by (35) is plotted in Fig. 6b, for $k=1$. For orientation angles in the range $\varphi \in [0,\pi /6]$, the following three-axis decomposition would be convenient:

$$\begin{aligned} \omega ^{2}\rightarrow a\cdot \left( {\omega _1 +\omega _2 } \right) ^{2}+b\cdot \left( {2\omega _1 +\omega _2 } \right) ^{2}+c\cdot \left( {\omega _1 +2\omega _2 } \right) ^{2} \end{aligned}$$

(36)

and we identify coefficients a, b, c by comparing mapping (36) with (9):

$$\begin{aligned} a= & {} k{\left( {-4+5\sin (2\varphi )} \right) }/2 \nonumber \\ b= & {} k{\left( {3+\cos (2\varphi )-3\sin (2\varphi )} \right) }/6 \nonumber \\ c= & {} k{\left( {3-\cos (2\varphi )-3\sin (2\varphi )} \right) }/6 \end{aligned}$$

(37)

The variation of coefficients a, b, c in this case is plotted in Fig. 6c. The axes $\omega _1 +\omega _2, 2\omega _1 +\omega _2$ and $\omega _1 +2\omega _2$ are shown in Fig. 5 (c). For the same values as before ($\varphi =\pi /6, k=4$) the following decomposition results:

$$\begin{aligned} H_G (\omega _1,\omega _2 )= & {} H_{G1} (\omega _1,\omega _2 )\cdot H_{G2} (\omega _1,\omega _2 )\cdot H_{G3} (\omega _1,\omega _2)\nonumber \\= & {} \exp \left( {-0.66025\cdot (\omega _1 +\omega _2 )^{2}} \right) \cdot \exp \left( {-0.60128\cdot (2\omega _1 +\omega _2 )^{2}} \right) \nonumber \\&\cdot \exp \left( {0.06538\cdot (\omega _1 +2\omega _2 )^{2}} \right) \end{aligned}$$

(38)

Obviously all exponents are smaller in absolute value than in decomposition (33), especially the positive one (with $c=0.06538$). This allows for a convenient, low-order approximation.

Fig. 6

Variation of coefficients a, b, c given by equations: a (18); b (35); c (37) with the orientation angle $\varphi$

The next design step is to find a trigonometric series approximation of each Gaussian in (38) and we use again the Chebyshev series. However, we will finally need a trigonometric expansion of each Gaussian $H_G (\omega )=\exp (-k\omega ^{2})$ in the variable $\cos (n\omega )$, rather than a polynomial in powers of the frequency $\omega$. Therefore, before calculating the Chebyshev series of a Gaussian $H_G (\omega )=\exp (-k\omega ^{2})$, with a specified k, the following variable change will be used:

$$\begin{aligned} \omega =\arccos \left( {x/\pi } \right) \;\;\leftrightarrow \;\;x=\pi \cos (\omega ) \end{aligned}$$

(39)

We get first the polynomial Chebyshev series expansion of $H_G (\arccos (x))$ in variable x, for $x\in [-\pi ,\pi ]$:

$$\begin{aligned} H_G (\arccos (x/\pi ))= & {} \exp \left( {-k\cdot \left( {\arccos (x/\pi )} \right) ^{2}} \right) \cong \sum _{n=0}^N {c_n \cdot x^{n}} \nonumber \\= & {} c_0 +c_1 x+c_2 x^{2}+c_3 x^{3}+ \ldots +c_N x^{N} \end{aligned}$$

(40)

where the number of terms N is chosen large enough to ensure the desired precision, specified by the maximum error. Substituting back $x=\pi \cos (\omega )$ in the polynomial expression (40), a trigonometric series results:

$$\begin{aligned} H_G (\omega )= & {} \exp (-k\omega ^{2})\cong H_P (\omega )=\sum _{n=0}^N {b_n \cdot \cos ^{n}(\omega )} =b_0 +b_1 \cos \omega +b_2 \cos ^{2}\omega \nonumber \\&+b_3 \cos ^{3}\omega + \ldots +b_N \cos ^{N}\omega \end{aligned}$$

(41)

with $b_0 =c_0,b_k =c_k \cdot \pi ^{k}$. This trigonometric approximation of the Gaussian $H_G (\omega )$ was denoted $H_P (\omega )$. According to the fundamental theorem of algebra, the polynomial (41) can be factored into first and second order polynomials in $\cos \omega$, as follows (where $n+2m=N$, the filter order):

$$\begin{aligned} H_P (\omega )=\gamma \cdot \prod _{i=1}^n {(\cos \omega +a_i )} \cdot \prod _{j=1}^m {(\cos ^{2}\omega +a_{1j} \cos \omega +a_{2j} )} \end{aligned}$$

(42)

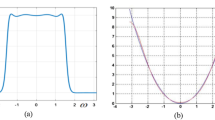
where $\gamma$ is a constant. Of course, for a more selective Gaussian (for a larger value of the selectivity parameter k), a larger number N of terms have to be taken into account in the Chebyshev series. In Fig. 7 the order N of Chebyshev series approximation vs. Gaussian selectivity parameter k is plotted for two imposed accuracy values, $\varepsilon =0.01$ and $\varepsilon =0.04$, respectively. In this paper we have used the accuracy value $\varepsilon =0.04$, sufficient for a good approximation. From both plots we notice that the most efficient approximation (i.e. fewer terms) results for k around 0.5.

Fig. 7

Order of Chebyshev series approximation vs. Gaussian selectivity parameter k for two imposed accuracy values: a $\varepsilon =0.01$; b $\varepsilon =0.04$

Therefore, a certain decomposition along three axes is most efficient if the parameters of the three Gaussian components result less than 1, or as small as possible, especially for selective Gaussians. Using this method for the Gaussian factors in (38) and also trigonometric identities, the following factored approximations result:

$$\begin{aligned} H_{G1} (\omega )\cong H_{P1} (\omega )= & {} 0.3469+0.4755\cdot \hbox {cos}\omega +0.1524\cdot \hbox {cos}(2\omega )+0.023122\cdot \hbox {cos}(3\omega )\nonumber \\= & {} 0.04624\cdot \left( {\hbox {cos}\omega +{1.0103}} \right) \left( {\hbox {cos}\hbox {(2}\omega )+{4.57063}\cdot \hbox {cos}\omega +{5.1643}} \right) \end{aligned}$$

(43)

$$\begin{aligned} H_{G2} (\omega )\cong H_{P2} (\omega )= & {} 0.3635+0.4803\cdot \hbox {cos}\omega +0.1375\cdot \hbox {cos}(2\omega )+0.017512\cdot \hbox {cos}(3\omega ) \nonumber \\= & {} 0.03502\cdot \left( {\hbox {cos}\omega +{1.037}} \right) \left( {\hbox {cos} (2\omega )+{5.7765} \hbox {cos} \omega +\hbox {7.223}} \right) \end{aligned}$$

(44)

$$\begin{aligned} H_{G3} (\omega )\cong H_{P3} (\omega )= & {} 1.264-0.340425\cdot \hbox {cos}\omega +0.11023\cdot \hbox {cos}(2\omega )-0.05233\cdot \hbox {cos}(3\omega )\nonumber \\&+\,0.03026\cdot \hbox {cos}(4\omega )\nonumber \\&-\,0.0197\cdot \hbox {cos}(5\omega )=-{0.0788}\cdot \left( {\hbox {cos}\omega -{1.541}} \right) ( \hbox {cos} (2\omega )\nonumber \\&+\,{4.0405} \hbox {cos}\omega +{4.2513})\left( {\hbox {cos} (2\omega )-{2.49458} \hbox {cos}\omega +{3.9986}} \right) \end{aligned}$$

(45)

and therefore the three Gaussian components from (38) along the axes $\omega _1 +\omega _2, 2\omega _1 +\omega _2$ and $\omega _1 +2\omega _2$ result as: $H_{G1} (\omega _{1},\omega _{2} )\cong H_{P1} (\omega _{1} +\omega _{2} ), H_{G2} (\omega _{1},\omega _{2} )\cong H_{P2} (2\omega _{1} +\omega _{2} ), H_{G3} (\omega _{1} ,\omega _{2} )\cong H_{P3} (\omega _{1} +2\omega _{2} )$. For example, using (43), the Gaussian along direction $\omega _1 +\omega _2$ (the frequency plane diagonal) is written in the form:

$$\begin{aligned} H_{G1} (\omega _{1},\omega _{2} )\cong & {} H_{P1} (\omega _{1} +\omega _{2} )=0.34696+0.47548\cdot \hbox {cos}(\omega _{1} +\omega _{2})\nonumber \\&+\,0.1524\cdot \hbox {cos}(2\omega _{1} +2\omega _{2} )+0.02312\cdot \hbox {cos}(3\omega _{1} +3\omega _{2} ) \end{aligned}$$

(46)

The frequency response and contour plot for the filter designed above are given in Fig. 8a, b. Also the filter components along the axes $\omega _1 +\omega _2, 2\omega _1 +\omega _2, \omega _1 +2\omega _2$ are displayed in Fig. 8c, (d), (e).

Example 4.5

For a more selective filter ($\varphi =\pi /6$ and $k=9)$, we obtain the decomposition along the same axes:

$$\begin{aligned} \exp (-9 \omega ^{2})\rightarrow & {} \exp \left( {-1.48557\cdot \left( {\omega _1 +\omega _2 } \right) ^{2}} \right) \cdot \exp \left( {-1.3529\cdot \left( {2\omega _1 +\omega _2 } \right) ^{2}} \right) \cdot \exp \nonumber \\&\quad \left( {0.14711\cdot \left( {\omega _1 +2\omega _2 } \right) ^{2}} \right) \nonumber \\= & {} H_{P1} (\omega _1 +\omega _2)\cdot H_{P2} (2\omega _1 +\omega _2 )\cdot H_{P3} (\omega _1 +2\omega _2) \end{aligned}$$

(47)

Using the method exposed above, we obtain the 2D filter frequency response and contour plot in Fig. 8f, g. Even for such a selective filter, the characteristic remains very uniform and linear along the filter longitudinal axis. For comparison, using decomposition (34) the same frequency response can be expressed as:

$$\begin{aligned} H_2 (\omega _1,\omega _2)=\exp \left( {-3.894\cdot \omega _1^2 } \right) \cdot \exp \left( {1.984\cdot (\omega _1 +\omega _2 )^{2}} \right) \cdot \exp \left( {-4.045\cdot (2\omega _1 +\omega _2 )^{2}} \right) \end{aligned}$$

(48)

which is much more difficult to approximate than (47), due to its larger exponents. This proves that a proper choice of decomposition axes is important. The following three-axis decomposition would be convenient for orientation angles around 0 (along frequency axis $\omega _{ 1}$), e.g. from the range $\varphi \in [0, { \pi }/8]$; the decomposition is made along the axes $\omega _{ 1}, 2\omega _{ 1} -\omega _{2}$ and $2\omega _{ 1} +\omega _{2}$, shown in the frequency plane in Fig. 5d:

$$\begin{aligned} \omega ^{2}\rightarrow & {} a\cdot \omega _{ 1}^2 +b\cdot \left( {2\omega _{ 1} -\omega _{2} } \right) ^{2}+c\cdot \left( {2\omega _{ 1} +\omega _{2} } \right) ^{2}\end{aligned}$$

(49)

$$\begin{aligned} a= & {} {\left( {-3+5\cos (2\varphi )} \right) }/2 \nonumber \\ b= & {} {\left( {2-2\cos (2\varphi )-\sin (2\varphi )} \right) }/8 \nonumber \\ c= & {} {\left( {2-2\cos (2\varphi )+\sin (2\varphi )} \right) }/8 \end{aligned}$$

(50)

The variation of a, b and c on the angle value range $\varphi \in [0, { \pi }/8]$ is displayed in Fig. 8h.

Fig. 8

a, b frequency response and contour plot of the Gaussian oriented filter $H_G (\omega _1,\omega _2 )$; c, d, e the component filters $H_{G1} (\omega _1,\omega _2 ), H_{G2} (\omega _1,\omega _2 )$ and $H_{G3} (\omega _1,\omega _2 )$ oriented along the directions $\omega _1 +\omega _2, 2\omega _1 +\omega _2$ and $\omega _1 +2\omega _2$; f, g frequency response and contour plot of the Gaussian oriented filter $H_G (\omega _1,\omega _2 )$based on $H_P (\omega )\,=\,\exp (-9\omega ^{2})$ and $\varphi =\pi /6$; h Variation of coefficients a, b, c given by (50) with the orientation angle $\varphi$

Fig. 9

a, b frequency response and contour plot of the Gaussian oriented filter $H_G (\omega _1,\omega _2 )$ with $\varphi =0.1 \pi$ and $k=4$, decomposed along the directions $\omega _{ 1} , 2\omega _{ 1} -\omega _{2}$ and $2\omega _{ 1} +\omega _{2}$

Example 4.6

For $\varphi =0.1 \pi$ and $k=4$, the following decomposition is derived along the specified axes:

$$\begin{aligned} H_G (\omega _1,\omega _2 )= & {} \exp \left( {-2.09017\cdot \omega _1^2 } \right) \cdot \exp \left( {0.10291\cdot (2\omega _1 -\omega _2 )^{2}}\right) \nonumber \\&\cdot \exp \left( {-0.4849\cdot (2\omega _1 +\omega _2 )^{2}} \right) \end{aligned}$$

(51)

The following approximations result:

$$\begin{aligned} H_{P1} (\omega )\cong & {} 0.19488+0.34582\cdot \hbox {cos}\omega +0.24153\cdot \hbox {cos}(2\omega )+0.1328\cdot \hbox {cos}(3\omega )\nonumber \\&+\,0.0575\cdot \hbox {cos}(4\omega )+0.01958\cdot \hbox {cos}(5\omega )\end{aligned}$$

(52)

$$\begin{aligned} H_{P2} (\omega )\cong & {} 1.47249-0.629866\cdot \hbox {cos}\omega +0.23045\cdot \hbox {cos}(2\omega )-0.11407\cdot \hbox {cos}(3\omega )\nonumber \\&+\,0.06717\cdot \hbox {cos}(4\omega )-0.04413\cdot \hbox {cos}(5\omega )\end{aligned}$$

(53)

$$\begin{aligned} H_{P3} (\omega )\cong & {} 0.40425+0.48515\cdot \hbox {cos}\omega +0.10173\cdot \hbox {cos}(2\omega ) \end{aligned}$$

(54)

The 2D straight directional filter for these parameters is shown in Fig. 9a, b. The filter characteristic shows a small ripple-like distortion along its longitudinal axis, but still the frequency response has a satisfactory shape.

4.2.2 Generalization

In a more general case, the direction $M\omega _1 +N\omega _2$ corresponds to an orientation angle $\varphi _{MN} =\hbox {arctg}(N/M)$, with M and N integers, and will result in an oriented Gaussian which will expand in a series of cosine terms of the form $\cos (M\omega _1 +N\omega _2 )$. In 2D Z-transform, this corresponds to a term $0.5\cdot \left( {z_1^M z_2^N +z_1^{-M} z_2^{-N} } \right)$. Of course, for larger M and N, higher order terms result, which implies a higher complexity of the 2D filter. The case $M=N$ is trivial, as the direction $M\omega _1 +N\omega _2$ would be the same as $\omega _{ 1} +\omega _2$, i.e. the diagonal of the frequency plane. For our purpose, the frequency combinations $\omega _{ 1} \pm 2\omega _2$ and $2\omega _{ 1} \pm \omega _2$ are sufficient to implement a 2D Gaussian oriented filter. The direction $2\omega _{ 1} +\omega _2$ corresponds to an angle of $\varphi _{21} =\hbox {arctg}(0.5)\cong 0.1476 \pi \cong 26.5 ^{\mathrm{o}}$.

4.2.3 Gaussian oriented filter with elliptically-shaped section

For a Gaussian oriented filter with elliptically-shaped section, we can apply the same method of decomposition along three convenient axes. Let us use first the decomposition along the axes $\omega _{ 1}, \omega _{ 2}$ and $\omega _{ 1} +\omega _{ 2}$.

Fig. 10

Variation of coefficients a, b, and c for: a $E = 2, F = 1$, variable orientation: $\varphi \in [0,\,\pi /4]$; b $\varphi =\pi /6$ and variable ellipse aspect ratio: $2<E/F<10\,(E=2, F\in [0.2,\;1])$

Identifying the coefficients in (10) and (17), the following expressions will result, where $p=1/{E^{2}}$ and $p=1/{F^{2}}$:

$$\begin{aligned} a= & {} 0.5 (p+q)+0.5 (p-q) (\sin 2\varphi +\cos 2\varphi ) \nonumber \\ b= & {} 0.5 (p+q)+0.5 (p-q) (\sin 2\varphi -\cos 2\varphi ) \nonumber \\ c= & {} 0.5 (q-p)\cdot \sin 2\varphi \end{aligned}$$

(55)

These coefficients depend both on orientation angle and ellipse semi-axes; for a given aspect ratio, these coefficients can be represented graphically. For instance with $E = 2, F = 1$ we obtain the variation of coefficients a, b, c in Fig. 10a. We notice that all coefficients are positive for orientation angles $\varphi \in [0, \;\pi /4]$. The coefficients (55) are also displayed in Fig. 10b for a fixed angle $\varphi =\pi /6$ and variable aspect ratio: $2<E/F<10$.

Example 4.7

For an orientation angle $\varphi =\pi /6$ and $E = 2, F = 0.8$, the following positive coefficients result: $a=0.01129, b=0.663455, c=0.564791$.

$$\begin{aligned} H_E (\omega _{ 1},\omega _{2})= & {} H_{G1} (\omega _{ 1} )\cdot H_{G2} (\omega _{ 2} )\cdot H_{G3} (\omega _{ 1} +\omega _{ 2} ) \nonumber \\= & {} \exp (-0.01129\cdot \omega _{ 1}^2 )\cdot \exp (-0.663455\cdot \omega _{ 2}^2 )\cdot \exp \left( {-0.564791\cdot (\omega _{1} +\omega _{ 2})^{2}} \right) \nonumber \\ \end{aligned}$$

(56)

and the accurate approximations are easily obtained:

$$\begin{aligned} H_{G1} (\omega )\cong H_{P1} (\omega )= & {} 0.96406+0.0432527\cdot \hbox {cos}\omega -0.010268\cdot \hbox {cos}(2\omega )\nonumber \\&+\,0.0045307\cdot \hbox {cos}(3\omega )\end{aligned}$$

(57)

$$\begin{aligned} H_{G2} (\omega )\cong H_{P2} (\omega )= & {} 0.34622+0.47539\cdot \hbox {cos}\omega +0.15325\cdot \hbox {cos}(2\omega )\nonumber \\&+\,0.023464\cdot \hbox {cos}(3\omega )\end{aligned}$$

(58)

$$\begin{aligned} H_{G3} (\omega )\cong H_{P3} (\omega )= & {} 0.37504+0.48282\cdot \hbox {cos}\omega +0.12728\cdot \hbox {cos}(2\omega )\nonumber \\&+\,0.01438\cdot \hbox {cos}(3\omega ) \end{aligned}$$

(59)

In this particular case, since the coefficient a is very close to zero, $H_{P1} (\omega _{ 1} )\cong 1$ and the frequency response $H_E (\omega _{ 1},\omega _{ 2} )$ can be approximated with a negligible error as

$$\begin{aligned} H_E (\omega _{ 1},\omega _{ 2} )\cong H_{P2} (\omega _{ 2} )\cdot H_{P3} (\omega _{ 1} +\omega _{ 2} ) \end{aligned}$$

(60)

It is displayed in Fig. 11a along with its contour plot in Fig. 11b and has a correct and undistorted elliptical shape.

Fig. 11

Frequency response (a) and contour plot (b) for an oriented elliptically-shaped Gaussian filter with $\varphi =\pi /6, E = 2, F = 0.8$, resulted by decomposition along axes $\omega _{1}, \omega _{2} , \omega _{1} +\omega _{2}$

In all the 2D frequency responses derived using this method, for implementation purposes we may substitute $\cos \omega _{ 1}, \cos \omega _{ 2}, \cos (\omega _{ 1} +\omega _{ 2} )$ and the general term $\cos (M\omega _{ 1} +N\omega _{ 2} )$ by ${(z_1 +z_1^{-1} )}/2, {(z_2 +z_2^{-1} )}/2, {(z_1 z_2 +z_1^{-1} z_2^{-1} )}/2$ and ${(z_1^M z_2^N +z_1^{-M} z_2^{-N} )}/2$ respectively. For example the factors $H_{P1} (\omega _{ 1} ), H_{P2} (\omega _{ 2} )$ and $H_{P3} (\omega _{ 1} +\omega _{ 2} )$ corresponding to approximations (57) - (59) can be expressed formally in complex variables $z_{1}$ and $z_{2}$ as:

$$\begin{aligned} H_{P1} (z_1)= & {} 0.96406+0.021626\cdot \left( {z_1 +z_1^{-1} } \right) -0.005134\cdot \left( {z_1^2 +z_1^{-2} }\right) \nonumber \\&+\,0.002265\cdot \left( {z_1^3 +z_1^{-3} } \right) \end{aligned}$$

(61)

$$\begin{aligned} H_{P2} (z_2)= & {} 0.34622+0.237695\cdot \left( {z_2 +z_2^{-1} } \right) +0.076625\cdot \left( {z_2^2 +z_2^{-2} }\right) \nonumber \\&+\,0.011732\cdot \left( {z_2^3 +z_2^{-3} } \right) \end{aligned}$$

(62)

$$\begin{aligned} H_{P3} (z_1 z_2)= & {} 0.37504+0.24141\cdot \left( {z_1 z_2 +z_1^{-1} z_2^{-1} } \right) +0.06364\cdot \left( {z_1^2 z_2^2 +z_1^{-2} z_2^{-2} } \right) \nonumber \\&+\,0.00719\cdot \left( {z_1^3 z_2^3 +z_1^{-3} z_2^{-3} } \right) \end{aligned}$$

(63)

Thus the overall 2D filter frequency response corresponds to a transfer function in the two-variable Z-transform:

$$\begin{aligned} H_E (z_{ 1},z_{ 2} )=H_{P1} (z_{ 1} )\cdot H_{P2} (z_{ 2} )\cdot H_{P3} (z_{ 1} z_{ 2} ) \end{aligned}$$

(64)

as a product of three partial transfer functions in the complex variables $z_{ 1}$ and $z_{ 2}$. For angles closer to $\varphi =\pi /4$, the filter is decomposed along the axes $\omega _1 +\omega _2, 2\omega _1 +\omega _2$ and $\omega _1 +2\omega _2$. Identifying coefficients from (10), (36) we get:

$$\begin{aligned} a= & {} -2(p+q)-2.5 (p-q)\sin 2\varphi \nonumber \\ b= & {} 0.5 (p+q)+{(p-q)\left( {3\sin 2\varphi +\cos 2\varphi } \right) }/6 \nonumber \\ c= & {} 0.5 (p+q)+{(p-q)\left( {3\sin 2\varphi -\cos 2\varphi } \right) }/6 \end{aligned}$$

(65)

For $E = 2$ and $F = 0.4$, the coefficients a, b and c from (65) are plotted for $\varphi \in [\pi /6,{ \pi }/{4]}$ in Fig. 12a. They can also be plotted for a fixed angle (e.g. $\varphi =\pi /6)$ and variable aspect ratio $(2<E/F<10)$ as in Fig. 12b.

Example 4.8

Let us design using this three-axis decomposition a Gaussian elliptically-shaped filter with parameters: $E = 2, F = 0.4$ (which gives an aspect ratio of $E/F=5)$ and the orientation angle $\varphi =\pi /{5=36^{\mathrm{o}}}$. From (65) the following coefficients result:$a=1.2658, b=0.0878, c=0.7058$; then the following approximations are derived:

$$\begin{aligned} H_{P1}(\omega )= & {} 0.25073+0.4116\cdot \hbox {cos} \omega +0.2276\cdot \hbox {cos} 2\omega +0.084764\cdot \hbox {cos} 3\omega \nonumber \\&+\,0.021272\cdot \hbox {cos} 4\omega \end{aligned}$$

(66)

$$\begin{aligned} H_{P2} (\omega )= & {} 0.77302+0.25484\cdot \hbox {cos}\;\omega -0.038876\cdot \hbox {cos} 2\omega +0.016849\cdot \hbox {cos} 3\omega \end{aligned}$$

(67)

$$\begin{aligned} H_{P3} (\omega )= & {} 0.33571+0.471376\cdot \hbox { cos}\omega +0.162723\cdot \hbox {cos} 2\omega +0.0278\cdot \hbox {cos} 3\omega \end{aligned}$$

(68)

Fig. 12

Variation of coefficients a, b, and c for: a $E = 2, F = 0.4$ and variable orientation: $\varphi \in [\pi /6,{\pi }/{4]}$; b $\varphi =\pi /6$ and variable ellipse aspect ratio: $2<E/F<10 (E=2, F\in [0.2,\;1])$

Fig. 13

Frequency response (a) and contour plot (b) for an oriented elliptically-shaped Gaussian filter with $\pi /5, E = 2, F = 0.4$, decomposed along the axes $\omega _1 +\omega _2, 2\omega _1 +\omega _2$ and $\omega _1 +2\omega _2$; c Error function $\Delta H(\omega _1,\omega _2)$

and the 2D filter frequency response is:

$$\begin{aligned} H_E (\omega _{ 1},\omega _{ 2} )= & {} \exp \left( {-1.2658\cdot (\omega _{1} +\omega _{2} )^{2}} \right) \cdot \exp \left( {-0.0878\cdot (2\omega _{1} +\omega _{ 2} )^{2}} \right) \nonumber \\&\cdot \exp \left( {-0.7058\cdot (\omega _{ 1} +2\omega _{ 2} )^{2}} \right) \nonumber \\= & {} H_{P1} (\omega _{1} +\omega _{2} )\cdot H_{P2} (2\omega _{1} +\omega _{2} )\cdot H_{P3} (\omega _{1} +2\omega _{2} ) \end{aligned}$$

(69)

We notice that all coefficients result positive for the chosen parameters. The frequency response and contour plot shown in Fig. 13a, b have a correct shape, with some distortions towards the margins of the frequency plane.

4.3 Distortion analysis

As in any design using analytical or numerical optimization techniques, the 2D filters obtained here inherently present some distortions. For instance, the ringing in the frequency domain, or ripple, visible in the stop band of the Gaussian characteristic in Fig. 1b appears due to the polynomial approximation (6) resulted using Chebyshev series expansion. Similarly, the approximated Gaussian response in Fig. 3b has a small ripple due to the combined approximation errors from (6) and (22). By substituting (22) into (6), a Fourier series approximation of the Gaussian is obtained. For a ripple of smaller amplitude, a higher order approximation is needed, which is not convenient for implementation, so an optimal trade-off must be reached. In the triple-axis decomposition method, the stop band ripple is further diminished because it results as a product of small ripples of the three oriented Gaussian responses.

The 2D FIR filters designed using the proposed analytical methods can be characterized by a distortion measure which describes the similarity between the frequency response of the designed filter and its ideal counterpart. For instance, if $H(\omega _1,\omega _2)$ and $H_I (\omega _1,\omega _2)$ are the frequency responses of the designed filter and ideal filter, respectively, their difference defines the error $\Delta H(\omega _1, \omega _2)=H(\omega _1 ,\omega _2 )-H_I (\omega _1,\omega _2)$. The error function for the filter in Fig. 13a is displayed in Fig. 13c. As can be noticed, the largest distortions are at the corners of the frequency plane. The frequency response is usually represented as a mesh or sampled surface in a convenient number of equally spaced points in the frequency plane, corresponding to a $N\times N$ matrix, where N is the number of points on the $[-\pi ,\pi ]$ range. A relevant measure of distortion may be the root of average value of the squared differences over all the sampling points, i.e the RMS. Taking N sampling points on both axes of the frequency plane, the distortion factor is defined as:

$$\begin{aligned} \delta =\frac{1}{N^{2}}\cdot \sqrt{\sum _{m=1}^N \sum _{n=1}^N {\left( {\Delta H({2m\pi }/N,{2n\pi }/N)} \right) ^{2}} } \end{aligned}$$

(70)

Using the expression (70), we can obtain the dependence of the distortion factor $\delta$ on the orientation angle $\varphi$ of the directional Gaussian filter, which is helpful in evaluating the design accuracy. Let us consider the filter with elliptical symmetry designed in Example 4.3, with parameter values $\varphi =\pi /6, E=4, F=1.5$. Keeping constant the semi-axes values E and F and varying the orientation angle $\varphi$ in the range $\varphi \in [0,{ \pi }/2]$ with a small step, the curve displayed in Fig. 14a is obtained, for $N=100$ points. The largest distortion is $\delta _{\max } \cong {0.031}=3.1\,\%$ and occurs at values of $\varphi$ close to 0 and $\pi /2$. There is also a local maximum of about $\delta \cong {0.0182}=1.82\,\%$ at $\varphi =\pi /4$. Due to symmetry, it is sufficient to analyze the filter distortions for $\varphi \in [0,{ \pi }/2]$. The factor $\delta$ depends weakly on the number N of sampling points. For example, taking instead $N=1000$, we obtain at $\varphi =\pi /4$ the value $\delta \cong {0.0181}=1.81\,\%$.

Fig. 14

Distortion factor $\delta$ vs. orientation angle $\varphi$ for the directional elliptically-shaped Gaussian filter with $k=4$ and: a $E=4, F=1.5$; b $F=1; E=3, E=4, E=5$ and $E=6$ respectively

Let us next consider another Gaussian elliptically-shaped filter, with $F=1$ and increasing aspect ratios E / F; taking $E=3, E=4, E=5$ and $E=6$ respectively, the curves shown in Fig. 14b are obtained, again for $N=100$ points. It can be noticed that the dependence of $\delta$ with $\varphi$ is symmetric about the angle $\varphi =\pi /4$, but not monotonic for $\varphi \in [0,{ \pi }/2]$, having three or five maxima. The largest distortion for $E=6$ is around $5\,\%$. Therefore, the filters designed using this method are quite accurate, even for large aspect ratios, i.e. high directional selectivity. For filters designed using the triple axis decomposition, a similar distortion analysis can be made.

4.4 Discussion

In many works on this topic, Gaussian directional filters are designed and implemented as IIR filters, due to their advantages, mainly higher processing speed and reduced computational complexity, like in Young and Vliet (1995), Geusebroek et al. (2003), Lam and Shi (2007), Lampert and Wirjadi (2006). The aim of our approach was to develop simple analytical design methods in the frequency domain for such filters, based on the approximation of the ideal 2D oriented Gaussian response. The main reason why a FIR version was approached here is that FIR filters are unconditionally stable. It is more difficult to design stable 2D IIR filters through analytical methods, due to stability restrictions. Even if the 1D IIR prototype used in design is stable, the applied frequency mappings may not preserve stability, so for 2D IIR filters, especially non-separable, the stability is difficult to guarantee. Moreover, the proposed 2D FIR Gaussian directional filters have some advantages. In both versions, i.e. based on mapping substitution and triple axis decomposition, the convolution kernel results directly decomposed into smaller size kernels, for instance $5\times 5$, allowing for the 2D oriented filter to be realized as a cascade of its component filters, which simplifies the implementation.

The matrix $\mathbf{M}_\varphi$ given by (27), and the filter kernel, expressed as a convolution of elementary kernels in (31), depend explicitly on specified parameters—the orientation $\varphi$ for straight directional filters, and additionally the semi-axes E and F,  for elliptically-shaped filters. Thus, the resulted filters are adjustable in orientation and aspect ratio. Using the second method, the designer can find an efficient Gaussian decomposition by properly choosing the set of three axes, such that the component filters result of minimum order. As shown in design examples, the resulted filters have accurate frequency responses for a wide range of specifications and present low distortions, mainly due to the small ripple present in the stop band. Moreover, the first proposed method is more general and is applicable for any zero-phase prototype with a polynomial approximation, not only Gaussian, for instance a maximally-flat prototype. The second method exploits the property of 2D Gaussian to be separable, so it is not suited for other types of filters.

The paper Lampert and Wirjadi (2006) proposes a technique in the space domain to separate the Gaussian kernel along arbitrary axes in $\mathbb {R}^{\mathrm{N}}$, with minimum number of interpolations. Our design is achieved in the frequency domain, the filter kernel resulting by coefficient identification from the factored frequency response, expressed as 2D DFT (Discrete Fourier Transform). The proposed approach eliminates interpolation between pixels because the decomposition axes are chosen along directions $M\omega _1 +N\omega _2$, with M and N integers, in particular $\omega _{ 1}, \omega _2, \omega _{ 1} \pm \omega _2, \omega _{ 1} \pm 2\omega _2$ and $2\omega _{ 1} \pm \omega _2$. Using the Chebyshev series approximation in design, the resulted 2D filters are accurate, efficient and of relatively low order for the given specifications.

Fig. 15

a binary test image; b FFT spectrum magnitude; c, d filtered output image for ${\varphi =\pi }/6$ and ${\varphi =5\pi }/{12}$; e straw texture image; f FFT spectrum magnitude; g, h, i, j filtered images with ${\varphi =\pi }/8,{\varphi =-\pi }/6, {\varphi =5\pi }/{12}$ and ${\varphi =-\pi }/3$; k, l binary images resulted from g and h by thresholding

5 Applications and simulation results

The designed Gaussian directional filters can be used to select from a given image the lines with a specified orientation. In order to prove the filtering capability of these filters, two test images were used. A binary image containing straight lines with gradually varying orientation is displayed in Fig. 15a, while Fig. 15e shows a real grayscale texture image of $1100\times 1100$ pixels, representing straws with random orientations. It is known that the spectrum of a straight line is oriented in the frequency plane $(\omega _{ 1},\omega _{ 2} )$ at an angle of $\pi /2$ with respect to the line direction. This can be seen in the FFT spectrum magnitude (b), displayed on the range $\omega _{ 1},\omega _{ 2} \in [{-\pi }/4,\pi /4]$ for better visibility. Only the lines for which the spectrum overlaps with the filter frequency response remain in the output image, while the rest are more or less blurred and are practically eliminated through directional low-pass filtering. For instance, with an orientation ${\varphi =\pi }/6$, in the output image (c), a single line and its closest neighbors are preserved. With ${\varphi =5\pi }/{12}$ we get the output image (d) in which only two lines are detected. The real texture image (e) has the FFT spectrum magnitude (f) displayed for $\omega _{ 1},\omega _{ 2} \in [{-\pi }/4,\pi /4]$, in which a fine structure of spectral lines is visible, corresponding to the straws which are roughly straight, thin lines. The images from Fig. 15g, h, i, j result using selective Gaussian straight directional filters with orientation angles ${\varphi =\pi }/8, {\varphi =-\pi }/6, {\varphi =5\pi }/{12}$ and ${\varphi =-\pi }/3$. A filter with ${\varphi =-\pi }/6$ is a filter with ${\varphi =\pi }/6$ whose kernel is mirrored left-right. Applying a convenient threshold to the directionally filtered image, a binary image results, where the detected objects are clearly visible. For example, the images (k) and (l) result from (g) and (h) by simple thresholding. Therefore, applying selective directional filters, we can detect the lines with roughly the same orientation and eliminate the others. The output images show the high directional resolution of these filters.

6 Conclusion

This work proposes two analytical design methods in the frequency domain for 2D orientation-selective Gaussian filters. The design relies on specific frequency transformations applied to a Gaussian prototype. In this paper, FIR filters were approached; this eliminates from the start the issue of ensuring stability, which for 2D recursive filters, especially non-separable, may be quite a difficult problem. These methods were applied to two types of oriented filters, having either a straight directional or an elliptically-shaped support in the frequency plane.

The first design method is generally easier to apply. For both types of oriented filters, for specified selectivity, the Gaussian polynomial approximation is found using the Chebyshev series. For a specified orientation, a certain frequency mapping is determined. Then the frequency response of the 2D filter results directly in a factored form, by a simple variable substitution. In the second method, depending on filter specifications, the first design step is to choose a set of three axes for the decomposition of the 2D oriented Gaussian filter, with straight or elliptical support. Then, using a Chebyshev series expansion, the Gaussian along each direction is expressed as a trigonometric polynomial in the two frequency variables. The desired 2D filter results as a cascade of the three component filters. Design examples show that the filters have accurate shapes, with relatively low distortions, for a large range of parameters.

This method yields a factored frequency response from which the filter kernel results directly as a convolution of small size matrices. The necessity of interpolation, solved by researchers in various ways, is completely eliminated. This analytical design approach based on 1D prototypes and frequency mappings is relatively simple, intuitive and accurate and uses polynomial approximations, but no other optimization algorithms are needed. The aim of this paper was limited to developing the proposed design methods and to present the design steps leading from the prototype and imposed specifications to the frequency response of the desired 2D filters. The actual implementation of the 2D filters was not approached here, but a large variety of existing methods can be applied. In future work on this topic, however, the filter implementation aspects, mainly regarding computational efficiency, will also be studied.