1 Introduction

Ever since the expansion of digital signal processing field, two-dimensional filters have been extensively studied by many researchers, due to the their essential applications in image processing, and many design techniques have been developed [1]. While algorithms involving numerical optimization generally yield optimal 2D filters, ensuring the best trade-off between accuracy and complexity, analytical design methods based on various transformations have also become popular due to their obvious advantages. The frequency response of the designed filter results in closed form, and it can be also made adjustable through specified parameters, when necessary. Generally, analytical methods are based on 1D prototypes with imposed shape and specifications, which then generate the desired 2D filters by applying various frequency mappings.

Researchers have developed a large variety of 2D filters, both of FIR and IIR type, with frequency response of various shapes, each finding specific applications in image processing. A widely-used technique for designing 2D FIR filters with various shapes is the McClellan transform [2, 3]. A particular class are elliptically-shaped filters, approached in works such as [4, 5, 6, 7]. In [4], design of oriented 2D filters with elliptical magnitude response is proposed, while [5] describes a multiscale region detector, based a set of elliptical Gaussian filters for low-level image analysis. Elliptical symmetry in 2D filters by adjusting parameters is studied in [6], and image filtering with a variable Gaussian elliptic window is investigated in [7]. Elliptical filters found useful applications in iris recognition [8], fingerprint enhancement [9] etc. Filters with circular symmetry are also widely used for their capabilities in image analysis; many design methods have been developed in papers such as [10,11,12,13,14,15]. Many works approach circular filters (CF) design using various methods. In the early papers [10, 11], 2D recursive filters with circular symmetry are designed. Wide-band FIR CFs using McClellan transform are studied in [12, 13], linear-phase CF using semi-definite programming in [14]. An efficient method to accelerate design of FIR CFs, using B-spline, piecewise Lagrange interpolation and nonlinear optimization is proposed in [15]. An interesting application of Gabor CFs in invariant texture segmentation is given in [16].

The author has also proposed various analytical design procedures for 2D filters with elliptical symmetry [17,18,19] and also with circular shape, in particular circular filter banks [20, 21, 22], useful in image analysis.

This work proposes an analytical design procedure for zero-phase 2D filters with elliptical and circular symmetry of their frequency response. They are derived applying a specific frequency transformation to the response of an adjustable 1D prototype. The filters result very selective at a relatively low order, inheriting the steepness from the corresponding prototypes. Their frequency responses have a very accurate shape in the frequency plane, and result directly in a factored form, which is a major advantage in implementation. Design examples are provided and also applications in image filtering are given, in order to illustrate their capabilities.

This work continues and expands the previous paper [22] which treated only circular filters. It extends the design procedure to the more general case of 2D filters with elliptically-shaped frequency response (low-pass, band-pass and directional) and includes circular filters as a particular case. Many typical design examples of 2D elliptical filters for various specifications were added. Several simulation results of filtering with elliptical and circular filters on several test images were included.

2 Low-pass and band-pass zero-phase prototypes

2.1 Low-pass zero-phase prototype

In the field of image processing, zero-phase filters are commonly used, as they do not introduce phase distortions in the filtered image. Let us consider the following real function, regarded as a simple, convenient approximation of a zero-phase low-pass (LP) filter with cut-off frequency \(\omega_{0} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\):

$$ H_{P0} (\omega ) = 0.5 \cdot \left( {\tanh \left( {a \cdot (\omega + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2})} \right) - \tanh \left( {a \cdot (\omega - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2})} \right)} \right) $$
(1)

In order to achieve more selective filters, the constant a should be larger. However, for larger values of parameter a, the prototype order will increase. Let us take the value \(a = 10\); next we need to find an accurate rational approximation of the prototype function \(H_{P0} (\omega )\), within a specified error, valid at least along the frequency interval \([ - \pi ,\pi ]\). We use for this purpose the efficient Chebyshev-Padé expansion, yielding a low-order, uniform rational approximation of a function on a specified range. It is easily derived using a symbolic calculation software like MAPLE. Thus, the following 8-th order rational approximation of \(H_{P0} (\omega )\) results:

$$ H_{P} (\omega ) \cong \xi \cdot {{P(\omega )} \mathord{\left/ {\vphantom {{P(\omega )} {Q(\omega )}}} \right. \kern-0pt} {Q(\omega )}} $$
(2)

where \(\xi = 0.010179\); here \(P(\omega )\) and \(Q(\omega )\) are even polynomials in factored form:

$$ P(\omega ) = (\omega^{2} - 4.099)(\omega^{2} - 5.8922)(\omega^{2} - 8.1354)(\omega^{2} - 9.5965) $$
(3)
$$ Q(\omega ) = (\omega^{4} { + 0}{\text{.2777}} \cdot \omega^{2} + 3.501)(\omega^{4} - 4.50512 \cdot \omega^{2} + 5.51545) $$
(4)

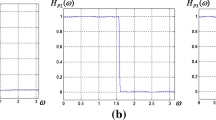
Thus, \(H_{P} (\omega )\) in (2) is the frequency response of a zero-phase low-pass filter (LPF) with cut-off frequency \(\omega_{0} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\) (shown on the range \([ - \pi ,\pi ]\) in Fig. 1(a)).

Fig. 1
figure 1

(a) Zero-phase LP prototype filter frequency response; (b) Parabolic function (blue) and its approximation (red)

Full size image

In order to obtain an adjustable LPF, we simply make prototype \(H_{P} (\omega )\) scalable on the frequency axis, by making the frequency scaling (substitution) \(\omega \to p \cdot \omega\), where \(p > 0\) is the scaling parameter; for \(p > 1\) the filter will be narrower, and for \(p < 1\) it will be wider. Thus the adjustable prototype has the frequency response:

$$ H_{P} (\omega ) \cong \xi \cdot \frac{{(p^{2} \omega^{2} - 4.099)(p^{2} \omega^{2} - 5.8922)(p^{2} \omega^{2} - 8.1354)(p^{2} \omega^{2} - 9.5965)}}{{(p^{4} \omega^{4} { + 0}{\text{.2777}} \cdot p^{2} \omega^{2} + 3.501)(p^{4} \omega^{4} - 4.50512 \cdot p^{2} \omega^{2} + 5.51545)}} $$
(5)

2.2 Design of band-pass prototype filters

Since we envisage to design next (in sub-Sect.  2.3) a uniform filter bank, we need to obtain a band-pass filter (BPF) with a specified central frequency and bandwidth from the designed parametric LPF. In general, shifting the LPF frequency response \(H_{LP} {(}\omega {) } = \xi \cdot {{P_{0} (\omega )} \mathord{\left/ {\vphantom {{P_{0} (\omega )} {Q_{0} (\omega )}}} \right. \kern-0pt} {Q_{0} (\omega )}}\) to the frequencies \(\pm \,\omega_{\,0}\), we obtain the following BPF:

$$ \begin{gathered} H_{BP} {(}\omega {) } = H_{LP} (\omega - \omega_{0} ) + H_{LP} (\omega + \omega_{0} ) \hfill \\ \, = \xi \cdot \frac{{P_{0} (\omega - \omega_{{{\kern 1pt} 0}} )Q_{0} (\omega + \omega_{{{\kern 1pt} 0}} ) + P_{0} (\omega + \omega_{{{\kern 1pt} 0}} )Q_{0} (\omega - \omega_{{{\kern 1pt} 0}} )}}{{Q_{0} (\omega - \omega_{{{\kern 1pt} 0}} )Q_{0} (\omega + \omega_{{{\kern 1pt} 0}} )}} = \frac{{H_{N} (\omega )}}{{H_{D} (\omega )}} \hfill \\ \end{gathered} $$
(6)

It can be shown that \(H_{BP} {(}\omega {) }\) results even, so it can always be expressed as a function of squared frequency variable \(\omega^{2}\).

Substituting now the shifted numerator \(P_{P} (\omega \pm \omega_{0} )\) and denominator \(Q_{P} (\omega \pm \omega_{0} )\) from (2) to (4) into (6), after doing the calculations, finally the BP filter frequency response \(H_{BP} (\omega )\) results as a ratio of two even polynomials of degree 16, where the numerator \(H_{N} (\omega )\) and denominator \(H_{D} (\omega )\) are even polynomials of the form:

$$ \begin{gathered} H_{N} (\omega ) = a_{8} \cdot \omega^{16} + a_{7} \cdot \omega^{14} + ... + a_{2} \cdot \omega^{4} + a_{1} \cdot \omega^{2} + a_{0} = \sum\limits_{k = 0}^{8} {a_{k} \cdot \omega^{2k} } \, \hfill \\ H_{D} (\omega ) = b_{8} \cdot \omega^{16} + b_{7} \cdot \omega^{14} + ... + b_{2} \cdot \omega^{4} + b_{1} \cdot \omega^{2} + b_{0} = \sum\limits_{k = 0}^{8} {b_{k} \cdot \omega^{2k} } \hfill \\ \end{gathered} $$
(7)

The coefficients of the above polynomials are found by simple identification and have the following expressions depending on the scaling parameter p and specified central frequency \(\omega_{0}\) of the BP prototype, where \(x = p^{2} \cdot \omega_{0}^{2}\):

$$ \begin{gathered} a_{0} = 2(x - 4.099)(x - 5.8922)(x - 8.1354)(x - 9.5965)(x^{2} + 0.2777x + 3.501) \hfill \\ \, \cdot (x^{2} - 4.50512x + 5.51545) \hfill \\ a_{1} = - 16p^{2} (x + 9.1163)(x - 1.75455)(x - 5.05279)(x - 7.56525) \hfill \\ \, \cdot (x - 14.09504)(x^{2} - 0.6177x + 0.7279) \hfill \\ a_{2} \, = \, 56p^{4} (x - 6.72613)(x - 14.55081)(x^{2} + 12.13664x + 38.1214) \hfill \\ \, \cdot (x^{2} - 1.12951x + 0.356516) \hfill \\ a_{3} \, = \, - 112p^{6} (x + 8.11544)(x - 0.3055)(x - 12.85724)(x^{2} + 2.19457x + 12.25043) \hfill \\ a_{4} \, = \, 140p^{8} (x - 0.69527)(x - 7.03916)(x^{2} + 10.01661x + 27.95546) \hfill \\ a_{5} \, = \, - 112p^{10} (x + 6.0369)(x^{2} - 0.902x + 7.7467) \hfill \\ a_{6} = 56p^{12} (x^{2} + 5.70545x + 14.441)...a_{7} = - 16p^{14} (x + 3.99381)...a_{8} = 2p^{16} \hfill \\ b_{0} = (x^{2} + 0.277753x + 3.5010423)(x^{2} + 0.277647x + 3.50096) \hfill \\ \, \cdot (x^{2} - 4.5051x + 5.515525)(x^{2} - 4.505134x + 5.5153753) \hfill \\ b_{1} = - 8p^{2} (x + 3.10388)(x - 1.65803)(x - 3.0089)(x^{2} - 0.677743x + 0.413973) \hfill \\ \, \cdot (x^{2} - 3.043441x + 10.724225) \hfill \\ b_{2} = \, 28p^{4} (x - 0.3087653)(x - 0.770433)(x^{2} + 3.7212x + 6.536534) \hfill \\ \, \cdot (x^{2} - 5.35963x + 11.546055) \hfill \\ b_{3} = - 56p^{6} (x + 2.0229)(x - 0.2743)(x - 2.808246)(x^{2} + 0.30475x + 4.40546) \hfill \\ b_{4} = 70p^{8} (x^{2} + 2.307184x + 2.91129)(x^{2} - 1.703266x + 1.076225) \hfill \\ b_{5} = - 56p^{10} (x + 1.304226)(x^{2} + 0.0545871x + 1.2889) \hfill \\ b_{6} = 28p^{12} (x^{2} + 1.5098x + 1.1929)...b_{7} = - 8p^{14} (x + 1.056855)...b_{8} = p^{16} \hfill \\ \end{gathered} $$
(8)

Thus, for any specified selectivity given by the scaling parameter p and a central frequency \(\omega_{0}\), the BPF coefficients result directly using expressions (8).

2.3 Design of a 1D uniform filter bank prototype

For an uniform filter bank (FB) with N components, the range \([0,\pi ]\) will be divided into N equal frequency intervals corresponding to the pass bands of the component filters. In this way, the cut-off frequency of first component filter (LPF) decreases to \(\omega_{\,1} = {\pi \mathord{\left/ {\vphantom {\pi N}} \right. \kern-0pt} N}\), so the prototype frequency response will be compressed along the frequency axis by a factor \(p = {{\omega_{\,0} } \mathord{\left/ {\vphantom {{\omega_{\,0} } {\omega_{\,1} }}} \right. \kern-0pt} {\omega_{\,1} }} = {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}\). The other BP filter bank components will have bandwidths equal to \(BW = {\pi \mathord{\left/ {\vphantom {\pi N}} \right. \kern-0pt} N}\), being derived from a LPF prototype with cut-off frequency \(\omega_{\,2} = {\pi \mathord{\left/ {\vphantom {\pi {(2N)}}} \right. \kern-0pt} {(2N)}}\) by shifting it along the frequency axis. Thus the k-th BPF is centered at frequency \(\omega_{\,0k} = {{(2k - 1)\,\pi } \mathord{\left/ {\vphantom {{(2k - 1)\,\pi } {(2N)}}} \right. \kern-0pt} {(2N)}}\) [22].

Next the components of a uniform FB are derived, based on the chosen prototype. Considering a uniform FB with 8 components, it divides the frequency interval \([ - \pi ,\pi ]\) into 8 equal sub-bands, each of bandwidth \(\omega_{\,B} = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}\) [22]. The first component is a LPF with cutoff frequency \(\omega_{\,C} = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}\) (in Fig. 2(a)). Since the cutoff frequency is \({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\), in order to obtain a LPF with \(\omega_{\,CLP2} = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}\), the former filter is compressed four times on the frequency axis, therefore in the frequency response we will impose the scaling \(\omega \to 4\omega\), thus obtaining the LPF \(H_{P1} {(}\omega {) }\) shown in Fig. 2(a), with cutoff frequency \(\omega_{\,C} = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}\) [22]:

$$ H_{P1} {(}\omega {) = 0}{\text{.010179}} \cdot \frac{{{(}\omega^{2} - {0}{\text{.256187)}} \cdot {(}\omega^{2} - 0.{036826)}}}{{{(}\omega^{4} { + 0}{\text{.1736}} \cdot \omega^{2} { + 0}{\text{.13676)}}}} \cdot \frac{{{(}\omega^{2} - {0}{\text{.508463)}} \cdot {(}\omega^{2} - {0}{\text{.59978)}}}}{{{(}\omega^{4} - {0}{\text{.28157}} \cdot \omega^{2} { + 0}{\text{.215447)}}}} $$
(9)
Fig. 2
figure 2

(a) LPF component of the prototype FB; (b) LPF which generates BP components; (c) first BPF component; (d) second BPF component; (e) uniform filter bank prototype

Full size image

The BP components of the FB will result by shifting the LPF frequency response. However, to obtain a bandwidth of \({\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}\), the LPF must have a cutoff frequency of \({\pi \mathord{\left/ {\vphantom {\pi {16}}} \right. \kern-0pt} {16}}\). Applying the scaling \(\omega \to 8\omega\) to prototype \(H_{LP} {(}\omega {) }\) given by (2)–(4), we obtain the LPF frequency response, where \(\xi = {0}{\text{.010179}}\) (shown in Fig. 2 (b)) [22]:

$$ H_{LP} {(}\omega {) = }\xi \cdot \frac{{{(}\omega^{2} - {0}{\text{.06405)}} \cdot {(}\omega^{2} - {0}{\text{.092066)}}}}{{{(}\omega^{4} { + 0}{\text{.00434}} \cdot \omega^{2} { + 0}{\text{.0008547)}}}} \cdot \frac{{{(}\omega^{2} - {0}{\text{.12712)}} \cdot {(}\omega^{2} - {0}{\text{.14995)}}}}{{{(}\omega^{4} - {0}{\text{.070393}} \cdot {\text{w + 0}}{.001346)}}} = \xi \cdot \frac{{P_{0} (\omega )}}{{Q_{0} (\omega )}} $$
(10)

For example, the second FB component is the first BP filter, with central frequency \(\omega_{\,P2} = \omega_{{{\kern 1pt} 0}} = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } {16}}} \right. \kern-0pt} {16}}\). Using coefficients expressions (8), after algebraic calculations, we obtain the frequency response \(H_{P2} {(}\omega {) }\) shown in Fig. 2(c):

$$ \begin{gathered} H_{P2} {(}\omega {) } = \xi \cdot \frac{{\left( {\omega^{4} - {0}{\text{.06687}} \cdot \omega^{2} { + 0}{\text{.00777}}} \right)\left( {\omega^{4} - {0}{\text{.23189}} \cdot \omega^{2} { + 0}{\text{.01375}}} \right)}}{{\left( {\omega^{4} - {0}{\text{.31754}} \cdot \omega^{2} { + 0}{\text{.02569}}} \right)\left( {\omega^{4} - {0}{\text{.41541}} \cdot \omega^{2} { + 0}{\text{.05718}}} \right)}} \hfill \\ \, \cdot \frac{{\left( {\omega^{4} - {1}{\text{.38799}} \cdot \omega^{2} { + 0}{\text{.4835876}}} \right)\left( {\omega^{4} - {1}{\text{.58783}} \cdot \omega^{2} { + 0}{\text{.721}}} \right)}}{{\left( {\omega^{4} - {0}{\text{.963444}} \cdot \omega^{2} { + 0}{\text{.26331}}} \right)\left( {\omega^{4} - {1}{\text{.21107}} \cdot \omega^{2} { + 0}{\text{.368513}}} \right)}} \hfill \\ \end{gathered} $$
(11)

where \(\xi = 0.{020358}\). Similarly, we obtain the BPF \(H_{P3} {(}\omega {) }\), shown in Fig. 2(d). The entire uniform FB prototype composed of the 8 filters is shown in Fig. 2(e). As an important remark, by scaling (compressing) along frequency axis the original LPF prototype \(H_{P} (\omega )\) from (2), the steepness of resulting filter increases accordingly, but without increasing the order, which is an advantage.

3 Design of elliptically-shaped filters

Next we propose an efficient design technique for 2D elliptically-shaped filters, based on 1D filters, considered as prototypes.

The specified parameters are the values of the ellipse semi-axes and the orientation, described by the angle formed by the large axis with frequency axis \(\omega_{\,1}\). From the frequency response (5) of the adjustable 1D prototype, a 2D filter with elliptical shape results using the frequency mapping \(\omega^{2} \to E_{\varphi } (\omega_{1} ,\omega_{2} )\), where [18]:

$$ \begin{gathered} E_{\varphi } (\omega_{1} ,\omega_{2} ) = \omega_{1}^{2} \left( {\frac{{\cos^{2} \varphi }}{{E^{2} }} + \frac{{\sin^{2} \varphi }}{{F^{2} }}} \right) + \omega_{2}^{2} \left( {\frac{{\sin^{2} \varphi }}{{E^{2} }} + \frac{{\cos^{2} \varphi }}{{F^{2} }}} \right) + \omega_{1} \omega_{2} \sin (2\varphi )\left( {\frac{1}{{F^{2} }} - \frac{1}{{E^{2} }}} \right) \hfill \\ \, = a_{0} \cdot \omega_{1}^{2} + b_{0} \cdot \omega_{2}^{2} + c_{0} \cdot \omega_{1} \omega_{2} \hfill \\ \end{gathered} $$
(12)

The parameters E and F are the ellipse semi-axes, where usually \(E > F\). Thus, starting from a 1D prototype, a 2D elliptical filter results, described by E, F and \(\varphi\). Using the identity \(\omega_{\,1} \omega_{\,2} = 0.5 \cdot \left( {(\omega_{\,1} + \omega_{\,1} )^{2} - \omega_{\,1}^{2} - \omega_{\,2}^{2} } \right)\), we get the mapping [18]:

$$ \omega^{2} \to E_{\varphi } (\omega_{1} ,\omega_{2} ) = a \cdot \omega_{1}^{2} + b \cdot \omega_{2}^{2} + c \cdot (\omega_{1} + \omega_{2} )^{2} $$
(13)

With notations \(q = {1 \mathord{\left/ {\vphantom {1 {E^{2} }}} \right. \kern-0pt} {E^{2} }} + {1 \mathord{\left/ {\vphantom {1 {F^{2} }}} \right. \kern-0pt} {F^{2} }}\), \(r = {1 \mathord{\left/ {\vphantom {1 {E^{2} }}} \right. \kern-0pt} {E^{2} }} - {1 \mathord{\left/ {\vphantom {1 {F^{2} }}} \right. \kern-0pt} {F^{2} }}\), coefficients a, b and c result as:

$$ \begin{gathered} a = a_{0} - 0.5\,c_{0} = q + r \cdot \cos (2\varphi ) + r \cdot \sin (2\varphi ) \hfill \\ b = b_{0} - 0.5\,c_{0} = q - r \cdot \cos (2\varphi ) + r \cdot \sin (2\varphi ) \hfill \\ c = 0.5\,c_{0} = - r \cdot \sin (2\varphi ) \hfill \\ \end{gathered} $$
(14)

To find a rational trigonometric approximation for \(\omega^{2}\) on the range \([ - \pi ,\pi ]\), we use the change of variable [18]:

$$ \omega = \arccos \left( {{x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi }} \right) \leftrightarrow x = \pi \cos \omega $$
(15)

First we find a rational approximation for function \((\arccos ({x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi }))^{2}\), applying (15). Thus, we obtain using MAPLE the first-order Chebyshev-Padé approximation in x:

$$ \left( {\arccos ({x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi })} \right)^{2} \cong {{\left( {{2}{\text{.35065 - 0}}{.7066} \cdot x} \right)} \mathord{\left/ {\vphantom {{\left( {{2}{\text{.35065 - 0}}{.7066} \cdot x} \right)} {\left( {1 + 0.149263 \cdot x} \right)}}} \right. \kern-0pt} {\left( {1 + 0.149263 \cdot x} \right)}} $$
(16)

Substituting back in (16) \(x = \pi \cos \omega\), we get the approximation for \(\omega^{2}\) (Fig. 1(b)):

$$ \omega^{2} \cong 2.3969 \cdot {{\left( {1 - \cos \omega } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \cos \omega } \right)} {\left( {1 + 0.364286 \cdot \cos \omega } \right)}}} \right. \kern-0pt} {\left( {1 + 0.364286 \cdot \cos \omega } \right)}} = {{P(\omega )} \mathord{\left/ {\vphantom {{P(\omega )} {Q(\omega )}}} \right. \kern-0pt} {Q(\omega )}} $$
(17)

This approximation turns out to be accurate for \(\omega \in [ - \pi ,\pi ]\), with visible errors only near the margins, where it diverges; being of minimum order, it is also very efficient. A circular filter obviously results using the mapping (12), taking equal semi-axes, \(E = F\). Thus we get the well-known mapping which yields circular filters:

$$ \omega^{2} \to \omega_{\,1}^{2} + \omega_{\,2}^{2} $$
(18)

Writing approximation (17) for frequency variables \(\omega_{1}\), \(\omega_{2}\) and their sum \(\omega_{\,1} + \omega_{\,2}\), the expressions of \(\omega_{\,1}^{2}\), \(\omega_{\,2}^{2}\) and \((\omega_{\,1} + \omega_{\,2} )^{2}\) are then replaced into (13), giving:

$$ \omega^{2} \to E_{\varphi } (\omega_{1} ,\omega_{2} ) = a \cdot \frac{{P(\omega_{1} )}}{{Q(\omega_{1} )}} + b \cdot \frac{{P(\omega_{2} )}}{{Q(\omega_{2} )}} + c \cdot \frac{{P(\omega_{1} + \omega_{2} )}}{{Q(\omega_{1} + \omega_{2} )}} = \frac{{M(\omega_{1} ,\omega_{2} )}}{{N(\omega_{1} ,\omega_{2} )}} $$
(19)

Making the calculations we obtain the numerator and denominator as:

$$ \begin{gathered} M(\omega_{1} ,\omega_{2} ) = a \cdot P(\omega_{1} ) \cdot Q(\omega_{2} ) \cdot Q(\omega_{1} + \omega_{2} ) + b \cdot Q(\omega_{1} ) \cdot P(\omega_{2} ) \cdot Q(\omega_{1} + \omega_{2} ) \hfill \\ \, + c \cdot Q(\omega_{1} ) \cdot Q(\omega_{2} ) \cdot P(\omega_{1} + \omega_{2} ) \hfill \\ \end{gathered} $$
(20)
$$ N(\omega_{1} ,\omega_{2} ) = Q(\omega_{1} ) \cdot Q(\omega_{2} ) \cdot Q(\omega_{1} + \omega_{2} ) $$
(21)

Using the expressions \(P(\omega )\), \(Q(\omega )\) from (17) and substituting them in (20), using also (14), the parametric expression of the numerator \(M(\omega_{1} ,\omega_{2} )\) can be written as:

$$ M(\omega_{1} ,\omega_{2} ) = q \cdot M_{0} (\omega_{1} ,\omega_{2} ) + r \cdot (\cos 2\varphi ) \cdot M_{1} (\omega_{1} ,\omega_{2} ) + r \cdot (sin2\varphi ) \cdot M_{2} (\omega_{1} ,\omega_{2} ) $$
(22)

Using the trigonometric identities \(\cos \omega_{\,1} = 0.5 \cdot (z_{1} + z_{1}^{ - 1} )\),\(\cos \omega_{2} = 0.5 \cdot (z_{2} + z_{2}^{ - 1} )\), in complex frequency variables \(z_{1} = e^{{j\omega_{1} }}\), \(z_{2} = e^{{j\omega_{2} }}\) and taking into account (17) and (19)–(21), the mapping (19) is expressed in matrix form as:

$$ \omega^{2} \to {{\left( {{\mathbf{z}}_{1} \times {\mathbf{M}} \times {\mathbf{z}}_{2}^{T} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{z}}_{1} \times {\mathbf{M}} \times {\mathbf{z}}_{2}^{T} } \right)} {\left( {{\mathbf{z}}_{1} \times {\mathbf{N}} \times {\mathbf{z}}_{2}^{T} } \right)}}} \right. \kern-0pt} {\left( {{\mathbf{z}}_{1} \times {\mathbf{N}} \times {\mathbf{z}}_{2}^{T} } \right)}} $$
(23)

where the vectors are: \({\mathbf{z}}_{1} = [1\;\;z_{1}^{ - 1} ...\;z_{1}^{ - 4} ]\) and \({\mathbf{z}}_{2} = [1\;\;z_{2}^{ - 1} ...\;z_{2}^{ - 4} ]\). Matrix \({\mathbf{M}}\) corresponding to numerator \(M(\omega_{1} ,\omega_{2} )\) in (19) is given by the linear combination:

$$ {\mathbf{M}} = q \cdot {\mathbf{M}}_{0} + r \cdot (\cos 2\varphi ) \cdot {\mathbf{M}}_{1} + r \cdot (sin2\varphi ) \cdot {\mathbf{M}}_{2} $$
(24)

where the component matrices \({\mathbf{M}}_{0}\),\({\mathbf{M}}_{1}\),\({\mathbf{M}}_{2}\) of size \(5 \times 5\) have constant elements and result through identifying corresponding coefficients from terms \(M_{0} (\omega_{1} ,\omega_{2} )\),\(M_{1} (\omega_{1} ,\omega_{2} )\), \(M_{2} (\omega_{1} ,\omega_{2} )\) of (22), interpreted as Discrete Space Fourier Transforms (DSFT), in frequency variables \(\omega_{1}\) and \(\omega_{2}\), of the matrices \({\mathbf{M}}_{0}\), \({\mathbf{M}}_{1}\) and \({\mathbf{M}}_{2}\), respectively. The denominator \(N(\omega_{1} ,\omega_{2} )\) in (19) corresponds to a \(5 \times 5\) matrix N with constant elements, resulted similarly by identifying coefficients of the terms of \(N(\omega_{1} ,\omega_{2} )\) in (21), regarded as DSFT. The matrices \({\mathbf{M}}_{0}\), \({\mathbf{M}}_{1}\), \({\mathbf{M}}_{2}\) and \({\mathbf{N}}\) are displayed below:

$$ {\mathbf{M}}_{0} = \left[ {\begin{array}{*{20}c} { - 0.07952} & { - 0.13877} & { - 0.07952} & 0 & 0 \\ { - 0.13877} & {\;\;0.43658} & { - 0.90064} & { - 0.43658} & 0 \\ { - 0.07952} & { - 0.90064} & {\;\;4.63476} & { - 0.90064} & { - 0.07952} \\ 0 & { - 0.43658} & { - 0.90064} & {\;\;0.43658} & { - 0.13877} \\ 0 & 0 & { - 0.07952} & { - 0.13877} & { - 0.07952} \\ \end{array} } \right] \, $$
(25)
$$ {\mathbf{M}}_{1} = \left[ {\begin{array}{*{20}c} 0 & {\;\;0.29781} & 0 & 0 & 0 \\ { - 0.29781} & 0 & {1.33722} & 0 & 0 \\ 0 & { - 1.33722} & 0 & { - 1.33722} & 0 \\ 0 & 0 & {1.33722} & 0 & { - 0.29781} \\ 0 & 0 & 0 & {\;\;0.29781} & 0 \\ \end{array} } \right] $$
(26)
$$ {\mathbf{M}}_{2} = \left[ {\begin{array}{*{20}c} { - 0.03976} & {\;\;0.07952} & { - 0.03976} & 0 & 0 \\ {\;\;0.07952} & {\;\;1.55551} & { - 1.11893} & { - 0.51610} & 0 \\ { - 0.03976} & { - 1.11893} & {\;\;2.31738} & { - 1.11893} & { - 0.03976} \\ 0 & { - 0.51610} & { - 1.11893} & {\;\;1.55551} & {\;\;0.07952} \\ 0 & 0 & { - 0.03976} & {\;\;0.07952} & { - 0.03976} \\ \end{array} } \right] \, $$
(27)
$$ {\mathbf{N}} = \left[ {\begin{array}{*{20}c} {0.00604} & {0.03318} & {0.00604} & 0 & 0 \\ {0.03318} & {0.21532} & {0.21532} & {0.03318} & 0 \\ {0.00604} & {0.21532} & {1.01209} & {0.21532} & {0.00604} \\ 0 & {0.03318} & {0.21532} & {0.21532} & {0.03318} \\ 0 & 0 & {0.00604} & {0.03318} & {0.00604} \\ \end{array} } \right] $$
(28)

As can be noticed, the matrices \({\mathbf{M}}_{0}\), \({\mathbf{M}}_{1}\), \({\mathbf{M}}_{2}\) and \({\mathbf{N}}\) have a “band” structure along the main diagonal, being symmetric with respect to the central element. Once specified the semi-axes E and F of the ellipse and the orientation angle \(\varphi\), the matrix \({\mathbf{M}}\) is determined from (24), using (25)–(27). Substituting mapping (19) into the expressions (7), the frequency response of the 2D elliptical filter can be written:

$$ \begin{gathered} H_{EBP} {(}\omega_{1} ,\omega_{2} {)} = {{H_{N} (\omega_{1} ,\omega_{2} )} \mathord{\left/ {\vphantom {{H_{N} (\omega_{1} ,\omega_{2} )} {H_{D} (\omega_{1} ,\omega_{2} )}}} \right. \kern-0pt} {H_{D} (\omega_{1} ,\omega_{2} )}} \hfill \\ \, = {{\sum\limits_{k = 0}^{8} {a_{k} \cdot \left( {M(\omega_{1} ,\omega_{2} )} \right)^{k} \left( {N(\omega_{1} ,\omega_{2} )} \right)^{8 - k} } } \mathord{\left/ {\vphantom {{\sum\limits_{k = 0}^{8} {a_{k} \cdot \left( {M(\omega_{1} ,\omega_{2} )} \right)^{k} \left( {N(\omega_{1} ,\omega_{2} )} \right)^{8 - k} } } {\sum\limits_{k = 0}^{8} {b_{k} \cdot \left( {M(\omega_{1} ,\omega_{2} )} \right)^{k} \left( {N(\omega_{1} ,\omega_{2} )} \right)^{8 - k} } }}} \right. \kern-0pt} {\sum\limits_{k = 0}^{8} {b_{k} \cdot \left( {M(\omega_{1} ,\omega_{2} )} \right)^{k} \left( {N(\omega_{1} ,\omega_{2} )} \right)^{8 - k} } }} \hfill \\ \end{gathered} $$
(29)

This can be written in the complex frequency variables \(z_{1}\) and \(z_{2}\), in matrix form:

$$ H_{EBP} {(}z_{1} {, }z_{2} {)} = {{\left( {{\mathbf{z}}_{1} \times {\mathbf{V}} \times {\mathbf{z}}_{2}^{T} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{z}}_{1} \times {\mathbf{V}} \times {\mathbf{z}}_{2}^{T} } \right)} {\left( {{\mathbf{z}}_{1} \times {\mathbf{U}} \times {\mathbf{z}}_{2}^{T} } \right)}}} \right. \kern-0pt} {\left( {{\mathbf{z}}_{1} \times {\mathbf{U}} \times {\mathbf{z}}_{2}^{T} } \right)}} $$
(30)

where \(\times\) is inner product and the vectors \({\mathbf{z}}_{{\mathbf{1}}}\), \({\mathbf{z}}_{2}\) are:

$$ {\mathbf{z}}_{1} = [1\;\;z_{1}^{ - 1} ...\;z_{1}^{ - 32} ] \, {\mathbf{z}}_{2} = [1\;\;z_{2}^{ - 1} ...\;z_{2}^{ - 32} ] $$
(31)

The matrices V and U from (30) result as weighted sums of multiple convolutions of the \(5 \times 5\) matrices M and N:

$$ {\mathbf{V}} = \sum\limits_{k = 0}^{8} {a_{k} \cdot {\mathbf{M}}^{(k)} * {\mathbf{N}}^{{\left( {8 - k} \right)}} } \, {\mathbf{U}} = \sum\limits_{k = 0}^{8} {b_{k} \cdot {\mathbf{M}}^{(k)} * {\mathbf{N}}^{{\left( {8 - k} \right)}} } $$
(32)

In (32), the notation \({\mathbf{M}}^{(k)} * {\mathbf{N}}^{{\left( {8 - k} \right)}}\) means convolution between matrix M convolved with itself k-1 times, and matrix N convolved with itself 7-k times, thus in each term of (32) there are k matrices M and (8-k) matrices N (in our case, 7 convolutions of 8 matrices). For instance, for \(k = 3\), we get the following term in the sums of (32):

$$ {\mathbf{M}}^{(3)} * {\mathbf{N}}^{\left( 5 \right)} = {\mathbf{M}} * {\mathbf{M}} * {\mathbf{M}} * {\mathbf{N}} * {\mathbf{N}} * {\mathbf{N}} * {\mathbf{N}} * {\mathbf{N}} $$
(33)

Let us consider the particular case of an elliptically-shaped filter with the following specifications:\(\omega_{\,0} = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {16}}} \right. \kern-0pt} {16}}\),\(\varphi = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}\),\(E = 2\),\(F = 0.5\),\(p = 6\). From the values \(E\) and \(F\), the values q and r result, then using \(\varphi\), the specific mapping matrix M results from (24). Then from the specified values \(\omega_{\,0}\) and p, the coefficients \(a_{k}\) and \(b_{k}\) are calculated from (8). If the polynomials \(H_{N} (\omega_{1} ,\omega_{2} )\) and \(H_{D} (\omega_{1} ,\omega_{2} )\) are factored (e.g. in MAPLE), after algebraic calculations we finally obtain the filter matrices V and U as the convolutions:

$$ \begin{gathered} {\mathbf{V}} = 2 \cdot \left( {{\mathbf{M}} * {\mathbf{M}} - 3.52959 \cdot {\mathbf{M}} * {\mathbf{N}} + 3.49381 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {{\mathbf{M}} * {\mathbf{M}} - 4.16118 \cdot {\mathbf{M}} * {\mathbf{N}} + 4.33978 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {{\mathbf{M}} * {\mathbf{M}} - 8.74286 \cdot {\mathbf{M}} * {\mathbf{N}} + 19.1324 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {{\mathbf{M}} * {\mathbf{M}} - 9.43632 \cdot {\mathbf{M}} * {\mathbf{N}} + 23.25748 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \end{gathered} $$
(34)
$$ \begin{gathered} {\mathbf{U}} = \left( {{\mathbf{M}} * {\mathbf{M}} - 4.58378 \cdot {\mathbf{M}} * {\mathbf{N}} + 5.26499 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {{\mathbf{M}} * {\mathbf{M}} - 5.14149 \cdot {\mathbf{M}} * {\mathbf{N}} + 6.89897 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {{\mathbf{M}} * {\mathbf{M}} - 7.33421 \cdot {\mathbf{M}} * {\mathbf{N}} + 13.86033 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {{\mathbf{M}} * {\mathbf{M}} - 8.15781 \cdot {\mathbf{M}} * {\mathbf{N}} + 16.65925 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \end{gathered} $$
(35)

Therefore, the matrix V can be generally expressed as a convolution of 4 matrices of the form \({\mathbf{V}} = 2 \cdot {\mathbf{V}}_{1} * {\mathbf{V}}_{2} * {\mathbf{V}}_{3} * {\mathbf{V}}_{4}\), where the 4 components have the general form:

$$ {\mathbf{V}}_{j} = {\mathbf{M}} * {\mathbf{M}} + c_{j1} \cdot {\mathbf{M}} * {\mathbf{N}} + c_{j2} \cdot {\mathbf{N}} * {\mathbf{N}} $$
(36)

and the matrix U is expressed similarly as \({\mathbf{U}} = {\mathbf{U}}_{1} * {\mathbf{U}}_{2} * {\mathbf{U}}_{3} * {\mathbf{U}}_{4}\), where

$$ {\mathbf{U}}_{j} = {\mathbf{M}} * {\mathbf{M}} + d_{j1} \cdot {\mathbf{M}} * {\mathbf{N}} + d_{j2} \cdot {\mathbf{N}} * {\mathbf{N}} $$
(37)

The frequency responses of the 2D LP elliptical and circular filters are obtained more easily than for BP filters.

From expression (5), applying the mapping (23), we get the two filter matrices corresponding to numerator and denominator, given by the following convolutions:

$$ \begin{gathered} {\mathbf{V}}_{ELP} = \left( {p^{2} \cdot {\mathbf{M}} - 4.099 \cdot {\mathbf{N}}} \right) * \left( {p^{2} \cdot {\mathbf{M}} - 5.8922 \cdot {\mathbf{N}}} \right) \hfill \\ \, * \left( {p^{2} \cdot {\mathbf{M}} - 8.1354 \cdot {\mathbf{N}}} \right) * \left( {p^{2} \cdot {\mathbf{M}} - 9.5965 \cdot {\mathbf{N}}} \right) \hfill \\ \end{gathered} $$
(38)
$$ \begin{gathered} {\mathbf{U}}_{ELP} = \left( {p^{4} \cdot {\mathbf{M}} * {\mathbf{M}} + 0.2777p^{2} \cdot {\mathbf{M}} * {\mathbf{N}} + 3.501 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \, * \left( {p^{4} \cdot {\mathbf{M}} * {\mathbf{M}} - 4.50512p^{2} \cdot {\mathbf{M}} * {\mathbf{N}} + 5.51545 \cdot {\mathbf{N}} * {\mathbf{N}}} \right) \hfill \\ \end{gathered} $$
(39)

The proposed design procedure (for elliptical BPF) is next presented in a synthetic form (the sequence of design steps can be regarded as an associated pseudo-code):

  1. (a)

    Calculate the parameters q and r, from the specified semiaxes values, E and F;

  2. (b)

    Read matrices \({\mathbf{M}}_{0}\), \({\mathbf{M}}_{1}\), \({\mathbf{M}}_{2}\), \({\mathbf{N}}\) with constant elements from (25)-(28);

  3. (c)

    Calculate the frequency mapping matrix \({\mathbf{M}}\)(being known q, r, \(\varphi\)), using (24);

  4. (d)

    Calculate using (8) the set of coefficients \(a_{0} ,...,a_{8}\), \(b_{0} ,..., \, b_{8}\), for given p and peak frequency \(\omega_{0}\);

  5. (e)

    Calculate the overall 2D filter matrices V and U, using (32) and the coefficients found at step (d);

  6. (f)

    Factoring the numerator \(H_{N} (\omega )\) and denominator \(H_{D} (\omega )\) given by (7) with coefficients (8), the filter matrices V and U are decomposed into convolutions of \(5 \times 5\) matrices as in (34), (35).

4 Design of circular filters

In order to generate circular filters from a given prototype, we apply the mapping \(\omega^{2} \to \omega_{\,1}^{2} + \omega_{\,2}^{2}\). Writing (17) for frequency variables \(\omega_{{{\kern 1pt} 1}}\) and \(\omega_{{{\kern 1pt} 2}}\), we get:

$$ \omega^{2} \to 2.3969 \cdot \left[ {\frac{{1 - \cos \omega_{{{\kern 1pt} 1}} }}{{1 + 0.36429 \cdot \cos \omega_{{{\kern 1pt} 1}} }} + \frac{{1 - \cos \omega_{{{\kern 1pt} 2}} }}{{1 + 0.36429 \cdot \cos \omega_{{{\kern 1pt} 2}} }}} \right] = \frac{{M_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )}}{{N_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )}} $$
(40)

Using the identities \(\cos \omega_{1} = 0.5 \cdot (z_{1} + z_{1}^{ - 1} )\) and \(\cos \omega_{2} = 0.5 \cdot (z_{2} + z_{2}^{ - 1} )\), in complex frequency variables \(z_{1} = e^{{j\omega_{1} }}\), \(z_{2} = e^{{j\omega_{2} }}\), the mapping (40) in matrix form results as:

$$ \omega^{2} \to {{M_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )} \mathord{\left/ {\vphantom {{M_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )} {N_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )}}} \right. \kern-0pt} {N_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )}} = {{\left( {{\mathbf{z}}_{1} \times {\mathbf{M}}_{C} \times {\mathbf{z}}_{2}^{T} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{z}}_{1} \times {\mathbf{M}}_{C} \times {\mathbf{z}}_{2}^{T} } \right)} {\left( {{\mathbf{z}}_{1} \times {\mathbf{N}}_{C} \times {\mathbf{z}}_{2}^{T} } \right)}}} \right. \kern-0pt} {\left( {{\mathbf{z}}_{1} \times {\mathbf{N}}_{C} \times {\mathbf{z}}_{2}^{T} } \right)}} $$
(41)

where the vectors are: \({\mathbf{z}}_{{\mathbf{1}}} = [\begin{array}{*{20}c} 1 & {z_{1}^{ - 1} } & {z_{1}^{ - 2} } \\ \end{array} ] \, \) and \({\mathbf{z}}_{{\mathbf{2}}} = [\begin{array}{*{20}c} 1 & {z_{2}^{ - 1} } & {z_{2}^{ - 2} } \\ \end{array} ]\). The numerator \(M_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )\) and denominator \(N_{C} (\omega_{{{\kern 1pt} 1}} ,\omega_{{{\kern 1pt} 2}} )\) in (40) are the Discrete Space Fourier Transforms (DSFT) of the \(3 \times 3\) centrally-symmetric matrices \({\mathbf{M}}_{C}\) and \({\mathbf{N}}_{C}\):

$$ {\mathbf{M}}_{C} = \left[ {\begin{array}{*{20}c} { - 0.4366} & { - 0.7618} & { - 0.4366} \\ { - 0.7618} & {\,\,\,4.7938} & { - 0.7618} \\ { - 0.4366} & { - 0.7618} & { - 0.4366} \\ \end{array} } \right]{ , }{\mathbf{N}}_{C} { = }\left[ {\begin{array}{*{20}c} {0.03317} & {0.18214} & {0.03317} \\ {0.18214} & 1 & {0.18214} \\ {0.03317} & {0.18214} & {0.03317} \\ \end{array} } \right] $$
(42)

Once found the frequency mapping for circular filters, the next steps of the design process are similar to those for elliptical filters, described in Sect. 3. A generic rational factor \(H_{Bj} {(}\omega {) }\) of the BP frequency response of type (11) is:

$$ H_{Bj} {(}\omega {) } = {{(\omega^{4} + \alpha_{{{\kern 1pt} 1j{\kern 1pt} }} \cdot \omega^{2} { + }\alpha_{0j} )} \mathord{\left/ {\vphantom {{(\omega^{4} + \alpha_{{{\kern 1pt} 1j{\kern 1pt} }} \cdot \omega^{2} { + }\alpha_{0j} )} {(\omega^{4} + \beta_{{{\kern 1pt} 1j{\kern 1pt} }} \cdot \omega^{2} { + }\beta_{0j} )}}} \right. \kern-0pt} {(\omega^{4} + \beta_{{{\kern 1pt} 1j{\kern 1pt} }} \cdot \omega^{2} { + }\beta_{0j} )}} $$
(43)

and applying the mapping (41), we obtain the transfer function of corresponding 2D circular filter factor, in matrix form:

$$ H_{BCj} {(}z_{1} {, }z_{2} {)} = {{\left( {{\mathbf{z}}_{1} \times {\mathbf{A}}_{Cj} \times {\mathbf{z}}_{2}^{T} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{z}}_{1} \times {\mathbf{A}}_{Cj} \times {\mathbf{z}}_{2}^{T} } \right)} {\left( {{\mathbf{z}}_{1} \times {\mathbf{B}}_{Cj} \times {\mathbf{z}}_{2}^{T} } \right)}}} \right. \kern-0pt} {\left( {{\mathbf{z}}_{1} \times {\mathbf{B}}_{Cj} \times {\mathbf{z}}_{2}^{T} } \right)}} $$
(44)

where \({\mathbf{z}}_{1} = [1\;\;z_{1}^{ - 1} ...\;z_{1}^{ - 4} ]\) and \({\mathbf{z}}_{2} = [1\;\;z_{2}^{ - 1} ...\;z_{2}^{ - 4} ]\). The \(5 \times 5\) matrices \({\mathbf{A}}_{Cj}\), \({\mathbf{B}}_{Cj}\) result as a weighted sum of convolutions of the \(3 \times 3\) matrices \({\mathbf{M}}_{C}\),\({\mathbf{N}}_{C}\) in (42):

$$ \begin{gathered} {\mathbf{A}}_{Cj} = {\mathbf{M}}_{C} * {\mathbf{M}}_{C} + \alpha_{{{\kern 1pt} 1j}} \cdot {\mathbf{M}}_{C} * {\mathbf{N}}_{C} + \alpha_{{{\kern 1pt} 0j}} \cdot {\mathbf{N}}_{C} * {\mathbf{N}}_{C} \, \hfill \\ {\mathbf{B}}_{Cj} = {\mathbf{M}}_{C} * {\mathbf{M}}_{C} + \beta_{{{\kern 1pt} 1j}} \cdot {\mathbf{M}}_{C} * {\mathbf{N}}_{C} + \beta_{{{\kern 1pt} 0j}} \cdot {\mathbf{N}}_{C} * {\mathbf{N}}_{C} \hfill \\ \end{gathered} $$
(45)

Using (45), we calculate the matrices \({\mathbf{A}}_{Cj}\), \({\mathbf{B}}_{Cj}\) (\(j = 1...4\)) for all 4 factors in (11); then, the matrices \({\mathbf{A}}_{C}\) and \({\mathbf{B}}_{C}\) of the overall circular filter \(H_{C} {(}z_{1} {, }z_{2} {)}\) will result by convolution:

$$ {\mathbf{A}}_{C} = {\mathbf{A}}_{C1} * {\mathbf{A}}_{C2} * {\mathbf{A}}_{C3} * {\mathbf{A}}_{C4} { ; }{\mathbf{B}}_{C} = {\mathbf{B}}_{C1} * {\mathbf{B}}_{C2} * {\mathbf{B}}_{C3} * {\mathbf{B}}_{C4} $$
(46)

so the designed circular filters can be implemented sequentially.

5 Design examples of elliptical LP and BP filters

In this section a few relevant design examples for elliptically-shaped LP and BP filters are provided, in order to illustrate the proposed analytical design method. For each filter with given parameters, its frequency response and associated contour plots are displayed in Fig. 3. Two wide-band, elliptical LP filters are shown in Fig. 3(a), (b). The filters (c–f) are a special case of LP filters, namely very selective (narrow) directional filters. They have a high ratio \(E/F\)(typically > 10) and also a large value of the scaling parameter p. Several elliptical BP filters are (g–j). These filters have the pass bandwidth adjustable through the parameters E, F and p.

Fig. 3
figure 3

Frequency responses and contour plots for various elliptical filters (a–f LP; g–j BP) with specified parameters: (a) \(\varphi = 0.25\pi\), \(E = 3\), \(F = 1\), \(p = 1.1\); (b) \(\varphi = 0.15\pi\), \(E = 4\), \(F = 1\), \(p = 2\); (c) \(\varphi = 0.1\pi\),\(E = 9\),\(F = 1\),\(p = 9\); (d) \(\varphi = 0.15\pi\), \(E = 9\), \(F = 1\), \(p = 9\); (e) \(\varphi = 0.2\pi\), \(E = 25\), \(F = 0.8\), \(p = 8\); (f) \(\varphi = 0.25\pi\), \(E = 25\), \(F = 1\), \(p = 9\); (g) \(\omega_{\,0} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}\), \(\varphi = 0.15\pi\), \(E = 3\), \(F = 1\), \(p = 3\); (h) \(\omega_{\,0} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}\), \(\varphi = 0.15\pi\), \(E = 3\), \(F = 1\), \(p = 9\); (i) \(\omega_{\,0} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}\), \(\varphi = 0.25\pi\), \(E = 4\), \(F = 1\), \(p = 9\); (j) \(\omega_{\,0} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}\), \(\varphi = 0.2\pi\), \(E = 4\), \(F = 1\), \(p = 30\)

Full size image

The BP filters (h), (i) are rather selective (\(p = 9\)), and filter (j) is extremely selective (\(p = 30\)). It can be noticed that all filters have an accurate elliptical shape, even for large values of semi-axes, without any visible distortions even near the margins of the frequency plane (as for filters (a), (g), (i)). The filters also have a very steep transition, and the pass region has a little ripple, while they have no visible ripple in the stop region. These features are directly inherited from its 1D prototype.

6 Uniform circular filter bank design example

In this section a design example for the components of a uniform CFB is provided [22]. The frequency responses and corresponding contour plots of the 8 components of the uniform CFB are displayed in Fig. 4. The first component is the circular LPF \(H_{CLP} {(}\omega_{{{\kern 1pt} 1}} {,}\omega_{{{\kern 1pt} 2}} {) }\) based on prototype \(H_{P1} {(}\omega {) }\) in (9), shown in Fig. 2 (a). The other frequency responses and constant level contours correspond to BP filters, denoted \(H_{CBPk} {(}\omega_{{{\kern 1pt} 1}} {,}\omega_{{{\kern 1pt} 2}} {) }\) with \(k = 1,...,7\). All filters have a bandwidth equal to \({\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}\) and central frequencies \(\omega_{{{\kern 1pt} 0k}} = {{(2k + 1) \cdot \pi } \mathord{\left/ {\vphantom {{(2k + 1) \cdot \pi } {16}}} \right. \kern-0pt} {16}}\). We notice that they are very selective, with a steep transition region, inherited from their prototypes, shown in Fig. 2(a)-(d). As can be noticed from the constant level contours, the first 7 components of the FB have an accurate circular shape, while filter \(H_{CBP7} {(}\omega_{{{\kern 1pt} 1}} {,}\omega_{{{\kern 1pt} 2}} {) }\) has the inner contour still circular and outer contour distorted, an effect of periodicity in the frequency plane, due to marginal distortions of approximation (17), visible in Fig. 1(b). Such a circular FB may have applications in a multi-resolution analysis of images [22].

Fig. 4
figure 4

Frequency responses and contour plots of the FB components

Full size image

7 Applications in image filtering

In this section, simulation results are provided of image filtering applications of the designed elliptical and circular LP and BP filters. Consider first the binary test image in Fig. 5 (a), containing various geometric shapes (circles, rings, ellipses, squares etc.) of various size and thickness. This image is first filtered with a circular LPF with two selectivities (\(p = 3\),\(p = 6\)), resulting in the blurred images (b), (c), depending on value p, in which the larger and thicker objects are more visible, while thinner and smaller ones are very blurred. If this LP filtering is followed by thresholding with various threshold values, we get the binary images (d), (e), (f) in which some objects from original image are preserved, while others vanish (like thinner rings), depending on the degree of blurring and threshold value. Therefore, this LPF can be used to select objects in images. The images (g), (h) result through elliptical LP filtering with the indicated parameters.

Fig. 5
figure 5

(a) Binary test image; image filtered with circular LPF: (b) \(p = 3\), (c) \(p = 6\); (d) image (b) thresholded with \(th = 0.75\); (e) image (b) thresholded with \(th = 0.5\); (f); image (c) thresholded with \(th = 0.5\); (g, h) images resulted through elliptical LP filtering with:\(E = 9\), \(F = 1\), \(p = 6\) and angle \(\varphi = 0.3\pi\) and \(\varphi = 0.8\pi\)

Full size image

Next, consider the binary image in Fig. 5(a) of size \(399 \times 399\) pixels, containing straight lines with gradually varying orientation. It is known that the spectrum of a straight line also looks as a straight line in frequency plane \((\omega_{1} ,\omega_{2} )\), perpendicular to the line direction. For a specified orientation angle, only the lines whose spectra overlap with filter characteristic are preserved in the output image, while the rest are more or less blurred, practically wiped out through directional LP filtering. The images filtered with a narrow elliptical filter (similar to the ones in Fig. 3(c)-(f)), choosing \(E = 9\),\(F = 1\),\(p = 12\) and a specified filter orientations, are displayed in Fig. 6(b–d). If the orientation angle is precisely chosen, the line appears sharply detected against the background, while the other lines are more or less blurred.

Fig. 6
figure 6

(a) Binary test image; (b–d) filtering results with an elliptical LPF with \(E = 9\), \(F = 1\), \(p = 12\) and orientation angles: (b) \(\varphi = 0.1\pi\); (c) \(\varphi = 0.26\pi\); (d) \(\varphi = 0.4\pi\); (e) test image “rice”; (f–j) results of directional filtering with an elliptical LPF with \(E = 9\), \(F = 1\), \(p = 6\) and orientation angles: (f) \(\varphi = - 0.1\pi\); (g) \(\varphi = - 0.15\pi\); (h) \(\varphi = - 0.25\pi\); (i) \(\varphi = 0.25\pi\); (j) \(\varphi = 0.1\pi\); (k) filtered with elliptical BPF (\(\omega_{\,0} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}\), \(\varphi = 0.25\pi\), \(E = 9\), \(F = 1\), \(p = 6\)); (l) filtered with circular BPF (\(\omega_{\,0} = 0.8\pi\), \(E = F = 1\), \(p = 6\))

Full size image

The third example is also a directional filtering, on texture-type image \((590 \times 590)\) in Fig. 6(e), containing rice grains, oriented randomly. Using an elliptical LPF with various specified parameters, the directionally filtered images (f–j) are obtained, in which only rice grains with selected orientation are visible, while others are more or less blurred. Images (k) and (l) result through BP elliptical and circular filtering. Another filtering example is a “real-life” grayscale image of \(600 \times 900\) pixels, in Fig. 7(a), showing a low-angle view (from ground level) of some high buildings (skyscrapers). This image is convenient for testing directional filtering as it contains straight lines oriented under various angles, marking the building structure. The images in Fig. 7(b–f) result from selective directional filtering, using an elliptical LPF, with parameter values: \(E = 9\), \(F = 1\), \(p = 6\) and various orientation angles. The directional filtering effect is clearly visible; for a specified filter orientation, some straight lines (contours or other details) are outlined, while others are more or less blurred, each depending on its orientation. Such directional filtering can be applied in detecting and selecting objects with various orientations from images.

Fig. 7
figure 7

(a) Skyscraper image; (b–f) results of directional filtering with an elliptical LPF with parameters: (b) \(\varphi = - 0.36\pi\), \(E = 6\), \(F = 1\), \(p = 6\): (c) \(\varphi = 0.4\pi\), \(E = 6\), \(F = 1\), \(p = 6\); (d)\(\varphi = - 0.1\pi\), \(E = 9\), \(F = 1\), \(p = 8\); (e) \(\varphi = 0.1\pi\), \(E = 9\), \(F = 1\), \(p = 6\); (f) \(\varphi = 0.48\pi\), \(E = 9\), \(F = 1\), \(p = 8\)

Full size image

8 Comparative discussion

The aim of this work was to propose an efficient analytical design procedure for a class of zero-phase 2D filters, namely elliptically-shaped, including circular filters as a particular case. Unlike the more traditional design based on global numerical optimization, the proposed analytical technique yields the desired 2D filter (in our case elliptical or circular LP/BP filter) with closed-form frequency response which results directly factored. In this method, the specific 1D-2D mapping is applied to each factor of the 1D prototype, thus yielding the corresponding factor of the desired 2D filter. This factorization is a major advantage, allowing for a sequential implementation. Correspondingly, filter matrices result as convolutions of smaller size (5×5) matrices. By comparison, global numerical optimization may lead to 2D frequency responses (two-variable polynomials for FIR filters, or rational functions for IIR filters) which in general cannot be factored, thus making the implementation more difficult.

Another advantage is that the original LP prototype can be scaled on frequency axis, yielding a LP prototype with adjustable selectivity, but keeping the same order. By shifting it along the frequency axis, we derive FB filters, which in turn generate the elliptical or circular 2D filter by applying specific frequency mappings.

The 2D filters inherit the characteristics of their 1D prototype (bandwidth, selectivity, steepness, ripple); by scaling (compressing) the LPF prototype along the frequency axis, the steepness of resulting filter increases accordingly, but without increasing the order, which is a useful advantage. For instance, all the components of the designed circular filter bank result or the same order.

The resulted 2D filters are parametric, since the design parameters (bandwidth, peak frequency, orientation angle) appear explicitly in the frequency response expression. Thus, when changing the specifications, the design process does not need to be resumed from the start, since the 2D frequency response is already determined by a simple substitution. The orientation angle, peak frequency and selectivity of the designed 2D filters can be adjusted independently through the imposed parameters.

As regards a comparison to other design methods for similar filters, available in the literature, this approach is substantially simpler, yielding filters with an accurate shape, even near frequency plane margins.

For a comparison with existing works, other analytical techniques for designing 2D elliptical and circular filters have been previously proposed by the author. The filters from [17] are based on zero-phase prototypes, being somewhat related to the ones proposed here; however, the frequency mapping uses Euler approximation and bilinear transform, which are known to introduce shape distortions. The filters in [18] rely on digital LP prototypes and the frequency mapping is more complicated, yielding LP elliptical filters with complex coefficients, more difficult to implement. In [19], a class of elliptical Gaussian FIR filters is proposed, for directional filtering of images; the filters are efficient, using three axis decomposition, but the method is more difficult to apply and the resulted filters cannot have a large bandwidth. Thus, the method proposed here is more convenient and easier to apply, yielding efficient, accurate elliptical filters, either wide-band or very selective. To the best of author’s knowledge, such filters have not been approached before by other researchers. Also the circular filters designed here (also as FB components) have better performances compared to previous approaches [20, 21]. Thus, the circular FB in [20] is based on digital prototypes and has complex coefficients, while in [21] it has a zero-phase prototype, but the frequency mapping is more complicated, increasing filter order. Some results of [22] have been included in this article, which approaches the more general case of the elliptical filter.

A rigorous comparison in terms of performance with filters of this shape proposed previously by other authors is quite difficult to be made, due to the large variety of filters and methods found in literature. Design techniques like [4] (using McClellan transform for magnitude approximation), [5] (a set of filters which use multiscale techniques), [6] (obtaining near-elliptical symmetry by adjusting parameters), or [7]9, as well as the circular filters in [10]15 are conceptually very different from the ones proposed here; they lead to filters with other purposes, specifications and characteristics, rather difficult to compare with the filters discussed here.

We may conclude that the proposed analytical design procedure is convenient, relatively easy to apply and yields efficient and accurate zero-phase 2D filters with elliptical and circular symmetry, which inherit the features of the chosen prototype. The orientation angle, peak frequency and selectivity of these filters can be adjusted independently through the imposed parameters. Following the steps of the design algorithm given in Sect. 3, the filter matrices result directly, in the form of sums of convolutions of small-size (\(5 \times 5\)) matrices (as in (34–39)), which allows for a convenient, sequential implementation. Because the filter matrices depend explicitly on the imposed specifications, they result by simply substituting parameter values.

9 Conclusions

The proposed analytical design technique is simple and efficient. The design starts from a parametric LP prototype, which is scalable along frequency axis, thus having adjustable selectivity. Also, BP filters result by shifting the LP prototype to a given central frequency. Applying frequency scaling, we can obtain filters with steep transition and high selectivity, while keeping the same relatively low order. In order to derive 2D elliptical or circular filters, a specific frequency mapping was determined, using Chebyshev-Padé approximation. This mapping is applied to the factored LP or BP prototype, leading directly to the closed-form frequency response of the desired 2D filter, which results factored, an advantage for implementation. The overall filter matrices result directly as a convolution of smaller size matrices. Various elliptical filters with specified parameters have been designed, including selective directional filters, useful in extracting oriented straight lines and details from a given image. The circular filters were designed as components of an uniform filter bank. Due to the accurate approximations used, the designed filters result with a precise shape, without visible distortions even near the frequency plane limits. Further research may envisage an efficient implementation of this class of filters.