Analytic design of directional and square-shaped 2D IIR filters based on digital prototypes

Abstract

This paper proposes an analytic design method for a class of 2D recursive filters, namely with directional and square-shaped frequency response. The design technique is based on a specified 1D digital prototype filter and a complex frequency transformation which is determined using various rational approximations. Several design examples are presented for given specifications. The resulted filters are efficient and adjustable, being at the same time of low complexity and relatively high selectivity. These filters may have useful applications in image processing, like detecting lines with a given orientation from an image, as shown through simulation results on test images. The novelty of the proposed method consists in deriving the transfer function of the desired 2D filter only by applying successive frequency transformations to a prototype filter. Its advantages over most state-of-the-art design methods, which generally use global optimization numerical algorithms, is the filter tunability, and also its versatility; since the filter parameters, namely orientation and selectivity appear explicitly in the 2D filter matrices, they result directly for any specified parameters, therefore the design procedure does not need to be resumed every time from the start.

1 Introduction

The field of two-dimensional (2D) filters has emerged almost four decades ago, along with the development of digital image processing (Dudgeon et al. 1984; Lu et al. 1992; Jain 1989). The analytic design methods for 2D FIR and IIR filters are generally based on 1D analog or digital filter prototypes with given specifications, to which various spectral transformations are applied, in order to derive a 2D filter with a desired frequency response. Some well-known early works such as Pendergrass et al. (1976), Harn and Shenoi (1986) and Chen and Lee (1994) have laid the foundations for these analytic methods applied in 2D filter design. There are a large variety of 2D filters with specific shapes of their frequency response, for instance circular or elliptically-shaped, fan, square-shaped or orientation-selective filters etc.

There are several types of filters with directional (orientation-selective) frequency response, very useful in some image processing tasks, such as edge detection (Paplinski 1998), texture analysis and classification, directional smoothing applied to weather images (Lakshmanan 2004), motion or optical flow analysis (Austvoll 2000) etc. A very efficient Gaussian smoothing filter is proposed in Charalampidis (2009), while a recursive anisotropic 2-D Gaussian filter based on a triple-axis decomposition is described in Lam and Shi (2007), and a recursive implementation of the Gaussian filter in Young and van Vliet (1995). Diamond filters have been mainly used as anti-aliasing filters in the conversion between signals sampled on the rectangular sampling grid and the quincunx sampling grid.

A symbolic implementation of the McClellan transformation for a 2D diamond-shaped filter was described in Tosic et al. (1997). In Low and Lim (1997) the authors present a complex design method based on frequency response masking approach for FIR diamond filters. An efficient diamond-shaped filter based on singular value decomposition is designed in Ito (2010) and also diamond and circular filters using semi-definite programming (Hung et al. 2007). Some other relevant works in this field approach the design of 2D IIR with approximately linear phase (Xiao and Agathoklis 1279; Wysocka-Schillak 2008) and a unified design algorithm for complex FIR and IIR filters (Lertniphonphun and McClellan 2001).

The optimization of 2-D IIR filters with separable or non-separable denominator is approached in Dumitrescu (2005). A design for separable-denominator 2-D IIR by successive projection methods using a stability criterion based on the system matrix is proposed in Miyata (2008). A sequential partial optimization method is presented in Lai et al. (2017) for minimax design of 2-D IIR filters with separable denominator. Some very recent papers propose new design methods using spectral transformations. For instance in Yan et al. (2015), zero-phase IIR notch filters are designed based on a state-space representation of a 2-D transformation. In Shahanas et al. (2017), a reconfigurable fan-type 2D FIR filter with a tunable pass-band inclination angle is designed.

Many researchers approached the issue of 2D recursive filter stability and also stabilization techniques. A comprehensive theoretical analysis for 2D IIR filter stability and some practical stability tests are given in O’Connor and Huang (1978). A more recent paper (Shao and Hou 2010) approached a new stability test algorithm based on discriminant systems of real polynomials. An extension of a stabilization technique for 1D IIR filters to 2D IIR filters is investigated in Jury et al. (1977). A powerful stabilization technique for unstable 2D IIR filters, based on planar least-squares inverse polynomials is proposed in Raghuramireddy et al. (1986).

Some analytic design methods based on frequency transformations were proposed by the author in previous works: orientation-selective 2D IIR filters (Matei and Matei 2009), directional Gaussian-shaped FIR filters (Matei 2018), directional IIR filters derived from digital 1D prototypes (Matei and Matei 2010) and a class of adjustable zero-phase square-shaped IIR filters (Matei 2013).

Some issues in the general field of 2D nonlinear systems are approached in recent papers like Xie et al. (2015a), which proposes a control scheme of Roesser type discrete-time 2D fuzzy systems and Xie et al. (2015b), where less conservative global asymptotic stability of 2D Roesser state-space digital filter is studied. The classical, well-known rational approximations used in this work, namely Padé and Chebyshev–Padé, are described in works like Brezenski (1996), Trefethen et al. (2013).

In this paper an analytic design method is proposed for 2D directional filters, which select narrow domains along given directions in the frequency plane, and also square-shaped filters. The design is achieved in the spatial frequency domain, starting from an efficient 1D digital prototype filter, to which specific frequency transformations are applied, in order to obtain a 2D filter with the desired shape in the frequency plane. The novelty and major advantage of the method is that the resulted 2D filter coefficients depend explicitly on the imposed specifications (orientation, bandwidth etc.) and can thus be tuned and adjusted according to the desired characteristics, without the need to resume each time the design procedure. The design method is mainly analytical and uses approximations, but not any numerical optimization algorithms.

As regards relationship to prior work in the field, while many design methods rely on optimization algorithms and usually yield filters of minimum order for given specifications, as in Wysocka-Schillak (2008), Dumitrescu (2005) and Lai et al. (2017), entirely analytical methods like the one proposed here were less approached, at least in this form. Some researchers used McClellan transform (Chen and Lee 1994; Tosic et al. 1997; Yan et al. 2015), state-space representation (Yan et al. 2015) or impulse response Gramians (Xiao and Agathoklis 1998). Since all these design techniques are very different, it is quite difficult to make a rigorous comparison with the proposed method, in terms of efficiency, performance in image filtering and computational complexity. For instance, most of the designed directional filters are Gaussian-shaped, like in Lakshmanan (2004), Charalampidis (2009), Young and van Vliet (1995), while the directional filter proposed here is based on a narrow elliptic prototype. The computational complexity of our directional filter is of the order obtained in Lakshmanan (2004).

The paper is organized as follows. In Sect. 2, the 1D prototype digital filters used in design are presented. Section 3 presents the proposed analytic design method, including filter shape specifications in the frequency plane and the mathematical derivation of frequency transformations. A correction filter which removes undesired parts of the resulted 2D filter characteristic is introduced as well. Further in Sect. 4 a few design examples of typical filters from this class for given specifications are provided. Section 4 also includes a distortion analysis of the designed filters and a discussion paragraph. In Sect. 5, simulation results are given for directional filtering of two types of test images.

2 Low-pass digital filter prototypes

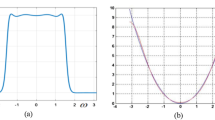
In designing the 2D orientation-selective filter, a very efficient 1D IIR digital filter prototype will be used. The most efficient analog or digital filter approximation for a specified steepness or selectivity is the elliptic filter, which results of a lower order than other approximations like Butterworth or Chebyshev, for the same specifications. Let us consider next a digital elliptic filter with order $N = 6$, peak-to-peak ripple $R_{P} = 0.1\,{\text{dB}}$, minimum stop-band attenuation $R_{S} = 36\,{\text{dB}}$ and normalized pass-band edge frequency $\omega_{P} = 0.01\pi$ (value 1 corresponding to half the sample rate). The specifications given above lead to the following transfer function in the complex frequency variable z:

$$ H_{P1} (z) = 0.012277 \cdot \frac{{\left( {z^{2} - 1.0202 \cdot z + 1} \right)}}{{\left( {z^{2} - 1.850147 \cdot z + 0.862316} \right)}} $$

(1)

The magnitude of the transfer function (1) is displayed in Fig. 1a on the frequency range $\omega \in [ - \;\pi ,\pi ]$; it has a steep transition and very small ripple in the pass-band and stop-band. This narrow filter will be the prototype for the designed 2D orientation-selective filters.

Fig. 1

Magnitudes of the prototype filter transfer functions given by (1), (2) and (3)

As the second prototype let us consider a digital elliptic filter with the following specifications: order $N = 6$, peak-to-peak ripple $R_{P} = 0.1\,{\text{dB}}$, minimum stop-band attenuation $R_{S} = 36\,{\text{dB}}$ and normalized pass-band edge frequency $\omega_{P} = 0.5\pi$, therefore a much wider bandwidth than prototype (1). These specifications give the following transfer function in variable z, in a factored form:

$$ \begin{aligned} H_{P2} (z) & = 0.11395 \cdot \frac{{\left( {z^{2} + 1.6501747 \cdot z + 1} \right)}}{{\left( {z^{2} + 0.057838 \cdot z + 0.916863} \right) \, }} \cdot \frac{{\left( {z^{2} + 0.627297 \cdot z + 1} \right)}}{{\left( {z^{2} - 0.072837 \cdot z + 0.63421} \right) \, }} \\ & \quad \cdot \frac{{\left( {z^{2} + 0.289093 \cdot z + 1} \right)}}{{\left( {z^{2} - 0.32878 \cdot z + 0.14951} \right) \, }} = k \cdot H_{B1} (z) \cdot H_{B2} (z) \cdot H_{B3} (z) \\ \end{aligned} $$

(2)

We can also use a 1D prototype with a narrower bandwidth than (2), for instance with normalized pass-band edge frequency $\omega_{P} = 0.25\pi$. In this case the factored prototype transfer function is the following:

$$ \begin{aligned} H_{P3} (z) & = 0.030383 \cdot \frac{{\left( {z^{2} + 0.636496 \cdot z + 1} \right)}}{{\left( {z^{2} - 1.167161 \cdot z + 0.399423} \right) \, }} \cdot \frac{{\left( {z^{2} - 0.970289 \cdot z + 1} \right)}}{{\left( {z^{2} - 1.262708 \cdot z + 0.724874} \right) \, }} \\ & \quad \cdot \frac{{\left( {z^{2} - 1.230289 \cdot z + 1} \right)}}{{\left( {z^{2} - 1.336221 \cdot z + 0.934522} \right) \, }} = k \cdot H_{B1} (z) \cdot H_{B2} (z) \cdot H_{B3} (z) \\ \end{aligned} $$

(3)

The low-pass elliptic transfer functions given in (1), (2) and (3) were obtained numerically from filter coefficients returned by the MATLAB function “ellip” for the given specifications; they result of low order, namely 2 and 6, finally leading to a low complexity 2D filter. The transfer functions in variable z given by (2) and (3) are factored into three bi-quad functions $H_{B1} (z)$, $H_{B2} (z)$ and $H_{B3} (z)$. The factors from the numerator and denominator in (2) and (3) can be coupled in pairs in several ways. The magnitude responses corresponding to the transfer functions in (2) and (3) are plotted in Figs. 1b and c, respectively over the frequency range $[0,\pi ]$.

3 Design of directional and square-shaped 2D IIR filters

In this main section, the analytical design method is described in detail for the two types of 2D filters, namely the directional and square-shaped filters. The 2D filters are specified in the frequency plane, then frequency transformations are found for each type of filter and finally the 2D filter matrices are obtained. A correction filter, necessary to eliminate marginal distortions, is also designed.

In this section, our proposed method will be compared to the one used in Chen and Lee (1994), where the frequency transformation is $z \to z_{1} \cdot z_{2}^{{{\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-0pt} \alpha }}}$, where $\alpha$ and $\beta$ are integers. The rotation angle in this case would be $\varphi = \arctan ({\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-0pt} \alpha })$. Using suitable interpolation functions, an interpolated array is generated, where signal values are defined on the new grid points. The whole scheme requires an input and an output interpolator. For an arbitrary angle, the values of $\alpha$ and $\beta$ may result inconveniently large, which might complicate the interpolation process.

3.1 Orientation specification for 2D directional filters

Starting from a zero-phase 1D prototype filter with a real transfer function $H(\omega_{\,1} )$ (which varies on one axis only), a two-dimensional oriented filter may be obtained by rotating the axes of the plane $(\omega_{\,1} ,\omega_{2} )$ with an angle $\varphi$. The rotation is defined by the linear transformation:

$$ \left[ {\begin{array}{*{20}c} {\omega_{\,1} } \\ {\omega_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\cos \varphi } \hfill & {\quad \sin \varphi } \hfill \\ { - \sin \varphi } \hfill & {\quad \cos \varphi } \hfill \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\bar{\omega }_{\,1} } \\ {\bar{\omega }_{2} } \\ \end{array} } \right] $$

(4)

where $\omega_{\,1}$, $\omega_{2}$ are the original frequency variables and $\bar{\omega }_{\,1}$,$\bar{\omega }_{2}$ the transformed variables. The spatial orientation is specified by angle $\varphi$ with respect to $\omega_{\,1} -$ axis and is defined by the following 1D to 2D spatial frequency transformation applied to the frequency response $H(\omega )$: $\omega \to \omega_{\;1} \cos \varphi + \omega_{2} \sin \varphi$. By substitution, the transfer function $H_{\varphi } (\omega_{\,1} ,\omega_{2} )$ of the 2D oriented filter results as:

$$ H_{\varphi } (\omega_{\,1} ,\omega_{2} ) = H(\omega_{\,1} \cos \varphi + \omega_{2} \sin \varphi ) $$

(5)

The directional filter $H_{\varphi } (\omega_{\,1} ,\omega_{2} )$ has the magnitude section along the line $\omega_{\,1} \cos \varphi + \omega_{2} \sin \varphi = 0$ identical with its prototype $H(\omega )$, and is constant along the perpendicular line $\omega_{\,1} \sin \varphi - \omega_{2} \cos \varphi = 0$ (the filter longitudinal axis). In Sect. 3.3 a convenient 1D to 2D frequency transformation is derived, which allows an oriented 2D filter to be obtained from a 1D prototype.

3.2 Frequency plane specification of square-shaped filters

A particular case of a square-shaped filter is the standard diamond filter; its shape in the frequency plane is shown in Fig. 2a. It is a square with a side length of $\pi \sqrt 2$, while its axis is tilted by an angle of $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$ radians about the two frequency axes. The orientation angle $\varphi$ is measured with respect to $\omega_{2}$ axis. A more general case is approached here, i.e. a 2D diamond-type filter with a square shape in the frequency plane, but with arbitrary side length and axis inclination angle, as shown in Fig. 2e. Next they will be referred to as square-shaped filters, since they are more general than the diamond filter from Fig. 2a, obtained as the intersection of the wide-band filter oriented diagonally (Fig. 2b) with its version rotated by 90°. In Fig. 2c and d, two wide-band directional responses are shown, whose axes form a 90° angle, described by the transfer functions $H_{D1} (z_{1} ,z_{2} )$ and $H_{D2} (z_{1} ,z_{2} )$. The square-shaped filter transfer function $H_{S} (z_{1} ,z_{2} )$ with response shown in Fig. 2e results as the product $H_{S} (z_{1} ,z_{2} ) = H_{D1} (z_{1} ,z_{2} ) \cdot H_{D2} (z_{1} ,z_{2} )$. Graphically, the square response with arbitrary orientation is the intersection of the two directional responses perpendicular to each other.

Fig. 2

a Diamond filter; b wide-band oriented filter; c, d wide-band oriented filters with orientations forming an angle $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$; e square-shaped filter resulted as product of the above oriented filters; f rhomboidal filter

The frequency response of $H_{D2} (z_{1} ,z_{2} )$ is ideally identical to the frequency response of $H_{D1} (z_{1} ,z_{2} )$, rotated by an angle of $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$. Since this axes rotation implies the frequency variable change:$\omega_{\,1} \to \omega_{2}$ and $\omega_{2} \to - \omega_{\,1}$, the transfer function $H_{D2} (z_{1} ,z_{2} )$ can be derived from $H_{D1} (z_{1} ,z_{2} )$ as $H_{D2} (z_{1} ,z_{2} ) = H_{D1} (z_{2} ,z_{1}^{ - 1} )$. A more general filter belonging to this class is a rhomboidal filter, as shown in Fig. 2f. In this case the two oriented low-pass component filters may have different band-widths and their axes are no longer perpendicular to each other (Matei 2013).

3.3 Frequency transformation for 2D directional and square-shaped filters

In this section a design method is proposed, which allows one to obtain a 2D discrete orientation-selective filter. The desired filter will be derived directly from a 1D prototype through a complex frequency transformation. A 1D discrete filter is generally described by a transfer function $H(z)$ like the ones given by Eqs. (1)–(3) from Sect. 2. The complex variable $z = e^{j\omega } = e^{s}$ is mapped into a 2D function $F_{\varphi } (z_{1} ,z_{2} )$, where the subscript $\varphi$ denotes the dependence upon the orientation angle $\varphi$. Using the linear frequency transformation (4) which defines the oriented filter, the following mapping results (Matei and Matei 2009):

$$ z \to e^{{j(\omega_{1} \cos \varphi + \omega_{2} \sin \varphi )}} = e^{{s_{1} \cos \varphi }} \cdot e^{{s_{2} \sin \varphi }} = (z_{1} )^{\cos \varphi } \cdot (z_{2} )^{\sin \varphi } = f_{1} (s_{1} ) \cdot f_{2} (s_{2} ) $$

(6)

Therefore the proposed complex frequency transformation is $z \to z_{1}^{\cos \varphi } \cdot z_{2}^{\sin \varphi }$. Our design method uses a simple technique which avoids the interpolation process, and is based on finding convenient approximations of the complex functions $f_{1} (s_{1} ) = e^{{s_{1} \cos \varphi }}$ and $f_{2} (s_{2} ) = e^{{s_{2} \sin \varphi }}$. These can be written as rational functions using the Padé or Chebyshev–Padé approximations. The Padé approximation is used here, which has the advantage of yielding analytical expressions of the coefficients, as a function of the orientation angle $\varphi$. The following approximations are easily derived using symbolic computation in MAPLE, as for real variable functions (Matei and Matei 2009):

$$ f_{1} (s_{1} ) \cong \frac{{1 + 0.5\cos \varphi \cdot s_{1} + 0.08333 \cdot \cos^{2} \varphi \cdot s_{1}^{2} }}{{1 - 0.5\cos \varphi \cdot s_{1} + 0.08333 \cdot \cos^{2} \varphi \cdot s_{1}^{2} }} = f_{a1} (s_{1} ) $$

(7)

$$ f_{2} (s_{2} ) \cong \frac{{1 + 0.5\sin \varphi \cdot s_{2} + 0.08333 \cdot \sin^{2} \varphi \cdot s_{2}^{2} }}{{1 - 0.5\sin \varphi \cdot s_{2} + 0.08333 \cdot \sin^{2} \varphi \cdot s_{2}^{2} }} = f_{a2} (s_{2} ) $$

(8)

They result directly using “pade” function, around value 0, and specifying the approximation order 2. The order of approximation can be chosen higher than 2, for better accuracy, but the expressions of the coefficients depending on angle $\varphi$ would be more complicated as well. In our case, the approximation was limited to second order, to obtain more efficient, low order 2D filters. The coefficients for the Padé approximations have closed-form expressions which are rather complicated for orders larger than 2, and the theory can be found in works like Xie et al. (2015a, b). Since $f_{1} (s_{1} )$ and $f_{2} (s_{2} )$ are complex functions ($s_{1} = j\omega_{1}$, $s_{2} = j\omega_{2}$), these approximations hold separately for real and imaginary parts, for instance:

$$ \text{Re} \left[ {f_{1} (j\omega_{\,1} )} \right] = \cos (\omega_{\,1} \cos \varphi ) \cong \text{Re} \left[ {f_{a1} (j\omega_{\,1} )} \right] $$

(9)

$$ \text{Im} \left[ {f_{1} (j\omega_{\,1} )} \right] = \sin (\omega_{\,1} \cos \varphi ) \cong \text{Im} \left[ {f_{a1} (j\omega_{\,1} )} \right] $$

(10)

and similarly for the other two. The real and imaginary parts of the two complex functions $f_{1} (s_{1} )$, $f_{2} (s_{2} )$ and of their rational approximations $f_{a1} (s_{1} )$, $f_{a2} (s_{2} )$ given by (7) and (8), are plotted comparatively in Fig. 3. It can be noticed that the proposed approximations are very accurate in the range $[ - \pi ,\pi ]$ and diverge outside this interval, because for a given order the Padé algorithm provides a good approximation, with a certain maximum error, on a limited range of values. The derived approximations (7) and (8) are scalable on the frequency axes, i.e. substituting the current frequency variable $\omega$ by $p \cdot \omega$ ($p > 0$), the approximation remains valid for a certain range of scaling parameter p (which means stretching for $p < 1$ and shrinking for $p > 1$). Thus (7) and (8) can be re-written as:

Fig. 3

Plots of exact functions versus their approximations: a$\cos (\omega_{1} \cos \varphi )$; b$\sin (\omega_{1} \cos \varphi )$; c$\cos (\omega_{1} \sin \varphi )$; d$\sin (\omega_{1} \sin \varphi )$

$$ f_{1} (ps_{1} ) \cong \frac{{1 + 0.5p\cos \varphi \cdot s_{1} + 0.08333p^{2} \cos^{2} \varphi \cdot s_{1}^{2} }}{{1 - 0.5p\cos \varphi \cdot s_{1} + 0.08333p^{2} \cos^{2} \varphi \cdot s_{1}^{2} }} = f_{a1} (ps_{1} ) $$

(11)

$$ f_{2} (ps_{2} ) \cong \frac{{1 + 0.5p\sin \varphi \cdot s_{2} + 0.08333p^{2} \sin^{2} \varphi \cdot s_{2}^{2} }}{{1 - 0.5p\sin \varphi \cdot s_{2} + 0.08333p^{2} \sin^{2} \varphi \cdot s_{2}^{2} }} = f_{a2} (ps_{2} ) $$

(12)

As show the design examples from Sect. 4, even using this low-order approximation, a very good directional filter results. Then the method can be generalized for higher orders for better performance. From the functions $f_{a1} (ps_{1} )$ and $f_{a2} (ps_{2} )$, two corresponding discrete functions in the complex variables $z_{1}$ and $z_{2}$ can be obtained. This can be achieved in various ways, for instance using Euler approximations, or the bilinear transform. However, these introduce relatively large errors, which result in large shape distortions of the designed 2D filter. Another approach would be to find more accurate discrete approximations for the variables $s_{1}$, $s_{2}$ and $s_{1}^{2}$, $s_{2}^{2}$. To find an efficient rational trigonometric approximation of the linear function $\omega$ on the range $[ - \pi ,\pi ]$ the simple change of variable is applied:

$$ \omega = \arccos \left( {{x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi }} \right) \leftrightarrow x = \pi \cos \omega $$

(13)

The approximation of the linear function ω is more easily derived indirectly, by finding the rational trigonometric approximation of ${\omega \mathord{\left/ {\vphantom {\omega {\sin \omega }}} \right. \kern-0pt} {\sin \omega }}$, an even function of $\cos \omega$. However, since we cannot find it directly, the change of variable (13) was used; by substituting in ${\omega \mathord{\left/ {\vphantom {\omega {\sin \omega }}} \right. \kern-0pt} {\sin \omega }}$ the variable ω by $\omega = \arccos \left( {{x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi }} \right)$, we find using MAPLE the following function and its first-order Chebyshev–Padé approximation in variable x:

$$ \frac{{\arccos ({x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi })}}{{\sin \left( {\arccos ({x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi })} \right)}} = \frac{{\arccos ({x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi })}}{{\sqrt {1 - ({x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0pt} \pi })^{2} } }} \cong \frac{1.553415 + 0.1099316x}{1 + 0.276857x} $$

(14)

Next, substituting back in (14) the variable $x = \pi \cos \omega$, the trigonometric approximation for ${\omega \mathord{\left/ {\vphantom {\omega {\sin \omega }}} \right. \kern-0pt} {\sin \omega }}$ is finally found. Here, x is an intermediate variable needed to obtain the desired approximations using MAPLE. Substituting back in (14) $x = \pi \cos \omega$, the approximation shown in Fig. 4a results:

Fig. 4

a The approximation (red curve) of the linear function (blue curve) on the frequency range $\omega \in [ - \pi ,\pi ]$; b The parabolic function (in blue) and its rational trigonometric approximation (in red) (Color figure online)

$$ \omega \cong {{\sin \omega \cdot \left( {1.553415 + 0.3451854 \cdot \cos \omega } \right)} \mathord{\left/ {\vphantom {{\sin \omega \cdot \left( {1.553415 + 0.3451854 \cdot \cos \omega } \right)} {\left( {1 + 0.869331 \cdot \cos \omega } \right)}}} \right. \kern-0pt} {\left( {1 + 0.869331 \cdot \cos \omega } \right)}} $$

(15)

For the squared frequency variable, the following rational trigonometric approximation is used:

$$ \omega^{2} \cong 2.357534 \cdot {{\left( {1 - 0.946216 \cdot \cos \omega } \right)} \mathord{\left/ {\vphantom {{\left( {1 - 0.946216 \cdot \cos \omega } \right)} {\left( {1 + 0.463012 \cdot \cos \omega } \right)}}} \right. \kern-0pt} {\left( {1 + 0.463012 \cdot \cos \omega } \right)}} $$

(16)

displayed in Fig. 4b. As can be noticed, these are very efficient and accurate approximations on the frequency range $\omega \in [ - \pi ,\pi ]$, having a small distortion only at the margins of the specified interval. Since on the two frequency axes, $s_{1,2} = j \cdot \omega_{\,1,2}$, $s_{1,2}^{2} = - \omega_{\,1,2}^{2}$ and $\cos \omega_{\,1,2} = 0.5 \cdot (z_{1,2} + z_{1,2}^{ - 1} )$, $\sin \omega_{\,1,2} = - j \cdot 0.5 \cdot (z_{1,2} - z_{1,2}^{ - 1} )$, functions (15), (16) can be expressed as complex frequency mappings:

$$ s_{1,2} \cong 0.198441 \cdot \frac{{\left( {z_{1,2}^{4} + 9.004834z_{1.2}^{3} + 2z_{1,2}^{2} + 9.004834z_{1,2} + 1} \right)}}{{z_{1,2} \left( {z_{1,2}^{2} + 2.300649z_{1,2} + 1} \right)}} $$

(17)

$$ s_{1,2}^{2} \cong - 4.81788 \cdot {{\left( {z_{1,2}^{2} - 2.113682 \cdot z_{1,2} + 1} \right)} \mathord{\left/ {\vphantom {{\left( {z_{1,2}^{2} - 2.113682 \cdot z_{1,2} + 1} \right)} {\left( {z_{1,2}^{2} - 4.319542 \cdot z_{1,2} + 1} \right)}}} \right. \kern-0pt} {\left( {z_{1,2}^{2} - 4.319542 \cdot z_{1,2} + 1} \right)}} $$

(18)

The approximations (17) and (18) are next substituted into (11) and (12) and finally the mapping (6) with the expression $z \to f_{a1} (ps_{1} ) \cdot f_{a2} (ps_{2} )$ may be written in the matrix form:

$$ z \to H(z_{1} ,z_{2} ) = \frac{{M(z_{1} ,z_{2} )}}{{N(z_{1} ,z_{2} )}} = \frac{{{\mathbf{z}}_{1} \times {\mathbf{M}} \times {\mathbf{z}}_{2}^{T} }}{{{\mathbf{z}}_{1} \times {\mathbf{N}} \times {\mathbf{z}}_{2}^{T} }} $$

(19)

where ${\mathbf{z}}_{1} = [\begin{array}{*{20}c} {z_{1}^{6} } & {z_{1}^{5} } & \ldots & {z_{1} } & 1 \\ \end{array} ]$, ${\mathbf{z}}_{2} = [\begin{array}{*{20}c} {z_{2}^{6} } & {z_{2}^{5} } & \ldots & {z_{2} } & 1 \\ \end{array} ]$ and the matrices M and N result from the vectors P and Q by outer product (two-dimensional convolution) as ${\mathbf{M}} = {\mathbf{P}} \otimes {\mathbf{P}}$ and ${\mathbf{N}} = {\mathbf{Q}} \otimes {\mathbf{Q}}$. The vectors P and Q corresponding to the numerator and denominator of functions $f_{a1} (ps_{1} )$ and $f_{a2} (ps_{2} )$ from (11), (12) are:

$$ {\mathbf{P}} = p \cdot \cos \varphi \cdot {\mathbf{A}}_{1} + p^{2} \cdot (\cos \varphi )^{2} \cdot {\mathbf{A}}_{2} $$

(20)

$$ {\mathbf{Q}} = p \cdot \sin \varphi \cdot {\mathbf{A}}_{1} + p^{2} \cdot (\sin \varphi )^{2} \cdot {\mathbf{A}}_{2} $$

(21)

where the component vectors are ${\mathbf{A}}_{1} = [\begin{array}{*{20}c} {\alpha_{1} } & {\beta_{1} } & {\gamma_{1} } & {\delta_{1} } & {\gamma_{1} } & {\beta_{1} } & {\alpha_{1} } \\ \end{array} ]$, with $\alpha_{1} = 0.0992205$, $\beta_{1} = 0.464877$, $\gamma_{1} = - 3.561694$, $\delta_{1} = 0.929754$ and ${\mathbf{A}}_{2} = [\begin{array}{*{20}c} {\alpha_{2} } & {\beta_{2} } & {\gamma_{2} } & {\delta_{2} } & {\gamma_{2} } & {\beta_{2} } & {\alpha_{2} } \\ \end{array} ]$, with $\alpha_{2} = 0$, $\beta_{2} = - 0.401474$, $\gamma_{2} = - 0.075062$, $\delta_{2} = 1.149356$. The matrices M and N depend only on the angle $\varphi$. Let us consider a generic bi-quad function $H_{Bi} (z)$ in the complex frequency plane variable z:

$$ H_{Bi} (z) = {{\left( {z^{2} + v_{1} \cdot z + v_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {z^{2} + v_{1} \cdot z + v_{0} } \right)} {\left( {z^{2} + u_{1} \cdot z + u_{0} } \right)}}} \right. \kern-0pt} {\left( {z^{2} + u_{1} \cdot z + u_{0} } \right)}} $$

(22)

Substituting the 1D to 2D mapping (19) into (22), the factor $H_{2Bi} (z_{1} ,z_{2} )$ results, corresponding to the generic bi-quad function $H_{Bi} (z)$:

$$ H_{Bi} (z) \to H_{2Bi} (z_{1} ,z_{2} ) = \frac{{V(z_{1} ,z_{2} )}}{{U(z_{1} ,z_{2} )}} = \frac{{{\mathbf{z}}_{1} \times {\mathbf{V}} \times {\mathbf{z}}_{2}^{T} }}{{{\mathbf{z}}_{1} \times {\mathbf{U}} \times {\mathbf{z}}_{2}^{T} }} $$

(23)

where $\times$ means inner product and the matrices U and V are given by:

$$ \begin{aligned} {\mathbf{V}} = {\mathbf{M}} * {\mathbf{M}} + v_{1} \cdot {\mathbf{M}} * {\mathbf{N}} + v_{0} \cdot {\mathbf{N}} * {\mathbf{N}} \hfill \\ {\mathbf{U}} = {\mathbf{M}} * {\mathbf{M}} + u_{1} \cdot {\mathbf{M}} * {\mathbf{N}} + u_{0} \cdot {\mathbf{N}} * {\mathbf{N}} \hfill \\ \end{aligned} $$

(24)

while the vectors ${\mathbf{z}}_{1}$ and ${\mathbf{z}}_{2}$ are: ${\mathbf{z}}_{1} = [\begin{array}{*{20}c} {z_{1}^{12} } & {z_{1}^{11} } & \ldots & {z_{1} } & 1 \\ \end{array} ]$; ${\mathbf{z}}_{2} = [\begin{array}{*{20}c} {z_{2}^{12} } & {z_{2}^{11} } & \ldots & {z_{2} } & 1 \\ \end{array} ]$. The numerator $V(z_{1} ,z_{2} )$ and the denominator $U(z_{1} ,z_{2} )$ are in fact the Discrete Space Fourier Transforms (DSFT) of the corresponding matrices V and U.

The resulted 2D filter preserves the characteristics of the 1D prototype filter, like cut-off frequency, steepness, pass-band and stop-band ripple etc. For instance, if the prototype filter is maximally flat, the resulted 2D filter will be also maximally flat; if the prototype has a small pass-band ripple, the 2D filter will inherit this ripple. For instance, a 2D wide-band filter oriented at $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$ as in Fig. 2b has a cut-off frequency of ${{\omega_{c1} = \pi \sqrt 2 } \mathord{\left/ {\vphantom {{\omega_{c1} = \pi \sqrt 2 } {2 \cong 0.7071\pi }}} \right. \kern-0pt} {2 \cong 0.7071\pi }}$; therefore, the 1D prototype filter should have exactly this cut-off frequency. We can use the 1D LP prototype $H_{P2} (z)$ given by (2), with cut-off frequency $\omega_{P2} = 0.5\pi$, which must be scaled (in this case dilated) on the frequency axis with the parameter p, as detailed in Sect. 3.3. The scaling parameter p in this case should be $p = \omega_{P2} /\omega_{c1} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}$, and so on. Depending on the desired 2D filter specifications, like cut-off frequency, we may choose the most convenient of the prototypes given by (1), (2) or (3) and apply the required scaling.

To summarize the design method, for a specified orientation $\varphi$ of the directional or square-shaped filter, the matrices M and N are determined as above. Depending on the filter selectivity, a suitable 1D low-pass prototype is chosen, for instance given by $H_{P1} (z)$, $H_{P2} (z)$ or $H_{P3} (z)$ as in (1)–(3) or a scaled version with a specified parameter p. As the following design examples show, an order $N = 6$ is sufficient for a very good selectivity or steepness. Each bi-quad factor function $H_{Bi} (z)$ of the factored prototype $H_{P} (z)$ is then simply mapped into $H_{2Bi} (z_{1} ,z_{2} )$ according to (23). The numerator and denominator of $H_{2Bi} (z_{1} ,z_{2} )$ correspond to matrices U and V given by (24). In the case of directional filters, the entire 2D filter will have the transfer function given by the product of bi-quads:

$$ H_{D} (z_{1} ,z_{2} ) = \prod\limits_{i = 1}^{3} {H_{2Bi} (z_{1} ,z_{2} )} $$

(25)

For square-shaped filters, using a wide LP prototype, the first partial transfer function $H_{D1} (z_{1} ,z_{2} )$ results as in (25), while its counterpart is given by $H_{D2} (z_{1} ,z_{2} ) = H_{D1} (z_{2} ,z_{1}^{ - 1} )$ and finally the transfer function of the square filter is $H_{S} (z_{1} ,z_{2} ) = H_{D1} (z_{1} ,z_{2} ) \cdot H_{D2} (z_{1} ,z_{2} )$, as shown in Sect. 3.2.

3.4 Correction filter design

For the two types of 2D filters, directional and square-shaped, we may need to remove some marginal distortions of the 2D filter frequency response by using a wide band low-pass (LP) filter which has the role of a masking filter and is applied over the desired frequency response; this means that the transfer functions of the desired filter and mask filter are multiplied in order to obtain the transfer function of the corrected square filter. A zero-phase correction filter will be used, which is easy to design and can be made scalable along the two frequency axes of the frequency plane. A relatively simple smooth function of frequency with a low-pass shape is the following:

$$ H_{PC} (\omega ) = 0.5\left( {\tanh \,(10 \cdot (\omega + {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 4}} \right. \kern-0pt} 4})) - \tanh \,(10 \cdot (\omega - {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 4}} \right. \kern-0pt} 4}))} \right) $$

(26)

There are also other functions with smooth low-pass shape which could be used. However, in terms of tanh, $H_{PC} (\omega )$ has a very simple expression. Moreover, its rational approximation can be easily derived using MAPLE, for the given order. For some functions, the algorithm for calculating the Chebyshev–Pade approximation does not converge. For the low-pass function chosen as in (26), the algorithm performs well and the following rational approximation of order 6 for $H_{PC} (\omega )$ is obtained, given in factored form, where q is a scaling parameter:

$$ H_{C} (\omega ) = 1.691967 \cdot \frac{{\left( {q^{2} \omega^{2} - 6.65275} \right)\left( {q^{2} \omega^{2} - 8.230488} \right)\left( {q^{2} \omega^{2} - 9.598568} \right)}}{{\left( {q^{2} \omega^{2} - 25.492071} \right)\left( {q^{4} \omega^{4} - 11.478865 \cdot q^{2} \omega^{2} + 34.824872} \right)}} $$

(27)

This can be regarded as a zero-phase LP filter with cut-off frequency ${{3\pi } \mathord{\left/ {\vphantom {{3\pi } 4}} \right. \kern-0pt} 4}$, being an accurate approximation of $H_{PC} (\omega )$ from (26), in which the tanh argument is shifted to the left and right by exactly 3π/4. This function is adjustable along the frequency axis through the parameter q. For $q = 1$, $H_{C} (\omega )$ is a very accurate approximation of $H_{PC} (\omega )$. If the frequency variable $\omega$ is replaced by $q \cdot \omega$, the function $H_{C} (\omega )$ becomes narrower for $q > 1$ and wider for $q < 1$. Figure 5c shows the function $H_{PC} (\omega )$ drawn in blue and $H_{C} (\omega )$ in red. In order to find a discrete version of the function (27) the approximation (16) is applied for $\omega^{2}$. Substituting (16) in each one of the factors of (27), a function in the variable $\cos \omega$ results. Since $\cos \omega = 0.5 \cdot (z + z^{ - 1} )$, a factored transfer function in variable z is derived in the matrix form:

$$ H_{C} (z) = \frac{{B_{C} (z)}}{{A_{C} (z)}} = \frac{{{\mathbf{B}}_{C} \times {\mathbf{z}}}}{{{\mathbf{A}}_{C} \times {\mathbf{z}}}} $$

(28)

where the vector is ${\mathbf{z}} = [\begin{array}{*{20}c} {z^{6} } & {z^{5} } & \ldots & z & 1 \\ \end{array} ]$, while ${\mathbf{B}}_{C}$ and ${\mathbf{A}}_{C}$ are vectors of size $1 \times 7$ which in turn can be written as convolution of $1 \times 3$ and $1 \times 5$ vectors as ${\mathbf{B}}_{C} = {\mathbf{B}}_{C1} * {\mathbf{B}}_{C2} * {\mathbf{B}}_{C3}$ and ${\mathbf{A}}_{C} = {\mathbf{A}}_{C1} * {\mathbf{A}}_{C2}$ where ${\mathbf{B}}_{C1} = \left[ {\begin{array}{*{20}c} {a_{1} } & {b_{1} } & {a_{1} } \\ \end{array} } \right]$,${\mathbf{B}}_{C2} = \left[ {\begin{array}{*{20}c} {a_{2} } & {b_{2} } & {a_{2} } \\ \end{array} } \right]$,${\mathbf{B}}_{C3} = \left[ {\begin{array}{*{20}c} {a_{3} } & {b_{3} } & {a_{3} } \\ \end{array} } \right]$, ${\mathbf{A}}_{C1} = \left[ {\begin{array}{*{20}c} {a_{4} } & {b_{4} } & {a_{4} } \\ \end{array} } \right]$, ${\mathbf{A}}_{C2} = [\begin{array}{*{20}c} a & b & c & b & a \\ \end{array} ]$ and the vector elements have the expressions depending on parameter q:

Fig. 5

a Frequency response $H_{\varphi 1} (\omega_{1} ,\omega_{2} )$ of the oriented filter with $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$; b its contour plot; c correction filter prototype; d correction filter characteristic; e–i frequency responses and contour plots for corrected oriented filters with various orientation angles: e, f$\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$; g, h$\varphi = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}$; i$\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$

$a_{1} = - 1.115368 \cdot q^{2} - 1.540152$; $b_{1} = 2.357534 \cdot q^{2} - 6.65275$; $a_{2} = - 1.115368 \cdot q^{2} - 1.905407$

$b_{2} = 2.357534 \cdot q^{2} - 8.230488$; $a_{3} = - 1.115368 \cdot q^{2} - 2.222126$; $b_{3} = 2.357534 \cdot q^{2} - 9.598568$

$a_{4} = - 1.115368 \cdot q^{2} - 5.901567$; $b_{4} = 2.357534 \cdot q^{2} - 25.492071$

$a = 1.244046 \cdot q^{4} + 2.964008 \cdot q^{2} + 1.86644$; $b = - 5.259037 \cdot q^{4} + { 6} . 5 3 8 1 8 9\cdot q^{2} + 16.124333\quad c = 8.046059 \cdot q^{4} - 21.133797 \cdot q^{2} + 38.557752$

Once known the 1D transfer function $H_{C} (z)$, the final transfer function of the 2D square-shaped correction filter results as $H_{COR} (z_{1} ,z_{2} ) = H_{C} (z_{1} ) \cdot H_{C} (z_{2} )$. This 2D LP filter is separable and results by applying successively the 1D filter along the two frequency axes. This correction filter is zero-phase and almost maximally-flat, as required. Its characteristic $H_{COR} (\omega \,_{1} ,\omega_{{{\kern 1pt} 2}} )$ is displayed in Fig. 5d.

4 Design examples

In this section, design examples of typical directional and square-shaped filters for given specifications are presented. Then a distortion analysis of their frequency responses is made and finally an extensive discussion on various design aspects is included.

4.1 Design examples of directional filters

Using the proposed method let us design a 2D directional filter with an orientation angle $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$. The frequency response $H_{\varphi 1} (\omega_{\,1} ,\omega_{2} )$ of the filter is displayed in Fig. 5a and the corresponding contour plot in Fig. 5b. As can be noticed, the filter characteristic has a good linearity, however it twists towards the margins of the frequency plane and some residual artifacts are also present. These marginal distortions can be corrected using an additional LP filter, like the one described in Sect. 3.4. Applying this correction filter $H_{COR} (\omega \,_{1} ,\omega_{{{\kern 1pt} 2}} )$, the undesired marginal parts of the designed filter frequency response are removed, thus resulting in a correct characteristic as in Fig. 5e, with the corresponding contour plot in Fig. 5f. The corrected directional filter has the frequency response given by $H_{\varphi 1C} (\omega_{1} ,\omega_{2} ) = H_{\varphi 1} (\omega_{1} ,\omega_{2} ) \cdot H_{COR} (\omega \,_{1} ,\omega_{{{\kern 1pt} 2}} )$. The frequency responses and contour plots of the corrected directional filters for other orientations, like $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}$ and $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$ are displayed in Fig. 5g, h, i. As can be noticed, all filters have very selective directional characteristics with good linearity along their axes. They are used in the next section in directional filtering of test images.

4.2 Design examples of square-shaped filters

Using the same method let us design some 2D square-shaped filters with specified orientation and bandwidth. The only difference compared to the directional filters derived previously is that the design starts from the second prototype filter, namely the wide bandwidth LP digital filter with transfer function $H_{P} (z)$ given by (2). The prototype, frequency response and contour plot of the correction filter with $q = 1$ are shown in Fig. 6a–c. Next, several examples of square filter design are given. The uncorrected characteristics of four square-shaped filters resulted directly by applying the steps of the proposed design method are shown in Figs. 6d, g, j and 7a, respectively.

Fig. 6

a 1D scalable prototype of the correction filter; b, c characteristic and contour plot of the correction filter with $q = 1$; d uncorrected frequency response of a square filter with $p = 1$ and $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$; e, f frequency response and contour plot of the corrected square filter; g uncorrected frequency response of a square filter with $p = 1$ and $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$; h, i frequency response and contour plot of the corrected square filter; j uncorrected frequency response of a square filter with $p = 1.4$ and $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$; k, l frequency response and contour plot of the corrected square filter

Fig. 7

a uncorrected frequency response of a square filter with $p = 1.6$ and $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}$; b, c frequency response and contour plot of the corrected square filter; d, e characteristic and contour plot of the uncorrected directional filter with $p = 1.6$ and $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}$; f, g characteristic and contour plot of the directional filter after applying a correction filter with $q = 1.1$

The marginal undesired distortions are clearly visible. The corresponding frequency responses and contour plots of the corrected filters are displayed in Figs. 6e, f, h, i, k, l and 7b, c respectively. Also in Fig. 7d–g an uncorrected and corrected wide oriented filter with $p = 1.6$, $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}$ is shown. All the corrected filters have small ripple distortions in the pass band and stop band and are very steep.

4.3 Distortion analysis

As in any design using analytical or numerical optimization techniques, the 2D filters obtained here inherently present some shape distortions, as compared to their ideal counterparts. These errors appear as a result of the approximations used to determine the specific frequency transformation, and occur mainly in the expressions (7), (8), (15), (16). The errors are larger at the limits of the frequency range, which is clearly visible in Figs. 3 and 4. These marginal errors of the used approximations result in the marginal artifacts which appear in the frequency response of the designed filters, both directional and square-shaped, as can be observed in Figs. 5a, 6b, g, j and 7a, d. These marginal errors in the frequency plane are removed using the correction LP filter which acts as a mask applied over the designed filter. A higher order approximation would be needed in order to have smaller distortions, which is not convenient for implementation, so an optimal trade-off must be reached. The 2D IIR filters designed using the proposed method can be characterized by a distortion measure which describes the similarity between the frequency response of the designed filter and its ideal counterpart. This distortion analysis was proposed by the author in Matei (2018) and is used here as well.

For instance, if $\left| {H_{R} (\omega_{1} ,\omega_{2} )} \right|$ and $\left| {H_{I} (\omega_{1} ,\omega_{2} )} \right|$ are the frequency response magnitudes of the designed filter and ideal filter, their difference defines the error $\Delta H(\omega_{1} ,\omega_{2} ) = \left| {H_{R} (\omega_{1} ,\omega_{2} )} \right| - \left| {H_{I} (\omega_{1} ,\omega_{2} )} \right|$. The frequency response is usually represented as a mesh or sampled surface in a convenient number of equally spaced points in the frequency plane, corresponding to a $N \times N$ matrix, where N is the number of points on the $[ - \pi ,\pi ]$ range. A relevant measure of distortion may be the root of average value of the squared differences over all the sampling points, i.e. the RMS. Taking N sampling points on both axes of the frequency plane, the distortion factor is defined as Matei (2018):

$$ \delta = \frac{1}{{N^{2} }} \cdot \sqrt {\sum\limits_{m = 1}^{N} {} \sum\limits_{n = 1}^{N} {\left( {\Delta H({{2m\pi } \mathord{\left/ {\vphantom {{2m\pi } N}} \right. \kern-0pt} N},{{2n\pi } \mathord{\left/ {\vphantom {{2n\pi } N}} \right. \kern-0pt} N})} \right)^{2} } } $$

(29)

Using the expression (29), one can obtain the dependence of the distortion factor $\delta$ on the orientation angle $\varphi$ of the oriented square-shaped filter, which is helpful in evaluating the design accuracy. Let us consider the square-shaped filter displayed in Fig. 6g–i, with parameter values $p = 1$, $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$. Keeping constant the filter bandwidth given by the parameter $p = 1$ and varying the orientation angle $\varphi$ in the range $\varphi \in [0,{{\,\pi } \mathord{\left/ {\vphantom {{\,\pi } 2}} \right. \kern-0pt} 2}]$ with a small step, the curve drawn in black displayed in Fig. 8 is obtained, for $N = 100$ points. In this particular case, the smallest distortion value is $\delta_{\hbox{min} } \cong 0. 0 2 3 4= 2.34\,\%$ and occurs exactly at the angle $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$ (for a diagonally-oriented filter), while the largest distortion value is $\delta_{\hbox{max} } \cong 0. 0 5 8 9= 5.89\,\%$, for values of $\varphi$ close to 0 and ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$. Due to symmetry in the frequency plane, it is sufficient to analyze the filter distortions for $\varphi \in [0,{{\,\pi } \mathord{\left/ {\vphantom {{\,\pi } 2}} \right. \kern-0pt} 2}]$. The factor $\delta$ depends weakly on the number N of sampling points. For example, taking $N = 1000$, for $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$ the value $\delta \cong 0. 0 2 3= 2.3\,\%$ is obtained. The curves plotted in Fig. 8 represent the variation of the distortion factor $\delta$ with orientation angle $\varphi$ for the indicated values of the parameter p. It can be noticed that the dependence of $\delta$ with $\varphi$ is symmetric about the angle $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$. A similar analysis can be made for the directional filters.

Fig. 8

Distortion factor $\delta$ versus orientation angle $\varphi$ for a typical square-shaped filter (Color figure online)

4.4 Discussion

The idea of the paper was to design two classes of 2D filters, namely directional and square-shaped filters using the same analytical method applied in each case to the appropriate 1D prototype filter. The IIR filters were chosen due to their low order (complexity) compared to the FIR version. It can be shown that FIR filters designed using a similar technique, namely frequency mappings applied to 1D prototypes, would result much more complicated and inefficient, of very high order, and the method would no longer be an alternative to numerical optimization design methods.

The two types of 2D filters approached here belong to the same class in the sense that the same frequency transformation was used to obtain them, applied to the same type of 1D prototype, namely an elliptic LP digital filter. The only difference is that a very narrow LP prototype is used to obtain a very selective directional filter, while a wider LP prototype is used to obtain the oriented square-shaped filter (in fact its two directional components).

The proposed analytic design method is relatively simple and efficient. Once chosen the suitable 1D recursive prototype filter, a specific frequency transformation is applied and the matrices of the 2D filter are determined in a straightforward way. Since the matrices M and N occurring in the mapping (19) are an outer product of the vectors P and Q given by (20), (21), the mapping is separable. Also the matrices U and V from (24) are a sum of three outer products of M and N, so three separable terms, we can consider that the numerator and denominator of the bi-quad $H_{Bi} (z_{1} ,z_{2} )$ in (23) are partially separable. The same is valid for the entire 2D filter $H_{D} (z_{1} ,z_{2} )$ given by (25), which may allow for an efficient implementation.

Both types of 2D filters designed using the proposed method are efficient, of relatively low order taking into account their high selectivity and steepness. As shown, both types of designed 2D filters are derived by applying the same 1D to 2D complex frequency mapping in matrix form given by (19) to different 1D LP prototypes, very narrow for directional filters and wide-band for square filters, respectively. Since the order of wide band prototype is 6 and the order of narrow prototype is only 2, the square-shaped filter is roughly speaking three times more complex than the directional one, since its order results three times higher. The function $H(z_{1} ,z_{2} )$ can be factored into 2 polynomials of order 6 in variables $z_{1}$ and $z_{2}$, corresponding to 2 matrices of size $7 \times 7$. Finally, the narrow directional filter results of order 12, corresponding to numerator and denominator matrices of size $13 \times 13$. However, both matrices can be written as sums of 3 convolution products of vectors of size $1 \times 13$. Thus, if q is the vector size and the image to be filtered is of size N (with $N^{2}$ pixels), the total computational complexity results of the order $(6q + 4)N^{2}$, which is comparable with the one in Austvoll (2000). In our case, for $q = 13$, we get $82N^{2}$ computations. By contrast, in the general case, the total number of computations would be roughly $2q^{2} N^{2}$ (in our case $338N^{2}$). Therefore, the proposed method is roughly 4 times more computationally efficient than in the general case of a non-separable filter.

Taking into account (19) and the prototype expression (1), it is easy to determine that the total number of multiplications needed in one filtering step is 338. In the same way, for the square-shaped or diamond filter given by prototype (2), consisting of a product of three bi-quad functions, the kernel size is $37 \times 37$ and thus the total number of multiplications is approximately 2700. This number is smaller than the one reported in Low and Lim (1997) for a diamond filter using the frequency masking technique, for which approximately 6500 multiplications are necessary. Therefore the implementation in our case would be about three times more efficient and the filter has a lower complexity.

The proposed directional filter is very selective by comparison to other orientation-selective filters from literature. Also, it has a straight, linear shape of the response in the frequency plane, and has a higher directional selectivity compared for instance with the Gaussian directional filter based on triple axis decomposition (Lam and Shi 2007), which has an elliptical shape in the frequency plane. The Gaussian directional filters applied in smoothing remote sensing images in Lakshmanan (2004) and Charalampidis (2009) also have elliptical shapes in the frequency plane. This method is somewhat related with the one proposed by the author in Matei (2018), for Gaussian directional FIR filters. The designed diamond filter has comparable characteristics with the diamond filter in Tosic et al. (1997). However, at roughly the same complexity, the shape of our proposed filter seems more precise in the frequency plane, it is almost maximally-flat and the transition region is narrower. Our approach also has comparable performance with the diamond filter with cascaded structure proposed in Ito (2010). Compared with the diamond filter in Hung et al. (2007), our method is relatively simpler and more versatile and also the designed filter seems to have a more precise shape of the frequency response.

The resulted 2D filters are comparable in efficiency with others described in the literature, while they also have the advantage of being adjustable or tunable, in the sense that their matrices depend explicitly on the specified parameters, in our case the orientation angle $\varphi$ and the scaling parameter p which gives the bandwidth. For different parameter values, the particular filter matrices result directly. Therefore an advantage of the method is its versatility; the design need not be resumed each time again from the start for various specifications.

The stability issue for the designed 2D filters was not approached here, but it will be studied in detail in further work on this topic. Generally the stability problem for 2D filters, especially non-separable, is a lot more difficult than for 1D filters. If the prototype filter is stable, and if the applied frequency transformations preserve stability, the derived 2D filters should also be stable. In the case of an analytical design method for recursive filters like the one proposed here, where the 2D filter transfer function results from its prototype through successive approximations and frequency mappings, the stability conditions are difficult to impose from the start. There are however in the literature various stability criteria (O’Connor and Huang 1978; Shao and Hou 2010) and also stabilization methods can be applied for unstable 2D filters (Jury et al. 1977; Raghuramireddy et al. 1986). As is well known, some filters are overall unstable (with poles both inside and outside the unit circle), but their transfer function can be separated into one stable part and one unstable part. This unstable part can be implemented using backward filtering. The input sequence is first filtered in the forward direction by the stable part, then the inverted sequence is filtered backwards by the unstable part. This technique is applied in Young and van Vliet (1995) for the implementation of a Gaussian recursive filter and since the 2D Gaussian filter is separable, this may be applied in principle also for a 2D filter, successively along the two directions. As a continuation of this work, the author intends to investigate first the stability of filters obtained through the proposed method, and also the applicability of such forward–backward filtering techniques in case the filters are not stable. Also further research envisages an efficient implementation of this class of filters and testing them on various real-life images.

5 Applications and simulation results

The designed directional filters can be used to select from a given image the lines with a specified orientation. In order to prove the filtering capability of these filters, two test images were used. A binary image containing straight lines with gradually varying orientation is displayed in Fig. 9a. It is known that the spectrum of a straight line is oriented in the frequency plane $(\omega_{1} ,\omega_{2} )$ at an angle of $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$ with respect to the line direction. This can be clearly seen in the 2D FFT spectrum magnitude (b) of image (a), displayed on the range $\omega_{\,1} ,\omega_{\,2} \in [{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0pt} 4},{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}]$ for better visibility. It can be noticed that the spectrum of image (a) consists of straight lines passing through the origin of the frequency plane. For a given orientation angle, only the lines whose spectrum overlaps with the filter frequency response remain in the output image, while the rest are more or less blurred and are practically eliminated through directional low-pass filtering. For instance, with ${{\varphi = \pi } \mathord{\left/ {\vphantom {{\varphi = \pi } 6}} \right. \kern-0pt} 6}$ and $p = 1.4$, in the output image (c), a single line and its closest neighbors are preserved; for the same $\varphi$ and $p = 2$ (a narrower filter), in image (d) practically a single line is detected, while the others are almost completely blurred. Other output images resulted through directional filtering are shown in Fig. 9e–i, for specified parameters. In most cases, due to directional selectivity, only a single line and nearest neighbors are preserved. The low-pass filtering effect is obvious from the filtered images in Fig. 9c–i. While the original image contains black lines (here corresponding to value 1) on a white background (associated to zero), in all the filtered images the background becomes a uniform light grey, which corresponds to the average pixel value, or zero frequency component. Also it can be noticed in the filtered images that for a specified orientation angle, one or two lines whose spectrum overlaps with filter frequency response remain almost unchanged in the filtered image; the other lines are blurred due to directional low-pass filtering. The larger the difference in angle between the line spectrum and the filter longitudinal axis, the more pronounced is the blurring. For instance, the horizontal line is completely blurred in Fig. 9c, d, h, i, while the vertical line is completely blurred in Fig. 9c–h.

Fig. 9

a binary test image; b FFT spectrum magnitude; c–i filtered output images for the following parameter values: c$p = 1.4, \, \varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$; d$p = 2, \, \varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$; e$p = 1.6, \, \varphi = {\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0pt} 8}$; f$p = 1.6, \, \varphi = {\pi \mathord{\left/ {\vphantom {\pi 9}} \right. \kern-0pt} 9}$; g$p = 1.6, \, \varphi = {\pi \mathord{\left/ {\vphantom {\pi {12}}} \right. \kern-0pt} {12}}$; h$p = 2, \, \varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$; i$p = 1.6, \, \varphi = {{7\pi } \mathord{\left/ {\vphantom {{7\pi } 9}} \right. \kern-0pt} 9}$; j binary test image; k, l filtering result with directional filter with $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$ and $\varphi = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-0pt} 3}$

The second binary image shown in Fig. 9j consists in straight lines of various lengths, roughly oriented along two orthogonal directions, namely with angles $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0pt} 6}$ and $\varphi = 2{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}$ about horizontal axis. Filtering this image with a directional filter with corresponding orientation angles, we get the images in Fig. 9k and l. The lines with spectra overlapping with the filter directional response remain almost unchanged, while the orthogonal lines are completely blurred.

The third test image displayed in Fig. 10a is a real grayscale texture image of $1100 \times 1100$ pixels, representing straws with random orientations. This image has the FFT spectrum magnitude (b) shown in the range $\omega_{\,1} ,\omega_{\,2} \in [{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0pt} 4},{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}]$, in which a fine structure of spectral lines is visible, corresponding to the straws which are roughly straight, thin lines. Applying a directional filtering to image (a), with $p = 2$ and ${{\varphi = - \pi } \mathord{\left/ {\vphantom {{\varphi = - \pi } 6}} \right. \kern-0pt} 6}$,${{\varphi = \pi } \mathord{\left/ {\vphantom {{\varphi = \pi } 4}} \right. \kern-0pt} 4}$ and ${{\varphi = \pi } \mathord{\left/ {\vphantom {{\varphi = \pi } 2}} \right. \kern-0pt} 2}$, the filtered images are (c), (d) and (e). It can be noticed that only the straws roughly corresponding to a given orientation remain visible in the output image, all the others being more or less blurred. The output images show the good directional resolution of these filters. Next, applying a convenient threshold to the directionally filtered image, a binary image results, where the detected objects are clearly visible. For example, the images (f), (g), (h) result from (c), (d), (e) by a simple thresholding with a convenient threshold value between 0 and 1. Another filtering example is shown in Fig. 10i–k. A set of such orientation-selective filters could be designed to form a directional filter bank, useful in detecting such linear objects in a pattern recognition application. The 2D filters used for filtering directional patterns (grayscale or binary images containing straight lines with various orientations) are very selective LP filters since their frequency response contains the origin of the frequency plane, corresponding to zero frequency. The directional filter passes the objects (in our case straight, thin lines) whose spectrum more or less overlaps with the filter response in the frequency plane, while the rest are more or less blurred, as an effect of directional LP filtering. We can notice that straws with specified orientation remain, while the others are filtered out. However, the smaller details, like short straws, are not blurred as clearly as in Fig. 9, because their spectra are rather narrow around the origin of frequency plane and the low-pass filtering effect is weaker.

Fig. 10

a straw texture image; b typical FFT spectrum magnitude; filtered output images for: c$p = 2$,${{\varphi = - \pi } \mathord{\left/ {\vphantom {{\varphi = - \pi } 6}} \right. \kern-0pt} 6}$; d$p = 2$,${{\varphi = \pi } \mathord{\left/ {\vphantom {{\varphi = \pi } 4}} \right. \kern-0pt} 4}$; e$p = 2$,${{\varphi = \pi } \mathord{\left/ {\vphantom {{\varphi = \pi } 2}} \right. \kern-0pt} 2}$; f, g, h binary images obtained by thresholding; i detail of straw texture image; j filtered output image with ${{\varphi = - \pi } \mathord{\left/ {\vphantom {{\varphi = - \pi } 4}} \right. \kern-0pt} 4}$; k binary image after thresholding

The last example provided is the real grayscale image of size 1000 × 1000 pixels in Fig. 11 a, showing a group of high buildings (skyscrapers) seen from ground level. Due to perspective effect, this image presents many straight lines oriented under various angles. The images in Fig. 11b and c are the result of very selective directional filtering with angles $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}$ and $\varphi = 2{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}$, respectively. The directional filtering effect is clearly visible in these images. Depending on filter orientation, different straight lines representing contours or details of the buildings are outlined, while others are more or less blurred, depending on their orientation.

Fig. 11

a Skyscrapers image; b, c image filtered with directional filter with $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}$ and $\varphi = 2{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3}$ respectively

6 Conclusion

An analytical design method is proposed for two types of 2D recursive filters, namely directional and square-shaped filters. The design is based on a 1D digital prototype, in particular an elliptic filter, and on a complex frequency transformation, which relies on a Chebyshev–Padé rational approximation. The designed filters are parametric, in the sense that the filter coefficients, given in matrix form, depend explicitly on the specifications, in our case the orientation angle and the scaling parameter. Some relevant design examples were provided and also some simulation results for directional filtering on test images were included.