Transversally higher-order interpolating polynomials for the two-dimensional shear deformable ANCF beam elements based on common coefficients

Abstract

The polynomial representation for describing the displacement field of the elements is the main factor that determines the performance of the shear deformable beam elements based on the absolute nodal coordinate formulation (ANCF). In order to resolve the locking problem of the ANCF beam elements, the transversally higher-order polynomial representation has been investigated frequently and applied to the displacement field of the elements by increasing the nodal coordinates of the beam elements. In this paper, transversally higher-order interpolating polynomials are added into the polynomial displacement field of the elements by using common coefficients which mean that the coefficients between the higher-order longitudinal and transversal polynomial components are common. The implementation does not require the increase of the nodal coordinates. Two new kinds of two-dimensional transversally higher-order ANCF beam elements are formulated by common coefficients. The effect of transversally higher-order interpolating polynomials on the performance of the proposed ANCF beam elements is studied by means of certain static and dynamic problems. It is shown that the transversally quadratic order polynomial component $y^{2}$ introduced by common coefficients can also relieve the problem of Poisson locking, and the proposed beam elements are effective and accurate in the static and dynamic analysis.

1 Introduction

The absolute nodal coordinate formulation (ANCF) is developed to study the nonlinear motion of structural components that undergo large displacements [1]. The ANCF employs the mathematical definition of the slopes to define the element coordinates. Therefore, the ANCF elements can be considered as isoparametric elements, and as a result, exact modeling of the rigid body dynamics can be obtained. In the ANCF, because the element coordinates are defined in the global system, not only the need for performing coordinate transformation is avoided, but also a simple expression for the inertia forces is obtained. The resulting mass matrix is constant. Nonetheless, the stiffness matrix becomes nonlinear function even in the case of small displacements.

Continuum mechanics approach [2, 3] was used to derive the expression of the elastic forces because of its simple formulation of the elastic forces and more appropriateness in the nonlinear case. But the proposed elements based on continuum mechanics approach have locking problems, leading to weak performance in the measurement of static and dynamic responses [4,5,6]. In order to avoid the locking problem, the accurate representations of the elastic forces [7,8,9,10,11,12,13,14], locking alleviation techniques [15,16,17], the polynomial expressions and the nodal coordinates in the kinematic description of the elements [16, 21, 24,25,26,27,28,29] have been studied frequently. An improvement proposal for the use of the continuum mechanics approach in deriving the expression of the elastic forces of the ANCF beam element was presented by Sopanen [7]. Reissner’s classical nonlinear rod theory was introduced into the ANCF and combined with continuum mechanics approach to obtain the elastic forces by Gerstmayr [8] and Nachbagauer [9,10,11]. The geometrically exact beam theory was used to formulate the strain energy by applying accurate curvature models of beam elements to the ANCF [12,13,14]. The ANCF and the geometrically exact formulation for nonlinear beams are compared regarding Poisson locking effects [15]. The strain split approach for ANCF locking alleviation was proposed by Mohil Patel and Shabana [16]. The shear and bending independently mode of deformation were evaluated [17]. It is important to note that the design and research of the polynomial expression and the nodal coordinates in the kinematic description of the elements has been implemented frequently to improve the performance of the shear deformable ANCF beam elements.

Presently, several shear deformable ANCF beam elements with different polynomial expressions have been proposed, including the two-dimensional ANCF beam elements [16, 18,19,20,21] and the three-dimensional ANCF beam elements [22,23,24,25,26,27,28,29]. When taking the shear deformation into account in the absolute nodal coordinate formulation, the polynomial expressions in the kinematic description of the elements are the terms of longitudinal and transversal coordinates of the element. A two-dimensional shear deformable absolute nodal coordinate beam element was firstly proposed by Omar [18]. In this beam element, it is assumed that cubic polynomials are used in the longitudinal direction and linear polynomials are used in the transverse direction. In order to obtain the unknown polynomial coefficients of the displacement field, six nodal coordinates need to be used and thus there are 12 nodal coordinates for an element. Then Kerkkänen [19] presented a linearly two-dimensional shear deformable beam element ignoring higher-order terms arising in the element proposed by Omar [18]. Therefore, a better convergence rate is achieved due to its symmetrically polynomial expression and a reduced number of nodal coordinates. The linear displacement field, nevertheless, leads to a problem called shear locking that the element stores excess shear strain energy leading to parasitic shear strain under pure bending especially in the thin structures. It is noteworthy that the shear locking disappears in the element proposed by Omar [18] because of its cubic interpolation polynomials along the longitudinal axis capable of describing the correct deformed mode under pure bending. But the shear locking still exists when the element proposed by Omar [18] is imposed on the linearly varying bending moment, which exhibits the quadratic shear strain distribution instead of the correct constant shear strain. To avoid the locking problems, a summary of the locking problems arising in the shear deformable ANCF beam element was addressed by Garcia Vallejo [20], Sopanen [7] and Gerstmayr [8, 25] including Poisson’s locking, the linear bending behavior, curvature thickness locking and shear locking. The polynomial component $x^{2} y$ was introduced to the new shear deformable ANCF beam element proposed by Garcia Vallejo [20], leading to linearly varying bending strain and eliminating the curvature thickness locking. But in this element, the shear locking and the Poisson locking still exist.

As pointed out in the literature, the longitudinal strain and the transverse strain of the assumed displacement field of the element do not satisfy the generalized Hooke’s law, leading to the problem of Poisson locking. A remedy to this problem is, e.g., a redesign of the element by introducing the transversally higher-order polynomial components to its displacement field. Firstly, the transversally higher-order polynomial component $x^{2} y^{2}$ is applied by Pengfei Li [21] using an additional nodal coordinate $\partial r / \partial x\partial y$, which allows for new cross-section deformation modes, including the warping effect and different stretch values at different points on the element cross-section. Then the transversally higher-order polynomial components $y^{2}$ is introduced by Patel and Shabana [16] with an addition of a curvature vector. The transversally higher-order polynomial components are also introduced into the three-dimensional transversally higher-order ANCF beam elements [24,25,26,27,28,29] by using additional nodal coordinates. In these transversally higher-order shear deformable beam elements, the problem of Poisson locking is well alleviated by using the transversally higher-order polynomial components. However, the way to introduce the transversally higher-order polynomial components to the displacement field of the element needs additional nodal coordinates which increase the degree of freedom of the element.

In this paper, the transversally higher-order polynomial components are investigated and are introduced into the displacement field of the beam elements based on common coefficients. It means that the coefficients between the higher-order longitudinal and transversal polynomial components are common. By this method, the transversally higher-order beam elements can be produced without additional nodal coordinates and two new two-dimensional transversally higher-order ANCF beam elements are proposed in this paper. The problem of Poisson locking of the proposed ANCF beam elements is examined in the static linear and nonlinear examples and proved to be relieved very well. In addition, the performance of these proposed ANCF transversally higher-order beam elements in the analysis of eigenfrequencies and modes, as well as in the dynamic analysis are presented. It is demonstrated that the results are in agreement with analytical solution and those obtained by the finite-element software.

Section 2 is devoted to a review of kinematics, inertia forces, elastic forces, external forces and the equation of motion. Section 3 shows the problem of Poisson locking. Section 4 presents two new kinds of two-dimensional transversally higher-order beam elements which are formulated based on common coefficients. In Sect. 5, static linear and nonlinear examples, and dynamic examples are examined to study the performance of the proposed elements. Finally, a summary and conclusions drawn from the present analysis are provided.

2 The shear deformable ANCF beam elements

2.1 Kinematics

The assumed displacement field of the ANCF shear deformable beam element requires the transversally interpolating polynomials. In the classically ANCF shear deformable beam element proposed by Omar and Shabana [18], linear polynomials in the transverse direction are used. The assumed displacement field of this element is defined using the following polynomials:

$$ \mathbf{r} = \left [ \textstyle\begin{array}{c} r_{1} \\ r_{2} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} a_{0} + a_{1}x + a_{2}y + a_{3}xy + a_{4}x^{2} + a_{5}x^{3} \\ b_{0} + b_{1}x + b_{2}y + b_{3}xy + b_{4}x^{2} + b_{5}x^{3} \end{array}\displaystyle \right ] $$

(1)

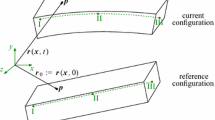
Here $\mathbf{r}$ is the global position vector of an arbitrary point on the beam, $x$ and $y$ are the local coordinates of the element, while $a_{i}$ and $b_{i}$ are the polynomial coefficients. The local element coordinate system is assumed to be located at the point $x{=}0$ and $y{=}0$ with the beam $x$ axis initially parallel to the element centerline. This element is a fully parameterized beam element having a complete set of position gradient vectors in the element nodal coordinates as follows:

$$\begin{gathered} \mathbf{e} = \left [ \textstyle\begin{array}{c@{\quad }c} \mathbf{e}^{i^{T}} & \mathbf{e}^{j^{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} \end{gathered}$$

(2a)

$$\begin{gathered} \mathbf{e}^{i} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} r_{1}^{i} & r_{2}^{i} & \frac{\partial r_{1}^{i}}{\partial x} & \frac{\partial r_{2}^{i}}{\partial x} & \frac{\partial r_{1}^{i}}{\partial y} & \frac{\partial r_{2}^{i}}{\partial y} \end{array}\displaystyle \right ]^{T} \end{gathered}$$

(2b)

$$\begin{gathered} \mathbf{e}^{j} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} r_{1}^{j} & r_{2}^{j} & \frac{\partial r_{1}^{j}}{\partial x} & \frac{\partial r_{2}^{j}}{\partial x} & \frac{\partial r_{1}^{j}}{\partial y} & \frac{\partial r_{2}^{j}}{\partial y} \end{array}\displaystyle \right ]^{T} \end{gathered}$$

(2c)

Here $\mathbf{e}$ is the vector of element nodal coordinates with two nodes $i$ and $j$, $\partial \mathbf{r} / \partial x$ and $\partial \mathbf{r} / \partial y$ are the position gradient vectors. The global position vector of an arbitrary point on the beam can be written as

$$ \mathbf{r} = \left [ \textstyle\begin{array}{c} r_{1} \\ r_{2} \end{array}\displaystyle \right ] = \mathbf{Se} $$

(3)

Here the element shape function matrix $\mathbf{S}$ is defined as

$$ \mathbf{S} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} s_{1}\mathbf{I} & s_{2}\mathbf{I} & s_{3}\mathbf{I} & s_{4}\mathbf{I} & s_{5}\mathbf{I} & s_{6}\mathbf{I} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \mathbf{S}_{1} \\ \mathbf{S}_{2} \end{array}\displaystyle \right ] $$

(4)

Here $\mathbf{I}$ is the 2×2 identity matrix and the shape function is defined as

$$ \left \{ \textstyle\begin{array}{l} s_{1} = 1 - 3\dfrac{x^{2}}{l^{2}} + 2\dfrac{x^{3}}{l^{3}}, \\ s_{2} = x - 2\dfrac{x^{2}}{l} + \dfrac{x^{3}}{l^{2}}, \\ s_{3} = y\left ( 1 - \dfrac{x}{l} \right ), \\ s_{4} = 3\dfrac{x^{2}}{l^{2}} - 2\dfrac{x^{3}}{l^{3}}, \\ s_{5} = - \dfrac{x^{2}}{l} + \dfrac{x^{3}}{l}, \\ s_{6} = \dfrac{xy}{l} \end{array}\displaystyle \right . $$

(5)

and $l$ is the element length.

2.2 Elastic forces

Continuum mechanics approach is employed to define the elastic forces of the ANCF beam elements. The strain-displacement relations are nonlinear. The position gradient can be defined as

$$ \mathbf{J} = \frac{\partial \mathbf{r}}{\partial \mathbf{r}_{0}} = \frac{\partial \mathbf{r}}{\partial \mathbf{x}}\frac{\partial \mathbf{x}}{\partial \mathbf{r}_{0}} = \left [ \textstyle\begin{array}{c@{\quad }c} \frac{\partial r_{1}}{\partial x} & \frac{\partial r_{1}}{\partial y} \\ \frac{\partial r_{2}}{\partial x} & \frac{\partial r_{2}}{\partial y} \end{array}\displaystyle \right ]\mathbf{J}_{0}^{ - 1} $$

(6)

Here the vector $\mathbf{r}_{0}$ defines the reference configuration and the matrix $\mathbf{J}_{0}$ is the identity matrix for initially horizontal beams. The Green-Lagrange strain tensor is used and can be written as

$$ \boldsymbol{\varepsilon } = \frac{1}{2}(\mathbf{J}^{\mathrm{T}}\mathbf{J} - \mathbf{I}) $$

(7)

Using the constitutive equation, the stress vector is related to the strain vector by

$$ \boldsymbol{\sigma } = \mathbf{D}\boldsymbol{\varepsilon } $$

(8)

Here $\mathbf{D}$ is the matrix of the elastic constants of the material. For isotropic homogeneous material, matrix $\mathbf{D}$ can be expressed in terms of Lamé’s constants $\lambda$ and $\mu$ as

$$ \mathbf{D} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda + 2\mu & \lambda & 0 \\ \lambda & \lambda + 2\mu & 0 \\ 0 & 0 & 2\mu \end{array}\displaystyle \right ] $$

(9)

Here, $\lambda = Ev/(1 - v^{2})$, $\mu = E/\left [ 2(1 + v) \right ]$, $E$ is Young’s modulus of elasticity, and $v$ is the Poisson ratio of the beam material. A general expression for the strain energy can be written using the strain vector $\boldsymbol{\varepsilon }$ and the stress vector $\boldsymbol{\sigma }$ as follows:

$$ U = \frac{1}{2}\int _{V} \boldsymbol{\varepsilon }^{\mathrm{T}}\mathbf{D}\boldsymbol{\varepsilon } dV $$

(10)

The elastic forces of the beam element can be defined using the strain energy as

$$ \mathbf{Q}_{e}^{\mathbf{T}} = \frac{\partial U}{\partial \mathbf{e}} = \mathbf{e}^{\mathbf{T}}\mathbf{K}(\mathbf{e}) $$

(11)

Here the stiffness matrix $\mathbf{K}$($\mathbf{e}$) is a nonlinear matrix in the ANCF, even in the static linear example.

2.3 The equation of motion

The Lagrange equations are employed to formulate the equation of motion. The expression of the equation of motion of a finite element can be obtained as

$$ \mathbf{M}\ddot{\mathbf{e}} = \mathbf{Q}_{k} - \mathbf{Q}_{e} $$

(12)

Here $\mathbf{M}$ is the mass matrix and can be obtained as

$$ \mathbf{M} = \frac{1}{2}\int _{V} \rho \mathbf{S}^{\mathrm{T}}\mathbf{S}dV $$

(13)

Here $\rho$ is the density of the material, $V$ is the volume of the element. It can be shown that the mass matrix $\mathbf{M}$ is a constant matrix.

$\mathbf{Q}_{k}$ is the externally applied force $\mathbf{F}$ acting on the element, and can be written as

$$ \mathbf{Q}_{k} = \mathbf{S}^{\mathrm{T}}\mathbf{F} $$

(14)

Thus the distributed gravity of the finite element can be obtained as

$$ \mathbf{Q}_{k} = \int _{V} \mathbf{S}^{\mathrm{T}}[\textstyle\begin{array}{c@{\quad }c} 0 & - \rho g \end{array}\displaystyle ]^{\mathrm{T}}dV $$

(15)

Here $g$ is the acceleration of gravity.

Equation (12) is a nonlinearly differential equation. For the static problem, the Newton iteration method can be applied to find the solution. For the dynamic problem, the Newmark method can be applied for solving.

3 The strain and the problem of Poisson locking

According to Eqs. (8) and (9), the relationship between strain and stress can be written as follows:

$$\begin{gathered} \varepsilon _{x} = \frac{\sigma _{x}}{E} - v\frac{\sigma _{y}}{E} - v^{2}\frac{\sigma _{x}}{E} - v^{2}\frac{\sigma _{y}}{E} \end{gathered}$$

(16)

$$\begin{gathered} \varepsilon _{y} = \frac{\sigma _{y}}{E} - v\frac{\sigma _{x}}{E} - v^{2}\frac{\sigma _{y}}{E} - v^{2}\frac{\sigma _{x}}{E} \end{gathered}$$

(17)

$$\begin{gathered} \varepsilon _{xy} = \frac{\sigma _{xy}}{E} + v\frac{\sigma _{xy}}{E} \end{gathered}$$

(18)

The equation is also termed a generalized Hooke’s law. It can be seen in the above equations that the Poisson ratio $v$ couples the longitudinal strain and the transverse strain. As pointed out in the literature [26], the longitudinal strain and the transverse strain of the assumed displacement field of the element do not satisfy the generalized Hooke’s law, leads to the problem of Poisson locking which must be resolved for obtaining the accurate results. When the Poisson ratio $v$ is nonzero, the residual transverse normal stress is produced which causes that the beam element predicts overly small displacements.

To explain this phenomenon, the linear strain is used here as follows:

$$ \varepsilon _{\mathit{lin}} = \frac{1}{2}(\bar{\mathbf{J}}^{\mathrm{T}} + \bar{\mathbf{J}}) $$

(19)

Here $\bar{\mathbf{J}}$ is the displacement vector gradient defined as

$$ \bar{\mathbf{J}} = \frac{\partial \mathbf{u}}{\partial \mathbf{r}_{0}} $$

(20)

Here $\mathbf{u}$ is the displacement vector defined as

$$ \mathbf{u} = \mathbf{r} - [x,y]^{\mathrm{T}} $$

(21)

Therefore, the strain can be obtained as

$$ \left \{ \textstyle\begin{array}{l} \varepsilon _{x} = \dfrac{\partial r_{1}}{\partial x} - 1 \\ \varepsilon _{y} = \dfrac{\partial r_{2}}{\partial y} - 1 \end{array}\displaystyle \right . $$

(22)

It can be obtained in Eq. (22) that the longitudinal strain $\varepsilon _{x}$ and the transverse strain $\varepsilon _{y}$ is related with the expressions of $\partial r_{1} / \partial x$ and $\partial r_{2} / \partial y$ which are determined by the assumed displacement field of the beam elements. When using the linear polynomials in the transverse direction [18,19,20], the expressions of $\partial r_{1} / \partial x$ and $\partial r_{2} / \partial y$ are written as

$$ \left \{ \textstyle\begin{array}{c} \dfrac{\partial r_{1}}{\partial x} = a_{3}y + 2a_{4}x + a_{1} + \cdots \\ \dfrac{\partial r_{2}}{\partial y} = b_{3}x + b_{2} \end{array}\displaystyle \right . $$

(23)

It can be obtained in Eq. (23) that the transverse strain is lack of transversally linear polynomial component $y$ and then leads to inconsistence between the longitudinal and transverse strain. This discard leads to that the longitudinal and transverse strain do not satisfy the generalized Hooke law stated in Eqs. (16) and (17). It is considered to be the main reason for the Poisson problem. In this point, it is pressing need for the transversally quadratic polynomial component in the assumed displacement field of the element.

In this paper, the transversally quadratic polynomial components are introduced based on common coefficients and then two new transversally higher-order ANCF beam elements are produced, which are in detail described in Sect. 4.

4 The two-dimensional transversally higher-order ANCF beam elements based on common coefficients

In this section, transversally quadratic polynomial component $y^{2}$ is introduced into displacement field of beam elements to satisfy the generalized Hooke’s law and try to resolve the problem of Poisson locking. If transversally quadratic polynomial is introduced by using independent coefficients, additional position gradient coordinates have to be added and lead to an increase in the number of nodal coordinates of the element. However, common coefficients, which are used between transversally and longitudinally quadratic interpolating polynomials, do not need to increase the nodal coordinates of the element.

4.1 Two-dimensional transversally higher-order beam element with two nodes (2d2n)

Transversally quadratic higher-order interpolating polynomial is introduced to the displacement field of the beam element by using common coefficient $a_{4}$ with longitudinally quadratic higher-order interpolating polynomial. Then the obtained displacement field of the beam element is proposed as

$$ \left \{ \textstyle\begin{array}{l} r_{1} = a_{0} + a_{1}x + a_{2}y + a_{3}xy + a_{4}(x^{2} + \mathrm{y}^{2}) + a_{5}x^{3} \\ r_{2} = b_{0} + b_{1}x + b_{2}y + b_{3}xy + b_{4}(x^{2} + \mathrm{y}^{2}) + b_{5}x^{3} \end{array}\displaystyle \right . $$

(24)

This element is a fully parameterized beam element having a complete set of position gradient vectors in the element nodal coordinates as Eqs. (2a)–(2c). There are two nodes and thus 12 nodal coordinates for an element. This proposed ANCF two-dimensional transversally high order beam element with two nodes is termed as 2d2n for short. Then its shape function is obtained as follows:

$$ \left \{ \textstyle\begin{array}{l} s_{1} = 1 - 3\dfrac{(x^{2} + y^{2})}{l^{2}} + 2\dfrac{x^{3}}{l^{3}}, \\ s_{2} = x - 2\dfrac{(x^{2} + y^{2})}{l} + \dfrac{x^{3}}{l^{2}}, \\ s_{3} = y\left ( 1 - \dfrac{x}{l} \right ), \\ s_{4} = 3\dfrac{(x^{2} + y^{2})}{l^{2}} - 2\dfrac{x^{3}}{l^{3}}, \\ s_{5} = - \dfrac{(x^{2} + y^{2})}{l} + \dfrac{x^{3}}{l^{2}}, \\ s_{6} = \dfrac{xy}{l} \end{array}\displaystyle \right . $$

(25)

4.2 Two-dimensional transversally higher-order beam element with three nodes (2d3n)

In this element, transversally quadratic higher-order interpolating polynomial is introduced to the displacement field of the beam element by using common coefficient $a_{4}$ with longitudinally quadratic higher-order interpolating polynomial. Then the obtained displacement field of the beam element is proposed as

$$ \left \{ \textstyle\begin{array}{l} r_{1} = a_{0} + a_{1}x + a_{2}y + a_{3}xy + a_{4}(x^{2} + \mathrm{y}^{2}) + a_{5}x^{2}y \\ r_{2} = b_{0} + b_{1}x + b_{2}y + b_{3}xy + b_{4}(x^{2} + \mathrm{y}^{2}) + b_{5}x^{2}y \end{array}\displaystyle \right . $$

(26)

This element is a gradient deficient beam element. Its position gradient vector only includes $\partial \mathbf{r} / \partial y$. The vector of nodal coordinates of this element is the same as the vector in Ref. [20] and expressed as follows:

$$ \mathbf{e} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \mathbf{r}^{i} & \frac{\partial \mathbf{r}^{i}}{\partial y} & \mathbf{r}^{j} & \frac{\partial \mathbf{r}^{j}}{\partial y} & \mathbf{r}^{k} & \frac{\partial \mathbf{r}^{k}}{\partial y} \end{array}\displaystyle \right ]^{\mathrm{T}} $$

(27)

Here i, j, k are nodes of the element. Therefore, there are three nodes and thus 12 nodal coordinates for an element. This proposed ANCF two-dimensional transversally higher-order beam element with three nodes is termed as 2d3n for short. Then its shape function can be obtained as follows:

$$ \left \{ \textstyle\begin{array}{l} s_{1} = 1 - 3\dfrac{x}{l} + 2\dfrac{(x^{2} + y^{2})}{l^{2}}, \\ s_{2} = y - 3\dfrac{xy}{l} + 2\dfrac{x^{2}y}{l^{2}}, \\ s_{3} = 4\dfrac{x}{l} - 4\dfrac{(x^{2} + y^{2})}{l^{2}}, \\ s_{4} = 4\dfrac{xy}{l} - 4\dfrac{x^{2}y}{l^{2}}, \\ s_{5} = - \dfrac{x}{l} + 2\dfrac{(x^{2} + y^{2})}{l^{2}}, \\ s_{6} = - \dfrac{xy}{l} + 2\dfrac{x^{2}y}{l^{2}} \end{array}\displaystyle \right . $$

(28)

5 Numerical examples

In this section, in order to show the effect of the transversely higher-order interpolating polynomials introduced by common coefficients on the relief from the Poisson locking problem, the static and dynamic problems are investigated.

5.1 The static linear problem

The static linear problem is considered using the simply supported beam structure shown in Fig. 1. The cross-section of the beam is a 0.1 m sided square and the length of the beam is 2.0 m. The material of the structure is assumed to be isotropic; the Young modulus of the material is 2.07*10¹¹ N/m², and the Poisson ratio is 0.3. A vertical load $F$ (1000N) is applied to the midpoint of the beam.

Fig. 1

The simply supported beam structure

In the linear case, the analytical solution of the vertical displacement of the midpoint of the beam can be obtained. On the other hand, the finite-element software “ANSYS” is used to solve this linear problem. The results of the proposed beam elements in this paper are compared with the results of BEAM3, BEAM 188 and the ANCF beam element in Ref. [18] which has the same nodal coordinates with the proposed element 2d2n and uses the linear polynomials in the transverse direction. It should be noted that the BEAM3 is based on the linear theory of small deformations and infinitesimal rotations, while the BEAM188 uses the linear interpolation and large-rotation theory; the BEAM189 uses the quadratic interpolation and large-rotation theory. Therefore, the BEAM3 can be used in this linear case, but is not applicable to the nonlinear case, while the BEAM188 and BEAM189 can also be used in the nonlinear case.

The results of the midpoint of the simply supported beam structure simulated by the elements 2d2n and 2d3n are obtained using a numerical integration method with two Gauss points. The results of the ANCF beam element in Ref. [18] are obtained with four Gauss points. And their boundary conditions are given to eliminate all position coordinates of the first node and the transversal position coordinates of the last node. The vertical displacements of the midpoint of the simply supported beam structure are shown in Table 1.

Table 1 Vertical displacements of the midpoint of the simply supported beam structure [mm]

It can be shown in Table 1 that the results of the proposed elements 2d2n and 2d3n, converge towards the analytical solution and the results of the BEAM 188 as the number of elements is increased. The result of BEAM3 is slightly low. The result of the ANCF beam element in Ref. [18] seems to suffer from Poisson locking problem. Therefore, it can be concluded that in the linear case, the proposed transversely high order elements in this paper, can eliminate the locking problem of Poisson.

The reason for this is related to the transversely quadratic interpolating polynomials $y^{2}$ which is applied in the displacement field of the element by using common coefficients with the longitudinally higher-order interpolating polynomials in this study, shown in Eqs. (24) and (26). Thus, the expressions of $\partial r_{1} / \partial x$ and $\partial r_{2} / \partial y$ of the proposed two–dimensional higher-order elements 2d2n and 2d3n can be written as follows:

$$ \left \{ \textstyle\begin{array}{c} (\dfrac{\partial r_{1}}{\partial x})_{2d} = a_{3}y + 2a_{4}x + a_{1} + \cdots \\ (\dfrac{\partial r_{2}}{\partial y})_{2d} = b_{3}x + 2b_{4}y + b_{2} + \cdots \end{array}\displaystyle \right . $$

(29)

It can be seen in Eq. (29) that the transverse strain of the proposed beam elements includes transversally linear polynomial component $y$ which does not exist in Eq. (23) with the transversally linear polynomial displacement field, thus the longitudinal and transverse strains of the proposed elements become consistent. Therefore, the longitudinal and transverse strains of the proposed elements can satisfy the generalized Hooke’s law stated in Eqs. (16) and (17). Although the transversally quadratic interpolating polynomials are introduced to the displacement field of the proposed elements by common coefficients, they act powerfully. The above points will be proved again in the next static nonlinear problem.

5.2 The static nonlinear problem

The static nonlinear problem is considered using the cantilever beam structure shown in Fig. 2. The cross-section of the beam is rectangular and a 0.1 m sided square, and the length of the cantilever beam is 2.0 m. The material of the structure is assumed to be isotropic, the Young modulus of the material is 2.07*10¹¹ N/m², the mass density is 7850 kg/m³, the Poisson ratio is 0.3. A vertical load $F$ (500000N) is applied to the endpoint of the beam.

Fig. 2

The cantilever beam structure subjected to a concentrated load

The displacements of the endpoint of the cantilever beam structure simulated by the elements 2d2n, 2d3n, and the ANCF beam element in Ref. [18] are obtained using a numerical integration method with two Gauss points. Their boundary conditions are given to eliminate all nodal coordinates of the first node. The results of the proposed elements are compared to the nonlinear solution of the BEAM188, BEAM189, and the ANCF beam element in Ref. [18], shown in Fig. 3 and Table 2.

Fig. 3

The displacements of the endpoint of the cantilever beam structure simulated by the elements 2d2n, 2d3n, BEAM188, BEAM189 and the ANCF beam element in Ref. [18] with the increasing numbers of elements

Table 2 The displacements of the endpoint of the cantilever beam structure using 128 elements

In Fig. 3, the convergence and accuracy of the proposed elements 2d2n and 2d3n are illustrated with the increasing numbers of elements compared with the BEAM188 and BEAM189. It can be seen in Fig. 3 that the vertical and longitudinal displacements of the proposed elements 2d2n and 2d3n are all convergent. The results of the proposed elements, the BAEM188 and BEAM189 tend to be consistent with the increasing numbers of elements. However, the vertical and longitudinal displacements of the ANCF beam element in Ref. [18] tend to a value different from the ones of the proposed elements, the BAEM188 and BEAM189.

In Table 2, the displacements of the endpoint of the cantilever beam structure with 128 numbers of elements are shown and prove that the solution of the proposed elements in this paper agree well with the solution of BAEM188 and BEAM189. However, the vertical and longitudinal displacements of the ANCF beam element in Ref. [18] are evidently lower than the results of the proposed elements, the BAEM188 and BEAM189.

In Fig. 4, the deformed configurations of the beam structure in the linear and nonlinear case simulated by the proposed elements and BEAM188 are shown. In Fig. 5, the absolute errors between the proposed elements and the BEAM188 are shown and very small compared with the deformation. Therefore, it can be seen that the deformed configurations of the proposed elements are identical to the deformed configurations of the BEAM188.

Fig. 4

The deformed configurations of the beam structure in the linear and nonlinear case simulated by 128 elements

Fig. 5

The absolute errors between the proposed elements and the BEAM188 in the linear and nonlinear static cases

Therefore, in static linear and nonlinear case, the elements proposed in this paper have no Poisson locking problem because of the application of the transversally quadratic interpolating polynomials. And the way that the transversally quadratic interpolating polynomials are introduced by common coefficients are effective.

5.3 Eigenfrequencies

The simply supported beam structure shown in Fig. 1 is used in this section to examine the deformation modes and eigenfrequencies of the proposed elements. The cross-section is rectangular, the length of the beam is 2.0 m, the height is 0.4 m, the width is 0.4 m, the Young modulus of the material is 2.07*10¹¹ N/m², the mass density is 7850 kg/m³, the Poisson ratio is 0.3. The analytical values of the eigenfrequencies which are provided in the reference [8] are employed here to be compared with the eigenfrequencies of the proposed elements in this paper. Table 3 shows the convergence and accuracy of the eigenfrequencies of the proposed elements with the increasing numbers of elements. Table 4 shows the modes and eigenfrequencies of the proposed elements with 16 elements.

Table 3 The eigenfrequencies of the proposed elements compared to the analytical solution

Table 4 The modes and eigenfrequencies of the proposed elements 2d2n and 2d3n

Numerical integration method cannot be used to obtain eigenfrequencies because of the numerical error. Therefore the eigenfrequencies and modes are obtained by the exact integration.

It can be concluded from the Table 3 that the bending, axial, shear and thick eigenfrequencies of the proposed elements are all convergent with the increasing elements, altogether lower than the analytical values. The first bending, axial and thick frequencies is slightly lower than the analytical values. While the errors between the second bending and axial frequencies and the analytical values are a little more. The second thick frequency is slightly larger than the analytical values. It should be noted that the first and second shear frequencies are observably lower than the analytical values. The reason for this is the use of the transversally higher-order polynomial component in the assumed displacement field.

5.4 Dynamic analysis: flexible pendulum

In this section, the free falling of a flexible pendulum under its own weight shown in Fig. 6 is considered to demonstrate the performance of the proposed elements. The pendulum is connected to the ground by a pin joint at one end. The pendulum is initially horizontal with zero initial velocity. The gravity constant is 9.81 m/s².

Fig. 6

The free falling flexible pendulum

In the first dynamic example, the length of the pendulum is 1.8 m, the height is 0.008 m, the width is 0.03125 m, the Young modulus of the material is 2.07*10¹¹ N/m², the mass density is 2766.67 kg/m³, the Poisson ratio is 0.3. In this example, the flexibility of the pendulum is low. The convergence and accurate of the results of the flexible pendulum under its own weight simulated by the proposed elements are studied, shown in Fig. 7-10.

Fig. 7

The position of the tip point of the flexible pendulum simulated by the elements 2d2n and 2d3n using 4, 8 and 16 elements

Figure 7 shows the position of the tip point of the flexible pendulum simulated by the elements 2d2n and 2d3n with 4, 8, and 16 elements. It can be concluded from Fig. 7 that the results obtained using 4, 8, and 16 elements are all identical and thus are convergent. Therefore, in the following study, the number of elements is chosen to be 8 elements.

In Fig. 8 and Fig. 9, the positions of the tip point of the flexible pendulum simulated by the elements 2d2n, 2d3n, are compared with the solution of the BEAM3, and BEAM188. It can be concluded from Fig. 8 and Fig. 9 that the solutions of the elements 2d2n, 2d3n, BEAM3 and BEAM188 agree very well and thus the Poisson locking problem is considered to be not existing in the proposed elements in the dynamic example.

Fig. 8

The position of the tip point of the flexible pendulum simulated by the elements 2d2n, 2d3n, BEAM3, and BEAM188 using 8 elements

Fig. 9

The vertical position of the tip point of the flexible pendulum simulated by the elements 2d2n, 2d3n, BEAM3, and BEAM188 using 8 elements

In the second dynamic example, the length of the pendulum is 1.2 m, the height is 0.2530 m, the width is 0.006335 m, the Young modulus of the material is 7*10⁵ N/m², the mass density is 5540 kg/m³, the Poisson ratio is 0.3. In this example, the flexibility of the pendulum is higher. Thus in the testing time period, the deformation of the pendulum becomes large. The flexibility of the pendulum can be obtained in Fig. 10 and Fig. 11 which show the falling flexible pendulum at different time steps simulated by the element 2d2n and 2d3n using 8 elements.

Fig. 10

The falling flexible pendulum at different time steps simulated by the elements 2d2n and 2d3n using 8 elements

Fig. 11

The falling flexible pendulum at different time steps simulated by the elements 2d2n and 2d3n using 8 elements

Under the case of large flexibility of the pendulum, the results simulated by the proposed elements 2d2n and 2d3n are in detail compared with the results obtained by BEAM3 and BEAM188, shown in Fig. 12, Fig. 13, and Fig. 14. And it can be seen that the consistency is still good between them. However, the absolute errors between the proposed elements and the BEAM188 shown in Fig. 15, in the first dynamic example with 1.8 m length and low flexibility, are obviously smaller than the ones in this dynamic example with 1.2 m length and high flexibility.

Fig. 12

The position of the tip point of the flexible pendulum simulated by the elements e2d2n, 2d3n, BEAM3 and BEAM188 using 8 elements

Fig. 13

The vertical position of the tip point of the flexible pendulum simulated by the elements 2d2n, 2d3n, BEAM3 and BEAM188 using 8 elements

Fig. 14

The falling flexible pendulum simulated by the element 2d2n, 2d3n, BEAM3 and BEAM188 using 8 elements at time 0.2 s, 0.5 s, 0.8 s and 1.1 s

Fig. 15

The absolute errors between the proposed elements and the BEAM188 in the two dynamic flexible pendulum

The results of the above flexible pendulum and the next standard slider-crank mechanism are all obtained by the numerical solution function of differential equation-ode45 in the software “Matlab”, which employs the Runge Kutta algorithm with adaptive step size.

5.5 Dynamic analysis: standard slider-Crank mechanism

In this section, the standard slider-crank mechanism shown in Fig. 16 is considered to demonstrate the performance of the proposed elements. The bar $O_{1} A$ is assumed to have a rectangular cross-section, the height is 0.0053 m, the width is 0.0053 m, the length is 0.15 m, the Young modulus of the material is 1.0*10¹¹ N/m², the mass density is 2770 kg/m³, the Poisson ratio is 0.3. The flexible connecting rod $AB$ is assumed to have the same mass density, cross-section. The length of the connecting rod $AB$ is 0.3 m, and the Young’s modulus of the material is 5.0*10⁸ N/m².

Fig. 16

The standard slider-crank mechanism

The initial configuration of the standard slider-crank mechanism is just as the configuration in Fig. 16. The end of the bar $O_{1} A$ is subjected to a concentrated force $F$ which is always tangent to the bar. In Fig. 17, the convergence of the proposed elements 2d2n and 2d3n are illustrated with the increasing number of elements. In Fig. 18 and Fig. 19, the accuracy of the proposed elements 2d2n and 2d3n are illustrated compared with the result obtained by the software “ABAQUS”, which can implement the dynamic simulation of flexible multibody system. In the software “ABAQUS”, a 3-node quadratic beam element “B32” is used. It can be seen in Fig. 17 that the vertical positions of the midpoint of the connecting rod tend to be identical with the increasing number of elements, therefore the proposed elements are convergent. It can be seen in Fig. 18 and Fig. 19 that the vertical positions of the midpoint of the connecting rod of the proposed 2d2n element is consistent with the results obtained in the software “ABAQUS”, and their errors compared with the software “ABAQUS” are very small.

Fig. 17

The vertical position of the midpoint of the connecting rod for different discretizations

Fig. 18

The vertical position of the midpoint of the connecting rod for different formulations

Fig. 19

The absolute errors in the vertical position between the proposed elements and the ABAQUS

6 Conclusions

Transversally higher-order interpolating polynomials have been introduced by several researchers to the shear deformable ANCF beam elements to resolve the locking problem of the ANCF beam elements. In this paper, common coefficients with the longitudinally higher-order interpolating polynomials are used to introduce the transversally higher-order interpolating polynomials to the polynomial displacement field of the beam elements. And, two new two-dimensional transversally higher-order ANCF beam elements are thus proposed, which have the same number of nodal coordinates of the element as the elements in the references [18, 20] with the linear polynomials in the transverse direction. Therefore, the way to combine the transversally higher-order interpolating polynomials by common coefficients can does not increase the number of nodal coordinates of the ANCF element. This character is very favorable for solution.

Several static and dynamic examples are examined to test the performance of the proposed elements. The convergence and accurate of the proposed elements are in detail studied. It can be concluded that there is no the problem of Poisson locking in the proposed elements because of the introduction of transversally quadratic interpolating polynomials and the proposed elements are all effective in the static and dynamic analysis. Therefore, the transversally higher-order polynomial components introduced by common coefficients can act as powerfully for solving the problem of Poisson locking, as the literature [16] in which the transversally higher-order polynomial components are introduced with independent coefficients and thus the nodal coordinates of the beam elements has to be increased.

The way that the transversally higher-order polynomial components are introduced by common coefficients is feasible in the two-dimensional shear deformable ANCF beam elements. For the three-dimensional shear deformable ANCF beam elements, the approach of “common coefficients” is investigated in progress to introduce the transversally higher-order interpolating polynomials to the displacement field of the beam element, which comes with additional complications. These additional complications will be studied in the future research.