1 Introduction

The absolute nodal coordinate formulation [1, 2] (ANCF) was a totally new finite element (FE) modeling method proposed by Shabana in 1996. This method was also mentioned by Rhim and Lee in 1998 [3]. ANCF is based on continuum mechanics and FE method, which not only promotes the deep combination of flexible multibody system dynamics and FE method, but is also widely considered by many scholars as a milestone in the history of flexible multibody system dynamics [4]. ANCF employs the position vector coordinates and gradient vector coordinates in the global coordinate system as the nodal generalized coordinates, which effectively avoids the parameterization problem of finite rotation and the analysis of the position vector in the local coordinate system, realizing the purpose of accurately investigating the spatial position and deformation characteristics of flexible parts in the global coordinate system within a nonincremental solution framework. Additionally, dynamic modeling based on ANCF offers several advantages, including that the equation has a constant mass matrix, no Coriolis force and centrifugal force terms, and the constraint equation is simple in form and does not need coordinate transformation [5, 6]. Over the past two decades, the absolute nodal coordinate formulation has been widely used in engineering, including the modeling of high-speed pantograph-catenary system, the recovery of tethered satellites, and the deployment of thin-film solar sails [7].

Locking phenomenon generally exists in classical finite elements such as beams, plates, and shells, and the locking mechanisms include shear locking, Poisson locking, curvature thickness locking, and volume locking [8]. To alleviate the locking problem of classical finite elements, Hughes et al. [9] used reduced and selective integration to effectively alleviate shear locking in the thin regime of plate elements. Malkus and Hughes [10] proposed the equivalence between mixed FE formulations and displacement formulations using the reduced integration technique, which saved the computing resources. Noor and Peters [11] also discussed and analyzed the approximate equivalence of different beam models with reduced integration. In addition, the mixed methods are also widely used to eliminate locking problems including volume locking and shear locking. Sussman and Bathe [12] used mixed displacement and pressure formulation to alleviate volume locking with the incompressible conditions. Pian [13] proposed a mixed element based on Hellinger–Reissner variational principle to improve the bending performance of beam and plate structures. Liu et al. [14] proposed a super-convergent element based on the Hu–Washizu variational principle. Bab et al. [15] developed a novel mixed FE laminated composite beam element, which is based on higher-order shear deformation theory, and validated the model through the comparison and convergence analysis of several laminated situations. Choi et al. [16] also established an efficient mixed FE formulation, aimed at the elastostatic beams, based on the Hu–Washizu variational principle, in which the strain distribution in the cross section is enriched by an enhanced assumed strain method to alleviate Poisson locking.

Similar to the traditional FE method, the beam elements based on ANCF are also impressionable to the occurrence of locking phenomenon, including shear locking, Poisson locking, etc. The illustrative example is the two-dimensional shear deformation beam element, which was proposed by Omar and Shabana [17]. The element configuration is completely determined through the nodal position vector and the gradient vector along the axial and transverse direction. Moreover, the displacement field uses cubic interpolation in the axial direction to determine the curvature of the beam with bending and linear interpolation in the transverse direction, describing the distribution of shear strain. Consequently, Dufva et al. [18] designed several static and dynamic examples, which proved that the beam element offers the ability to simulate highly nonlinear behavior and solve large deformation problems. However, due to the inconsistency between the axial higher-order interpolation and the transverse low-order interpolation in the Omar–Shabana beam element, stresses in different directions are coupled with each other, resulting in pseudo-stresses during the bending process, excessive stiffness with decline of element’s performance, and demonstrating a distinct phenomenon of bending locking [19]. Gerstmayr, Sopanen, and Garcia-Vallejo et al. [20–22] analyzed and discussed the mechanical mechanism of Poisson locking in relevant literature, respectively.

Some typical ANCF studies aimed at alleviating Poisson locking are as follows:

  1. (1)

    Methods for eliminating Poisson effect.

Gerstmayr and Matikainen [23] artificially set Poisson’s ratio of 0 to eliminate Poisson effect. Kerkkaenen et al. [24] eliminated Poisson effect and alleviated Poisson locking by simplifying stress tensor. However, these approaches all are based on eliminating the Poisson effect of beam element, which is quite different from the actual situation.

  1. (2)

    Methods based on reduced-based integration, enriching interpolation field and split methods.

Gerstmayr et al. [20] reconstructed the elastic force matrix of plane beam element by using the selective reduced integration technique and effectively alleviated the locking phenomenon of beam element by only considering Poisson effect in the axial direction. Garcia-Vallejo et al. [22] also developed a novel locking-free shear deformation beam element based on reduced integration. Dufva et al. [18] used mixed displacement field and shear strain interpolation to improve element’s bending performance and to alleviate Poisson locking by neglecting Poisson coupling between axial and transverse normal strains. Matikainen et al. [25] developed a higher-order three-dimensional ANCF beam element, in which quadratic interpolation is used for the cross section, effectively alleviating Poisson locking, whereas the beam element has too many degrees of freedom, resulting in high-cost calculating consumption. Shen et al. [26] proposed a series of higher-order beam elements utilizing Pascal trigonometric polynomials. These elements employ a great number of generalized coordinates and more complex interpolation functions to capture the distortion and warping deformation of the cross-section accurately. Zhao et al. [27] added transversally higher-order interpolating polynomials into the polynomial displacement field, which enriched the distribution of transverse strain and alleviated Poisson locking. Hurskainen et al. [28] proposed a planar ANCF beam element based on mixed interpolation by using the independent interpolation technique of transverse deformation field on the basis of planar ANCF beam element and proved that the element has high accuracy and convergence for bending deformation through a series of numerical examples. Additionally, reconstructing the elastic force formulation based on the variational principle is also an effective method to alleviate Poisson locking [29, 30]. Schwab and Meijaard [31] introduced the shear stress and strain field through Hellinger–Reissner and Hu–Washizu variational principles respectively and reconstructed the elastic force formulation with the elastic line method, which eliminated the higher-order coupling term of axial and lateral deformation and alleviated the locking problem. Hussein et al. [32] used the elastic line method without Poisson coupling and the independent shear stress interpolation technique based on Hellinger–Reissner variational principles to eliminate the shear locking problem of two-dimensional (2D) ANCF full parameter beam elements. Gerstmayr and Irschik [33] used the elastic line method to study the bending deformation of ANCF beam in detail and gave a modifier formulation of strain measurement. Strain split method (SSM) is a new method to suppress Poisson locking [34–36]. Patel and Shabana [37] decomposed Green–Lagrange strain into axial strain and cross-section strain of the element and modified the constitutive model. It is assumed that only the low-order strain related to the axial deformation of the beam has Poisson effect, whereas ignoring the Poisson effect of the higher-order term of the normal strain significantly improves the bending performance of the beam, consequently. In addition, Patel and Shabana [37] also developed a 2D ANCF beam element, which can alleviate Poisson locking through introducing higher-order curvature vectors. This element can be regarded as a special (two-dimensional) case of three-dimensional higher-order elements proposed by Shen et al. [26] and analyzed by Orzechowski and Shabana [38].

The paper is arranged as follows: Sect. 2 introduces the global position interpolation field, gradient vector distribution, nodal generalized coordinates, and shape function of the proposed beam element models. Section 3 analyzes mechanical mechanism of alleviating Poisson locking of the proposed model in detail. Section 4 gives the general process of dynamic modeling based on ANCF. Section 5 compares and investigates the performance of beam elements through a series of numerical examples of statics and dynamics, demonstrating the rationality and effectiveness of a series of beam element models proposed in this paper. Finally, some conclusions are presented in Sect. 6.

2 A series of beam models

2.1 Global position interpolation field

A beam in mechanical structure can be abstracted as a one-dimensional object based on its center line, and the position vector of any material point can be defined as follows:

$$ \mathbf{r}(X,Y,Z,t) = \sum _{i = 1}^{n} f_{i}(Y,Z)\mathbf{u}_{i}(X,t), $$
(1)

where \(X\), \(Y\), and \(Z \) respectively donate the three coordinates of any point in the local coordinate system, \(\mathbf{u}_{i}\) is a vector used to describe the beam axis configuration, \(f_{i}\), which is a characteristic function, is used to characterize the deformation of cross-section, \(n\) is the number of expansion terms, t represents time variable.

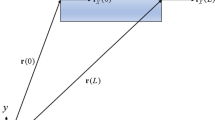
Here, the beam configuration in the global coordinate system is shown in Fig. 1.

Fig. 1
figure 1

Beam configuration in the global coordinate system

Full size image

In case of plane problem (\(x\)-\(y\)), Equation (1) can be simplified as follows:

$$ \mathbf{r}(X,Y,t) = \sum _{i = 1}^{n} f_{i}(Y)\mathbf{u}_{i}(X,t). $$
(2)

Generally, the cubic interpolation of global position coordinates along the axial direction is enough to ensure the precision of calculating normal strain \(\varepsilon _{x}\) generated in bending. Additionally, \(\mathbf{u}_{i}(X,t)\) can be further decoupled as follows:

$$ \mathbf{u}_{i}(X,t) = \left [ \textstyle\begin{array}{c} a_{i}(t) \\ b_{i}(t) \end{array}\displaystyle \right ]g_{i}(X), $$
(3)

where \(a_{i}(t)\) and \(b_{i}(t)\) are defined as time coefficient components, along the \(x\) and \(y\) direction in the global coordinate system (\(O\)-\(xy\)), \(g_{i}(X)\) is a decoupled position function. Consequently, the \(f_{i}(Y)\) term of \(f_{i}(Y)g_{i}(X)\) must be fully rational based on the consideration of Poisson effect because it not only determines the distribution of transverse strain \(\varepsilon _{y}\) along the cross section, but is also the key to alleviate the Poisson locking of ANCF beam element.

In this paper, partial Pascal trigonometric polynomials are used to represent the function \(f_{i}(Y)\mathbf{g}_{i}(X)\) due to the categoricalness of Pascal’s triangle. Hence, a detail position interpolation field function \(\mathbf{r}(X,Y,t)\) can be constructed as follows, accordingly:

$$ \mathbf{r}(X,Y,t) = \left [ \textstyle\begin{array}{c} x(X,Y,t) \\ y(X,Y,t) \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \sum _{i = 1}^{2N + 4} a_{i}(t)h_{i}(X,Y) \\ \sum _{i = 1}^{2N + 4} b_{i}(t)h_{i}(X,Y) \end{array}\displaystyle \right ](N = 1,2, \ldots ), $$
(4)

where \(x\) and \(y \) respectively denote the coordinate components of vector \(\mathbf{r}\) in the global coordinate system, \(h_{i}(X,Y)\) is equal to \(g_{i}(X)f_{i}(Y)\), and \(N\) is defined as the order of the beam model. The Pascal trigonometric polynomials, corresponding to \(h_{i}(X,Y)\) of beam models with different orders, are shown in Fig. 2.

Fig. 2
figure 2

Interpolation trigonometric polynomials

Full size image

In Fig. 2, idle items in the shaded part are not introduced in the beam models proposed in this paper, the items in red solid box are all necessary for interpolation, which represents that the interpolation along the axial direction of the beam has cubic accuracy, which is enough, and the item in the dotted box indicates additional terms included in the beam models with different orders, and these additional terms including coordinate \(Y\) determine the distribution of transverse strain \(\varepsilon _{y}\) in the cross-section.

Note that the order of the model can be improved only by adding two terms along the right-hand side of Pascal’s triangle, and the higher the order of interpolation polynomial along the Y direction, the more accurate the complicated distribution of \(\varepsilon _{y}\) along the cross-section, which can alleviate Poisson locking effectively.

Accordingly, the position field of the first four order beam models in the global coordinates system can be written as follows:

$$\begin{aligned} \begin{aligned} \mathbf{r}_{1 - order} &= \left [ \textstyle\begin{array}{c} a_{0} + a_{1}X + a_{2}Y + a_{3}XY + a_{4}X^{2} + a_{5}X^{3} \\ b_{0} + b_{1}X + b_{2}Y + b_{3}XY + b_{4}X^{2} + b_{5}X^{3} \end{array}\displaystyle \right ] \\ \mathbf{r}_{2 - order} &= \left [ \textstyle\begin{array}{c} a_{0} + a_{1}X + a_{2}Y + a_{3}XY + a_{4}X^{2} + a_{5}Y^{2} + a_{6}XY^{2} + a_{7}X^{3} \\ b_{0} + b_{1}X + b_{2}Y + b_{3}XY + b_{4}X^{2} + b_{5}Y^{2} + b_{6}XY^{2} + b_{7}X^{3} \end{array}\displaystyle \right ] \\ \mathbf{r}_{3 - order} &= \left [ \textstyle\begin{array}{l} a_{0} + a_{1}X + a_{2}Y + a_{3}XY + a_{4}X^{2} + a_{5}Y^{2} + a_{6}XY^{2} + a_{7}X^{3} \\ \quad{} + a_{8}Y^{3} + a_{9}XY^{3} \\ b_{0} + b_{1}X + b_{2}Y + b_{3}XY + b_{4}X^{2} + b_{5}Y^{2} + b_{6}XY^{2} + b_{7}X^{3} \\ \quad{} + b_{8}Y^{3} + b_{9}XY^{3} \end{array}\displaystyle \right ] \\ \mathbf{r}_{4 - order}& = \left [ \textstyle\begin{array}{l} a_{0} + a_{1}X + a_{2}Y + a_{3}XY + a_{4}X^{2} + a_{5}Y^{2} + a_{6}XY^{2} + a_{7}X^{3} + a_{8}Y^{3} \\ \quad{} + a_{9}XY^{3} + a_{10}Y^{4} + a_{11}XY^{4} \\ b_{0} + b_{1}X + b_{2}Y + b_{3}XY + b_{4}X^{2} + b_{5}Y^{2} + b_{6}XY^{2} + b_{7}X^{3} + b_{8}Y^{3} \\ \quad{} + b_{9}XY^{3} + b_{10}Y^{4} + b_{11}XY^{4} \end{array}\displaystyle \right ] \end{aligned}. \end{aligned}$$
(5)

2.2 Nodal generalized coordinates

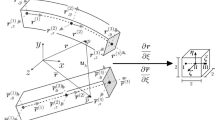
To coordinate with the global position interpolation field function, the corresponding gradient vectors, distributed along the transverse direction, are arranged on the cross-section of the beam element to capture the higher-order transverse strain \(\varepsilon _{y}\) accurately, which is different from the traditional ANCF beam element due to non-common nodes between gradient vector \(\mathbf{r}_{Y}\) and position vector \(\mathbf{r}\). Nevertheless, similar to the tradition ANCF beam element, the position vector \(\mathbf{r}\) is only used to determine the spatial position of the nodes at both ends of the central axis of the beam, and the gradient vector \(\mathbf{r}_{X}\) distributed along the axial direction and the position vector \(\mathbf{r}\) still maintain the strategy of co-nodes.

In this paper, boundary nodes and Chebyshev interpolation nodes all are considered to determine the distribution of the transverse gradient vector \(\mathbf{r}_{Y}\) along the cross-section, in which Chebyshev interpolation is used to avoid the unexpected Runge phenomenon in transverse higher-order interpolation. The first three Chebyshev interpolation polynomials are as follows (\(x \in [ - 1,1]\)):

$$ \begin{aligned} T_{1}(x) &= x \\ T_{2}(x) &= 2x^{2} - 1 \\ T_{3}(x) &= 4x^{3} - 3x \end{aligned}. $$
(6)

In case of 2D beam element, Fig. 3 shows the distribution of gradient vectors \(\mathbf{r}_{Y}\) of the first four beam models, accordingly.

Fig. 3
figure 3

Distribution of transverse gradient vectors (first four orders)

Full size image

In Fig. 3, the first-order model employs the coordinate origin as the node of the gradient vectors \(\mathbf{r}_{y}\), the second-order model only uses two boundary point as the interpolation node, and the third-order model uses three interpolation nodes, namely the boundary points and zero point of the first-order Chebyshev polynomial. Regularly, the \(i\) th (\(i\geq 3\)) order ANCF beam model uses \(i \) nodes to determine the distribution of gradient vectors \(\mathbf{r}_{y}\), which includes two boundary points and \(i\)-2 zero points of the \(i\)-2 th order Chebyshev polynomial. Correspondingly, Fig. 4 displays the proposed ANCF beam elements.

Fig. 4
figure 4

First four order ANCF beam elements

Full size image

As can be seen from Fig. 4, with the increase of the order, more gradient vectors \(\mathbf{r}_{Y}\) will be proposed in the cross-section without disturbing the distribution of axial gradient vectors \(\mathbf{r}_{X}\) and position vectors \(\mathbf{r}\). In this way, the interpolation accuracy along the transverse direction will be greatly improved, and the Poisson locking can be suppressed without introducing the higher-order curvature vectors \(\mathbf{r}_{YY}\).

According to Fig. 4, the generalized coordinates of node \(i\) can be expressed as follows:

$$ \begin{aligned} \mathbf{q}_{i(1 - order)} &= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{r}_{i(0,0)}^{T} & \mathbf{r}_{iX(0,0)}^{T} & \mathbf{r}_{iY(0,0)}^{T} \end{array}\displaystyle \right ]^{T} \\ \mathbf{q}_{i(2 - order)} &= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{r}_{i(0,0)}^{T} & \mathbf{r}_{iX(0,0)}^{T} & \mathbf{r}_{iY(0, - \frac{h}{2})}^{T} & \mathbf{r}_{iY(0,\frac{h}{2})}^{T} \end{array}\displaystyle \right ]^{T} \\ \mathbf{q}_{i(3 - order)} &= \left [ \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} \mathbf{r}_{i(0,0)}^{T} & \mathbf{r}_{iX(0,0)}^{T} & \mathbf{r}_{iY(0,0)}^{T} & \mathbf{r}_{iY(0, - \frac{h}{2})}^{T} & \mathbf{r}_{iY(0,\frac{h}{2})}^{T} \end{array}\displaystyle \right ]^{T} \\ \mathbf{q}_{i(4 - order)} &= \left [ \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} \mathbf{r}_{i(0,0)}^{T} & \mathbf{r}_{iX(0,0)}^{T} & \mathbf{r}_{iY(0, - \frac{h}{2})}^{T} & \mathbf{r}_{iY(0, - \frac{\sqrt{2} h}{4})}^{T} & \mathbf{r}_{iY(0,\frac{\sqrt{2} h}{4})}^{T} & \mathbf{r}_{iY(0,\frac{h}{2})}^{T} \end{array}\displaystyle \right ]^{T} \end{aligned}. $$
(7)

Here, \(h\) denotes the height of the beam element, \(\mathbf{r}_{i}\) represents the position vector of node \(i\), and \(\mathbf{r}_{iX}\) and \(\mathbf{r}_{iY}\) represent two gradient vectors of node \(i\), respectively. Accordingly, the number of generalized coordinates of the corresponding order beam element is consistent with the time coefficient undetermined in Equation (5). This explicitly reflects the formal coordination of the beam element models.

Especially, when the proposed beam model is reduced to the first order, the ANCF element is essentially Omar–Shabana element, and when the model is improved to the second order, it evolves into the element model developed by Zheng et al. [7].

2.3 Shape functions

This section will take the third-order beam model as an illustrative example to introduce the derivation process of a shape function in detail.

Based on Equation (5), the position interpolation field function of the third-order ANCF beam element can be rewritten in matrix as follows:

$$ \mathbf{r} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{A} & \mathbf{0} \\ \mathbf{0} & \mathbf{A} \end{array}\displaystyle \right ]\mathrm{C}, $$
(8)

where the form of \(\mathbf{A} \) is

$$ \mathbf{A} = \left [ \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & X & Y & XY & X^{2} & Y^{2} & XY^{2} & X^{3} & Y^{3} & XY^{3} \end{array}\displaystyle \right ], $$
(9)

and the coefficient matrix \(\mathbf{C}\) can be expressed as follows:

$$ \mathbf{C} = \left [ \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} a_{0} & \cdots & a_{9} & b_{0} & \cdots & b_{9} \end{array}\displaystyle \right ]^{T}. $$
(10)

Ulteriorly, all generalized coordinates of ANCF element can be written as follows, according to Equation (8):

$$ \mathbf{q} = \mathbf{Q}\mathbf{C}, $$
(11)

where \(\mathbf{q} \) is a generalized coordinates matrix with the size of 20 × 1 for the third-order model, and \(\mathbf{Q} \) is a nonsingular constant matrix with a size of 20 × 20.

Substituting Equation (11) into (8), Equation (8) can be rewritten as follows:

$$ \mathbf{r} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{A} & \mathbf{0} \\ \mathbf{0} & \mathbf{A} \end{array}\displaystyle \right ]\mathbf{Q}^{ - 1}\mathbf{q} = \mathbf{S}\mathbf{q}. $$
(12)

Here, \(\mathbf{S}\) is defined as shape function matrix and the reversibility of \(\mathbf{Q}\) is the key to determine whether \(\mathbf{S}\) exists.

For the third-order ANCF beam model, its shape function matrix is

$$ \mathbf{S} = \left [ \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} S_{1} & 0 & S_{2} & 0 & \cdots & S_{10} & 0 \\ 0 & S_{1} & 0 & S_{2} & \cdots & 0 & S_{10} \end{array}\displaystyle \right ], $$
(13)

where \(S_{1} \sim S_{10}\) can be expressed as follows:

$$ \textstyle\begin{array}{l@{\qquad }l@{\qquad }l} & S_{1} = 1 - 3\xi ^{2} + 2\xi ^{3} & S_{2} = L(\xi -2\xi ^{2} + \xi ^{3}) \\ &\displaystyle S_{3} = h(1 - \xi )(1 - \frac{4}{3}\eta ^{2})\eta &\displaystyle S_{4} = h(1 - \xi )(\frac{2}{3}\eta - \frac{1}{2})\eta ^{2} \\ &\displaystyle S_{5} = h(1 - \xi )(\frac{2}{3}\eta + \frac{1}{2})\eta ^{2} &\displaystyle S_{6} = 3\xi ^{2} - 2\xi ^{3} \\ &\displaystyle S_{7} = L( - \xi ^{2} + \xi ^{3}) &\displaystyle S_{8} = h\xi (1 -\frac{4}{3}\eta ^{2})\eta \\ &\displaystyle S_{9} = h\xi (\frac{2}{3}\eta - \frac{1}{2})\eta ^{2} &\displaystyle S_{10} = h\xi(\frac{2}{3}\eta + \frac{1}{2})\eta ^{2} \end{array}\displaystyle . $$
(14)

Here, \(L \) and \(h\) represent the length and height of the beam element, respectively, and \(\xi = \frac{X}{L}\), \(\eta = \frac{Y}{h}\). Additionally, the shape function of the fourth-order beam model is given in the Appendix.

3 Mechanism of alleviating locking

Zheng discussed the mechanism of the second-order beam model in alleviating locking and obtained a pivotal point that the linear interpolation of two gradient vectors \(\mathbf{r}_{Y}\), located in the cross-section, enriches the transverse strain \(\varepsilon _{y}\) distribution along the thickness direction. This method increases the order of transverse interpolation and solves the locking problem. Based on the novel idea, this paper introduces more gradient vectors \(\mathbf{r}_{Y}\) to improve the order of the model and popularize this method.

To present the mechanism of alleviating locking, the third-order beam model is taken as an example to analyze.

Based on continuum mechanics [39], the strain \(\varepsilon _{y}\) located at \(X= 0\) is given by

$$ \varepsilon _{y} = \frac{1}{2}(\left | \mathbf{r}_{Y(0,\eta )} \right |^{2} - 1). $$
(15)

Substituting Equations (12), (13), and (14) into (15), Equation (16) can be obtained as follows:

$$ \begin{gathered} \varepsilon _{y} = \frac{1}{2}(\delta _{x}^{2} + \delta _{y}^{2} - 1) \\ \delta _{x} = (1 - 4\eta ^{2})k_{5} + (2\eta ^{2} - \eta )k_{7} + (2\eta ^{2} + \eta )k_{9} \\ \delta _{y} = (1 - 4\eta ^{2})k_{6} + (2\eta ^{2} - \eta )k_{8} + (2\eta ^{2} + \eta )k_{10} \end{gathered}. $$
(16)

Here, \(k_{5}\) and \(k_{6}\) represent two components of the gradient vector \(\mathbf{r}_{Y}(0,0)\) in the global coordinate system, respectively, \(k_{7}\) and \(k_{8}\) represent two components of the curvature vector \(\mathbf{r}_{Y}(0, - \frac{h}{2})\) in the global coordinate system, respectively, and \(k_{9}\), \(k_{10}\) represent two components of the curvature vector \(\mathbf{r}_{Y}(0,\frac{h}{2})\) in the global coordinate system, respectively.

Essentially, three gradient vectors \(\mathbf{r}_{Y}|_{(X,Y) = (0, - \frac{h}{2})} \), \(\mathbf{r}_{Y}|_{(X,Y) = (0,0)} \), \(\mathbf{r}_{Y} |_{(X,Y) = (0,\frac{h}{2})} \) arranged in the cross-section are equivalent to three-node quadratic interpolation of \(\mathbf{r}_{Y}\), which generates gradient vectors with high accuracy distributed along the transverse direction as follows:

$$ \mathbf{r}_{Y}\left |_{X = 0,Y \in [ - \frac{h}{2},\frac{h}{2}]} \right . = \left [ \textstyle\begin{array}{c@{\quad}c} \delta _{x} & \delta _{y} \end{array}\displaystyle \right ]^{T}. $$
(17)

Consequently, the third-order ANCF beam model can capture the transverse strain \(\varepsilon _{y}\) with high order distribution along the section.

Additionally, the above analysis is still valid for higher-order beam models.

4 Dynamic modeling

4.1 Kinetic energy

The kinetic energy \(T\) of one element can be conventionally written as follows, according to Equation (12):

$$ T = \frac{1}{2}\int _{V} \rho \dot{\mathbf{r}}^{T}\dot{\mathbf{r}}dV = \frac{1}{2}\dot{\mathbf{q}}^{T}\int _{V} \rho \mathbf{S}^{T}\mathbf{S}dV \dot{\mathbf{q}} = \frac{1}{2}\dot{\mathbf{q}}^{T}\mathbf{M}\dot{\mathbf{q}}, $$
(18)

where \(\rho \), \(V\) represent the density and volume domain of the element, respectively, and \(\mathbf{M}\) is defined as a positive definite constant mass matrix, which is equal to \(\int _{V} \rho \mathbf{S}^{T}\mathbf{S}dV\).

4.2 Strain energy

Conventionally, the strain energy \(U\) of one element can be written as follows:

$$ U = \frac{1}{2}\int _{V} \varepsilon ^{T}\mathbf{D}\varepsilon dV, $$
(19)

where \(\varepsilon \) represents a strain array with six components including three normal strains and three shear strains, and the matrix of elasticities \(\mathbf{D}\) takes the form in case of linear elastic material.

$$ \mathbf{D} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \lambda + 2\mu & \lambda & \lambda & 0 & 0 & 0 \\ \lambda & \lambda + 2\mu & \lambda & 0 & 0 & 0 \\ \lambda & \lambda & \lambda + 2\mu & 0 & 0 & 0 \\ 0 & 0 & 0 & \mu & 0 & 0 \\ 0 & 0 & 0 & 0 & \mu & 0 \\ 0 & 0 & 0 & 0 & 0 & \mu \end{array}\displaystyle \right ], $$
(20)

where \(\lambda \) and \(\mu \) can be expressed as follows:

$$ \begin{aligned} \lambda &= \frac{Ev}{(1 + v)(1 - 2v)} \\ \mu &= \frac{E}{2(1 + v)} \end{aligned} $$
(21)

Here, \(E \) and \(v\) represent Yong’s modulus and Poisson’s ratio of the beam, respectively.

4.3 Equilibrium equation

According to Hamiliton’s principle, the weak form of equilibrium equation is

$$ \delta \int _{t_{0}}^{t_{f}} (T - U + W)dt = 0, $$
(22)

where \(t_{0}\) and \(t_{f}\) represent the initial and final moments of the integral, respectively, and \(W \) denotes the work done by external force, which can be written as

$$ W = \mathbf{r}_{(X_{0},Y_{0},Z_{0})}^{T}\mathbf{F}. $$
(23)

In Equation (23), note that the external force \(\mathbf{F} \) acts on the material point located at \((X_{0}, Y_{0}, Z_{0})\).

In this way, substituting Equations (12), (18), (19), (23) into Equation (22), the following equation can be obtained:

$$ \int _{t_{0}}^{t_{f}} \delta \mathbf{q}^{T}[\mathbf{M}\ddot{\mathbf{q}} + (\frac{\partial \varepsilon}{\partial \mathbf{q}})^{T}\mathbf{D}\varepsilon - \mathbf{S}_{(X_{0},Y_{0},Z_{0})}^{T}\mathbf{F}] dt = 0. $$
(24)

In addition, considering the arbitrariness of variation \(\delta \mathbf{q}\), the equilibrium equation of a single ANCF beam element can be expressed as follows:

$$ \mathbf{M}\ddot{\mathbf{q}} + \mathbf{K}(\mathbf{q}) = \mathbf{Q}(\mathbf{q}), $$
(25)

where \(\mathbf{K}(\mathbf{q})\) is a generalized elastic force array, which is equal to \((\frac{\partial \varepsilon}{\partial \mathbf{q}})^{T}\mathbf{D}\varepsilon \), and \(\mathbf{Q}(\mathbf{q})\) is a generalized external force array, which is equal to \(\mathbf{S}_{(X_{0},Y_{0},Z_{0})}^{T}\mathbf{F}\).

Furthermore, for a constrained mechanical system, the equilibrium equation can be written as follows:

$$ \begin{aligned} & \mathbf{M}\ddot{\mathbf{q}} + \Phi _{\mathbf{q}}^{T}\lambda = \mathbf{Q}(\mathbf{q}) - \mathrm{K}(\mathbf{q}) \\ & \Phi (\mathbf{q},t) = 0 \end{aligned}, $$
(26)

where \(\Phi (\mathbf{q},t)\) represents the constraint equations, and \(\lambda \) is defined as Lagrange multiplier array.

5 Numerical examples

To demonstrate higher-order ANCF beam models (second-order, third-order, fourth-order models), proposed in this paper, can alleviate Poisson locking effectively, this section specially takes the first four order beam models, Patel–Shabana beam element, and enhanced continuum mechanics (ECM) approach as the subject for numerical simulation analysis, in which the first-order beam model is Omar–Shabana element [17] and the second-order beam model is beam element proposed by Zheng [7], essentially. Thus, six numerical examples are involved, namely, three static examples and three dynamic examples. The first static example is that of a slender cantilever beam subjected to small deformation. The second static example involves a slender beam subjected to large deformation. The last static example is that of a thick cantilever beam subjected to large deformation. Additionally, the first dynamic analysis example is a beam pendulum with small deformation under gravity loading. The second dynamic analysis example is a beam pendulum with large deformation under gravity loading, and the last dynamic example considers a cantilever beam subjected to gravity loading.

5.1 Slender beam (small deformation)

A slender cantilever beam with a tip force \(F\) is investigated as shown in Fig. 5. Table 1 gives the parameters of the beam, including the geometry properties and materials properties.

Fig. 5
figure 5

Slender cantilever beam subjected to small deformation

Full size image
Table 1 Parameters of the slender beam (small deformation)
Full size table

The tip force is 10 N in the vertical direction. Consequently, the analytical vertical displacement of the free end is calculated to be −0.02 m in this case, based on the Euler–Bernoulli beam theory.

Figure 6 displays the displacement convergence results of four models with different finite element numbers. As can be seen from Fig. 6, no matter how many ANCF elements are used, the convergent tip deflection of the first-order ANCF beam model (Omar–Shabana element) is smaller than that of the theoretical solution −0.02 m, which explains why the Omar–Shabana beam element cannot converge to the correct solution due to excessive stiffness. Contrary, the deflection solution under the second-, third-, and fourth-order models can approach the analytical solution with only eight elements, effectively, and this consistency will be enhanced with an increase of the element number, greatly.

Fig. 6
figure 6

Tip deflection with different element number

Full size image

Figure 7 shows the distribution of transverse strain \(\varepsilon _{y}\) located at cantilever end along height direction. In Fig. 7, as was mentioned previously, the strain \(\varepsilon _{y}\) of the first-order model along the transverse direction is a constant with a value of 0, which demonstrated that Omar–Shabana elements are susceptible to Poisson locking. However, for the other three beam models, it is linearly distributed due to the higher-order interpolation along the transverse direction, and the strain \(\varepsilon _{y}\) at the end of the rectangular section is close to the theoretical value ±90 μ\(\varepsilon\).

Fig. 7
figure 7

Strain \(\varepsilon _{y}\) of cantilever end along height direction

Full size image

5.2 Slender beam (large deformation)

A slender cantilever beam subjected to gravity loading is investigated to test the element’s effectiveness under highly nonlinear conditions. In this numerical example, gravity load is considered to be the external force with uniform distribution, as shown in Fig. 8. Table 2 gives the geometry properties and materials properties of the beam.

Fig. 8
figure 8

Slender cantilever beam subjected to large deformation

Full size image
Table 2 Parameters of the slender beam (large deformation)
Full size table

Tables 3 and 4 indicate the tip horizontal and vertical displacement of the tips of Patel–Shabana element, the ECM model, and the first four order models in different element numbers, respectively. Figure 9 displays the equilibrium configuration of flexible slender beam, which has 16 ANCF elements under different models.

Fig. 9
figure 9

Equilibrium configuration of different beam models

Full size image
Table 3 Beam tip horizontal displacement (m) in different element numbers
Full size table
Table 4 Beam tip vertical displacement (m) in different element numbers
Full size table

From the convergent tip displacement and equilibrium configuration of beam it can be seen that the deformation of the first-order model is always smaller than that of the higher-order models, which indicates that the Omar–Shabana element is also susceptible to the occurrence of bending locking phenomenon in highly nonlinear problems. Additionally, with the increase of the number of elements, the number of generalized coordinates of the beam model, especially for the fourth-order beam model, will greatly increase, and the cost of numerical calculation will continue to increase, and the tip displacement results of higher-order beam models will gradually be consistent with the high-performance Patel–Shabana element and ECM approach. Meanwhile, the equilibrium configurations of beam under different higher-order models are all close to the result of Patel–Shabana beam model, which also proves that the proposed higher-order beam model is effective and reasonable in alleviating Poisson locking in large deformation statics problem.

5.3 Thick beam (large deformation)

A thick cantilever beam with a tip force \(F\) is investigated as shown in Fig. 10. Table 5 gives the basic parameters of the beam and the shear correction factor \(k_{s} = \frac{10(1 + v)}{12 + 11v}\).

Fig. 10
figure 10

Thick cantilever beam subjected to large deformation

Full size image
Table 5 Basic parameters of the beam (thick cantilever beam)
Full size table

The tip force is \(1\times 10^{6}~\text{N}\) in the vertical direction. To demonstrate the reliability of the numerical solution, a referenced vertical displacement solution (−0.21912 m) of the beam tip is obtained by using ABAQUS, which employs a total of 8000 C3D8R elements (\(400\times 50\times 4\)) for FE simulation. Figure 11 shows the vertical displacement of different models with different element numbers.

Fig. 11
figure 11

Tip vertical displacement with different element number

Full size image

Analogously, the tip vertical displacement of the first-order beam model is obviously small due to the excessive stiffness caused by Poisson locking, and it converges to about −0.2 m. Oppositely, the solutions of higher-order models (second-order, third-order, and fourth-order models) and the Patel–Shabana beam model are consistent with reference solution −0.214791 m, which also verifies that the developed higher-order beam models can alleviate Poisson locking in geometric nonlinear problems.

5.4 Beam pendulum (small deformation)

A dynamic beam pendulum problem is presented to demonstrate that the newly proposed beam models can contribute to locking alleviation in dynamic problems as well. The beam pendulum subjected to gravity loading \(q \) is shown in Fig. 12. The basic parameters of the beam pendulum are also described in Table 1. Obviously, a sufficient elastic modulus is provided in Table 1 to ensure that the beam only undergoes small deformation during free-falling.

Fig. 12
figure 12

Beam pendulum with small deformation

Full size image

To compare the simulation results of the four models and the Patel–Shabana model effectively, beam pendulum meshed with 16 ANCF elements is considered. The configurations of the third-order beam model at every 0.25 s for 0 ∼ 1 s are shown in Fig. 13. Figures 14 and 15 represent the curves of the horizontal and vertical position of the beam tip with time, respectively. As can be seen from these results, because the motion of the beam is basically a large-scale rigid motion, the small-scale elastic deformation caused by Poisson effect has little influence on the displacement result of the tip, which is also a crucial reason why the simulation results of four models, the Patel–Shabana model and the ECM model are highly consistent. Meanwhile, it also reveals that Poisson locking has little influence on dynamic problems dominated by large-scale rigid motion and small-scale elastic deformation.

Fig. 13
figure 13

Configurations of beam for pendulum motion (beam pendulum with small deformation)

Full size image
Fig. 14
figure 14

Beam tip horizontal position of different models (beam pendulum with small deformation)

Full size image
Fig. 15
figure 15

Beam tip vertical position of different models (beam pendulum with small deformation)

Full size image

5.5 Beam pendulum (large deformation)

To further investigate the influence of Poisson locking in dynamic problems dominated by large-scale rigid motion and large-scale elastic deformation, beam pendulum adopts the physical parameters in Table 2. Obviously, an insufficient elastic modulus is provided in Table 2 to ensure that the beam engenders large elastic deformation during free-falling, as shown in Fig. 16.

Fig. 16
figure 16

Beam pendulum with large deformation

Full size image

Similarly, the ANCF beam models also used 16 elements. The configurations of the third-order beam model at every 0.25 s for 0 ∼ 1 s are shown in Fig. 17. Figures 18 and 19 represent the curves of the horizontal and vertical position of the beam tip with time, respectively, and Fig. 20 represents the strain energy of different beam models. As can be seen from Figs. 17–20, although the beam has undergone the large elastic deformation during free-falling, the difference in beam tip displacement and strain energy between different models, including low-precision Omar–Shabana element, other higher-order beam models, and ECM approach is small due to the large-scale rigid movement caused by the rotation of the hub. Consequently, the influence of Poisson locking on the different beam models cannot be distinguished, clearly.

Fig. 17
figure 17

Configurations of beam for pendulum motion (beam pendulum with large deformation)

Full size image
Fig. 18
figure 18

Beam tip horizontal position of different models (beam pendulum with large deformation)

Full size image
Fig. 19
figure 19

Beam tip vertical position of different models (beam pendulum with large deformation)

Full size image
Fig. 20
figure 20

Strain energy of different beam models (beam pendulum with large deformation)

Full size image

5.6 Cantilever beam

Finally, a cantilever beam structure is presented in this section, to study the characteristics of Poisson locking in dynamic problems dominated by small-scale rigid motion and large-scale elastic deformation. This problem is consitent with the one considered by Orzechowski and Shabana [38]. The parameters of the beam are shown in Table 6. Obviously, cantilever boundary conditions and an insufficient elastic modulus ensures that the beam motion is mainly large-scale elastic deformation, as shown in Fig. 21.

Fig. 21
figure 21

Cantilever beam subjected to gravity loading

Full size image
Table 6 Basic parameters of the beam (cantilever beam subjected to gravity loading)
Full size table

The configurations of the third-order beam model at every 0.1 s for 0 ∼ 0.3 s are shown in Fig. 22. Figures 23 and 24 display the curves of the horizontal and vertical position of the beam tip with time, respectively. From these results, the tip displacement of the first-order beam model is obviously smaller than that of the higher-order models similarly, and Poisson locking exists in the Omar–Shabana beam element, objectively. For other higher-order models, including the Patel–Shabana beam model, their tip displacement solutions show high consistency with ECM approach, which demonstrates that proposed higher-order models have enough accuracy and can alleviate locking in dynamic problems as well.

Fig. 22
figure 22

Configurations of beam for cantilever beam

Full size image
Fig. 23
figure 23

Beam tip horizontal position of different models (cantilever beam subjected to gravity loading)

Full size image
Fig. 24
figure 24

Beam tip vertical position of different models (cantilever beam subjected to gravity loading)

Full size image

6 Conclusions

Locking phenomenon objectively exists in classical ANCF elements. To alleviate the problem of excessive stiffness caused by Poisson locking, a series of higher-order ANCF beam elements are developed based on the absolute nodal coordinate formulation, and the proposed beam models are highly generalized and consolidated in theory, in which the first-order beam model is Omar–Shabana element and the second-order beam model is Zheng et al. higher-order element. Additionally, the effectiveness and high-accuracy of the proposed higher-order beam model are demonstrated by comparing the proposed beam model with the Patel–Shabana model and ECM approach in six numerical examples. Correspondingly, in three static numerical examples, the beam tip displacement of higher-order beam models converges well in both small deformation problems and large deformation problems, which demonstrated that the higher-order ANCF beam models can alleviate locking in statics problems effectively. However, in the two dynamic beam pendulum problems, the numerical simulation results of low-precision Omar–Shabana element, high-performance Patel–Shabana model, and ECM approach have little difference, including tip displacement and strain energy characteristics, and it indicates that the elastic deformation caused by Poisson effect has little influence on the dynamic response of the whole system in case of the dynamic problems dominated by large-scale rigid motion. Finally, in the dynamic cantilever beam problem, the excessive stiffness caused by Poisson locking is obviously manifested in the first-order model, and the tip displacement between several higher-order models and ECM approach display high-level consistency, which establishes that the higher-order ANCF beam models can simulate complex dynamic problems with high accuracy on the basis of alleviating locking.