A unified formulation for mechanical joints with and without clearances/bushings and/or stops in the framework of multibody systems

Abstract

Virtually all machines and mechanisms use mechanical joints that are not perfect from the kinematic point of view and for which tolerances, in the fitting of their components, are specified. Together with such controlled clearances, mechanical joints may require the use of bushing elements, such as those used in vehicle suspensions. Furthermore, in many situations the joints exhibit limits (stops) in their translational or rotational motion that have to be taken into account when modeling them. The dynamic response of the mechanical systems that use such realistic mechanical joints is largely dependent on their characteristic dimensions and material properties of the compliant elements, implying that correct models of these systems must include realistic models of the bushing/clearance joints and of the joint stops. Several works addressed the modeling of imperfect joints to account for the existence of clearances and bushings, generally independently of the formulation of the perfect kinematic joints. This work proposes a formulation in which both perfect and clearance/bushing joints share the same kinematic information making their modeling data similar and enabling their easy permutation in the context of multibody systems modeling. The proposed methodology is suitable for the most common mechanical joints and easily extended to many other joint types benefiting the exploration of a wide number of modeling applications, including the representation of cut-joints required for some formulations in multibody dynamics. The formulation presented in this work is applied to several demonstrative examples of spatial mechanisms to show the need to consider the type of imperfect joints and/or joints with stops modeling in practical applications.

1 Introduction

Mechanical joints in any natural or man-made mechanism allow for the relative motion between the connected elements of the system. The function and durability of mechanical and biological joints is not only associated with the geometry of the mating pairs, which in turn guarantee the correct mobility of the system, but also to the materials used in the interface, which may allow for some level of energy dissipation and provide local flexibility, and to the tribological fluids to ensure the proper friction characteristics and wear control. Joints in mechanisms subjected to impact loading or with large transient loads, such as virtually all joints in road or railway vehicles, need not only to exhibit some level of compliance but also to provide some isolation to the transmission of vibrations between connecting bodies.

From the physical point of view, when the modeling of local compliance, energy dissipation or vibrational isolation/modification on the system kinematics are due to features of the mechanical joints, it is necessary that these are modelled as clearance/bushing joints and not as perfect kinematic pairs. From the mathematical, or computational, point of view it is often necessary to allow for the modeling of kinematic chains to have cutoff joints, i.e., kinematic joints modelled as contact pairs, either because the formulations used cannot handle closed kinematic loops, or because the multibody system only works due to slight misalignment of joints or even because it is a suitable modeling strategy to overcome the numerical difficulties associated with the existence of redundant constraints in the multibody system. In these cases, the availability of efficient and accurate models of clearance/bushing joints is a valuable feature in multibody computational tools for the development of realistic multibody systems.

The need for the modeling of clearance joints, in the framework of the dynamics of mechanical system, has recognized in earlier theoretical and experimental work by Dubowsky [11], Dubowsky and Gardner [12], Grant and Fawcett [23], Haines [26] or Soong and Thompson [47], among many others. This work showed how clearances can condition the dynamical response of mechanisms, affect performance and even interfere with machine control systems. In the framework of multibody dynamics Ravn [44], Schwab et al. [46] or Flores and Ambrósio [14] and Flores et al. [16, 19] presented some of the basic work for the generalized modeling of clearance joints. Most of this work focuses on the planar systems involving either revolute or translation joints. Based on that early work, the modeling of planar clearance joints has been explored by a wide number of researchers to model their lubrication [30], to understand the systems behavior in the presence of multiple joints [7], to apply their basic formulations in a wider range of contact problems [40], to devise controlling strategies for systems in their presence [1, 51] or simply to implement them in computer codes based on different formulations [24].

The solution of any contact problem is not simple and the modeling of clearance joints is not an exception. The solution of the contact problem is divided in two parts: the contact detection and the modeling of the contact force. Particular care must be put in the numerical issues associated with the integration of the equations of motion in the presence of sudden change of forces or even discontinuities. The contact detection for planar joints is rather simple being solutions for the most common type of joints available in the work of Flores et al. [16] or Zhang and Wang [53]. The modeling of the contact force is either approached by using penalty formulations, generally based on Hertz elastic contact [28, 41], or by using unilateral constraints in the framework of non-smooth contact dynamics [2, 18, 22]. A critical issue in the numerical solution of multibody dynamics problems in the presence of contact, or impact, is the fitting of the numerical integration method and of the time-step selected to the correct integration of the equations of motion. This issue is discussed by Flores and Ambrosio [17] in the framework of continuous contact force models using penalty formulations, and by Förg et al. [20] or Brogliato [9] in the context of unilateral constraints or non-smooth contact dynamics.

The use of multibody models for 3D systems that use of spatial clearance/bushing joints is required for a wide number of realistic problems. Road vehicles, whose suspensions use bushing elements in the joints [3], railway vehicles for which the extra degrees associated with the clearance joints provides the compliance of the suspension systems that promote a better wheel–rail contact [33] or in the multibody modeling of high-speed train pantographs in which some of the fundamental features of their dynamic response are associated with the existence of imperfect joints [50] or even in the modeling of mechanical watches [45] are examples of the need for using imperfect joints. In general, while the numerical issues associated with the numerical methods and time-stepping procedures in contact problems are similar in spatial and planar multibody systems, the contact detection and the use of the contact force models have different issues in planar and spatial clearance/bushing joints. Different computational models for spatial clearance joints, mostly revolute joints, are proposed in the literature. Flores et al. [15] propose a new revolute joint model which is revisited later by the same authors, together with models for spatial spherical and translation joints [16]. Alternative formulations for spatial revolute and translation joints are proposed by different authors [10, 49, 52, 53]. The main differences between the various formulations consist in the approaches used for the contact detection and on the description of the continuous contact force model. The contact force models used in most of the current formulations for clearance joints are inherited from the analysis of planar contact problems, without fully taking into account the characteristics of the three dimensional contact geometry. Continuous force models such as that proposed by Lankarani and Nikravesh [28] or by Pereira et al. [41] are examples of models that are suitable to be used in planar clearance joints but cannot be applied in the exact same manner in general spatial cylindrical or revolute clearance joints. The bushing joints, whose use in vehicle suspensions, in particular, are of fundamental importance, are examples of joints in which the force models are associated with the material that is included between the contacting surfaces, generally elastomers [3]. The use the strip method, in which one of the cylindrical contact surfaces of the clearance joint is discretized in cylindrical patches, being each one of these patches checked independently for contact with the mating cylindrical surface, has been proposed to address the roller bearing contact [25]. This approach provides a methodology for using continuous contact models, originally developed for planar problems, in the context of spatial clearance joints that is applied here.

This work proposes a novel approach to the modeling of perfect kinematic joints and of clearance/bushing joints in the sense that they both share a similar basic mathematical description in terms of the algebraic operations required for their formulation. By also ensuring a common set of modeling data, it is simple not only to ensure a computational implementation of the kinematic and clearance/bushing joints in a common framework, allowing for the existence of joints with mixed features, but also to develop easily recyclable multibody models in which the nature of the mechanical joints is interchangeable. Besides the unifying characteristics of the formulation used, also the compliance of the joints is treated in the same form, being this the result of contact or of the existence of bushing elements. It is also shown that the modeling of joint stops in revolute, cylindrical or translation joints is just a particular case of the modeling of clearance joints. Finally, two demonstration cases are used to show the performance of the formulations proposed in this work with respect to the geometrical and material features of the clearance/bushing joints developed here.

2 Multibody formulation of kinematic and contact joints

2.1 Multibody formulation with cartesian coordinates

Without loss of generality, let Cartesian coordinates be used to describe the equations of motion of the constrained multibody system. Let $\mathbf{q}$ denote the vector of the system coordinates, composed with the translation and rotation coordinates of the individual rigid bodies, and $\dot{\mathbf{q}}$ and $\ddot{\mathbf{q}}$ be the velocity and acceleration vectors of the system, respectively [37]. The constraint equations associated with the kinematic constraints are denoted by $\boldsymbol{\varPhi}$, being their Jacobian matrix, i.e., the matrix with their derivatives with respect to the system coordinates, denoted by $\boldsymbol{\varPhi} _{\mathbf{q}}$. Then the dynamic response of the system is obtained by solving the system equilibrium equations

$$ \left [ \textstyle\begin{array}{c@{\quad }c} \mathbf{M} & \boldsymbol{\varPhi}_{\mathbf{q}}^{T}\\ \boldsymbol{\varPhi}_{\mathbf{q}} & \mathbf{0} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \mathbf{g} \\ \boldsymbol{\gamma} \end{array}\displaystyle \right \} $$

(1)

to obtain $\ddot{\mathbf{q}}$, which in turn is integrated in time to obtain $\dot{\mathbf{q}}$ and $\mathbf{q}$. In Eq. (1) $\mathbf{M}$ is the mass matrix, $\mathbf{g}$ the force vector, $\boldsymbol{\lambda}$ is the vector of Lagrange multipliers, which are related to the joint reaction forces, and $\boldsymbol{\gamma}$ is the right-hand-side of the acceleration constraint equations. Note that, depending on the rotation coordinates used to describe the spatial kinematics of the rigid bodies, the velocity vector $\dot{\mathbf{q}}$ may not be simply the time derivative of vector $\mathbf{q}$. When using Euler parameters to describe rotations, as in the case of this work, the coordinates that describe the position and orientation of a rigid body $i$ are $\mathbf{q}_{i}^{*} = [ \mathbf{r}^{T} \ \ \mathbf{p}^{T} ]_{i}^{T}$, where $\mathbf{p} = [e_{0} \ \ e_{1} \ \ e_{2} \ \ e_{3} ]^{T}$ are the Euler parameters. The time the velocities of the rigid body can be expressed as $\dot{\mathbf{q}}_{i}^{*} = [ \dot{\mathbf{r}}^{T} \ \ \dot{\mathbf{p}}^{T} ]_{i}^{T}$ or as $\dot{\mathbf{q}}_{i} = [ \dot{\mathbf{r}}^{T} \ \ \boldsymbol{\omega} ^{\prime\,T} ]_{i}^{T}$, in which $\boldsymbol{\omega}'_{i}$ is the body angular velocity, expressed in the body-fixed coordinate system. The relation between the time derivatives of the Euler parameters and the angular velocities of the rigid body are given by $\boldsymbol{\omega} '_{i} = 2\mathbf{L}_{i}\dot{\mathbf{p}}_{i}$, where the $3\times4$ $\mathbf{L} _{i}$ matrix, made of the Euler parameters is defined in [37].

Of particular interest for the developments reported in this work are the kinematic joint reaction forces, included in Eq. (1), and highlighted here as

$$ \mathbf{g}^{(c)} = - \boldsymbol{\varPhi}_{\mathbf{q}}\boldsymbol{\lambda} $$

(2)

which derive from the application of the Augmented Lagrangian method to add the kinematic constraints to the equations of motion. The first row of Eq. (1) can be written as

$$ \mathbf{M}\ddot{\mathbf{q}} = \mathbf{g} + \mathbf{g}^{(c)} $$

(3)

When some joints of the mechanical system are not perfect kinematic joints but, instead, exhibit joint clearances and/or bushings, their corresponding joint reaction forces are replaced, in Eq. (3), by specific force elements. In this case, the system equations of motion are

$$ \mathbf{M}\ddot{\mathbf{q}} = \mathbf{g} + \mathbf{g}^{(c_{k})} + \mathbf{g}^{(c/b)} $$

(4)

in which $\mathbf{g}^{(c_{k})}$ represents the joint reaction forces of the remaining kinematic joints and $\mathbf{g}^{(c/b)}$ are the forces in the clearance/bushing joints. In what follows, the clearance/bushing joints are derived by using the same vector operations required to evaluate the kinematic joints constraints and suitable force constitutive equations.

The integration of the accelerations and velocities of the multibody system lead to a numerical drift in the position and velocity constraint equations of the kinematic constraints, as these are not explicitly used in the solution process. In all that follows the Baumgarte stabilization method [6, 37] is used to control the violation of the constraint equations. For the joints represented as contact pairs, instead of kinematic constraints, there are, naturally, no constraint violations and, consequently, no stabilization method required.

When dealing with impact/contact between the bodies of a system, such as those that form the contact pair in clearance/bushing joints, the detection of the time of initiation of contact is fundamental. When variable time-step integration algorithms are used and the pre-impact dynamics does not involve high frequencies the integration algorithms may use larger time steps and the contact between two surfaces may start with initial penetrations that are artificially high. Either this fact leads to a stall of the integration algorithm or to contact forces that are physically impossible which, in turn, lead to post-impact dynamics that is unrelated to the physical problem. The procedure proposed by Flores and Ambrosio [17] that ensures that for any impact in a multibody system the time step of the integration is such that any initial penetration is below a prescribed threshold is applied here. When any new contact start, and after a time step is complete, the numerical error control of the selected integration algorithm is forced to handle the physical criteria to accept/reject time steps in equal terms with the numerical error control that it normally uses. In this case, if the initial penetration is higher than the threshold the integrator is instructed to reject the time step, implying that its internal control decreases it until the threshold is met.

2.2 Perfect kinematic joints: an alternative view

Although the general approach proposed in this work can be used for the formulation of all types of kinematic and clearance/bushing joints, only the cylindrical, revolute, translation and rigid joints are considered here. The formulation for the spherical clearance/bushing joint used in the applications presented here is that proposed by Flores et al. [16] in what contact detection is concerned while the use of general constitutive models for the contact force is discussed hereafter.

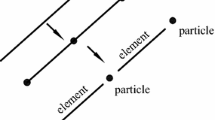
A general representation for cylindrical, revolute, translation or even rigid joints is depicted in Fig. 1(a). The input required to define the constraint equations of any of the kinematic joints referred are the positions of points $P$ and the vectors aligned with the joint axis in bodies $i$ and $j$, respectively denoted as $\mathbf{s}_{i}^{\prime\,P}$, $\mathbf{s}_{j}^{\prime\,P}$, $\mathbf{s}'_{i}$ and $\mathbf{s}'_{j}$. The superscript $(\bullet)'$ denotes that the quantity (•) is defined in the body-fixed coordinate system of the body used in the subscript of the same quantity.

Fig. 1

Generic representation of perfect cylindrical, revolute, translation or rigid kinematic joints; (a) identification of the points required; (b) vectors based on pre-defined points

In all that follows, and without loss of generality, let it be assumed a set of rules to be used in the construction of the multibody models that has to be followed for the definition of the perfect and clearance/bushing joints:

• Body $j$ includes the bearing while body $i$ includes the journal;

• The location of point $P _{j}$ is half-way along the bearing axial length, defined as $l _{j}$;

• The location of point $P _{i}$ is half-way along the journal axial length, defined as $l _{i}$;

• The location of point $Q _{j}$ is in one of the ‘edges’ of the bearing axis, such that $l_{j} = 2\overline{P_{j} Q_{j}}$

• The location of point $Q _{i}$ is in one of the ‘edges’ of the journal axis, such that $l_{i} = 2\overline{P_{i} Q_{i}}$

• The journal length is always longer or equal to the bearing length, i.e., $l _{i} \geq l _{j}$.

Note that for perfect kinematic joints the concept of bearing and journal, or of their length, is not important. However, for clearance joints not only the knowledge of the lengths is important but also the location of the points defining the joint axis is used to define the application of the joint reactions. Therefore, it is preferred that the same set of rules is used for the definition of mechanical joints, regardless of them being perfect or not.

Let two orthogonal sets of vectors be defined, in each one of the body-fixed coordinate frames, as seen in Fig. 1(b), such that

$$ \begin{aligned} &\mathbf{h}'_{i} \bot \mathbf{s}'_{i}; \quad \mathbf{t}'_{i} \bot \mathbf{s}'_{i}; \quad \mathbf{h}'_{i} \bot \mathbf{t}'_{i} \\ &\mathbf{h}'_{j} \bot \mathbf{s}'_{j}; \quad \mathbf{t}'_{j} \bot \mathbf{s}'_{j}; \quad \mathbf{h}'_{j} \bot \mathbf{t}'_{j} \end{aligned} $$

(5)

Start with vectors $\mathbf{b} _{i}$ and $\mathbf{b} _{j}$, in Fig. 1(b), which not only are parallel to $\mathbf{s} _{i}$ and $\mathbf{s} _{j}$, but also have the same orientation of $\mathbf{s} _{i}$, i.e., $\mathbf{b}'_{i} = \mathbf{s}'_{i}/ \vert \mathbf{s}'_{i} \vert$ and $\mathbf{b}'_{j} = \mathbf{A}_{j}^{T}\mathbf{A}_{i}\mathbf{b}'_{i}$ at time $t _{0}$, where matrices $\mathbf{A} _{i}$ and $\mathbf{A} _{j}$ are the transformation matrices from bodies $i$ and $j$ coordinate systems, respectively, to the inertial referential. Generate vector $\mathbf{h}'_{i}$, in Eq. (5), to be orthogonal to $\mathbf{b}'_{i}$, for instance by using a Householder transformation [31]. From the numerical point of view it is assumed that the vectors are generated such a way that $\mathbf{h}'_{i} = \mathbf{A}_{i}^{T}\mathbf{h}_{i}$ and $\mathbf{h}'_{j} = \mathbf{A}_{j}^{T}\mathbf{h}_{i}$. Finally, the vectors $\mathbf{t}'_{i}$ and $\mathbf{t}'_{j}$ are such that not only Eq. (5) is fulfilled but also such that right-hand vector triads are obtained. A joint coordinate system $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{i}$ is associated with the journal and another coordinate system $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{j}$ is associated with the bearing, being these parallel to each other in the initial time $t _{0}$ of the analysis. Of particular importance in what follows is the transformation of coordinates from the journal coordinate system to the body $i$ coordinate system, which is expressed by the constant transformation matrix $\mathbf{A}_{\mathit{joint}} = [ \mathbf{h}'_{i} \ \ \mathbf{t}'_{i} \ \ \mathbf{b}'_{i} ]$. In all time steps during the numerical integration of the equations of motion of a multibody system, the distance vector $\mathbf{d}$, depicted in Fig. 1(b), is

$$ \mathbf{d} = \bigl(\mathbf{r}_{j} + \mathbf{A}_{j} \mathbf{s}_{j}^{\prime\,P}\bigr) - \bigl(\mathbf{r}_{i} + \mathbf{A}_{i}\mathbf{s}_{i}^{\prime\,P}\bigr) $$

(6)

The different perfect kinematic joints are described by defining the convenient vector operations with the quantities presented in Eqs. (5) and (6). The constraint equations for a cylindrical joint are defined as

$$ \boldsymbol{\varPhi}^{(c,4)} \equiv \left \{ \textstyle\begin{array}{c} \mathbf{h}_{i}^{T}\mathbf{b}_{j} \\ \mathbf{t}_{i}^{T}\mathbf{b}_{j} \\ \mathbf{h}_{i}^{T}\mathbf{d} \\ \mathbf{t}_{i}^{T}\mathbf{d} \end{array}\displaystyle \right \} = \mathbf{0} $$

(7)

For a revolute joint the constraint equations are obtained by adding to the cylindrical joint constraint equations a restriction that prevents the axial displacement of body $i$ with respect to body $j$, i.e.,

$$ \boldsymbol{\varPhi}^{(r,5)} \equiv \left \{ \textstyle\begin{array}{c} \boldsymbol{\varPhi}^{(c,4)} \\ \mathbf{d}^{T}\mathbf{d} - d_{0}^{2} \end{array}\displaystyle \right \} = \mathbf{0} $$

(8)

in which the square of the axial distance between points $P$ in bodies $i$ and $j$, defining the joint, $d_{0}^{2} = ( \mathbf{d}^{T}\mathbf{d} )_{\mathit{time} = t_{0}}$, is evaluated for time $t _{0}$. For a translation joint the constraints equations are obtained by adding to the cylindrical joint constraints a restraint that prevents the rotation of body $i$ with respect to body $j$,

$$ \boldsymbol{\varPhi}^{(t,5)} \equiv \left \{ \textstyle\begin{array}{c} \boldsymbol{\varPhi}^{(c,4)} \\ \mathbf{h}_{i}^{T}\mathbf{t}_{j} - h_{0}^{2} \end{array}\displaystyle \right \} = \mathbf{0} $$

(9)

being the square of the angular alignment of bodies $i$ and $j$ along the joint axis, $h_{0}^{2} = ( \mathbf{h}_{i}^{T}\mathbf{t}_{j} )_{\mathit{time} = t_{0}}$, evaluated for time $t _{0}$.

The rigid joint is obtained with the cylindrical joint constraints plus the restrictions for the axial displacement and rotation about the axis defined between bodies $i$ and $j$, as

$$ \boldsymbol{\varPhi}^{(\mathit{rig},6)} \equiv \left \{ \textstyle\begin{array}{c} \boldsymbol{\varPhi}^{(c,4)} \\ \mathbf{d}^{T}\mathbf{d} - d_{0}^{2} \\ \mathbf{h}_{i}^{T}\mathbf{t}_{j} - h_{0}^{2} \end{array}\displaystyle \right \} = \mathbf{0} $$

(10)

Note that the rigid joint can be expressed by a formulation alternative to that used here, in which the set of constraints defining a spherical joint are complemented by a frame alignment constraint as that used in the path motion constraint proposed by Pombo and Ambrósio [42]. In fact, if $d _{0} =0$ and the frames defined by vectors $\mathbf{h}$, $\mathbf{t}$, $\mathbf{b}$, associated with each body, are substituted by the unit vectors associated with the body-fixed coordinate systems both formulations become identical.

2.3 General description of imperfect kinematic joints or contact joints

Equation (7) through (9) define the perfect kinematic joints that need to be included in Eq. (1) using the Augmented Lagrangian method [37]. However, in many applications the kinematic joints are not perfect, as that illustrated in Fig. 2. Instead of enforcing kinematic constraints between rigid bodies, the relative displacements and rotations between them lead to contact forces which are related to the relative displacements by appropriate constitutive relations.

Fig. 2

General representation of clearance/bushing cylindrical, revolute and translation joints with the identification of specific relative motions required for their formulation

A general clearance/bushing joint that restricts all relative motions between two connected bodies requires that the axial and radial displacements, axial misalignment and axial rotation, identified in Fig. 2, are penalized. The penalization forces must be evaluated and applied in the bodies constrained by the joint in specific interaction points, which must be clearly defined also. The contact forces between the two bodies are proposed by Ambrosio and Verissimo [3], in the case of pure bushing joints, and by Flores et al. [16], in the case of clearance joints. These contact force constitutive models are revisited here with several enhancements, not only to accommodate for the simultaneous application of clearances and bushings but also to explicitly use the same vectors obtained for the definition of the perfect joints, while providing improved numerical performance.

2.3.1 Relative displacements/rotations

The concepts of axial and radial displacements, axial misalignment and axial rotation, visualized in the graphical aids depicted in Fig. 2, are defined first. For this purpose, let the distance vector $\mathbf{d}$ be decomposed, as illustrated in Fig. 2, into axial displacement component along vector $\mathbf{b} _{i}$, which specifies the joint axis in body $j$, defined as

$$ \mathbf{d}_{t} = \bigl(\mathbf{d}^{T} \mathbf{b}_{i}\bigr)\mathbf{b}_{i} $$

(11)

and an orthogonal component, the radial displacement with respect to the joint axis, defined as

$$ \mathbf{d}_{n} = \mathbf{d} - \mathbf{d}_{t} $$

(12)

The radial displacement, denoted by $\delta _{n}$, and the radial direction, $\mathbf{u} _{rd}$, are obtained:

$$\begin{aligned} \delta_{n} =& \sqrt{\mathbf{d}_{n}^{T} \mathbf{d}_{n}} \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{u}_{rd} =& \mathbf{d}_{n} / \delta_{n} \end{aligned}$$

(14)

The axial displacement, denoted by $\delta _{t}$, and the radial direction, $\mathbf{u} _{\mathit{ad}}$, are obtained:

$$\begin{aligned} \delta_{t} =& \sqrt{\mathbf{d}_{t}^{T} \mathbf{d}_{t}} \end{aligned}$$

(15)

$$\begin{aligned} \mathbf{u}_{\mathit{ad}} =& \mathbf{d}_{t} / \delta_{t} \end{aligned}$$

(16)

The axial misalignment of joint axis in bodies $i$ and $j$ is described by an angle $\theta _{\mathit{am}}$ measured about a vector $\mathbf{u} _{\mathit{am}}$ written as

$$\begin{aligned} \theta_{\mathit{am}} =& \arcsin \bigl( \vert \tilde{\mathbf{b}}_{i} \mathbf{b}_{j} \vert \bigr) \end{aligned}$$

(17)

$$\begin{aligned} \mathbf{u}_{\mathit{am}} =& \tilde{\mathbf{b}}_{i} \mathbf{b}_{j} / \vert \tilde{\mathbf{b}}_{i} \mathbf{b}_{j} \vert \end{aligned}$$

(18)

in which the skew-symmetric matrix of a vector $\mathbf{b}$, denoted by $\tilde{\mathbf{b}}$, is defined in Nikravesh [37]. It must be noted that if the axial misalignment is null, i.e., $\vert \tilde{\mathbf{b}}_{i} \mathbf{b}_{j} \vert \approx 0$, Eq. (18) is not required because the conditions of alignment of the axis of the bearing and journal are fulfilled and no penalization force needs to be calculated. The axial rotation of the bearing with respect to the journal is defined by angle $\alpha _{\mathit{ar}}$, obtained:

$$ \alpha_{\mathit{ar}} = \operatorname{arc} \sin \bigl(\mathbf{h}_{i}^{T} \mathbf{t}_{j}\bigr) $$

(19)

The measures of misalignments and relative displacements between the joint bearing and journal are used to define the clearance/bushing joints. Note that in their definition only the vectors already used for the definition of the perfect kinematic joints are required.

2.3.2 Forces in clearance/bushing joints

A cylindrical clearance/bushing joint is defined by using a proper penalization of the relative motion between bearing and journal, i.e., the radial displacement and the axial misalignment lead to contact forces during the contact phase. Based on the joint description in Fig. 2 and using the definitions of Eqs. (11) through (18), the clearance/bushing cylindrical joint, requires that the forces are applied in points $P _{i}$ and $P _{j}$, of bodies $i$ and $j$, respectively, defined by

$$ \begin{aligned} \mathbf{f}_{i}^{(\mathit{cyl})}& = \mathbf{f}_{\mathit{cyl}}(\delta_{n},\dot{\delta}_{n},\delta_{t},\dot{\delta}_{t},\theta_{\mathit{am}},\dot{\theta}_{\mathit{am}}) \\ \mathbf{f}_{j}^{(\mathit{cyl})} &= - \mathbf{f}_{i}^{(\mathit{cyl})} \end{aligned} $$

(20)

The force constitutive equation $\mathbf{f}_{\mathit{cyl}}(\delta_{n},\dot{\delta}_{n},\delta_{t},\dot{\delta}_{t},\theta_{\mathit{am}},\dot{\theta}_{\mathit{am}})$ is, in general, a relation in which all relative displacements and misalignments are coupled but that also involves the clearance size, bearing and journal geometry and the material constitutive properties, which is discussed in next section. Besides the force penalization, also a penalization moment must be considered in the cylindrical joint, written in its general form as

$$ \begin{aligned} \mathbf{n}_{i}^{\prime\,(\mathit{cyl})} &= \mathbf{n}_{\mathit{cyl},i}(\delta_{n},\dot{\delta}_{n},\delta_{t},\dot{\delta}_{t},\theta_{\mathit{am}},\dot{\theta}_{\mathit{am}}) \\ \mathbf{n}_{j}^{\prime\,(\mathit{cyl})} &= \mathbf{n}_{\mathit{cyl},j}(\delta_{n},\dot{\delta}_{n},\delta_{t},\dot{\delta}_{t},\theta_{\mathit{am}},\dot{\theta}_{\mathit{am}}) \end{aligned} $$

(21)

For a clearance/bushing revolute joint, the penalization forces due to the axial displacement, presented in Fig. 2, is also required. Besides the penalization forces and moments expressed by Eqs. (20) and (21) the revolute joint also requires the application of contact forces in points $P _{i}$ and $P _{j}$, of bodies $i$ and $j$, respectively, defined by

$$ \begin{aligned} \mathbf{f}_{i}^{(\mathit{ad})} &= f_{\mathit{ad}}(\delta_{t},\dot{\delta}_{t})\mathbf{u}_{\mathit{ad}} \\ \mathbf{f}_{j}^{(\mathit{ad})} &= - \mathbf{f}_{i}^{(\mathit{ad})} \end{aligned} $$

(22)

The axial displacement $\mathbf{d} _{t}$ is calculated by using Eq. (11). The force relation $f_{\mathit{ad}}(\delta_{t},\dot{\delta}_{t})$ is a nonlinear relation that involves the axial displacement, its speed and the geometric and material characteristics of the joint.

For a clearance/bushing translation joint, the penalization forces due to the axial rotation between bearing and journal, shown in Fig. 2, is required together with the contact forces and moments expressed by Eqs. (20) and (21). The penalization of the axial rotation requires the application of penalty moments in bodies $i$ and $j$ defined by

$$ \begin{aligned} \mathbf{n}_{i}^{\prime\,(\mathit{ar})} &= f_{\mathit{ar}}(\alpha,\dot{\alpha} )\mathbf{A}_{i}^{T}\mathbf{b}_{i} \\ \mathbf{n}_{j}^{\prime\,(\mathit{ar})} &= - \mathbf{A}_{j}^{T}\mathbf{A}_{i}\mathbf{n}_{i}^{\prime\,(\mathit{ar})} \end{aligned} $$

(23)

The relation $f_{\mathit{ar}}(\alpha,\dot{\alpha} ) f_{\mathit{ar}}(\alpha_{\mathit{ar}},\dot{\alpha}_{\mathit{ar}})$ is a nonlinear relation that includes the axial rotation angle, its speed and the geometric and material characteristics of the joint.

The total forces and moments to be applied on bodies $i$ and $j$ resulting from the clearance/bushing constitutive equations are defined independently by Eqs. (20) through (23), being the forces applied on points $P _{i}$ and $P _{j}$, in bodies $i$ and $j$, respectively. Therefore, their transference to the center of mass of each body, where the fixed coordinate system is assumed to be attached, must be considered. The contribution of the clearance/bushing joints to the force vector of the bodies connected by one of those joints is given by

$$\begin{aligned} \begin{aligned} \mathbf{g}_{i}& = \left \{ \textstyle\begin{array}{c} ( \mathbf{f}_{i}^{(\mathit{cyl})} + \mathbf{f}_{i}^{(\mathit{ad})} ) \\ {\tilde{\mathbf{s}}}_{i}^{\prime\,P}\mathbf{A}_{i}^{T} ( \mathbf{f}_{i}^{(\mathit{cyl})} + \mathbf{f}_{i}^{(\mathit{ad})} ) + \mathbf{n}_{i}^{\prime\,(\mathit{cyl})} + \mathbf{n}_{i}^{\prime\,(\mathit{ar})} \end{array}\displaystyle \right \} \\ \mathbf{g}_{j} &= \left \{ \textstyle\begin{array}{c} \mathbf{f}_{j}^{(\mathit{cyl})} + \mathbf{f}_{j}^{(\mathit{ad})} \\ {\tilde{\mathbf{s}}}_{j}^{\prime\,P}\mathbf{A}_{j}^{T} ( \mathbf{f}_{j}^{(\mathit{cyl})} + \mathbf{f}_{j}^{(\mathit{ad})} ) + \mathbf{n}_{j}^{\prime\,(\mathit{cyl})} + \mathbf{n}_{j}^{\prime\,(\mathit{ar})} \end{array}\displaystyle \right \} \end{aligned} \end{aligned}$$

(24)

All penalization forces and moments defined in Eqs. (20) through (23) involve relative displacements and rotations and their time derivatives. For the evaluation of the relative displacement and rotation speeds the reader is directed to reference [3]. In the definition of the penalty moments, defined by Eqs. (21) and (23) the penalization of the axial displacement and axial rotation are decoupled from each other, and from the other relative motion penalizing force components. In some particular applications, the relative motion components may be coupled as, for instance, in biological structures, such as intervertebral disk in the human spine, where the axial deformation is coupled with the axial rotation.

2.4 Application to a clearance/bushing cylindrical joint

The computational treatment of a clearance/bushing joint has a computational implementation similar to that of any other contact problem. First the general contact detection has to be solved. The contact detection depends on the geometry of the contact pair being its implementation more or less specialized for particular geometries [27, 36], being in general the most, computationally, expensive part of the solution of the contact problem. When contact is detected, an appropriate constitutive force model is applied to obtain the contact forces. The force modeling may be more or less costly, depending on the constitutive relations involved, eventually leading to numerical integration difficulties that need to be handled [9, 17, 20]. To overcome the computational cost of solving the contact problem online, it is common the use of contact lookup tables to obtain the contact forces based on the relative position of the two surfaces of the contact pair [8, 32], represented in this work by Eqs. (20) through (23). To demonstrate the calculations required for the solution of the contact detection problem in clearance/bushing joints, the case of a cylindrical joint is presented here.

2.4.1 Contact detection

Let the clearance/bushing cylindrical joint be shown in Fig. 3(a). Let the journal be a cylinder defined in the journal coordinate system $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{i}$ by the parameters $\theta _{i}$ and $b _{i}$, shown in Fig. 3(b), and the bearing be another cylinder discretized by a selected number of circular patches defined in the bearing coordinate system $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{j}$ by parameters $\theta _{j}$, also shown in Fig. 3(b).

Fig. 3

Representation of clearance/bushing cylindrical joint: (a) Exploded view for contact detection; (b) Parametric description of the surfaces in the contact pair

Let two points, $C _{i}$ and $C _{j}$, in bodies $i$ and $j$, respectively, be candidates to contact points. Their coordinates, in journal and bearing coordinate systems, are written as:

$$\begin{aligned} \mathbf{s}_{i}^{\prime\prime\,C} =& \left \{ \textstyle\begin{array}{c} R_{i}\cos \theta_{i} \\ R_{i}\sin \theta_{i} \\ b_{i} \end{array}\displaystyle \right \} \end{aligned}$$

(25)

$$\begin{aligned} \mathbf{s}_{j}^{\prime\prime\,C} =& \left \{ \textstyle\begin{array}{c} R_{j}\cos \theta_{j} \\ R_{j}\sin \theta_{j} \\ b_{j} \end{array}\displaystyle \right \} \end{aligned}$$

(26)

in which the circumference located with the coordinate $b _{j}$ along the axis of the bearing cylinder is considered for contact. Note that in what follows $b _{j}$ is known while $\theta _{j}$, $\theta _{i}$ and $b _{i}$ are unknown parameters that need to be calculated. The bearing surface tangent vector at point $C _{j}$ is defined by

$$ \mathbf{t}_{j}^{\prime\prime\,C} = \left \{ \textstyle\begin{array}{c} - \sin \theta_{j} \\ \cos \theta_{j} \\ 0 \end{array}\displaystyle \right \} $$

(27)

The normal, tangent and binormal vectors to the journal cylindrical surface at point $C _{i}$ are

$$\begin{aligned} \mathbf{h}_{i}^{\prime\prime\,C} =& \left \{ \textstyle\begin{array}{c} \cos \theta_{i} \\ \sin \theta_{i} \\ 0 \end{array}\displaystyle \right \} \end{aligned}$$

(28)

$$\begin{aligned} \mathbf{t}_{i}^{\prime\prime\,C} =& \left \{ \textstyle\begin{array}{c} - \sin \theta_{i} \\ \cos \theta_{i} \\ 0 \end{array}\displaystyle \right \} \end{aligned}$$

(29)

$$\begin{aligned} \mathbf{b}_{i}^{\prime\prime\,C} =& \left \{ \textstyle\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\displaystyle \right \} \end{aligned}$$

(30)

For convenience, the local journal coordinate system $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{i}$ is used to carry all the calculations required for the contact search. The rotation of the bearing coordinate frame to the journal coordinate frame is defined by a sequence of two rotations. The first rotation, by $\theta _{\mathit{am}}$, represented in Fig. 2 and described by Eqs. (17) and (18), leads to the alignment of axis $\mathbf{b} _{j}$ with $\mathbf{b} _{i}$ by a set of Euler parameters $\mathbf{p} _{\mathit{am}}$, which are related to the axial misalignment as:

$$ \mathbf{p}_{\mathit{am}} = \left \{ \textstyle\begin{array}{c} e_{\mathit{am},0} \\ e_{\mathit{am},1} \\ e_{\mathit{am},2} \\ e_{\mathit{am},3} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} e_{\mathit{am},0} \\ \mathbf{e}_{\mathit{am}} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \cos ( \theta_{\mathit{am}} / 2 ) \\ \sin ( \theta_{\mathit{am}} / 2 )\mathbf{u}_{\mathit{am}} \end{array}\displaystyle \right \} $$

(31)

The transformation matrix, for the first rotation, defined as $\mathbf{A} _{\mathit{am}}$, is obtained by using the Euler parameters as shown in [37]. The second rotation, $\alpha _{\mathit{ar}}$, represented in Fig. 2, defined about the axis $\mathbf{b} _{i}$ leads to a transformation matrix $\mathbf{A} _{\mathit{ar}}$. Therefore, the rotation that aligns $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{j}$ to $(\mathbf{h}, \mathbf{t}, \mathbf{b})_{i}$, is defined as $\mathbf{A}_{ j2 i } = \mathbf{A} _{\mathit{ar}} \mathbf{A} _{\mathit{am}}$.

The location of point $C _{j}$ with respect to point $C _{i}$, represented in Fig. 3, is given by

$$ \mathbf{d}^{C} = \mathbf{d} + \mathbf{A}_{ j} \mathbf{A}_{\mathit{bearing}2 j}\mathbf{s}_{j}^{\prime\prime\,C} - \mathbf{A}_{ i}\mathbf{A}_{\mathit{journal}2 i}\mathbf{s}_{i}^{\prime\prime\,C} $$

(32)

where the transformation matrices from bearing to body $j$ frame and from journal to body $i$ frame are given by $\mathbf{A}_{\mathit{bearing}2 j} = [ \mathbf{h}'_{j} \ \ \mathbf{t}'_{j} \ \ \mathbf{b}'_{j} ]$ and $\mathbf{A}_{\mathit{journal}2 i} = [ \mathbf{h}'_{i} \ \ \mathbf{t}'_{i} \ \ \mathbf{b}'_{i} ]$, respectively. Vector $\mathbf{d}_{i}^{\prime\,C}$ is now expressed, in the journal coordinate system, as:

$$ \mathbf{d}_{i}^{\prime\prime\,C} = \mathbf{A}_{\mathit{bearing}2 i}^{T}\mathbf{A}_{i}^{T} \mathbf{d} + \mathbf{A}_{\mathit{bearing}2 i}^{T}\mathbf{A}_{i}^{T} \mathbf{A}_{ j}\mathbf{A}_{\mathit{journal}2 j}\mathbf{s}_{j}^{\prime\prime\,C} - \mathbf{s}_{i}^{\prime\prime\,C} $$

(33)

by observing Eq. (33) it is clear that the transformation from the journal frame to the bearing frame is given by $\mathbf{A}_{j2i} = \mathbf{A}_{\mathit{bearing}2 i}^{T}\mathbf{A}_{i}^{T}\mathbf{A}_{ j}\mathbf{A}_{\mathit{journal}2 j}$. Noticing that the same transformation is, alternatively, given by $\mathbf{A}_{ j2 i } = \mathbf{A} _{\mathit{ar}} \mathbf{A} _{\mathit{am}}$, Eq. (33) is re-written as

$$ \mathbf{d}_{i}^{\prime\prime\,C} = \mathbf{A}_{\mathit{bearing}2 i}^{T}\mathbf{A}_{i}^{T} \mathbf{d} + \mathbf{A}_{\mathit{\mathit{ar}}}\mathbf{A}_{\mathit{am}} \mathbf{s}_{j}^{\prime\prime\,C} - \mathbf{s}_{i}^{\prime\prime\,C} $$

(34)

The conditions for points $C _{j}$ and $C _{i}$ to be candidates to contact points require not only that the displacement between them is normal to the journal surface, but also that the journal normal vector in point $C _{i}$ is normal to the tangent vector in point $C _{j}$, written as [43]:

$$ \boldsymbol{\varPhi} \equiv \left \{ \textstyle\begin{array}{c} ( \mathbf{b}_{i}^{C} )^{T}\mathbf{d}_{i}^{C} \\ ( \mathbf{t}_{i}^{C} )^{T}\mathbf{d}_{i}^{C} \\ ( \mathbf{h}_{i}^{C} )^{T}\mathbf{t}_{j}^{C} \end{array}\displaystyle \right \} = \mathbf{0} $$

(35)

which is transformed to the journal coordinate system leading to

$$ \boldsymbol{\varPhi} \equiv \left \{ \textstyle\begin{array}{c} ( \mathbf{b}_{i}^{\prime\prime\,C} )^{T}\mathbf{d}_{i}^{\prime\prime\,C} \\ ( \mathbf{t}_{i}^{\prime\prime\,C} )^{T}\mathbf{d}_{i}^{\prime\prime\,C} \\ ( \mathbf{h}_{i}^{\prime\prime\,C} )^{T}\mathbf{t}_{ji}^{\prime\prime\,C} \end{array}\displaystyle \right \} = \mathbf{0} $$

(36)

where $\mathbf{t}_{ji}^{\prime\prime\,C} = \mathbf{A}_{\mathit{bearing}2 i}^{T}\mathbf{A}_{i}^{T}\mathbf{A}_{ j}\mathbf{A}_{\mathit{journal}2 j}\mathbf{t}_{j}^{\prime\prime\,C}$ or, using the sequence of two rotations between the bearing and journal frames, is given by $\mathbf{t}_{ji}^{\prime\prime\,C} = \mathbf{A}_{j2i}\mathbf{t}_{j}^{\prime\prime\,C}$. Equation (36) is a nonlinear system that must be solved for $\theta _{j}$, $\theta _{i}$ and $b _{i}$ in order to identify the candidates to contact points, as defined in Eqs. (25) and (26). The interference between the journal and bearing at these points is evaluated as

$$ \delta = \bigl( \mathbf{h}_{i}^{\prime\prime\,C} \bigr)^{T}\mathbf{d}_{i}^{\prime\prime\,C} $$

(37)

If $\delta >0$ there is contact, being $C _{j}$ and $C _{i}$ the contact points, the contact forces need to be calculated. Otherwise, there is no contact and no force penalization is applied in the clearance/bushing joint.

In the case of contact, the normal and tangential contact forces need to be applied on points $P _{i}$, of the journal, and $P _{j}$, of the bearing, so that the expressions for the body forces, given by Eq. (24), can be applied. The contact forces applied at point $C _{i}$, of the journal are written as:

$$ \mathbf{f}_{i}^{(\mathit{cyl})} = - f_{\mathit{normal}} \mathbf{h}_{i}^{C} + f_{\mathit{tangential}}^{t} \mathbf{t}_{i}^{C} + f_{\mathit{tangential}}^{b} \mathbf{b}_{i}^{C} $$

(38)

where the normal and tangential components of the contact force, $f _{\mathit{normal}}$, $f ^{t} _{\mathit{tangential}}$ and $f ^{b} _{\mathit{tangential}}$ are discussed in Sect. 2.4.2. The normal and tangential vectors of the journal cylindrical surfaces, in global coordinates, are defined as:

$$\begin{aligned} \begin{aligned} \mathbf{h}_{i}^{C} &=\mathbf{A}_{i}\mathbf{A}_{\mathit{bearing}2i}\mathbf{h}_{i}^{\prime\prime\,C} \\ \mathbf{t}_{i}^{C} &=\mathbf{A}_{i}\mathbf{A}_{\mathit{bearing}2i}\mathbf{t}_{i}^{\prime\prime\,C} \\ \mathbf{b}_{i}^{C} &=\mathbf{A}_{i}\mathbf{A}_{\mathit{bearing}2i}\mathbf{b}_{i}^{\prime\prime\,C} \end{aligned} \end{aligned}$$

(39)

The moment $\mathbf{n}_{i}^{\prime\,(\mathit{cyl})}$ applied in the journal body is the result, in the case of the cylindrical clearance/bushing joint proposed here, of the transport of the force from point $C _{i}$ to $P _{i}$, is:

$$ \mathbf{n}_{i}^{\prime\,(\mathit{cyl})} = {\tilde{\mathbf{s}}}_{i}^{\prime\,C}\mathbf{A}_{i}^{T} \mathbf{f}_{i}^{(\mathit{cyl})} $$

(40)

where $\mathbf{s}_{i}^{\prime\,C} = \mathbf{A}_{\mathit{bearing}2 i}\mathbf{s}_{i}^{\prime\prime\,C}$ is the vector of the position of point $C _{i}$ with respect to point $P _{i}$ in the coordinates of body $i$. Similarly, the bearing transport moment due to moving the point of application of force $\mathbf{f}_{j}^{(\mathit{cyl})}$ from point $C _{j}$ to $P _{j}$, is evaluated as

$$ \mathbf{n}_{j}^{\prime\,(\mathit{cyl})} = {\tilde{\mathbf{s}}}_{j}^{\prime\prime\,C}\mathbf{A}_{j}^{T} \mathbf{f}_{j}^{(\mathit{cyl})} $$

(41)

The contact search with the bearing must be done for the top circle of the bearing cylindrical surface, defined by Eq. (26) when $b _{j} = l _{j}/2$, and, at least, also for the lower circle in the same surface. In general, it is better that the complete bearing cylindrical surface is discretized by a finite number of contact patches, as seen in Fig. 4. The discretization of the surface in this form easily accommodates surfaces of revolution for the bearing that are not necessarily cylindrical. Let each of the $N$ contact patch of the bearing cylindrical surface, with a length of $l _{j}$/$N$, be represented by its mid-circle. The bearing cylindrical surface is discretized by $N$ circles, defined by

$$ \mathbf{s}_{k,j}^{\prime\prime\,C} = \left \{ \textstyle\begin{array}{c} R_{j}\cos \theta_{j} \\ R_{j}\sin \theta_{j} \\ ( \frac{N - 2k + 1}{2} )\frac{l_{j}}{N} \end{array}\displaystyle \right \},\quad k = 1, \ldots,N $$

(42)

Then the contact search problem is solved for each one of the circles, using Eqs. (25) through (41), playing $\mathbf{s}_{k,j}^{\prime\prime\,C}$ in Eq. (42) the role of $\mathbf{s}_{j}^{\prime\prime\,C}$ in Eq. (26). The sum of all contributions of all patches are accounted for in the vector of the bodies forces by using Eqs. (38) through (41). Note that the constitutive force model must take it into account the discretization in contact patches.

Fig. 4

Discretization of the surface of the bearing and its contact with the cylindrical surface of the journal

2.4.2 Clearance/bushing constitutive force models

The penalization forces for the clearance/bushing joints, defined by Eqs. (20) through (24) require that proper constitutive relations for the continuous contact force models are used. Here, the contact detection problem is solved independently for each strip of the bearing, illustrated in Fig. 4. It is shown by Pereira et al. [41] that in the internal cylindrical contact the Hertz elastic contact theory can still be applied. Therefore, any of the cylindrical contact force models overviewed by Pereira et al. [39] can be applied to the problem in hand, within the limitation inherent to each one of the models, identified in the referenced work.

In general, the penalization of displacements, or moments, is described by a force-displacement relation as that depicted in Fig. 5(a). A known model, for spherical clearance joints, is the contact force model proposed by Lankarani and Nikravesh [28], suitable for low impact velocities in which local plasticity effects do not develop or are negligible, is given by

$$ f_{\mathit{normal}} = \left \{ \textstyle\begin{array}{l@{\quad }l} 0 & \delta \le 0 \\ f^{(c)} ( \delta,\dot{\delta} ) = \frac{4E^{*}}{3N} ( \frac{R_{j}R_{i}}{\boldsymbol{\Delta} R} )^{1 / 2}\delta^{n} [ 1 + \frac{3(1 - c_{e}^{2})}{4}\frac{\dot{\delta}}{\dot{\delta}^{{( - )}}} ] & \delta > 0 \end{array}\displaystyle \right . $$

(43)

where $\delta$ is evaluated using Eq. (37) and include $E^{*} = E / 2 ( 1 - \nu^{2} )$, which is the composite modulus, assuming materials with similar elastic modulus, $E$, and Poisson coefficients, $\upsilon$, and $\Delta R=R _{j}-R _{i}$, is the radial clearance between the two contacting bodies, the pseudo-penetration exponent $n$ and the restitution coefficient $c_{e}$ dependent on the geometry and material of the contacting surfaces. $\dot{\delta}$ is the velocity of indentation and $\dot{\delta}^{{( - )}}$ is the velocity of indentation at the initial instant of contact. Note that in Eq. (43) the number of cylindrical stripes that discretize the journal is $N$, shown in Fig. 4.

Fig. 5

Representation of force-displacement constitutive relations for: (a) Clearance with free-flight displacement $\delta _{c}$; (b) Bushing with maximum compression of $\delta _{b}$; (c) Clearance with a free-flight displacement, a bushing compression and ‘hard’ material deformation

The Lankarani and Nikravesh contact force model (1994) provides a representation of the damping coefficient present in the Hunt–Crossley model as hysteresis damping, which in turn is related to the material properties and coefficient of restitution, leading to Eq. (43). It must also be noted that ratio $\delta /\dot{\delta}^{{( - )}}$ leads to numerical problems for very small velocities of indentation at the start of contact, i.e., when $\dot{\delta}^{{( - )}} \approx 0$. In the computational implementation of the Lankarani and Nikravesh model, or any other that has the dissipative part written in the same form, the ratio $\delta /\dot{\delta}^{{( - )}} = 1$ anytime the penetration velocity $\dot{\delta}$ exceeds $\dot{\delta}^{{( - )}}$ or when $\dot{\delta}^{{( - )}} \approx 0$.

Of practical interest to the modeling of the forces in cylindrical and revolute clearance joints are the cylindrical contact force models. After a critical overview of the most commonly used cylindrical contact models Pereira et al. [39] concluded that all of them have serious limitations on their range of application. As a result of this study, Pereira et al. [41] proposed an enhanced cylindrical contact model suitable for the type of geometries and materials more commonly encountered in clearance joints. The cylindrical contact force model is

$$ f_{\mathit{normal}} = \frac{ ( a \boldsymbol{\Delta} R + b ) L E^{{*}}}{N \boldsymbol{\Delta} R}\delta^{n} \biggl[ 1 + \frac{3(1 - c_{e}^{2})}{4}\frac{\dot{\delta}}{\dot{\delta}^{{( - )}}} \biggr] $$

(44)

in which

$$\begin{aligned} a =& \left \{ \textstyle\begin{array}{l@{\quad }l} 0.965 & \mbox{for internal contact} \\ 0.39 & \mbox{for external contact} \end{array}\displaystyle \right . \end{aligned}$$

(45)

$$\begin{aligned} b =& \left \{ \textstyle\begin{array}{l@{\quad }l} 0.0965 & \mbox{for internal contact} \\ 0.85 & \mbox{for external contact} \end{array}\displaystyle \right . \end{aligned}$$

(46)

$$\begin{aligned} n =& \left \{ \textstyle\begin{array}{l@{\quad }l} Y\Delta R^{ - 0.005} & \mbox{for internal contact} \\ 1.094 & \mbox{for external contact} \end{array}\displaystyle \right . \end{aligned}$$

(47)

$$\begin{aligned} Y =& \left \{ \textstyle\begin{array}{l@{\quad }l} 1.51 [ \ln ( 1000 \Delta R ) ]^{ - 0.151} & \mbox{if } \Delta R \in [0.005, 0.34954[~\mbox{mm} \\ 0.0151 \Delta R + 1.151 & \mbox{if } \Delta R \in [0.34954, 10.0[~\mbox{mm} \end{array}\displaystyle \right . \end{aligned}$$

(48)

For internal contact $\Delta R=R _{j}-R _{i}$ and for external contact $\Delta R=R _{j}+R _{i}$. The remaining quantities in Eq. (44) are similar to those used in the Lankarani and Nikravesh model.

Note that the relative displacement refers, in this section, in generic terms to the axial or radial displacements present in Eqs. (20) and (22), i.e., $\delta = \delta _{n}$ or $\delta = \delta _{t}$, respectively, or to the radial and axial displacements in Eqs. (13), (15) or (37). The same type of penalization constitutive relation can be used for the angular misalignment or rotation appearing in Eqs. (17) or (19), for which $\delta = \theta _{\mathit{am}}$ and $\delta =\alpha_{\mathit{ar}}$, respectively, provided that proper penalization parameters are identified.

For bushing joints several models are available in the literature [3, 29, 38]. The common approach is to penalize the relative displacement between two bodies by a constitutive force relation that reflects the material response of the deformable media, such as that shown in Fig. 5(b). The constitutive relations, obtained by experimental testing, detailed finite element analysis, such as those proposed by Ambrosio and Verissimo [3] or analytical approaches, are written in the form

$$ f_{\mathit{normal}} = f^{(b)} ( \delta,\dot{\delta} ) = f ( \delta ) + b \dot{\delta} $$

(49)

where $f ( \delta )$ is the radial stiffness and $b$ is the damping characteristics of the bushing. Depending on the material properties, including its strain-rate sensitiveness, and geometry the relation expressed by Eq. (49) may be a nonlinear function of both relative displacement and relative velocity.

Assume that a bushing element can only be compressed until a point after which it either breaks or becomes excessively rigid. Afterwards, the relation between the force and the displacement becomes similar to that of the dry contact model, expressed by Eq. (44), for cylindrical contact. A unified formulation for joints with clearances and bushings is expressed by allowing an initial clearance on the joint, followed by a bushing loading relation that is maintained until a maximum compression, after which dry contact starts. In order to have a smooth numerical transition between the constitutive relations either a weighted sum [16] or an exponential blending function [48] can be used, over a preset range. Using a weighted sum blending function, the general constitutive relation for the clearance/bushing penalization forces is

$$ f_{\mathit{normal}} = \left \{ \textstyle\begin{array}{l@{\quad }l} 0 & \delta \le \delta_{c} \\ f^{(b)} ( \delta_{1},\dot{\delta} ) & \delta_{c} < \delta \le \delta_{b} \\ \frac{(\delta_{b} + \varepsilon ) - \delta}{\varepsilon} f^{(b)} ( \delta_{1},\dot{\delta} ) + \frac{\delta - \delta_{b}}{\varepsilon} f^{(c)} ( \delta_{2},\dot{\delta} ) & \delta_{b} < \delta < \delta_{b} + \varepsilon \\ f^{(c)} ( \delta_{2},\dot{\delta} ) & \delta \ge \delta_{b} + \varepsilon \end{array}\displaystyle \right . $$

(50)

in which $\delta_{1} = \delta - \delta_{c}$ and $\delta_{2} = \delta - \delta_{b}$, being the free-flight displacement $\delta _{c}$, and the maximum bushing compression $\delta _{b}$, shown in Fig. 5. Functions $f^{(b)} ( \delta_{1},\dot{\delta} )$, representing the bushing normal force, and $f^{(c)} ( \delta_{2},\dot{\delta} )$, representing the ‘hard’ material contact force due to a pure clearance joint, which appear in Eq. (50) are defined in Eqs. (49) and (43), or (44), respectively. The blending displacement $\epsilon$ is a small number define by the user, for instance $\epsilon = 0.01 \delta _{b}$. The relative velocity between the two bodies connected by the joint, referred to in Eqs. (43) through (50), is given in references [3, 16] for the different displacement/rotation penalizations.

Although the modeling of friction forces in the clearance/bushing joints is not explicitly described in this example, they can be included in the force contact model in the same way they are in any contact application using a formulation with the nature of that presented in this work. After evaluating the location of the contact points, the component of the relative velocity between the contacting points along the tangent plane to the contacting surfaces is easily obtained by subtracting the normal component of the relative velocity from the total relative velocity. Then any selected friction force model can be applied [34], being the friction force calculated in this form added to bodies force vectors $\mathbf{g} _{i}$ and $\mathbf{g} _{j}$, depicted by Eq. (24).

2.5 Joint motion limits

Translation and cylindrical joints are, often, subject to limits on the relative translation motion between the two bodies, such as that pictured in Fig. 6(a). Revolute joints can also have a limited range for the relative rotation between its two bodies, as the joint exemplified in Fig. 6(b). The definition of the joint motion limits, for perfect kinematic joints or for clearance/bushing joints, can now be handled as a penalization on the joint motion to which limits are defined.

Fig. 6

Kinematic joints with limits in their range of motion: (a) cylindrical joint with limits on its translation displacement; (b) revolute joint with limits on its rotation range

The penalization is achieved by including in the force vector of the bodies that share the joint the appropriate force relation, i.e., one of the relations defined by Eqs. (20) through (23). For instance, a perfect kinematic translation joint, with limits in the translation degree-of-freedom, includes the following contributions to the system constraint equations and force vector:

$$ \textstyle\begin{array}{l@{\quad }l} \mbox{in constraint equations:} & \boldsymbol{\varPhi}^{(t,5)} = \mathbf{0} \\ \mbox{in force vector:} & \left \{ \textstyle\begin{array}{l} \mathbf{f}_{i} = \mathbf{f}_{i}^{(\mathit{ad})} \\ \mathbf{f}_{j} = - \mathbf{f}_{i}^{(\mathit{ad})} \\ \mathbf{n}'_{i} = \mathbf{A}_{i}^{T}{\tilde{\mathbf{s}}}_{i}^{P}\mathbf{f}_{i} \\ \mathbf{n}'_{j} = \mathbf{A}_{j}^{T}{\tilde{\mathbf{s}}}_{j}^{P}\mathbf{f}_{j} \end{array}\displaystyle \right . \end{array} $$

(51)

in which the range of motion is defined in Fig. 6(a) as $\delta _{c}$. For a revolute joint with limits on its rotation degree of freedom, as that shown in Fig. 6(b), the contributions for the constraint equations and force vector are

$$ \textstyle\begin{array}{l@{\quad }l} \mbox{in constraint equations:} & \boldsymbol{\varPhi}^{(r,5)} = \mathbf{0} \\ \mbox{in force vector:} & \left \{ \textstyle\begin{array}{l} \mathbf{f}_{i} = \mathbf{0} \\ \mathbf{f}_{j} = \mathbf{0} \\ \mathbf{n}'_{i} = \mathbf{n}_{i}^{\prime\,(\mathit{ar})} \\ \mathbf{n}'_{j} = - \mathbf{A}_{j}^{T} \mathbf{A}_{i} \mathbf{n}_{i}^{\prime\,(\mathit{ar})} \end{array}\displaystyle \right . \end{array} $$

(52)

where the range of motion is defined in Fig. 6(b) as $\theta _{c}=\theta _{c1}+ \theta _{c2}$. For a cylindrical joint with limits on translation and rotation d.o.f. the contributions to the constraint equations and force vector are

$$ \textstyle\begin{array}{l@{\quad }l} \mbox{in constraint equations:} & \boldsymbol{\varPhi}^{(c,4)} = \mathbf{0} \\ \mbox{in force vector:} & \left \{ \textstyle\begin{array}{l} \mathbf{f}_{i} = \mathbf{f}_{i}^{(\mathit{ad})} \\ \mathbf{f}_{j} = - \mathbf{f}_{i} \\ \mathbf{n}'_{i} = \mathbf{A}_{i}^{T}{\tilde{\mathbf{s}}}_{i}^{P}\mathbf{f}_{i}^{(\mathit{ad})} + \mathbf{n} _{i}^{\prime\,(\mathit{ar})} \\ \mathbf{n}'_{j} = - \mathbf{A}_{j}^{T}{\tilde{\mathbf{s}}}_{j}^{P}\mathbf{f}_{i}^{(\mathit{ad})} - \mathbf{A}_{j}^{T}\mathbf{A}_{i}\mathbf{n}_{i}^{\prime\,(\mathit{ar})} \end{array}\displaystyle \right . \end{array} $$

(53)

When the joint motion limits are hard stops the penalization of the relative motion is defined only with the clearance part of the constitutive relation defined by Eq. (50), i.e., by defining $\delta _{b}= \delta _{c}$ and $\epsilon =0$. When the joint limits are defined with soft stops, such as the bounce stops in the vehicle suspensions, all terms in Eqs. (49) through (53) must be defined according to their physical characteristics.

3 Demonstrative applications

3.1 3D slider–crank mechanism

Consider the 3D rigid slider–crank mechanism depicted in Fig. 7, part of the library of multibody benchmark problems [35]. The mechanism consists of a crank AB of length 0.08 m, a connecting rod BC of length 0.3 m, and a sliding block DE. The crank, connected to the ground by revolute joint A, is driven from initial position $\theta = 0$ rad with initial angular speed of 6 rad/s. There is a spherical joint at B and a universal joint at C. The block is constrained to the ground by a translation joint DE, allowing only its sliding displacement. All joints are frictionless.

Fig. 7

3D slider–crank mechanism

Three rigid bodies, plus the ground, are used to represent the 3D slider crank. A local reference frame ($\xi$, $\eta$, $\zeta$) is rigidly attached to the center of mass of each body in such a way that the axes are aligned with the principal inertia directions of the bodies. In this way, the inertial tensor of the bodies is completely defined by the inertia moments $I _{\xi \xi}$, $I _{\eta \eta}$ and $I _{\zeta \zeta}$. The mass and the inertia properties of each body are defined in Table 1. The first column of the table lists the reference numbers that identify the bodies in the model shown in Fig. 7.

Table 1 Mass and moments of inertia of rigid bodies of the slider crank

The Cartesian coordinates and Euler parameters, which define, respectively, the initial position of the center of mass and the orientation of the local frame of each body with respect to the global reference frame ($x$, $y$, $z$), are defined in Table 2 according to the benchmark problem specifications [35]. Also the initial Cartesian velocities, with respect to the global frame, and the angular velocities, defined with respect to the local reference frames ($\xi$, $\eta$, $\zeta$) are specified in Table 2.

Table 2 Initial position and velocity of rigid bodies of the slider crank

Five scenarios are considered here to demonstrate the methodology presented in this work. First, the dynamic behavior of the 3D slider crank is analyzed considering all its joints as perfect, i.e., considering the classical kinematic formulation [37]. The second and third scenarios consider that the mechanism has an imperfect spherical joint and an imperfect revolute joint, respectively, with clearances of 0, $10^{-3}$, $10^{-1}$ and 1 mm. Notice that when the joints have clearances of 0 mm, it means that, although these are perfect joints, as there are no gaps between the ball/journal and the socket/bearing, they are still modeled as clearance/bushing joints. In all cases the clearance sizes refer to radial direction, for the spherical joints, and to axial and radial displacements, for the revolute joints.

The contact force model with hysteresis damping proposed by Lankarani and Nikravesh [28], in Eq. (43), is considered for the imperfect spherical kinematic joints while the cylindrical contact model, in Eq. (44), is used for the revolute joints. It is assumed a stiffness coefficient $K = 5.0\times 10^{6}~\mbox{N}/\mbox{m}$, an exponent of the Hertz contact force model $n = 1.5$ and a restitution coefficient $e = 0.75$. The MUltiBOdy Dynamic analysis program MUBODyn [5] is used to perform the dynamic analyses of the scenarios described here. The differential and algebraic equations of motion are numerically integrated with the Gear multistep integration algorithm [21] and a sparse matrix solver [13] is used for the system of linear equations. The time-stepping physical control procedure proposed by Flores and Ambrosio [17] is applied to detect the start of contact. The dynamic analyses are carried out for 5 s simulation time.

The time histories of the slider block position and crank angle, for all scenarios with null or small spherical clearances, are presented in Figs. 8 and 9, respectively. The results show that, for the perfect kinematic joints, the amplitude of the slider motion is constant, as there is no friction or energy dissipation in the joints due to the contact, being the results coincident with those of the benchmark [35]. When the clearance in the spherical joint starts to increase it is observed that not only the slider position but also the crank angle start to have some delay with respect to that of the benchmark in virtue of the energy dissipation that occurs in the clearance and bushing joints. For longer simulations the energy dissipated eventually leads to a point in which the crank is unable to complete a rotation and starts to work as a pendulum.

Fig. 8

Slider position of the slider–crank model with spherical clearance joint for: (a) null or small clearances; (b) large clearances

Fig. 9

Crank angle of the slider–crank model with spherical clearance joint for: (a) null or small clearances; (b) larger clearances

The joint reaction forces observed in the spherical joint, along X, are displayed in Fig. 10 for the cases with perfect kinematic joints and clearance joints. It is observed that large peaks in the force develop at the instants that the slider reaches its end of range, or end of the stroke, and inverts the direction of the motion. For perfect spherical joints modeled either as spherical kinematic constraints or as imperfect joints with null clearance the response is rather smooth, i.e., no oscillations in the reaction force are observed. However, when the clearance increases the joint reaction force exhibits oscillations during the slider mid-stroke, being the amplitude of the force oscillations higher as the clearance increases.

Fig. 10

Joint reaction force in the spherical joint (X component) for: (a) null or small clearances; (b) larger clearances

Selected results for the slider–crank models with a clearance revolute joint are presented in Fig. 11 through Fig. 13. The results, depicted in Fig. 11(a) show that, as the clearance in the revolute joint starts to increase, the time at which the slider reaches its end of stroke is increasingly delayed. For a clearance of 1 mm it is observed, in Fig. 11(b), that the crank angle is unable to develop more than two revolutions, after which the crank starts to oscillate about its static equilibrium position. The effect of the energy dissipation due to the inclusion of the non-elastic restitution parameter in the contact force model is visible when comparing the responses of the models with a null clearance revolute joint with and without damping. It is visible in Fig. 11(a) and (b) that just the existence of the damping favors that the slider oscillation experiences an increasing delay reaching its end of stroke.

Fig. 11

Slider–crank model with revolute clearance joint: (a) slider position; (b) crank angle

The joint reaction forces observed in the revolute joint, along X and Z, are displayed in Fig. 12 for the cases with perfect kinematic joints and revolute clearance joints. Just as for the cases in which the models considered the spherical clearance joints, for the models with perfect revolute joints modeled either as revolute kinematic constraints or as imperfect joints with null clearance no oscillations in the reaction force are observed. However, when the clearance increases the joint reaction force exhibits oscillations, mostly during the slider mid-stroke, being the amplitude of the force oscillations higher as the clearance increases.

Fig. 12

Joint reaction force for the revolute joint slider–crank models with perfect and with clearance revolute joint: (a) force component X; (b) force component Z

It is interesting to observe the effect of the damping, due to the use of non-elastic restitution parameters in the contact force models, on the joint reaction forces. The joint reaction forces in the revolute joint, along X and Z, are displayed in Fig. 13 for the model with a null clearance of the revolute joint. It is clear that, if no damping is considered, the oscillations in the contact force develop mostly as a result of the slider reaching its end of stroke, which enhances the impact of the journal and bearing, leads to alternate periods of relative free-flight motion and contact following motions.

Fig. 13

Joint reaction force for the revolute joint slider–crank models with perfect and with clearance revolute joint with and without damping in the contact model: (a) force component X; (b) force component Z

The presence of hysteresis damping in the normal contact model of the clearance joint eliminates the oscillations of the joint reaction forces observed in Fig. 13. It has been observed in some cases that the friction forces, when present, also mitigate the oscillatory behavior observed in the contact joint [4]. The use of different numerical integrator schemes, with fixed or variable time steps or with internal damping can also mask, or emphasize, the observed oscillatory behavior. In any case, the clearance joint behavior for a null clearance can be expected to be similar to that of a perfect kinematic joint not only in terms of kinematic behavior, as observed on the displacements depicted by Figs. 8, 9 or 11, but also in terms of its kinetic response. Therefore, not only the source of the large amplitude oscillations but also the numerical methods used to handle the dynamics of the problem are worth being investigated in future work.

3.2 Triple pendulum with joint limits

Consider the triple-pendulum mechanism depicted in Fig. 14. Body 1, of length 0.6 m, is constrained to the ground by a revolute joint with a horizontal axis. Body 2 has also a length of 0.6 m and is linked to body 1 by the vertical cylindrical joint with limits on its translation displacement. Body 3, of length 0.3 m, is connected to body 2 by the revolute joint with limits on its rotation range, with an orientation of $45^{\circ}$ with respect to the Z axis. The bodies have no initial velocity being acted by gravitational forces only. All joints are frictionless.

Fig. 14

Triple pendulum with joint limits

The mass and the inertia properties of the bodies that compose the triple-pendulum mechanism are defined in Table 3. The reference numbers in the first column of the table identify the bodies in the model shown in Fig. 14. The Cartesian coordinates that define the initial position of the center of mass of each body are also defined in Table 3, together with the Euler parameters that express the orientation of the body-fixed frames ($\xi$, $\eta$, $\zeta$) with respect to the global reference frame ($x$, $y$, $z$).

Table 3 Mass, moments of inertia, and initial position and orientation of rigid bodies of the triple pendulum

Two scenarios are considered to demonstrate the joint motion limits methodology. Both consider all joints modelled by using kinematic constraints in which limits in the relative motion between the joined bodies are included. Limits of $\theta _{c1} = \theta _{c2} = 45^{\circ}$ are imposed on the rotation range of the revolute joint connecting bodies 2 and 3, as shown in Fig. 14. The triple pendulum has a revolute joints between bodies 0 and 1 and a cylindrical joint, between bodies 1 and 3 with relative translation limits $\delta _{c1} = \delta _{c2} = 0.25~\mbox{m}$, as represented in Fig. 14.

In the first scenario the penalization force is described by the Lankarani and Nikravesh model (1994) being $K=1.0\times 10^{5}$, $n=1.5$ and $e=0.75$ for the translational joint stops of the cylindrical joint and $K=1.0\times 10^{3}$ for the rotation joint stops. In the second scenario a modified Kelvin–Voigt viscoelastic contact model [16, 19] is used in both joint stops, formulated as,

$$ f_{\mathit{normal}} = \left \{ \textstyle\begin{array}{l@{\quad }l} K\delta c_{e} & \dot{\delta} \le 0 \\ K\delta [ c_{e} + ( 1 - c_{e} ) ( 3r^{2} - 2r^{3} ) ] & 0 < \dot{\delta} < v_{0} \\ K\delta & \dot{\delta} \ge v_{0} \end{array}\displaystyle \right . $$

(54)

with the ratio between the penetration velocity and the penetration velocity tolerance being $r = \dot{\delta} /v_{0}$. In this case the penalty stiffness $K$ is equal to that in the first scenario, the coefficient of restitution is $c _{e}=0.01$ and the penetration velocity tolerance is $v _{0} =0.1~\mbox{m}/\mbox{s}$. Note that the modified Kelvin–Voigt normal contact force model includes the penetration velocity tolerance to smooth the discontinuity in the contact force in the transition between compression and restitution.

The dynamic analyses are carried out for 4 s simulation time. Snapshots representative of the motion of the triple pendulum are depicted in Fig. 15.

Fig. 15

Kinematics of the triple pendulum, using the Lankarani and Nikravesh contact force model, with joint stops in key positions: (a) Sequence of snapshots; (b) Forward swing (1st); (c) Backward swing (1st)

The behavior of the joint stops and contact forces that develop are of interest to understand of the methodology proposed here. The time history of the relative translation between bodies 1 and 2, the corresponding joint stops contact forces, and the relative rotation between bodies 2 and 3, and respective joint stops moments, are depicted in Fig. 16, using the Lankarani and Nikravesh contact force, and in Fig. 17, using the Kelvin–Voigt contact force model.

Fig. 16

Relative translation between bodies 1 and 2, with the corresponding joint stops contact forces, relative orientation between bodies 2 and 3, with the joint stops moments, in which the joint limit forces/moments use the Lankarani and Nikravesh force model

Fig. 17

Relative translation between bodies 1 and 2, with corresponding joint stops contact forces, and relative orientation between bodies 2 and 3, with respective joint stops moments, in which the joint limit forces/moments use the Kelvin–Voigt force model

As expected the contact with the end stops in the pendulum model in which the Lankarani and Nikravesh contact force model is used have a lower energy dissipation and do not present any residual deformation. Therefore, the bodies rebound from contact when a joint stop is reached, eventually leading the joint displacement, or rotation, to be such that soon after the contact takes place with the joint stop in the other side of the joint.

When the Kelvin–Voigt contact model is used, with a residual restitution coefficient value, not only there is an appreciable energy dissipation during the contact but also there is a residual deformation, as seen in Fig. 17 in which the contact deformation in the cylindrical joint translation stops becomes permanent. For the rotation stops the same tendency for the permanent deformation during contact exists. It is only due to the gravitational acceleration that the body 3 tend to rotate with respect to body 2 bringing the joint out of contact with its end stops. It is also observed that while for the model in which the Lankarani and Nikravesh contact force is used the amplitude of the pendulum swing decreases slightly in each period, for the model using the Kelvin–Voigt contact force the amplitude of the pendulum swings decreases very quickly in each following period. Actually, for the scenario with the Kelvin–Voigt contact with null restitution coefficient the swing amplitude decreases there are no more contact events with any of the joint stops, remaining basically constant afterwards as no more energy dissipative events take place. This behavior is shown in Fig. 18 in which the angular velocity of body 1 is displayed together with the relative displacements and orientations of bodies connected with joints with joint stops.

Fig. 18

Response of the triple-pendulum model with the Kelvin–Voigt contact model, with a null restitution coefficient, for a long simulation: Angular velocity of body 1; Relative translation between bodies 1 and 2; Relative orientation between bodies 2 and 3

4 Conclusions

The work now presented proposes a common framework for the formulation of common kinematic joints and mechanical joints with clearances and/or bushings, with or without joint stops. This formulation is novel in the sense that it not only unifies the different vector quantities required for the formulation of the joints as kinematic constraints or as contact force elements but also because the input data for each type of approach is composed with a common set of topological information. This approach leads to the ability to have mixed descriptions of a joint in which some relative motions are prevented by kinematic constraints while others are penalized by contact force elements, as for instance in the case of the joint stops. The formulation is demonstrated by studying two mechanical systems, a spatial slider crank and a triple pendulum, that include some of the features that can be represented by the formulations proposed here. In the process of presenting the proposed formulation a new model for contact detection of the pairs of cylindrical clearance joints is developed.

The study of two demonstrative mechanisms allows verifying the use of clearance/bushing joints with extremely small clearances have a kinematic behavior very similar to that of the mechanisms modeled with perfect kinematic joints, as expected. The size of the clearances and their contact mechanics becomes determinant in the mechanism behavior for large clearance sizes but is almost unobservable for very small clearances, i.e., for clearances generally associated with precision machining tolerances. The energy dissipation, not existing in mechanisms with perfect kinematic joints, is represented in clearance/bushing joints via the contact force models used. Actually, joints with larger clearances and with contact models, even with contact models in which the energy dissipation is small, lead to a behavior of the mechanism in which the continued motion is not possible without external actions applied to the system, as shown in the case of the spatial slider crank demonstrates in which the crank is unable to continue having a complete 360° rotation after some revolutions. One of the aspects of the formulation of the clearance joints concerns the penalty factor for the contact force law which is of primary importance. When the contact stiffness is underestimated the differences in mechanical behavior between mechanisms with different clearance sizes becomes difficult to appraise. Therefore, it is recommended to use penalty factors that result from elastic contact theories, such as those based on Hertzian contact or obtained via experimental identification.

In the process of testing the new formulations proposed here no evidence that the computational time required for the simulations increase when clearance/bushing joints are used in the model instead of the perfect kinematic joints. In one hand the lower number of equations used to describe the constrained equations of motion, as the number of constraint equations decreases leads to lower computational times. On the other hand the contact models with less energy dissipation, used here, introduce higher frequency contents in the dynamic response that require a reduction on the variable time-step integrators, which lead to smaller time steps and higher computational costs, while the lack of constraint violations associated with these joints removes an important dynamic contribution to the increase of higher frequencies in the system dynamic response, thus removing this contributions for the decrease their time step in virtue of such violations. Future studies should be developed to clarify the relative computational efficiency of either of the modeling approaches, i.e., the use of kinematic perfect joints versus the use of clearance/bushing joints in the models of multibody systems.