Vector form intrinsic finite element method for planar multibody systems with multiple clearance joints

Abstract

A new computational methodology is presented for the dynamic analysis of multibody systems with multiple clearance joints by vector form intrinsic finite element method. A joint model is developed to simulate the motion of ideal and clearance joints for multibody systems. The dynamic behaviour of a four-bar mechanism with three clearance joints in continuous contact mode is analysed. The results show that the dynamic performance of the mechanism with three clearance joints in continuous contact mode is not similar to that with ideal joints and is fluctuating and affected by the clearance size of the joints and input crank speed.

1 Introduction

Many revolute joints with clearance exist in real mechanisms, and such joints are generally assumed to be perfect or ideal for general dynamic analysis. However, the clearance between the bearing and journal of the joint leads to collision; thus, the real mechanism with revolute clearance joints has a different dynamic response from the ideal mechanism.

In recent years, many researchers have conducted extensive work on the dynamic response of mechanisms with clearance joints. Khulief [1] reviewed different approaches for modelling the dynamics of impact in rigid multibody mechanical systems. Flores et al. [2] extensively investigated the kinematic and dynamic characteristics of multibody systems with clearance joints. Muvengei et al. [3] investigated the effects on the dynamic responses of a mechanical system by the location of the clearance, the clearance size and the operating speed. In addition to the rigid multibody mechanical systems, numerical and experimental studies of the partly compliant mechanism were carried out by Erkaya and Dogan [4] and Erkaya et al. [5]. The dynamic responses of some complex mechanisms were also investigated. Pereira et al. [6] carried out the dynamic simulation of roller chain drivers, and Tian et al. [7] studied the coupling dynamics of a geared multibody system. The clearance joints of the mechanism can lead to poor dynamic performance; therefore, time-dependent reliability of mechanisms [8], optimal dynamic design [9, 10] and bifurcation of mechanisms [11] were also investigated.

The contact force model plays a key role in simulation of dynamic response of multibody mechanical systems with clearance joints [12]. The extensively used contact force model was proposed by Lankarani and Nikravesh [13], which used a modified Hertz’ law to include energy dissipation in the form of internal damping. Pereira et al. [14, 15] discussed the shortcomings of the cylinder contact force models, and an enhanced cylindrical contact force model was proposed. These contact models are suitable for planar revolute clearance joints. For the spatial revolute joints with clearance, the model was presented [16–18]. Alves et al. [19] studied viscoelastic contact force models. For soft materials, Flores et al. [20] proposed a continuous contact force model in multibody dynamics. Lubricated revolute joints [21, 22] were also carried out on the dynamic response of multibody systems. An efficient computational method was investigated to deal with contact detection in multibody dynamics [23], and an approach to stabilizing the constraint violations in dynamic simulation was studied [24].

Multibody system dynamics is generally used to simulate the influence of the dynamic response of a mechanism with revolute clearance joints [25–27]. The modelling method of a revolute joint with clearance is different from that of the ideal joint in multibody system dynamics. The revolute joint with clearance is modelled by contact force, whereas the ideal revolute joint is modelled by kinematic constraint. All revolute joints with clearance should be modelled to efficiently reveal the real dynamic response of the mechanism with multiple clearance joints [28]. Given the increasing number of modelled clearance joints in the mechanism, the constrained multibody system gradually becomes an unconstrained or joint-force system [29]. Furthermore, due to the interaction between the clearance joints, the dynamic analysis becomes complex.

Most of the previous works considered only one clearance joint in mechanisms, some recent papers focus on the nonlinear dynamic analysis of a planar mechanism with two or three clearance joints [28–33]. A three-mode model has been proposed for a planar revolute clearance joint with a journal inside the bearing; the three modes are the free flight, impact and continuous contact modes [2, 4, 25, 31, 33]. Flores carried out a parametric study for quantifying the influence of the clearance size, input crank speed and number of clearance joints for the dynamic response of multibody systems with multiple clearance joints. The results showed that one clearance joint would always be in continuous contact mode in some parametric conditions [29, 33]. Muvengei et al. [28] discussed nine possible modes of the motion of a slide-crank mechanism with two clearance joints. They concluded that the motion mode in one revolute clearance joint determines the motion mode in the other clearance joint and affects the dynamic behaviour of the mechanism. Megahed and Haroun [30] also investigated nine possible modes of motion of a slide-crank mechanism with two clearance joints and concluded that the maximum impact force at joints occurs at the joint nearest to the input link. Their studies indicated that the dynamic performance of the mechanism is affected by the motion mode combinations of clearance joints.

Studies on a mechanism with multiple clearance joints have sought to predict and reduce the influence of the mechanism’s kinematic and dynamic performance caused by clearance joints and to explore the motion of the mechanism under ideal conditions. Under some conditions, the clearance joints are all in continuous contact mode in the mechanism. In fact, all parts of the ideal joint are in contact state. At this time, the physical contact state of the mechanism with multiple joints is similar to that of a mechanism with ideal joints, but the dynamic difference between the two states of the mechanisms is not widely concerned.

Ting et al. [34, 35] and Shih et al. [36] proposed the vector form intrinsic finite element (VFIFE) method, which is based on vector mechanics without invoking continuum governing equations. The structure is divided into particles, and the governing equations are the equation of the motion of the particles. The equation of motion for each particle is directly formulated by Newton’s law. The explicit time integration method and central difference integration are used to solve the equations without introducing matrix calculation. Therefore, VFIFE is an effective method of processing issues of large deformations and large displacements. The method can effectively handle the nonlinear statics of frame structures and obtain satisfactory results [37–40]. Wu et al. [41] analysed the planar motion of solids through the triangular solid element of VFIFE and demonstrated the capability and accuracy of the method. Liao [42] studied the motion analysis of a mechanism with joint clearance using the fragmentation method of VFIFE.

VFIFE method is the combination of Newtonian vector mechanics method and finite element theory. Natural coordinates method [43] uses points and unit vectors to describe solids, and nonlinear finite element method can deal with multibody dynamics [44]. VFIFE method may be similar to these method, but actually they are quite different.

Natural coordinates method has an important advantage in computational efficiency because of their simple modelling of rigid bodies [43, 45]. Natural coordinates method uses the Cartesian coordinates of three (or more) non-aligned points to define the position of a solid in the 3-D space. In other words, each element and its motion are defined by a set of points and unit vectors rigidly attached to it. VFIFE is a Newtonian vector mechanic method and uses a finite number of particles to define a rigid body. In addition, the natural coordinate formulations of the multibody system are differential algebraic equations (DAE), but the particles motion formulations obtained by using VFIFE are ordinary differential equations (ODE).

Ambrosio [44] and Ambrosio and Nikravesh [46] proposed a novel methodology for nonlinear finite element description of the flexible part of a multibody system, which can deal with structural systems experiencing geometric and material nonlinear deformations. Dynamic models of rigid–flexible multibody systems have been developed using Newton–Euler equations. Using lumped mass formulation and static condensation, the flexible body is described by a small number of generalised coordinates. VFIFE method can also use a lumped mass matrix. The difference with usage of the mass matrix is that the components of the mass matrix belong to the finite elements in nonlinear finite element method and the components of the mass matrix belong to the particles in VFIFE method. Moreover, to decouple the rigid body motion and deformation of the bodies of the system, the floating frame approach was adopted in nonlinear finite element method and the fictitious reversed rigid body motion method was employed in VFIFE method.

From the theory of VFIFE, the governing equation of a particle is the motion equation of the particle. The motion equation is actually a force equilibrium of the internal and external forces applied to the particle. In other words, the governing equation of particle motion is a force equation. The algebraic constraints of the structure are constant and are described by lumped mass and forces, including internal and external, in the motion equation of the particle. During the numerical simulation process, the internal and external forces of the particle are always updated with the particle motion, without involving algebraic constraints.

The primary objective of this work is to extend the VFIFE method into dynamic analysis of planar multibody systems with multiple clearance joints. A planar revolute joint is usually treated as one particle in the conventional VFIFE theory. The mass of the particle and the forces applied to the particle are lumped from the connecting elements. The force between the joint components cannot be calculated. A new motion model of the planar revolute joint is developed to simulate the motion of ideal and clearance joints in this study. The contact force of ideal and clearance joints is obtained, as well as the local deformation of clearance joint components. The joint model is easily introduced with the VFIFE method.

If the clearance joints are modelled using the new motion model of the VFIFE theory in a multibody system, the governing equations of the clearance joints are force equilibrium equations. With an increasing number of clearance joints in the mechanism, the number of force equilibrium equations also increases; however, this does not increase the difficulty of solving the equations. This characteristic makes VFIFE different from multibody system dynamics.

In this work, the VFIFE method is adopted to study the dynamics of planar multibody systems with multiple clearance joints, and a parameter study of a four-bar mechanism with three clearance joints in continuous contact mode. Section 2 briefly introduces using the VFIFE method in handling motion of the multibody system. Section 3 develops the joint model; the contact force of the ideal joint is derived by the same motion, whereas that of the clearance joint is simulated by an enhanced cylindrical contact force model [14] with friction [47]. To demonstrate and validate the proposed model, Sect. 4 verifies the journal moving within the bearing and a four-bar mechanism with one clearance joint by comparing it with the published model. Section 5 presents the simulation results of a four-bar mechanism with multiple clearance joints; the difference between the ideal state and all clearance joints in continuous contact mode state is studied. Section 6 presents the main conclusions of this study.

2 Motion analysis of planar multibody systems using the VFIFE method

A planar mechanism can be divided into multiple rigid bodies, and each body is represented by a finite number of particles with mass. The governing equation is the equation of motion of each particle, which is directly formulated by Newton’s law. The approach to calculating the motion of the mechanism consists of four parts: (a) discretization of the mechanism, (b) discretization of the particle path, (c) motion calculation of the mechanism by time integration and (d) evaluation of internal forces. For simplicity only a brief summary of the fundamental theory is provided. The theory and some numerical examples of the VFIFE approach have been well documented in the references [34, 36–39, 41].

2.1 Discretization of mechanism

The analysed mechanism is represented by some rigid frames. A frame can be divided into some particles and elements, as shown in Fig. 1. Each particle has mass, whereas the element does not have mass. The element has two nodes, and each node has two translations and one rotation of freedom. Each element is defined by nodal displacements and equivalent nodal force. The equivalent internal nodal forces are induced by element deformation. The internal and external nodal forces of one element apply to the particles connected with the element. Each node displacement is caused by particle motion. The particle motion can be calculated by Newton’s law.

Fig. 1

Discretization of a frame

2.2 Discretization of particle path

A basic assumption exists about the path of particle motion. The arbitrary particle analysis period $t_0 \le t\le t_f$ can be split into discrete time segments, $t_0<t_1<t_2<\cdots<t_a<t_b<\cdots<t_n<\cdots <t_f$, as shown in Fig. 2. (1) Each discrete time segment is named a path unit, such as $t_a \le t\le t_b$. The configuration at time $t_a$ is the reference configuration for the element stress calculation. (2) The deformation in path unit $t_a \le t\le t_b$ is infinitesimal; thus, infinitesimal strain and engineering stress are adopted [41].

Fig. 2

Discretization of a particle path

Fig. 3

Forces on a particle

2.3 Motion calculation of planar mechanism by time integration

Considering all the forces on a specific particle with mass m at time t, as illustrated in Fig. 3, the equation of motion for the particle can be derived via Newton’s second law:

$$\begin{aligned} \left[ {{\begin{array}{ccc} m&{} 0&{} 0 \\ 0&{} m&{} 0 \\ 0&{} 0&{} I \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\ddot{d}_x } \\ {\ddot{d}_y } \\ {\ddot{\theta }_z } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {F_x } \\ {F_y } \\ {Q_z } \\ \end{array} }} \right\} -\sum _{i=1}^{nc} {\left\{ {{\begin{array}{c} {f_{ix} } \\ {f_{iy} } \\ {m_{iz} } \\ \end{array} }} \right\} \quad } t_a \le t\le t_b \end{aligned}$$

(1a)

or via the following simplified equation:

$$\begin{aligned} m{\ddot{\mathbf{d}}}=\mathbf{F}-\sum \mathbf{f} \quad t_a \le t\le t_b \end{aligned}$$

(1b)

where $\mathbf{d}$ is the particle displacement vector on plane (x, y), $\mathbf{F}$ is the external force vector on the particle, $\mathbf{f}$ is the equivalent internal nodal force vector on the node due to the deformations in the elements, derivation outlined below, and nc is the number of elements connected with particle. m and I are defined as follows:

$$\begin{aligned} m= & {} m_\alpha +\sum _{i=1}^{nc} {\frac{1}{2}\rho _i l_i } \nonumber \\ I= & {} I_\alpha +\sum _{i=1}^{nc} {\frac{1}{2}m_i r_i^2 } \end{aligned}$$

(2)

where $m_\alpha$ and $I_\alpha$ are the mass and moment inertia of the mass attached to particle $\alpha$, respectively, $\rho$ is the mass per unit length, l is the length of element and r is the radius of the gyration of the cross section at the node connected to particle $\alpha$.

The explicit time integration method and central difference integration are used to solve Eq. (1). The acceleration and velocity of each particle can be approximated as follows:

$$\begin{aligned} ({\ddot{\mathbf{d}}}_n )_\alpha= & {} \frac{1}{(\Delta t)^{2}}(\mathbf{d}_{n+1} -2\mathbf{d}_n +\mathbf{d}_{n-1} )_\alpha \end{aligned}$$

(3)

$$\begin{aligned} ({\dot{\mathbf{d}}}_n )_\alpha= & {} \frac{1}{2(\Delta t)}(\mathbf{d}_{n+1} -\mathbf{d}_{n-1} )_\alpha \end{aligned}$$

(4)

where $\Delta t$ is the time increment. Substituting Eq. (3) into Eq. (1b), the displacement of each particle can be written as follows:

$$\begin{aligned} (\mathbf{d}_{n+1} )_\alpha =\frac{(\Delta t)^{2}}{m_\alpha }\left( \mathbf{F}-\sum \mathbf{f}\right) _\alpha +(2\mathbf{d}_n -\mathbf{d}_{n-1} )_\alpha \end{aligned}$$

(5)

Hence, the displacement, velocity and acceleration of each particle are calculated after the motion is completed for the time increment.

2.4 Evaluation of internal forces

The initial conditions for each particle are known and used to solve Eqs. (3)–(5). In addition, external and internal nodal forces are required. The external forces of each node in a path unit can be either physical forces or equivalent force according to the principle of virtual work. The equivalent internal forces of each node in a path unit are derived using the fictitious reversed rigid body motion.

Fig. 4

Nodal displacement of a two-node plane frame element

A plane frame element with nodal numbers (1, 2) at different times is shown in Fig. 4. The position of the two nodes is $(1_{0},2_{0})$ at initial time $t_0 , (1_{\mathrm{a}},2_{\mathrm{a}})$ at time $t_a$ and (1, 2) at current time t. Within a path unit, $t_a \le t\le t_b$, the displacement increment vector of nodes $\Delta \mathbf{u}_i$ is calculated with a reference coordinate at time $t_a$, as illustrated in Fig. 4:

$$\begin{aligned} \Delta \mathbf{u}_i =\mathbf{u}_i -\mathbf{u}_{ia} \quad i=1,2 \end{aligned}$$

(6)

To decouple the rigid body motion and deformation for each displacement increment, a fictitious reversed rigid body motion, including translation and rotation, is adopted. The element (1, 2) at current time t first translates a displacement vector $-\Delta \mathbf{u}_1$ and then rotates an angle $-\Delta \varphi$ to the direction of element $(1_{\mathrm{a}},2_{\mathrm{a}})$ at time $t_a$, as shown in Fig. 5. The deformation of vector $\Delta \mathbf{d}$ in each displacement increment can be obtained as follows:

$$\begin{aligned} \Delta \mathbf{d}=\Delta \mathbf{u}-\Delta \mathbf{u}^{r} \end{aligned}$$

(7)

where $\Delta \mathbf{u}$ is the total displacement increment vector and $\Delta \mathbf{u}^{r}$ is the displacement increment vector induced by rigid body motion [37].

Fig. 5

Fictitious reversed rigid body motion of an element

Three independent variables of deformation exist for a planar frame element,

$$\begin{aligned} \Delta \mathbf{d}=[\Delta _e \;\theta _1 \;\theta _2 ]^{T} \end{aligned}$$

(8)

where $\Delta _e$ is the axial deformation increment and $\theta _1$ and $\theta _2$ are the deformation of the nodal rotations.

The virtual internal energy increment of the planar frame element induced by the element stresses and virtual deformations is equivalent to that induced by the nodal internal forces and virtual deformations. Therefore, the incremental nodal force vector is calculated as

$$\begin{aligned} \Delta \mathbf{f}^{*}=\left\{ {{\begin{array}{c} {\Delta f_{2x} } \\ {\Delta m_{1z} } \\ {\Delta m_{2z} } \\ \end{array} }} \right\} \end{aligned}$$

(9)

According to the material frame of the element at time $t_a$, the total internal nodal force vector at time t can be written as

$$\begin{aligned} \mathbf{f}^{*}=\left\{ {{\begin{array}{c} {f_{2x} } \\ {m_{1z} } \\ {m_{2z} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {f_{a2x} +\Delta f_{2x} } \\ {m_{a1z} +\Delta m_{1z} } \\ {m_{a2z} +\Delta m_{2z} } \\ \end{array} }} \right\} \end{aligned}$$

(10)

From the force equilibrium conditions of the element, the other three nodal forces can be obtained as follows:

$$\begin{aligned}&\sum {F_x=0} \quad f_{1x} =-f_{2x} \nonumber \\&\sum {M_1 =0\quad f_{2y} =-(m_{1z} +m_{2z} )/l_a } \nonumber \\&\sum {F_y=0} \quad f_{1y} =-f_{2y} \end{aligned}$$

(11)

The total internal nodal force vector referred to the reference coordinate is

$$\begin{aligned} \mathbf{f}_r ^{\mathrm{int}}=\left\{ {f_{1x} \;f_{1y} \;m_{1z} \;f_{2x} \;f_{2y} \;m_{2z} } \right\} ^{T} \end{aligned}$$

(12a)

In initial condition, $\mathbf{f}_r^{\mathrm{int}}$ can be written as [34]

$$\begin{aligned} \mathbf{f}_r^{\mathrm{int}} =\left\{ {{\begin{array}{c} {f_{1x} } \\ {f_{1y} } \\ {m_{1z} } \\ {f_{2x} } \\ {f_{2y} } \\ {m_{2z} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {-(AE/l)\Delta _e } \\ {(6EI/l^{2})(\theta _1 +\theta _2 )} \\ {(2EI/l)(2\theta _1 +\theta _2 )} \\ {(AE/l)\Delta _e } \\ {-(6EI/l^{2})(\theta _1 +\theta _2 )} \\ {(2EI/l)(\theta _1 +2\theta _2 )} \\ \end{array} }} \right\} \end{aligned}$$

(12b)

If node 1 can rotate freely, such as a revolute joint, then the internal force component $m_{1z} =0$. If nodes 1 and 2 can rotate freely under the special condition, the components of internal force $m_{1z} =0$ and $m_{2z} =0$. In this case, the element is very similar to the bar element of finite element method and it can be used to simulate the rigid bar.

Fig. 6

Motion model of the planar revolute joints. a Physical models of ideal and clearance joints. b Ideal and clearance joints model with elements. c Force equilibrium of the joints

Finally, the element is subjected to a forward motion, including a translation $\Delta \mathbf{u}_1$ and a rotation $\Delta \varphi$. The total global internal nodal force vector $\mathbf{f}^{\mathrm{int}}$ is obtained as follows:

$$\begin{aligned} \mathbf{f}^{\mathrm{int}}=\mathbf{T}^{T}{} \mathbf{f}_r^{\mathrm{int}} \end{aligned}$$

(13)

where $\mathbf{T}^{T}$ is the transformation matrix between the global coordinate and the reference coordinate.

The VFIFE method uses finite element theory, an independent solution method can be obtained for the motion equations of the particles, and this is not the same as traditional finite element method. The use of a central difference time integrator has a standard solving efficiency in this study. The solution methods of traditional finite element method and dynamics of multibody systems are plentiful and have highly solving efficiency.

3 Motion model of a planar revolute joint

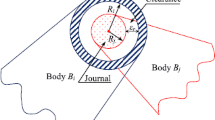
The force between the joint parts cannot be calculated in the conventional VFIFE theory because the joint was assumed as a particle. A planar revolute joint consists of two components, the bearing and journal, as shown in Fig. 6a. A contact force occurs between bearing and journal during joint motion. The contact force is defined as $\mathbf{f}_\mathrm{c}$. Due to different causes of the contact force, different calculation models are used to calculate the contact force. For the ideal and clearance joints, the contact force is caused by the same motion of bearing and journal as in an ideal revolute joint, but is altered by the impact of bearing and journal which results from clearance in the joint.

Therefore, a new motion model of the planar revolute joint is built to calculate the motion of the joint and the contact force in the joint. The bearing and journal of the planar joint are modelled as colliding bodies. According to the above VFIFE theory, the bearing and journal are treated as separate particles with mass and connected to the element, as shown in Fig. 6b. The contact force between the bearing and journal is $\mathbf{f}_\mathrm{c}$, and the nodal internal forces of the elements are $\mathbf{f}_q$ and $\mathbf{f}_s$, as shown in Fig. 6c. The external forces are omitted here for simplicity. The force equilibrium equations of particles B and J are obtained as follows:

$$\begin{aligned} m_B {\ddot{\mathbf{d}}}_B= & {} \mathbf{f}_\mathrm{c} -\mathbf{f}_q \nonumber \\ m_J {\ddot{\mathbf{d}}}_J= & {} -\mathbf{f}_\mathrm{c} -\mathbf{f}_s \end{aligned}$$

(14)

Equation (14) is the governing equation of motion about the bearing and journal in an ideal planar revolute joint or a joint with clearance. Hence, the motion of the joint can be illuminated by the equation above. The contact force $\mathbf{f}_\mathrm{c}$ will be carried out in the following derivation.

Equation (14) is the same as the equation of one arbitrary particle, namely Eq. (1); they are independent and are not combined with each other. The motion of the mechanism with an ideal planar revolute joint or a joint with clearance is solved by adding Eq. (14) to the equation group of the mechanism. With an increase in the number of joints, the number of equations of motion for the mechanism also increases; this in turn increases the amount of calculation, but will not increase the complexity of solving the equations. This characteristic is an advantage in solving the motion of the mechanism with multiple ideal joints or joints with clearance.

3.1 Contact force in an ideal planar revolute joint

Throughout the ideal planar revolute joint path unit, the bearing and journal combine closely, rotate coaxially and freely. Two particles, B and J, always coincide; thus, the accelerations of the two particles are the same:

$$\begin{aligned} {\ddot{\mathbf{d}}}_B ={\ddot{\mathbf{d}}}_J \end{aligned}$$

(15)

Substituting Eq. (15) into (14) to obtain the ideal contact force vector $\mathbf{f}_{\mathrm{ic}}$:

$$\begin{aligned} \mathbf{f}_{\mathrm{ic}} =\frac{m_J \mathbf{f}_q -m_B \mathbf{f}_s }{m_J +m_B } \end{aligned}$$

(16)

Substituting Eq. (16) into (14) yields

$$\begin{aligned} m_B {\ddot{\mathbf{d}}}_B= & {} -\frac{m_B }{m_J +m_B }(\mathbf{f}_q +\mathbf{f}_s ) \nonumber \\ m_J {\ddot{\mathbf{d}}}_J= & {} -\frac{m_J }{m_J +m_B }(\mathbf{f}_q +\mathbf{f}_s) \end{aligned}$$

(17)

Fig. 7

Revolute joint with clearance. a Physical model of the clearance joint. b Contact forces and penetration depth. c Three-mode model of the clearance joint

Equations (17) and (14) are essentially the same for the bearing and journal in one ideal revolute joint. The motion of the ideal joint is the same as that of the bearing or journal.

3.2 Contact force in a planar revolute joint with clearance

A planar revolute joint with clearance is shown in Fig. 7a. The size of clearance is

$$\begin{aligned} c=R_\mathrm{B} -R_\mathrm{J} \end{aligned}$$

(18)

The bearing and journal of a revolute clearance joint can move freely, and the journal is bound to move within the bearing boundary. A relative penetration $\delta$ occurs during the contact between the bearing and journal, as defined in Fig. 7b. $\delta$ is enlarged for clarity, but it is actually very small. A normal contact force $F_\mathrm{N}$ together with a friction force $F_\mathrm{T}$ is evaluated from impact of the bearing wall by the journal. Therefore, three different motion states of the journal exist inside the bearing boundary. The three motion states are the free flight, impact and continuous contact motions, as shown in Fig. 7c. Three modes are associated with $\delta$ and $F_\mathrm{N}$:

$$\begin{aligned}&\left\{ {{\begin{array}{ll} \delta <0\;F_\mathrm{N} =0 &{} \mathrm{free \,flight\, mode}\\ \delta =0\;F_\mathrm{N} =0 &{} \mathrm{impact\, mode}\\ \delta>0\;F_\mathrm{N} >0 &{} \mathrm{continuous\,contact\, mode}\\ \end{array}}}\right. \end{aligned}$$

(19)

$$\begin{aligned}&\delta =e-c\quad (\delta \ge 0) \end{aligned}$$

(20)

where e is the magnitude of the eccentricity

$$\begin{aligned} e=\sqrt{\mathbf{e}_{ij}^T \mathbf{e}_{ij} } \end{aligned}$$

(21)

where $\mathbf{e}_{ij}$ is eccentricity vector, which connects the centre of the bearing and journal, that is,

$$\begin{aligned} \mathbf{e}_{ij} =\mathbf{X}_\mathrm{J} -\mathbf{X}_\mathrm{B} \end{aligned}$$

(22)

where $\mathbf{X}_\mathrm{B}$ and $\mathbf{X}_\mathrm{J}$ are the coordinate vectors of the bearing and journal centres, and they can be obtained by the motion of particles B and J.

The contact force vector between the bearing and journal of the revolute clearance joint is defined as follows:

$$\begin{aligned} \mathbf{f}_{rc} =F_\mathrm{N} \mathbf{n}+F_\mathrm{T} \mathbf{t} \end{aligned}$$

(23)

where $\mathbf{n}$ is the vector that defines the normal direction of the plane of collision between the bearing and journal, given as

$$\begin{aligned} \mathbf{n}=\frac{\mathbf{e}_{ij} }{e} \end{aligned}$$

(24)

where $\mathbf{t}$ is obtained by $\mathbf{n}$ rotating anticlockwise by $90^{\circ }$.

Substituting Eq. (23) into (14) yields

$$\begin{aligned}&m_\mathrm{B} {\ddot{\mathbf{d}}}_\mathrm{B} =F_\mathrm{N} \mathbf{n}+F_\mathrm{T} \mathbf{t}-\mathbf{f}_q \nonumber \\&m_\mathrm{J} {\ddot{\mathbf{d}}}_\mathrm{J} =-F_\mathrm{N} \mathbf{n}-F_\mathrm{T} \mathbf{t}-\mathbf{f}_s \end{aligned}$$

(25)

The motion of the bearing and journal of the revolute clearance joint can be obtained using Eq. (25).

In this work, an enhanced cylindrical contact force model [14] is used to evaluate the normal reaction force $F_\mathrm{N}$. The contact force model is expressed as

$$\begin{aligned} F_\mathrm{N} =\frac{(a\Delta R+b)LE^{*}}{\Delta R}\delta ^{n}\left[ {1+\frac{3(1-c_e^2 )}{4\dot{\delta }^{(-)}}\dot{\delta }} \right] \end{aligned}$$

(26)

where

$$\begin{aligned} a= & {} \left\{ {{\begin{array}{ll} 0.965 &{} \hbox {for internal contact}, \\ 0.39 &{} \hbox {for external contact}, \\ \end{array} }} \right. \end{aligned}$$

(27a)

$$\begin{aligned} b= & {} \left\{ {{\begin{array}{ll} 0.0965 &{} \hbox {for internal contact}, \\ 0.85 &{} \hbox {for external contact}, \\ \end{array}}} \right. \end{aligned}$$

(27b)

$$\begin{aligned} n= & {} \left\{ {{\begin{array}{ll} Y\Delta R^{-0.005} &{} \hbox {for internal contact}, \\ 1.094 &{} \hbox {for external contact}, \\ \end{array} }} \right. \end{aligned}$$

(27c)

$$\begin{aligned} Y= & {} \left\{ {{\begin{array}{ll} 1.51[\ln (1000\Delta R)]^{-0.151} &{} \hbox {if }\;\Delta R\in [0.005,0.34954]\;\hbox {mm}, \\ 0.0151\Delta R+1.151 &{} \hbox {if}\;\Delta R\in [0.34954,10.0]\;\hbox {mm}, \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(27d)

where the composite modulus $E^{*}$ is given as

$$\begin{aligned} E^{*}=E/2(1-v^{2}) \end{aligned}$$

(28)

where v is the Poisson’s ratio and $\Delta R=R_i -R_j$ is the radial clearance between the two cylinders of radii $R_i$ and $R_j$ with axial length L. Note that $\Delta R=R_i -R_j$ for internal contact and $\Delta R=R_i +R_j$ for external contact. $c_e$ is the restitution coefficient.

In Eq. (26), $\delta$ is the relative penetration depth, as shown in Fig. 7b, $\dot{\delta }$ is the relative penetration velocity, and $\dot{\delta }^{(-)}$ is the initial impact velocity between the bearing and journal.

When simulating the process of contact, how initial contact is detected Flores [23] proposed a very good method for detecting initial contact. The same method is utilised in this study. Using Eq. (20), at time $t^{-}$ penetration is defined as $\delta ^{-}$, after time period $\Delta t$ at time $t^{+}$ penetration is defined as $\delta ^{+}$,

$$\begin{aligned} \delta ^{-}\delta ^{+}\le 0 \end{aligned}$$

(29)

When the condition of Eq. (29) is reached, this means initial contact has occurred. Initial contact time is

$$\begin{aligned} t^{c}=t^{-}+\frac{\delta ^{-}}{\delta ^{+}-\delta ^{-}}(t^{+}-t^{-}) \end{aligned}$$

(30)

$\delta _{\max }$ is the threshold for iteration time step adjustment for simulating the contact process.

During the contact process, at the time increment of $t-\Delta t$ to t, the penetration is $\delta _{t-\Delta t}$ at time $t-\Delta t$ and $\delta _t$ at time t. These are calculated by the coordinate vectors of the bearing and journal centres using Eqs. (20)–(22). The relative penetration velocity $\dot{\delta }$ is expressed by:

$$\begin{aligned} \dot{\delta }=(\delta _t -\delta _{t-\Delta t} )/\Delta t \end{aligned}$$

(31)

From Eqs. (20) and (31), it can be seen that if the contact force expression is an explicit formulation for contact force, the proposed motion model described in this study can be used to calculate it. If the contact force uses implicit formulation, then the proposed motion model described in this study cannot be used to calculate it. At the same time, it can be seen that the proposed motion model can simulate point contact mode. In respect of line contact and surface contact modes, a new model still needs to be researched.

A central difference time integrator is adopted in this study for numerical implementations, and the size of iteration time steps should be selected carefully. When modelling the contact force, the iteration time step size also needs to be carefully selected. Therefore, restrictions were met from the time steps’ size of the integrator and contact force calculation. This became a very time-consuming method, which resulted in standard efficiency.

In order to avoid a highly nonlinear phenomenon of the original Coulomb’s friction law, a modified Coulomb law is used [47]

$$\begin{aligned} F_T =-c_\mathrm{f} c_\mathrm{d} F_\mathrm{N} \frac{\mathbf{V}_\mathrm{T} }{v_{T} } \end{aligned}$$

(32)

where $c_\mathrm{f}$ is the friction coefficient, $\mathbf{V}_\mathrm{T}$ is the relative tangential velocity between the contact surfaces and $v_{T}$ is magnitude. The dynamic correction coefficient $c_\mathrm{d}$ is

$$\begin{aligned} c=\left\{ {{\begin{array}{ll} 0 &{} \quad \hbox {if}\quad v_T \le v_0\\ \frac{v_T -v_0 }{v_1 -v_0 }&{} \quad \hbox {if}\quad v_0 \le v_T \le v_1 \\ 1 &{} \quad \hbox {if}\quad v_T \ge v_1 \\ \end{array}}}\right. \end{aligned}$$

(33)

where $v_0$ and $v_1$ are given tolerances for the tangential velocity.

The velocity of the bearing and journal is given as

$$\begin{aligned} \mathbf{V}_\mathrm{B}= & {} (\mathbf{X}_{B t} -\mathbf{X}_{B t-\Delta t} )/(2\Delta t)\end{aligned}$$

(34)

$$\begin{aligned} \mathbf{V}_\mathrm{J}= & {} (\mathbf{X}_{J t} -\mathbf{X}_{J t-\Delta t} )/(2\Delta t) \end{aligned}$$

(35)

The magnitude of the relative velocity of the bearing and journal is written as

$$\begin{aligned} v_T =\sqrt{(\mathbf{V}_\mathrm{B} -\mathbf{V}_\mathrm{J} )^{T}(\mathbf{V}_\mathrm{B} -\mathbf{V}_\mathrm{J} )} \end{aligned}$$

(36)

The relative tangential velocity $\mathbf{V}_\mathrm{T}$ is

$$\begin{aligned} \mathbf{V}_\mathrm{T} =\mathbf{V}_\mathrm{B} -\mathbf{V}_\mathrm{J} \end{aligned}$$

(37)

4 Numerical examples

The proposed motion model of the planar revolute joint is expanded from the VFIFE theory. The simulation results are verified by comparison with published results [14, 48]. The slider-crank mechanism and four-bar mechanism are often used to demonstrate the dynamic response of a multibody system with clearance joint. The four-bar mechanism is more complex than the slider-crank mechanism. Therefore, the journal motion of a revolute joint with clearance and a four-bar mechanism with one clearance joint are studied.

4.1 Journal motion of a revolute joint with clearance

A revolute joint with clearance is used to simulate the motion of the journal using the proposed motion model of a planar revolute joint. A clearance joint exists, as shown in Fig. 7a. The bearing is fixed. The journal moves freely within the bearing boundary and exerts an impact on the bearing. The initial horizontal velocity $v=1$ m/s, the radius of journal $R_\mathrm{J} = 9.5$ mm, and the radius of the bearing $R_\mathrm{B}= 10$ mm. Young’s modulus $E=2.07$ GPa and Poisson’s ratio $v_n =0.3$ are the joint material parameters. The effect of gravity on the journal is not considered.

When the Lankarani and Nikravesh contact force model is employed, the generalised stiffness coefficient used is $6.6\times 10^{10}\,\hbox {N/m}^{1.5}$. The variation of the contact force with time for the different coefficients of restitution is shown in Fig. 8a, and the hysteresis loops are shown in Fig. 8b. Figure 8 is similar to Fig. 4 in published results [48].

Fig. 8

Influence of the coefficient of restitution for the Lankarani and Nikravesh contact force model. a Contact force versus time. b Force–penetration depth relationship

The enhanced cylindrical contact force model can also account for dissipated energy from contact. This method is an improvement on the Lankarani and Nikravesh contact force model. Results of using the enhanced model to calculate contact force of a revolute joint with clearance are compared with those of the Lankarani and Nikravesh model. The penetration depth of the enhanced model is smaller than that used in the Lankarani and Nikravesh model as shown in Fig. 9. The comparison result is similar to the published results as shown in Fig. 17 [14].

Fig. 9

Force–penetration depth relationship

Figure 10 shows the variation of the contact force during a period of time. The journal motion state changes amongst the three known motion states, which are the free flight, impact and continuous contact motions, as shown in Fig. 7c. Figure 10 also shows that the second peak is less than the first peak of the curve, thereby indicating the loss of dissipation during the impact process. The proposed model can simulate different contact force models. All results conclude that the proposed model can simulate the impact process of the clearance joint.

Fig. 10

Contact force and journal motion

4.2 Motion of four-bar mechanism with one clearance joint

The planar academic four-bar mechanism is often used as a model to demonstrate how a revolute joint with clearance affects mechanism behaviour [48]. Figure 11 shows the initial simulation configuration of a four-bar mechanism with one revolute joint clearance between the coupler and follower. The mechanism consists of crank, coupler and follower. Four joints exist in the four-bar mechanism. Three ideal revolute joints connect the ground to the crank, the crank to the coupler and the ground to the follower. A revolute joint with clearance exists between the coupler and follower. For illustration, an enlarged clearance joint is shown in Fig. 11, but the clearance of real joint is in fact much smaller. The four-bar mechanism is used to calculate the motion of the mechanism using the proposed motion model of a planar revolute joint. The dimension and mass of each body are listed in Table 1. The parameters used in the dynamic simulations are listed in Table 2.

Fig. 11

Four-bar mechanism with one revolute joint clearance between the coupler and follower

Table 1 Dimension and mass of each body

Table 2 Simulation parameters for the four-bar mechanism

Each body of the four bars mechanism is considered as a rigid body. The motion of the mechanism with one clearance joint is simulated, and that with all ideal joints is also calculated using the proposed model. The follower angular velocity, follower angular acceleration and journal centre path relative to the bearing are obtained using the Lankarani and Nikravesh contact force model, as shown in Fig. 12. The simulation results of the mechanism are in accord with Fig. 6 in published results [48].

Fig. 12

Simulation results for the four-bar mechanism with one clearance joint. a Follower angular velocity. b Follower angular acceleration. c Journal centre path relative to the bearing

When the enhanced model is used with a modified Coulomb’s law, the normal contact force and penetration depth are obtained, as shown in Fig. 13. These results are compared with results from the Lankarani and Nikravesh model simulation. As the results show, it can be seen that the enhanced model’s calculation of the penetration is smaller than the results of the calculation of the Lankarani and Nikravesh model. The influence of the friction force reduces the frequency of penetration. All results show that the proposed motion model of the planar revolute joint can simulate and calculate the mechanism’s motion.

Fig. 13

Contact force and penetration depth of the four-bar mechanism with one clearance joint. a Contact force between the bearing and journal. b Penetration depth

5 Dynamic behaviour of a mechanism with three clearance joints in continuous contact mode

The motion of the journal inside the internal boundaries of the bearing is classified into three different states: the continuous contact, free flight and impact motions. The $3^{m}$ combinations of the motion modes exist in the mechanism when the total number of the joints with clearance is m, and the dynamic behaviour of the mechanism is different across different combinations. With some parameters, the journal of all the clearance joints is always in continuous contact with the bearing wall during the entire motion cycle of the mechanism. In other words, only one type of motion mode arises in all the clearance joints of the mechanism, namely the continuous contact mode, throughout the entire motion cycle. In this situation, the physical mechanism model with multiple joints is similar to the model with ideal joints. However, the numerical simulation results indicate a significant dynamic difference between the two mechanism models.

The four-bar mechanism with three revolute clearance joints, named joints 1, 2 and 3, as shown in Fig. 14, is presented and investigated in this work to demonstrate how the clearance joints in the continuous contact mode affect the dynamic behaviour of the mechanisms. In the four-bar mechanism, each body is considered as a rigid body. The joint connecting the crank and the ground is assumed to be ideal because of the fact that, in the simulation, the crank is the driving link and rotates at a constant angular velocity. Different numerical examples are conducted to quantify the influence of the clearance size and input crank speed on the dynamic response of the four-bar mechanism with three clearance joints.

All the simulation parameters of the mechanism are listed in Tables 1 and 2. The values of n, which is the constant angular velocity of crank, are $10\,\pi , 20\,\pi$ and $50\,\pi$ rad/s. The values of c, which is the clearance size of joints, vary amongst 0.1, 0.2 and 0.5 mm. The contact force of clearance joint 2 and the angular acceleration of the follower in the mechanism with three clearance joints are selected for the study in this work. The modified Coulomb law [47] was chosen to model the friction at the clearance joints, and a friction coefficient of 0.1 is used.

The dynamic influences of one cycle on the mechanism with clearance joints after the steady state is reached are analysed against those obtained for the mechanism with ideal joints. In order to better understand the influences during the cycle, dimensionless local influence parameters (LIPs) are redefined to evaluate how the level of the dynamic response maximum is increased during a cycle [48].

The dimensionless LIP for the contact force of the clearance joint is expressed by

$$\begin{aligned} \hbox {LIP(F)}=\frac{F_{\mathrm{c},\max } -F_{\mathrm{i},\max } }{F_{\mathrm{i},\max }}\times 100 \end{aligned}$$

(38)

Fig. 14

Four-bar mechanism with three clearance joints

Fig. 15

Journal centre path relative to the bearing centre for the three clearance joints with different clearance sizes ($\hbox {n} = 50\,\pi$ rad/s). a 0.1 mm. b 0.2 mm. c 0.5 mm

where $F_{\mathrm{c},\max }$ and $F_{\mathrm{i},\max }$ are the maximum contact forces of the clearance joint and ideal joint, respectively. Similarly, the dimensionless LIP for the angular acceleration of the follower is expressed as

$$\begin{aligned} \hbox {LIP(a)}=\frac{a_{\mathrm{c},\max } -a_{\mathrm{i},\max } }{a_{\mathrm{i},\max } }\times 100 \end{aligned}$$

(39)

where $a_{\mathrm{c},\max }$ and $a_{\mathrm{i},\max }$ are the maximum follower angular accelerations of the mechanism with clearance joints and ideal joints, respectively.

Fig. 16

Contact force of joint 2 under different clearance sizes of the joints ($\hbox {n} = 50\,\pi$ rad/s). a 0.1 mm. b 0.2 mm. c 0.5 mm

Fig. 17

Acceleration of the follower under different clearance sizes of the joints ($\hbox {n} = 50\,\pi$ rad/s). a 0.1 mm. b 0.2 mm. c 0.5 mm

5.1 Influence of the clearance size of the joints on the dynamic response of the mechanism under the same crank speed

The influence of the clearance size of the joints on the dynamic response of the four-bar mechanism is investigated in this subsection. The radial clearances of the three clearance joints are identical and chosen to be 0.1, 0.2 and 0.5 mm. The crank speed is equal to $50\,\pi$ rad/s. Figure 15 demonstrates the journal centre path relative to the bearing centre of all the joints during the entire motion cycle. The journal path outside the circle with a radius of clearance size means the journal is in continuous contact motion. With the different clearance size of the joints, the continuous contact mode arises between the journal and the bearing wall of the three clearance joints during the entire motion cycle, as shown in Fig. 15.

Table 3 Dimensionless parameters of the joint 2

Fig. 18

Journal centre path relative to the bearing centre of the three clearance joints under different crank speeds (c $=$ 0.2 mm). a $10\,\pi$. b $20\,\pi$. c $50\,\pi$

Figures 16 and 17 illustrate the contact force of joint 2 and the acceleration of the follower of the four-bar mechanism under different values of the joint clearance. The crank speed is chosen to be $50\,\pi$ rad/s.

Although the journal of all the three clearance joints is always in contact with the bearing wall during the entire motion cycle of the mechanism, the curves of the reaction force of joint 2 and of the follower acceleration in Figs. 16 and 17 are both fluctuating instead of smooth, which generally happens in the curves of the ideal four-bar mechanism. Therefore, the dynamic performances of the mechanism with all clearance joints in continuous contact mode are different from those of the mechanism with all ideal joints. Figures 16 and 17 also indicate that differences in clearance size significantly influence the joint contact force and the follower acceleration. To quantify these differences during a motion cycle, the dimensionless LIPs evaluating the contact force of joint 2 and the follower acceleration are listed in Table 3, respectively.

Fig. 19

Contact force of joint 2 under different crank speeds (c $=$ 0.2 mm). a $10\,\pi$. b $20\,\pi$. c $50\,\pi$

The values listed in Table 3 show that the values of the dimensionless parameters of the joint contact force and the follower acceleration both increase with the clearance size. Hence, the local fluctuating characteristics of the mechanism increase with the clearance size. Similar behaviours of slider-crank mechanism with one clearance joint are reported [14].

The analyses immediately show that strong vibration exists in the four-bar mechanism with clearance joints after the motion has been triggered. The vibration then gradually declines and finally stabilises. The mechanism behaviour tends to be periodic. The periodic vibration after the steady state is reached is caused by the initial vibration of the mechanism. The initial vibration increases with the size of the joint clearance. These are reasonable explanations for the results.

5.2 Influence of the input crank speed on the dynamic response of the mechanism under the same clearance size

In this subsection, the influence of the input crank speed on the dynamic response of the four-bar mechanism is investigated. The radial clearance of the three clearance joints is identical and is equal to 0.2 mm. The values of the crank speed are chosen to be 10, 20 and $50\,\pi$ rad/s. Figure 18 demonstrates that, during the entire motion cycle, only the continuous contact mode arises between the journal and the bearing wall of the three clearance joints.

Figures 19 and 20 illustrate the contact force of joint 2 and the acceleration of the follower under different crank speeds. The clearance size of the three joints is chosen to be 0.2 mm.

Figures 19 and 20 show that the differences in crank speed significantly influence the joint contact force and the follower acceleration. The dimensionless LIPs that evaluate the contact force of joint 2 and the follower acceleration are listed in Table 4, respectively.

Fig. 20

Acceleration of the follower under different crank speeds (c $=$ 0.2 mm). a $10\,\pi$. b $20\,\pi$. c $50\,\pi$

These values show that the dimensionless parameters of the joint contact force and the follower acceleration both decrease with an increase in crank speed. Thus, the local fluctuating characteristics of the mechanism decline with an increase in crank speed. Simulation results of this study are similar to results shown in Figs. 11 and 12 of slider-crank mechanisms with one clearance joint [33].

The values of the contact force in the clearance joints and follower acceleration significantly increase with an increase in crank speed. The contact force in the clearance joints must increase with the crank speed because the greater the acceleration of the bodies of the mechanism, the greater the required force. The relative penetration depth between the journal and the bearing consequently increases with crank speed, as shown in Fig. 18. Collision time becomes considerable with an increase in penetration depth; therefore, the change in the contact force becomes slow. The dynamic performances under the contact force last for a long time. The difference between the dynamic performance of the mechanism with all clearance joints in continuous contact mode and that of the mechanism with all ideal joints becomes insignificant.

Table 4 Dimensionless parameters of the joint 2

6 Conclusions

A new computational methodology is presented for the dynamic analysis of multibody systems with multiple clearance joints. The VFIFE method is employed to simulate the motion of the mechanism without utilising matrix calculation. A motion model for ideal and clearance joints is proposed. The motions of the journal and bearing of joint are modelled and the motion-governing equations are formulated. The motion equations for the journal and bearing of joints are simply added to the motion equation group of the mechanism. With an increase in the number of joints, the number of the equations of motion for the mechanism with joints increases as well, which in turn increases the amount of calculation, but without increasing the complexity of solving the equations. This characteristic is beneficial for solving the motion of a mechanism with multiple clearance joints. The simulation results for the proposed joint model are verified and agree well with published results.

With some simulation parameters in the demonstrated examples, only the continuous contact mode between the journal and the bearing arises, which can be confirmed from the relative path of the journal centre to the bearing centre of the three clearance joints. The analyses indicate that the behaviour of the four-bar mechanism with multiple clearance joints tends to be periodic after reaching the steady state. The curves of the joint reaction force and follower acceleration during one cycle are both fluctuating and different from those of the mechanism with ideal joints, which are smooth. This particular issue has not been addressed in other studies.

The level of the periodic vibration depends on the crank speed and the clearance size of joints. For the joint contact force and the follower acceleration, the local fluctuating characteristics all increase with the clearance size under the same crank speed. Although the absolute values of the joint contact force and follower acceleration both increase with the crank speed under the same clearance size, the local fluctuating characteristics decline with an increase in the crank speed.