1 Introduction

Nowadays, there is a variety of mechanical systems which describe large translational and rotational motions, suitable for many types of engineering applications. These systems may be regarded as multibody mechanical systems as they are constituted by rigid or deformable bodies connected to each other by means of kinematic pairs. There are several types of kinematic joints, among which the most common include revolute, translational, and spherical joints. Due to its importance, in this work, the modeling of spherical joints is analyzed in the context of multibody systems dynamic simulations.

From the mechanical design point of view, in spherical joints, a spherical part of one component, the ball, resides inside a spherical part of the connected component, the socket [1]. Bearing in mind the type of applications in which they are designed to operate, spherical joints may be modeled using different formulations. The simplest and most common approach is to consider the spherical joint as an ideal joint, being modeled with three kinematic constraints. An ideal spherical joint constrains three relative translations and allows three relative rotations of the bodies that it connects, yielding three degrees-of-freedom. In certain application scenarios, the assumption of a perfect relative motion between the ball and the socket components is not acceptable due to the fact that, in an actual spherical joint, there is always a certain amount of clearance. In those cases, the three kinematic constraints used in the ideal joint case are eliminated, resulting in the introduction of three additional degrees-of-freedom into the system. Moreover, the dynamics of the joint is governed by contact forces, which occur as a result of the collision between the surfaces of the ball and the socket, therefore being referred to as force joint [2].

One of the most critical issues when dealing with the analysis of multibody systems with dry clearance joints is the process of modeling the contact-impact phenomena. A good number of contact force models have been proposed and are critically documented in several studies [3–15]. Due to the collisions between the ball and the socket, spherical joints with clearance often exhibit nonlinear dynamic response [16]. Apart from this, uncertainty is also characteristic of clearance joints, and it may lead to angular and positional errors in mechanical systems. In high precision tasks, accuracy is always of utmost importance and, thus, clearance joints should be taken seriously because the cumulative error is considerable, and the system’s accuracy is affected by the joint clearances even if the active joints are frozen [17]. Besides normal contact, friction forces are present in dry spherical joints due to the resistance to the local relative tangential motion between the contacting surfaces. Over the last years, several review papers on the friction force models have been available in the literature [18–21].

Clearance is necessary and inevitable to allow the assembly and correct operation of the mechanical components of a system. Clearance may arise from different and diverse sources, such as the manufacturing tolerances, wear, thermal effects, and local deformations. It results in the development of friction, vibration, and fatigue phenomena or even in the random overall behavior of the system [22]. The dynamic response of the system can be greatly affected by the contact forces generated at clearance joints. Additionally, they might explain the deviation between the numerical and experimental findings and, eventually, lead to significant discrepancies between the projected behavior of the mechanical system and its real outcome. These forces might also be the source of high-frequency vibration and joint wear, which penalizes the performance and service life of the mechanism [23–27]. Several researchers have analyzed the influence of modeling clearance in spherical joints on the response of mechanical systems. Liu et al. [28] developed a contact force model for spherical joints with clearance that is simple and straightforward. Their contact model has its basis on Winkler’s elastic foundation approach and considers the modeling of the compliance of the contacting surfaces. Flores et al. [2] established a model to deal with dry frictionless spherical clearance joints. The authors concluded that clearance considerably increased the peaks in the acceleration and reaction moments and that the response of the system tended to become nonperiodic when compared with the ideal joint case. Wang et al. [29] studied the influence of the spherical clearance joint caused by wear on the dynamic performance of mechanical systems. The results showed that clearance had significant effects on the joint reaction forces when compared with the ideal case and that the wear depth along the socket surface was found to be nonuniform. Marques et al. [30] analyzed spatial mechanisms with spherical clearance joints, which main focus was on the influence of the friction effect. It was shown that the existence of friction in the spherical clearance joint stabilized the response of the system, making it less chaotic compared with the frictionless case. More recently, Gao et al. [31] analyzed the influence of spherical clearance joints on a spatial 4-UPS (universal joint-prismatic pair-spherical joint)-RPU (revolute joint-prismatic pair-universal joint) parallel mechanism. The work developed by Tian and co-workers [32] provides a detailed review of clearance joints considering analytical, numerical, and experimental methodologies.

Adding a lubricant in the space between the socket and the ball is one of the most common solutions to prevent or reduce the solid-to-solid contact on dry clearance joints, as well as to minimize energy dissipation. The ball and socket are kept apart by the high pressures that develop in this fluid, which prevents direct contact between these two mechanical components. Furthermore, the use of a fluid to promote lubrication in a clearance joint, besides helping in friction and wear reduction, also provides load-carrying capacity and adds damping to dissipate undesirable mechanical vibrations [23, 33–37]. In general, lubricants consist of mineral, synthetic or biological oils containing low concentrations of different additives [38]. Some authors have been studying the influence of lubrication in spherical clearance joints. Tian et al. [39] presented a computational methodology for the dynamic analysis of spatial flexible multibody systems with dry and lubricated spherical joints. The existence of friction in the dry joint was modeled with Coulomb’s law. The authors concluded that the direct contact between the ball and the socket arising from the dry joint could be avoided if a lubricant was introduced into the joint. Lubrication allowed the performance of the system to become closer to the ideal joint case. Flores and Lankarani. [24] compared dry and lubricated spherical clearance joints in spatial mechanisms. In their study, the response of the system with lubrication presented fewer peaks in the kinematic and dynamic outputs when compared with the results of the dry joint model. Both studies analyzed the influence of the squeeze-film effect in lubricated spherical clearance joints and based their approaches on Reynold’s theory.

Clearance and lubrication are also present in biomechanical systems. Considering specifically spherical joints, the human hip articulation may be considered as a spherical clearance joint with and without lubrication. Considering the physiological terminology, these joints are referred to as synovial joints, where there is the presence of a lubricant called synovial fluid, which prevents the occurrence of friction between the cartilage. Askari et al. [40] modeled and analyzed the influence of friction-induced vibration on the predicted wear rate of artificial hip articulations. For that, a dry spherical clearance joint was utilized, accompanied by appropriate normal, friction, and wear constitutive laws. Askari and Flores [34] proposed a new approach to model the hydrodynamic lubrication in spherical clearance joints that considers the dynamic motion of the articulating components, as well as both the squeeze- and wedge-film effects. The developed approach was based on Reynold’s equation and was applied to a hip prosthesis lubricated by synovial fluid.

In some practical applications, lubrication may not be intended, and bushing elements may be utilized instead. These are usually composed of elastomeric materials and are placed between the inner and outer sleeves of the joints. Bushing elements are present in some actual situations, including road vehicles, whose suspension systems use these flexible components in their joints. Ledesma et al. [41] developed a formulation able to incorporate bushing elements in multibody systems. The nonlinear viscoelastic bushing forces were modeled as massless force elements between two bodies and were dependent not only on the instantaneous bushing deformation but also on the time history of that deformation. Ambrósio and Veríssimo [42] proposed a constitutive law to model bushing elements associated with mechanical joints used in road and rail vehicles. The bushing elements were modeled as nonlinear restrains that relate the relative displacement between the connected bodies with the joint reaction forces. Ambrósio and Pombo [43] proposed an approach to model perfect kinematic joints and clearance/bushing joints in the framework of multibody systems methodologies. In this sense, as the joints shared the same kinematic information, their modeling data was similar, which enabled their easy permutation when modeling multibody systems.

The goal of this work is to provide a comparative analysis between different spherical joint models and to analyze their influence on the dynamic response of different multibody mechanical systems. For this purpose, the kinematic and dynamic aspects associated with four different models are presented, namely the ideal, dry, lubricated, and bushing formulations. The dry clearance model is analyzed utilizing several normal contact force models and taking into consideration the tangential forces between the contacting surfaces. The lubricated joint model considers the influence of the squeeze-film action. Finally, the bushing approach is based on elastomer deformation, as well as on stiffness and damping properties. In the aftermath of this process, two examples of application are considered with the purpose of demonstrating the influence of each spherical joint model on their response, namely the spatial four-bar mechanism and a car suspension. This study provides a simple and direct comparison between different methodologies that can be considered to model mechanical systems with spherical joints. Herewith and by acknowledging the advantages of each approach, this study allows a better understanding of the model to adopt for a certain application.

The remaining paper is organized as follows. In Sect. 2, the Newton-Euler method of the dynamic equations of motion for constrained multibody mechanical systems is described. Then, in Sects. 3 and 4, a comprehensive explanation of the kinematic and dynamic characteristics of the spherical joint models is provided. In this regard, various approaches are investigated and studied, considering the normal, tangential, lubrication, and bushing forces experienced by the multibody systems due to the incorporation of the spherical joints models. In Sect. 5, the considered joint models are applied to the dynamic modeling and simulation of two multibody systems, and their influence on the dynamic response of those systems is assessed. The results are obtained from computational simulations of the four spherical joint models. Finally, this work ends with some concluding remarks described in Sect. 6.

2 Spatial multibody dynamics

The multibody dynamics analysis includes the development of mathematical models of the equations of motion of the systems under analysis, as well as the implementation of computational procedures to simulate, analyze, and optimize the global motion produced. The Newton-Euler approach with absolute coordinates is amongst the most widely used methods in several engineering fields because it is simple, direct, and quite intuitive for general-purpose codes to model multibody mechanical systems [44–46].

By and large, a multibody mechanical system comprises two main features that is, rigid and/or deformable bodies describing large rotational and translational motions and joints that kinematically constrain the relative motion of the mechanical components [45]. By assembling the Newton-Euler equations of motion for a constrained multibody system and the accelerations constraints equations, the governing equations for a dynamic multibody system with holonomic constraints are formulated as

$$ \left[ \textstyle\begin{array}{c@{\quad }c} \mathbf{M} & \mathbf{D}^{\mathrm{T}} \\ \mathbf{D} & \mathbf{0} \end{array}\displaystyle \right]\left\{ \textstyle\begin{array}{c} \dot{\mathbf{v}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right\} = \left\{ \textstyle\begin{array}{c} \mathbf{g} \\ \boldsymbol{\upgamma} \end{array}\displaystyle \right\} $$
(1)

where \(\mathbf{M}\) is the system mass matrix, \(\mathbf{D}\) represents the Jacobian matrix of the constraint equations, \(\dot{\mathbf{v}}\) denotes the vector containing the system accelerations, \(\boldsymbol{\lambda}\) is Lagrange multipliers vector that contains the reaction forces and moments on the kinematic joints, \(\mathbf{g}\) represents the generalized vector of applied forces and moments, and \(\boldsymbol{\upgamma}\) denotes the right-hand side vector of the acceleration equations [1].

Equation (1) may be described as a combination of the equations of motion and the kinematic constraint equations, often referred to as a set of differential-algebraic equations (DAE). The first step in the standard resolution of the equations of motion is to define the initial time and initial conditions of the system. Then, \(\mathbf{M}\), \(\mathbf{D}\), \(\boldsymbol{\upgamma}\) and \(\mathbf{g}\) are evaluated, and Eq. (1) is solved for the constrained multibody system to obtain \(\dot{\mathbf{v}}\) and \(\boldsymbol{\lambda}\) at time instant \(t\). The auxiliary vector \(\dot{\mathbf{y}}_{t}\) for time \(t\), which gathers the velocity and acceleration of the system, is assembled and numerically integrated for time instant \(t\)+\(\Delta t\) to obtain vector \(\mathbf{y}\)t+Δt. Thus, the new velocities and positions of the system are obtained. To complete the simulation, the time variable is updated. If the final simulation time has not been reached yet, the simulation continues, and these steps are repeated for the following time steps [47].

Equation (1) does not explicitly include the position, \(\boldsymbol{\Phi}\), and velocity, \(\dot{\boldsymbol{\Phi}} \), constraint equations, which, for moderate or long simulations, results in the violation of those original constraints. This occurrence might be associated with the integration procedures, time step selected, and/or inaccurate initial conditions. In order to overcome or minimize this problem, several strategies can be implemented, namely stabilization techniques, coordinate partitioning methods, and direct correction formulations [47]. In this work, the Baumgarte stabilization technique was used, and Eq. (1) is modified as

$$ \left[ \textstyle\begin{array}{c@{\quad }c} \mathbf{M} & \mathbf{D}^{\mathrm{T}} \\ \mathbf{D} & \mathbf{0} \end{array}\displaystyle \right]\left\{ \textstyle\begin{array}{c} \dot{\mathbf{v}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right\} = \left\{ \textstyle\begin{array}{c} \mathbf{g} \\ \boldsymbol{\upgamma} - \mathbf{2}\alpha \dot{\boldsymbol{\Phi}} - \beta^{2}\boldsymbol{\Phi} \end{array}\displaystyle \right\} $$
(2)

where \(\alpha\) and \(\beta\) represent the feedback control parameters for velocity and position constraint violations, respectively, and are taken as positive constants.

3 Kinematics of spherical joints

A comprehensive description of the formulations considered in this work to model spherical joints under the multibody system’s framework is included in this section. Four different cases are presented, namely the ideal, dry, lubricated, and bushing models.

3.1 Ideal joint

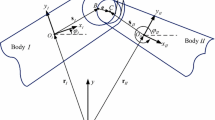
Ideal spherical joints allow the relative rotations between two adjacent bodies \(i \) and \(j\), while the three relative translations are constrained. Consequently, the center of the ideal joint holds constant coordinates relative to both local coordinate systems. This means that point \(P_{i}\) on body \(i\) is coincident with point \(P_{j}\) on body \(j\), and, thus, the relative position between those bodies is restricted [45].

A schematic representation of an ideal spherical joint is depicted in Fig. 1, in which the centers of mass of bodies \(i\) and \(j\) are \(O_{i}\) and \(O_{j}\), respectively. The global coordinate system is represented by xyz, and the body-fixed coordinate systems \(\xi\eta\zeta\) are attached to their corresponding center of mass [1]. Using the nomenclature described in Fig. 1, the condition defining that points \(P_{i}\) and \(P_{j}\) are coincident can be written in vector form as

$$ \boldsymbol{\Phi}^{(s,3)} \equiv \mathbf{r}_{j}^{P} - \mathbf{r}_{i}^{P} = \mathbf{r}_{j} + \mathbf{s}_{j}^{P} - \mathbf{r}_{i} - \mathbf{s}_{i}^{P} = \mathbf{0} $$
(3)

where \(\mathbf{r}_{k}^{P}\) represents the global position vector of point \(P\) located on body \(k\), \(\mathbf{r}_{k}\) denotes the position vector of the center of mass of body \(k\) in global coordinates and \(\mathbf{s}_{k}^{P}\) is the global position vector of point \(P\) located on body \(k\) with respect to the body’s local coordinate system. \(\boldsymbol{\Phi}^{(s,3)}\) refers to a spherical (s) joint constraint with three (3) equations [1]. The local and global components of \(\mathbf{s}_{k}^{P}\) relate as

$$ \mathbf{s}_{k}^{P} = \mathbf{A}_{k}\mathbf{s}_{k}^{\prime\,P} $$
(4)

where \(\mathbf{A}_{k}\) is the transformation matrix of body \(k\) and \(\mathbf{s}_{k}^{\prime\,P}\) refers to the position of point \(P\) on the body’s local coordinates.

Fig. 1
figure 1

Schematic representation of an ideal spherical joint connecting bodies \(i\) and \(j\)

Full size image

The velocity constraint equations for an ideal spherical joint are obtained by taking the first time derivative of Eq. (3), yielding

$$ \dot{\boldsymbol{\Phi}}^{(s,3)} = \dot{\mathbf{r}}_{j} + \dot{\mathbf{s}}^{P}_{j} - \dot{\mathbf{r}}_{i} - \dot{\mathbf{s}}^{P}_{i} = \mathbf{0} $$
(5)

in which the dot represents the derivative with respect to time.

Considering the following condition

$$ \dot{\mathbf{s}} = \tilde{\boldsymbol{\upomega }} \mathbf{s} = - \tilde{\mathbf{s}}\boldsymbol{\upomega } $$
(6)

where the symbol (∼) represents the skew-symmetric matrix and \(\boldsymbol{\upomega }\) is the angular velocity vector on global coordinates, then Eq. (5) can be rewritten as

$$ \dot{\boldsymbol{\Phi}}^{(s,3)} = \dot{\mathbf{r}}_{j} - \tilde{\mathbf{s}}_{j}^{P}\boldsymbol{\upomega }_{j} - \dot{\mathbf{r}}_{i} + \tilde{\mathbf{s}}_{i}^{P}\boldsymbol{\upomega }_{i} = \mathbf{0} $$
(7)

Consequently, the contribution to the Jacobian matrix of the spherical joint constraints can be yielded as follows

$$ \mathbf{D}^{(s,3)} = \left[ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} - \mathbf{I} & \tilde{\mathbf{s}}_{i}^{P} & \mathbf{I} & - \tilde{\mathbf{s}}_{j}^{P} \end{array}\displaystyle \right] $$
(8)

The time derivative of Eq. (7) yields the acceleration constraint equations of the ideal spherical joint as

$$ \ddot{\boldsymbol{\Phi}}^{(s,3)} = \ddot{\mathbf{r}}_{j} - \tilde{\dot{\mathbf{s}}}_{j}^{P}\boldsymbol{\upomega }_{j} - \tilde{\mathbf{s}}_{j}^{P}\dot{\boldsymbol{\upomega }}_{j} - \ddot{\mathbf{r}}_{i} + \tilde{\dot{\mathbf{s}}}_{i}^{P}\boldsymbol{\upomega }_{i} + \tilde{\mathbf{s}}_{i}^{P}\dot{\boldsymbol{\upomega }}_{i} = \mathbf{0} $$
(9)

The contribution to the right-hand side of the acceleration equations of the ideal spherical joint constraints yields

$$ \boldsymbol{\upgamma}^{(s,3)} = - \tilde{\dot{\mathbf{s}}}_{i}^{P}\boldsymbol{\upomega }_{i} + \tilde{\dot{\mathbf{s}}}_{j}^{P}\boldsymbol{\upomega }_{j} $$
(10)

3.2 Dry clearance joint

The condition defining that the center points of the socket and ball, \(P_{i}\) and \(P_{j}\), are coincident, which was assumed in the previous section, is not considered in the case of the clearance joint. Hence, the three kinematic constraints presented in Eq. (3) are eliminated, which means that the two bodies are separated and free to move in relation to one another. Contrary to the ideal joint case, no degree-of-freedom is constrained from the system in the case of the spherical clearance joint [24, 33]. Figure 2 depicts a general configuration of a spherical joint with clearance in a multibody system. The convex portion of body \(j\), the ball, is situated inside the concave portion of body \(i\), the socket. The radii of the socket and the ball are \(R_{i}\) and \(R_{j}\), respectively, and the difference between these parameters represents the radial clearance as [24, 33]

$$ c = R_{i} - R_{j} $$
(11)
Fig. 2
figure 2

Schematic representation of a spherical clearance joint connecting bodies \(i \) and \(j\)

Full size image

According to the nomenclature utilized in Fig. 2, the vector connecting point \(P_{i}\) to point \(P_{j}\) defines the eccentricity vector, \(\mathbf{e}\), which is given by

$$ \mathbf{e} = \mathbf{r}_{j}^{P} - \mathbf{r}_{i}^{P} $$
(12)

The magnitude of the eccentricity vector is given by

$$ e = \sqrt{\mathbf{e}^{\mathrm{T}}\mathbf{e}} $$
(13)

and the time rate of the eccentricity in the radial direction, that is, in the direction of the line of centers of the socket and the ball, is written as

$$ \dot{e} = \frac{\mathbf{e}^{\mathrm{T}}\dot{\mathbf{e}}}{ e} $$
(14)

The situation in which the socket and the ball contact with each other, which is identified by the existence of a relative pseudo-penetration \(\delta\), is shown in Fig. 3. The unit vector \(\mathbf{n}\) is normal to the collision surface between the socket and the ball, and it is aligned with the eccentricity vector [24, 33], that is

$$ \mathbf{n} = \frac{\mathbf{e}}{ e} $$
(15)
Fig. 3
figure 3

Schematic representation of the penetration depth between the socket and the ball during contact

Full size image

The contact points on bodies \(i\) and \(j\) are denoted by \(Q_{i}\) and \(Q_{j}\), respectively, and their global position vectors are given by

$$ \mathbf{r}_{k}^{Q} = \mathbf{r}_{k} + \mathbf{s}_{k}^{P} + R_{k}\mathbf{n} \quad (k = i,j) $$
(16)

The velocities of the contact points are obtained by differentiating Eq. (16) concerning time, yielding

$$ \dot{\mathbf{r}}_{k}^{Q} = \dot{\mathbf{r}}_{k} + \dot{\mathbf{s}}^{P}_{k} + R_{k}\dot{\mathbf{n}} \quad (k = i,j) $$
(17)

The relative normal and tangential velocities of the contact points determine whether the bodies in contact are approaching or separating and whether they are sliding or sticking, respectively [24, 33]. These velocities are obtained by projecting the relative contact velocity onto normal and tangential directions, as

$$\begin{aligned} & \mathbf{v}_{\mathrm{n}} = \left[ \left( \dot{\mathbf{r}}_{j}^{Q} - \dot{\mathbf{r}}_{i}^{Q} \right)^{\mathrm{T}}\mathbf{n} \right]\mathbf{n} \end{aligned}$$
(18)
$$\begin{aligned} & \mathbf{v}_{\mathrm{t}} = \left( \dot{\mathbf{r}}_{j}^{Q} - \dot{\mathbf{r}}_{i}^{Q} \right)^{\mathrm{T}} - \mathbf{v}_{\mathrm{n}} \equiv v_{\mathrm{t}}\mathbf{t} \end{aligned}$$
(19)

where \(v_{t}\) is the magnitude of the tangential velocity and \(\mathbf{t}\) is the tangential direction of the relative velocity associated with the contacting surfaces represented as

$$ \mathbf{t} = \frac{\mathbf{v}_{\mathrm{t}}}{v_{\mathrm{t}}} $$
(20)

Through the observation of Fig. 3, it is evident that the geometric condition for the contact between the socket and the ball is defined as

$$ \delta = e - c $$
(21)

and the relative normal contact velocity, \(\dot{\delta} \), is given by

$$ \dot{\delta} = \left( \dot{\mathbf{r}}_{j}^{Q} - \dot{\mathbf{r}}_{i}^{Q} \right)^{\mathrm{T}}\mathbf{n} $$
(22)

In the dry spherical clearance joint model, the ball and the socket are allowed to move freely in relation to one another, which results in distinct types of motion of the ball inside the socket. The contact or following mode is characterized by the continuous contact interaction, and it is accompanied by a sliding motion of both components relative to each other. This mode ends with ball and socket separation and the ball entering free flight mode. In this motion mode, since there is no contact, the ball can freely move inside the socket, which results in the absence of a joint reaction force. Finally, the impact mode occurs at the end of the free flight motion, and it is characterized by the application of contact-impact forces to the system. Due to these forces, the kinematic and dynamic responses of the system are subjected to abrupt discontinuities. Besides, a significant momentum exchange between the two impact bodies is also observed. At the end of the impact mode, the ball enters either free flight or the following modes [33].

3.3 Lubricated joint

In the case of a lubricated spherical joint (Fig. 4), a lubricant is used to fill the space between the ball and the socket. When the load is applied to the joint, the ball moves with respect to the socket, and the lubricant is forced into the clearance space, which results in a buildup of pressure. The high pressures developed in the lubricant film maintain the surfaces of the spherical joint apart. In this regard, lubricated joints are designed so that the socket and the ball do not contact with each other [24]. However, this condition might be violated when high external forces are involved.

Fig. 4
figure 4

Schematic representation of a lubricated spherical clearance joint

Full size image

The main kinematic aspects of spherical clearance joints with lubrication are similar to those described for the dry spherical joint. The main difference is in the relative radial velocity given by Eq. (14), which results in lubricant squeeze action when the ball and the socket surfaces are not in contact [24].

3.4 Bushing joint

Bushing elements, as one illustrated in Fig. 5, are commonly utilized in mechanical systems, such as vehicle suspensions, to act as shock and vibration absorbers, to handle misalignments, and to reduce the transmissibility of irregularities to the system. These elements are usually composed of elastomeric material combined with steel sleeves and can be found in various mechanical joints, such as spherical, revolute, and translational joints, allowing the connection of rigid components of the mechanical system. The relative motion of these components deforms the bushing element, involving radial, torsional, and a combination of radial-torsional deformation. Bushing elements generally used in energy dissipation present a nonlinear viscoelastic relation between the forces and moments and their corresponding displacement and rotations [42, 48]. Similarly to the dry and lubricated cases, using bushing elements instead of an ideal joint decreases the number of kinematic constraints required to model the system.

Fig. 5
figure 5

Schematic representation of a bushing element in a spherical joint

Full size image

The formulation utilized in this study is based on the methodology presented by Ambrósio and Veríssimo [42], in which the bushing elements are modeled as nonlinear restrains and are characterized by a matrix constitutive relation. The relative displacements between the connected bodies are related to the joint reaction forces. The kinematic aspects of the bushing joint are similar to those of the dry spherical joint.

4 Dynamics of spherical joints

This section includes a brief description of the methodologies utilized to compute the forces involved in the modeling of the dynamics of spherical joints in a given multibody system. The normal, tangential, and lubrication force models are characterized, followed by the bushing approach. The resulting forces can be introduced into the equations of motion of a multibody system, that is, in Eq. (1), as external generalized forces in vector \(\mathbf{g}\).

4.1 Normal force models

In the case of the dry spherical clearance model, the dynamics of the joint is controlled by contact-impact forces arising from the interaction between the connected bodies [24, 33]. In contact mechanics, the evaluation of normal contact forces resulting from collisions between bodies is an aspect of utmost importance to take into consideration. Concerning the capacity of dissipating energy, normal contact force models might be classified as purely elastic or dissipative.

Using the theory of elasticity, Hertz [49] developed the most popular purely elastic contact force model to represent the collision between two spheres of linear and isotropic materials [47]. The contact force can be expressed as

$$ f_{\mathrm{n}} = K\delta^{n} $$
(23)

where \(K\) is the generalized contact stiffness, \(n\) denotes the nonlinear exponent factor, and \(\delta\) is the penetration calculated by Eq. (21).

The generalized stiffness parameter, \(K\), depends on the material properties and the local geometry of the contacting surfaces. For two spheres \(i \) and \(j\) in contact, this parameter is computed based on the radii of the spheres and on the material properties, as [47]

$$ K = \frac{4}{3\left( \sigma_{i} + \sigma_{j} \right)}\sqrt{\frac{R_{i}R_{j}}{R_{i} + R_{j}}} $$
(24)

where the material properties \(\sigma_{i}\) and \(\sigma_{j}\) are given by

$$ \sigma_{k} = \frac{1 - \upsilon_{k}^{2}}{E_{k}}\quad (k = i,j) $$
(25)

in which the quantities \(\upsilon_{k}\) and \(E_{k}\) represent Poisson’s ratio and Young’s modulus associated with each sphere, respectively.

It is important to note that in Eq. (24), the radius is a negative value for concave surfaces, such as the socket, and assumes a positive value for convex surfaces, such as the ball.

The contact law (23) is limited to contacts with elastic deformations and does not consider energy dissipation. Hence, alternative models have been proposed to extend the application of the Hertz contact force model to include energy dissipation [47]. Within the scope of this study, only dissipative contact force models are analyzed. In this work, four models were selected as the targets of the analysis, namely the ones developed by Hunt and Crossley [50], Lankarani and Nikravesh [51], Gonthier et al. [52], and Flores et al. [53]. These four models were chosen so that the analysis would include approaches suitable for different values of the restitution coefficient.

The nonlinear Hunt and Crossley contact force model [50] represents the contact force proposed by Hertz’s law together with a nonlinear viscoelastic element, as

$$ f_{\mathrm{n}} = K\delta^{n}\left[ 1 + \frac{3(1 - c_{\mathrm{r}})}{2}\frac{\dot{\delta}}{\dot{\delta}^{( - )}} \right] $$
(26)

where \(\dot{\delta}^{( - )}\) represents the initial contact velocity, \(c_{\mathrm{r}}\) denotes the restitution coefficient, \(K \) is calculated by Eq. (24), and \(\dot{\delta} \) is the penetration rate, and it is given by Eq. (22).

Lankarani and Nikravesh [51] also proposed a continuous contact force model, which uses the Hertz contact law combined with a hysteresis damping factor to accommodate energy dissipation in the form of internal damping. The contact force model is expressed as

$$ f_{\mathrm{n}} = K\delta^{n}\left[ 1 + \frac{3(1 - c_{\mathrm{r}}^{2})}{4}\frac{\dot{\delta}}{\dot{\delta}^{( - )}} \right] $$
(27)

The Lankarani and Nikravesh contact force model is valid for cases where the dissipated energy during the contact process is relatively small compared with the maximum absorbed elastic energy. This means that the model presented in Eq. (27) is valid for values of the coefficient of restitution close to unity [47].

A simplified contact model developed by Gonthier et al. [52] can be utilized to simulate fully elastic to completely plastic impacts, which is represented as

$$ f_{\mathrm{n}} = K\delta^{n}\left[ 1 + \frac{1 - c_{\mathrm{r}}^{2}}{c_{\mathrm{r}}}\frac{\dot{\delta}}{\dot{\delta}^{( - )}} \right] $$
(28)

Finally, Flores and co-workers [53] proposed a contact force model for hard and soft materials that closely follows the methodology proposed by Lankarani and Nikravesh [51]. This model was developed considering the energy dissipation during contact. To this end, the model was described with the foundation of the Hertz law together with a hysteresis damping factor. The normal contact force model presented by Flores et al. [53] yields

$$ f_{\mathrm{n}} = K\delta^{n}\left[ 1 + \frac{8(1 - c_{\mathrm{r}})}{5c_{\mathrm{r}}}\frac{\dot{\delta}}{\dot{\delta}^{( - )}} \right] $$
(29)

The Hunt and Crossley [50] and Lankarani and Nikravesh [51] models have been proposed for nearly elastic contacts, that is, for values of the restitution coefficient close to unity. These two models do not respond adequately to reduced values of this parameter. The Hunt and Crossley and Lankarani and Nikravesh models dissipate less energy during the impact event than the Gonthier et al. [52] and Flores et al. [53] models, as seen from the narrower force pseudo-penetration diagrams in Fig. 6. The Gonthier et al. and Flores et al. models present an adequate behavior for low values of the restitution coefficient, meaning they perform satisfactorily for perfectly inelastic contacts. The area inside the contact force pseudo-penetration loop represents the amount of energy dissipation during a compression-restitution cycle [11, 47]. The Hertz [49] model does not dissipate energy during the contact event, as observed by the absence of a hysteresis loop in Fig. 6. The Hertz model is presented here to provide a comparative basis between the purely elastic and dissipative contact force models.

Fig. 6
figure 6

Contact force versus pseudo-penetration relation for different contact force models

Full size image

4.2 Tangential force models

A substantial number of friction force models that can be used in the context of multibody systems formulations are available in the literature. They might be classified as static or dynamic models [18]. The steady-state behavior of the friction force-relative velocity relation is usually considered in the static models, making them easier to implement in multibody dynamics codes. The second group of friction models, the dynamic ones, illustrates the friction phenomena more realistically since extra state variables are considered in the formulation, which provides additional degrees-of-freedom for each frictional contact [18, 19].

The Coulomb model is the most well-known friction force model. This model postulates that the relative tangential motion between two contacting points is always opposed by friction force, being its magnitude proportional to the normal contact force, as follows

$$ \mathbf{f}_{\mathrm{t}} = \left\{ \textstyle\begin{array}{l@{\quad}l} f_{\mathrm{c}}\mathbf{t} & \mbox{if }v_{\mathrm{t}} \neq 0 \\ \min (f_{\mathrm{e}},f_{\mathrm{c}}){\operatorname{sgn}} (\mathbf{f}_{\mathrm{e}}) & \mbox{if }v_{\mathrm{t}} = 0 \end{array}\displaystyle \right. $$
(30)

where \(v_{\mathrm{t}}\) is the magnitude of the relative tangential velocity, \(\mathbf{t}\) is given by Eq. (20), \(\mathbf{f}_{\mathrm{e}}\) denotes the external tangential force vector and \(f_{\mathrm{c}}\) represents the magnitude of Coulomb’s friction denoted as

$$ f_{\mathrm{c}} = \mu_{\mathrm{k}}f_{\mathrm{n}} $$
(31)

in which \(\mu_{\mathrm{k}}\) is the kinetic coefficient of friction, and \(f_{\mathrm{n}}\) is the normal contact force magnitude.

Even though this model is mathematically simple, it introduces several numerical difficulties as it does not specify a friction force at null velocity. To avoid such discontinuity, several modifications to Coulomb’s friction force model have been proposed [18, 30]. Within the scope of this study, static tangential force models are considered, namely the Threlfall [54], Bengisu and Akay [55], Ambrósio [56], and Brown and McPhee [57] models.

In the model presented by Threlfall [54], an exponential function relates the friction force and tangential velocity. The purpose of this approach is to deal with the numerical difficulties inherent to the discontinuity present in Coulomb’s law. This model was the starting point for the development of other friction force models, such as the continuous function expressed as [18, 30]

$$ \mathbf{f}_{\mathrm{t}} = f_{\mathrm{c}}\tanh \left( \frac{v_{\mathrm{t}}}{v_{1}} \right)\mathbf{t} $$
(32)

where \(v_{1}\) denotes the threshold for the velocity. This methodology to smooth the original Coloumb’s model will, hereafter, be designated Threlfall-based model.

Bengisu and Akay [55] presented a distinct friction force model that is capable of describing both the slope and the Stribeck effect by using two different expressions. The model can be given as

$$ \mathbf{f}_{\mathrm{t}} = \left\{ \textstyle\begin{array}{l@{\quad }l} \left( - \frac{f_{\mathrm{s}}}{v_{0}^{2}}\left( v_{\mathrm{t}} - v_{0} \right)^{2} + f_{\mathrm{s}} \right)\mathbf{t} & \mbox{if }v_{\mathrm{t}} < v_{0} \\ \left( f_{\mathrm{c}} + \left( f_{\mathrm{s}} - f_{\mathrm{c}} \right)\mathrm{e}^{ - \kappa (v_{\mathrm{t}} - v_{0})} \right)\mathbf{t} & \mbox{if }v_{\mathrm{t}} \ge v_{0} \end{array}\displaystyle \right. $$
(33)

where \(v_{0}\) is the threshold for the velocity, \(\kappa\) is a positive parameter representing the negative slope of the sliding state, and \(f_{\mathrm{s}}\) denotes the magnitude of the static friction as

$$ f_{\mathrm{s}} = \mu_{{\mathrm{S}}}f_{\mathrm{n}} $$
(34)

in which \(\mu_{\mathrm{s}}\) is the static coefficient of friction.

Ambrósio [56] also proposed a modification to the original Coulomb’s friction model by incorporating a tolerance around null velocity. When the relative velocity approaches zero, this model avoids direction change in the friction force. The ramps model can be formulated as

$$ \mathbf{f}_{\mathrm{t}} = \left\{ \textstyle\begin{array}{l@{\quad}l} \mathbf{0} & \mbox{if }v_{\mathrm{t}} \le v_{0} \\ \frac{v_{\mathrm{t}} - v_{0}}{v_{1} - v_{0}} f_{\mathrm{c}}\mathbf{t} & \mbox{if }v_{0} < v_{\mathrm{t}} < v_{1} \\ f_{\mathrm{c}}\mathbf{t} &\mbox{if }v_{\mathrm{t}} \ge v_{1} \end{array}\displaystyle \right. $$
(35)

The last model considered is the one proposed by Brown and McPhee [57]. Neglecting the viscous friction term, the model is expressed as

$$ \mathbf{f}_{\mathrm{t}} = \left( f_{\mathrm{c}}\tanh \left( 4\frac{v_{\mathrm{t}}}{v_{\mathrm{s}}} \right) + \left( f_{\mathrm{s}} - f_{\mathrm{c}} \right)\frac{\left( \frac{v_{\mathrm{t}}}{v_{\mathrm{s}}} \right)}{\left( \frac{1}{4}\left( \frac{v_{\mathrm{t}}}{v_{\mathrm{s}}} \right)^{2} + \frac{3}{4} \right)^{2}} \right)\mathbf{t} $$
(36)

where \(v_{\mathrm{s}}\) represents the Stribeck velocity. This model is suitable for real-time simulations and optimization problems because it is continuously differentiable and only velocity dependent.

The characteristic diagram of the friction force-velocity dependence for each of the four friction force models is depicted in Fig. 7. The Coulomb friction force model is used as a reference for comparison purposes with the remaining friction force models.

Fig. 7
figure 7

Friction force models for different approaches

Full size image

4.3 Lubricated model

The hydrodynamic lubricated spherical joints are dynamically loaded through squeeze-film and wedge-film actions. The squeeze-film effect occurs when there is no significant rotation of the ball about its center; but instead, this component moves along some path inside the socket boundaries. In these situations, the relative rotational velocity between the ball and the socket is not significant when compared with the relative radial velocity. On the other hand, when the rotational velocity is high, the wedge-film effect is predominant [24].

When two lubricated spherical surfaces approach each other, the lubricant begins experiencing normal pressures, leading to the phenomenon of squeeze-film action. In these cases, the distribution of pressure can be obtained if a suitable set of boundary conditions is used to integrate the pressure gradient. To this end, there are two types of boundary conditions that can be considered, that is, concerning either the entire domain - Sommerfeld’s boundary condition - or half domain - Gümbel’s boundary condition. In Gümbel’s condition, the pressure field is integrated solely over the positive part by considering that the pressure in the remaining section is null. Since the cavitation phenomenon is not considered in Sommerfeld’s boundary condition, negative pressures can occur. However, in many applications, the fluid is not capable of sustaining significant sub-ambient pressures, and therefore this case is not fulfilled [58].

The hydrodynamic lubrication force due to squeeze-film action developed between the socket and the ball can be modeled using a law presented by Pinkus and Sternlicht [59], which can be formulated as

$$ f_{\mathrm{l}} = \frac{6\uppi \nu \dot{e}R_{i}}{(c/R_{i})^{3}}\left[ \frac{1}{\varepsilon^{3}}\ln (1 - \varepsilon ) + \frac{1}{\varepsilon^{2}(1 - \varepsilon )} - \frac{1}{2\varepsilon} \right] $$
(37)

where \(\nu\) represents the dynamic lubricant viscosity, \(\dot{e}\) is the eccentricity rate given by Eq. (14), and \(\varepsilon\) denotes the eccentricity ratio given by

$$ \varepsilon = \frac{ e}{ c} $$
(38)

where \(e\) and \(c\) are given by Eq. (13) and Eq. (11), respectively.

The direction of the lubrication force (37) is collinear with the line of centers of the socket and ball [24], and the condition utilized for the lubricant flow is Gümbel’s boundary condition.

Since the lubrication force due to the squeeze-film effect is proportional to the rate of decrease of the fluid thickness, it is clear that the lubricant acts as a nonlinear viscous damper that resists the load when the fluid thickness is decreasing. As the fluid thickness becomes very thin, that is, the ball surface is very close to the socket surface, and the lubrication force evaluated from Eq. (37) becomes very large. Consequently, a discontinuity appears when the fluid thickness approaches zero and the lubrication force tends to infinity. It is assumed that, for a certain fluid thickness, called the boundary layer, the fluid can no longer be squeezed out, and the ball and the socket surfaces are considered to be in contact. This situation is similar to the dry contact described in Sect. 4.1 [60]. In order to overcome this shortcoming, Flores and co-workers [60] proposed a hybrid model, which combines the squeeze film action with the dry contact model. In the hybrid model, the ball and the socket can operate in two different modes

  • Mode 1: there is no contact between the surfaces of the ball and the socket. For the dry model, when the eccentricity is smaller than the clearance, the ball is in free flight motion, and there are no forces associated with the ball and the socket. Considering the lubricated model, a force is transmitted through the lubricant. This force must be evaluated from the state variables of the system using Eq. (37).

  • Mode 2: the ball and the socket surfaces are in contact, and the force between these two components can be evaluated using one of the contact force models described in Sect. 4.1.

When the ball reaches the boundary layer, the lubrication force due to the squeeze film effect is replaced by the dry contact force model, as represented in Fig. 8. The change between the two contact modes is performed using a transition stage in which the force is computed recurring to a weighted sum of both lubrication and dry contact force models to avoid discontinuities. Mathematically, the hybrid force model proposed by Flores et al. [60] is expressed as

$$ f_{\mathrm{h}} = \left\{ \textstyle\begin{array}{l@{\quad }l} f_{\mathrm{l}} & \mbox{if }e \le c \\ \frac{(c + e_{\mathrm{h}0}) - e}{e_{\mathrm{h}0}}f_{\mathrm{l}} + \frac{e - c}{e_{\mathrm{h}0}}f_{\mathrm{n}} & \mbox{if }c \le e \le c + e_{\mathrm{h}0} \\ f_{\mathrm{n}} & \mbox{if }e \ge c + e_{\mathrm{h}0} \end{array}\displaystyle \right. $$
(39)

where the lubrication force, \(f_{\mathrm{l}}\), is calculated as in Eq. (37) and, to avoid numerical issues, Eq. (38) is replaced by

$$ \varepsilon = \frac{ e}{ c + e_{\mathrm{h}1}} $$
(40)

where \(e\)h0 and \(e\)h1 are given tolerances for the eccentricity, as observed in Fig. 8.

Fig. 8
figure 8

Schematic representation of the force-eccentricity relation of the hybrid model

Full size image

4.4 Bushing formulation

The eccentricity vector \(\mathbf{e}\), represented in Fig. 2 and given by Eq. (12), is related to the deformation of the elastomer in a spherical joint with a bushing element [42]. The approach utilized in this study is based on the formulation proposed by Ambrósio and Veríssimo [42], which obtained the constitutive equations for several bushing joint models through a finite element analysis using a nonlinear finite element code. A linear force-displacement relation was obtained for the spherical bushing joint from which the elastic part of the constitutive relation considers a constant stiffness. To introduce dissipation in the constitutive equation of the spherical bushing joint and to provide more realistic results, the authors [42] suggested a stiffness proportional damping parameter, which is obtained by a trial-and-error approach. In this sense, the expression of the force due to the bushing deformation is as follows

$$ \mathbf{f}_{\mathrm{b}} = \left[ k\left( \delta + b\dot{\delta} \right) \right]\mathbf{n} $$
(41)

where \(k\) is the stiffness of the bushing element, \(b \) denotes the stiffness proportional damping parameter, \(\delta\) represents the bushing deformation, and \(\dot{\delta} \) is the deformation rate. In this study, it is assumed that no gap exists between the bushing and the ball. In this sense, \(e = \delta\) and, thus, \(\delta \) and \(\dot{\delta} \) are given by Eq. (13) and Eq. (14), respectively.

5 Demonstrative examples of application

The objective of this section is to examine the influence of using different cases for modeling spherical joints on the dynamic response of multibody systems. To this end, two application examples are utilized, namely a spatial four-bar mechanism and a car suspension model. All simulations were run in Matlab® R2020b using an in-house code.

5.1 Spatial four-bar mechanism

The spatial four-bar mechanism considered in this work has four rigid bodies: the ground, crank, coupler, and rocker. The local coordinate systems of each body of the mechanism and their associated number are shown in Fig. 9.

Fig. 9
figure 9

Schematic representation of the spatial four-bar mechanism

Full size image

Two revolute and two spherical joints are utilized in order to kinematically connect the bodies to each other. The revolute joints are applied between the ground and the crank and between the ground and the rocker. On the other hand, the two spherical joints connect the crank to the coupler and the coupler to the rocker. Realistic characteristics of nonideal cases are introduced in the spherical joint connecting the coupler and the rocker to analyze the dry, lubricated, and bushing joint models. All the other joints are considered to be ideal.

The initial configuration of the spatial four-bar mechanism is illustrated in Fig. 9, and the associated initial conditions are presented in Table 1. The system is released from the initial configuration with no velocity. Apart from the forces developed in the joint, gravitational action is the only external force considered, and it is assumed to act in the negative \(z\)-direction. For the nonideal joint models, these initial conditions force the ball and the socket of the spherical clearance joint to be concentric at the initial instant of time.

Table 1 Initial configuration of the spatial four-bar mechanism
Full size table

The dimensions and inertial properties of each body of the spatial four-bar mechanism are listed in Table 2.

Table 2 Dimensions and inertial properties of the spatial four-bar mechanism
Full size table

The simulation parameters used in all dynamic simulations and in the numerical methods required to solve the dynamics of the system are displayed in Table 3.

Table 3 Parameters used in the dynamic simulation of the four-bar mechanism
Full size table

For the case of the dry clearance joint, two different types of analysis are performed, that is, without and with friction. Concerning the frictionless joint, the study of the effect of the clearance size and contact force model on the response of the system is carried out. For the dry clearance joint with friction, the same analyses are conducted, together with the study of the friction force model. Regarding the lubricated joint, the clearance size is examined. In the bushing joint model, both the stiffness and damping are studied. The socket radius has a constant value of 10 mm. When clearance is added to the system, the ball radius is adjusted accordingly. Table 4 shows the parameters for each simulation.

Table 4 Parameters for the performed simulations
Full size table

In what follows, several numerical results obtained from various computational simulations are presented to assess the response of the spatial four-bar mechanism considering the different spherical joint models. All simulations are compared with the ideal joint case. The \(z\)-component of the position, velocity, and acceleration was chosen to be evaluated because it is the one in which more differences can be observed, facilitating the comparison amongst the joint models analyzed. We chose to analyze the rocker because it is the output body of the mechanism.

The first analysis for each joint model includes four plots, namely the \(z\)-component of the position, velocity and acceleration of the rocker, and the variation of the mechanical energy of the system. The acceleration and the mechanical energy are more sensitive quantities than the position and velocity, in a sense that their evolution is more affected by the simulation conditions. Therefore, the acceleration and the mechanical energy are subsequently considered as the main variables analyzed.

Concerning the frictionless case, the influence of the radial clearance size on the \(z\)-component of the position, velocity, and acceleration of the rocker center of mass and on the mechanical energy of the system is presented in the plots in Fig. 10. It can be observed that the mechanism tends to exhibit a similar response to the ideal joint case when the clearance size is equal to 0.05 mm. This is the clearance size that leads to less energy dissipation. In addition, the larger the clearance size, the higher the oscillations observed in the response of the system, mainly in terms of the velocity and acceleration plots. Regarding the mechanical energy of the system, it can be concluded that, for the initial contacts, the larger the clearance size, the higher the energy dissipated by the system. However, due to the chaotic motion associated with clearance, in the subsequent contacts, the motion of the system is no longer predictable, and no relationship can be established.

Fig. 10
figure 10figure 10

Influence of the clearance size on the response of the spatial four-bar mechanism with a dry spherical clearance joint without friction. (a) Position, (b) velocity and (c) acceleration of the rocker, (d) mechanical energy

Full size image

The influence of different normal contact force models on the response of the spatial four-bar mechanism is shown in the plots in Fig. 11. The Gonthier et al. model produces higher acceleration peaks when compared with the remaining contact force models. In turn, the Lankarani and Nikravesh model dissipates the highest amount of energy of all models studied, which is sound because this model is valid for values of the restitution coefficient close to unity.

Fig. 11
figure 11

Influence of the normal contact force model on the response of the spatial four-bar mechanism with a dry spherical clearance joint without friction. (a) Rocker’s acceleration, (b) mechanical energy

Full size image

The introduction of friction on the spherical clearance joint model of the spatial four-bar mechanism produces the diagrams represented in Fig. 12.

Fig. 12
figure 12figure 12

Influence of the clearance size on the response of the spatial four-bar mechanism with a dry spherical clearance joint with friction. (a) Position, (b) velocity and (c) acceleration of the rocker, (d) mechanical energy

Full size image

In a similar manner to the frictionless joint model, when the clearance size is small (0.05 mm), the mechanism tends to have a response closer to the ideal joint case. Regarding the acceleration and mechanical energy plots, the behavior of the system with friction presents fewer oscillations than the frictionless model (see Fig. 12). Concerning only the model with friction, the system tends to be less chaotic for smaller clearance sizes. In addition, the decrease in the clearance size leads to a more conservative system, as the variation of the mechanical energy is smaller.

The four normal contact force models considered above are also compared when the joint is modeled with friction. From the analysis of the plots in Fig. 13, it can be concluded that no significant differences are visible among the models analyzed for both the \(z\)-component of the acceleration of the rocker and the variation of the mechanical energy of the system. This feature arises from the fact that, for this application example, the friction forces have a more important role in the energy dissipation during the contact process than the normal contact force model. Comparing with the frictionless joint, the joint with friction presents smoother acceleration curves.

Fig. 13
figure 13

Influence of the normal contact force model on the response of the spatial four-bar mechanism with a dry spherical clearance joint with friction. (a) Rocker’s acceleration, (b) mechanical energy

Full size image

With the intention of analyzing the response of the system with a spherical clearance joint with friction, four different friction force models are considered. The kinematic response of the rocker, as well as the variation of the mechanical energy of the system, are presented in Fig. 14. It can be observed that there are no significant deviations between the different friction force models. The main differences may occur in the vicinity of the null relative sliding velocity. Thus, to show discrepancies in the response of the system, a detailed view is plotted in Fig. 14(c) for the acceleration of the rocker. As described in Sect. 4.2, the Threlfall-based [54] and the Ambrósio [56] friction force models do not consider the static coefficient of friction in the calculation of the friction force. As seen in Fig. 14(c), these friction force models exhibit smaller peaks in the acceleration than the models that consider the static coefficient of friction, namely the Bengisu and Akay [55] and the Brown and McPhee [57] approaches. Moreover, those acceleration peaks better describe the friction phenomena since they represent the increase in friction force when the relative tangential velocity approaches zero, which might allow capturing the stick-slip effect.

Fig. 14
figure 14

Influence of the friction force model on the response of the spatial four-bar mechanism with a dry spherical clearance joint with friction. (a) Rocker’s acceleration and (b) mechanical energy, (c) detailed view of the acceleration in which the relative sliding velocity is close to zero

Full size image

The following outcomes concern the inclusion of a lubricant between the ball and the socket of the coupler and rocker components of the spatial four-bar mechanism. The value considered for the dynamic lubricant viscosity is 400 cP, which corresponds to the oil viscosity at 40 °C.

The effect of the clearance size on the dynamic response of the four-bar mechanism with a lubricated spherical joint is presented in Fig. 15. Concerning the \(z\)-component of the position of the rocker, it can be stated that the smaller the clearance size, the closer the behavior of the mechanism is to the ideal joint case. In addition, as can be observed in Fig. 15, higher values of the radial clearance induce higher velocity and acceleration peaks on the \(z\)-component of the rocker. Besides, higher values of clearance size also lead to an increase in the oscillations of these curves, indicating an increase in the chaotic behavior of the system, as seen in Fig. 15(b) and (c). Similarly, the energy dissipation is higher for larger values of the radial clearance.

Fig. 15
figure 15figure 15

Influence of the clearance size on the response of the spatial four-bar mechanism with a lubricated spherical clearance joint (a) Position, (b) velocity and (c) acceleration of the rocker, (d) mechanical energy

Full size image

The results regarding the introduction of a bushing element to the spherical joint of the four-bar mechanism are presented in the following paragraphs. It is evident that the lower the stiffness of the bushing, the higher the differences of the bushing model curves when compared with the ideal joint case. This phenomenon is particularly evident for both the position and velocity plots, as seen in Fig. 16(a) and (b), respectively. These results are expected in the measure that, in the ideal joint model, the ball and the socket of the spherical joint are considered to be rigid bodies and are in continuous contact with each other. On the contrary, the bushing element is a flexible component that is introduced between these two rigid components. Thus, the rigid ball and socket elements are not in direct contact with each other. Instead, they contact with a flexible bushing element, causing a response of the system different from the ideal joint case. Observing Fig. 16(c), no significant differences in acceleration are found with the modification of the stiffness of the bushing element. The variation of the mechanical energy of the system indicates that the higher the value of the stiffness, the lower the energy dissipation since a stiffer bushing allows less relative displacement and velocity between the ball and the socket elements, which decreases the damping.

Fig. 16
figure 16figure 16

Influence of the stiffness on the response of the spatial four-bar mechanism with a spherical bushing joint. (a) Position, (b) velocity and (c) acceleration of the rocker, (d) mechanical energy

Full size image

Observing the acceleration plot of Fig. 17, no significant differences are noted for the different values tested for the damping of the bushing element. However, taking a close look at the variation of the mechanical energy, it can be stated that at the beginning of the analysis, the lowest damping value is a cause of an overestimation of the energy. As the simulation proceeds, the higher the value of the damping, the higher the energy dissipation.

Fig. 17
figure 17

Influence of the damping on the response of the spatial four-bar mechanism with a spherical bushing joint. (a) Rocker’s acceleration, (b) mechanical energy

Full size image

To analyze the effect of the different spherical joint models, a detailed comparison concerning the \(z\)-component of the position, velocity, and acceleration of the rocker and the variation of the mechanical energy of the system for the spherical joint models analyzed in this study is provided in Fig. 18.

Fig. 18
figure 18figure 18

Influence of the spherical joint model on the response of the spatial four-bar mechanism (a) Position, (b) velocity and (c) acceleration of the rocker, (d) mechanical energy

Full size image

Concerning the analyses done so far, it can be stated that the dynamic response of the four-bar mechanism is influenced by the model selected to characterize the spherical joint. In general, the dry clearance joint model, that is, the frictionless model, is the one exhibiting the highest number of oscillations when compared with the other joint models. Moreover, it is clear that the four-bar mechanism incorporating the frictionless dry spherical joint model generates larger velocities and accelerations than those observed in the ideal dry joint with friction and lubricated models. This suggests that when friction is not considered in the analysis, the response of the system becomes chaotic. In fact, the introduction of friction in the dry spherical clearance joint has a tendency to smooth the behavior of the system, leading to a less chaotic motion. The observation of Fig. 18(c) indicates that the spatial four-bar mechanism produces lower accelerations with the ideal joint model compared with the other approaches. Concerning the variation of the mechanical energy, the model with friction exhibits the highest energy dissipation, followed by the frictionless and lubricated models, as can be seen in Fig. 18(d). As expected, the results presented by the bushing joint model are closer to the ideal joint case. This means that the inclusion of the bushing element is, in fact, decreasing the noise associated with clearance and stabilizing the system, making it less chaotic. The bushing model is the model that dissipates less amount of energy compared with the other spherical joint models. These results are expected as the bushing element is intended to handle deviations from the ideal alignment, constraining the system and, consequently, limiting its chaotic response.

In order to study the level of nonlinearity associated with the response of a specific system, it is a common practice to analyze the phase portraits. In this sense, the \(z\)-component of the position of the rocker versus its velocity and the velocity versus the acceleration are the variables considered to plot the phase portraits of all spherical joint models analyzed in this work. The phase portraits can be observed in Fig. 19 (a)-(j). A detailed analysis of Fig. 19 leads to the conclusion that the four-bar mechanism exhibits a non-smooth behavior when the spherical clearance joint is modeled without friction. This phenomenon is directly related to the level and degree of the impacts between the surfaces of the ball and the socket. When the joint is frictionless, the system requires more time to ensure continuous or permanent contact between the joint elements. It is also evident that the initial impacts are followed by rebounds, which helps explain the more complex nature of the phase portraits. This phenomenon indicates chaotic behavior and can be observed in Fig. 19 (c) and (d). Contrarily to the frictionless joint model, the dynamic behavior of the system modeled with a spherical clearance joint with friction is smoother and closer to the ideal joint case, which can be confirmed in the diagram of Fig. 19 (a), (b), (e) and (f). The smoother behavior can be associated with the dissipative nature related to the friction effect, which facilitates the accommodation between the ball and the socket surfaces. In the model with friction, the system produces impacts with lower magnitude.

Fig. 19
figure 19figure 19

Phase portraits of \(z\)-position vs. \(z\)-velocity and \(z\)-velocity vs. \(z\)-acceleration: (a), (b) ideal; (c), (d) dry clearance, (e), (f) dry clearance with friction; (g), (h) lubricated; (i), (j) bushing

Full size image

Concerning the lubricated model, the response of the four-bar mechanism tends to be close to the ideal joint case because the lubricant acts as a filter by reducing the level of the peaks due to severe dry impact. This phenomenon is observed by the simple and less chaotic behavior visible in the phase portraits of Fig. 19 (a), (b), (g), and (h). The shape of the phase portrait diagrams of the bushing joint is the closest to that of the ideal joint case. This occurrence is related to the fact that the bushing element constrains the motion of the ball and socket relative to each other, acting closer to the ideal joint.

The time evolution of the eccentricity for the spherical joint models analyzed is presented in Fig. 20. The black line represents the maximum eccentricity, which is equal to the radial clearance and equal to 0.10 mm. For the dry joint models, it is clear that in the beginning of the simulation, the ball and the socket are concentric and start to separate until a maximum eccentricity is reached. The subsequent impacts are followed by rebounds, which are visible in the diagrams of Fig. 20 (a) and (b), where the system changes from free flight mode to impact mode. After that, the ball enters contact mode and continues this motion until the end of the simulation. By observing Fig. 20(a) and (b), in the dry joint with friction, the contacts have a smaller magnitude than in the frictionless joint model. This fact might be related to the dissipative nature associated with the friction effect, which promotes the accommodation between the ball and the socket surfaces.

Fig. 20
figure 20

Evolution of the eccentricity ratio with time for the four-bar mechanism: (a) dry clearance joint, (b) dry clearance joint with friction, (c) lubricated joint, (d) bushing joint

Full size image

Concerning the lubricated spherical joint model, the ball surface does not reach the socket surface (see Fig. 20(c)). This phenomenon is logical since the lubricant that fills the space between the socket and the ball keeps the two bodies apart due to the high pressures generated when the bodies tend to approximate each other. As discussed above, the bushing joint model does not consider clearance. Therefore, this model tends to present a behavior close to the ideal joint case, and, thus, the ball and the socket tend to remain concentric throughout the simulation, as shown in Fig. 20(d). Consequently, when analyzing the bushing joint model, the resulting eccentricity is not comparable to that of the other joint models, as they consider clearance.

Finally, the computational efficiency of the different spherical joint models considered in the spatial four-bar mechanism is compared through the computational time ratio, which allows a fair comparison regardless of the computer and programming language used, and it is plotted in Fig. 21. As expected, the ideal joint model is the most efficient approach. Thus, the elapsed time of the ideal joint simulation was considered the reference, and all joint models studied were divided by this reference to provide the computational time ratio. The introduction of clearance penalizes the efficiency of the simulation. However, the addition of friction to the clearance joint leads to an increase in computational efficiency. Both the lubricated and bushing joint models decrease the computational efficiency of the system, with the bushing model being the worst in terms of efficiency.

Fig. 21
figure 21

Computational time ratio for the different spherical joint models for the four-bar mechanism

Full size image

5.2 Right front suspension of a car

The second example of application is a multibody model of a right front suspension of a car that passes over a bump. The European automobile industry proposed the 4×4 BOMBARDIER ILTIS vehicle to validate multibody dynamic codes [61]. For the sake of simplicity, the vehicle chassis is omitted, and the suspension components are considered to be attached to the ground. The model is composed of four bodies, namely the wheel with a hub and break assembly, the A-arm, the leaf spring, and the tie rod. These bodies are kinematically connected to each other by two revolute and four spherical joints (see Fig. 22). The revolute joints connect the A-arm to the ground and the leaf spring to the ground. The spherical joints link the wheel to the A-arm, the leaf spring to the A-arm, the A-arm to the tie rod, and the tie rod to the ground. Clearance and bushing are introduced in the spherical joint connecting the wheel and the A-arm, which is highlighted in Fig. 22, in order to analyze the dry, lubricated, and bushing joint models on the system’s response.

Fig. 22
figure 22

Schematic representation of a right front suspension of a car

Full size image

The initial conditions for the right front suspension of a car are presented in Table 5. The system is assumed to move with a constant linear velocity of 5 m/s in the \(x\)-direction. For the nonideal joint models, at the initial instant of time, the ball and the socket of the spherical clearance joint are concentric.

Table 5 Initial configuration of the right front suspension of a car
Full size table

The mass and moment of inertia of the wheel and A-arm bodies of the right front suspension of a car are listed in Table 6, the inertial properties of the remaining bodies neglected.

Table 6 Inertial properties of the right front suspension of a car
Full size table

The gravitational force acts on the negative \(z\)-direction. Apart from this force, the system is also incorporated with a shock absorber connected to the A-arm, generating both elastic, \(f_{\mathrm{k}}\), and damping, \(f_{\mathrm{d}}\), forces as [61]

$$\begin{aligned} & f_{\mathrm{k}} = - 4.0092 \times 10^{6} + 2.8397 \times 10^{7}x - 6.7061 \times 10^{7}x^{2} + 5.2796 \times 10^{7}x^{3} \end{aligned}$$
(42)
$$\begin{aligned} & f_{\mathrm{d}} = \left\{ \textstyle\begin{array}{l@{\quad }l} - 416.42 + 1844.3\dot{x} & \mbox{if }\dot{x} < - 0.20 \\ 9945.627\dot{x} + 33955.72 \dot{x}^{2} - 59832.25\dot{x}^{3} - 395651.0\dot{x}^{4} & \mbox{if }- 0.20 < \dot{x} < 0.21 \\ 1919.1638 + 1634.727\dot{x} & \mbox{if } \dot{x} > 0.21 \end{array}\displaystyle \right. \end{aligned}$$
(43)

where \(x\) is the distance between the two ends of the shock absorber, and \(\dot{x}\) represents the corresponding velocity.

The leaf spring is modeled considering two stiffnesses. This means that, for deformations smaller than 145 mm, the leaf spring behaves similarly to a linear spring with 35900 N/m. For higher deformations, a bump stop contact occurs, and a second spring with a stiffness equal to 107 N/m is activated. The tire is modeled as a linear spring with an unloaded radius of 0.36325 m and stiffness of 460×103 N/m. The tire passes over a bump with a profile described by the following condition [61]

$$\begin{aligned} & z_{\mathrm{B}} = \left\{ \textstyle\begin{array}{l@{\quad }l} 0 & \mbox{if }x_{\mathrm{B}} < 15 \\ 0.1\left[ 1 - \cos \left( \frac{2\uppi (x_{\mathrm{B}} - 15)}{5} \right) \right] & \mbox{if }15 < x_{\mathrm{B}} < 20 \\ 0 & \mbox{if }x_{\mathrm{B}} > 20 \end{array}\displaystyle \right. \end{aligned}$$
(44)

where \(x_{\mathrm{B}}\) is the horizontal position of the bump profile in meters obtained from the wheel center position and \(z_{\mathrm{B}}\) is the vertical position of the bump profile.

The simulation parameters utilized to solve the dynamics of the right front suspension of a car are similar to those considered for the four-bar mechanism (see Table 3). However, the integration algorithm utilized to simulate the right front suspension model is ode45, which is an explicit method from the Runge-Kutta family [62], instead of ode15s, which uses Gear’s method based on backward differentiation formulas [63, 64]. The ode45 is suitable and efficient for the suspension multibody model since the resolution of its equations of motion results in a “non-stiff” problem. This integrator is classified as a variable step type, as it adjusts the time step in order to increase accuracy in quickly changing events and to avoid taking too many steps if the model’s variables are very stable. The simulation time is also set to 6 seconds so the tire could pass over the bump with the profile (44).

The results obtained from the computational simulations are presented in the plots of Fig. 23, which show the response of the right front suspension of a car considering the different spherical joint models described previously. The car passes over the bump between the 3 and 4 seconds of simulation time, as seen from the abrupt variation of the plots in Fig. 23. It can be observed that no significant differences are found among the different spherical joint models used. Since the system comprises several elastic and damping forces arising from the shock absorber and from the leaf spring, the influence of those forces on the dynamic response of the system might be much more relevant than the influence of the spherical joint model. Thus, the type of joint model has very little influence on the overall response of the system.

Fig. 23
figure 23figure 23

Influence of the spherical joint model on the response of the right front suspension of a car. (a) Position, (b) velocity and (c) acceleration of the wheel, (d) mechanical energy

Full size image

With intend to provide a more detailed analysis, the eccentricity evolution throughout the simulation time for the different spherical joint models is plotted in Fig. 24. For all models, at some point, the eccentricity is higher than the clearance size (represented by the black line, as in the case of the four-bar mechanism), meaning that there is an extra penetration between the ball and the socket associated with the bump. This phenomenon occurs when the system passes over the bump with the profile described by Eq. (44). For the joint without friction, joint with friction and lubricated joint models, concerning the analysis of the joint reaction forces on the spherical clearance joint, it is possible to determine the maximum value for the \(z\)-component of the joint reaction force, which is, approximately, 20 kN. Knowing that the generalized stiffness, \(K\), is 1.5089×1011 N/m\(^{3/2}\) (obtained with Eq. (24)) and taking into account Eq. (23), then the maximum pseudo-penetration yields 0.026 mm. Considering now Eq. (21), it can be concluded that the maximum eccentricity has a value of 0.130 mm. The outer circle in the eccentricity plots for these three models has a value of 0.150 mm. Therefore, it is logical that the eccentricity plots for the joint without friction, joint with friction, and lubricated joint models present an eccentricity that goes beyond the maximum clearance of 0.10 mm when the system passes over the bump.

Fig. 24
figure 24

Evolution of the eccentricity ratio with time for the right front suspension of a car: (a) dry clearance joint, (b) dry clearance joint with friction, (c) lubricated joint, (d) bushing joint

Full size image

Regarding only the lubricated joint model, throughout most of the simulation time, the ball is in contact mode. This phenomenon is associated with the fact that the hydrodynamic effect produced by the lubricant cannot support such a high load that is imposed on it due to the dynamics of the entire system. Thus, the hybrid force model represented by Eq. (39) remains in the contact zone using the chosen contact force model. In the results obtained for the eccentricity of the bushing joint model, the outer circle of Fig. 24(d) has a value of 1.10 mm. Based on the results obtained by Ambrósio and Veríssimo [42], a penetration of 1.50 mm was expected. In fact, the findings observed in Fig. 24(d) are in accordance with this value of penetration. These results are expected since the bushing is a flexible element enabling higher deformations than the rigid ball and socket components, as occurs in the other joint models. Besides these results, it can also be concluded that both the lubricated and dry clearance joint with friction models dampen the peaks associated with the initial impacts compared with the dry spherical clearance joint case.

The computational efficiency of the spherical joint models is also examined for the right front suspension of a car (see Fig. 25). The conclusions drawn for the four-bar mechanism concerning the ideal joint, frictionless joint, and joint with friction are similar to the ones drawn for the suspension model. In addition, both the lubricated and bushing joint models decrease the computational efficiency of the system. However, the lubricated joint model is less efficient, meaning that the model (39) may not be appropriate for the suspension from the physical point of view. The best approaches to computational efficiency are the ideal and dry joint with friction models.

Fig. 25
figure 25

Computational time ratio for the different spherical joint models for the right front suspension

Full size image

6 Concluding remarks

A comparative analysis of several approaches for the dynamic modeling of spherical joints in spatial multibody systems is examined in this work. For that, the kinematics of the ideal, dry, lubricated and bushing spherical joint modeling strategies are revisited. Subsequently, the main dynamic aspects of these types of spherical joint models are briefly described, taking into account the corresponding normal, tangential, lubrication and bushing forces. In the aftermath of this process, two demonstrative examples of application are considered to study the influence of the joint modeling approaches, namely a spatial four-bar mechanism and a right front suspension of a car. The dynamic response of these multibody models with the different spherical joint modeling strategies described, together with their computational efficiency, is assessed. The performance of the four-bar mechanism is strongly affected by the spherical joint modeling, which is essentially visible in terms of accelerations, the mechanical energy of the system, and joint eccentricity. On the contrary, no significant differences are observed for the right front suspension of a car model. Overall, the influence of the spherical joint modeling strategy on the dynamic response of mechanical multibody systems depends on the dynamics of the system under analysis. Although the selected spherical joint model affects the dynamics of the joint and, consequently, the mechanical system, it is not possible to establish a hierarchy among the studied approaches. The selection of each of these strategies relies on the required degree of accuracy and, mainly, on the topology of the spherical joint to be modeled.