1 Introduction

Multibody dynamic models are commonly employed in the design, analysis, and control of systems in a wide range of applications. It is often most convenient to model a multibody system using more generalized coordinates than there are degrees-of-freedom in the system. The presence of dependent coordinates results in a system of index-3 differential-algebraic equations (DAEs) of motion—that is, the second-order ordinary differential equations (ODEs) governing the dynamics of the system are coupled to a set of algebraic constraint equations. For these equations to accurately predict the response of a physical system, suitable system parameters must be determined, either through direct physical measurement or using parameter identification. If experimental measurements can be obtained from the physical system, the parameters in the mathematical model can be determined using optimization techniques. The optimal system parameters for the mathematical model are those that minimize the error between the model response and the experimental data. Note that the identified parameters may differ from the parameters of the physical system in the presence of modeling errors.

Linear regression [10, 17] is one of the simplest, yet most powerful, tools available for identifying parameters in a mathematical model. One of the key advantages of linear regression is that it always leads to a convex optimization problem and, as such, the identified parameters are guaranteed to be globally optimal. A drawback of this method is that the parameters being sought must appear linearly in the mathematical model. When absolute coordinates are used to model a multibody system, the inertial parameters appear linearly in the equations of motion [2, 3, 8, 14], and the parameter identification problem can be readily solved using linear regression. In many applications, however, it is more convenient to model the system using joint coordinates. In this case, the geometric and inertial parameters are coupled, and a new set of barycentric parameters [1, 4, 5, 12] can be defined to facilitate the application of linear regression. In all existing work on parameter identification using linear regression, the Lagrange multipliers are first eliminated from the dynamic equations to obtain a system of ODEs in the independent coordinates [2, 3, 8, 14]. Using the conventional approach, linear regression can be applied only once the Lagrange multipliers have been eliminated. Eliminating the Lagrange multipliers may be a nontrivial task, however, as it requires the assembly of an orthogonal complement of the Jacobian [9], which can be onerous if a symbolic formulation is used.

In this work, we present an approach for using linear regression to identify the inertial system parameters and time-varying Lagrange multipliers simultaneously, thereby avoiding the need to eliminate the latter from the dynamic equations. Since linear regression can be implemented as a recursive algorithm, the proposed approach facilitates the real-time identification of inertial parameters and Lagrange multipliers in applications requiring online identification. For instance, the health of a multibody system can be monitored by detecting changes in the behavior of the Lagrange multipliers, which often represent reaction forces in kinematic joints. The mathematical details of our approach are presented in Sect. 2. In Sect. 3, we present two numerical examples—the first, using absolute coordinates; the second, using joint coordinates—to demonstrate the application of this approach. We use Monte Carlo simulation [11] to investigate the identification of parameters when the experimental data are corrupted by measurement noise, and justify the use of such an approach. Finally, conclusions and future work are outlined in Sect. 4.

2 Mathematical modeling

The equations governing the motion of a multibody system can be expressed as follows:

$$\begin{aligned} \mathbf{M}( \mathbf{q}, \mathbf{p}, \mathbf{k} ) \,\ddot{\mathbf{ q}} + \mathbf{J}( \mathbf{q}, \mathbf{k} )^{\mathrm{T}} \boldsymbol{ \lambda}(t) =& \mathbf{f}( \mathbf{q}, \dot{\mathbf{q}}, \mathbf {p}, \mathbf{k} ) + \mathbf{f}_{\text{e}}(t) \end{aligned}$$
(1)
$$\begin{aligned} \boldsymbol{\Phi}( \mathbf{q}, \mathbf{k} ) =& \mathbf{0} \end{aligned}$$
(2)

where q=[q 1(t),q 2(t),…,q n (t)]T is a vector containing the n time-dependent modeling coordinates, and p=[ p 1,p 2,…,p r ]T contains the unknown system parameters, which can be masses, moments of inertia, or barycentric parameters, depending on the topology of the system and the choice of modeling coordinates. M(q,p,k) is the n×n configuration- and parameter-dependent mass matrix; Φ(q,k) represents the m nonlinear algebraic constraint equations, which are functions of known geometric parameters (i.e., lengths) k; J(q,k)=∂ Φ/∂ q is the m×n Jacobian matrix; and λ(t)=[λ 1(t),λ 2(t),…,λ m (t)]T are the Lagrange multipliers. The first term on the right-hand side of (1) contains the quadratic velocity terms; the second term, f e(t), contains the externally applied forces and torques.

We are interested in determining the parameters p given experimental measurements for q, \(\dot{\mathbf{q}}\), \(\ddot{\mathbf {q}}\), and f e at equally-spaced time points [t 1,t 2,…,t f ], where δt≜t i+1−t i . Provided the parameters p appear linearly, the dynamic equations (1) can be expressed in the following alternate form:

$$ \boldsymbol{\Gamma}( \mathbf{q}, \dot{\mathbf {q}}, \ddot{\mathbf{ q}}, \mathbf{k} )_{n \times r} \,\mathbf{p}_{r \times1} + \mathbf{J}( \mathbf{q}, \mathbf{k} )^{\mathrm{T}} \boldsymbol{\lambda}(t) = \mathbf{h}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf{q}}, \mathbf{k} ) + \mathbf {f}_{\text{e}}(t) $$
(3)

where \(\mathbf{h}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf{q}}, \mathbf{k} )\) contains terms involving inertial parameters that are known, should any exist. In this work, the conversion of (1) into the form shown in (3) is facilitated by the use of a symbolic formulation. Note that (3) cannot be used to perform linear regression directly, as the Lagrange multipliers λ(t) are unknown.

We proceed by expanding each Lagrange multiplier λ i (t) in a piecewise linear form over equally-spaced time points (Δ) t=[1 t,2 t,…,ℓ t]:

$$\begin{aligned} \lambda_i(t) =& \sum_{j=1}^{\ell-1} \biggl[ {}^{j}\lambda _i \biggl( 1 - \frac{t - {}^{j}t}{\Delta t} \biggr) + {}^{j+1}\lambda _i \biggl( \frac{t - {}^{j}t}{\Delta t} \biggr) \biggr] \bigl[ H\bigl(t - {}^{j}t \bigr) - H\bigl( t - {}^{j+1}t\bigr) \bigr] \\ \triangleq&\mathbf{b} \mathbf{a}_i \end{aligned}$$
(4)

where H(x) is the Heaviside step function, Δt=j+1 t−j t, and a i =[1 λ i ,2 λ i ,…,ℓ λ i ]T. Introducing the notation \(H_{j}^{j+1} = H(t - {}^{j}t) - H( t - {}^{j+1}t)\) and β j =(t−j t)/Δt, we can express b as follows:

$$\begin{aligned} \mathbf{b} =& \bigl[ ( 1 - \beta_1 ) H_1^2, \beta_1 H_1^2 + ( 1 - \beta_2 ) H_2^3, \ldots, \\ & \quad\beta_{\ell-2} H_{\ell-2}^{\ell-1} + ( 1 - \beta_{\ell-1} ) H_{\ell-1}^{\ell}, \;\; \beta_{\ell-1} H_{\ell -1}^{\ell} \bigr] \end{aligned}$$
(5)

The objective is now to determine the value of each Lagrange multiplier λ i (t) at time points (Δ) t along with the parameters p. We can now express the Lagrange multipliers as follows:

$$ \boldsymbol{\lambda}(t) = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{b} & \mathbf{0} & \ldots& \mathbf{0} \\ \mathbf{0} & \mathbf{b} & \ldots& \mathbf{0} \\ \vdots& \vdots& \ddots& \vdots\\ \mathbf{0} & \mathbf{0} & \ldots& \mathbf{b} \end{array} \right] _{m \times\ell m} \left\{ \begin{array}{c} \mathbf{a}_1 \\ \mathbf{a}_2 \\ \vdots\\ \mathbf{a}_m \end{array} \right\} _{\ell m \times1} \triangleq\mathbf{B} \;\!\mathbf{a} $$
(6)

Upon substitution of (6) into (3), we obtain the following:

$$ \left[ \begin{array}{c@{\quad}c} \boldsymbol{\Gamma}( \mathbf{q}, \dot{\mathbf{q}}, \ddot {\mathbf {q}}, \mathbf{k} ) & \mathbf{J}( \mathbf{q}, \mathbf{k} )^{\mathrm{T}} \mathbf{B} \end{array} \right] \left\{ \begin{array}{c} \mathbf{p} \\ \mathbf{a} \end{array} \right\} = \mathbf{h}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf{q}}, \mathbf{k} ) + \mathbf{f}_{\text{e}}(t) $$
(7)

Finally, we assemble (7) at each point in time for which experimental data are collected:

$$ \left[ \begin{array}{c@{\quad}c@{\quad}c} [ \boldsymbol{\Gamma}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf{q}}, \mathbf{k} ) & & \mathbf{J}(\mathbf{q}, \mathbf{k} )^{\mathrm{T}} \,\mathbf{B} ]_{t = t_1} \\ {} [ \boldsymbol{\Gamma}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf{q}}, \mathbf{k} ) & &\mathbf{J} (\mathbf{q}, \mathbf{k})^{\mathrm{T}} \,\mathbf{B} ]_{t =t_2} \\ & \vdots& \\ {} [ \boldsymbol{\Gamma}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf{q}}, \mathbf{k} )& &\mathbf{J}(\mathbf{q}, \mathbf{k} )^{\mathrm{T}} \,\mathbf{B} ]_{t = t_{\!f} } \end{array} \right] \left\{ \begin{array}{c} \mathbf{p} \\ \mathbf{a} \end{array} \right\} = \left\{ \begin{array}{c} \mathbf{h}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf {q}}, \mathbf{k} )_{t = t_1} + \mathbf{f}_{\text{e}}(t_1) \\ \mathbf{h}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf {q}}, \mathbf{k} )_{t = t_2} + \mathbf{f}_{\text{e}}(t_2) \\ \vdots\\ \mathbf{h}( \mathbf{q}, \dot{\mathbf{q}}, \ddot{\mathbf {q}}, \mathbf{k} )_{t = t_{\!f}} + \mathbf{f}_{\text{e}}(t_{\!f}) \end{array} \right\} $$
(8)

Standard least-squares algorithms can be used to solve (8) and obtain the r system parameters p and ℓm Lagrange multiplier values a (provided r+ℓm≤nf and the system is not underdetermined). Note, however, that (8) is not of the form used in standard linear regression problems (i.e., y=Ax+ϵ, where ϵ is noise). In standard linear regression problems, the noise appears linearly and, when assumed to be Gaussian, can be accounted for explicitly when determining x to minimize the variance of the parameter estimates. Since the noise appears nonlinearly in (8) (due, in part, to the presence of trigonometric terms), we use Monte Carlo simulation to investigate the effect of measurement noise on the identified parameters. The identification procedure is repeated using different noise signals sampled from the same distribution, thereby allowing us to investigate the anticipated effect of noise on the parameter estimates. Statistical data are generated for each parameter estimate; a small statistical variance corresponds to a parameter whose identified value is most reliable.

It is important to note that the systems encountered using the proposed approach are of size nf×(r+ℓm), which can be substantially larger than the systems of size nf×r obtained using existing approaches. Once the problem has been transformed into a system of linear equations, however, very efficient solution techniques can be employed. Furthermore, since the Lagrange multiplier points 1..ℓ λ 1..m are localized in time, reducing the size of the time window used for identification will reduce the size of the system. Alternatively, a recursive least-squares algorithm could be used to solve the identification problem, in which case the system that must be solved at each time step is only of size n×(r+ℓm).

3 Example systems

Two numerical examples are presented in this section: a planar pendulum modeled with absolute coordinates, and a spatial slider-crank mechanism modeled with joint coordinates. All equations are generated using the Multibody library in MapleSimFootnote 1; the required expressions are then exported to Matlab Footnote 2 for simulation. We assume full state measurement in both examples. For situations in which it is not possible to obtain either direct or indirect measurements of all displacements, velocities, and accelerations in the system, we recommend adopting one of several existing strategies (e.g., by considering only linear or linearized systems with noiseless displacement data [13], by solving a general nonlinear programming problem using an initial-value or a multiple-shooting approach [6], or using single-shooting homotopy optimization [16]).

3.1 Planar pendulum

We first consider the single planar pendulum shown in Fig. 1. When modeled with absolute coordinates q=[x,y,θ]T, the following DAEs govern the motion of this system:

$$\begin{aligned} \left[ \begin{array}{c@{\quad}c@{\quad}c} M & 0 & 0 \\ 0 & M & 0 \\ 0 & 0 & I \end{array} \right] \left\{ \begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{\theta} \end{array} \right\} + \left[ \begin{array}{c@{\quad}c} 1 & 0 \\ 0 & 1 \\ L \sin(\theta) & -L \cos(\theta) \end{array} \right] \left\{ \begin{array}{c} \lambda_1 \\ \lambda_2 \end{array} \right\} =& \left\{ \begin{array}{c} Mg \\ 0 \\ 0 \end{array} \right\} \end{aligned}$$
(9)
$$\begin{aligned} \left\{ \begin{array}{c} x - L \cos(\theta) \\ y - L \sin(\theta) \end{array} \right\} =& \mathbf{0} \end{aligned}$$
(10)

where M, I, and L are the mass, centroidal inertia, and length of the pendulum, and gravity acts in the X-direction. Experimental data are generated using the following parameters: M=10 kg, \(I = 0.2~\mbox{kg\,m$^{2}$}\), L=0.5 m, δt=10 ms, t f =5 s, and Δt=50 ms (i.e., the piecewise linear approximation for each Lagrange multiplier consists of ℓ=101 points spaced 50 ms apart); the pendulum is initially at rest with displacement θ(0)=π/2 rad. We shall assume that the mass and length are known, as are experimental measurements for all positions, velocities, and accelerations; the inertia and the m=2 Lagrange multipliers are to be identified. Note that a total of r+ℓm=1+101⋅2=203 parameters are being sought, which does not exceed the number of equations available (namely, nf=1503). The dynamic equations (9) are rearranged into the form shown in (3):

$$ \left[ \begin{array}{c} 0 \\ 0 \\ \ddot{\theta} \end{array} \right] \left\{ \begin{array}{c} I \end{array} \right\} + \left[ \begin{array}{c@{\quad}c} 1 & 0 \\ 0 & 1 \\ L \sin(\theta) & -L \cos(\theta) \end{array} \right] \left\{ \begin{array}{c} \lambda_1 \\ \lambda_2 \end{array} \right\} = \left\{ \begin{array}{c} Mg - M\ddot{x} \\ -M\ddot{y} \\ 0 \end{array} \right\} $$
(11)

which is assembled at each point in time for which experimental data are collected. The least-squares solution is then computed using the Matlab backslash operator, which employs the efficient QR factorization routines available in the Linear Algebra PACKage (LAPACK) library [15]; the slower lsqr routine produces nearly identical results. Excellent estimates are obtained: the identified inertia is \(0.199991~\mbox{kg\,m$^{2}$}\) and, as shown in Fig. 2, the identified Lagrange multipliers deviate only slightly from the experimental data, which can be attributed to the piecewise linear approximations used to represent these curves.

Fig. 1
figure 1

Planar pendulum

Full size image
Fig. 2
figure 2

Identified Lagrange multipliers for the planar pendulum, which represent the reaction forces at the pin (a) in the X-direction and (b) in the Y-direction

Full size image

We now repeat the identification procedure using experimental data corrupted by white Gaussian measurement noise, as demonstrated in Fig. 3 for θ(t) with signal-to-noise ratios (SNRs) of 30 dB and 15 dB. The identified inertias and errors of the identified Lagrange multipliers are shown in Fig. 4 for decreasing SNRs. The statistical data are generated by repeating the identification procedure 1000 times for each SNR. As expected, the accuracy of the estimates degrades as the SNR decreases; however, as shown in Fig. 5, reasonable results are obtained even when the SNR is 15 dB. In practice, it may be beneficial to smooth or otherwise filter noise-corrupted data before proceeding with parameter identification.

Fig. 3
figure 3

Experimental data and noise-corrupted measurements for θ(t) with signal-to-noise ratios of (a) 30 dB and (b) 15 dB

Full size image
Fig. 4
figure 4

Identification of (a) inertia, (b) λ 1(t), and (c) λ 2(t) for the planar pendulum using noise-corrupted experimental data

Full size image
Fig. 5
figure 5

Identified Lagrange multipliers for the planar pendulum using noise-corrupted experimental data with SNR of 15 dB (shown here is the sample whose root-mean-square error was closest to the average)

Full size image

3.2 Spatial slider-crank mechanism

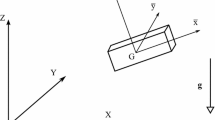
We now consider the spatial slider-crank mechanism shown in Fig. 6. We model this system with joint coordinates q=[θ,α,β,s]T, as shown in the figure, again obtaining a system of index-3 DAEs. Experimental data are generated using the system parameters shown in Table 1, and the following simulation parameters: δt=1 ms, t f =2 s, and Δt=5 ms (i.e., the piecewise linear approximation for each Lagrange multiplier consists of ℓ=401 points spaced 5 ms apart). In addition to gravity, which acts in the −Z-direction, an external torque τ C(t)=0.1sin(2πt) Nm is applied to the crank, and an external force F P(t)=−0.05sin(πt) N is applied to the piston. The system is initially at rest with θ(0)=0 rad. In this example, we identify the three moments of inertia of the connecting rod, as well as the m=3 Lagrange multipliers, which represent the reaction forces in the spherical joint between the crank and the connecting rod. Thus, a total of r+ℓm=3+401⋅3=1206 parameters are being sought, which does not exceed the number of equations available (in this case, nf=8004). It is assumed that noise-corrupted experimental data are available for only θ, \(\dot{\theta}\), \(\ddot{\theta}\), τ C, and F P; the remaining positions, velocities, and accelerations are determined using the constraint equations and their derivatives.

Fig. 6
figure 6

Spatial slider-crank mechanism (adapted from Haug [7])

Full size image
Table 1 System parameters used for spatial slider-crank mechanism example
Full size table

The linear regression problem is solved as before. The identified inertias and errors of the identified Lagrange multipliers are shown in Figs. 7 and 8 for decreasing SNRs. In this example, the statistical data are generated by repeating the identification procedure 100 times for each SNR. The statistical trends are similar to those observed in the first example. Once again, reasonable results are obtained even when the experimental data are corrupted by measurement noise, as shown in Fig. 9.

Fig. 7
figure 7

Identification of (a) I xxR, (b) I yyR, and (c) I zzR for the spatial slider-crank mechanism using noise-corrupted experimental data

Full size image
Fig. 8
figure 8

Identification of (a) λ 1(t), (b) λ 2(t), and (c) λ 3(t) for the spatial slider-crank mechanism using noise-corrupted experimental data

Full size image
Fig. 9
figure 9

Identified Lagrange multipliers for the spatial slider-crank mechanism using noise-corrupted experimental data with SNR of 40 dB (shown here is the sample whose root-mean-square error was closest to the average)

Full size image

4 Conclusions and future work

A new approach has been proposed for identifying inertial parameters in multibody systems governed by DAEs. Existing approaches involve first eliminating the Lagrange multipliers from the dynamic equations using an orthogonal complement of the Jacobian. The proposed approach avoids this pre-processing step by identifying a piecewise linear approximation for each Lagrange multiplier along with the unknown inertial parameters. Numerical examples have demonstrated the efficacy of this approach using both absolute and joint coordinate formulations, and in the presence of measurement noise.

While inertial system parameters may not vary under normal operating conditions, estimates of these parameters can be used to monitor the health of a system over time. Changes in the behavior of the Lagrange multipliers, which often represent reaction forces in kinematic joints, can also be important indicators of system health. In applications involving unknown masses (e.g., washing machines and amusement park rides), the estimation of inertias may be necessary for control purposes. Future work will focus on applying the proposed approach to the problem of fault detection and isolation in multibody systems. It may also be possible to extend this approach to the identification of parameters in vehicle tire models, such as lateral and longitudinal slip coefficients. Estimates of these parameters are required by dynamic controllers, and approximations of the reaction forces in vehicular systems could provide valuable suspension load data.