Abstract
In this study, a review is presented of recent work of the authors on a class of multibody dynamic systems, involving bilateral motion constraints. First, the Analytical Dynamics framework is adopted and the basic theoretical ingredients of a method leading to a new set of equations of motion are presented. According to this method, the motion constraints are treated as an integral part of the overall analytical process. Consequently, this yields the equations of motion as a set of pure second-order ordinary differential equations in a natural way. Then, this set is put in an appropriate weak form and a suitable numerical discretization scheme is developed, respecting the geometric properties of the configuration space. This scheme is also capable of handling cases involving redundant constraints and singular positions, through a proper extension to an augmented Lagrangian form. Finally, the accuracy and efficiency of the new numerical scheme are demonstrated by examining a selected set of mechanical examples, including a benchmark problem. An extensive comparison with classical numerical schemes, based on equations of motion expressed as sets of differential–algebraic equations, is also performed.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This work is concerned with dynamics of a wide class of multibody mechanical systems subject to motion constraints. Both the theoretical and the numerical aspects of setting up and solving the governing equations are quite challenging [1,2,3,4,5]. Moreover, such systems appear in many engineering disciplines, like mechanisms, robotics, biomechanics, ground vehicles, naval and aerospace structures, to just mention a few of them [6,7,8]. As a result, a large amount of research effort has already been devoted to understanding, improving and controlling their dynamic response [9,10,11,12].
In general, the motion constraints imposed on a mechanical system are divided into bilateral or unilateral constraints, depending on whether they appear in an equality or inequality form, respectively. Typically, the latter case appears in problems involving contact, impact and friction between the members of the system examined and are not considered here [13, 14]. Instead, the present study focuses on systems subject to equality motion constraints. Also, the work focuses on systems possessing discrete dynamic characteristics. In the great majority of previous publications on the subject, the constraint equations are just appended to the set of equations governing the dynamics. This leads to a set of differential algebraic equations (DAEs) of high index [8, 15]. Such equations are known to involve severe singularities and lead to drift in the lower kinematical levels (velocities, displacements) and instabilities [16,17,18,19,20]. As a consequence, a lot of research effort has been devoted to several typical activities aiming at overcoming these difficulties. For instance, these activities include scaling the equations of motion [18, 19], performing projections to eliminate the drift in the solution [20], lowering the DAE index or even producing convenient sets of ordinary differential equations (ODEs) [15, 21, 22]. However, in all those cases, the emphasis was given to a rather mathematical or numerical treatment of the constraint equations, which does not lead to a definite cure or elimination of the inherent problems of a DAE-based formulation. A comprehensive review of such methods can be found in [8].
Over the last years, a new methodology has emerged, where the motion constraints are treated as an integral part of the whole process of deriving the equations of motion (EOM) [23]. This led to derivation of a new set of equations of motion, through the introduction of suitable linear operators, originating from the motion constraints, as well as by a consistent application of Newton’s second law on the configuration space. Eventually, this gives rise to a set of pure second-order ODEs, in a natural way. A distinct feature of these equations of motion is that they involve inertia, damping and stiffness terms in both the original equations of motion and those resulting by the constraint equations [24]. This, in turn, provides mechanisms for an automatic scaling and stabilization of these equations. Then, more numerical benefits are gained by putting the original second-order (strong) form of these equations into an equivalent first-order three-field weak form [25]. Simultaneously, a suitable numerical discretization procedure is applied, respecting and exploiting the geometric properties of the configuration manifold. Finally, a special augmented Lagrangian methodology has also been developed, in order to handle cases related to the presence of redundant coordinates and the appearance of singular positions during the motion [26].
The outline of the present work is as follows: First, in Sect. 2, the emphasis is put on a presentation of the general analytical setting, leading to derivation of the new set of equations of motion governing the behavior of the class of dynamic systems examined. Then, the basic ingredients of an appropriate weak form of these equations are presented in Sect. 3. This provides a foundation for the derivation of an equivalent set of equations of motion in first-order form and a solid basis for its geometrically consistent temporal discretization. Some representative numerical integration methodologies are presented in Sect. 4, including a suitable augmented Lagrangian formulation. Next, a collection of mechanical examples, illustrating the advantages of employing the new set of equations of motion, in comparison with classical DAE formulations, is presented in Sect. 5. Finally, the highlights of this work, together with some directions for future work, are summarized in Sect. 6.
2 Derivation of the equations of motion
In this section, a brief but quite complete summary of the essential steps and the main theoretical results obtained in previous publications of the authors on the subject are presented [23,24,25,26]. Specifically, the equations of motion are derived by adopting the classical Analytical Dynamics framework [2, 22, 27]. First, the general analytical setting is provided by considering mechanical systems described by Lagrangian coordinates. Then, the effect of imposing motion constraints in deriving a new set of equations of motion in a second-order (strong) ODE form is investigated. Finally, some important theoretical issues which are frequently overlooked in the literature are considered.
2.1 General analytical setting
According to the classical viewpoint of Analytical Dynamics, the motion of a mechanical system in the three-dimensional physical space can be described by a set of generalized coordinates, say \(q = (q^{1} \ldots \;q^{n} )\) [1,2,3,4,5]. Consequently, the motion of the same system can be represented by the motion of a fictitious point \(p\) along a curve \(\gamma (t)\) of an \(n\)-dimensional abstract manifold \(M\), parameterized by time \(t\) [9,10,11]. In fact, the coordinates of point \(p\) are obtained through a local smooth map:
acting from a neighborhood of point \(p\) to an n-dimensional Euclidean manifold. Moreover, the tangent vector \(\underline {v} = {{{\text{d}}\gamma } \mathord{\left/ {\vphantom {{{\text{d}}\gamma } {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}}\) to the motion curve \(\gamma (t)\) at point \(p\) of manifold \(M\) belongs to an n-dimensional vector space \(T_{p} M\) [28]. This vector is known as generalized velocity, and if \({\mathfrak{B}}_{e} = \{ \underline {e}_{1} \ldots \; \underline {e}_{n} \}\) is a basis of \(T_{p} M\) it can be put in the compact form
by using the usual summation convention on repeated indices [5]. Also, to each tangent space \(T_{p} M\) there corresponds a cotangent (or dual) space \(T_{p}^{ * } M\), with elements known as covectors. In fact, to each vector \(\underline {u}\) corresponds a covector \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u}}^{ * }\), established through the duality or natural pairing:
where \(\langle \cdot , \cdot \rangle\) is the inner product on \(T_{p} M\). In this way, a dual basis \({\mathfrak{B}}_{e}^{*} = \{ \underline {e}^{1} \ldots \; \underline {e}^{n} \}\) to \({\mathfrak{B}}_{e}\) can be created for \(T_{p}^{ * } M\), through application of the condition \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{i} ({\kern 1pt} \underline {e}_{{{\kern 1pt} j}} ) = \delta_{j}^{i}\), where \(\delta_{\,j}^{i}\) is a Kronecker delta [28].
The inner product on \(T_{p} M\) is expressed in terms of the components
of the metric tensor \(g \equiv g_{ij} \,{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{i} \otimes {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{j}\) at point \(p\) and is useful in measuring lengths of and angles between vectors of \(T_{p} M\). In dynamics, these components are determined through consideration of the kinetic energy of the system, so that
Then, it is easy to verify that covectors \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{p}}_{M}^{*} = p_{i} \,{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{i}\) represent generalized momenta, with components
in the dual basis \({\mathfrak{B}}_{e}^{*}\).
In general, the geometry of the configuration manifold \(M\) is non-Euclidean. For this reason, the exact solution path on \(M\) is determined by application of Newton’s second law in the form
provided that the generalized coordinates selected form an independent set [23]. In particular, the term in the right-hand side of Eq. (6) is a covector, \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{f}}_{M}^{*} = f_{i} {\kern 1pt} \,{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{i}\), representing the applied forces, while the term in the left-hand side is the covariant derivative of the generalized momentum \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{p}}_{M}^{*}\) along a path on \(M\) with tangent vector \(\underline {v}\). The latter term can be expressed in the following component form
with \(i,j,k = 1, \ldots ,n\). The quantities \(\Lambda_{{j{\kern 1pt} i}}^{k}\), known as affinities, are components of the affine connection \(\nabla\) of the manifold, satisfying the definition
They dictate the transition from a tangent space to a neighboring tangent space of manifold \(M\) [5, 28]. In this respect, they determine the parallel translation of vectors along a curve of \(M\) as well as some vital geometric properties of \(M\), like its torsion and curvature [5, 29]. Therefore, the connection, together with the abstract set of points \(p\) belonging to \(M\) and the metric tensor \(g\), provides the geometry of the configuration manifold \(M\) in a complete manner. Since their definition depends directly on motion constraints, some more details on their selection are provided in Sect. 2.3.
Among all the bases of \(T_{p} M\), any special basis \({\mathfrak{B}}_{g} = \{ \underline {g}_{1} \ldots \; \underline {g}_{\,n} \}\), having base vectors tangent to the coordinate lines corresponding to the coordinate map (chart) defined by Eq. (1), is called natural (or holonomic) basis. In this basis, the velocity components are simply
By introducing the classical matrix notation
and selecting a natural basis for simplicity, Eq. (6) can eventually be cast in the form
where the array \(\underline {h} (\underline {q} ,\underline {\dot{q}} )\) includes the inertia terms related to the affinities \(\Lambda_{ij}^{k}\) only [24].
The extension to quasi-coordinates is straightforward. Such coordinates do not appear explicitly in the equations of motion and are not so useful, since they depend on the specific path followed on a manifold [27]. However, their time derivatives, known as quasi-velocities, are employed in several practical cases, like in rigid body rotation or in systems involving nonholonomic constraints [30]. Such velocities are related to anholonomic bases \({\mathfrak{B}}_{e}\), where the equations of motion appear in a bit more involved form. Namely, if the elements of a basis \({\mathfrak{B}}_{e}\) are related to the elements of a natural basis through the transformation
with \(A_{\,i}^{j} B_{k}^{i} = \delta_{k}^{j}\) [31], then
Finally, direct substitution of the last expression in Eq. (9) provides the equations of motion in terms of the set of quasi-velocities selected.
2.2 Mechanical systems with additional motion constraints
A new picture arises when the system examined is subjected to an additional set of motion constraints. In particular, the class of mechanical systems examined is assumed to be subject to a set of \(k\) scleronomic, catastatic and linearly independent constraints, with general form
where \(R = 1, \ldots ,k\) and \(A = [a_{i}^{R} (q)]\) is a known \(k \times n\) matrix (cases with rheonomic, acatastatic or inequality constraints need more involved but similar treatment [32, 33]). In some cases, the equation of a constraint can be integrated and put in the (holonomic) form
The manipulation of these constraint equations is quite critical for the derivation of the new set of equations of motion. Essentially, they provide the tools to decompose the original configuration manifold \(M\) locally into an (\(n - k\))-dimensional manifold \(M_{A}\), described by an appropriate set of \(m = n - k\) minimal coordinates, say \(\theta = (\theta^{1} \ldots \;\theta^{m} )\), plus \(k\) one-dimensional manifolds \(M_{R}\), one for each constraint. This is achieved by first using Eq. (12) to derive a linear relation
with
where \(\alpha = 1, \ldots m\), \(v^{\alpha } = \dot{\theta }^{\alpha }\) and \(\underline {e}_{\;\alpha }\) is an element of a basis of the vector space \(T_{{p_{A} }} M_{A}\) at point \(p_{A}\) of manifold \(M_{A}\), related to \(p\) through the constraints [24]. In the last expression and in the sequel, Latin and Greek lower-case indices correspond to components of entities defined on manifold \(M\) and \(M_{A}\), respectively. Then, Eq. (14) provides a foundation for defining a suitable set of linear operators, acting between the tangent and dual spaces of these manifolds. For instance, the operator
helps in rewriting Eq. (14) in the alternative form
which illustrates that \(E_{S}\) acts as a linear transformation from \(T_{{p_{A} }} M_{A}\) to \(T_{p} M\). Likewise, the dual operator
helps in transferring covectors from the corresponding cotangent space \(T_{p}^{*} M\) to \(T_{{p_{A} }}^{\;*} M_{A}\). Specifically, after defining the special covectors
on \(T_{p}^{*} M\), then operator \(E_{SD}\) helps in determining the corresponding covectors
on \(T_{{p_{A} }}^{\;*} M_{A}\). Covectors \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{h}}_{M}^{ * }\) are called Newton covectors on \(M\), since they are equal to zero when there are no additional motion constraints, according to Newton’s second law expressed by Eq. (6) [23].In a similar manner, the communication between the tangent and cotangent spaces of the configuration manifold \(M\) and each of the single dimensional constraint manifolds \(M_{R}\), \(R = 1, \ldots ,k\) is established through the pair of operators
for each constraint. Then,
with
expressing a vector and a covector of spaces \(T_{{p_{R} }} M_{R}\) and \(T_{{p_{R} }}^{*} M_{R}\), respectively. In Eqs. (20)–(22) and in the sequel, the convention on repeated indices does not apply to index \(R\).
Among other things, the set of linear operators introduced based on the constraints helps in splitting each element of the cotangent space \(T_{p}^{ * } M\) in a unique manner [24]. More specifically, a Newton covector on \(M\) is expressed in the form
with
The linear operators \(E_{TD}\) and \(T_{RD}\) transfer the corresponding Newton covectors \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{h}}_{A}^{ * }\) from \(T_{{p_{A} }}^{\;*} M_{A}\) and \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{h}}_{R}^{ * }\) from each of the \(T_{{p_{R} }}^{*} M_{R}\), respectively, back to \(T_{p}^{ * } M\). The special covectors \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{h}}_{A}^{ * }\) and \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{h}}_{R}^{ * }\) are defined in accordance with Eq. (18).
Due to the presence of the motion constraints, expressed by Eq. (12), the original set of coordinates \(q = (q^{1} \ldots \;q^{n} )\) becomes redundant. Consequently, Eq. (6) is no longer valid and is replaced by
instead. Then, by taking Eqs. (24) and (25) into account, Eq. (23) becomes
Next, substitution of Eqs. (5) and (7) in Eq. (18) yields
with components
Likewise, each Newton covector \({\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{h}}_{R}^{*}\) on the constraint manifolds \(M_{R}\) (for \(R = 1, \ldots ,k\)) takes the form of Eq. (22) with components
Moreover, during the solution process, the terms
are determined through a projection along special directions \(\underline {c}_{{{\kern 1pt} R}}\) on \(T_{p} M\), defined for each of the constraints. In particular, the components of the \(n\)-vector \(\underline {c}_{{{\kern 1pt} R}}\) are chosen so that
Finally, each coefficient \(\overline{c}_{RR}\) and \(\overline{k}_{RR}\) is selected so that the corresponding term in Eq. (29) represents a corrective force applied to the figurative point (particle), when a constraint violation tends to develop along direction \(\underline {c}_{{{\kern 1pt} R}}\). For instance, if the applied forces depend on the generalized coordinates and velocities, a convenient choice is
Next, by combining Eqs. (20) and (26)–(29), it easily turns out that
or eventually
for \(i = 1, \ldots ,n\). Therefore, after enhancing the matrix notation introduced by Eq. (9) with
and the array \(\underline {\overline{f}}\), as determined by Eqs. (30)–(32), Eq. (34) can be cast in the following matrix form
Equation (34), or Eq. (36), corresponds to a set of \(n\) second-order ODEs, involving the \(n + k\) unknowns \(q^{i}\) and \(\lambda^{R}\). A complete mathematical formulation is obtained by including the \(k\) equations of the constraints. Originally, these are expressed by Eq. (12) but can eventually be put in the second-order ODE form:
through appropriate mappings from \(M\) to \(M_{R}\), forcing \(\phi^{R}\) or \(\dot{\psi }^{R}\), respectively, to become zero for \(R = 1, \ldots ,k\).
A complete picture of the formulation presented in this section, together with an extensive comparison with previous theoretical formulations on the subject, is provided in earlier publications [23, 24]. Briefly, compared to previous approaches in the field of constrained multibody dynamic systems, the present approach brings significant advantages. These advantages arise from the physically consistent application of Newton’s second law, leading to a natural and correct elimination of the singularities associated with the sets of high-index DAEs of motion, obtained in earlier studies [8, 17]. More specifically, in the new formulation the motion constraints are treated as an integral part of the overall process yielding the equations of motion, which leads to a set of dynamic Lagrange multipliers, expressed by Eq. (29). As an outcome, each constraint introduces effective inertia and damping terms, in addition to restoring terms, in Eqs. (36) and (37). In this way, the overall set of equations of motion appears now in a pure second-order ODE form, from the onset. Moreover, all the extra terms appearing in the new set of equations of motion are determined in a systematic and analytical manner. This is achieved through a proper application of Newton’s law of motion on configuration manifolds with general geometric properties. Consequently, there is no need for an ad hoc choice of parameter values in order to stabilize the constraints numerically. Likewise, no scaling of the equations of motion is necessary, since the \(\lambda\)’s are now treated as coordinates and not as forces. Finally, additional advantages arise during the numerical integration, because the equations of motion are first put in an appropriate three-field weak form and are then discretized in time by respecting and exploiting the geometric properties of the configuration space, as explained in Sects. 3 and 4, respectively.
2.3 Selection of the affinities—metric compatibility conditions
Some results are presented in this section, which are usually overlooked in setting up the equations of motion of constrained mechanical systems in the literature. First, if the motion on the original manifold \(M\) is governed by Newton’s law in the form of Eq. (6), then this form remains invariant on the constrained manifold \(M_{A}\), only when two dynamic conditions are satisfied, which were produced in a previous study [23]. Specifically, through the use of the linear operators established by the set of the additional motion constraints, expressed by Eq. (12), it was shown that Newton’s law of motion is transferred from \(M\) to \(M_{A}\) in a form similar to that expressed by Eq. (6), provided that the components of the metric and connection on \(M_{A}\) satisfy the following conditions:
and
respectively [23]. Then, given the metric components and the affinities of \(M\), together with the elements of the \(n \times m\) matrix \(N = [N_{\alpha }^{i} ]\), defined by Eq. (14), relation (38) fixes the metric on manifold \(M_{A}\) completely, while (39) provides a condition on the selection of the corresponding connection, involving some freedom.
In several earlier studies, the connection on manifold \(M\) is chosen to be fully compatible with its metric, by directly adopting the common choice in abstract Riemannian geometries [28, 31]. This means that the components of the connection are determined by imposing the condition
for all vectors \(\underline {v}\), \(\underline {u}\) and \(\underline {w}\) of \(T_{p} M\), where the metric tensor appears in the form \(g \equiv g_{ij} \,{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{i} \otimes {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{e}}^{j}\). Then, the affinities are selected by satisfying the conditions
and depend solely on the components of the metric tensor on \(M\). Consequently, we assume that the connection is torsionless and provides the extra conditions needed for a full determination of the affinities. The same selection is also performed on the constrained manifold \(M_{A}\). In contrast, the affinities selected by using Eq. (39) are more appropriate for the class of systems examined since they depend on these constraints explicitly, through the elements of matrix \(N\). Specifically, based on condition (39), the affinities on \(M_{A}\) are split in the general form
where the component \(\overline{\Lambda }_{\gamma \alpha }^{\rho }\) is determined completely by
while the component \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Lambda }_{\gamma \alpha }^{\rho }\) satisfies the condition
Since \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Lambda }_{\gamma \alpha }^{\rho } g_{\rho \beta } v^{\beta } v^{\gamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Lambda }_{\gamma \alpha }^{\rho } p_{\rho } v^{\gamma }\), a simple inspection of Eq. (7) verifies that this component of the affinities does not affect the equations of motion. However, the addition of such a component affects some of the crucial geometric properties of \(M_{A}\), like its autoparallel curves. Finally, when Eq. (14) is interpreted as a simple velocity transformation in the same manifold, then Eq. (43) provides the affinities in the new basis.
Obviously, Eq. (43) fixes an appropriate connection on manifold \(M_{A}\), given the set of additional motion constraints and the geometric properties of the original manifold M [23]. According to a common view of Analytical Mechanics [1,2,3,4,5], the equations of motion on M can be obtained by reference to the archetypal Euclidean configuration manifold \(E^{3N}\), corresponding to motion of N unconstrained particles in the three-dimensional physical space. The motion on manifold \(E^{3N}\) is described by a set of \(3N\) Cartesian coordinates. Then, imposing a set of holonomic/nonholonomic motion constraints leads through a coordinate/velocity transformation, respectively, to a system whose configuration manifold is M, where the motion is described by a set of Lagrangian coordinates \(q\) [11, 27]. The manifold \(E^{3N}\) possesses a constant diagonal metric and zero affinities. Therefore, the metric and the affinities on M can be established once the set of motion constraints leading from \(E^{3N}\) to M is known. In this sense, even the motion on M can be considered as a constrained motion. This procedure has already been illustrated in a previous study, where the affinities corresponding to rigid body motion have been evaluated as an example [23].
An alternative, more common and popular way to derive the equations of motion of mechanical systems is based on using the classical Lagrange equations. However, this derivation is subject to some conditions, which are usually overlooked and lead to mistakes. More specifically, the Euler–Lagrange operator on manifold M is defined by:
where T is the kinetic energy of the dynamical system examined, furnished by Eq. (4). Also, Eq. (7) can be rewritten and put in the form
with
Then, it was shown in a previous study [23] that the following relation holds on \(M\)
where the derivative term \(D_{i} {\kern 1pt} g_{{j{\kern 1pt} k}}\) is defined by Eq. (41), while \(c_{{k{\kern 1pt} i}}^{m}\) are the Hamel transitivity coefficients or structure constants [5, 28]. These quantities are defined through the Lie bracket of the base vectors in the form
They are related to the properties of the basis of the tangent space \(T_{p} M\) and are equal to zero for a holonomic basis. Moreover, the terms \(\tau_{{k{\kern 1pt} i}}^{m}\) are the components of the torsion of the connection [28], found in the form
For instance, when a body frame is selected in studying rotation of a rigid body about a fixed point, it is easy to verify that the correction terms in the right-hand side of Eq. (47) provide the quadratic angular velocity terms, which are missing when using the Lagrange operator as defined by Eq. (45).
Equation (47) is of fundamental importance in the dynamics of constrained systems. It shows that the Euler–Lagrange operator \(L_{i}\) coincides with the (correct) Newton operator \(\nabla_{{\underline {v} }} p_{i}\) only when three conditions are satisfied simultaneously. Namely, the application of these operations on the configuration manifold \(M\) yields the same set of equations of motion only when the connection is torsionless and satisfies the metric compatibility condition (41), while the basis employed on the tangent space \(T_{p} M\) is natural. These requirements are too restrictive and are not satisfied in general (e.g., in rigid body dynamics). In fact, the well-known Boltzmann–Hamel or Poincare equations are a special case of the above, since they are derived by employing the Euler–Lagrange operator and include the correction terms, arising when an anholonomic basis is used [27, 34].
3 Three-field weak form of the equations of motion
In many cases, it is more convenient to work with systems of equations of motion, which are dynamically equivalent to a set of first-order ODEs. Such a set was derived in an earlier work and was shown to correspond to the classical Hamilton’s canonical equations [25]. Briefly, the process leading to that result starts from Eq. (26), which is first put in the integral form
for arbitrary time instances \(t_{1}\) and \(t_{2}\). A similar treatment of each constraint equation, expressed by Eq. (37), leads first to
Then, by performing lengthy mathematical operations, involving a typical step with an appropriate integration by parts on a manifold leads eventually to a set of first-order ODEs of the generalized coordinates \(q^{i}\) and the dynamic Lagrange multipliers \(\lambda^{R}\). Moreover, in order to exploit more theoretical and numerical advantages of the weak formulation, the position, velocity and momentum variables can be considered as independent quantities, according to the Veubeke–Washizu methodology, applied earlier to systems with a flat configuration manifold [35, 36]. For this, a new velocity field \(\underline {\upsilon }\) is introduced on manifold \(M\), which is forced to become identical to the true velocity field \(\underline {v}\) in an average rather than a pointwise sense through the relations
where \(\delta \pi_{i}\) are arbitrary constants. Likewise, a new quantity \(\mu^{R}\) is introduced for each constraint, which is forced to become identical to \(\dot{\lambda }^{R}\), by imposing the conditions
where \(\delta \sigma_{R}\) are arbitrary constants. In addition, the last two sets of equations are enhanced by an accompanying set of integral conditions, consisting of
and
where \(\pi_{i}\) and \(\sigma_{R}\) are appropriate Lagrange multipliers, leading to independent variations \(\delta \upsilon^{i}\), \(\delta v^{i}\) and \(\delta \mu^{R}\), \(\delta \dot{\lambda }^{R}\), respectively. Therefore, by augmenting Eq. (50) with Eq. (54) and performing another round of manipulations, it can be shown (see [25] for details) that this leads eventually to the following variational equation
where the quantities \(\sigma_{{j{\kern 1pt} k}}^{i}\) are arbitrary constants, with \(\sigma_{kj}^{i} = - \sigma_{{j{\kern 1pt} k}}^{i}\), while
with partial derivatives \(a_{{{\kern 1pt} i,j}}^{R} \equiv {{\partial a_{{{\kern 1pt} i}}^{R} } \mathord{\left/ {\vphantom {{\partial a_{{{\kern 1pt} i}}^{R} } {\partial q^{j} }}} \right. \kern-\nulldelimiterspace} {\partial q^{j} }}\) and \(\pi_{i,j} \equiv {{\partial \pi_{i} } \mathord{\left/ {\vphantom {{\partial \pi_{i} } {\partial q^{j} }}} \right. \kern-\nulldelimiterspace} {\partial q^{j} }}\). Finally, a similar manipulation of Eqs. (51) and (55) yields
Note that the holonomic version of the constraints, as expressed by Eq. (37), is employed in Eqs. (56) and (58). A similar form is obtained for each nonholonomic constraint by eliminating the terms involving \(\overline{k}_{RR}\).
By construction, the variations \(w^{i}\) (representing \(\delta q^{i}\) for a true coordinate \(q^{i}\)), \(\delta \lambda^{R}\), \(\delta \upsilon^{i}\), \(\delta \mu^{R}\), \(\delta \pi_{i}\) and \(\delta \sigma_{R}\) are independent for all \(i = 1, \ldots ,n\) and \(R = 1, \ldots ,k\). Therefore, collecting the terms of Eqs. (56) and (58), multiplied by the variations \(w^{i}\) and \(\delta \lambda^{R}\), yields
and
respectively. Then, collecting the terms of the same equations, multiplied by \(\delta \upsilon^{i}\) and \(\delta \mu^{R}\), yields
and
respectively. The last two equations can be used in order to obtain updates of the values of the generalized momenta \(\pi_{i}\) and \(\sigma_{R}\), respectively, when necessary. Likewise, Eqs. (52) and (53) are used in order to obtain updates of the values of the generalized coordinates \(q^{i}\) and the Lagrange multipliers \(\lambda^{R}\), respectively. The above results provide a solid foundation for performing an appropriate temporal discretization of the equations of motion, based on the weak form, as explained in Sect. 4.2.
4 Numerical integration of the equations of motion
The equations of motion of the class of mechanical systems examined comprise strongly nonlinear sets of ODEs in both the strong form, expressed by Eqs. (36) and (37), and in the first-order weak form, expressed by Eqs. (59)–(62), (52) and (53). Therefore, their solution can be determined by applying a plethora of suitable numerical integration techniques. Next, a sample of such techniques is presented, starting from the simplest and concluding with the most involved and effective methodology.
4.1 Direct integration of the strong form
The easiest and most direct way to integrate the equations of motion of the class of systems examined is to consider their strong form, expressed by Eqs. (36) and (37). Specifically, Eq. (36) is first rewritten in the second-order ODE form
Likewise, taking into account Eq. (12), Eq. (37) is put in the form
Therefore, combination of Eqs. (63) and (64) leads eventually to the composite form
The above represents a strongly nonlinear set of second-order ODEs for the generalized coordinates \(q^{i}\) and the Lagrange multipliers \(\lambda^{R}\). Therefore, given any appropriate set of initial conditions, this system of equations can be solved by using any numerical integration method which is suitable for ODEs.
Based on the existing literature on the subject, both implicit and explicit numerical integration methods can be developed and applied in solving Eq. (65). In fact, special methods exploiting the Lie group structure and possible symmetries of the configuration space can be developed [9, 37]. In particular, the existence of group properties provides the ground for a definition of appropriate left and right translation operators, which in turn furnish valuable analytical tools, such as the identification of one-parameter subgroups and the generation of the corresponding exponential matrices [28, 31]. Then, these tools can be used for the development of suitable numerical algorithms, so that all the integration points remain on the manifold [38,39,40]. Such methods have already been developed for solving the equations of motion of multibody systems in DAE form [41, 42]. In cases where the system examined possesses redundant coordinates or passes from singular positions, it is advantageous to apply an augmented Lagrangian formulation [43,44,45,46]. Here, the application of such methods can lead to additional advantages, in both cases, since the equations of motion appear in an ODE rather than a DAE form.
4.2 Direct integration of the weak form
In general, the presence of motion constraints causes a non-flatness (i.e., appearance of curvature and/or torsion) to the configuration space of the class of systems examined. Therefore, it is useful to utilize special types of curves in performing the temporal discretization, in order to exploit the geometric properties of this space. For instance, the most natural curves to select are the autoparallels, corresponding to the “straightest” curves on the configuration manifold [28, 29]. Likewise, the one-parameter subgroups are the most appropriate curves on the manifold, when the manifold possesses group properties. In fact, in rigid body spherical motion it was possible to select the affinities on the configuration manifold so that the autoparallel curves coincide with the curve on the manifold corresponding to one-parameter subgroups and their left translation [47, 48].
Among all the possible choices, a special temporal discretization is performed. Specifically, taking into account earlier approaches applied to flat spaces [49], all the variations in Eqs. (52), (53) and (59)–(62) are assumed to remain constant within each time interval [\(t_{m} ,t_{m + 1}\)], while the corresponding variables vary linearly in time. Then, these conditions help to convert Eqs. (52) and (53) into relations with the following general form:
and
where \(\Delta t = t_{m + 1} - t_{m}\) is the time step. In particular, the function \(\underline {g} (\underline {\upsilon }_{{{\kern 1pt} m + 1}} ,\underline {\upsilon }_{{{\kern 1pt} m}} )\) in Eq. (66) is determined in terms of the components of the connection selected. For instance, in a Euclidean configuration space [23], where \(\Lambda_{ij}^{k} = 0\), it turns out that
Equations (66) and (67) represent update formulas for the generalized coordinates and the Lagrange multipliers, respectively. For simplicity and clarity, the numerical implementation of the algorithm employed for solving the discretized set of equations of motion, given by Eqs. (59) and (60), is presented next for mechanical systems possessing rigid bodies only. In this case, through the choices \(\sigma_{ij}^{\ell } = 0\) and \(\tau_{ij}^{\ell } = \Lambda_{ij}^{\ell }\), with the affinities as determined in [23], Eqs. (59) and (60) are replaced by
and
respectively. Then, Eq. (68) can be put in the matrix form
with
where the terms \(\dot{a}_{{{\kern 1pt} i}}^{R}\) are defined by Eq. (57). In addition, the action of operator \(\mathcal{A}\) is equivalent to the identity matrix or the corresponding rotation matrix of a rigid body when it applies to its translational or rotational degrees of freedom, respectively. Likewise, Eq. (69) is also put in the matrix form
with
Therefore, the application of the classical trapezoidal rule to Eqs. (70) and (72) leads eventually to the equations
and
respectively.
In summary, the set of unknowns arising by application of the three-field weak formulation includes the generalized coordinates \(q^{i}\) and \(\lambda^{R}\), the corresponding generalized velocities \(\upsilon^{i}\) and \(\mu^{R}\) as well as the generalized momenta \(\pi_{i}\) and \(\sigma_{R}\). Therefore, it includes \(3(n + k)\) unknowns, satisfying the system of \(3(n + k)\) nonlinear algebraic equations consisting of Eqs. (61), (62), (66), (67), (74) and (75). This set of equations is solved by applying a block-type iterative technique within each time step [50], as explained next.
First, it is assumed that the values of all the unknowns but the components of the weak velocity vectors, \(\underline {\upsilon } = (\upsilon^{1} \ldots\; \upsilon^{n} )^{{\text{T}}}\) and \(\underline {\mu } = (\mu^{1} \ldots \;\mu^{k} )^{{\text{T}}}\), are fixed. Then, the application of Eqs. (74) and (75) leads to a set of \(n + k\) nonlinear algebraic equations only, with form
where \(\underline {\upsilon }_{{{\kern 1pt} m + 1}}\) and \(\underline {\upsilon }_{{{\kern 1pt} m}}\) represent the values of \(\underline {\upsilon }\) at times \(t_{m + 1}\) and \(t_{m}\), respectively, while a similar meaning is given to the quantities \(\underline {\mu }\), \(\underline {q}\), \(\underline {\lambda }\), \(\underline {\pi }\) and \(\underline {\sigma }\). Then, Eq. (76) is solved by applying a Newton–Raphson approach, with respect to the unknowns
In brief, given an estimate \(\underline {x}_{{{\kern 1pt} m + 1}}^{\ell }\), a corrected value \(\underline {x}_{{{\kern 1pt} m + 1}}^{\ell + 1}\) is obtained, according to
where the correction \(\Delta {\kern 1pt} \underline {x}^{\ell }\) is determined by solving the linearized problem
resulting by substituting Eq. (78) into Eq. (76), with Jacobian matrix
and residual vector
In fact, the residual covector can be split in the form
where \(\mathcal{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{R}}}_{v}\) and \( \mathcal{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{R}}}_{\mu } \) are the numerical residual of Eqs. (74) and (75), respectively. Then, the square of the norm of the total residual is evaluated in the form
Likewise, the square of the norm of the residual of the equation constraints, given by Eq. (12), is obtained by
For a given tolerance level, the calculations are assumed to have converged when both \(||\mathcal{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{R}}}_{\,T} ||\) and \(||\mathcal{\underline {R} }_{\,C} ||\) are smaller than the selected tolerance value.
When the norms of vector \(\underline {x}_{{{\kern 1pt} m + 1}}\) and the constraint equations become smaller than a pre-specified numerical value, the computations are stopped. Also, if the iterations exceed a critical number, the time step \(\Delta t\) is reduced and the process is restarted [51]. After determining the generalized velocities \(\underline {x}_{{{\kern 1pt} m + 1}}\), the generalized coordinates \(\underline {q}_{m + 1}\) and \(\underline {\lambda }_{{{\kern 1pt} m + 1}}\) are determined by a direct update, using Eqs. (66) and (67), respectively. Next, if the residual in the right-hand side of Eq. (79) becomes sufficiently small, the iterations are considered to be complete. Otherwise, the time step is decreased and the process is repeated. Eventually, the updated values of the generalized momentum variables \(\underline {\pi }_{m + 1}\) and \(\underline {\sigma }_{m + 1}\) can also be obtained, by employing the equations resulting by direct application of Eqs. (61) and (62), respectively.
4.3 An augmented Lagrangian formulation
In multibody dynamics, there appear many occasions where the system examined involves redundant constraints or passes through singular positions. To overcome the difficulties arising in such cases, it is convenient to apply an augmented Lagrangian approach [43,44,45,46]. Then, the equations of motion are derived by applying optimization techniques to an appropriate objective function. Based on recent work of the authors, a suitable objective function is the following:

with
where the positive constants \(\xi_{R}\) are known as penalty factors, while
Then, performing appropriate mathematical operations on this objective function leads eventually to a new weak form [26]. Essentially, this form becomes identical to that represented by Eqs. (52)–(56) and (58), provided that the terms \(\mu^{R}\) and \(\lambda^{R}\) are substituted by
when they are multiplied by \(\overline{m}_{RR}\) or \(\overline{c}_{RR}\) and \(\overline{k}_{RR}\), respectively. This permits to include only the weak velocity \(\underline {\upsilon } = (\begin{array}{*{20}c} {\upsilon^{1} } & \cdots & {\upsilon^{n} )^{\rm T} } \\ \end{array}\) in the original set of unknowns. Then, the solution of each linear problem, as expressed by Eq. (79), is stopped when vector \(\underline {x} = \underline {\upsilon }\) is determined up to a pre-specified accuracy or the iterations exceed a critical number. In the latter case, the process is restarted after reducing the time step \(\Delta t\). Next, based on Eq. (84), the new values of \(\underline {\mu }\) are determined by the augmentation:
where the diagonal matrix
includes the penalty values. Τhe new round of iterations is completed when a suitable augmentation criterion is satisfied. If this is not feasible, the values of the penalty parameters are increased according to common practice [52, 53]. Then, the process is repeated up to satisfaction of the convergence criteria set on the accurate enforcement of the motion constraints on the velocity level. Following determination of \(\underline {\upsilon }_{\;m + 1}\), the generalized coordinates \(\underline {q}_{m + 1}\) and \(\underline {\lambda }_{{{\kern 1pt} m + 1}}\) of the augmented system are evaluated by a direct update, using Eqs. (66) and (67), respectively. When both the residual in the right-hand side of Eq. (79) and the error in the motion constraints, expressed by Eq. (37), become also sufficiently small, the iterations are stopped. Otherwise, the time step is decreased and the process is repeated. After all these iterations are finished, the values of the generalized momenta \(\underline {\pi }_{m + 1}\) and \(\underline {\sigma }_{m + 1}\) can also be determined by employing the equations resulting from application of Eqs. (61) and (62), respectively.
5 Numerical results
In this section, the theoretical and numerical advantages of the new set of equations of motion, obtained for the class of constrained dynamic systems examined, are supported and illustrated by numerical results. Specifically, a selected set of results is presented for five challenging mechanical examples. The attention is focused on comparisons with analytical results as well as with results produced by employing standard DAE solvers and codes. Finally, comparison with results from a benchmark problem is also performed.
5.1 Torque-free motion of a rigid body with spherically symmetric inertia
In the first example, torque-free motion of a rigid body with spherically symmetric inertia is investigated. Namely, the body has equal mass moments of inertia along the axes of an orthonormal Cartesian frame \(Oxyz\), which is fixed in the body and has origin at its center of mass O. That is,
Therefore, the mass moment of inertia matrix with respect to the center of mass O has the form \(I = I_{O} I_{3}\), where \(I_{3}\) is the \(3 \times 3\) identity matrix. In fact, this implies that the mass moment of inertia of the body along any axis passing through point O is equal to \(I_{O}\) (equimomental [27, 54]). For such bodies, by a simple inspection of the Euler equations
it can be verified that they accept simple solutions with form
This means that the body preserves its original angular velocity \(\underline {\Omega }_{0}\), and it therefore undergoes a pure rotation about the axis defined by \(\underline {\Omega }_{0}\), throughout its subsequent motion.
If \(OXYZ\) is a fixed (inertial) frame, the body orientation is specified completely by using the corresponding 3–1-3 set of Euler angles \(\underline {\theta }_{\;E} = (\begin{array}{*{20}c} \varphi & \theta & \psi \\ \end{array} )^{\rm T}\), where \(\varphi\), \(\theta\) and \(\psi\) represent precession, nutation and spin angles, respectively [6, 55]. Starting from Eq. (87), the equations governing the rotational part of a torque-free motion of a rigid body become:
where
and \(T\) represents the transformation matrix between \(\underline {\Omega }\) and \(\underline {\dot{\theta }}_{\,E}\) [6]. Furthermore, the translation of the body under no external forcing is described by the equations of motion
where \(M = m\,I_{3}\) is the mass matrix of the body. Obviously, the rotational and translational components of the motion, governed by Eqs. (89) and (91), respectively, are decoupled. Moreover, if the initial conditions \(\underline {r}_{\,O} (0) = \underline {0}\) and \(\dot{\underline {r} }_{\,O} (0) = \underline {0}\) are imposed, it can easily be proved that \(\underline {r}_{\,O} (t) = \underline {0}\).
Next, numerical integration of Eqs. (89) and (91) was performed, after imposing the condition \(\underline {\phi } = \underline {r}_{\,O} (t) = \underline {0}\) as a motion constraint, instead, through a spherical joint at the mass center O. The specific body examined consists of three identical rods, connected at their centers, as shown in Fig. 1a. Each rod has mass \(m = 1\;{\text{kg}}\) and length \(\ell = 1\;{\text{m}}\). Also, each rod axis is aligned with one of the axes of the body frame \(Oxyz\), so that \(I_{O} = \frac{1}{6}\;{\text{ml}}{}^{2}\). In addition, the example body starts moving from an initial position with \((\varphi_{0} ,\theta_{0} ,\psi_{0} ) = (0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2},0)\) and an angular velocity having components \(\Omega_{x0} = 1\;{{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\), \(\Omega_{y0} = 2\;{{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\) and \(\Omega_{z0} = 3\;{{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\).
Torque-free motion: a mechanical example, b angular velocity components and c mechanical energy of the example body, using the ODE-GC (geometrically consistent) new method and the MATLAB ODE-45 solver with Eq. (65)
First, in Fig. 1b, c are shown numerical results obtained by integrating the new set of the equations of motion. Specifically, in Fig. 1b are depicted the time histories of the angular velocity components \(\Omega_{x}\), \(\Omega_{y}\) and \(\Omega_{z}\), over the first 50 s of the motion. The corresponding mechanical energy of the body is included in Fig. 1b. The results presented were obtained by employing the numerical integration of the strong form and the weak form, as presented in Sect. 4.1 and 4.2, respectively. The strong form, expressed by Eq. (65), was integrated by using the MATLAB solver ode45. In brief, this is a single-step solver, based on an explicit Runge–Kutta (4, 5) formula [56]. This method is labeled by ODE-45, while the integration method of the weak form is labeled by ODE-GC. For the ODE-45 method, the maximum time step was set equal to 0.1 s, while three different values were selected for the numerical tolerance. Specifically, the tolerance value was chosen so that the relative tolerance is equal to the absolute tolerance. Also, for the ODE-GC method, the tolerance value is chosen by Eq. (80).
It is remarkable that the new method ODE-GC captures the correct time history in just one step, independently on the duration of the motion and the magnitude of the tolerance value. This is so because this method is geometrically consistent (GC), since it takes full advantage of the manifold geometry. Namely, the temporal discretization is performed by using the autoparallel curves on the manifold. For rigid body rotation, these curves correspond to pure rotation, by definition [48]. On the other hand, the discretization employed in ode45 needs a sufficiently small time step to run, since this solver does not respect the manifold geometry and the integration is not performed along curves of the manifold corresponding to pure rotation. Consequently, the results start deviating from the expected pure rotation along the original axis of rotation, so that smaller time steps are required for the same level of accuracy.
In the results presented, the accuracy level of the computations is governed by the tolerance parameter. Obviously, the solution deviates from the exact solution in all cases, eventually. However, the smaller the tolerance value, the closer the numerical solution comes to the exact motion. This effect is also reflected in the corresponding mechanical energy, shown in Fig. 1c, indicating that the numerical solution converges to the exact solution, as the numerical accuracy level is increased.
Next, the equations of motion were put in a classical DAE form. More specifically, the following set of equations of motion was employed:
accompanied by the equations of constraint in the form
corresponding to the index-3 and index-1 formulation, respectively [6, 8]. These equations were integrated by employing the MATLAB solvers ode15i and ode15s. In brief, the former is a fully implicit solver (DAE-FI), based on the backward differentiation formulas (BDFs) of orders 1 to 5 [57], while the latter is a semi-explicit solver (DAE-SE), based on the numerical differentiation formulas (NDFs) of orders 1 to 5 [58]. In both cases, Eq. (93) was replaced by
where the elements of the diagonal matrices \(C_{B}\) and \(K_{B}\) were selected according to the classical constraint stabilization approach suggested by Baumgarte [8, 59].
First, results obtained by using the fully implicit DAE formulation (DAE-FI) are presented in Fig. 2, for a maximum time step of 0.1 s and three different values of the tolerance. The angular velocity components are depicted in Fig. 2a, while the mechanical energy of the rigid body is shown in Fig. 2b. For comparison purposes, the corresponding results of the geometrically consistent new method (ODE-GC) are also included. The results indicate that the predictions of the DAE-FI solver exhibit a continuous divergence from the exact motion, which is also reflected in the mechanical energy history. For the largest tolerance value, the energy reaches levels about two orders of magnitude larger than the initial energy, while for the intermediate tolerance value the integration fails at about 72 s, as indicated by the star symbol in Fig. 2b. Finally, for the smallest tolerance value, this DAE integration method led to a pure rotation about an axis which is different than the original axis, after a long transient period. This is illustrated by including the time interval between 290 and 300 s in the right side of Fig. 2a. This deviation cannot be eliminated by decreasing the value of the numerical tolerance.
Next, similar results obtained by using the semi-explicit DAE formulation (DAE-SE) are presented in Fig. 3. Here, the emerging picture is much worse, since there is no evidence of even converging to a pure rotation solution by decreasing the tolerance. More specifically, a new solution arises by changing the tolerance value. In addition, quite large oscillations of the mechanical energy are observed to occur in all cases examined.
5.2 Motion of a spherical pendulum
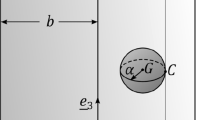
In the second example, motion of a rigid pendulum, with mass \(m = 1\;kg\) and length \(2\ell = 1\;m\), is examined. Its cross-section is circular, with radius \(r = 0.1\;m\), while its end Ο is supported on the ground through a spherical joint. Moreover, its longitudinal axis is aligned with the axis \(Cx\) of an orthonormal Cartesian frame \(Cxyz\), which is fixed in the body, with origin at its center of mass \(C\), as shown in Fig. 4. In addition, the orientation of the body with respect to a fixed frame \(OXYZ\) is determined by using the corresponding 3–1-3 set of Euler angles \(\underline {\theta }_{\;E} = (\begin{array}{*{20}c} \varphi & \theta & \psi \\ \end{array} )^{\rm T}\), again. Finally, the pendulum moves inside a gravity field with a constant gravity acceleration \(g = 9.81\;{m \mathord{\left/ {\vphantom {m {s^{2} }}} \right. \kern-\nulldelimiterspace} {s^{2} }}\), acting along the \(OY\) axis.
The first set of numerical results was obtained by assuming that the pendulum has an initial position with \(\underline {r}_{\;\;C} (0) = (\begin{array}{*{20}c} \ell & 0 & 0 \\ \end{array} )^{\rm T}\), \((\varphi_{0} ,\theta_{0} ,\psi_{0} ) = (0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2},0)\) and starts from rest (i.e., with \(\dot{\underline {r} }_{\;\;C} (0) = \underline {0}\) and \(\underline {\Omega } (0) = \underline {0}\)), as depicted in Fig. 4. First, in Fig. 5 are shown the time histories of the norm of the motion constraint function \(\underline {\phi }\), the norm of \(\underline {\dot{\phi }}\), the time step employed during numerical integration and the mechanical energy of the body over the first two seconds of the motion. In particular, the constraint function is defined by
with \(\underline {s} = (\begin{array}{*{20}c} { - \ell } & 0 & 0 \\ \end{array} )^{\rm T}\). Then, differentiation of Eq. (95) leads to
which specifies the constraint matrix \(A = [\begin{array}{*{20}c} {I_{3} } & { - R\,\tilde{s}\,T} \\ \end{array} ]\), required in Eq. (92).
The numerical methods applied to the first example are also applied to this, a little more involved, mechanical example. More specifically, a comparison is performed between results obtained by employing the geometrically consistent new method (ODE-GC) and by integrating Eq. (65) using the MATLAB solver ode45 (ODE-45) and Eqs. (92) and (94) using the MATLAB solvers ode15s (DAE-SE) and ode15i (DAE-FI). When using the ODE-GC method, the time step was set equal to the constant value 0.01 s. In all other cases, the maximum time step was set equal to 0.01 s, since these methods employ a variable time step. Also, in all cases, a tolerance value equal to 0.001 was selected.
First, the results shown in Fig. 5a, b reveal that the norms of \(\| {\underline {\phi } } \|\) and \(\| {\underline {\dot{\phi }} } \|\) are sufficiently small in all methods. In particular, the results of the ODE-GC method are close to the required accuracy level. Also, the biggest values for both of these norms appear for the DAE-FI method, while the smallest values are obtained by ODE-45. The last observation is justified by the high order of accuracy of the ode45 Runge–Kutta solver [56]. In fact, all these are also reflected by the results of Fig. 5c, providing the history of the time step selected by each method. The last results reveal that the DAE-FI method exhibits the most irregular variation of the time step. Finally, the corresponding mechanical energy is depicted in Fig. 5d. Again, the DAE-FI solver exhibits the worst performance.
Under the initial conditions selected, the pendulum is expected to undergo planar motion (within the \(OXY\) plane). This was found to be the case by using the geometrically consistent ODE-GC and the ODE-45 solver, indeed. However, integration with the DAE methods led to different results. For instance, in Fig. 6a, b are presented results obtained for the displacement of the pendulum center along the direction of the \(OX\) and the \(OZ\) axes, respectively, over the first 40 s of the motion. First, the DAE-SE solver exhibited an instability at about 20 s and failed to run further at about 32 s, as indicated by the star symbol. In fact, this instability is related to the appearance of a strong out of plane displacement, as shown in Fig. 6b. Also, the DAE-FI solver run through the whole time interval considered but gave acceptable results at the beginning of the motion only. The corresponding histories of the time step and the mechanical energy are also included in Fig. 6c, d. Obviously, both DAE solvers exhibit very large and irregular variations in the time step. Moreover, direct comparison with the results of the geometrically consistent new method shows that the numerical instability developed at about 20 s when using the DAE-SE solver is also related to an exceeding increase in the mechanical energy within the time interval 20–32 s, which destroys the subsequent solution.
Next, a second set of numerical results was obtained by assuming that the initial conditions are the same as before, but with \(\Omega_{z} (0) = 0.1\;{{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\). Under this new set of initial conditions, the pendulum is expected to exhibit a spatial motion. First, in Fig. 7a–d are shown the time histories of the norms of \(\underline {\phi }\) and \(\underline {\dot{\phi }}\), the time step of integration and the mechanical energy of the body, by applying the same numerical integration methods. The results reveal that the DAE-SE solver run over the time interval examined. However, it gave acceptable results at the very beginning of the motion, only, as confirmed by the results of Fig. 7a, b. In contrast, the DAE-FI solver failed in this case, at about 5.5 s. The history of the time step and the energy, shown in Fig. 7c, d, respectively, provides a justification for the unusual behavior observed. Finally, in Fig. 7e, f are presented results obtained for the displacement of the pendulum center along the direction of the \(OX\) and the \(OZ\) axes, respectively. Once again, the results obtained by the DAE methods are problematic. More specifically, the DAE-FI solver provided results which appear to be reasonably close to the solution obtained by both the ODE solvers, but it failed to continue after 5.5 s. In addition, the DAE-SE solver provided highly inaccurate results from the very beginning of the motion. On the other hand, the predictions of both ODE-GC and ODE-45 stay close throughout the motion, which now becomes spatial, by developing a significant displacement component along the OZ axis in a gradual manner.
Time histories of: a the norm of the motion constraint function \(\underline {\phi }\), b the norm of \(\underline {\dot{\phi }}\), c the time step of numerical integration, d the mechanical energy, e the center of mass displacement along the OX axis and (f) along the OZ axis, for motion of a spherical pendulum
5.3 Chain motion
In the third example, motion of a chain, involving fifteen identical members and suspended at four points, is investigated. The suspension points A, B, C and D are located at a distance of \(b = 0.9144\;{\text{m}}\) apart, as shown in Fig. 8. Each member is a bar with mass \(m = 1\;{\text{kg}}\) and length \(\ell = 0.3048\;{\text{m}}\), all interconnected with spherical joints. At some moment, while the chain is at rest, the supports at the intermediate points B and C are removed suddenly and the chain starts moving under the action of gravity. Specifically, the gravity acceleration is \(g = 9.81\;{\text{m/s}}^{2}\) and acts along the negative AY axis of a fixed frame AXYZ. Finally, each bar is modeled as a rigid body with six generalized coordinates, so that the total system is described by 90 generalized coordinates and involves 48 motion constraints. More details about the chain configuration can be found in the original reference [60].
Next, in Fig. 9 are presented and compared results obtained by using the ODE-GC numerical integration with results derived by employing two state-of-the-art commercial codes [61, 62]. In those codes, the equations of motion are first set up as a system of high-index DAEs, which are then solved numerically, by employing classical backward differentiation formulas (BDFs). In particular, the GSTIFF and DASPK methods were selected in solving the equations of motion by ADAMS and Motion Solve, respectively. In brief, GSTIFF is a variable-order, variable-step, multi-step integrator with a maximum integration order of six. The BDF coefficients it uses are calculated by assuming that the step size of the model is mostly constant [61]. Likewise, DASPK solves a system of differential/algebraic equations of the form \(\underline {G} (t,\underline {y} ,\underline {y^{\prime}} ) = \underline {0}\), using a combination of BDF methods [62]. For each of the two codes, the numerical results were determined for a maximum allowable time step of 0.001 s. Instead, the time step is kept constant to the value of 0.001 s in ODE-GC.
Originally, the history of the mechanical energy of the system over the first two seconds of the motion is shown in Fig. 9a. According to the analytical predictions, the mechanical energy of the system should remain constant, through the entire duration of the motion. The results of the codes were obtained for two widely different values of the numerical tolerance parameter. In all cases, a sudden and large drop in the mechanical energy is observed at the time where point E reaches its lowest position for the first time. At that instant, the forces developed at the joints become very large temporarily. As an outcome, the results obtained by the DAE solvers for the larger tolerance value present a drop in the energy, which continuous afterward. In contrast, the ODE solution and the solutions obtained by both the DAE solvers for the smaller tolerance seem to return to the correct value, after that moment. However, the results presented in Fig. 9b, showing the history of the mechanical energy of the system over the first twenty seconds of the motion, indicate that only the new method conserves the energy eventually. This is attributed to the way the constraints are treated and imposed in the overall formulation. On the other hand, this is not the case for the results obtained by both the DAE solvers. For scaling purposes, only the results corresponding to the smaller tolerance value are included in Fig. 9b, c. These results illustrate that an increase in the numerical accuracy level has only a temporary effect, but it cannot eliminate the inherent problems of the DAE solvers.
Also, despite the fact that the initial static position and the forcing are planar, the two DAE solvers predict significant levels of out-of-plane motion. For instance, in Fig. 9c are presented the time histories obtained for the displacement of the middle point E along the AZ axis. The new method (ODE-GC) predicts a virtually zero value for the out-of-plane displacement. However, both ADAMS and Motion Solve (even with the smaller tolerance value) predict the development of significant levels of out-of-plane motion, after an initial short interval of plane motion. Finally, the time evolution of the time steps required during the direct integration is included in Fig. 9d. The new method produces quite satisfactory results with the selected time step, throughout the computations. However, the DAE solvers require a much smaller time step, compared to the time step needed in ODE-GC.
5.4 Motion of a spinning top
In the fourth example, motion of a spinning top is examined. In particular, the top has a symmetry axis Oz, whose point \(O\) is fixed on the ground, as shown in Fig. 10. Consequently, if frame Oxyz is fixed in the body and frame OXYZ is fixed on the ground, the configuration of the top is specified completely by the 3–1–3 set of Euler angles \(\underline {\theta }_{E} = (\begin{array}{*{20}c} \varphi & \theta & \psi \\ \end{array} )^{{\text{T}}}\). Moreover, the top is under the action of a uniform gravity field, acting along the negative \(OZ\) axis, while the friction effects are negligible. Finally, the top center of mass \(C\) is located at a distance \(\ell\) from point \(O\) and the mass of the top is \(m\). In addition, the mass moment of inertia with respect to point \(O\) is \(I_{zz} = I_{a}\) about the symmetry axis and \(I_{xx} = I_{yy} = I_{t}\) about the other body axes.
The spinning top was selected as a mechanical example since its dynamics is quite interesting and admits an exact solution [54, 55]. This provides the ground to evaluate the numerical performance and accuracy of both the new ODE methods and the DAE solvers, by direct comparison with existing analytical solutions. For instance, in Fig. 11 are presented results for one of the most characteristic motions of a heavy symmetrical top, known as cuspidal motion. These motions appear under the following special choice of the initial conditions.
During such a motion, the analysis predicts that the top nutates between the angles \(\theta_{0}\) and \(\theta_{1} > \theta_{0}\), while it precesses and spins, simultaneously, with time-varying angular rates \(\dot{\varphi }\) and \(\dot{\psi }\).
The spinning top was modeled as a constrained 6-dof rigid body, where the constraint function is given by Eq. (95), again, with \(\underline {s} = (\begin{array}{*{20}c} 0 & 0 & { - \ell } \\ \end{array} )^{{\text{T}}}\). In particular, the set of numerical results presented in Fig. 11 were obtained for the following set of numerical values: \(m = 5\;{\text{kg}}\), \(\ell = 0.1\;{\text{m}}\), \(I_{a} = 0.01\;{\text{kg}}\;{\text{m}}^{2}\), \(I_{t} = 0.1\;{\text{kg}}\;{\text{m}}^{2}\) and a gravity acceleration \(g = 9.81\;{\text{m/s}}^{2}\). Moreover, \(\theta_{0} = 20\) °, \(\omega_{3} = \Omega_{z} (0) = 50\;{\text{rad/s}}\), while the tolerance value was selected equal to 10–4. Finally, a fixed time step of 0.001 s was chosen for ODE-GC, while a maximum time step of 0.001 s was allowed for all the other solvers.
First, in Fig. 11a, b is presented the time history of the nutation angle and the angular rate \(\dot{\varphi }\), over the initial 5 s of the motion. The results demonstrate that the predictions of both the ODE solvers (ODE-45 and ODE-GC) are virtually coincident with the analytical results. However, the ODE-45 solver achieves that objective at the expense of a large decrease in the time step, as is illustrated by Fig. 11c. In contrast, the results obtained by either DAE-SE or DAE-FI are not appropriate. More specifically, the DAE-FI solver provides results of acceptable accuracy, only during a short initial interval, and it then fails suddenly to continue. In addition, the DAE-SE solver runs throughout the time interval examined, but the solution obtained is inaccurate. Also, its time step varies rapidly, by about four orders of magnitude during the computations. These results are also reflected by Fig. 11d, where the mechanical energy of the system is plotted.
5.5 Motion of a multi-bar system
In the last example, motion of a multiple four-bar mechanism, possessing five degrees of freedom, is investigated. In fact, the system examined is a benchmark problem, where the main objective is to assess the efficiency of a multibody formulation in the dynamic simulation as well as to test the handling of redundant constraint equations and singular positions [63]. More specifically, the system consists of a 5 × 5 grid of four-bar mechanisms, with members aligned with the \(OY\) and \(OZ\) axes of a fixed coordinate system \(OXYZ\). The initial static position of the system is depicted in Fig. 12a.
The members of the system examined are modeled as three-dimensional bodies. This implies that the system is mechanically over-constrained. Specifically, the bodies are connected through revolute joints, which are parallel to the OX axis. Also, all the bars have a length of 1 m, a uniformly distributed mass of 1 kg and a negligible mass moment of inertia with respect to their longitudinal axis. Moreover, the mechanism is under the action of gravity, which acts along the negative \(OZ\) axis, with a gravity acceleration of \(g = 9.81\;{\text{m/s}}^{2}\). In addition, the initial velocity of the six top bodies is \(\dot{\varphi }_{1} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-\nulldelimiterspace} 3}\;\)rad/s, while the simulation is run for 10 s. Furthermore, the total number of moving bodies is 55, while the number of joints is 80. Finally, the mechanical energy of the system is evaluated at every time step. After defining the energy drift as the absolute value of the difference between the current and the initial system energy, the simulation error is computed as the maximum energy drift, with maximum allowable value 1 J.
Next, in Fig. 12b–f are presented numerical results obtained by applying the numerical integration of the new method and compared with the benchmark results. Due to the presence of redundant coordinates and multiple singular solutions, the augmented Lagrangian version of the ODE-GC solver was employed for this set of calculations [26]. Direct comparison demonstrates that the results on the response quantities are virtually indistinguishable. In fact, ODE-GC leads to a much better energy prediction. All these results illustrate the numerical accuracy and efficiency of the new method.
6 Synopsis and extensions
In the first part of this work, the essential steps of a theoretical procedure were presented, leading to a new set of equations governing the motion of a general class of multibody dynamic systems subjected to equality motion constraints. This procedure was founded on fundamental concepts of Analytical Mechanics and provided a set of pure second-order ODEs in a natural manner. Then, this set was converted to an equivalent first-order three-field weak form. This provided the foundation to develop an appropriate numerical integration scheme, respecting the geometric properties of the configuration space and avoiding the singularities and instabilities related to existing DAE formulations. Moreover, to cover cases involving redundant coordinates and singular positions, this scheme was also extended and put to a convenient Augmented Lagrangian form.
In the second part of this study, the numerical effectiveness and accuracy of the scheme developed were tested in several mechanical example systems. This was done by comparison of numerical results with similar results obtained by using analytical solutions as well with results determined by employing DAE solvers. In particular, the results of the new method were found to be virtually coincident with the analytical predictions and the results of a benchmark problem. Also, the robustness, accuracy and efficiency of the new numerical method were demonstrated by comparison with classical DAE solvers. These solvers exhibited the usual pathologies related to their singular form and expressed by gradual and eventually large deviations from the solution or by appearance of sudden instabilities. Even worse, it was found that application of typical numerical procedures, like the reduction of the time step or the allowable tolerance level, does not guarantee an improvement in the quality of the numerical results of the DAE solvers. All these are in agreement with findings of previous studies on the subject [8, 18,19,20,21, 64, 65]. The superior performance of the new method over the classical DAE solvers is due to the consistent and systematic exploitation of the complex geometric properties characterizing the configuration space of the class of systems examined. This is reflected both by the extra terms appearing in the equations of motion and by the consistent geometric discretization performed. The former causes a natural stabilization and scaling of the equations of motion, while the latter adds robustness to the numerical discretization process.
The new method can be applied to more complex and challenging mechanical systems. For instance, it can easily be extended to systems with rheonomic characteristics, where the new set of equations of motion is also available [32]. Furthermore, a related area, with an enormous theoretical and engineering significance, is the area of multibody systems involving contacts, impacts and friction, where the geometry and dynamics of the motion are more complex, since some of the constraints appear in an inequality form [66,67,68]. Some preliminary work, applicable to single contact events, indicates that similar methodologies are applicable and equally beneficial. Specifically, the equations of motion can be put in a second-order ODE form, again. Moreover, development and application of geometrically consistent methodologies are still available [69, 70]. Another possible extension is to multibody dynamic systems where some of the members of the system exhibit significant deformability [6, 8]. In this respect, it is of interest to investigate how do the motion constraints applied to bodies with a general three-dimensional geometry affect the geometric properties (mainly the affinities) of the resulting two-dimensional (e.g., plates, shells) and one-dimensional (e.g., rods, rings, beams) counterparts [71]. In addition, investigation of similar effects of the classical geometric discretization procedures applied to the original continuous body (e.g., finite element methods [72]) is also desirable. Furthermore, an area with large engineering significance for the application of the new method is the special but large class of mechanical systems with linear characteristics, subject to linear motion constraints [73, 74]. This will also be useful in efforts to investigate the stability properties of the numerical integration schemes. Finally, the ODE form of the new equations of motion makes amenable the development of new robust implicit or explicit numerical integration methods, depending on the specific characteristics and properties of the system examined, as well as their application to large-scale mechanical systems [74, 75].
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Lanczos, C.: The Variational Principles of Mechanics. University of Toronto Press, Toronto (1952)
Pars, L.Α: A Treatise on Analytical Dynamics. Heinemann Educational Books, London (1965)
Greenwood, D.T.: Classical Dynamics. Dover Publications, New York (1977)
Rosenberg, R.M.: Analytical Dynamics of Discrete Systems. Plenum Press, New York (1977)
Papastavridis, J.G.: Tensor Calculus and Analytical Dynamics. CRC Press, Boca Raton (1999)
Geradin, Μ, Cardona, Α: Flexible Multibody Dynamics. John Wiley & Sons, New York (2001)
Shabana, A.A.: Dynamics of Multibody Systems, 3rd edn. Cambridge University Press, New York (2005)
Bauchau, O.A.: Flexible Multibody Dynamics. Springer Science+Business Media, London (2011)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry, 2nd edn. Springer Science+Business Media Inc., New York (1999)
Murray, R.M., Li, Ζ, Sastry, S.S.: A Mathematical Introduction to Robot Manipulation. CRC Press, Boca Raton (1994)
Bloch, A.M.: Nonholonomic Mechanics and Control. Springer, New York (2003)
Selig, J.M.: Geometric Fundamentals of Robotics, 2nd edn. Springer, New York (2005)
Pfeiffer, F., Glocker, Ch.: Multibody Dynamics with Unilateral Contacts. Wiley, New York (1996)
Natsiavas, S.: Analytical modeling of discrete mechanical systems involving contact, impact and friction. ASME J. Appl. Mech. Rev. 71, 050802–050825 (2019)
Nikravesh, P.E.: Computer-Aided Analysis of Mechanical Systems. Prentice-Hall Inc, Englewood Cliffs (1988)
Petzold, L.: Differential/algebraic equations are not ODE’s. SIAM J. Sci. Stat. Comput. 3, 367–384 (1982)
Βrenan, K.E., Campbell, S.L., Petzhold, L.R.: Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations. North-Holland, Νew York (1989)
García Orden, J.C., Conde, S.C.: Controllable velocity projection for constraint stabilization in multibody dynamics. Nonlinear Dyn. 68, 245–257 (2012)
Bottasso, C.L., Dopico, D., Trainelli, L.: On the optimal scaling of index three DAEs in multibody dynamics. Multibody Syst. Dyn. 19, 3–20 (2008)
Bauchau, ΟΑ, Epple, Α, Bottasso, C.L.: Scaling of constraints and augmented Lagrangian formulations in multibody dynamics simulations. ASME J. Comput. Nonlinear Dyn. 4, 021007 (2009)
Wehage, R.A., Haug, E.J.: Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems. ASME J. Mech. Des. 104, 247–255 (1982)
Udwadia, F.E., Kalaba, R.E.: Analytical Dynamics A New Approach. Cambridge University Press, Cambridge (1996)
Paraskevopoulos, E., Natsiavas, S.: On application of Newton’s law to mechanical systems with motion constraints. Nonlinear Dyn. 72, 455–475 (2013)
Natsiavas, S., Paraskevopoulos, E.: A set of ordinary differential equations of motion for constrained mechanical systems. Nonlinear Dyn. 79, 1911–1938 (2015)
Paraskevopoulos, E., Natsiavas, S.: Weak formulation and first order form of the equations of motion for a class of constrained mechanical systems. Int. J. Non-linear Mech. 77, 208–222 (2015)
Potosakis, N., Paraskevopoulos, E., Natsiavas, S.: Application of an augmented Lagrangian approach to multibody systems with equality motion constraints. Nonlinear Dyn. 99, 753–776 (2020)
Greenwood, D.T.: Advanced Dynamics. Cambridge University Press, New York (2003)
Frankel, T.: The Geometry of Physics: An Introduction. Cambridge University Press, New York (1997)
Shabanov, S.V.: Constrained systems and analytical mechanics in spaces with torsion. J. Phys. A Math. Gen. 31, 5177–5190 (1998)
Νeimark, J.I., Fufaev, N.A.: Dynamics of Nonholonomic Systems. Translations of Mathematical Monographs, vol. 33. American Mathematical Society, Providence (1972)
Bowen, R.M., Wang, C.-C.: Introduction to Vectors and Tensors, 2nd edn. Dover Publications Inc, Mineola (2008)
Natsiavas, S., Paraskevopoulos, E.: Application of Newton’s law of motion to constrained mechanical systems possessing configuration manifolds with time dependent geometric properties. Nonlinear Dyn. 85, 2583–2610 (2016)
Natsiavas, S., Paraskevopoulos, E.: A boundary layer approach to multibody systems involving single frictional impacts. ASME J. Comput. Nonlinear Dyn. 14, 011002–011016 (2019)
Chetaev, N.G.: Theoretical Mechanics. Mir Publishers, Moscow (1989)
Washizu, K.: Variational Methods in Elasticity and Plasticity, 3rd edn. Pergamon Press, Oxford (1982)
Felippa, C.: On the original publication of the general canonical functional of linear elasticity. ASME J. Appl. Mech. 67, 217–219 (2000)
Simo, J., Wong, K.: Unconditionally stable algorithms for rigid body dynamics that exactly preserve energy and momentum. Int. J. Num. Meth. Eng. 31, 19–52 (1991)
Crouch, P., Grossman, R.: Numerical integration of ordinary differential equations on manifolds. J. Nonlinear Sci. 3, 1–33 (1993)
Munthe-Kaas, H.: Runge-Kutta methods on Lie groups. BIT Numer. Math. 38, 92–111 (1998)
Iserles, A., Munthe-Kaas, H.Z., Nørsett, S.P., Zanna, A.: Lie-group methods. Acta Num. 215–365 (2000)
Negrut, D., Haug, E.J., German, H.C.: An implicit Runge-Kutta method for the integration of differential-algebraic equations of multibody dynamics. Multibody System Dyn. 9, 121–142 (2003)
Brüls, O., Cardona, A., Arnold, M.: Lie group generalized-α time integration of constrained flexible multibody systems. Mech. Mach. Theory 48, 121–137 (2012)
Bayo, E., Ledesma, R.: Augmented Lagrangian and mass-orthogonal projection methods for constrained multibody dynamics. Nonlinear Dyn. 9, 113–130 (1996)
Blajer, W.: Augmented Lagrangian formulation: geometrical interpretation and application to systems with singularities and redundancy. Multibody Syst. Dyn. 8, 141–159 (2002)
Dopico, D., Gonzalez, F., Cuadrado, J., Kövecses, J.: Determination of holonomic and nonholonomic constraint reactions in an index-3 augmented Lagrangian formulation with velocity and acceleration projections. ASME J. Comput. Nonlinear Dyn. 9, 041006 (2014)
Gonzalez, F., Dopico, D., Pastorino, R., Cuadrado, J.: Behaviour of augmented Lagrangian and Hamiltonian methods for multibody dynamics in the proximity of singular configurations. Nonlinear Dyn. 85, 1491–1508 (2016)
Bertram, W.: Differential geometry, Lie groups and symmetric spaces over general base fields and rings. Mem. Am. Math. Soc. 192, 1–202 (2008)
Paraskevopoulos, E., Natsiavas, S.: A new look into the kinematics and dynamics of finite rigid body rotations using Lie group theory. Int. J. Solids Struct. 50, 57–72 (2013)
Paraskevopoulos, E.A., Panagiotopoulos, C.G., Talaslidis, D.G.: Rational derivation of energy/momentum-preserving time integration algorithms. Application to dynamic response under moving vehicles. In: ECCOMAS Conference, Crete, Greece (2007)
Benzi, M., Golub, G.H., Liesen, J.: Numerical solution of saddle point problems. Acta Num. 1–137 (2005)
Passas, P., Natsiavas, S., Paraskevopoulos, E.: Numerical integration of multibody dynamic systems involving nonholonomic equality constraints. Nonlinear Dyn. 105, 1191–1211 (2021)
Bertsekas, D.P.: Constraint Optimization and Lagrange Multiplier Methods. Academic Press, NY (1982)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer Series in Operations Research, New York (1999)
Greenwood, D.T.: Principles of Dynamics, 2nd edn. Prentice-Hall Inc, Englewood Cliffs (1988)
Goldstein, H.: Classical Mechamics, 2nd edn. Addison-Wesley, Menlo Park (1981)
Dormand, J.R., Prince, P.J.: A family of embedded Runge–Kutta formulae. J. Comp. Appl. Math. 6, 19–26 (1980)
Shampine, L.F., Reichelt, M.W.: The MATLAB ODE Suite. SIAM J. Sci. Comput. 18, 1–22 (1997)
Shampine, L.F.: Solving 0 = F(t, y(t), y′(t)) in MATLAB. J. Num. Math. 10, 291–310 (2002)
Baumgarte, J.: Stabilization of constraints and integrals of motion in dynamical systems. Comput. Methods Appl. Mech. Eng. 1, 1–16 (1972)
Kamman, J.W., Huston, R.L.: Dynamics of constrained multibody systems. ASME J. Appl. Mech. 51, 899–903 (1984)
MSC ADAMS 2018.1, User Guide, MSC Software Corporation, California, USA.
MotionSolve v19.0, User Guide, Altair Engineering Inc., Irvine, California, USA.
IFToMM T.C. for Multibody Dynamics, Library of Computational Benchmark Problems, http://www.iftomm-multibody.org/benchmark
Arnold, M., Cardona, A., Bruls, O.: Order reduction in time integration caused by velocity projection. J. Mech. Sci. Technol. 29, 2579–2585 (2015)
de Bustos, I.F., Uriarte, H., Urkullu, G., Garcia-Marina, V.: A non-damped stabilization algorithm for multibody dynamics. Meccanica (2021). https://doi.org/10.1007/s11012-021-01433-0
Brogliato, B.: Nonsmooth Mechanics: Models, Dynamics and Control, 3rd edn. Springer, London (2016)
Khulief, Y.A.: Modeling of impact in multibody systems: an overview. ASME J. Comput. Nonlinear Dyn. 8(2), 021012 (2013)
Tian, Q., Flores, P., Lankarani, H.M.: A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 122, 1–57 (2018)
Natsiavas, S., Paraskevopoulos, E.: An analytical dynamics approach for mechanical systems involving a single frictional contact using b-geometry. Int. J. Solids Struct. 148–149, 140–156 (2018)
Passas, P., Natsiavas, S.: A time-stepping method for multibody systems involving frictional impacts and phases with persistent contact. Mech. Mach. Theory 169, 104591 (2022)
Fung, Y.C., Tong, P.: Classical and Computational Solid Mechanics. World Scientific, Singapore (2001)
Hughes, T.J.R.: The Finite Element Method. Prentice-Hall Inc, Englewood Cliffs (1987)
Géradin, M., Rixen, D.J.: Mechanical Vibrations: Theory and Application to Structural Dynamics. Wiley, New York (2014)
Craig, R.R., Jr.: Structural Dynamics—An Introduction to Computer Methods. Wiley, New York (1981)
Papalukopoulos, C., Natsiavas, S.: Dynamics of large scale mechanical models using multi-level substructuring. ASME J. Comput. Nonlinear Dyn. 2, 40–51 (2007)
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Natsiavas, S., Passas, P. & Paraskevopoulos, E. Nonlinear dynamics of constrained multibody systems based on a natural ODE formulation. Nonlinear Dyn 110, 2951–2977 (2022). https://doi.org/10.1007/s11071-022-07748-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-07748-1