On the Lagrange multipliers of the intrinsic constraint equations of rigid multibody mechanical systems

Abstract

This paper deals with the Lagrange multipliers corresponding to the intrinsic constraint equations of rigid multibody mechanical systems. The intrinsic constraint equations are algebraic equations that are associated with nonminimal sets of orientation parameters employed for the kinematic representation of large finite rotations. Two coordinate formulations are analyzed in this investigation, namely the reference point coordinate formulation (RPCF) with Euler parameters and the natural absolute coordinate formulation (NACF). While the RPCF with Euler parameters employs the four components of a unit quaternion as rotational coordinates, the NACF directly uses the orthonormal set of nine direction cosines for describing the orientation of a rigid body in the three-dimensional space. In the multibody approaches based on the RPCF with Euler parameters and on the NACF, the use of a nonminimal set of rotational coordinates facilitates a general and systematic formulation of the differential–algebraic equations of motion. Considering the basic equations of classical mechanics, the fundamental problem of constrained motion is formalized and solved in this paper by using a special form of the Udwadia–Kalaba method. By doing so, the Udwadia–Kalaba equations are employed for obtaining closed-form analytical solutions for the Lagrange multipliers associated with the intrinsic constraint equations that appear in the differential–algebraic dynamic equations developed by using the RPCF with Euler parameters and the NACF multibody approaches. Two simple numerical examples support the analytical results found in this paper.

1 Introduction

This investigation is concerned with the nonlinear constraint equations of two coordinate formulations commonly used in multibody system applications. In particular, the multibody approaches that are based on redundant sets of orientation parameters are the object of this study. Background materials, the formulation of the problem of interest for this investigation, the scope, the contributions, and the organization of the paper are discussed in this section.

1.1 Background

In industrial manufacturing and vehicle engineering applications, mechanical systems such as machines and mechanisms are often modeled as multibody mechanical systems [1,2,3,4,5,6,7,8]. Numerous engineering examples of mechanical systems that can be modeled using the multibody system approach can be found for robotic systems, automotive systems, watercraft, aircraft, and spacecraft [9,10,11,12,13,14,15]. The mechanical part of a multibody system is subjected to nonlinear force fields and is connected by mechanical joints that can allow large translations and large finite rotations with respect to each other [16,17,18,19,20]. Therefore, in the analytical description of a multibody system and in the subsequent computer implementation of the equations of motion, the system nonlinearities must be correctly modeled using suitable formulation approaches in order to correctly take into account the inherent nature of the multibody mechanical system under consideration [21,22,23,24,25]. As thoroughly discussed in the literature, this problem is particularly important for lightweight machines and mechanisms in which, in order to meet increasing performance specifications, the structural components have a more complex dynamical behavior in addition to the geometric nonlinearity that is due to the mechanical deformations [26,27,28,29].

In the last two decades, multibody dynamics has emerged as an interdisciplinary research field firmly grounded in analytical mechanics, mutually interconnected with the finite element analysis of flexible structures, and strongly related to the nonlinear control theory of machines and mechanisms [30,31,32,33,34]. Since the dynamics of multibody mechanical systems is highly nonlinear because of the geometric nonlinearities and the possible presence of mechanical deformations, standard control strategies based on the linearization approach are inappropriate and more complex control methods are required in order to obtain robust, effective, and efficient control policies for this class of mechanical systems [35,36,37,38]. In general, multibody dynamics can be subdivided in two complementary research fields: rigid multibody dynamics, which deals only with rigid bodies, and flexible multibody dynamics, which includes both rigid and deformable bodies [39]. In flexible multibody system applications, it is necessary to use a sound analysis approach in order to correctly capture the effect of the mechanical deformations of flexible bodies [40,41,42,43]. This is necessary because the system components can undergo large finite rotations and can experience small and/or large deformations [44,45,46,47]. In particular, among all the analytical descriptions available in the literature for flexible multibody mechanical systems, the floating frame of reference formulation (FFRF) and the absolute nodal coordinate formulation (ANCF) are nonlinear formulation approaches for flexible multibody systems which yield accurate descriptions of three-dimensional geometry and allow for the development of nonincremental solution procedures for the computer implementation of the resulting set of differential–algebraic equations of motion [48]. In the ANCF computational framework, accurate mathematical models of flexible multibody systems can be obtained because a unique geometric representation is used for both the displacement field and the rotation field of a continuum body [49]. Thus, in recent years, ANCF finite elements have been successfully used in several engineering applications to develop large models with complex three-dimensional shapes and significant model details [50,51,52,53,54,55,56].

1.2 Formulation of the problem of interest for this investigation

It is well known that a rigid body has only three degrees of freedom in a two-dimensional space and six degrees of freedom in a three-dimensional space. A continuum body can be considered as a rigid body when its deformation is very small and, therefore, the effect of the deformation on the resulting global motion can be neglected. However, the mathematical description of the geometric configuration of a three-dimensional rigid body is not unique and, for this purpose, independent or redundant sets of configuration parameters featuring more than six generalized coordinates can be employed. To this end, minimal and nonminimal mathematical descriptions of the rigid body configuration in the three-dimensional space are often used to develop kinematic and dynamic formulations for rigid multibody mechanical systems. A minimal description of the motion of a rigid body with respect to an inertial frame of reference is based on three translational coordinates and three rotational coordinates. In virtue of their clear physical interpretation, the sets of three rotational coordinates that are widely employed to describe the orientation of a rigid body are the three independent Euler angles and the three independent Tait–Bryan angles also called Cardan angles. The Euler angles and the Tait–Bryan angles involve three successive rotations about three body-fixed axes which, in general, are not orthogonal. For example, the Euler angles frequently employed in the classical mechanics consider three successive rotations about the z–x–z axes, whereas the Tait–Bryan angles or Cardan angles used in vehicle engineering applications are obtained from three successive rotations about the x–y–z axes which are called, respectively, roll, pitch, and yaw [57]. However, there are available in the literature other sets of three orientation coordinates that are seldom employed for practical applications due to their more abstract mathematical nature and, more importantly, because of the presence of critical configurations called kinematic singularities [58]. In fact, since it can be mathematically proved that each kinematic formulation based on a minimal set of three rotational coordinates suffers from the serious problem of having kinematic singularities, a redundant set of orientation parameters is often employed for modeling complex rigid multibody mechanical systems and solve this important issue related to the geometric description of the body orientation in a three-dimensional space [59]. A kinematic singularity is a point of the configuration space of the rigid body where the rotation matrix and the Jacobian matrix of the body angular velocity computed with respect to the time derivative of the set of rotational coordinates degenerate and lose their full rank. It is important to understand that the nature of the kinematic singularity is purely mathematical, it depends on the formulation strategy adopted to describe the kinematics and dynamics of the rigid body, and this undesirable phenomenon has no physical counterpart. Since the angular velocity of a rigid body is not an exact differential, which means that it cannot be obtained as the time derivative of some vector quantity related to the orientation of the rigid body, devising a robust mathematical approach for the definition of the body angular orientation in a three-dimensional space is challenging.

In order to solve the kinematic singularity problem, two rigid multibody formulations that are of interest for this investigation can be effectively employed, namely the reference point coordinate formulation (RPCF) with Euler parameters [60] and the natural absolute coordinate formulation (NACF) [61]. In the RPCF, the kinematic issues associated with the presence of critical configurations are eliminated employing as rotational coordinates the four components of a unit quaternion which identify the set of Euler parameters. In the NACF, on the other hand, the singularity problems are solved from the outset using the set of nine direction cosines as orientation parameters. Since both the set of four Euler parameters and the set of nine direction cosines do not suffer from the kinematic singularity problem encountered when each set of three rotational coordinates is employed, they are extensively used in engineering applications for the kinematic and dynamic analysis of rigid multibody mechanical systems. Therefore, the RPCF with Euler parameters uses only one additional rotational coordinate when compared with respect to the other minimal coordinate formulations, whereas the NACF employs six extra rotational coordinates with respect to the minimal number of orientation parameters. Nevertheless, since in the kinematic description adopted in the NACF the separation of variables technique is employed, the dynamic formulation based on the NACF leads to a convenient structure of the differential–algebraic equations of motion which are sparse and easy to implement in a general-purpose multibody computer program [62]. Furthermore, unlike the conventional multibody approaches based on natural coordinates [63,64,65,66,67], the NACF allows for a systematic formulation of the constraint equations that enter in the formulation of the differential–algebraic equations of motions leading to effective and efficient dynamic simulations.

The coordinate redundancy employed in the geometric descriptions of the RPCF and of the NACF implies the mathematical formulation of an additional set of algebraic constraint equations which do not have a straightforward physical interpretation. However, by using the basic mathematical tools of linear algebra and employing some continuum mechanics concepts such as the definition of the Green–Lagrange strain tensor, it can be easily demonstrated that the algebraic constraints arising from the use of redundant orientation parameters are associated with the body rigidity conditions. For this reason, in this work these algebraic constraints are referred to as intrinsic constrains, whereas the algebraic constrains associated with the kinematic joints are called extrinsic constrains. The entire group of algebraic equations made of intrinsic and extrinsic constraints form a set of holonomic constraints which can be included in the equations of motion of a rigid multibody system using the Lagrange multipliers technique. The vector of Lagrange multipliers represents an additional vector of unknown functions which must be computed together with the system configuration vector and its time derivatives in order to predict the motion of the multibody mechanical system of interest. It is well known that the vector of Lagrange multipliers associated with the extrinsic constraints can be used to recover the generalized reaction forces of the kinematic joints which have a clear physical interpretation. A similar procedure can be applied to compute the generalized constraint forces associated with the intrinsic constraint equations by means of the corresponding vector of Lagrange multipliers. The main object of this investigation is, therefore, to analyze the generalized constraint forces associated with the Lagrange multipliers relative to the set of intrinsic constraint equations, corroborate the mathematical derivation developed in the paper with simple numerical experiments, and discuss the nontrivial physical interpretation of the mathematical results found.

1.3 Scope and contributions of this study

This paper represents an attempt to shed more light on the issues associated with the intrinsic constraint equations employed in the nonminimal representation of the orientation of rigid bodies. The goal of this investigation is, therefore, to gain physical insights into the mathematical behavior of the multibody differential–algebraic equations of motion and obtain a deeper understanding of the kinematics and dynamics of rigid multibody mechanical systems. A powerful mathematical tool is employed for this purpose, namely the fundamental equations of constrained motion that are also known as Udwadia–Kalaba equations [68]. The Udwadia–Kalaba equations originate from recent findings in the field of analytical dynamics and represent a simple and general method for deriving the equations of motion of a multibody mechanical system constrained by a general set of algebraic equations [69,70,71]. Furthermore, by using the fundamental equations of constrained motion, a unified approach can be developed for modeling complex multibody mechanical systems and also for the design of nonlinear control strategies [72, 73]. Applying the Udwadia–Kalaba method in conjunction with the theory of constrained motion in Lagrangian mechanics, both holonomic and nonholonomic constraints are treated in the same way without the need to resort to the Lagrange multiplier technique [74]. However, the vector of Lagrange multipliers can still be recovered from the generalized acceleration vector obtained employing the Udwadia–Kalaba equations by using the hypothesis of workless constraints that is typically employed in classical mechanics. This effective method allows for obtaining an explicit closed-form analytical solution for the equations of motion for constrained multibody mechanical systems even in the case of kinetic singularity, that is, when the system mass matrix become a symmetric positive semi-definite singular matrix [75]. In analogy with the kinematic singularity, a kinetic singularity is a point in the configuration space of the rigid body where the mass matrix of the body degenerates and loses its full rank [76]. The kinetic singularity has no physical justification and depends on the mathematical approach adopted for representing the orientation of a rigid body in the three-dimensional space. As discussed in the literature, assuming precise mathematical restrictions on the structure of the mass matrix and on the form of the algebraic constrains, the resulting explicit form of the system equations of motion exists and is unique [77]. This is the case of main interest for this investigation. In fact, considering, for example, a single rigid body modeled using the RPCF with Euler parameters, it can be shown that the resulting mass matrix is a symmetric positive semi-definite (singular) matrix and both the body mass matrix and the intrinsic constraint equation are amenable to be treated with the general from of the Udwadia–Kalaba equations [78]. On the other hand, as discussed in the paper, the equations of motion of a rigid body modeled employing the NACF lead to a symmetric positive definite mass matrix and, therefore, the original form of the Udwadia–Kalaba equations can be used to rewrite the equations of motion in a special mathematical form and analyze the closed-form expressions of the corresponding generalized constraint force vectors obtained in the NACF computational framework [79]. The analytical results developed in the paper are obtained by using the Udwadia–Kalaba equations in order to calculate the Lagrange multipliers associated with the intrinsic constraint equations arising both in the RPCF with Euler parameters and in the NACF together with the corresponding generalized constraint forces. Furthermore, the analytical results found in the paper are supported by a set of numerical results obtained by means of dynamic simulations.

Another important contribution of the present study is the reformulation of the fundamental equations of constrained motion in a mathematical form that is compact and easy to implement in a general-purpose multibody computer program. By doing so, the computational efficiency of the methodology developed by Udwadia and Kalaba can be considerably improved and, at the same time, the efficacy of the Udwadia–Kalaba equations is conserved. To this end, a general matrix called kinetic matrix that is associated with the multibody formulation strategy employed for deriving the differential–algebraic equations of motion is introduced. Employing the concept of the Moore–Penrose pseudoinverse matrix, the kinetic matrix is subsequently used for computing the constraint feedback matrix that allows for obtaining the generalized force vector and the Lagrange multiplier vector associated with the algebraic constraints. The alternative form of the Udwadia–Kalaba equations developed in this investigation can be applied to the equations of motion obtained by using both the RPCF with Euler parameters and the NACF. However, in the case of the RPCF with Euler parameters, the system mass matrix is a singular symmetric mass matrix and, therefore, the introduction of an auxiliary multibody mechanical system is needed in order to obtain the generalized acceleration vector and the generalized constraint force vector of the original multibody system. As discussed in details in the paper, this analytical calculation can be readily performed by using the kinetic matrix associated with the auxiliary multibody mechanical system. For this purpose, in this investigation, the fundamental equations of constrained motion are used for the analytical treatment of the set of intrinsic constraint equations resulting from the nonminimal representation of large finite rotations.

1.4 Organization of the paper

The organization of this paper is as follows. In Sect. 2, background materials and important concepts related to the two multibody formulations used in the paper for the description of the kinematics and dynamics of rigid multibody mechanical systems are reviewed. In this section, particular attention is given to the basic equations that will be extensively used in this investigation for the RPCF with Euler parameters and the NACF. In Sect. 3, the fundamental equations of constrained motion, also known as Udwadia–Kalaba equations, are discussed. In particular, in this section, the Udwadia–Kalaba equations are expressed in a special analytical form suitable for obtaining in a closed form the Lagrange multipliers of the intrinsic constraint equations that appear in the differential–algebraic equations of motion derived by using the RPCF with Euler parameters and the NACF. In Sect. 4, the numerical results obtained using two illustrative examples of rigid multibody mechanical systems are analyzed. In order to provide a numerical verification of the analytical results developed in the paper, in this section two simple mechanical systems are considered as an example of an unconstrained rigid body and as an example of a rigid body constrained by kinematic joints. In Sect. 5, the summary and the conclusions drawn from this investigation are provided.

2 Equations of motion of three-dimensional rigid multibody mechanical systems

In this section, the basic multibody equations employed in the paper and useful background material for explaining the main ideas behind the present study are provided. In particular, the equations of motion of a generic rigid body i that belongs to a three-dimensional mechanical system are derived considering two general coordinate formulations for rigid multibody systems, namely the RPCF with Euler parameters and the NACF. While in the kinematic description of the RPCF the orientation of the body-fixed reference system is commonly represented using the set of Euler parameters, in the kinematic description of the NACF the set of direction cosines is employed to represent large finite rotations of the rigid body i. A brief summary of the fundamental equations concerning the RPCF with Euler parameters and the NACF is given below.

2.1 Kinematic analysis based on the reference point coordinate formulation with Euler parameters

In this subsection, the kinematic description of the RPCF featuring the set of Euler parameters as rotational coordinates is briefly recalled. In particular, the position, velocity, and acceleration fields of a general rigid body i are derived in terms of the reference point coordinates based on the Euler parameters. In the kinematic descriptions of both the RPCF with Euler parameters and the NACF, two types of frame of reference are considered. The first type of coordinate system is an inertial frame of reference which is simply called global reference system. Without loss of generality, the global reference system can be considered fixed in space and time so that it can serve as a unique standard for the kinematic analysis of the rigid multibody system under consideration. The second type of coordinate system is a frame of reference attached to a given point ${O^i}$ of the rigid body i that forms the multibody systems and, therefore, this local reference system translates and rotates with the body i. The point ${O^i}$ is thus selected as a reference point on the rigid body i. For a three-dimensional multibody system, the global position vector of the reference point ${O^i}$ defined in the global coordinate system is denoted with ${\mathbf{{R}}^i}$ and is given by:

$$\begin{aligned} {\mathbf{{R}}^i} = \left[ {\begin{array}{*{20}{c}} {R_1^i}\\ {R_2^i}\\ {R_3^i} \end{array}} \right] \end{aligned}$$

(1)

where $R_1^i$, $R_2^i$, and $R_3^i$ are the Cartesian components of the reference point ${O^i}$ defined in the global coordinate system. On the other hand, the position vector of an arbitrary point ${P^i}$ on the rigid body i defined in the local coordinate system is denoted with ${{\bar{\mathbf{u}}}^i}$ and is given by:

$$\begin{aligned} {{\bar{\mathbf{u}}}^i} = \left[ {\begin{array}{*{20}{c}} {{{\bar{x}}^i}}\\ {{{\bar{y}}^i}}\\ {{{\bar{z}}^i}} \end{array}} \right] \end{aligned}$$

(2)

where ${\bar{x}^i}$, ${\bar{y}^i}$, and ${\bar{z}^i}$ are the Cartesian components of the arbitrary point ${P^i}$ defined in the local coordinate system. In the RPCF with Euler parameters, the global position vector of an arbitrary point ${P^i}$ on the rigid body i is denoted with ${\mathbf{{r}}^i}$ and can be written as:

$$\begin{aligned} {\mathbf{{r}}^i} = {\mathbf{{R}}^i} + {\mathbf{{A}}^i}{{\bar{\mathbf{u}}}^i} \end{aligned}$$

(3)

where ${\mathbf{{R}}^i}$ is the global position vector of the reference point ${O^i}$ associated with the local coordinate system on the rigid body i, ${\mathbf{{A}}^i}$ is the rotation matrix that defines the orientation of the body frame of reference with respect to the inertial coordinate system, and ${{\bar{\mathbf{u}}}^i}$ is the position vector of an arbitrary point ${P^i}$ on the rigid body i defined in the local coordinate system. The rotation matrix ${\mathbf{{A}}^i}$ transforms vector quantities expressed in the local frame of reference into their global counterparts represented in the inertial coordinate system. The rotation matrix ${\mathbf{{A}}^i}$ can be expressed employing the set of Euler parameters denoted with ${{\varvec{\theta }}^i}$ and given by:

$$\begin{aligned} {\varvec{\theta }}^{i} = \left[ {\begin{array}{*{20}{c}} {\theta _0^i}\\ {\theta _1^i}\\ {\theta _2^i}\\ {\theta _3^i} \end{array}} \right] \end{aligned}$$

(4)

where the four scalar quantities ${\theta _0^i}$, ${\theta _1^i}$, ${\theta _2^i}$, and ${\theta _3^i}$ are the Euler parameters associated with the orientation of the rigid body i. The set of Euler parameters ${{\varvec{\theta }}^i}$ is a nonminimal set of orientation coordinates and, therefore, it must satisfy the following normalization condition:

$$\begin{aligned} {\varvec{\varphi }} ^{i} = {\left( {\varvec{\theta }}^{i} \right) ^T}{\varvec{\theta }}^{i} - 1 = 0 \end{aligned}$$

(5)

where ${{\varvec{\varphi }}^i}$ is a constraint vector which contains the intrinsic constraint equation corresponding to the rigidity condition of the rigid body i. In fact, the algebraic equation associated with the set of Euler parameters ${{\varvec{\theta }}^i}$ guarantees that the rotation matrix ${\mathbf{{A}}^i}$ is an orthogonal matrix. Thus, it can be proved that the normalization condition of the Euler parameters is a mathematical formulation of the physical rigidity of a given rigid body i and, therefore, it represents an intrinsic constraint equation. One can show that the rotation matrix ${\mathbf{{A}}^i}$ can be expressed in terms of the Euler parameters ${{\varvec{\theta }}^i}$ as follows:

$$\begin{aligned} {\mathbf{A}^i} = {\mathbf{E}^i}{\left( {{{\bar{\mathbf{E}}}^i}} \right) ^T} \end{aligned}$$

(6)

where the matrices ${\mathbf{{E}}^i}$ and ${{\bar{\mathbf{E}}}^i}$ can be explicitly written in terms of the set of Euler parameters as:

$$\begin{aligned} {\mathbf{{E}}^i}= & {} \left[ {\begin{array}{*{20}{c}} { - \theta _1^i}&{} \quad {\theta _0^i}&{} \quad { - \theta _3^i}&{} \quad {\theta _2^i}\\ { - \theta _2^i}&{} \quad {\theta _3^i}&{} \quad {\theta _0^i}&{} \quad { - \theta _1^i}\\ { - \theta _3^i}&{} \quad { - \theta _2^i}&{} \quad {\theta _1^i}&{} \quad {\theta _0^i} \end{array}} \right] \end{aligned}$$

(7)

$$\begin{aligned} {{\bar{\mathbf{E}}}^i}= & {} \left[ {\begin{array}{*{20}{c}} { - \theta _1^i}&{} \quad {\theta _0^i}&{} \quad {\theta _3^i}&{} \quad { - \theta _2^i}\\ { - \theta _2^i}&{} \quad { - \theta _3^i}&{} \quad {\theta _0^i}&{} \quad {\theta _1^i}\\ { - \theta _3^i}&{} \quad {\theta _2^i}&{} \quad { - \theta _1^i}&{} \quad {\theta _0^i} \end{array}} \right] \end{aligned}$$

(8)

As a result, the configuration of a rigid body i of the three-dimensional multibody system can be identified univocally considering a generalized coordinate vector ${\mathbf{{q}}^i}$ in which the translational coordinates ${\mathbf{{R}}^i}$ and the rotational coordinates ${{\varvec{\theta }}^i}$ of the rigid body i are grouped as follows:

$$\begin{aligned} {\mathbf{{q}}^i} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{R}}^i}}\\ {{{\varvec{\theta }}^i}} \end{array}} \right] \end{aligned}$$

(9)

From the kinematic description of the RPCF with Euler parameters, it is clear that the position field of a rigid body ${\mathbf{{r}}^i}$ is a nonlinear function of the configuration vector ${\mathbf{{q}}^i}$. On the other hand, one can easily show that in the RPCF with Euler parameters the virtual displacement field $\delta {\mathbf{{r}}^i}$ and the velocity field ${{\dot{\mathbf{r}}}^i}$ of a rigid body i are nonlinear functions of the generalized coordinate vector ${\mathbf{{q}}^i}$ and are linear functions of, respectively, the virtual change in the generalized coordinate vector $\delta {\mathbf{{q}}^i}$ and in the generalized velocity vector ${{\dot{\mathbf{q}}}^i}$. Thus, in the RPCF featuring Euler parameters, the virtual displacement field $\delta {\mathbf{{r}}^i}$ and the velocity field ${{\dot{\mathbf{r}}}^i}$ of a rigid body i are, respectively, given by:

$$\begin{aligned} \delta {\mathbf{{r}}^i}= & {} {\mathbf{{L}}^i}\delta {\mathbf{{q}}^i} \end{aligned}$$

(10)

$$\begin{aligned} {{\dot{\mathbf{r}}}^i}= & {} {\mathbf{{L}}^i}{{\dot{\mathbf{q}}}^i} \end{aligned}$$

(11)

where ${\mathbf{{L}}^i}$ is the Jacobian matrix of the position field ${\mathbf{{r}}^i}$ of the rigid body i computed with respect to the generalized coordinate vector ${\mathbf{{q}}^i}$ that can be written as:

$$\begin{aligned} {\mathbf{{L}}^i} = \left[ {\begin{array}{*{20}{c}} \mathbf{{I}}&{{\mathbf{{H}}^i}} \end{array}} \right] \end{aligned}$$

(12)

In this equation, $\mathbf{{I}}$ is an appropriate identity matrix and ${\mathbf{{H}}^i}$ is a matrix which depends on the rotational coordinates given by:

$$\begin{aligned} {\mathbf{{H}}^i} = {\mathbf{{A}}^i}{\left( {{{{\tilde{\bar{\mathbf{u}}}}}^i}} \right) ^T}{{\bar{\mathbf{G}}}^i} \end{aligned}$$

(13)

where ${{\tilde{\bar{\mathbf{u}}}}^i}$ is a skew-symmetric matrix associated with the cross product of the axial vector ${{\bar{\mathbf{u}}}^i}$ and ${{\bar{\mathbf{G}}}^i}$ is the transformation matrix that allows to express the angular velocity vector defined in the local coordinate system ${{\bar{\varvec{\omega }}}^i}$ as a linear combination of the time derivatives of the vector of Euler parameters ${{\dot{\varvec{\theta }}}^i}$ as follows:

$$\begin{aligned} {{\bar{\varvec{\omega }}}^i} = {{\bar{\mathbf{G}}}^i}{\dot{\varvec{\theta }}^i} \end{aligned}$$

(14)

where in the RPCF with Euler parameters the transformation matrix ${{\bar{\mathbf{G}}}^i}$ is given by:

$$\begin{aligned} {{\bar{\mathbf{G}}}^i} = 2{{\bar{\mathbf{E}}}^i} \end{aligned}$$

(15)

Furthermore, in the RPCF with Euler parameters, the acceleration field ${{\ddot{\mathbf{r}}}^i}$ of the rigid body i can be readily calculated as:

$$\begin{aligned} {{\ddot{\mathbf{r}}}^i} = {\mathbf{{L}}^i}{{\ddot{\mathbf{q}}}^i} + {{\dot{\mathbf{L}}}^i}{{\dot{\mathbf{q}}}^i} \end{aligned}$$

(16)

In this equation, the time derivative of the Jacobian matrix ${{\dot{\mathbf{L}}}^i}$ can be easily computed to yield:

$$\begin{aligned} {{\dot{\mathbf{L}}}^i} = \left[ {\begin{array}{*{20}{c}} \mathbf{{O}}&{{{{\dot{\mathbf{H}}}}^i}} \end{array}} \right] \end{aligned}$$

(17)

where the time derivative of the matrix associated with the rotational coordinates ${{\dot{\mathbf{H}}}^i}$ can be explicitly computed as follows:

$$\begin{aligned} {{{\dot{\mathbf{H}}}}^i}= & {} {{{\dot{\mathbf{A}}}}^i}{\left( {{{{\tilde{\bar{\mathbf{u}}}}}^i}} \right) ^T}{{{\bar{\mathbf{G}}}}^i} + {\mathbf{{A}}^i}{\left( {{{{\tilde{\bar{\mathbf{u}}}}}^i}} \right) ^T}{{{\dot{\bar{\mathbf{G}}}}}^i} \nonumber \\= & {} {\mathbf{{A}}^i}{{{\tilde{\bar{{\varvec{\omega }} }}}}^i}{\left( {{{{\tilde{\bar{\mathbf{u}}}}}^i}} \right) ^T}{{{\bar{\mathbf{G}}}}^i} + {\mathbf{{A}}^i}{\left( {{{{\tilde{\bar{\mathbf{u}}}}}^i}} \right) ^T}{{{\dot{\bar{\mathbf{G}}}}}^i} \end{aligned}$$

(18)

where ${\tilde{\bar{{\varvec{\omega }}}}}^{i}$ is a skew-symmetric matrix associated with the cross product of the axial vector ${{\bar{\varvec{\omega }}}^i}$. From this equation, it is apparent that the acceleration field ${{\ddot{\mathbf{r}}}^i}$ of rigid body i is a nonlinear function of the generalized coordinate vector ${\mathbf{{q}}^i}$, a nonlinear function of the generalized velocity vector ${{\dot{\mathbf{q}}}^i}$, and a linear function of the generalized acceleration vector ${{\ddot{\mathbf{q}}}^i}$. The explicit derivations of the position, velocity, and acceleration fields complete the kinematic description of a given rigid body i in the RPCF based on the set of Euler parameters.

2.2 Dynamic analysis based on the reference point coordinate formulation with Euler parameters

In this subsection, the equations of motion of a three-dimensional rigid multibody mechanical system are derived using the kinematic description of the RPCF and employing the set of Euler parameters as rotational coordinates. In particular, the mass matrix, the quadratic velocity vector associated with the generalized inertia effects, the generalized external force vector, and the constraint quadratic velocity vector relative to the intrinsic constraint are derived for a general rigid body i in terms of the reference point coordinates based on the Euler parameters. The equations of motion for a general rigid body i represented in terms of the reference point coordinates based on the set of Euler parameters can be obtained by using the D’Alembert–Lagrange principle of virtual work in conjunction with the method of Lagrange multipliers. To this end, one can write the virtual work of the complete set of generalized forces which act on a general rigid body i as follows:

$$\begin{aligned} \delta W_i^i + \delta W_e^i + \delta W_c^i = 0 \end{aligned}$$

(19)

where $\delta W_i^i$ represents the virtual work of the generalized inertia forces of the rigid body i, $\delta W_e^i$ denotes the virtual work of the generalized external forces acting on the rigid body i, and $\delta W_c^i$ is the virtual work of the generalized constraint forces associated with the intrinsic constraint equation of the rigid body i. In the RPCF with Euler parameters, the virtual work of the generalized inertia forces associated with a given rigid body i can be written as:

$$\begin{aligned} \delta W_i^i= & {} - \int _{{\Omega ^i}} {{\rho ^i}{{\left( {{{{\ddot{\mathbf{r}}}}^i}} \right) }^T}\delta {\mathbf{{r}}^i}\hbox {d}{V^i}} \nonumber \\= & {} \left( { - {{\left( {{{{\ddot{\mathbf{q}}}}^i}} \right) }^T}\int _{{\Omega ^i}} {{\rho ^i}{{\left( {{\mathbf{{L}}^i}} \right) }^T}{\mathbf{{L}}^i}\hbox {d}{V^i}} - {{\left( {{{{\dot{\mathbf{q}}}}^i}} \right) }^T}\int _{{\Omega ^i}} {{\rho ^i}{{\left( {{{{\dot{\mathbf{L}}}}^i}} \right) }^T}{\mathbf{{L}}^i}\hbox {d}{V^i}} } \right) \delta {\mathbf{{q}}^i} \nonumber \\= & {} {\left( { - {\mathbf{{M}}^i}{{{\ddot{\mathbf{q}}}}^i} + \mathbf{{Q}}_v^i} \right) ^T}\delta {\mathbf{{q}}^i} \end{aligned}$$

(20)

In this equation, ${\Omega ^i}$ denotes the volume of the rigid body i, ${\rho ^i}$ is the rigid body mass density, ${\mathbf{{M}}^i}$ represents the mass matrix of the rigid body i, and $\mathbf{{Q}}_v^i$ is the generalized force vector that contains the terms which are quadratic in the generalized velocities expressed in terms of reference point coordinates. The mass matrix ${\mathbf{{M}}^i}$ of the rigid body i can be explicitly computed to yield:

$$\begin{aligned} {\mathbf{{M}}^i}= & {} \int _{{\Omega ^i}} {{\rho ^i}{{\left( {{\mathbf{{L}}^i}} \right) }^T}{\mathbf{{L}}^i}\hbox {d}{V^i}} \nonumber \\= & {} \left[ {\begin{array}{ll} {{m^i}{} \mathbf{{I}}}&{} \quad {{m^i}{\mathbf{{A}}^i}{{\left( {{\tilde{\bar{\mathbf{u}}}}_{{G^i}}^i} \right) }^T}{{{\bar{\mathbf{G}}}}^i}}\\ {{m^i}{{\left( {{{{\bar{\mathbf{G}}}}^i}} \right) }^T}{\tilde{\bar{\mathbf{u}}}}_{{G^i}}^i{{\left( {{\mathbf{{A}}^i}} \right) }^T}}&{} \quad {{{\left( {{{{\bar{\mathbf{G}}}}^i}} \right) }^T}{\bar{\mathbf{I}}}_{{O^i}}^i{{{\bar{\mathbf{G}}}}^i}} \end{array}} \right] \end{aligned}$$

(21)

where $\mathbf{{I}}$ is an appropriate identity matrix, ${m^i}$ denotes the mass of the rigid body i, ${G^i}$ is the center of mass of the rigid body i, ${\bar{\mathbf{u}}}_{{G^i}}^i$ is the position vector of the centroid of the rigid body i expressed in the body-fixed coordinate system, ${\tilde{\bar{\mathbf{u}}}}_{{G^i}}^i$ is a skew-symmetric matrix associated with the cross product of the axial vector ${\bar{\mathbf{u}}}_{{G^i}}^i$, and ${\bar{\mathbf{I}}}_{{O^i}}^i$ is the matrix of mass moments of inertia relative to the rigid body i computed with respect to the local frame of reference. It is important to note that, in the RPCF with Euler parameters, the mass matrix ${\mathbf{{M}}^i}$ of the rigid body i is a symmetric positive semi-definite matrix which has a degree of singularity equal to one, that is, the rank of the mass matrix ${\mathbf{{M}}^i}$ is equal to its dimension minus one. In fact, the mass matrix ${\mathbf{{M}}^i}$ of the rigid body i depends explicitly on the orientation of the rigid body through the redundant set of Euler parameters ${{\varvec{\theta }}^i}$, thus reducing the matrix rank. For a general rigid multibody mechanical system, the rank deficiency of the system mass matrix is equal to the number of intrinsic constraint equations associated with each set of Euler parameters employed in the description of the system orientation and, therefore, the degree of singularity of the mechanical system is equal to the number of bodies in the rigid multibody system. This issue relative to the mass matrix ${\mathbf{{M}}^i}$ of the rigid body i modeled employing the RPCF based on the set of Euler parameters is called kinetic singularity in contrast to the kinematic singularity that characterizes each set of three orientation parameters in the representation of the rotation, such as the Euler angles or the Tait–Bryan angles. In particular, if the reference point ${O^i}$ coincides with the center of mass ${G^i}$ of the rigid body i and, at the same time, if the axes of the body-fixed reference frame coincide with the principal inertia axes of the rigid body i, then the body mass matrix ${\mathbf{{M}}^i}$ is a block diagonal matrix that assumes the following special form:

$$\begin{aligned} {\mathbf{{M}}^i} = \left[ {\begin{array}{*{20}{c}} {{m^i}{} \mathbf{{I}}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad {{{\left( {{{{\bar{\mathbf{G}}}}^i}} \right) }^T}{\bar{\mathbf{I}}}_{{G^i}}^i{{{\bar{\mathbf{G}}}}^i}} \end{array}} \right] \end{aligned}$$

(22)

where ${\bar{\mathbf{I}}}_{{G^i}}^i$ is the matrix of principal mass moments of inertia for the rigid body i computed with respect to the body-fixed reference frame. On the other hand, the quadratic velocity vector associated with the centrifugal and Coriolis generalized inertia effects $\mathbf{{Q}}_v^i$ can be computed as follows:

$$\begin{aligned} \mathbf{Q}_{v}^{i}= & {} - \int _{{\Omega ^{i}}} {{\rho ^{i}} {{\left( \mathbf{L}^{i} \right) }^{T}}{{{\dot{\mathbf{L}}}}^i}\hbox {d}{V^i}} {\dot{\mathbf{q}}}^{i} \nonumber \\= & {} \left[ {\begin{array}{*{20}{l}} {m^{i}}{\mathbf{A}^{i}}{\tilde{\bar{\varvec{\omega }}}}^{i}{\tilde{\bar{\mathbf{u}}}}_{{G^i}}^{i}\bar{{\varvec{\omega }}}^{i}\\ - {\left( {\bar{\mathbf{G}}}^{i}\right) }^{T}{\tilde{\bar{\varvec{\omega }}}}^{i}{\bar{\mathbf{I}}}_{{O^i}}^{i}{{{\bar{\varvec{\omega }}}}^{i}} \end{array}} \right] \end{aligned}$$

(23)

Even in this case, when the reference point ${O^i}$ coincides with the center of mass ${G^i}$ of the rigid body i and the axes of local reference system coincide with the principal inertia axes of the rigid body i, the inertia quadratic velocity vector $\mathbf{{Q}}_v^i$ assumes the following simplified form:

$$\begin{aligned} \mathbf{{Q}}_v^i = \left[ {\begin{array}{*{20}{c}} \mathbf{{0}}\\ { - {{\left( {{{{\bar{\mathbf{G}}}}^i}} \right) }^T}{{{{\tilde{\bar{\varvec{\omega }}} }}}^i}{\bar{\mathbf{I}}}_{{G^i}}^i{{{\bar{\varvec{\omega }}}}^i}} \end{array}} \right] \end{aligned}$$

(24)

Employing the set of reference point coordinates featuring the Euler parameters as rotational coordinates, the virtual work of the generalized external forces acting on the rigid body i can be written as:

$$\begin{aligned} \delta W_e^i= & {} \int _{{\Omega ^i}} {{{\left( {\mathbf{{f}}_e^i} \right) }^T}\delta {\mathbf{{r}}^i}\hbox {d}{V^i}} \nonumber \\= & {} \int _{{\Omega ^i}} {{{\left( {\mathbf{{f}}_e^i} \right) }^T}{\mathbf{{L}}^i}\hbox {d}{V^i}} \delta {\mathbf{{q}}^i}\nonumber \\= & {} {\left( {\mathbf{{Q}}_e^i} \right) ^T}\delta {\mathbf{{q}}^i} \end{aligned}$$

(25)

where $\mathbf{{f}}_e^i$ is a general external force vector distributed on the rigid body i, such as a constant force vector given by the product of the body mass density ${\rho ^i}$ multiplied by the gravity vector ${\mathbf{{g}}^i}$, and $\mathbf{{Q}}_e^i$ is the generalized external force vector acting on the rigid body i which is given by:

$$\begin{aligned} \mathbf{{Q}}_e^i = \int _{{\Omega ^i}} {{{\left( {{\mathbf{{L}}^i}} \right) }^T}{} \mathbf{{f}}_e^i\hbox {d}{V^i}} \end{aligned}$$

(26)

Moreover, in the RPCF with Euler parameters, the virtual work of the generalized constraint forces associated with the intrinsic constraint equation of the rigid body i can be obtained employing the Lagrange multiplier technique as follows:

$$\begin{aligned} \delta W_c^i= & {} - {\left( {{{\varvec{\lambda }}^i}} \right) ^T}\delta {{\varvec{\varphi }}^i} \nonumber \\= & {} - {\left( {{{\varvec{\lambda }}^i}} \right) ^T}{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i\delta {\mathbf{{q}}^i}\nonumber \\= & {} {\left( { - {{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}} \right) ^T}\delta {\mathbf{{q}}^i} \nonumber \\= & {} {\left( {\mathbf{{Q}}_c^i} \right) ^T}\delta {\mathbf{{q}}^i} \end{aligned}$$

(27)

where ${\varvec{\lambda }}^{i}$ is the Lagrange multiplier relative to the intrinsic constraint equation of the Euler parameters, ${\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i$ denotes the Jacobian matrix of the intrinsic constraint vector ${{\varvec{\varphi }}^i}$ calculated with respect to the reference point coordinates ${\mathbf{{q}}^i}$, and $\mathbf{{Q}}_c^i$ represents the generalized force vector associated with the Euler parameters normalization condition. The intrinsic constraint Jacobian matrix ${\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i$ and the intrinsic constraint generalized force vector $\mathbf{{Q}}_c^i$ are, respectively, given by:

$$\begin{aligned} {\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i= & {} \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&\quad {2{{\left( {{{\varvec{\theta }}^i}} \right) }^T}} \end{array}} \right] \end{aligned}$$

(28)

$$\begin{aligned} \mathbf{{Q}}_c^i= & {} - {\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) ^T}{{\varvec{\lambda }}^i} \end{aligned}$$

(29)

By substituting the explicit expressions of the virtual works for the generalized inertia, external, and constraint forces into the D’Alembert–Lagrange principle of virtual work and employing the Lagrange multiplier method, one obtains the following set of equations of motion for a general rigid body i modeled employing the RPCF with Euler parameters:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{M}}^i}{{{\ddot{\mathbf{q}}}}^i} = \mathbf{{Q}}_v^i + \mathbf{{Q}}_e^i - {{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}}\\ {{{\varvec{\varphi }}^i} = \mathbf{{0}}} \end{array}} \right. \end{aligned}$$

(30)

The equations of motion relative to the rigid body i modeled using the reference point coordinates with the set of Euler parameters form a set of differential–algebraic dynamic equations (DAE). These index-three dynamic equations of motion can be transformed into their index-one counterpart differentiating twice with respect to time the intrinsic constraint equation of the normalization condition for the Euler parameters leading to the following set of ordinary differential dynamic equations (ODE):

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{M}}^i}{{{\ddot{\mathbf{q}}}}^i} = \mathbf{{Q}}_v^i + \mathbf{{Q}}_e^i - {{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}}\\ {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i{{{\ddot{\mathbf{q}}}}^i} = \mathbf{{Q}}_d^i} \end{array}} \right. \end{aligned}$$

(31)

where $\mathbf{{Q}}_d^i$ is a constraint quadratic velocity vector associated with the intrinsic constraint that absorbs the terms which are quadratic in the generalized velocities expressed in terms of reference point coordinates. Considering the second time derivative of the normalization condition associated with the set of Euler parameters, the corresponding constraint quadratic velocity vector can be readily computed to yield:

$$\begin{aligned} \mathbf{{Q}}_d^i = - 2{\left( {{{{\dot{\varvec{\theta } }}}^i}} \right) ^T}{{\dot{\varvec{\theta } }}^i} \end{aligned}$$

(32)

The explicit derivations of the mass matrix, the quadratic velocity vector associated with the generalized inertia effects, the generalized external force vector, and the constraint quadratic velocity vector associated with the intrinsic constraint of the reference point coordinates complete the description of dynamic equations of a rigid body i based on the RPCF with Euler parameters.

2.3 Kinematic analysis based on the natural absolute coordinate formulation

In this subsection, the kinematic description of the NACF featuring the direction cosines as orientation parameters is concisely illustrated. In particular, the position, velocity, and acceleration fields of a general rigid body i are derived in terms of the set of natural absolute coordinates. In the NACF, the global position vector of an arbitrary point ${P^i}$ on the rigid body i is defined as:

$$\begin{aligned} {\mathbf{{r}}^i} = {\mathbf{{S}}^i}{\mathbf{{e}}^i} = {\mathbf{{R}}^i} + {\bar{x}^i}{{\varvec{\alpha }}^i} + {\bar{y}^i}{{\varvec{\beta }}^i} + {\bar{z}^i}{{\varvec{\gamma }}^i} \end{aligned}$$

(33)

In this equation, ${\mathbf{{S}}^i}$ is the matrix of the shape functions of the rigid body i and ${\mathbf{{e}}^i}$ is the vector of natural absolute coordinates which identifies the configuration of the rigid body i that are, respectively, given by:

$$\begin{aligned} {\mathbf{{S}}^i}= & {} \left[ {\begin{array}{*{20}{c}} \mathbf{{I}}&{{{\bar{x}}^i}{} \mathbf{{I}}}&{{{\bar{y}}^i}{} \mathbf{{I}}}&{{{\bar{z}}^i}{} \mathbf{{I}}} \end{array}} \right] \end{aligned}$$

(34)

$$\begin{aligned} {\mathbf{{e}}^i}= & {} \left[ {\begin{array}{*{20}{c}} {{\mathbf{{R}}^i}}\\ {{{\varvec{\delta }}^i}} \end{array}} \right] \end{aligned}$$

(35)

where ${{\varvec{\delta }}^i}$ is the orientation vector that contains the direction cosines associated with the body-fixed coordinate system defined as:

$$\begin{aligned} {{\varvec{\delta }}^i} = \left[ {\begin{array}{*{20}{c}} {{{\varvec{\alpha }}^i}}\\ {{{\varvec{\beta }}^i}}\\ {{{\varvec{\gamma }}^i}} \end{array}} \right] \end{aligned}$$

(36)

where ${{\varvec{\alpha }}^i}$, ${{\varvec{\beta }}^i}$, and ${{\varvec{\gamma }}^i}$ identify three unit vectors which contains the direction cosines of the rotation matrix ${\mathbf{{A}}^i}$ of the rigid body i and are, respectively, given by:

$$\begin{aligned} {{\varvec{\alpha }}^i}= & {} \left[ {\begin{array}{*{20}{c}} {\alpha _1^i}\\ {\alpha _2^i}\\ {\alpha _3^i} \end{array}} \right] \end{aligned}$$

(37)

$$\begin{aligned} {{\varvec{\beta }}^i}= & {} \left[ {\begin{array}{*{20}{c}} {\beta _1^i}\\ {\beta _2^i}\\ {\beta _3^i} \end{array}} \right] \end{aligned}$$

(38)

$$\begin{aligned} {{\varvec{\gamma }}^i}= & {} \left[ {\begin{array}{*{20}{c}} {\gamma _1^i}\\ {\gamma _2^i}\\ {\gamma _3^i} \end{array}} \right] \end{aligned}$$

(39)

where ${\alpha _1^i}$, ${\alpha _2^i}$, and ${\alpha _3^i}$ are the direction cosines associated with the unit vector directed along the ${\bar{x}^i}$ axis of the local frame of reference, ${\beta _1^i}$, ${\beta _2^i}$, and ${\beta _3^i}$ are the direction cosines relative to the unit vector directed along the ${\bar{y}^i}$ axis of the body-fixed reference system, and ${\gamma _1^i}$, ${\gamma _2^i}$, and ${\gamma _3^i}$ are the direction cosines of the unit vector directed along the ${\bar{z}^i}$ axis of the floating coordinate system. The set of direction cosines that forms the orientation vector ${{\varvec{\delta }}^i}$ is a nonminimal set of rotation coordinates and, therefore, it must fulfill the following normalization conditions:

$$\begin{aligned} {{\varvec{\varphi }}^i} = \left[ {\begin{array}{l} {{{\left( {{{\varvec{\alpha }}^i}} \right) }^T}{{\varvec{\alpha }}^i} - 1}\\ {{{\left( {{{\varvec{\beta }}^i}} \right) }^T}{{\varvec{\beta }}^i} - 1}\\ {{{\left( {{{\varvec{\gamma }}^i}} \right) }^T}{{\varvec{\gamma }}^i} - 1}\\ {{{\left( {{{\varvec{\alpha }}^i}} \right) }^T}{{\varvec{\beta }}^i}}\\ {{{\left( {{{\varvec{\alpha }}^i}} \right) }^T}{{\varvec{\gamma }}^i}}\\ {{{\left( {{{\varvec{\beta }}^i}} \right) }^T}{{\varvec{\gamma }}^i}} \end{array}} \right] = \mathbf{{0}} \end{aligned}$$

(40)

where ${{\varvec{\varphi }}^i}$ is a constraint vector which incorporates the intrinsic constraint equations relative to the rigidity conditions of the rigid body i. Indeed, the algebraic equations associated with the set of direction cosines ${{\varvec{\alpha }}^i}$, ${{\varvec{\beta }}^i}$, and ${{\varvec{\gamma }}^i}$ ensure that the rotation matrix ${\mathbf{{A}}^i}$ is an orthogonal matrix. Thus, it can be proved that the normalization conditions of the direction cosines are a mathematical representation of the physical rigidity of a general rigid body i and, therefore, they represent a set of intrinsic constraint equations. The rotation matrix ${\mathbf{{A}}^i}$ relative to the local frame of reference for the rigid body i can be expressed in terms of the set of direction cosines as follows:

$$\begin{aligned} {\mathbf{{A}}^i} = \left[ {\begin{array}{*{20}{c}} {{{\varvec{\alpha }}^i}}&{{{\varvec{\beta }}^i}}&{{{\varvec{\gamma }}^i}} \end{array}} \right] \end{aligned}$$

(41)

On the other hand, in the NACF, the angular velocity vector expressed in the body-fixed coordinate system ${{\bar{\varvec{\omega }}}^i}$ can be written in terms of the time derivative of the orientation vector ${{\dot{\varvec{\delta }}}^i}$ as follows:

$$\begin{aligned} {{\bar{\varvec{\omega }}}^i} = {{\bar{\mathbf{G}}}^i}{{\dot{\varvec{\delta } }}^i} \end{aligned}$$

(42)

where in the NACF the transformation matrix ${{\bar{\mathbf{G}}}^i}$ is defined as:

$$\begin{aligned} {{\bar{\mathbf{G}}}^i} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad { - {{\left( {{{\varvec{\beta }}^i}} \right) }^T}}\\ { - {{\left( {{{\varvec{\gamma }}^i}} \right) }^T}}&{} \quad {{\mathbf{{0}}^T}}&{}{{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad { - {{\left( {{{\varvec{\alpha }}^i}} \right) }^T}}&{} \quad {{\mathbf{{0}}^T}} \end{array}} \right] \end{aligned}$$

(43)

From the kinematic description of the NACF, it is apparent that the global position vector ${\mathbf{{r}}^i}$ of the rigid body i can be written as the product of a spatial-dependent shape function matrix ${\mathbf{{S}}^i}$ and a time-dependent vector of natural absolute coordinates ${\mathbf{{e}}^i}$. Consequently, the position field of a rigid body ${\mathbf{{r}}^i}$ is a linear function of the configuration vector ${\mathbf{{e}}^i}$. Also, the virtual displacement field $\delta {\mathbf{{r}}^i}$ and the velocity field ${{\dot{\mathbf{r}}}^i}$ of a rigid body i are linear functions of, respectively, the virtual change in the natural absolute coordinate vector $\delta {\mathbf{{e}}^i}$ and in the generalized velocity vector associated with the natural absolute coordinates ${{\dot{\mathbf{e}}}^i}$. Therefore, in the NACF, the virtual displacement field $\delta {\mathbf{{r}}^i}$ and the velocity field ${{\dot{\mathbf{r}}}^i}$ of the rigid body i can be, respectively, written as:

$$\begin{aligned} \delta {\mathbf{{r}}^i}= & {} {\mathbf{{S}}^i}\delta {\mathbf{{e}}^i} = \delta {\mathbf{{R}}^i} + {\bar{x}^i}{\delta } {{\varvec{\alpha }^i}} + {\bar{y}^i}{\delta }{{\varvec{\beta }^i}} + {\bar{z}^i}{\delta } {\varvec{{\gamma }^i}} \end{aligned}$$

(44)

$$\begin{aligned} {{\dot{\mathbf{r}}}^i}= & {} {\mathbf{{S}}^i}{{\dot{\mathbf{e}}}^i} = {{\dot{\mathbf{R}}}^i} + {\bar{x}^i}{{\dot{\varvec{\alpha }}}^i} + {\bar{y}^i}{{\dot{\varvec{ \beta }}^i}} + {\bar{z}^i}{{\dot{\varvec{\gamma }}^i}} \end{aligned}$$

(45)

Furthermore, in the NACF, the acceleration field ${{\ddot{\mathbf{r}}}^i}$ of the rigid body i can be readily computed as follows:

$$\begin{aligned} {{\ddot{\mathbf{r}}}^i} = {\mathbf{{S}}^i}{{\ddot{\mathbf{e}}}^i} = {{\ddot{\mathbf{R}}}^i} + {\bar{x}^i}{{\ddot{\varvec{\alpha }}^i}} + {\bar{y}^i}{{\ddot{\varvec{\beta }}^i}} + {\bar{z}^i}{{\ddot{\varvec{\gamma }}^i}} \end{aligned}$$

(46)

From this equation, it is clear that the acceleration field of rigid body i is a linear function of the generalized accelerations associated with the natural absolute coordinates ${{\ddot{\mathbf{e}}}^i}$. The explicit derivations of the position, velocity, and acceleration fields of a general rigid body i complete the kinematic description of the NACF.

2.4 Dynamic analysis based on the natural absolute coordinate formulation

In this subsection, the equations of motion of a three-dimensional rigid multibody mechanical system are obtained employing the kinematic description of the NACF. In particular, the mass matrix, the generalized external force vector, and the constraint quadratic velocity vector associated with the intrinsic constraints are developed for a general rigid body i in terms of the set of natural absolute coordinates. The equations of motion for a given rigid body i expressed in terms of the natural absolute coordinates can be readily derived employing the D’Alembert–Lagrange principle of virtual work combined with the method of Lagrange multipliers. To this end, one can write the virtual work of the complete set of generalized forces that acts on a given rigid body i as follows:

$$\begin{aligned} \delta W_i^i + \delta W_e^i + \delta W_c^i = 0 \end{aligned}$$

(47)

where $\delta W_i^i$ is the virtual work of the generalized inertia forces of the rigid body i, $\delta W_e^i$ represents the virtual work of the generalized external forces acting on the rigid body i, and $\delta W_c^i$ denotes the virtual work of the generalized constraint forces associated with the intrinsic constraint equations of the rigid body i. In the NACF, the virtual work of the generalized inertia forces associated with a given rigid body i can be written as:

$$\begin{aligned} \delta W_i^i= & {} - \int _{{\Omega ^i}} {{\rho ^i}{{\left( {{{{\ddot{\mathbf{r}}}}^i}} \right) }^T}\delta {\mathbf{{r}}^i}\hbox {d}{V^i}} \nonumber \\= & {} - {\left( {{{{\ddot{\mathbf{e}}}}^i}} \right) ^T}\int _{{\Omega ^i}} {{\rho ^i}{{\left( {{\mathbf{{S}}^i}} \right) }^T}{\mathbf{{S}}^i}\hbox {d}{V^i}} \delta {\mathbf{{e}}^i}\nonumber \\= & {} {\left( { - {\mathbf{{M}}^i}{{{\ddot{\mathbf{e}}}}^i}} \right) ^T}\delta {\mathbf{{e}}^i} \end{aligned}$$

(48)

In this equation, ${\Omega ^i}$ denotes the volume of the rigid body i, ${\rho ^i}$ is the rigid body mass density, and ${\mathbf{{M}}^i}$ represents the mass matrix of the rigid body i expressed in terms of natural absolute coordinates. The mass matrix ${\mathbf{{M}}^i}$ of the rigid body i can be explicitly calculated as follows:

$$\begin{aligned} {\mathbf{{M}}^i}= & {} \int _{{\Omega ^i}} {{\rho ^i}{{\left( {{\mathbf{{S}}^i}} \right) }^T}{\mathbf{{S}}^i}\hbox {d}{V^i}} \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} {{m^i}{} \mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{x}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{y}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{z}}^i}}^i\mathbf{{I}}}\\ {\bar{J}_{{O^i},{{\bar{x}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{y}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{z}}^i}}^i\mathbf{{I}}}\\ {\bar{J}_{{O^i},{{\bar{y}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{y}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{z}}^i}}^i\mathbf{{I}}}\\ {\bar{J}_{{O^i},{{\bar{z}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{z}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{z}}^i}}^i\mathbf{{I}}}&{} \quad {\bar{J}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i\mathbf{{I}}} \end{array}} \right] \end{aligned}$$

(49)

where $\mathbf{{I}}$ denotes an appropriate identity matrix, ${m^i}$ is the mass of the rigid body i, while ${\bar{J}_{{O^i},{{\bar{x}}^i}}^i}$, ${\bar{J}_{{O^i},{{\bar{y}}^i}}^i}$, and ${\bar{J}_{{O^i},{{\bar{z}}^i}}^i}$ indicate the first moments of mass of the rigid body i computed with respect to the three local axes passing through the body reference point ${O^i}$, whereas $\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i$, $\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i$, $\bar{J}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i$, $\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{y}}^i}}^i$, $\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{z}}^i}}^i$, and $\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{z}}^i}}^i$ denote the second moments of mass of the rigid body i computed with respect to the three local axes passing through the body reference point ${O^i}$ which can be written as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\bar{J}_{{O^i},{{\bar{x}}^i}}^i = {m^i}\bar{x}_{{G^i}}^i}\\ {\bar{J}_{{O^i},{{\bar{y}}^i}}^i = {m^i}\bar{y}_{{G^i}}^i}\\ {\bar{J}_{{O^i},{{\bar{z}}^i}}^i = {m^i}\bar{z}_{{G^i}}^i}\\ {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i = \frac{1}{2}\left( {\bar{I}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i + \bar{I}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i - \bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i} \right) }\\ {\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i = \frac{1}{2}\left( {\bar{I}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i + \bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i - \bar{I}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i} \right) }\\ {\bar{J}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i = \frac{1}{2}\left( {\bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{I}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i - \bar{I}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i} \right) }\\ {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{y}}^i}}^i = - \bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{y}}^i}}^i}\\ {\bar{J}_{{O^i},{{\bar{x}}^i}{{\bar{z}}^i}}^i = - \bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{z}}^i}}^i}\\ {\bar{J}_{{O^i},{{\bar{y}}^i}{{\bar{z}}^i}}^i = - \bar{I}_{{O^i},{{\bar{y}}^i}{{\bar{z}}^i}}^i} \end{array}} \right. \end{aligned}$$

(50)

where ${G^i}$ identifies the centroid of the rigid body i, whereas $\bar{x}_{{G^i}}^i$, $\bar{y}_{{G^i}}^i$, and $\bar{z}_{{G^i}}^i$ represents the three Cartesian coordinates of the center of mass of the rigid body i represented with respect to the body-fixed frame of reference, $\bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i$, $\bar{I}_{{O^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i$, and $\bar{I}_{{O^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i$ are the mass moments of inertia of the rigid body i computed with respect to the three local axes passing through the body reference point ${O^i}$, while $\bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{y}}^i}}^i$, $\bar{I}_{{O^i},{{\bar{x}}^i}{{\bar{z}}^i}}^i$, and $\bar{I}_{{O^i},{{\bar{y}}^i}{{\bar{z}}^i}}^i$ are the mass products of inertia of the rigid body i calculated with respect to the three local axes passing through the body reference point ${O^i}$. It is important to note that in the NACF the mass matrix ${\mathbf{{M}}^i}$ of a general rigid body i is constant, symmetric, and positive definite and features a full rank. As a result, in the NACF the quadratic velocity vector $\mathbf{{Q}}_v^i$ associated with the centrifugal and Coriolis generalized inertia effects is equal to zero. This peculiar property of the mass matrix ${\mathbf{{M}}^i}$ of the rigid body i modeled employing the set of natural absolute coordinates is a direct consequence of the separation of variables carried out in the kinematic description of the position field of the rigid body i and is advantageous for performing effective and efficient dynamical simulations. In the special case in which the reference point ${O^i}$ coincides with the center of mass ${G^i}$ of the rigid body i and when the axes of the body-fixed reference frame coincide with the principal inertia axes of the rigid body i, the mass matrix ${\mathbf{{M}}^i}$ reduces to a constant diagonal matrix given by:

$$\begin{aligned} {\mathbf{{M}}^i} = \left[ {\begin{array}{*{20}{c}} {{m^i}{} \mathbf{{I}}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad {\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\mathbf{{I}}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad {\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i\mathbf{{I}}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad {\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i\mathbf{{I}}} \end{array}} \right] \end{aligned}$$

(51)

where $\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i$, $\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i$, and $\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i$ are the principal second moments of mass relative to the rigid body i calculated with respect to the local reference system. By using the kinematic description based on the set of natural absolute coordinates, the virtual work of the generalized external forces acting on the rigid body i can be written as:

$$\begin{aligned} \delta W_e^i= & {} \int _{{\Omega ^i}} {{{\left( {\mathbf{{f}}_e^i} \right) }^T}\delta {\mathbf{{r}}^i}\hbox {d}{V^i}} \nonumber \\= & {} \int _{{\Omega ^i}} {{{\left( {\mathbf{{f}}_e^i} \right) }^T}{\mathbf{{S}}^i}\hbox {d}{V^i}} \delta {\mathbf{{e}}^i}\nonumber \\= & {} {\left( {\mathbf{{Q}}_e^i} \right) ^T}\delta {\mathbf{{e}}^i} \end{aligned}$$

(52)

where $\mathbf{{f}}_e^i$ is a general external force vector distributed on the rigid body i, such as a constant force vector given by the product of the body mass density ${\rho ^i}$ multiplied by the gravity vector ${\mathbf{{g}}^i}$, and $\mathbf{{Q}}_e^i$ is the generalized external force vector acting on the rigid body i that can be computed as follows:

$$\begin{aligned} \mathbf{{Q}}_e^i = \int _{{\Omega ^i}} {{{\left( {{\mathbf{{S}}^i}} \right) }^T}{} \mathbf{{f}}_e^i\hbox {d}{V^i}} \end{aligned}$$

(53)

Moreover, in the NACF, the virtual work of the generalized constraint forces related to the set of intrinsic constraint equations of the rigid body i can be derived using the Lagrange multiplier technique as:

$$\begin{aligned} \delta W_c^i= & {} - {\left( {{{\varvec{\lambda }}^i}} \right) ^T}\delta {{\varvec{\varphi }}^i} \nonumber \\= & {} - {\left( {{{\varvec{\lambda }}^i}} \right) ^T}{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i\delta {\mathbf{{e}}^i} \nonumber \\= & {} {\left( { - {{\left( {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}} \right) ^T}\delta {\mathbf{{e}}^i} \nonumber \\= & {} {\left( {\mathbf{{Q}}_c^i} \right) ^T}\delta {\mathbf{{e}}^i} \end{aligned}$$

(54)

where ${{\varvec{\lambda }}^i}$ is a vector of Lagrange multipliers corresponding to the intrinsic constraint equations of the direction cosines, ${\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i$ represents the Jacobian matrix of the intrinsic constraint vector ${{\varvec{\varphi }}^i}$ computed with respect to the set of natural absolute coordinates ${\mathbf{{e}}^i}$, and $\mathbf{{Q}}_c^i$ denotes the generalized force vector relative to the direction cosines normalization conditions. The intrinsic constraint Jacobian matrix ${\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i$ and the intrinsic constraint generalized force vector $\mathbf{{Q}}_c^i$ can be are, respectively, written as:

$$\begin{aligned} {\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i= & {} \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&{} \quad {2{{\left( {{{\varvec{\alpha }}^i}} \right) }^T}}&{} \quad {{\mathbf{{0}}^T}}&{}{{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {2{{\left( {{{\varvec{\beta }}^i}} \right) }^T}}&{}{{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {2{{\left( {{{\varvec{\gamma }}^i}} \right) }^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{{\left( {{{\varvec{\beta }}^i}} \right) }^T}}&{} \quad {{{\left( {{{\varvec{\alpha }}^i}} \right) }^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{{\left( {{{\varvec{\gamma }}^i}} \right) }^T}}&{} \quad {{\mathbf{{0}}^T}}&{}{{{\left( {{{\varvec{\alpha }}^i}} \right) }^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{{\left( {{{\varvec{\gamma }}^i}} \right) }^T}}&{}{{{\left( {{{\varvec{\beta }}^i}} \right) }^T}} \end{array}} \right] \end{aligned}$$

(55)

$$\begin{aligned} \mathbf{{Q}}_c^i= & {} - {\left( {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i} \right) ^T}{{\varvec{\lambda }}^i} \end{aligned}$$

(56)

By substituting the analytical expressions of the virtual works for the generalized inertia, external, and constraint forces into the D’Alembert–Lagrange principle of virtual work and using the Lagrange multiplier method, one obtains the following set of equations of motion for a general rigid body i modeled using the NACF:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{M}}^i}{{{\ddot{\mathbf{e}}}}^i} = \mathbf{{Q}}_e^i - {{\left( {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}}\\ {{{\varvec{\varphi }}^i} = \mathbf{{0}}} \end{array}} \right. \end{aligned}$$

(57)

The equations of motion for the rigid body i modeled employing the natural absolute coordinates form a set of differential–algebraic dynamic equations (DAE). These index-three equations of motion can be transformed into their index-one counterpart differentiating twice with respect to time the intrinsic constraint equations relative to the normalization conditions of the direction cosines leading to the following set of ordinary differential dynamic equations (ODE):

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{M}}^i}{{{\ddot{\mathbf{e}}}}^i} = \mathbf{{Q}}_e^i - {{\left( {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}}\\ {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i{{{\ddot{\mathbf{e}}}}^i} = \mathbf{{Q}}_d^i} \end{array}} \right. \end{aligned}$$

(58)

where $\mathbf{{Q}}_d^i$ is a constraint quadratic velocity vector corresponding to the intrinsic constraints that contains the terms which are quadratic in the generalized velocities expressed in terms of natural absolute coordinates. Considering the second time derivative of the normalization conditions relative to the direction cosines, the associated constraint quadratic velocity vector can be explicitly written as follows:

$$\begin{aligned} \mathbf{{Q}}_d^i = \left[ {\begin{array}{*{20}{l}} { - 2{{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) }^T}{{{\dot{\varvec{\alpha }}}}^i}}\\ { - 2{{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) }^T}{{{\dot{\varvec{\beta }}}}^i}}\\ { - 2{{\left( {{{{\dot{\varvec{\gamma }}}}^i}} \right) }^T}{{{\dot{\varvec{\gamma }}}}^i}}\\ { - 2{{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) }^T}{{{\dot{\varvec{\beta }}}}^i}}\\ { - 2{{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) }^T}{{{\dot{\varvec{\gamma }}}}^i}}\\ { - 2{{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) }^T}{{{\dot{\varvec{\gamma }}}}^i}} \end{array}} \right] \end{aligned}$$

(59)

The explicit derivations of the mass matrix, the generalized external force vector, and the constraint quadratic velocity vector for the intrinsic constraints of the natural absolute coordinates complete the description of dynamic equations of a rigid body i based on the NACF.

3 Fundamental equations of constrained motion

In this section, the fundamental equations of constrained motion are discussed. The fundamental equations of constrained motion are also known as Udwadia–Kalaba equations by the names of their discoverers [80]. Udwadia and Kalaba developed the fundamental equations of constrained motion employing the Gauss principle of least constraint as a fundamental principle of analytical mechanics combined with modern linear algebra techniques [81]. In particular, in this section the fundamental equations of constrained motion are reformulated in an analytical form suitable for modeling the generalized constraint forces of rigid multibody mechanical systems. The Udwadia–Kalaba equations represent an efficient and effective analytical method for solving the central problem of constrained motion. In fact, this method allows for obtaining closed-form expressions of the generalized constraint forces and of the corresponding Lagrange multipliers for a rigid multibody mechanical system subjected to a broad class of holonomic and nonholonomic constraints [82]. In the general case in which a set of nonholonomic constraints is considered, the Udwadia–Kalaba equations can be applied as long as the algebraic constraint equations depend linearly on the system generalized accelerations, whereas a general nonlinear dependence can be assumed in terms of the system generalized coordinates and velocities [83]. Two general cases are considered in this section. In the first general case, a multibody mechanical system having a positive semi-definite mass matrix is considered. On the other hand, the second general case concerns a multibody mechanical system having a positive definite mass matrix. In both cases, a general set of holonomic constraint equations is assumed as a restriction of the motion of the multibody mechanical system. Subsequently, the two general forms of the Udwadia–Kalaba equations developed in this section are used to analytically determine the Lagrange multipliers and the corresponding generalized constraint forces associated with the set of intrinsic constraint equations. The analytical calculation of the Lagrange multipliers is performed for a multibody mechanical system modeled employing both the RPCF featuring the Euler parameters as orientation coordinates and the NACF based on the set of direction cosines.

3.1 Udwadia–Kalaba equations for positive semi-definite multibody mechanical systems

In this subsection, the Udwadia–Kalaba equations for a general positive semi-definite multibody mechanical system are briefly reviewed. In particular, in this subsection the fundamental equations of constrained motion for positive semi-definite multibody mechanical systems are reformulated in a compact mathematical form which can be readily implemented in a general-purpose multibody computer program. By doing so, the computational efficiency of the methodology developed by Udwadia and Kalaba can be considerably improved and, at the same time, the efficacy of the Udwadia–Kalaba method is conserved. To this end, consider a rigid multibody mechanical systems described by the following index-one form of equations of motion:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{M}\ddot{\mathbf{q}}} = {\mathbf{{Q}}_b} + {\mathbf{{Q}}_c}}\\ {{\mathbf{{C}}_\mathbf{{q}}}{\ddot{\mathbf{q}}} = {\mathbf{{Q}}_d}} \end{array}} \right. \end{aligned}$$

(60)

where $\mathbf{{q}}$ is the system generalized coordinate vector, $\mathbf{{M}}$ represents the symmetric positive semi-definite mass matrix of the multibody system, ${\mathbf{{Q}}_b}$ denotes the complete vector of generalized forces acting on the mechanical system, ${\mathbf{{Q}}_c}$ identifies the constraint generalized force vector, $\mathbf{{C}}$ is the constraint vector which contains the intrinsic and extrinsic constraint equations that restrict the motion of the multibody mechanical system, ${\mathbf{{C}}_\mathbf{{q}}}$ represents the Jacobian matrix of the kinematic constraints, and ${\mathbf{{Q}}_d}$ is the quadratic velocity vector associated with the complete set of algebraic constraints. In order to be able to apply the Udwadia–Kalaba equations to a general positive semi-definite multibody mechanical system, an auxiliary mechanical system must be employed. The auxiliary mechanical system is a dual multibody mechanical system that has the same generalized acceleration vector as well as the same time evolution of the original rigid multibody mechanical system. To this end, consider an auxiliary mechanical system characterized by the following set of dynamic equations:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\bar{\mathbf{M}}\ddot{\mathbf{q}}}} = {{{\bar{\mathbf{Q}}}}_b} + {\mathbf{{Q}}_c}\\ {{\mathbf{{C}}_\mathbf{{q}}}{\ddot{\mathbf{q}}} = {\mathbf{{Q}}_d}} \end{array}} \right. \end{aligned}$$

(61)

where ${\bar{\mathbf{M}}}$ is a symmetric positive definite matrix that represents the mass matrix of the auxiliary mechanical system and ${{\bar{\mathbf{Q}}}_b}$ denotes the vector of generalized forces acting on the auxiliary mechanical system that are, respectively, defined as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{\bar{\mathbf{M}}} = \mathbf{{M}} + \mathbf{{C}}_\mathbf{{q}}^T{\mathbf{{C}}_\mathbf{{q}}}}\\ {{{{\bar{\mathbf{Q}}}}_b} = {\mathbf{{Q}}_b} + \mathbf{{C}}_\mathbf{{q}}^T{\mathbf{{Q}}_d}} \end{array}} \right. \end{aligned}$$

(62)

Employing the previous definitions for the mass matrix ${\bar{\mathbf{M}}}$ and for the generalized force vector ${{\bar{\mathbf{Q}}}_b}$, it can be proved that the generalized acceleration vector of the auxiliary mechanical system is equal to the generalized acceleration vector of the multibody mechanical system under examination [84]. The analytical method based on the Udwadia–Kalaba equations for positive semi-definite multibody mechanical systems leads to a closed-loop solution for the generalized acceleration vector of the multibody mechanical system ${{\ddot{\mathbf{q}}}}$, for the complete vector of Lagrange multipliers ${\varvec{\lambda }}$, and for the total generalized constraint force vector ${\mathbf{{Q}}_c}$. Using a Lagrangian formulation suitable for the dynamic analysis of rigid multibody mechanical systems, the Udwadia–Kalaba equations for positive semi-definite mechanical systems can be written as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\bar{\mathbf{a}}} = {{{\bar{\mathbf{M}}}}^{ - 1}}{{{\bar{\mathbf{Q}}}}_b}}\\ {{\bar{{\varvec{\varepsilon }}}} = {\mathbf{{Q}}_d} - {\mathbf{C}_{\mathbf{q}}}{\bar{\mathbf{a}}}}\\ {{\bar{\mathbf{K}}} = {\mathbf{C}_{\mathbf{q}}}{{{\bar{\mathbf{M}}}}^{ - 1}}{} \mathbf{C}_{\mathbf{q}}^{T}}\\ {{\bar{\mathbf{F}}} = {{{\bar{\mathbf{K}}}}^ + }}\\ {\varvec{\lambda }} = - {\bar{\mathbf{F}} {\bar{\varvec{\varepsilon }}}}\\ {\mathbf{Q}_{c}} = - {\mathbf{C}}_{\mathbf{q}}^{T}{\varvec{\lambda }} \\ {\bar{\mathbf{a}}}_{c} = {{\bar{\mathbf{M}}}}^{- 1}{} \mathbf{Q}_{c}\\ {\ddot{\mathbf{q}}} = {\bar{\mathbf{a}}} + {{\bar{\mathbf{a}}}}_{c} \end{array}} \right. \end{aligned}$$

(63)

where ${{\bar{\mathbf{a}}}}$ is the generalized acceleration vector corresponding to the unconstrained multibody mechanical system, ${{\bar{\varvec{\varepsilon }}}}$ denotes the constraint generalized error vector that analytically quantifies how much the generalized acceleration vector of the unconstrained system ${{\bar{\mathbf{a}}}}$ violates the constraint equations, ${{\bar{\mathbf{K}}}}$ identifies the kinetic matrix of the auxiliary mechanical system, ${{\bar{\mathbf{F}}}}$ represents the constraint feedback matrix that arises from the application of the kinematic constraints on the multibody mechanical system, ${\varvec{\lambda }}$ is the vector of Lagrange multipliers associated with the algebraic constrains, ${{\mathbf{{Q}}_c}}$ denotes the generalized constraint force vector, ${{{{\bar{\mathbf{a}}}}_c}}$ represents the system generalized acceleration vector induced by the action of the kinematic constraints, and ${{\ddot{\mathbf{q}}}}$ is the resultant generalized acceleration vector of the multibody mechanical system. In these equations, ${{{{\bar{\mathbf{K}}}}^ + }}$ indicates the Moore–Penrose pseudoinverse matrix of the kinetic matrix ${{\bar{\mathbf{K}}}}$ of the auxiliary mechanical system. However, if the Jacobian matrix of the kinematic constraints ${{\mathbf{{C}}_\mathbf{{q}}}}$ features a full row rank, which means that there are no redundant constraint equations in the vector of kinematic constraints $\mathbf{{C}}$, the generalized inverse which defines the Moore–Penrose pseudoinverse matrix coincides with the regular inverse matrix.

3.2 Lagrange multiplier associated with the set of Euler parameters for the unconstrained rigid body

In this subsection, the Udwadia–Kalaba equations for positive semi-definite multibody mechanical systems are employed for obtaining a closed-form solution for the Lagrange multiplier and for the generalized constraint forces of the intrinsic constraint of a rigid body modeled using the RPCF with Euler parameters. The frame of reference associated with the rigid body i is assumed to be located in the center of mass of the rigid body ${G^i}$ and the directions of the reference axes are assumed to be parallel to the body principal axes of inertia. Therefore, the local position vector ${\bar{\mathbf{u}}}_{{G^i}}^i$ of the body centroid ${G^i}$ is assumed as a zero vector and the matrix of mass moments of inertia ${\bar{\mathbf{I}}}_{{G^i}}^i$ is assumed to be a diagonal matrix. To this end, consider an auxiliary rigid body associated with the rigid body i and described by the following index-one form of equations of motion:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{{\bar{\mathbf{M}}}}^i}{{{\ddot{\mathbf{q}}}}^i} = {\bar{\mathbf{Q}}}_b^i + \mathbf{{Q}}_c^i}\\ {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i{{{\ddot{\mathbf{q}}}}^i} = \mathbf{{Q}}_d^i} \end{array}} \right. \end{aligned}$$

(64)

where ${{{{\bar{\mathbf{M}}}}^i}}$ is the mass matrix of the auxiliary rigid body i and ${{\bar{\mathbf{Q}}}_b^i}$ is the total vector of generalized forces acting on the auxiliary rigid body i given by:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{{{\bar{\mathbf{M}}}}^i} = {\mathbf{{M}}^i} + {{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i}\\ {{\bar{\mathbf{Q}}}_b^i = \mathbf{{Q}}_b^i + {{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}{} \mathbf{{Q}}_d^i} \end{array}} \right. \end{aligned}$$

(65)

The application of the Udwadia–Kalaba method to the equations of motion of a rigid body i modeled using the RPCF with Euler parameters leads to the following set of equations:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{{\bar{\mathbf{a}}}}^i} = {{\left( {{{{\bar{\mathbf{M}}}}^i}} \right) }^{ - 1}}{\bar{\mathbf{Q}}}_b^i}\\ {{{{\bar{\varvec{\varepsilon }}}}^i} = \mathbf{{Q}}_d^i - {\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i{{{\bar{\mathbf{a}}}}^i}}\\ {{{{\bar{\mathbf{K}}}}^i} = {\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i{{\left( {{{{\bar{\mathbf{M}}}}^i}} \right) }^{ - 1}}{{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}}\\ {{{{\bar{\mathbf{F}}}}^i} = {{\left( {{{{\bar{\mathbf{K}}}}^i}} \right) }^{ - 1}}}\\ {{{\varvec{\lambda }}^i} = - {{{\bar{\mathbf{F}}}}^i}{{{\bar{\varvec{\varepsilon }}}}^i}}\\ {\mathbf{{Q}}_c^i = - {{\left( {{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}}\\ {{\bar{\mathbf{a}}}_c^i = {{\left( {{{{\bar{\mathbf{M}}}}^i}} \right) }^{ - 1}}{} \mathbf{{Q}}_c^i}\\ {{{{\ddot{\mathbf{q}}}}^i} = {{{\bar{\mathbf{a}}}}^i} + {\bar{\mathbf{a}}}_c^i} \end{array}} \right. \end{aligned}$$

(66)

By means of symbolic manipulations and considering the explicit expressions for the mass matrix ${{\mathbf{{M}}^i}}$, the inertia quadratic velocity vector ${\mathbf{{Q}}_v^i}$, the Jacobian matrix of the intrinsic constraint equation associated with the set of Euler parameters ${{\varvec{\varphi }}_{{\mathbf{{q}}^i}}^i}$, and the constraint quadratic velocity vector ${\mathbf{{Q}}_d^i}$ for the rigid body i given in Sect. 2 of the paper for the RPCF with Euler parameters, the kinetic matrix ${{\bar{\mathbf{K}}}^i}$ of the rigid body i degenerates into a scalar quantity that can be obtained as:

$$\begin{aligned} {{\bar{\mathbf{K}}}^i} = 1 \end{aligned}$$

(67)

Thus, the constraint feedback matrix ${{\bar{\mathbf{F}}}^i}$ of the rigid body i is reduced to a scalar quantity as well:

$$\begin{aligned} {{\bar{\mathbf{F}}}^i} = 1 \end{aligned}$$

(68)

Also, the Lagrange multiplier ${{{\varvec{\lambda }}^i}}$ associated with the normalization condition of the Euler parameters is a constant quantity that can be explicitly computed to yield:

$$\begin{aligned} {{\varvec{\lambda }}^i} = 0 \end{aligned}$$

(69)

As a result, the Udwadia–Kalaba equations lead to the closed-form solution of the vector of generalized constraint forces ${\mathbf{{Q}}_c^i}$ associated with the intrinsic constraint of the Euler parameters as a zero vector:

$$\begin{aligned} \mathbf{{Q}}_c^i = \mathbf{{0}} \end{aligned}$$

(70)

It can be shown by means of the fundamental equations of constrained motion that the solution for the Lagrange multiplier ${{{\varvec{\lambda }}^i}}$ relative to the intrinsic constraint of the Euler parameters ${{\varvec{\theta }}^i}$ is a general analytical result valid also in the case in which the origin of the local reference system ${O^i}$ is assumed to be located in a generic point ${P^i}$ on the rigid body i and when the directions of the local reference axes are assumed to be arbitrary. This important analytical result may seem somehow counterintuitive because it means that the set of Euler parameters automatically satisfies the intrinsic constraint equation. However, other researchers also obtained the same mathematical result based on different considerations and, therefore, this paper can be considered an extension of their work and provides an important analytical proof derived from the basic principles of analytical mechanics [85, 86]. Furthermore, as far as the authors know, before this investigation there was no mathematical proof of this important analytical result based on the fundamental principles of mechanics. On the other hand, this important analytical result still lacks an obvious physical meaning. Numerical simulations also confirm this analytical result, as shown in Sect. 4 of the paper. Moreover, it is important to note that, among all the real numbers, zero is a valid value for the Lagrange multiplier ${{{\varvec{\lambda }}^i}}$ associated with the vector of Euler parameters ${{\varvec{\theta }}^i}$ that does not contradict the basic theoretical hypotheses employed to derive the equations of motion. Consequently, in theory, in the RPCF with Euler parameters there is no need to include in the equations of motion the terms associated with the intrinsic constraints ${{\varvec{\varphi }}^i}$ of the set of Euler parameters ${{\varvec{\theta }}^i}$. On the other hand, in practical applications where complex rigid multibody mechanical systems are considered and involve dynamical simulations that encompass a long time span, the numerical errors that arise from the use of numerical integration schemes for the approximate solution of the equations of motion can cause a violation of the intrinsic constraint equations. Therefore, it is not recommended to remove the constraint equations for the set of Euler parameters in the development of general-purpose rigid multibody codes. Furthermore, obtaining a vector of zero Lagrange multipliers associated with the normalization condition of the Euler parameters can serve an useful benchmark for evaluating the effectiveness and the robustness of new numerical procedures for the approximate solutions of the set of differential–algebraic multibody equations of motion obtained using the RPCF with Euler parameters.

3.3 Udwadia–Kalaba equations for positive definite multibody mechanical systems

In this subsection, the Udwadia–Kalaba equations for a general positive definite multibody mechanical system are briefly recalled. In particular, in this subsection the fundamental equations of constrained motion for positive definite multibody mechanical systems are rewritten in a concise mathematical form which can be easily implemented in a general-purpose multibody computer program. In this way, the computational efficiency of the method developed by Udwadia and Kalaba can be considerably improved and, at the same time, the efficacy of the Udwadia–Kalaba methodology is conserved. To this end, consider a rigid multibody mechanical systems described by the following index-one form of equations of motion:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\mathbf{M}{\ddot{\mathbf{e}}}} = {\mathbf{{Q}}_b} + {\mathbf{{Q}}_c}\\ {{\mathbf{{C}}_\mathbf{{e}}}{\ddot{\mathbf{e}}} = {\mathbf{{Q}}_d}} \end{array}} \right. \end{aligned}$$

(71)

where $\mathbf{{e}}$ denotes the system configuration vector, $\mathbf{{M}}$ identifies the symmetric positive definite mass matrix of the mechanical system, ${\mathbf{{Q}}_b}$ represents the total vector of generalized forces acting on the multibody system, ${\mathbf{{Q}}_c}$ is the constraint generalized force vector, $\mathbf{{C}}$ is the constraint vector that contains the kinematic constraint equations which restrict the motion of the multibody mechanical system, ${\mathbf{{C}}_\mathbf{{e}}}$ represents the Jacobian matrix of the algebraic constraints, and ${\mathbf{{Q}}_d}$ is the quadratic velocity vector relative to the complete set of kinematic constraints. The analytical technique based on the Udwadia–Kalaba equations for positive definite multibody mechanical systems provides a closed-loop solution for the generalized acceleration vector of the multibody mechanical system ${{\ddot{\mathbf{e}}}}$, for the complete vector of Lagrange multipliers ${\varvec{\lambda }}$, and for the total generalized constraint force vector ${\mathbf{{Q}}_c}$. Considering the original Lagrangian form, the Udwadia–Kalaba equations for positive definite mechanical systems are given by:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\mathbf{{a}} = {\mathbf{{M}}^{ - 1}}{\mathbf{{Q}}_b}}\\ {{\varvec{\varepsilon }} = {\mathbf{{Q}}_d} - {\mathbf{{C}}_\mathbf{{e}}}{} \mathbf{{a}}}\\ {\mathbf{{K}} = {\mathbf{{C}}_\mathbf{{e}}}{\mathbf{{M}}^{ - 1}}{} \mathbf{{C}}_\mathbf{{e}}^T}\\ {\mathbf{{F}} = {\mathbf{{K}}^ + }}\\ {{\varvec{\lambda }} = - \mathbf{{F \varvec{\varepsilon }}}}\\ {{\mathbf{{Q}}_c} = - \mathbf{{C}}_\mathbf{{e}}^T{\varvec{\lambda }}}\\ {{\mathbf{{a}}_c} = {\mathbf{{M}}^{ - 1}}{\mathbf{{Q}}_c}}\\ {{\ddot{\mathbf{e}}} = \mathbf{{a}} + {\mathbf{{a}}_c}} \end{array}} \right. \end{aligned}$$

(72)

where $\mathbf{{a}}$ denotes the generalized acceleration vector relative to the unconstrained multibody mechanical system, ${\varvec{\varepsilon }}$ is the constraint generalized error vector that analytically quantifies how much the generalized acceleration vector of the unconstrained system $\mathbf{{a}}$ violates the constraint equations, $\mathbf{{K}}$ represents the kinetic matrix of the multibody mechanical system, $\mathbf{{F}}$ is the constraint feedback matrix which comes from the application of the algebraic constraints on the multibody mechanical system, ${\varvec{\lambda }}$ is the vector of Lagrange multipliers corresponding to the set of kinematic constrains, ${{\mathbf{{Q}}_c}}$ identifies the generalized constraint force vector, ${{\mathbf{{a}}_c}}$ is the system generalized acceleration vector induced by the action of the algebraic constraints, and ${{\ddot{\mathbf{e}}}}$ represents the resultant generalized acceleration vector of the multibody mechanical system. Even in this case, if the Jacobian matrix of the kinematic constraints ${{\mathbf{{C}}_\mathbf{{e}}}}$ features a full row rank, the Moore–Penrose pseudoinverse matrix coincides with the regular inverse matrix.

3.4 Lagrange multipliers associated with the set of direction cosines for the unconstrained rigid body

In this subsection, the Udwadia–Kalaba equations for positive definite multibody mechanical systems are used for obtaining a closed-form solution for the Lagrange multipliers and for the generalized constraint forces of the intrinsic constraints of a rigid body modeled employing the NACF. Even in this case, the body-fixed reference system is assumed to be coincident with the center of mass of the rigid body ${G^i}$ and the directions of the axes of the local frame of reference are assumed to be parallel to the body principal axes of inertia. Thus, the local position vector ${\bar{\mathbf{u}}}_{{G^i}}^i$ of the body centroid ${G^i}$ is a zero vector and the matrix of mass moments of inertia ${\bar{\mathbf{I}}}_{{G^i}}^i$ is a diagonal matrix. To this end, consider a general rigid body i described by the following index-one form of equations of motion:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{M}}^i}{{{\ddot{\mathbf{e}}}}^i} = \mathbf{{Q}}_b^i + \mathbf{{Q}}_c^i}\\ {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i{{{\ddot{\mathbf{e}}}}^i} = \mathbf{{Q}}_d^i} \end{array}} \right. \end{aligned}$$

(73)

The application of the Udwadia–Kalaba method to the equations of motion of a rigid body i modeled using the NACF leads to the following set of equations:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{a}}^i} = {{\left( {{\mathbf{{M}}^i}} \right) }^{ - 1}}{} \mathbf{{Q}}_b^i}\\ {{{\varvec{\varepsilon }}^i} = \mathbf{{Q}}_d^i - {\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i{\mathbf{{a}}^i}}\\ {{\mathbf{{K}}^i} = {\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i{{\left( {{\mathbf{{M}}^i}} \right) }^{ - 1}}{{\left( {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i} \right) }^T}}\\ {{\mathbf{{F}}^i} = {{\left( {{\mathbf{{K}}^i}} \right) }^{ - 1}}}\\ {{{\varvec{\lambda }}^i} = - {\mathbf{{F}}^i}{{\varvec{\varepsilon }}^i}}\\ {\mathbf{{Q}}_c^i = - {{\left( {{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i} \right) }^T}{{\varvec{\lambda }}^i}}\\ {\mathbf{{a}}_c^i = {{\left( {{\mathbf{{M}}^i}} \right) }^{ - 1}}{} \mathbf{{Q}}_c^i}\\ {{{{\ddot{\mathbf{e}}}}^i} = {\mathbf{{a}}^i} + \mathbf{{a}}_c^i} \end{array}} \right. \end{aligned}$$

(74)

By means of symbolic manipulations and employing the explicit expressions for the mass matrix ${{\mathbf{{M}}^i}}$, the Jacobian matrix of the intrinsic constraint equations associated with the direction cosines ${{\varvec{\varphi }}_{{\mathbf{{e}}^i}}^i}$, and the constraint quadratic velocity vector ${\mathbf{{Q}}_d^i}$ for the rigid body i given in Sect. 2 of the paper for the NACF, the kinetic matrix ${{\mathbf{{K}}^i}}$ of the rigid body i is a diagonal matrix given by:

$$\begin{aligned} {\mathbf{{K}}^i}= & {} \mathrm{{diag}}\left( \frac{4}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i}},\frac{4}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}},\frac{4}{{\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}},\right. \nonumber \\&\left. \frac{1}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i}} + \frac{1}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}},\frac{1}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i}} + \frac{1}{{\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}},\frac{1}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}} + \frac{1}{{\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}\right) \end{aligned}$$

(75)

Consequently, the constraint feedback matrix ${\mathbf{{F}}^i}$ of the rigid body i is a diagonal matrix which can be written as:

$$\begin{aligned} {\mathbf{{F}}^i}= & {} \mathrm{{diag}}\left( \frac{1}{4}\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i,\frac{1}{4}\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i,\frac{1}{4}\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i,\right. \nonumber \\&\left. \frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}},\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}},\frac{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}\right) \end{aligned}$$

(76)

Furthermore, the vector of Lagrange multipliers ${{{\varvec{\lambda }}^i}}$ associated with the normalization condition of the direction cosines can be explicitly calculated and is given by:

$$\begin{aligned} {{\varvec{\lambda }}^i} = \left[ {\begin{array}{*{20}{l}} {\frac{1}{2}\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i{{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) }^T}{{{\dot{\varvec{\alpha }}}}^i}}\\ {\frac{1}{2}\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i{{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) }^T}{{{\dot{\varvec{\beta }}}}^i}}\\ {\frac{1}{2}\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i{{\left( {{{{\dot{\varvec{\gamma }}}}^i}} \right) }^T}{{{\dot{\varvec{\gamma }}}}^i}}\\ {2\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) }^T}{{{\dot{\varvec{\beta }}}}^i}}\\ {2\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) }^T}{{{\dot{\varvec{\gamma }}}}^i}}\\ {2\frac{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) }^T}{{{\dot{\varvec{\gamma }}}}^i}} \end{array}} \right] \end{aligned}$$

(77)

Thus, the vector of generalized constraint forces ${\mathbf{{Q}}_c^i}$ corresponding to the intrinsic constraints of the direction is a nonzero vector that can be analytically computed by using the Udwadia–Kalaba method to yield:

$$\begin{aligned} \mathbf{{Q}}_c^i = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} \mathbf{{0}}\\ \end{array}\\ \begin{array}{l} \bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i{{\varvec{\alpha }}^i}{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) ^T}{{{\dot{\varvec{\alpha }}}}^i} + 2\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\varvec{\beta }}^i}{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) ^T}{{{\dot{\varvec{\beta }}}}^i}\\ + 2\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\varvec{\gamma }}^i}{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) ^T}{{{\dot{\varvec{\gamma }}}}^i}\\ \end{array}\\ \begin{array}{l} \bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i{{\varvec{\beta }}^i}{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) ^T}{{{\dot{\varvec{\beta }}}}^i} + 2\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i}}{{\varvec{\alpha }}^i}{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) ^T}{{{\dot{\varvec{\beta }}}}^i}\\ + 2\frac{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\varvec{\gamma }}^i}{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) ^T}{{{\dot{\varvec{\gamma }}}}^i}\\ \end{array}\\ \begin{array}{l} \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i{{\varvec{\gamma }}^i}{\left( {{{{\dot{\varvec{\gamma }}}}^i}} \right) ^T}{{{\dot{\varvec{\gamma }}}}^i} + 2\frac{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{x}}^i}{{\bar{x}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\varvec{\alpha }}^i}{\left( {{{{\dot{\varvec{\alpha }}}}^i}} \right) ^T}{{{\dot{\varvec{\gamma }}}}^i}\\ + 2\frac{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i\bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\bar{J}_{{G^i},{{\bar{y}}^i}{{\bar{y}}^i}}^i + \bar{J}_{{G^i},{{\bar{z}}^i}{{\bar{z}}^i}}^i}}{{\varvec{\beta }}^i}{\left( {{{{\dot{\varvec{\beta }}}}^i}} \right) ^T}{{{\dot{\varvec{\gamma }}}}^i} \end{array} \end{array}} \right] \end{aligned}$$

(78)

As expected, it is apparent from the derivation presented in this subsection that, for a rigid body i modeled using the NACF, the vector of Lagrange multipliers associated with the intrinsic constraints of the direction cosines ${{\varvec{\lambda }}^i}$ does not vanish and, therefore, the vector of generalized constraint forces ${\mathbf{{Q}}_c^i}$ is not a null vector. This important analytical result derived from the basic principles of classical mechanics is new and it is also confirmed by numerical results obtained from dynamical simulations, as shown in Sect. 4 of the paper. In principle, in the NACF one can directly use the analytical expression of the generalized constraint force vector ${\mathbf{{Q}}_c^i}$ in order to transform the differential–algebraic equations of motion of the rigid body i in a set of ordinary differential equations. However, this method is not recommended in the dynamic analysis of complex rigid multibody mechanical systems because of the occurrence of the drift phenomenon of the kinematic constraints. The drift phenomenon of the kinematic constraints is the violation of the constraint equations at the position and velocity levels caused by the numerical solution of the differential–algebraic equations of motion expressed in the index-one form. The drift phenomenon of the algebraic constraints can be significantly contrasted employing some effective constraint stabilization techniques such as the Baumgarte stabilization method, the penalty method, or the well-known generalized coordinate partitioning algorithm. On the other hand, the analytical expression of the vector of Lagrange multipliers ${{\varvec{\lambda }}^i}$ associated with the intrinsic constraints of a rigid body i can be used as a benchmark for the development of general-purpose multibody computer programs based on the NACF.

4 Numerical results and discussion

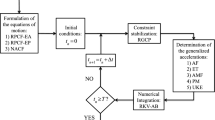
In this section, two numerical examples are discussed in order to illustrate the analytical results developed in the paper. The numerical examples considered in this sections are a spinning projectile and a simple pendulum. The spinning projectile represents an example of an unconstrained rigid body, whereas the simple pendulum is representative of a rigid body constrained by kinematic joints. In the first numerical example, an unconstrained rigid body is considered and the analytical results derived in Sect. 3 of the paper are directly verified in comparison with the numerical results obtained by means of dynamical simulations. The second numerical example, on the other hand, concerns a rigid body constrained by a revolute joint. In this case, the analytical expressions of the generalized constraint forces are not amenable to be transformed into compact mathematical expressions by means of symbolic manipulations. Therefore, in the second numerical example, the fundamental equations of constrained motion are implemented and solved in a multibody computer program developed in the MATLAB simulation environment and the numerical results obtained are compared with those derived by using the well-known augmented formulation.

The equations of motion of the two mechanical systems employed in this section as numerical examples are formally derived by using the RPCF with Euler parameters and the NACF. Subsequently, the resulting index-three systems of differential–algebraic equations of motion are reduced to the corresponding index-one forms. The numerical integration method implemented to solve the index-one ordinary differential equations of motion is the sixth-order Adams–Bashforth algorithm, which is an explicit linear multistep scheme with a constant size of the time step. The time span considered for the numerical simulation is $T = 5\;\hbox {s}$, while the constant time step used is $\Delta t = 5 \times {10^{ - 3}}\;\hbox {s}$. In the numerical implementation of the equations of motion, both the augmented formulation and the Udwadia–Kalaba approach are used to solve for the generalized acceleration vector and the vector of Lagrange multipliers that appear in the index-one form of the dynamic equations [87]. Also, two cases are considered in the numerical procedure used for solving the equations of motion. In the first case, the algebraic constraint equations are enforced at the position and velocity levels employing the generalized coordinate partitioning algorithm [88]. For this purpose, a constraint tolerance equal to $\varepsilon = {10^{ - 9}}$ is considered in the Newton–Raphson loop for enforcing the total set of algebraic constraint equations at both the position and velocity levels. In the second case, no constraint stabilization methods are used in the numerical solution procedure.

4.1 Spinning projectile

In this subsection, a simple numerical example is presented in order to numerically verify the analytical expressions of the Lagrange multipliers given by Eqs. (69) and (77) employed for determining the generalized constraint forces associated with the orientation parameters of an unconstrained rigid body. To this end, a single unconstrained rigid body shown in Fig. 1 is considered. The rigid body translates and rotates in the space as a spinning projectile under the action of the gravity field. The spinning projectile has a mass $m = 3\;\hbox {kg}$ and principal moments of inertia ${\bar{I}_{\bar{x}\bar{x}}} = 2\;\hbox {kg} \; {\hbox {m}^2}$, ${\bar{I}_{\bar{y}\bar{y}}} = 2\;\hbox {kg} \; {\hbox {m}^2}$, and ${\bar{I}_{\bar{z}\bar{z}}} = 2\;\hbox {kg} \; {\hbox {m}^2}$ which form the body matrix of inertia defined as ${{\bar{\mathbf{I}}}_G} = \mathrm{{diag}}({\bar{I}_{\bar{x}\bar{x}}},{\bar{I}_{\bar{y}\bar{y}}},{\bar{I}_{\bar{z}\bar{z}}})$. The gravitational acceleration is assumed $g = 9.81\;{\hbox {m}/ {{\hbox {s}^2}}}$ and the body weight vector is defined as ${\mathbf{{F}}_g} = {\left[ {\begin{array}{*{20}{c}}0&\quad 0&\quad { - mg}\end{array}} \right] ^T}$. Employing the RPCF with Euler parameters, the index-one form of the equations of motion of the spinning projectile can be readily written as:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbf{M}\ddot{\mathbf{q}}} = {\mathbf{{Q}}_v} + {\mathbf{{Q}}_e} - \mathbf{{C}}_\mathbf{{q}}^T{\varvec{\lambda }}\\ {\mathbf{{C}}_\mathbf{{q}}}{\ddot{\mathbf{q}}} = {\mathbf{{Q}}_d} \end{array} \right. \end{aligned}$$

(79)

where the matrix and vector terms that appear in the equations of motion of the spinning projectile based on the RPCF with Euler parameters can be, respectively, computed using the definitions presented in the paper as follows:

$$\begin{aligned} \mathbf{{M}}= & {} \left[ {\begin{array}{*{20}{c}} {m\mathbf{{I}}}&{}\mathbf{{O}}\\ \mathbf{{O}}&{} \quad {{{{\bar{\mathbf{G}}}}^T}{{{\bar{\mathbf{I}}}}_G}{\bar{\mathbf{G}}}} \end{array}} \right] ,\quad {\mathbf{{Q}}_v} = \left[ {\begin{array}{*{20}{c}} \mathbf{{0}}\\ { - {{{\bar{\mathbf{G}}}}^T}{{\tilde{\bar{\varvec{\omega }}}}}{{{\bar{\mathbf{I}}}}_G}{\bar{\varvec{{\omega }}}}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_g}= & {} \mathbf{{L}}_G^T{\mathbf{{F}}_g},\quad \mathbf{{C}} = {\varvec{\varphi }} = {{\varvec{\theta }}^T}{\varvec{\theta }} - 1,\quad {\mathbf{{C}}_\mathbf{{q}}} = {{\varvec{\varphi }}_\mathbf{{q}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&{2{{\varvec{\theta }}^T}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_d}= & {} {\mathbf{{Q}}_{d,\varphi }} = - 2{{{\dot{\varvec{\theta }}}}^T}{\dot{\varvec{\theta }}} \end{aligned}$$

(80)

On the other hand, by using the NACF, the index-one form of the equations of motion of the spinning projectile can be readily written as:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbf{M}\ddot{\mathbf{e}}} = {\mathbf{{Q}}_e} - \mathbf{{C}}_\mathbf{{e}}^T{\varvec{\lambda }}\\ {\mathbf{{C}}_\mathbf{{e}}}{\ddot{\mathbf{e}}} = {\mathbf{{Q}}_d} \end{array} \right. \end{aligned}$$

(81)

Fig. 1

Spinning projectile

where the matrix and vector terms that appear in the equations of motion of the spinning projectile based on the NACF can be, respectively, computed using the definitions presented in the paper as follows:

$$\begin{aligned} \mathbf{{M}}= & {} \left[ {\begin{array}{*{20}{c}} {m\mathbf{{I}}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad {\frac{{ - {{\bar{I}}_{\bar{x}\bar{x}}} + {{\bar{I}}_{\bar{y}\bar{y}}} + {{\bar{I}}_{\bar{z}\bar{z}}}}}{2}{} \mathbf{{I}}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad {\frac{{{{\bar{I}}_{\bar{x}\bar{x}}} - {{\bar{I}}_{\bar{y}\bar{y}}} + {{\bar{I}}_{\bar{z}\bar{z}}}}}{2}{} \mathbf{{I}}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad {\frac{{{{\bar{I}}_{\bar{x}\bar{x}}} + {{\bar{I}}_{\bar{y}\bar{y}}} - {{\bar{I}}_{\bar{z}\bar{z}}}}}{2}{} \mathbf{{I}}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_g}= & {} \mathbf{{S}}_G^T{\mathbf{{F}}_g},\quad \mathbf{{C}} = {\varvec{\varphi }} = \left[ {\begin{array}{*{20}{c}} {{{\varvec{\alpha }}^T}{\varvec{\alpha }} - 1}\\ {{{\varvec{\beta }}^T}{\varvec{\beta }} - 1}\\ {{{\varvec{\gamma }}^T}{\varvec{\gamma }} - 1}\\ {{{\varvec{\alpha }}^T}{\varvec{\beta }}}\\ {{{\varvec{\alpha }}^T}{\varvec{\gamma }}}\\ {{{\varvec{\beta }}^T}{\varvec{\gamma }}} \end{array}} \right] ,\quad {\mathbf{{C}}_\mathbf{{e}}} = {{\varvec{\varphi }}_\mathbf{{e}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&{} \quad {2{{\varvec{\alpha }}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {2{{\varvec{\beta }}^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {2{{\varvec{\gamma }}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\beta }}^T}}&{} \quad {{{\varvec{\alpha }}^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\gamma }}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\alpha }}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\gamma }}^T}}&{} \quad {{{\varvec{\beta }}^T}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_d}= & {} {\mathbf{{Q}}_{d,\varphi }} = \left[ {\begin{array}{*{20}{c}} { - 2{{{\dot{\varvec{\alpha }}}}^T}{\dot{\varvec{\alpha }}}}\\ { - 2{{{\dot{\varvec{\beta }}}}^T}{\dot{\varvec{\beta }}}}\\ { - 2{{{\dot{\varvec{\gamma }}}}^T}{\dot{\varvec{\gamma }}}}\\ { - 2{{{\dot{\varvec{\alpha }}}}^T}{\dot{\varvec{\beta }}}}\\ { - 2{{{\dot{\varvec{\alpha }}}}^T}{\dot{\varvec{\gamma }}}}\\ { - 2{{{\dot{\varvec{\beta }}}}^T}{\dot{\varvec{\gamma }}}} \end{array}} \right] \end{aligned}$$

(82)

The initial position of the centroid of the spinning projectile coincides with the origin of the inertial reference system, while the rigid body initial orientation is represented using the following set of Euler parameters:

$$\begin{aligned} {\varvec{\theta }} = \left[ {\begin{array}{*{20}{c}} {{\theta _0}}\\ {{\theta _1}}\\ {{\theta _2}}\\ {{\theta _3}} \end{array}} \right] \end{aligned}$$

(83)

where ${\theta _0} = {{0}}{{.924}}$, ${\theta _1} = 0$, ${\theta _2} = - \,{{0}}{{.382}}$, and ${\theta _3} = 0$. The orientation of the spinning projectile is identified by the vector of Euler parameters ${\varvec{\theta }}$ and corresponds to the direction cosine vectors ${\varvec{\alpha }}$, ${\varvec{\beta }}$, and ${\varvec{\gamma }}$ defined as:

$$\begin{aligned} {\varvec{\alpha }} = \left[ {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\alpha _2}}\\ {{\alpha _3}} \end{array}} \right] ,\quad \quad {\varvec{\beta }} = \left[ {\begin{array}{*{20}{c}} {{\beta _1}}\\ {{\beta _2}}\\ {{\beta _3}} \end{array}} \right] ,\quad \quad {\varvec{\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\gamma _1}}\\ {{\gamma _2}}\\ {{\gamma _3}} \end{array}} \right] \end{aligned}$$

(84)

where ${\alpha _1} = {{0}}{{.707}}$, ${\alpha _2} =0$, ${\alpha _3} = {{0}}{{.707}}$, ${\beta _1} = 0$, ${\beta _2} =1$, ${\beta _3} = 0$, ${\gamma _1} = {{- \, 0}}{{.707}}$, ${\gamma _2} =0$, and ${\gamma _3} = {{0}}{{.707}}$. The spinning projectile is launched with the following initial linear velocity:

Fig. 2

Centroid vertical position of the spinning projectile, (circle) NACF, (square) RPCF with Euler parameters

Fig. 3

Third component of the third direction cosine of the spinning projectile, (circle) NACF, (square) RPCF with Euler parameters

$$\begin{aligned} {\dot{\mathbf{R}}} = {U_0}\left[ {\begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}}\\ {{v_3}} \end{array}} \right] \end{aligned}$$

(85)

where ${U_0} = 15\;\frac{\hbox {m}}{\hbox {s}}$, ${v_1} = {{0}}{{.707}}$, ${v_2} = 0$, and ${v_3} = {{0}}{{.707}}$. The initial angular velocity of the spinning projectile expressed in the body-fixed reference frame is assumed as:

$$\begin{aligned} {\bar{\varvec{\omega }}} = {\Omega _0}\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}} \end{array}} \right] \end{aligned}$$

(86)

where ${\Omega _0} = 5\;\frac{{\hbox {rad}}}{\hbox {s}}$, ${w_1} = 1$, ${w_2} = 0$, and ${w_3} = 0$. The vertical position of the centroid of the spinning projectile computed employing both the NACF and the RPCF with Euler parameters is shown in Fig. 2. In Fig. 3, the third component of the third direction cosine of the spinning projectile corresponding to the NACF solution and to the RPCF solution is represented in order to show the large rotation of the rigid body. The violations of the intrinsic constraint equations that appear in the equations of motion obtained using the NACF and the RPCF with Euler parameters are, respectively, shown in Tables 1 and 2. In this numerical example, the Lagrange multipliers associated with the intrinsic constraint equations can be considered constant for the entire time span of the numerical simulation with a very good approximation. Thus, the comparison between the solution obtained by using the Udwadia–Kalaba equations and the numerical solution for the Lagrange multiplier corresponding to the set of direction cosines is reported in Table 3. Moreover, the solution obtained employing the Udwadia–Kalaba equations and the numerical solution procedure found for the Lagrange multipliers relative to the set of Euler parameters is reported in Table 4. Considering an unconstrained rigid body such as the spinning projectile modeled employing both the NACF and the RPCF with Euler parameters and observing Tables 3 and 4, it is clear that the numerical results obtained using the augmented formulation are in a very good agreement with the analytical results predicted employing the Udwadia–Kalaba equations.

Table 1 Violations of the constraint equations in the NACF for the spinning projectile

Table 2 Violations of the constraint equations in the RPCF with Euler parameters for the spinning projectile

Table 3 Lagrange multiplier associated with the intrinsic constraint equations of the direction cosines for the spinning projectile

Table 4 Lagrange multiplier associated with the intrinsic constraint equation of the Euler parameters for the spinning projectile

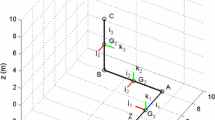
4.2 Simple pendulum

Fig. 4

Simple pendulum

In this subsection, a second simple numerical example is shown to numerically verify the general analytical expressions of the Lagrange multipliers obtained using the general expressions of the Udwadia–Kalaba equations. To this end, Eqs. (63) and (72) are used to compute the generalized constraint forces associated with the intrinsic constraint equations of a constrained rigid body. In this numerical example, a simple pendulum constrained to the ground by means of a revolute joint as shown in Fig. 4 is considered. The simple pendulum has a mass $m = 3\;\hbox {kg}$ and principal moments of inertia ${\bar{I}_{\bar{x}\bar{x}}} = {{0}}{{.0}}8\;\hbox {kg} \; {\hbox {m}^2}$, ${\bar{I}_{\bar{y}\bar{y}}} = {{1}}{{.04}}\;\hbox {kg} \; {\hbox {m}^2}$, and ${\bar{I}_{\bar{z}\bar{z}}} = {{1}}{{.04}}\;\hbox {kg} \; {\hbox {m}^2}$ which form the body matrix of inertia defined as ${{\bar{\mathbf{I}}}_G} = \mathrm{{diag}}({\bar{I}_{\bar{x}\bar{x}}},{\bar{I}_{\bar{y}\bar{y}}},{\bar{I}_{\bar{z}\bar{z}}})$. The gravitational acceleration is assumed $g = 9.81\;{\hbox {m}}/{{\hbox {s}^2}}$ and the body weight vector is defined as ${\mathbf{{F}}_g} = {\left[ {\begin{array}{*{20}{c}}0&\quad 0&\quad { - mg}\end{array}} \right] ^T}$. Employing the RPCF with Euler parameters, the index-one form of the equations of motion of the simple pendulum can be readily written as:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbf{M}\ddot{\mathbf{q}}} = {\mathbf{{Q}}_v} + {\mathbf{{Q}}_e} - \mathbf{{C}}_\mathbf{{q}}^T{\varvec{\lambda }}\\ {\mathbf{{C}}_\mathbf{{q}}}{\ddot{\mathbf{q}}} = {\mathbf{{Q}}_d} \end{array} \right. \end{aligned}$$

(87)

where the matrix and vector terms that appear in the equations of motion of the simple pendulum based on the RPCF with Euler parameters can be, respectively, computed using the definitions presented in the paper as follows:

$$\begin{aligned} \mathbf{{M}}= & {} \left[ {\begin{array}{*{20}{c}} {m\mathbf{{I}}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad {{{{\bar{\mathbf{G}}}}^T}{{{\bar{\mathbf{I}}}}_G}{\bar{\mathbf{G}}}} \end{array}} \right] ,\quad {\mathbf{{Q}}_v} = \left[ {\begin{array}{*{20}{c}} \mathbf{{0}}\\ { - {{{\bar{\mathbf{G}}}}^T}{{\tilde{\bar{\varvec{\omega }} }}}{{{\bar{\mathbf{I}}}}_G}{\bar{\varvec{\omega }}}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_g}= & {} \mathbf{{L}}_G^T{\mathbf{{F}}_g},\quad \mathbf{{C}} = \left[ {\begin{array}{*{20}{c}} {\varvec{\varphi }}\\ {\varvec{\psi }} \end{array}} \right] ,\quad {\varvec{\varphi }} = {{\varvec{\theta }}^T}{\varvec{\theta }} - 1,\quad {\varvec{\psi }} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{r}}_O}}\\ {{\mathbf{{a}}^T}{} \mathbf{{c}}}\\ {{\mathbf{{b}}^T}{} \mathbf{{c}}} \end{array}} \right] ,\nonumber \\ {\mathbf{{C}}_\mathbf{{q}}}= & {} \left[ {\begin{array}{*{20}{c}} {{{\varvec{\varphi }}_\mathbf{{q}}}}\\ {{{\varvec{\psi }}_\mathbf{{q}}}} \end{array}} \right] ,\quad {{\varvec{\varphi }}_\mathbf{{q}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&\quad {2{{\varvec{\theta }}^T}} \end{array}} \right] ,\quad {{\varvec{\psi }}_\mathbf{{q}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{L}}_O}}\\ {{\mathbf{{c}}^T}{\mathbf{{D}}_a}}\\ {{\mathbf{{c}}^T}{\mathbf{{D}}_b}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_d}= & {} \left[ {\begin{array}{*{20}{c}} {{\mathbf{{Q}}_{d,\varphi }}}\\ {{\mathbf{{Q}}_{d, {\psi } }}} \end{array}} \right] ,\quad {\mathbf{{Q}}_{d,\varphi }} = - 2{{{\dot{\varvec{\theta }}}}^T}{\dot{\varvec{\theta }}},\quad {\mathbf{{Q}}_{d, {\psi }}} = \left[ {\begin{array}{*{20}{c}} { - {{{\dot{\mathbf{L}}}}_O}{\dot{\mathbf{q}}}}\\ { - {\mathbf{{c}}^T}{{{\dot{\mathbf{D}}}}_a}{\dot{\mathbf{q}}}}\\ { - {\mathbf{{c}}^T}{{{\dot{\mathbf{D}}}}_b}{\dot{\mathbf{q}}}} \end{array}} \right] \end{aligned}$$

(88)

where $\mathbf{{a}}$ and $\mathbf{{b}}$ are two directions vectors, whereas $\mathbf{{c}}$ is a fixed unit vector that identifies the axis of the revolute joint. On the other hand, by using the NACF, the index-one form of the equations of motion of the simple pendulum can be readily written as:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbf{M}\ddot{\mathbf{e}}} = {\mathbf{{Q}}_e} - \mathbf{{C}}_\mathbf{{e}}^T{\varvec{\lambda }}\\ {\mathbf{{C}}_\mathbf{{e}}}{\ddot{\mathbf{e}}} = {\mathbf{{Q}}_d} \end{array} \right. \end{aligned}$$

(89)

where the matrix and vector terms that appear in the equations of motion of the simple pendulum based on the NACF can be, respectively, computed using the definitions presented in the paper as follows:

$$\begin{aligned} \mathbf{{M}}= & {} \left[ {\begin{array}{*{20}{c}} {m\mathbf{{I}}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad {\frac{{ - {{\bar{I}}_{\bar{x}\bar{x}}} + {{\bar{I}}_{\bar{y}\bar{y}}} + {{\bar{I}}_{\bar{z}\bar{z}}}}}{2}{} \mathbf{{I}}}&{} \quad \mathbf{{O}}&{} \quad \mathbf{{O}}\\ \mathbf{{O}}&{} \quad \mathbf{{O}}&{} \quad {\frac{{{{\bar{I}}_{\bar{x}\bar{x}}} - {{\bar{I}}_{\bar{y}\bar{y}}} + {{\bar{I}}_{\bar{z}\bar{z}}}}}{2}{} \mathbf{{I}}}&{}\mathbf{{O}}\\ \mathbf{{O}}&{} \quad \mathbf{{O}}&{}\mathbf{{O}}&{} \quad {\frac{{{{\bar{I}}_{\bar{x}\bar{x}}} + {{\bar{I}}_{\bar{y}\bar{y}}} - {{\bar{I}}_{\bar{z}\bar{z}}}}}{2}{} \mathbf{{I}}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_g}= & {} \mathbf{{S}}_G^T{\mathbf{{F}}_g},\quad \mathbf{{C}} = \left[ {\begin{array}{*{20}{c}} {\varvec{\varphi }}\\ {\varvec{\psi }} \end{array}} \right] ,\quad {\varvec{\varphi }} = \left[ {\begin{array}{*{20}{c}} {{{\varvec{\alpha }}^T}{\varvec{\alpha }} - 1}\\ {{{\varvec{\beta }}^T}{\varvec{\beta }} - 1}\\ {{{\varvec{\gamma }}^T}{\varvec{\gamma }} - 1}\\ {{{\varvec{\alpha }}^T}{\varvec{\beta }}}\\ {{{\varvec{\alpha }}^T}{\varvec{\gamma }}}\\ {{{\varvec{\beta }}^T}{\varvec{\gamma }}} \end{array}} \right] ,\quad {\varvec{\psi }} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{r}}_O}}\\ {{\mathbf{{a}}^T}{} \mathbf{{c}}}\\ {{\mathbf{{b}}^T}{} \mathbf{{c}}} \end{array}} \right] ,\nonumber \\ {\mathbf{{C}}_\mathbf{{e}}}= & {} \left[ {\begin{array}{*{20}{c}} {{{\varvec{\varphi }}_\mathbf{{e}}}}\\ {{{\varvec{\psi }}_\mathbf{{e}}}} \end{array}} \right] ,\quad {{\varvec{\varphi }}_\mathbf{{e}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}^T}}&{} \quad {2{{\varvec{\alpha }}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {2{{\varvec{\beta }}^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{}{2{{\varvec{\gamma }}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\beta }}^T}}&{} \quad {{{\varvec{\alpha }}^T}}&{} \quad {{\mathbf{{0}}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\gamma }}^T}}&{} \quad {{\mathbf{{0}}^T}}&{} \quad {{{\varvec{\alpha }}^T}}\\ {{\mathbf{{0}}^T}}&{} \quad {{\mathbf{{0}}^T}}&{}{{{\varvec{\gamma }}^T}}&{}{{{\varvec{\beta }}^T}} \end{array}} \right] ,\quad {{\varvec{\psi }}_\mathbf{{e}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{S}}_O}}\\ {{\mathbf{{c}}^T}{\mathbf{{N}}_a}}\\ {{\mathbf{{c}}^T}{\mathbf{{N}}_b}} \end{array}} \right] ,\nonumber \\ {\mathbf{{Q}}_d}= & {} \left[ {\begin{array}{*{20}{c}} {{\mathbf{{Q}}_{d,\varphi }}}\\ {{\mathbf{{Q}}_{d, {\psi } }}} \end{array}} \right] ,\quad {\mathbf{{Q}}_{d,\varphi }} = \left[ {\begin{array}{*{20}{c}} { - 2{{{\dot{\varvec{\alpha }}}}^T}{\dot{\varvec{\alpha }}}}\\ { - 2{{{\dot{\varvec{\beta }}}}^T}{\dot{\varvec{\beta }}}}\\ { - 2{{{\dot{\varvec{\gamma }}}}^T}{\dot{\varvec{\gamma }}}}\\ { - 2{{{\dot{\varvec{\alpha }}}}^T}{\dot{\varvec{\beta }}}}\\ { - 2{{{\dot{\varvec{\alpha }}}}^T}{\dot{\varvec{\gamma }}}}\\ { - 2{{{\dot{\varvec{\beta }}}}^T}{\dot{\varvec{\gamma }}}} \end{array}} \right] ,\quad {\mathbf{{Q}}_{d, {\psi }}} = \mathbf{{0}} \end{aligned}$$

(90)

where $\mathbf{{a}}$ and $\mathbf{{b}}$ are two directions vectors, whereas $\mathbf{{c}}$ is a fixed unit vector that identifies the axis of the revolute joint. The initial position of the centroid of the simple pendulum is represented by the following global position vector:

$$\begin{aligned} \mathbf{{R}} = \left[ {\begin{array}{*{20}{c}} {{X_0}}\\ {{Y_0}}\\ {{Z_0}} \end{array}} \right] \end{aligned}$$

(91)

where ${X_0} = 1$, ${Y_0} = 0.2$, and ${Z_0} = 0$. The rigid body initial orientation is identified by the following set of Euler parameters:

$$\begin{aligned} {\varvec{\theta }} = \left[ {\begin{array}{*{20}{c}} {{\theta _0}}\\ {{\theta _1}}\\ {{\theta _2}}\\ {{\theta _3}} \end{array}} \right] \end{aligned}$$

(92)

where ${\theta _0} = {{1}}$, ${\theta _1} = 0$, ${\theta _2} = 0$, and ${\theta _3} = 0$. The orientation of the simple pendulum is defined by the vector of Euler parameters ${\varvec{\theta }}$ and corresponds to the direction cosine vectors ${\varvec{\alpha }}$, ${\varvec{\beta }}$, and ${\varvec{\gamma }}$ defined as:

$$\begin{aligned} {\varvec{\alpha }} = \left[ {\begin{array}{*{20}{c}} {{\varvec{\alpha }_1}}\\ {{\varvec{\alpha }_2}}\\ {{\varvec{\alpha }_3}} \end{array}} \right] ,\quad \quad {\varvec{\beta }} = \left[ {\begin{array}{*{20}{c}} {{\varvec{\beta }_1}}\\ {{\varvec{\beta }_2}}\\ {{\varvec{\beta }_3}} \end{array}} \right] ,\quad \quad {\varvec{\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\varvec{\gamma }_1}}\\ {{\varvec{\gamma }_2}}\\ {{\varvec{\gamma }_3}} \end{array}} \right] \end{aligned}$$

(93)

where ${\alpha _1} = 1$, ${\alpha _2} =0$, ${\alpha _3} = 0$, ${\beta _1} = 0$, ${\beta _2} =1$, ${\beta _3} = 0$, ${\gamma _1} = 0$, ${\gamma _2} =0$, and ${\gamma _2} =1$. The initial linear and angular velocities of the simple pendulum are assumed zero. The vertical position of the centroid of the simple pendulum computed employing both the NACF and the RPCF with Euler parameters is shown in Fig. 5. The violations of the intrinsic constraint equations relative to the NACF and to the RPCF with Euler parameters are, respectively, shown in Tables 5 and 6. In this numerical example, some Lagrange multipliers associated with the intrinsic constraint equations can be considered constant for the entire time span of the numerical simulation with a very good approximation. This is the case of the Lagrange multiplier associated with the set of Euler parameters and for the second, fourth, and sixth Lagrange multipliers relative to the direction cosines. The comparison between the solution obtained employing the Udwadia–Kalaba equations the and the numerical solution procedure for the Lagrange multiplier corresponding to the set of direction cosines is reported in Table 7. Furthermore, the solution obtained by using the Udwadia–Kalaba equations and the numerical solutions found for the Lagrange multipliers relative to the set of Euler parameters is reported in Table 8. On the other hand, the comparison between the time evolution of the first, third, and fifth Lagrange multipliers associated with the direction cosines obtained by using the Udwadia–Kalaba equations and the numerical solution procedure are, respectively, shown in Figs. 6, 7, and 8. Observing Tables 7 and 8, and considering Figs. 6, 7, and 8, it is clear that the numerical results obtained using the augmented formulation are in a very good agreement with the analytical results predicted employing the Udwadia–Kalaba equations even in the case of a constrained rigid body such as the simple pendulum modeled employing both the RPCF with Euler parameters and the NACF.

Fig. 5

Centroid vertical position of the simple pendulum, (circle) NACF, (square) RPCF with Euler parameters

Fig. 6

First Lagrange multiplier of the intrinsic constraints associated with the direction cosines for the simple pendulum, (circle) Udwadia–Kalaba equations, (square) augmented formulation with generalized coordinate partitioning, (diamond) augmented formulation without constraint stabilization

Fig. 7

Third Lagrange multiplier of the intrinsic constraints associated with the direction cosines for the simple pendulum, (circle) Udwadia–Kalaba equations, (square) augmented formulation with generalized coordinate partitioning, (diamond) augmented formulation without constraint stabilization

Fig. 8

Fifth Lagrange multiplier of the intrinsic constraints associated with the direction cosines for the simple pendulum, (circle) Udwadia–Kalaba equations, (square) augmented formulation with generalized coordinate partitioning, (diamond) augmented formulation without constraint stabilization

Table 5 Violations of the constraint equations in the NACF for the simple pendulum

Table 6 Violations of the constraint equations in the RPCF with Euler parameters for the simple pendulum

Table 7 Lagrange multiplier associated with the intrinsic constraint equations of the direction cosines for the simple pendulum

Table 8 Lagrange multiplier associated with the intrinsic constraint equation of the Euler parameters for the simple pendulum

5 Summary and conclusions

The principal research goals of the authors are focused on the development of new, effective, and efficient methods to carry out accurate analytic modeling [89,90,91], experimental system identification [92,93,94], and numerical control optimization of rigid–flexible multibody mechanical systems exploiting the deep connections between multibody dynamics, system identification, and nonlinear control theory [95,96,97]. In particular, this work is an analytical study and numerical investigation on the intrinsic constraint equations that play a fundamental role in the mathematical formulation of the differential–algebraic equations of motion of rigid multibody mechanical systems described by using a nonminimal set of rotational coordinates.

In this investigation, two general forms of the differential–algebraic equations of motion of three-dimensional rigid bodies were examined. In the first form of the dynamic equations, the RPCF with Euler parameters was discussed, whereas a multibody approach based on the NACF was considered as the second analytical formulation. While the RPCF with Euler parameters conveniently employs the components of a unit quaternion for representing the orientation of a rigid body in the space, in the NACF the configuration of a rigid body is represented by using the set of direction cosines that identifies the unit vectors associated with the body-fixed reference system. The RPCF with Euler parameters and the NACF employ, therefore, two different mathematical descriptions which lead to effective representations of large finite rotations of rigid multibody systems. Furthermore, the analytical approaches based on the RPCF with Euler parameters and on the NACF allow for circumventing the kinematic singularity issues associated with critical configurations which affect each minimal set of three orientation coordinates such as the Euler angles, the Tait–Bryan angles, and the Cardan angles. However, both in the RPCF with Euler parameters and in the NACF, two different nonminimal sets of rotational coordinates are used. Therefore, in the mathematical models developed by using these multibody formulations for rigid mechanical systems, two different sets of normalization conditions must be employed for obtaining a consistent description of arbitrary rotations free of kinematic singularities. Consequently, the normalization equations associated with the rotational coordinates represent an additional set of algebraic constraints that must be considered in order to obtain reliable dynamic simulations.

In this work, the additional normalization conditions associated with the rotational coordinates are referred to as intrinsic constraint equations in order to conceptually distinguish them from the algebraic constraints that arise from the kinematic joints. On the other hand, the algebraic equations that mathematically model the mechanical joints are called in this paper extrinsic constraint equations. It can be proved that the algebraic constraints arising from the geometrical representation of arbitrary rotations, which are identified in this paper as intrinsic constraint equations, are also associated with the rigidity of the bodies that from the multibody mechanical system. In the analytical formulation of the equations of motion based on the fundamental laws of classical mechanics, the set of intrinsic constraint equations can be treated with the Lagrange multiplier technique. Thus, a vector of kinematic constraints and a vector of generalized constraint forces associated with the intrinsic constraint equations enter in the formulation of the equations of motion. The main goal of this investigation was, therefore, to shed more light on the role of the intrinsic constraint equations that appear in the mathematical formulations of the equations of motion of rigid multibody systems. To this end, closed-form analytical expressions of the Lagrange multipliers associated with the intrinsic constraint equations were found for both the RPCF with Euler parameters and the NACF. For this purpose, the fundamental equations of constrained motion were effectively employed in order to obtain in a straightforward manner the desired analytical results. The Udwadia–Kalaba equations are based on the approach to the analytical mechanics recently developed by Udwadia and Kalaba [98]. The fundamental equations of constrained motion represent a general analytical method which allows for obtaining the generalized constraint forces together with the generalized acceleration vector of a multibody mechanical system subjected to a set of holonomic and/or nonholonomic constraint equations. Another important application of the Udwadia–Kalaba method is in the field of nonlinear control. Following the Udwadia–Kalaba approach to the nonlinear control theory, prescribed control requirements are viewed as additional algebraic constraints which can be of holonomic or nonholonomic nature. By using the Udwadia–Kalaba method for solving the problem of interest of this investigation, the Lagrange multiplier associated with the normalization condition of the Euler parameters was found to be always equal to zero. On the other hand, the Lagrange multipliers corresponding to the orthonormality conditions of the directions cosines were found to have always nonzero values which can be readily computed in a closed-form. These analytical findings represent important results for the dynamic analysis of rigid multibody systems that are confirmed by numerical experiments.

In this paper, simple numerical examples were used for performing the numerical experiments necessary to confirm the analytical results and the mathematical derivations developed in this investigation. For this purpose, two simple numerical examples were used, namely the unconstrained motion of a spinning projectile translating and rotating in the space and the constrained motion of a simple pendulum. The differential–algebraic equations of motion of a single rigid body were derived in terms of reference point coordinates and also in terms of natural absolute coordinates. In the computer implementation of the dynamic equations, the augmented formulation and the Udwadia–Kalaba approach were employed in conjunction with the generalized coordinate partitioning technique in order to numerically solve the resulting index-one form of the differential–algebraic equations of motion. A very good agreement was found between the analytical formulas developed in the paper and the numerical results obtained by means of dynamic simulations. However, the analytical expressions and the numerical values of the Lagrange multipliers associated with both the set of Euler parameters and the set of direction cosines still lack a clear physical meaning. For example, the Lagrange multipliers associated with the intrinsic constraint equations of the direction cosines can be interpreted as mathematical quantities related to the generalized intrinsic constraint forces that guarantee the rigidity of the body and, therefore, they can have an intuitive physical interpretation. On the other hand, the mechanical interpretation of the zero value of the Lagrange multiplier associated with the normalization condition of the unit quaternion corresponding to the set of Euler parameters is still not obvious. Shedding more light on these important issues will be the object of future investigations.