Fluid–structure interaction analysis of free convection in an inclined square cavity partitioned by a flexible impermeable membrane with sinusoidal temperature heating

Abstract

The problem of unsteady natural convection inside an inclined square cavity partitioned by a flexible impermeable membrane is studied numerically using the finite-element method along with the Arbitrary Lagrangian–Eulerian (ALE) approach. The bottom and top walls of the cavity are kept adiabatic. The left side wall is kept isothermal at a high temperature, while the right wall is cooled in a sinusoidal fashion. The cavity is provided by two eyelets to compensate volume changes due to the movement of the flexible membrane. The studied pertinent parameters are the Rayleigh number (in the range of 1E4–1E7), the amplitude of the sinusoidal wall temperature (A in the range of 0–1.0), the inclination angle of the cavity (in the range of −π/3 to π/3), and the body force parameter (Fv in the range of −1.64E−2 to +1.64E−2) whereas the Prandtl number is fixed at 6.2. The results show that at a low Rayleigh number, the membrane shape is a function of the imposed body force. While at a high Rayleigh number, the buoyancy force becomes responsible for the membrane deflection. The natural convection is appreciably affected by the inclination angle of the cavity which in turn, affects the concave or convex shape of the membrane.

1 Introduction

The importance of natural convection in industry and engineering applications has produced abundant developments and innovations that improved the process efficiency. The convection inside enclosures has received numerous investigations because of its vast environmental and industrial applications. So, the relevant literature manifests different designs of the domain enclosing the natural convection process [1–6], different cooling or heating arrangements [7–10], different nanoparticles addition to improve the thermal properties of regular liquids [11–15]. Alternatively, some applications require retarding the natural convection process, so an external magnetic field is applied upon electrically-conducting liquids [16–18] to suppress the natural convection. Inserting baffles or fins or even tilting the whole cavity are some techniques followed in controlling the natural convection inside clear or saturated porous cavities [19–27]. Natural convection in cavities composed of two different layers with impermeable interface has its substantial area in industrial applications [28, 29]. It is essential to consider the transient numerical solutions to investigate the transient features of the coupled thermal boundary layers adjacent to a partition that splits a cavity [30], to simulate a time varying thermal boundary conditions [31], or for the simulation of fluid‐structure interaction [32].

During the last two decades, various methods have been considered to enhance the natural convection by exciting the entire cavity or its boundary using an external mechanical or electrical force. Hence, this mechanism is unrestricted by the electrical or thermal properties of the fluid. The analysis of such a problem is classified as a moving boundary problem which is encountered in many engineering applications and in nature as well. A cooling fan-induced vibration in electronic devices, biological micro-scale experiments, mixing and sterling devices, and heat exchangers are examples of these applications. The effects of vertical vibration and gravity on the induced convection inside an enclosure were simulated by Fu and Sheih [33, 34]. Kimoto and Ishidi [35] investigated the vibration effects on the natural convection heat transfer in a square enclosure. Fu et al. [36] reported a remarkable increase in heat transfer associated with laminar forced convection in a parallel-plate channel including an oscillating block. Florio and Harnoy [37] studied the enhancement of natural convection cooling of discrete heat source in a vertical channel using a vibrating plate. Convection in porous media undergoing mechanical vibration is reported by Razi et al. [38]. Chung and Vafai [39] investigated the vibrational and buoyancy-induced convection in a vertical porous channel with an open-ended top and a vibrating left wall. Cheng et al. [40] proposed a novel approach to enhance the convective heat transfer in a heat exchanger by using the flow-induced vibration instead of strictly avoiding it. D’Orazio et al. [41] performed mixed convection in an inclined enclosure for the case of an imposed non-zero heat flux.

In some applications, flexible boundaries oscillate periodically resulting in a deformable domain. For example, flow through a diaphragm pump, diaphragm sensors, flow through elastic pipes as in arteries or other blood vessels, moving pistons or sloshing of fluids in elastic containers [42] are problems with deformable domains. However, this type of problems is an interesting vehicle to mathematicians and those whom delineated in computational fluid dynamics in understanding the physics and flow characteristics. An efficient numerical simulation technique that deals with this time-dependent moving boundary problem is the Arbitrary Lagrangian–Eulerian (ALE) approach. It is a technique that discourses the drawbacks associated with the Lagrangian and Eulerian methods individually. According to the ALE technique, the mesh nodes of the computational domain may be moved (according to the Lagrangian method), held fixed (according to the Eulerian approach), or moved in an arbitrary procedure. Details of this technique are illustrated in the works of Hirt et al. [43], Hughes et al. [44], and Donea et al. [45]. Fu and Huang [46] utilized the ALE technique to investigate natural convection of a heated plate in a vertical channel under vibrational motion. One of their main conclusions was that for a given Rayleigh number, natural convection for a certain combination of frequency and amplitude was possibly smaller than that of the stationary state.

A critical survey of natural convection inside a cavity partitioned by a flexible impermeable membrane has shown that no published works on this topic exist. As such, the authors of this paper have found that it is essential to discover the features of natural convection in a cavity containing one or more fluids separated by a thin flexible membrane. To make the present study comprehensive, the inclination of the whole cavity is considered. Moreover, the cavity is equipped by two ports (eyelets) to compensate the increase or decrease of fluid volume in both sides due to the membrane deformation.

2 Problem description and mathematical formulation

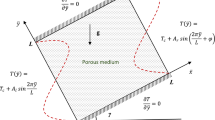
A schematic diagram of the cavity geometry under investigation is shown in Fig. 1. The bottom wall of the square cavity (x ^*-axis) makes an angle γ with the horizontal axis. The temperature is assumed to be constant along the left wall and sinusoidal spatially-varying on the right wall, whereas the top and bottom horizontal walls are assumed thermally insulated. Also, the sinusoidal distribution of temperature expresses that the mean temperature is T ^* _c along the right sidewall. The cavity walls are stationary and it is assumed that the no-slip boundary condition is acceptable on them. The square cavity is divided into two equal parts using a thin flexible membrane perpendicular to the x ^*-axis. The thickness of the flexible membrane is t* _p and is considered to be isotropic, uniform and dense. The temperature gradient and the energy storage are ignored in the membrane because the membrane is very thin and has a high thermal conductivity. All walls of the cavity as well as the membrane are impermeable. Two eyelets are embedded on the left and right sidewalls in order to control the volume changes caused by the movement of the flexible membrane in both parts.

Fig. 1

A schematic of the problem and coordinates system

The working fluid is assumed incompressible and Newtonian and the fluid flow is considered to be laminar and unsteady. The thermophysical properties of the fluid are assumed constant except the density variation in the body force term of the momentum equation which is satisfied by the Boussinesq’s approximation. The inclined cavity is under the influence of the gravity field in the vertical direction. Also, the viscous dissipation can be neglected compared to the convection and conduction terms. The body force exerted on the membrane is taken into consideration in this study. This force includes the effects of the weight of the membrane and the buoyancy force of the fluid. Applying the mentioned presumptions and using the Arbitrary Lagrangian–Eulerian (ALE) technique, the governing equations for the fluid flow and heat transfer consist of the balance laws of mass, momentum and energy and can be written as follows:

$$\nabla^{*} \cdot {\mathbf{u}}^{*} = 0$$

(1)

$$\frac{{\partial {\mathbf{u}}^{*} }}{\partial t} + \left( {{\mathbf{u}}^{*} - {\mathbf{w}}^{*} } \right) \cdot \nabla^{*} {\mathbf{u}}^{*} = - \frac{1}{{\rho_{f} }}\nabla^{*} P^{*} + v_{f} \nabla^{*2} {\mathbf{u}}^{*} + \beta {\mathbf{g}}\left( {T^{*} - T_{c}^{*} } \right)$$

(2)

$$\frac{{\partial T^{*} }}{\partial t} + \left( {{\mathbf{u}}^{*} - {\mathbf{w}}^{*} } \right).\nabla^{*} T^{*} = \alpha_{f} \nabla^{*2} T^{*}$$

(3)

Also, the structural displacement of the flexible membrane is described using the following nonlinear elasto-dynamic equation:

$$\rho_{s} \frac{{d^{2} {\mathbf{d}}_{s}^{*} }}{{dt^{2} }} - \nabla^{*} {\varvec{\upsigma}}^{*} = {\mathbf{F}}_{v}^{*}$$

(4)

In these equations, u ^* is the fluid velocity field, u ^* = (u ^*,v ^*), w ^* denotes the moving coordinate system velocity, w ^* = (u ^* _s ,v ^* _s ), P ^* is the fluid pressure, T ^* is the fluid temperature, g is the acceleration vector. ∇^* is a dimensional gradient operator, d ^*_s is the displacement vector of membrane such that d d ^*_s /dt = w ^*, σ ^* is the solid stress tensor, F ^*_v represents the imposed body forces on the flexible membrane and includes the components F ^* _v cos γ and F ^* _v sin γ along the x ^*- and y ^*-axes, respectively. In both of the components, F ^* _v and γ are the values of the body force vector and inclination angle, respectively. It is clear that F ^* _v , the body force caused by the weight of the membrane and the buoyancy force, is (ρ _f –ρ _s )g acting in the vertical direction. ρ _f and ρ _s are the densities of the fluid and the solid, respectively, ν _f and α _f are the kinematic viscosity and thermal diffusivity of the fluid, respectively and finally, β is the volumetric thermal expansion coefficient.

As shown in Fig. 1, the velocity and thermal boundary conditions imposed on the geometry are

$$\begin{aligned} & {\text{On}}\;{\text{all}}\;{\text{walls}}\;{\text{of}}\;{\text{cavity}}\;u^{*} = v^{*} = 0 \\ & {\text{On}}\;{\text{the}}\;{\text{top}}\;{\text{and}}\;{\text{bottom}}\;{\text{walls}}\;{\text{of}}\;{\text{cavity}}\;\frac{{\partial T^{*} }}{{\partial y^{*} }} = 0 \\ & {\text{On}}\;{\text{the}}\;{\text{left}}\;{\text{wall}}\;{\text{of}}\;{\text{cavity}}\;T^{*} = T_{h}^{*} \\ & {\text{On}}\;{\text{the}}\;{\text{right}}\;{\text{wall}}\;{\text{of}}\;{\text{the}}\;{\text{cavity}}\;T^{*} = T_{c}^{*} + A\left( {T_{h}^{*} - T_{c}^{*} } \right)\sin \left( {2\pi \frac{{y^{*} }}{L}} \right) \\ \end{aligned}$$

(5)

In the above equation, A is the amplitude of the sinusoidal distribution of temperature. In Eq. (4), the stress tensor can be defined using the Neo-Hookean solid model. A Neo-Hookean solid is defined as a hyper-elastic material model that can be employed for describing the non-linear stress–strain behavior of materials with large deformations. This model can be expressed by the following equation:

$${\varvec{\upsigma}}^{*} = J^{ - 1} FSF^{T}$$

(6)

In the aforementioned equation, $F = \left( {I + \nabla^{*} {\mathbf{d}}_{s}^{*} } \right)$, J = det(F), S = ∂W _s /∂ε, and superscript T denotes the transpose of the matrix F. W _s and ε are the strain energy density function and the strain, respectively and can be expressed by the following equations:

$$W_{s} = \frac{1}{2}\mu_{l} \left( {J^{ - 1} I_{1} - 3} \right) - \mu_{l} \ln \left( J \right) + \frac{1}{2}\lambda \left( {\ln \left( J \right)} \right)^{2}$$

(7)

$$\varepsilon = \frac{1}{2}\left( {\nabla^{*} {\mathbf{d}}_{s}^{*} + \nabla^{*} {\mathbf{d}}_{s}^{*T} + \nabla^{*} {\mathbf{d}}_{s}^{*T} \nabla^{*} {\mathbf{d}}_{s}^{*} } \right)$$

(8)

In Eq. (7), λ and μ _l are separately referred to as the Lame’s first and second parameters, respectively and are evaluated by µ _l  = E/(2(1 + ν)) and λ = Eν/((1 + ν)(1 − 2ν)). Also, I ₁ refers to the first invariant of the right Cauchy–Green deformation tensor. Two boundary conditions applied for simulation of the fluid–solid interaction are the continuity of the kinematic forces and the dynamic motions. The dimensional fluid–solid interface boundary conditions for the fluid at the flexible membrane surface can be written as follows:

$$\frac{{\partial {\mathbf{d}}_{s}^{*} }}{\partial t} = {\mathbf{u}}^{*} \;{\text{and}}\;{\varvec{\upsigma}}^{*} \cdot n = - P^{*} + \mu_{f} \nabla {\mathbf{u}}^{*}$$

(9)

Also, it is necessary to depict the conservation of energy requirement for the flexible membrane. Therefore, two control surfaces are placed on either side of the flexible membrane. In this case, the energy generation and storage are no longer relevant for as much as the membrane is very thin and has a high thermal conductivity. Finally, the conservation of energy and continuity of temperature lead to the following equations, respectively:

$$\frac{\partial T}{\partial n}^{* + } = \frac{\partial T}{\partial n}^{* - } {\text{ and }}T^{* + } { = }T^{* - }$$

(10)

In the above equation, the positive and negative superscripts refer to the right and left surfaces of membrane wall, respectively. For the two eyelets embedded on the walls perpendicular to the x ^*-axis, the following equation is satisfied:

$$\left[ { - P^{*} + \mu \nabla {\mathbf{u}}^{*} } \right] \cdot n = 0$$

(11)

The dimensional governing Eqs. (1)–(4) are converted into non-dimensional equations using the following dimensionless parameters:

$${\mathbf{d}}_{s} = \frac{{{\mathbf{d}}_{s}^{*} }}{L},\quad {\varvec{\upsigma}} = \frac{{{\varvec{\upsigma}}^{*} }}{E},\quad \tau = \frac{{t\alpha_{f} }}{{L^{2} }},\quad (x,y)\frac{{x^{*} ,y^{*} }}{L},$$

(12a)

$${\mathbf{u}} = \frac{{{\mathbf{u}}^{*} L}}{{\alpha_{f} }},\quad {\mathbf{w}} = \frac{{{\mathbf{w}}^{*} L}}{{\alpha_{f} }},\quad P = \frac{{L^{2} }}{{\rho_{f} \alpha_{f}^{2} }}P^{*} ,\quad T = \frac{{T^{*} - T_{c}^{*} }}{{T_{h}^{*} - T_{c}^{*} }}$$

(12b)

$$\nabla = \frac{\nabla^{*} }{{{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}}},\quad \nabla = \frac{{\nabla^{*2} }}{{{1 \mathord{\left/ {\vphantom {1 {L^{2} }}} \right. \kern-0pt} {L^{2} }}}},\quad t_{p} = \frac{{t_{p}^{*} }}{L}$$

(12c)

Thus, in the dimensionless coordinate, the governing equations are:

$$\frac{1}{{\rho_{R} }}\frac{{d^{2} {\mathbf{d}}_{s} }}{{d\tau^{2} }} - E_{\tau } \nabla {\varvec{\upsigma}} = E_{\tau } {\mathbf{F}}_{v}$$

(13)

$$\nabla \cdot {\mathbf{u}} = 0$$

(14)

$$\frac{{\partial {\mathbf{u}}}}{\partial \tau } + \left( {{\mathbf{u}} - {\mathbf{w}}} \right) \cdot \nabla {\mathbf{u}} = - \nabla P + \text{Pr}\nabla^{2} {\mathbf{u}} + \Pr {\mathbf{Ra}}T$$

(15)

$$\frac{\partial T}{\partial \tau } + \left( {{\mathbf{u}} - {\mathbf{w}}} \right) \cdot \nabla T = \nabla^{2} T$$

(16)

where

$${\mathbf{Ra}} = \frac{{{\mathbf{g}}\beta \left( {T_{h} - T_{c} } \right)L^{3} }}{{\upsilon_{f} \alpha_{f} }},\quad \text{Pr} = \frac{{\upsilon_{f} }}{{\alpha_{f} }},\quad E_{\tau } = \frac{{EL^{2} }}{{\rho_{f} \alpha_{f}^{2} }},\quad {\mathbf{F}}_{v} = \frac{{\left( {\rho_{f} - \rho_{s} } \right)L{\mathbf{g}}}}{E},\quad \rho_{R} = \frac{{\rho_{f} }}{{\rho_{s} }}$$

(17)

are the Rayleigh number vector, Prandtl number, non-dimensional elasticity modulus, non-dimensionless body force vector and the density ratio number, respectively. It is necessary to mention that the Rayleigh number vector has two components; Ra sin γ along the x-axis and Ra cos γ along the y-axis. In these components, Ra is the value of the Rayleigh number vector and is called Rayleigh number. Also, F _v has two components; F _v sin γ and F _v cos γ along the x- and y-axes, respectively.

The boundary conditions imposed on the geometry in the dimensionless coordinate are changed as follows:

$$\begin{aligned} & {\text{On}}\;{\text{all}}\;{\text{walls}}\;{\text{of}}\;{\text{cavity}}\;u = v = 0 \\ & {\text{On}}\;{\text{the}}\;{\text{top}}\;{\text{and}}\;{\text{bottom}}\;{\text{walls}}\;{\text{of}}\;{\text{cavity}}\;\frac{\partial T}{\partial y} = 0 \\ & {\text{On}}\;{\text{the}}\;{\text{left}}\;{\text{wall}}\;{\text{of}}\;{\text{cavity}}\;T = 1 \\ & {\text{On}}\;{\text{the}}\;{\text{right}}\;{\text{wall}}\;{\text{of}}\;{\text{the}}\;{\text{cavity}}\;T = A\sin \left( {2\pi y} \right) \\ & {\text{For}}\;{\text{the}}\;{\text{flexible}}\;{\text{membrane}}\frac{\partial T}{\partial n}^{ + } = \frac{\partial T}{\partial n}^{ - } \;{\text{and}}\;T^{ + } = T^{ - } \\ \end{aligned}$$

(18)

At time t = 0, the fluid is quiescent (u (x,y,0) = 0). At this time, the temperatures of the fluid in the left and right sub-cavities are the temperatures of the hot and cold walls, respectively. In other words, the left sub-cavity is initially at the uniform temperature T _h while the right-sub cavity is initially at the uniform temperature T _c . The dimensionless boundary conditions for the fluid–solid interface are

$$\frac{{\partial {\mathbf{d}}_{s} }}{\partial \tau } = {\mathbf{u}}\;{\text{and}}\;E_{\tau } {\varvec{\upsigma}} \cdot n = - P + \Pr \nabla {\mathbf{u}}$$

(19)

Finally, the dimensionless boundary conditions for both of the eyelets are provided as follows:

$$\left[ { - P + \Pr \nabla {\mathbf{u}}} \right] \cdot n = 0$$

(20)

In order to estimate the heat transfer rate, the local Nusselt number for the vertical walls is given as

$$Nu_{local} = - \frac{\partial T}{\partial x}$$

(21)

The average Nusselt number can be obtained by integrating the local Nusselt number as follows:

$$Nu_{avg} = \int\limits_{0}^{1} {Nu_{local} } dy$$

(22)

Eventually, in order to describe the fluid motion, it is worthwhile to define another parameter namely, the stream function ψ that can be expressed as follows:

$$u\text{ = }\frac{\partial \psi }{\partial y}, \, v\text{ = } - \frac{\partial \psi }{\partial x}$$

(23)

3 Numerical solution and validations

3.1 Grid independency test

The dimensionless governing partial differential Eqs. (13)–(16) subjected to the mentioned boundary conditions (18)–(20) are transformed into the weak form and solved numerically by the Galerkin finite-element method. The details of this method are discussed in [47]. The Arbitrary Lagrangian–Eulerian (ALE) approach is followed to interpret the moving boundary originated by the flexible motion of the impermeable membrane. The quadratic elements with the Lagrangian shape function are used in the finite-element method. The governing equations for the continuity, momentum, solid structure and the heat transfer are fully coupled by employing the damped Newton method. Then, the Parallel Sparse Direct Solver (PSDS) is utilized to solve the obtained algebraic equations corresponding to the governing equations.

The convergence criterion is based on the condition that the residuals for the defined dependent variables are below 10⁻⁶. The 2D mesh that has been used in this work is a non-uniform unstructured mesh. Prior to starting the calculations, a grid-independence test has been performed to ensure that the results do not depend on the grid size. For this purpose, the average Nusselt number history on the right wall (the wall with the sinusoidal distribution of temperature) is evaluated for several different grids at Ra = 10⁷, γ = 0, A = 1, E _τ  = 10¹⁴ and F _v  = 1.64 × 10⁻². As shown in Fig. 1, the variations of the obtained results versus the dimensionless time are congruent for the grid size more than 37,029. Therefore, we have chosen to continue the computing with the grid size of 37,209 (Fig. 2).

Fig. 2

Grid independence test for Ra = 10⁷, A = 1, F _v  = 1.64 × 10⁻², E _τ  = 10¹⁴ and γ = 0

3.2 Numerical code verification

The accuracy of the numerical approach applied in the present study has been assessed by comparing our results with several test cases. The first test case is unsteady natural convection in a square cavity that has been divided into two equal parts using a vertical rigid membrane. Figure 3 depicts the comparison of the dimensionless temperature history obtained from the current study with the results reported by Xu et al. [30] at the specified point (0.0083, 0.375). The very good agreement between both of the graphs confirms the validity of our study. The second test case for validation is an inclined square cavity with adiabatic top and bottom walls and constant temperature vertical right wall. The temperature of the vertical left wall varies in a sinusoidal fashion with time. Also, it is assumed that the time-averaged temperature is the same on the both of vertical walls. The results of the present study and those obtained by Kalabin et al. [31] are in an excellent agreement as show in Fig. 4.

Fig. 3

Comparison of temperature variations versus dimensionless time between the present results and those reported by Xu et al. [30] for Ra = 9.2 × 10⁸, Pr = 6.63 and t _p  = 10⁻⁴

Fig. 4

Variations of the average Nusselt number versus dimensionless time for the present results and those reported by Kalabin et al. [31] for various values of γ = 0°, γ = 36°, γ = 89° at Ra/Pr = 2 × 10⁵

In another test case, the accuracy of the results is assessed by comparing the results of this study with those of Cheong et al. [10] who performed a numerical investigation on natural convection in an inclined rectangular cavity with angle γ and aspect ratio Ar (Ar = height/width). In their study, the bottom and top walls of the cavity are adiabatic; a sinusoidal temperature profile is imposed on the left wall and the right wall is at a low constant temperature T_c. As can be seen in Fig. 5, the results in terms of the average Nusselt number on the left wall are highly consistent with each other. The last validation compares the deformation of a flexible wall of a lid-driven cavity in the investigation examined by Küttler and Wall [32] and the present study. As illustrated in Fig. 6, the accuracy of the solution method is confirmed. In this verification, the maximum difference between the present result and that reported by Küttler and Wall [32] is about 1% of the length of the membrane and it occurs at x = 0.46.

Fig. 5

Comparison of the average Nusselt number obtained in the present study and those reported by Cheong et al. [10] for Ar = 1, Pr = 0.71, 10³ ≤ Ra ≤ 10⁶ and 0° ≤ γ ≤ 90°

Fig. 6

The deformation of the flexible bottom wall of the lid-driven cavity perused by Küttler and Wall [32] and the present study at t = 7.5 s

4 Results and discussion

This section presents the numerical results obtained by solving the problem under investigation. In this study, the effects of the following variable parameters are examined on the characteristics of the fluid flow and heat transfer: the Rayleigh number (10⁴ ≤ Ra ≤ 10⁷), the amplitude of sinusoidal function (0.0 ≤ A ≤ 1), the inclination angle of cavity (−π/3 ≤ γ ≤ π/3) and the body force parameter (F _v  = ± 1.64 × 10⁻²). Whereas, the Prandtl number Pr and the non-dimensional elasticity modulus E _τ are kept fixed at 6.2 and 10¹⁴, respectively.

Figures 7 and 8 depict the contours of the streamlines and isotherms for several time steps until reaching the steady-state condition. At the time step of τ = 10⁻⁸, due to the very low streamlines density and also, the distribution of the streamlines, it can be seen that the velocity of the fluid is zero. Entrance and ventilation of the fluid from the embedded eyelets creates secondary vortices in the upper corners of the cavity. The negative and positive signs of the stream function indicate that the fluid flow circulates in the clockwise and counter-clockwise directions, respectively. Therefore, it is clear that the secondary vortices created in the vicinity of the eyelets circulate in a direction opposite to the circulation of the primary circulations.

Fig. 7

Streamlines at various dimensionless times for A = 0.5, F _ν  = −1.64 × 10⁻², Ra = 10⁷, γ = π/3

Fig. 8

Isotherms for various dimensionless times for A = 0.5, F _ν  = −1.64 × 10⁻², Ra = 10⁷, γ = π/3

The fluid flow tends to enter the right sub-cavity as the flexible membrane moves to the left side. At the same time, some of the fluid exactly equals to the fluid incoming from the right sub-cavity comes out from the left sub-cavity. Finally, the entrance and ventilation of the fluid from the eyelets result in the increase and decrease of the volumes of the right and left sub-cavities, respectively. As is shown in Fig. 8, at τ = 10⁻⁸, the cavity is divided into two isothermal regions. With time evolution, the heat transfer starts from areas very close to the membrane and the right-hand wall. At these stages, heat transfer occurs by the thermal conduction predominantly. Then, the advection heat transfer dominates as the thermal mixing of the fluid increases.

Generally, it can be said that there are two types of forces applied to the membrane. As explained earlier, one force is produced by gravity and buoyancy which is called the static force or the body force F _v . The other force is applied to the membrane causing the fluid motion and pressure distribution and is called the dynamic force. The resultant of these two forces determines the final shape of the flexible membrane. Here, we have examined the effect of the body force parameter on the final shape of the membrane at low and high Rayleigh numbers 10⁴ and 10⁷, respectively. For this scrutiny, two values for the body force F _v (± 1.64 × 10⁻²) are considered whereas γ and A are kept fixed at −π/6 and 0.50, respectively.

According to the relationship listed for F _v in Eq. (17), it is obvious that F _v is greater than zero when the density of the fluid is higher than the density of the membrane. Similarly, an opposite state exists for F _v less than zero. The results shown in Fig. 9 demonstrate the effects of the body force applied to the flexible membrane F _v on the countors of the streamlines and the isotherms and most importantly, the final shape of the membrane. As it can be seen, in the case of F _v  = −1.64 × 10⁻² (indicated by I), the mentioned two forces contradict with each other. For this reason, the final shape of the membrane is defined based on the larger force. Because at the Rayleigh number of 10⁴, the flow circulation manifests low strength, the body force F _v is dominant against the dynamic force caused by the distribution of the fluid flow. Therefore, the membrane deformation is concave upward, or in accordance with Fig. 9, it is to the left direction. In contrast, when the Rayleigh number is 10⁷, the strength of the fluid flow is very high and the dynamic force due to the velocity and the pressure distributions overcome the body force F _v , the results presented in Fig. 9a-I, b-II confirm our attribution. Both the dynamic and body forces are aligned and have the same direction in the case of F _v  = 1.64 × 10⁻². In such a case, it is obvious that the membrane moves upward. Also, it can be seen that for F _v  = 1.64 × 10⁻² and at the Rayleigh number of 10⁷, the streamlines are very similar to those in F _v  = −1.64 × 10⁻². However, the streamlines associated with the Rayleigh number of 10⁴ are somewhat different for both positive and negative body force F _v values.

Fig. 9

The effects of body force (I): −1.64 × 10⁻² and (II): +1.64 × 10⁻² on the final shape of membrne, countors of streamlines (a) and isotherms (b)

Figure 10 presents the effect of varying the inclination angle of the cavity on the isotherms and streamlines for Ra = 10⁷, F _v  = 1.64 × 10⁻², A = 1. It should be noted that these contours are for steady state. It can be observed that the isotherms and streamlines at different inclination angles of the cavity are very dissimilar. As shown, the strength of the fluid flow |ψ| _max increases with the change of the cavity angle from –π/3 to π/3 in both partitions. The counter-clockwise vortex area formed in the right partition diminishes and moves upward with revolving the cavity from –π/3–0. Then, this vortex is shifted to the upper right-hand corner of the enclosure for γ = π/6. As mentioned earlier, the Rayleigh number vector Ra has two components, Ra sin γ and Ra cos γ along the x and y axes, respectively. Ra cos γ is the component that causes the fluid to rise along the hot wall (or the flexible membrane) and then to come down along the membrane (or the wall with sinusoidal temperature) in the left side sub-cavity (or right side sub-cavity). However, if γ > 0 (right lateral inclination), the component Ra sin γ, is from the hot left wall (or flexible membrane) to the membrane (or the wall with sinusoidal temperature), and as a result, it improves the natural convection (motion) of the fluid. On the contrary, in the case where the inclination is to left lateral (γ < 0), this component is from the wall with sinusoidal temperature (the flexible membrane) to membrane (the hot wall), and hence it acts against the typical motion of the fluid as a drag force. The contours of isotherms display that the non-uniformity in the membrane temperature is too high for γ = −π/3 and decreases with increasing values of the inclination angle of the cavity from –π/3 to π/3. The thermal mixing of the fluid gets better due to increasing the strength of the fluid flow as the inclination angle varies from −π/3 to π/3 and consequently, the isotherms are more distorted.

Fig. 10

Streamlines (left) and isotherms (right) for inclination angles γ of a −π/3, b −π/6, c 0.0, d π/6, and e π/3 for Ra = 10⁷, F _v  = 1.64 × 10⁻², A = 1

In order to make better imagination of the deformations of the flexible membrane of Fig. 10, we have collected all those together in Fig. 11. As shown, the deformation of the membrane is the same for inclination angles γ = −π/3 and γ = −π/6. The resultant of the body force F _v and the dyanmic force are consistent with each other causing such deformations. The membrane deviation from a straight-line shape decreases when the cavity is vertical. This can be attributed to the fact that the body force F _v does not have a signifcant effect on the membrane deflection. It is observed also that the concavity deformation of the membrane is changed when the cavity rotates in the counter-clockwise (γ = π/3 and γ = π/6) direction. This behavior demonstrates that the body force F _v is dominant against the dynamic force applied to the membrane.

Fig. 11

Effect of inclination angle of cavity on the final shape of the flexible membrane for Ra = 10⁷, F _v  = 1.64 × 10⁻², A = 1

Figure 12a, b depicts the variations of the average Nusselt number on the hot wall and the average temperature inside the whole cavity with the dimensionless time for five different inclination angles of the cavity between γ = −π/3 and γ = π/3 at Ra = 10⁷, F _v  = 1.64 × 10⁻², A = 1. As seen, at the initial stages of natural convection, the average Nusselt number at the hot wall is exactly zero for all inclination angles of the cavity. This is due to the fact that there is no convected fluid during these stages. The average Nusselt number overshoots for clockwise cavities (γ = −π/6 and –π/3) before reaching the steady-state condition. It can be seen also that the heat transfer rate rises as the inclination angle changes from –π/3 to π/6, and afterwards, it decreases when γ reaches π/3. The variations of the dimensionless temperature with time, shown in Fig. 12b, illustrates that the average temperature inside the whole cavity is exactly 0.5 for the initial stages. This result adapts with the initial conditions defined by us. For the clockwise tilted caviteis (γ = −π/3 and γ = −π/6), a slight drop can be seen at τ = 4 × 10⁻³, afterwards, the temperature rises over time until it reaches the constant values of 0.712 and 0.533 at γ = −π/3 and γ = −π/6, respectively. Also, the results indicate that for a non-inclined (γ = 0.0) and anti-clockwise (γ = π/3 and γ = π/6) cavites, the mean temperature decreases and this process continues until reaching the constant values.

Fig. 12

Variations of average Nusselt number on the hot wall (a) and the average temperature (b) versus the dimentionless time for different inclination angles of cavity at A = 1, F _v  = 1.64 × 10⁻², Ra = 10⁷

Table 1 includes the maximum stress (σ _m ) at all times and the stress at the steady state (σ _SS ) for various inlication angles of the cavity at A = 1, F _v  = −1.64 × 10⁻², Ra = 10⁷. σ _m is reduced with changing of the inclination angle from −π/3 until π/3. This procedure is also seen for σ _SS except in γ = π/3. As it is seen, σ _SS decreases with revolving the cavity from −π/3 to π/6, then, it increases at π/3.

Table 1 The effectof γ on σ _m and σ _SS

Figure 13 illustrates the influence of varying the amplitude of the sinusoidal function of temperature A on the contours of the streamlines and the isotherms, whereas Ra, γ and F _v are kept fixed at 10⁶, −π/6 and −1.64 × 10⁻², respectively. As is seen from Fig. 13, the vortex localized in the right sub-cavity breaks up into two vortices as A increases from 0 to 0.25. On the left sub-cavity, the pattern of the streamlines remains constant while the vortex weakens. Then, rising the amplitude from 0.25 to 0.5 makes a small counter-clockwise vortex that is created in the vicinity of the right wall and particularly in the middle of the right sub-cavity. Afterwards, the domain occupied by a counter-clockwise vortex in the right sub-cavity is developed with the increase of the amplitude so that three completely separate vortices can be observed clearly for A = 1. Also, it should be said that the strength of the vortex |ψ| _max formed in the left sub-cavity slightly decreases as the amplitude of the sinusoidal distribution of the temperature augments until A = 1. Whilst the trend is slightly different in the other sub-cavity. In the right sub-cavity, first, the strength of the vortex |ψ| _max is reduced until A = 0.75, then grows for A = 1.0.

Fig. 13

Streamlines (left) and isotherms (right) for a A = 0, b A = 0.25, c A = 0.5, d A = 0.75, and e A = 1 at Ra = 10⁶, F _v  = −1.64 × 10⁻², γ = −π/6

The results indicated in Fig. 14a state that the heat transfer rate is approximately equal for all amplitudes of the sinusoidal function of the temperature in the initial stages of natural convection defined with (I) range. It is evident that the Nusselt number, as representation of the heat transfer, reduces with the increase of the amplitude. This can be attributed to the fact that a local mometum exhange takes place close to the right wall due to the relatively high temperature difference. This weakens the fluid flow in the sub-cavity adjacent to the hot wall. The ifluence of the amplitude on the mean temperature versus the dimensionless time is depicted in Fig. 14b.

Fig. 14

Variations of the average Nusselt number on the hot wall (a) and the average temperature (b) versus the dimentionless time for different values of A at γ = −π/6, F _v  = −1.64 × 10⁻², Ra = 10⁶

The amplitude of the temperature slightly affects the deflection of the membrane as shown in Fig. 15. This figure shows that an increase of A can increase the membrane deviation.

Fig. 15

Effect of the amplitude of the sinusoidal distribution of the temperature on the final shape of the flexible membrane at γ = −π/6, F _v  = −1.64 × 10⁻², Ra = 10⁶

The parameters used in plotting Fig. 14 are adopted for demonstrating the effect of the amplitude of the sinusoidal temperature on σ _m and σ _SS as presented in Table 2.

Table 2 The effect of A on σ _m and σ _SS

The effects of the Rayleigh number on the contours of the streamlines and isotherms are presented in Fig. 16 for A = 1, F _v  = −1.64 × 10⁻², γ = π/3. At the low Rayleigh number of 10⁴, the streamlines are on a regular basis and smooth so that the streamlines close to the center of the vortex formed in the right sub-cavity are almost a circle. As the Rayleigh number increases, both primary vortices are stretched until the vortex in the left sub-cavity breaks up into two vortices at 10⁶. It is also clear that the centers of the primary vortices shift towards the walls as the Rayleigh number increases. However, the strengths of the primary vortices and the secondary vortex formed in the upper right corner of the cavity increase with the increase of the Rayleigh number. The reason is that the buoyancy force acting on the flow field increases as Ra increases. The form of the isotherms depicted in Fig. 16 indicates how predominant mechanisms of heat transfer change with the increase of the Rayleigh number. At the low Rayleigh number of 10⁴, the vertical isotherms state that the predominant mechanism of heat transfer is conduction. Increasing the Rayleigh number makes the impact of conduction heat transfer dwindles compared to advection heat transfer. This is due to the fact that the thermal mixing of the fluid increases with the Rayleigh number.

Fig. 16

Streamlines (left) and isotherms (right) for a Ra = 10⁴, b Ra = 10⁵, c Ra = 10⁶, and d Ra = 10⁷ at A = 1, F _v  = −1.64 × 10⁻², γ = π/3

The influence of Ra on the final shape of the membrane is depicted in Fig. 17. As a whole, the membrane deviation increases noticeably with the increase of Ra. In fact, the fluid–structure interaction increases with Ra.

Fig. 17

Effect of Rayleigh number on the final shape of the flexible membrane at A = 1, F _v  = −1.64 × 10⁻², γ = π/3

Figure 18a, b demonstrates the influence of the Rayleigh number on the mean Nusselt number and the mean temperature inside the whole cavity according to the dimensionless time. There is a certain trend for both the heat transfer rate and the mean temperature with increasing values of Ra. The increase of Ra causes a rapid increase in Nu _av and a rapid decrease in T.

Fig. 18

Variations of the average Nusselt number on the hot wall (a) and the average temperature (b) versus the dimentionless time for the different Rayleigh numbers at A = 1, F _v  = −1.64 × 10⁻², γ = π/3

The maximum transient and steady stresses in the flexible membrane for the different Rayleigh numbers at A = 1, F _v  = −1.64 × 10⁻², γ = π/3 are presented in Table 3. When the Rayleigh number increases, the stress in the flexible number becomes forcible. This is due to the fact that increasing the Rayleigh number increases the strength of the fluid flow and accordingly, the interaction between the fluid and the flexible membrane augments. A comparison between the maximum stress and tension at the steady-state conditions shows that the maximum stress occurs at the steady state.

Table 3 The effect of Ra on σ _m and σ _SS

5 Conclusions

Unsteady natural convection inside an inclined square cavity partitioned by a flexible impermeable membrane is studied numerically using the Arbitrary Lagrangian–Eulerian (ALE) approach. The cavity bottom and top walls are kept adiabatic. The left side wall is kept isothermal at a high temperature, while the right wall is cooled in a sinusoidal fashion. The results have led to the following concluding remarks:

• 1. With time evolution, there is a continuous deformation of the flexible membrane before it reaches its final configuration at steady state.

• 2. In the case of a low Rayleigh number, the shape of the memberahne is under a significant influence of the body force F_v. However, as the Rayleigh number increases, the interaction between the fluid and the membrane gets important. Hence, in the case of high values of the Rayleigh number, the body force is not significant compared to the fluid and membrabne interaction forces. Thus, the shape of the membrane is mainly a function of the flow patterns and interaction between the fluid and the membrane.

• 3. The contours of the isotherms display that the non-uniformity in the membrane temperature is too high for γ = −π/3 and decreases with increasing values of the inclination angle of the cavity from −π/3 to π/3.

• 4. The natural convection is appreciably affected by the tilting angle of the cavity, and as such, the concave or convex fashion of the membrane is appreciably affected by the cavity tilting angle.

• 5. The effect of the sinusoidal distribution amplitude of the cold temperature on the membrane deformation is found to be small in the simulations. Whereas, the Rayleigh number manifests noticeable deformation of the membrane.

• 6. The maximum convective heat transfer is attained with the counter-clockwise cavity inclination i.e. at γ > 0, and particularly at γ = π/6°. On the other hand, the convective heat transfer is a decreasing function of the sinusoidal distribution amplitude of the cold temperature.