Lattice Boltzmann method with heat flux boundary condition applied to mixed convection in inclined lid driven cavity

Abstract

Mixed convection in a inclined cavity has not been investigated by LBM in case of an imposed non zero heat flux. This type of boundary condition, representing very usual situations in physical world, is not simple to model in lattice Boltzmann schemes. In effect, the only boundary condition able to simulate an imposed temperature and an imposed heat flux at a boundary has been presented by D’Orazio et al. in previous works, where the boundary was at rest. In this work, laminar mixed convective heat transfer in two-dimensional rectangular inclined driven cavity is studied numerically by means of a double population thermal Lattice Boltzmann method. The counter-slip internal energy density boundary condition, able to simulate an imposed heat flux at the wall, is applied. Through the top moving lid the heat flux enters the cavity and it leaves the system through the bottom wall; side walls are adiabatic. Results are analyzed over a range of the Richardson numbers and tilting angles of the enclosure, encompassing the dominating forced convection, mixed convection, and dominating natural convection flow regimes. The results show that, as expected, heat transfer rate increases as increases the inclination angle, but this effect is significant for higher Richardson numbers, when buoyancy forces dominate the problem; for horizontal cavity, average Nusselt number decreases with the increase of Richardson number because of the stratified field configuration. This study shows that the counter-slip internal energy density boundary condition can be effectively used to simulate heat transfer phenomena also in case of moving walls and it makes the Lattice Boltzmann Method able to simulate a wide class of cooling process where a given thermal power must be removed.

1 Introduction

The lattice Boltzmann equation (LBE) is a minimal form of the Boltzmann kinetic equation, which is the evolution equation for a continuous one-body distribution function, wherein all details of molecular motion are removed except those that are strictly needed to represent the hydrodynamic behaviour at the macroscopic scale; it has gained much attention for its ability to simulate fluid flows, and for its potential advantages over conventional numerical solution of the Navier–Stokes equations. The kinetic nature of Lattice Boltzmann Method (LBM) introduces key advantages, including easy implementation of boundary conditions and fully parallel algorithms. In addition, the convection operator is linear, no Poisson equation for the pressure must be resolved and the translation of the microscopic distribution function into the macroscopic quantities consists of simple arithmetic calculations [1–4]. LBM have met with significant success for the numerical simulation of a large variety of fluid flows, including real-world engineering applications and physical phenomena of various complexities as multiphase flows, complex geometries and interfacial flows [5–12]. The application to fluid flow coupled with non negligible heat transfer turned out to be much more difficult. The LBE thermal models fall into three categories: the multi-speed approach, the passive scalar approach and the doubled populations approach. In this latter, successful, strategy [13] thermal energy density and heat flux are expressed as kinetic moments of a thermal distribution function, so that no kinetic moment beyond the first order is ever required, thus providing numerical stability, also in case of significant temperature gradient [14]; in addition, with respect to the previous approaches, viscous heat dissipation and compression work done by the pressure were naturally incorporated and the boundary conditions are easily implemented because both populations live in the same lattice, where additional speeds are not necessary. The doubled population model has been widely applied to several and complex flow configuration (see for example [15, 16]). Dixit and Babu [17] simulated high Ra natural convections in a square cavity using LBM. Barrios et al. [18] used LBM in two dimensions to solve natural convective flow in an open cavity in which the lower part of a vertical wall was conductive and the upper part and all other walls were adiabatic; they validated the results obtained from LBM with related experimental results. Nazari and Ramzani [19] studied natural convective heat transfer in a cavity in thr presence of internal straight obstacle by means of double population LBM. Kao et al. [20] investigated 2D natural convection flows with nonlinear phenomena within enclosed rectangular cavities, at the reference Rayleigh numbers of Ra ≤ 2 × 10⁴ at the macroscopic scale (Kn = 10⁻⁴) and the mesoscopic scale (Kn = 10⁻²). Natural convection heat transfer in cavities has already been considered extensively, because of its wide applications in manufacturing of solar collectors and heat exchangers, or designing of cooling systems of electronic devices, or heat transfer in buildings. Most investigations have already been dedicated to horizontal cavities, in which gravitational acceleration is parallel to their sidewalls, and the reader is referred to the large number of papers available in the open literature, which testifies the great interest of this topic. However, in many cases it is necessary to use inclined cavities, in which, according to inclination angle of the cavities, the shear stress applied by lid on the flow increases or decreases the buoyancy force. Also this flow configuration has been widely studied, for different aspect ratio and thermal boundary conditions (with regard to lattice Boltzmann method, see for example recent papers [21] ). Numerous investigations have been conducted in the past on lid-driven cavity flow and heat transfer considering various combinations of the imposed temperature gradients and cavity configurations. M.A.R. Sharif [22] studied numerically two-dimensional shallow rectangular driven cavities of aspect ratio 10 for Rayleigh numbers ranging from 10⁵ to 10⁷, keeping the Reynolds number fixed at 408.21, and Prandtl number taken as 6 representing water; the effects of inclination of the cavity on the flow and thermal fields are investigated for inclination angles ranging from 0° to 30°. Basak et al. [23] performed finite element simulations to investigate the influence of linearly heated side wall(s) or cooled right wall on mixed convection lid-driven flows in a square cavity; numerical solutions were obtained for Gr = 10³ ÷ 10⁵, Pr = 0.015 ÷ 10 and Re = 1 ÷ 10² with uniform heating of the bottom wall where the two vertical walls are linearly heated or the right wall is kept at cold temperature and the top wall is well insulated with a horizontal velocity U. Sivasankaran et al. [24] performed a numerical study, with finite volume method, on mixed convection in a lid-driven cavity with the vertical sidewalls maintained with sinusoidal temperature distribution and top and bottom wall adiabatic; results were analyzed over a range of the Richardson numbers, amplitude ratios and phase deviations. T.S. Cheng [25] investigated the flow and heat transfer in a 2-D square cavity where the flow is induced by a shear force resulting from the motion of the upper lid combined with buoyancy force due to bottom heating. The numerical simulations covered a wide range of Reynolds (10 ≤ Re ≤ 2,200), Grashof (100 ≤ Gr ≤ 4.84 × 10⁶), Prandtl (0.01 ≤ Pr ≤ 50), and Richardson (0.01 ≤ Ri ≤ 100) numbers. The top and bottom walls were maintained isothermally at temperatures T _c and T _h , respectively, with $T_{h} > T_{c}$. The vertical side walls were thermally insulated. Mixed convection in an inclined cavity has not been investigated by LBM, to the authors’ knowledge, except for a recent previous work by Karimipour et al. [26], in which laminar mixed convection in a two-dimensional rectangular inclined cavity with moving top lid is investigated numerically for Richardson number ranging from 0.1 to 10 and inclination angle ranging from 0° to 90° in case of imposed temperature at top and bottom walls. Mixed convection in an inclined cavity has not been investigated by LBM in case of imposed non zero heat flux. This type of boundary condition, representing very usual situations in physical world, is not simple to model in lattice Boltzmann schemes. In effect, the only boundary condition able to simulate imposed temperature and imposed heat flux at a boundary has been presented by D’Orazio et al. in [27] where the boundary were at rest. In this work, laminar mixed convection in a two-dimensional rectangular inclined cavity with moving top lid is investigated numerically. Top lid motion results in fluid motion inside. Inclination of the cavity causes horizontal and vertical components of velocity to be affected by buoyancy force, since the heat flux enters the cavity through the top moving lid and it leaves the system through the bottom wall, side walls being adiabatic. To include this effect, collision term of Boltzmann equation is modified and the counter-slip internal energy density boundary condition by [14, 27, 28], able to simulate an imposed heat flux at the wall, is applied. The effects of the variations of Richardson number and inclination angle on the thermal and flow behaviour of the fluid inside the cavity are investigated. The results are presented as velocity and temperature profiles, stream function contours and isotherms. Simulations are performed for Pr = 0.7 and Re = 200 and for three value of the Richardson number Ri = 0.1, Ri = 1, Ri = 10; the effects of the inclination angle γ = 0°, 30°, 60°, 90° on fluid flow and heat transfer are studied in case of positive and negative moving lid velocity.

2 Thermal and hydrodynamic Lattice Boltzmann Method

The lattice Boltzmann equation with a single relaxation time from the BGK model [29, 30] can be expressed as

$$ \widetilde{f}_{i } \left( {\vec{x} + \vec{c}_{i} dt, t + dt} \right) - \widetilde{f}_{i } \left( {\vec{x},t} \right) = - \frac{dt}{{\tau_{f} + 0.5dt}}\left[ {\widetilde{f}_{i } - \widetilde{f}_{i}^{e} } \right] $$

(1)

$$ \widetilde{g}_{i } \left( {\vec{x} + \vec{c}_{i} dt, t + dt} \right) - \widetilde{g}_{i } \left( {\vec{x},t} \right) = - \frac{dt}{{\tau_{g} + 0.5dt}}\left[ {\widetilde{g}_{i } - \widetilde{g}_{i}^{e} } \right] - \frac{{\tau_{g} dt}}{{\tau_{g} + 0.5dt}}f_{i} Z_{i} $$

(2)

where the populations $\widetilde{f}_{i }$ carry mass and momentum and the populations $\widetilde{g}_{i }$ carry internal energy and heat flux.

The discrete distribution functions $\widetilde{\text{f}}_{\text{i}}$ and $\widetilde{\text{g}}_{\text{i}}$ are introduced as in [13]:

$$ \widetilde{f}_{i} = f_{i} + \frac{dt}{{2\tau_{f} }}\left( {f_{i} - f_{i}^{e} } \right) $$

(3)

$$ \widetilde{g}_{i} = g_{i} + \frac{dt}{{2\tau_{g} }}\left( {g_{i} - g_{i}^{e} } \right) + \frac{dt}{2}f_{i} Z_{i} $$

(4)

$$ Z_{i} = \left( {\vec{c}_{i} - \vec{u}} \right)D_{i} \vec{u} , D_{i} = \partial_{t} + \vec{c}_{i} \cdot \nabla $$

(5)

where f_i and g_i are the discrete populations which evolve when a standard first order integration strategy is adopted, the term ${\text{Z}}_{\text{i}} = \left( {{\vec{\text{c}}}_{\text{i}} - {\vec{\text{u}}}} \right){\text{D}}_{\text{i}} {\vec{\text{u}}}$ represents the effects of viscous heating (${\text{D}}_{\text{i}} = \partial_{\text{t}} + {\vec{\text{c}}}_{\text{i}} \cdot \nabla$ is the material derivative along direction c_i), τ _f and τ _g are relaxations times and ${\text{f}}_{\text{i}}^{\text{e}}$ and ${\text{g}}_{\text{i}}^{\text{e}}$ are the equilibrium distribution functions. Throughout of this work, two-dimensional square lattice with the nine speeds, as shown in Fig. 1, is used.

Fig. 1

Nine-speed square lattice

The discrete particle lattice speeds are:

$$ c_{i} = \left( {{\text{cos}}\frac{i - 1}{2}\pi,\; {\text{sin}}\frac{i - 1}{2}\pi } \right)c,\quad i = 1, 2, 3, 4 $$

(6)

$$ c_{i} = \sqrt 2 \left[ {{\text{cos}}\left( {\frac{i - 5}{2}\pi + \frac{\pi }{4}} \right),\; {\text{sin}}\left( {\frac{i - 5}{2}\pi + \frac{\pi }{4}} \right)} \right]c,\quad i = 5,6, 7, 8 $$

(6′)

$$ c_{0} = \left( {0, 0} \right) $$

(6″)

where c ² = 3RT and T is the temperature. The equilibrium density distributions are chosen as follows:

$$ f_{i}^{e} = \omega_{i} \rho \left[ {1 + \frac{{3\vec{c}_{i} \cdot \vec{u}}}{{c^{2} }} + \frac{{9\left( {\vec{c}_{i} \cdot \vec{u}} \right)^{2} }}{{2c^{4} }} - \frac{{3\left( {u^{2} + v^{2} } \right)}}{{2c^{2} }}} \right] $$

(7)

$$ g_{0}^{e} = - \omega_{0} \left[ {\frac{{3\rho e\left( {u^{2} + v^{2} } \right)}}{{2c^{2} }}} \right] $$

(8)

$$ g_{1, 2, 3, 4}^{e} = \omega_{1} \rho e\left[ {1.5 + 1.5\frac{{\vec{c}_{i} \cdot \vec{u}}}{{c^{2} }} + 4.5\frac{{\left( {\vec{c}_{i} \cdot \vec{u}} \right)^{2} }}{{c^{4} }} - 1.5\frac{{\left( {u^{2} + v^{2} } \right)}}{{c^{2} }}} \right] $$

(9)

$$ g_{5, 6, 7, 8}^{e} = \omega_{2} \rho e\left[ {3 + 6\frac{{\vec{c}_{i} \cdot \vec{u}}}{{c^{2} }} + 4.5\frac{{\left( {\vec{c}_{i} \cdot \vec{u}} \right)^{2} }}{{c^{4} }} - 1.5\frac{{\left( {u^{2} + v^{2} } \right)}}{{c^{2} }}} \right] $$

(10)

where $\vec{u} = \left( {u,v} \right)$ and ρe = ρRT (in two-dimensional geometry). The weights of the different populations are ω ₀ = 4/9, ω _i  = 1/9 for i = 1, 2, 3, 4 and ω _i  = 1/36 for i = 5, 6, 7, 8. The terms enclosed by the square bracket, multiplied by the corresponding weights ω _i , will be called corresponding form for equilibrium.

Finally, using ${\text{f}}_{\text{i}}^{\text{e}}$ and ${\text{g}}_{\text{i}}^{\text{e}}$, hydrodynamic and thermal variables are calculated as follows:

$$ \rho = \sum\limits_{i} {\widetilde{f}_{i} } \rho e = \sum\limits_{i} {\widetilde{g}_{i} } - \frac{dt}{2}\mathop \sum \limits_{i} f_{i} Z_{i} $$

(11)

$$ \rho \vec{u} = \sum\limits_{i} {\vec{c}_{i} \widetilde{f}_{i} } \vec{q} = \left[ {\mathop \sum \limits_{i} \vec{c}_{i} \widetilde{g}_{i} - \rho e\vec{u} - \frac{dt}{2}\mathop \sum \limits_{i} \vec{c}_{i} f_{i} Z_{i} } \right]\frac{{\tau_{g} }}{{\tau_{g} + 0.5dt}} $$

(12)

The kinematic viscosity and the thermal diffusivity in the two-dimensional geometry are given by [13]:

$$ \nu = \tau_{f} R\overline{T} , \chi = 2\tau_{g} R\overline{T} $$

(13)

In this problem shear stress applied by moving lid on the fluid layers results in fluid motion, thus creating suitable temperature gradient that enhances buoyancy forces. Therefore, mixed convection is produced in the fluid confined in the cavity. With the Boussinesq approximation, all the fluid properties are considered as constant, except in the body force term in the Navier–Stokes equations, where the fluid density is assumed $\uprho = \overline{\uprho} \left[ {1 -\upbeta\left( {{\text{T}} - \overline{\text{T}} } \right)} \right]$, in which β is volumetric expansion coefficient, $\overline{\uprho}$ and $\overline{\text{T}}$ are the average fluid density and temperature. In order to simulate the mixed convection of nearly incompressible flows, buoyancy force per unit mass is defined as

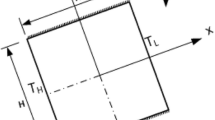
$\text{G} = {\beta g}\left( {{\text{T}} - \overline{\text{T}} } \right)$ and this is used to drive the flow. By considering inclination angle, coordinate axis and gravity acceleration direction, as shown in Fig. 2, all of the aforementioned relations are maintained and used except those that are modified below:

Fig. 2

Geometry and coordinates axis in the inclined cavity

$$ \begin{aligned} \widetilde{f}_{i } \left( {\vec{x} + \vec{c}_{i} dt, t + dt} \right) - \widetilde{f}_{i } \left( {\vec{x},t} \right) = &- \frac{dt}{{\tau_{f} + 0.5dt}}\left[ {\widetilde{f}_{i } {-}f_{i}^{e} } \right] \\ &+ \left[ {\frac{{dt\tau_{f} }}{{\tau_{f} + 0.5dt}}\frac{{3G\left( {c_{ix} - u} \right)}}{{c^{2} }}f_{i}^{e} } \right]{\text{sin}}\gamma + \left[ {\frac{{dt\tau_{f} }}{{\tau_{f} + 0.5dt}}\frac{{3G\left( {c_{iy} - v} \right)}}{{c^{2} }}f_{i}^{e} } \right] {\text{cos}}\gamma \end{aligned} $$

(14)

According to Eq. (3), we have:

$$ f_{i} = \frac{{\tau_{f} \widetilde{f}_{i } + 0.5dtf_{i}^{e} }}{{\tau_{f} + 0.5dt}} + \left[ {\frac{{0.5dt\tau_{f} }}{{\tau_{f} + 0.5dt}}\frac{{3G\left( {c_{ix} - u} \right)f_{i}^{e} }}{{c^{2} }}} \right]{\text{sin}}\gamma + \left[ {\frac{{0.5dt\tau_{f} }}{{\tau_{f} + 0.5dt}}\frac{{3G\left( {c_{iy} - v} \right)f_{i}^{e} }}{{c^{2} }}} \right] {\text{cos}}\gamma $$

(15)

In this case hydrodynamic macroscopic variables are calculated as follows:

$$ \rho = \sum\limits_{i} {\widetilde{f}_{i } } , u = \frac{1}{\rho }\mathop \sum \limits_{i} \widetilde{f}_{i } c_{ix} + \frac{dt}{2}G{\text{sin}}\gamma , v = \frac{1}{\rho }\mathop \sum \limits_{i} \widetilde{f}_{i } c_{iy} + \frac{dt}{2}G{\text{cos}}\gamma $$

(16)

where ${\vec{\text{c}}}_{\text{i}} = \left( {{\text{c}}_{\text{ix}} , {\text{c}}_{\text{iy}} } \right)$ denotes discrete particle speeds.

3 Boundary conditions

With regard to hydrodynamic boundary condition, no slip boundary condition is applied; it is obtained by means of the non-equilibrium bounce back rule [31] as applied to the population perpendicular to the boundary. As an example, for the west wall we impose $\widetilde{f}_{1 } {-}f_{1}^{e} = \widetilde{f}_{3 } {-}f_{3}^{e}$. With regard to thermal boundary conditions, the top cavity lid and bottom wall are heated and cooled respectively by an uniform and constant heat flux entering and leaving respectively, and the sidewalls are insulated. These boundary conditions are obtained by means a thermal counter-slip approach as proposed by [14, 27, 28], in which the incoming unknown thermal populations are assumed to be equilibrium distribution functions with a counterslip thermal energy density e′, which is determined so that suitable constraints are verified. For the top wall of the cavity, named as “north wall”, in which entering heat flux is constant and equal to q_N, the unknown $\widetilde{\text{g}}_{4 } ,\widetilde{\text{g}}_{7 }$, and $\widetilde{\text{g}}_{8 }$ are chosen as follows.

$$ \widetilde{g}_{i } = \rho \left( {e_{N} + e^{'} } \right) \times \left[ {corresponding form for equilibrium} \right] \quad i = 4, 7, 8 $$

(17)

By definition:

$$ \sum\limits_{i} { c_{iy} \widetilde{g}_{i } } = \frac{dt}{2}\mathop \sum \limits_{i} c_{iy} f_{i} Z_{i} + \rho e_{N} V_{N} + \frac{{\tau_{g} + 0.5dt}}{{\tau_{g} }}q_{y} $$

(18)

which yields to:

$$ \rho e_{N} + \rho e^{\prime} = \left[ {K - \frac{dt}{2}\sum\limits_{i} {\frac{{c_{iy} }}{c}f_{i} Z_{i} } - \rho e_{N} \frac{{V_{N} }}{c} - \frac{{\tau_{g} + 0.5dt}}{{\tau_{g} }}\frac{{q_{y} }}{c}} \right]\Bigg/\left[ {\frac{1}{3} - \frac{1}{2}\frac{{V_{N} }}{c} + \frac{1}{2}\frac{{V_{N}^{2} }}{{c^{2} }}} \right] $$

(19)

where V _N is the component normal to the wall of flow velocity at the wall, K is the sum of the three known populations ($\widetilde{g}_{2 } ,\widetilde{g}_{5 }$ and $\widetilde{g}_{6 }$) e _N denotes the current value of thermal energy density at the north wall. At the insulated walls, the constraint on the heat flux is obtained by imposing q _x  = 0 in Eq. (24), for example for the west wall, so that we have [27]

$$ \sum\limits_{i} { c_{ix} \widetilde{g}_{i } } = 0.5 dt\sum\limits_{i} { c_{ix} f_{i} Z_{i} + \rho e_{W} U_{W} } $$

(20)

where e _W denotes the thermal energy density current value (coming from the run) at the West wall. The unknown populations $\widetilde{\text{g}}_{1 } ,\widetilde{\text{g}}_{5}$ and $\widetilde{\text{g}}_{8 }$ are chosen as

$$ \widetilde{\text{g}}_{i } = \rho \left( {e_{W} + e^{'} } \right) \times \left[ {corresponding form for equilibrium} \right] i = 1, 5, 8 $$

(21)

and become

$$ \begin{aligned} \widetilde{\text{g}}_{i } & = \left[ {K + \frac{dt}{2}\mathop \sum \limits_{i} \frac{{c_{i} }}{c}f_{i} Z_{i} + \rho e_{W} \frac{{U_{W} }}{c}} \right]\Bigg/\left[ {\frac{1}{3} + 0.5\frac{{U_{W} }}{c} + 0.5\frac{{U_{W}^{2} }}{{c^{2} }}} \right] \\ & \quad \times \left[ {corresponding form for equilibrium} \right] \quad i = 1, 5, 8 \\ \end{aligned} $$

(22)

where $U_{W}$ is the component normal to the wall of the flow velocity at the wall and K is the sum of the known populations ($\widetilde{\text{g}}_{3 } ,\widetilde{\text{g}}_{6}$ and $\widetilde{\text{g}}_{7 }$ in this case). The corners nodes are treated similarly and the counter-slip procedure can be applied to the five unknown incoming populations at the corner; more details can be found in [27].

The same relations are used for the bottom wall (named as “south wall”), in which leaving heat flux is constant and equal to q _S and the unknown populations are $\widetilde{\text{g}}_{2 } ,\;\widetilde{\text{g}}_{5}$ and $\widetilde{\text{g}}_{6 }$.

With regard to the initial conditions, the velocities of all nodes inside the cavity are taken as zero initially. The initial density is set to a value of 2.7 [32]. The initial equilibrium distribution functions are evaluated correspondingly. The initial distribution functions are taken as the corresponding equilibrium values [33].

4 Problem statement

Laminar mixed convection of a fluid inside a rectangular cavity with moving top lid and aspect ratio AR = L/H = 3, in which L and H are shown in Fig. 2, is studied numerically using Lattice Boltzmann Method previously described. The bottom wall is cooled and the top lid is heated, and side walls are assumed insulated. Top lid moves with constant velocity ${\text{U}}_{0}$. Characteristic dimensionless number in the analysis of mixed convection problems is Richardson number defined as ${\text{Ri}} = {\text{Ra}}/{\text{PrRe}}^{2}$. As stated before, lattice Boltzmann method is used for near-incompressible flows and therefore Mach number is assumed as ${\text{Ma}} \ll 1$. More specifically, the characteristic velocity of the flow for both natural regime, ${\text{U}}^{\ast} = \sqrt {\beta {\text{gH}}\Delta {\text{T}}}$, and forced regime ${\text{U}}^{*} = {\nu Re}/{\text{H}}$ must be small compared with the fluid speed of sound; in present study the velocity ${\text{U}}_{0}$ was selected as ${\text{U}}_{0} = 0.1$. The Prandtl and Reynolds numbers are assumed as ${ \Pr } = 0.7$ and ${\text{Re}} = 200$ respectively and the effects of the variations of the Richardson number ${\text{Ri}}$ and angle γ on the flow and heat transfer are studied. Inclination angle varies from zero degree, horizontal cavity, to 90º, vertical cavity. To avoid ambiguity, the cavity’s walls are referred to according to the coordinates shown in Fig. 2.

In the following the macroscopic variables of fluid flow are made dimensionless as follows, respectively for dimensionless coordinates, dimensionless velocity components, dimensionless temperature, dimensionless time

$$ Y = \frac{y}{H } ,\quad X = \frac{x}{H },\quad U = \frac{u}{{U_{0} }},\quad V = \frac{v}{{U_{0} }},\quad \Theta = \frac{{T - T_{c} }}{{T_{h} - T_{c} }},\quad \tau = \frac{{tU_{0} }}{H } $$

(23)

with ${\text{T}}^{\ast\ast} =\upchi \upnu {\text{Ra}}^{4/5} \big/\upbeta{\text{gH}}^{3}$. Therefore, local and average Nusselt numbers along the lid and bottom wall are calculated using following relations

$$ Nu_{X} = \frac{qH}{{k\Delta T}} = - \left( {\frac{{\partial\Theta }}{\partial Y}} \right)_{wall} , \quad Nu_{m} = \frac{1}{AR} \mathop \smallint \limits_{0}^{AR} Nu_{X} dX $$

(24)

The top lid is the hot moving wall at Y = 1, the bottom wall is the cold wall at Y = 0 and two insulated side walls are at X = 0 and X = 3.

5 Numerical validation

In order to obtain grid independent solution, a grid refinement study is performed for a horizontal cavity (γ = 0). Grid independence of the results has been established in term of average Nusselt number on the lid and dimensionless values of x-velocity U, y-velocity V, and temperature $\Theta$ at X = 1.5 and Y = 0.5 (cavity center) for three different grid size, namely 300 × 100, 450 × 150 and 600 × 200 lattice nodes. In Table 1 results are reported as obtained for Ri = 0.1, Re = 200 and Pr = 0.7; due to small difference between the results of the last two grid sizes, the 450 × 150 grid is chosen as a suitable one in this work.

Table 1 Grid dependence study for mixed convection for Ri = 0.1, Re = 200, Pr = 0.7 at X = 1.5 and Y = 0.5

To validate the computer code, the comparison with the analytical solution given by Kimura and Bejan [34] is examined. Results for the Rayleigh number equal to 10⁶ and the Prandtl number equal to 2.0 are considered. Table 2 reports the value of the average Nusselt number Nu _m (for ${\text{Ra}} = 10^{5}$ and ${\text{Ra}} = 10^{6}$) obtained in present work as compared with theoretical value by [35] and the value obtained by D’Orazio et al. [27]. Results of Table 2 show good agreement with those of Bejan et al. [34] and of D’Orazio et al. [27], with a maximum error equal to 18.6 %.

Table 2 Natural convection in a square cavity with uniform heat flux from vertical walls: average Nusselt number at the hot-wall for different Rayleigh numbers and ${ \Pr } = 2.0$; comparison of laminar solution with previous work [27] and theoretical solution [34]

6 Results and discussion

In order to show the effect of inclination angles on the flow field and heat transfer, in Figs. 3, 4 and 5 streamlines and isotherms are reported at different inclination angles γ = 0, 30, 60 and 90^∘ for the cases Ri = 0.1, 1 and 10 respectively. The motion of the cavity lid, with positive lid velocity, causes the fluid motion in the cavity and produces a strong clockwise rotational cell in it. This motion transfers hot fluid to the lower parts and enhances favourable pressure gradient along the vertical direction, leading to the generating buoyancy motions and transferring hot fluid to the upper parts. Therefore, the combination of free and forced convection, called “mixed convection”, is made. In Fig. 3, the Richardson number is Ri = 0.1, with forced convection dominant with respect to natural convection, and it implies that by increasing γ, the rotational power of the cell in the center of the cavity increases slightly and it does not affect significantly the other moving and thermal behaviour of the fluid.

Fig. 3

Streamlines and isotherms for Ri = 0.1, at γ = 0°, 30°, 60° and 90°, U ₀ > 0

Fig. 4

Streamlines and isotherms for Ri = 1, at γ = 0°, 30°, 60° and 90°, U ₀ > 0

Fig. 5

Streamlines and isotherms for Ri = 10, at γ = 0°, 30°, 60° and 90°, U ₀ > 0

When buoyancy forces dominate the problem, as for Ri = 10 reported in Fig. 5, inclination angle has significant effect on the flow field and heat transfer. For γ = 0, a strong cell in the upper half and a weak cell in the lower half of the cavity, are generated due to the forcing of moving wall. In addition, for γ = 0, isotherms in the lower half of the cavity are straight lines and perpendicular to the side walls, indicating that conduction heat transfer is dominant in this region and that, without the forced convection contribution, no motion occurs, due the stratified fluid. As the inclination angle increases, the two cells merge, so that for γ = 90 a large rotational cell covers the whole space of the cavity, with the central part practically motionless.

Figures 6 and 7 show the profile of longitudinal component of dimensionless velocity, U, and temperature, $\Theta$, along the transverse centerline of the cavity respectively, at different inclination angles for Ri = 0.1. Figure 8 shows the profile of transverse component of dimensionless velocity, V, along the longitudinal centerline of the cavity, for the same inclination angles and Richardson number. It is seen that U is zero at Y = 0 and it decreases as Y increases, so that it is negative at 0 < Y < 0.75. For higher values of Y, U increases and approaches to the velocity of moving lid at Y = 1. The increase of inclination angle does not have a significant effect on U and V. The V profile shows the strong downward flow in the right part of the cavity. Then, from middle and left side of the cavity fluid flow moves upward with lower velocity. The cold fluid with high variations of temperature can be seen in the lower part of the cavity space.

Higher value of Richardson number leads to higher sensibility of U, V and $\Theta$ to the inclination angle.

Fig. 6

Normalized longitudinal velocity U at x/H = 1.5 (transverse centerline) for Ri = 0.1 and U ₀ > 0

Fig. 7

Normalized temperature profile $\Theta$ at x/H = 1.5 (transverse centerline) for for Ri = 0.1 and U ₀ > 0

Fig. 8

Normalized transverse velocity V at y/H = 0.5 (longitudinal centerline) for Ri = 0.1 and U ₀ > 0

Figures 9, 10, 11, 12, 13 and 14 show profiles of U, V and $\Theta$ for Ri = 1 and Ri = 10 respectively. Increasing the inclination angle from 30º to higher values, causes the increase of the absolute value of U and V. The most temperature difference between the top and the bottom walls can be seen in the temperature profile of this figure for horizontal cavity.

Fig. 9

Normalized longitudinal velocity U at x/H = 1.5 (transverse centerline) for Ri = 1 and U ₀ > 0

Fig. 10

Normalized transverse velocity V at y/H = 0.5 (longitudinal centerline) for Ri = 1 and U ₀ > 0

Fig. 11

Normalized temperature profile $\Theta$ at x/H = 1.5 (transverse centerline) for for Ri = 1 and U ₀ > 0

Fig. 12

Normalized longitudinal velocity U at x/H = 1.5 (transverse centerline) for Ri = 10 and U ₀ > 0

Fig. 13

Normalized transverse velocity V at y/H = 0.5 (longitudinal centerline) for Ri = 10 and U ₀ > 0

Fig. 14

Normalized temperature profile $\Theta$ at x/H = 1.5 (transverse centerline) for for Ri = 10 and U ₀ > 0

All simulations have been performed also in case of negative top lid velocity, that is directed towards x < 0. In Figs. 15, 16 and 17, streamlines and isotherms are shown for Richardson number equal to 0.1, 1 and 10 respectively and for inclination angle ranging from 30° to 90°, being the case γ = 0 not depending on the moving lid direction. With regard to the velocity and temperature profiles, only the case with some difference with respect to the case of positive velocity are shown. Figure 18 refers to profiles of temperature, $\Theta$, along the transverse centerline of the cavity, at different inclination angles for Richardson number equal to 0.1; Figs. 19, 20 and 21 show the profile of longitudinal component of dimensionless velocity, U, along the transverse centerline of the cavity, the profile of transverse component of dimensionless velocity, V, along the longitudinal centerline of the cavity, and the profiles of temperature, $\Theta$, along the transverse centerline of the cavity, at different inclination angles for Richardson number equal to 1; finally Figs. 22 and 23 show the profile of longitudinal component of dimensionless velocity, U, and the profiles of temperature, $\Theta$, along the transverse centerline of the cavity, at different inclination angles for Richardson number equal to 10. When the buoyancy effect is predominant (Ri = 10), the effect of the direction of the moving wall, in term of modified flow field, can be detected. While for ${\text{U}}_{0} > 0$ the two rotational cells lose their individuality already for low inclination angles, for ${\text{U}}_{0} < 0$ they remain distinct because the hot moving wall has an opposite effect with respect to the buoyancy. It can be noted that longitudinal velocity profiles, shown in Fig. 22 and referred to transversal centerlines, don’t undergo significant changes, provided to consider the upper part of the longitudinal profile as reversed, and the same does the temperature profile shown in Fig. 23; the transverse velocity profiles are practically the same of the case with positive velocity and are not shown; instead streamlines and isotherms, describing the whole flow and thermal field, show the influence of the direction of the lid motion into the near wall region; more specifically, we find different values of temperature with respect to the core of the cavity and this effect is more evident for low values (γ = 30°) of inclination angle, that is when, being equal the driving thermal contribution, the geometrical factor of natural convection flow is lowest.

Fig. 15

Streamlines and isotherms for Ri = 0.1, at γ = 30°, 60° and 90°, U ₀ < 0

Fig. 16

Streamlines and isotherms for Ri = 1, at γ = 30°, 60° and 90°, U ₀ < 0

Fig. 17

Streamlines and isotherms for Ri = 10, at γ = 30°, 60° and 90°, U ₀ < 0

Fig. 18

Normalized temperature profile $\Theta$ at x/H = 1.5 (transverse centerline) for for Ri = 0.1 and U ₀ < 0

Fig. 19

Normalized longitudinal velocity U at x/H = 1.5 (transverse centerline) for Ri = 1 and U ₀ < 0

Fig. 20

Normalized transverse velocity V at y/H = 0.5 (longitudinal centerline) for Ri = 1 and U ₀ < 0

Fig. 21

Normalized temperature profile $\Theta$ at x/H = 1.5 (transverse centerline) for for Ri = 1 and U ₀ < 0

Fig. 22

Normalized temperature profile ${\text{U}}$ at x/H = 1.5 (transverse centerline) for for Ri = 10 and U ₀ < 0

Fig. 23

Normalized temperature profile $\Theta$ at x/H = 1.5 (transverse centerline) for for Ri = 10 and U ₀ < 0

When Ri = 1, it becomes evident as the contribution of the moving wall and the buoyancy due to gravity acceleration have opposite effects on the fluid field; it gives rise to the formation of two rotational cell into the cavity. This balancing of opposite contribution, equally important, can be observed in Figs. 19, 20 and 21, where the velocity and temperature profiles aim at to become symmetric.

For Ri = 0.1, when forced convection is the dominant effect on the flow field, streamlines and isotherms, reported in Fig. 15, have the same behaviour shown in case of positive wall velocity, although as in a mirror, but the result of the two cited opposing effects is the persistence of the two rotational cells. The velocity and temperature profiles don’t change with the inclination angle when wall velocity is negative. It can be noted from Fig. 18 that the temperature difference between the cold region (at the bottom of the cavity) and the core are more pronounced than in the case of positive velocity.

In Fig. 24, the average Nusselt number on the lid surface is reported as a function of inclination angle for different Richardson number in both case of positive and negative moving wall velocity. It has to be noted that for γ = 0, Nu_m decreases when Ri increases, since it implies to go to a stratified field configuration. With regard to $\upgamma \ne 0$, it is observed that for positive lid velocity when Ri = 0.1,Nu_m increases slightly with the increase of γ. At ${\text{Ri}} \ge 1,\;{\text{Nu}}_{\text{m}}$ is increased more intensively. In fact at ${\text{Ri}} = 10$, it is increased by a factor of 5 when γ varies from 0 to 90°, indicating that in this case free convection effect is enhanced and its contribution can be added to the forced convection effect. When γ = 0 (horizontal cavity) Nu_m is maximum at Ri = 0.1 (significant forced convection), but for inclined cavity, the maximum Nu_m occurs at Ri = 10 (significant natural convection). For negative velocity of moving wall, the opposite effect of buoyancy and forced convection contribution can be observed since the Nusselt number results ever lower than the value corresponding to the case of positive velocity. For low inclination angle, the contribution of natural convection is less important than the hindering effect of the negative moving wall velocity, whereas for increasing γ angle the importance of natural convection becomes predominant.

Fig. 24

Average Nusselt number Nu _m on the hot surface as a function of inclination angle γ for different Richardson number and in case of U ₀ > 0 and U ₀ < 0

7 Conclusions

A thermal lattice Boltzmann BGK model with a dedicated boundary condition was used to study numerically laminar two-dimensional mixed convection heat transfer inside an inclined rectangular cavity when he heat transfer rate is imposed at the boundaries. Since the inclination of the cavity enhances the buoyancy force, which affects the velocity components of the flow, the forcing term simulating the buoyancy effect in the lattice Boltzmann equation were modified. The results show that, as expected, heat transfer rate increases as increases the inclination angle, but this effect is significant for the higher Richardson numbers, when buoyancy forces dominate the problem; for horizontal cavity, average Nusselt number decreases with the increase of the Richardson number because of the stratified field configuration. The effects of forced convection and natural convection can be considered as cooperating for positive velocity of the moving lid, while on the contrary they can be considered as opposite for negative velocity. This study shows that lattice Boltzmann method together with the counter-slip thermal energy density boundary condition can be effectively used to simulate heat transfer phenomena also in case of moving walls. The method can be successfully applied to simulate a wide class of cooling process where a given thermal power must be removed.